马艳丽1,范璐洋1,2,吕天玲3,郭琳3
(1.哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090;2.中国电建集团成都勘测设计研究院有限公司, 成都 610072; 3.黑龙江省劳动安全科学技术研究中心, 哈尔滨 150040)
摘要:
为评估自然驾驶过程中车辆运行存在的交通风险,采用贝叶斯网络对车辆运行风险进行量化研究. 首先开展自然驾驶试验,获取车辆距离控制指标、加速度、方向盘转向熵车辆控制数据及驾驶人视线转移时间、扫视速度、眨眼频率眼动数据. 然后,分析了各项指标的风险概率,确定各项指标阈值对应风险等级. 最后,构建了基于贝叶斯网络的车辆运行风险评估模型,给出了风险量化分级方法,确定了车辆运行风险等级,并对模型进行了敏感性分析. 结果表明:基于车辆控制和眼动表征的贝叶斯网络模型能够有效地对驾驶过程中车辆运行风险进行定量评估. 研究结果可评估自然驾驶过程中的车辆运行风险,并为运行风险进行量化分级.
关键词: 交通工程 运行风险 贝叶斯网络 量化分级 自然驾驶
DOI：10.11918/201810126
分类号:U491
文献标识码:A
基金项目:国家重点基础研究发展计划(2017YFC0803901); 国家自然科学基金(51108136)
Quantification classification method for driving risk quantization using Bayesian network
MA Yanli1,FAN Luyang1,2,Lü Tianling3,GUO Lin3
(1. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China; 2. Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China; 3. Heilongjiang Administration of Work Safety, Harbin 150040, China)
Abstract:
In order to evaluate the risk in the process of natural driving, Bayesian network was used to carry out quantitative research on driving risk. First, natural driving test was conducted to obtain the vehicle control data of vehicle spacing, acceleration, and steering entropy, as well as the eye movement data, including the driver’s sight transfer time, saccade speed, and blink frequency. Then, the risk rule of each index data was analyzed, and the risk level threshold of each index was determined. Finally, a vehicle operation risk assessment model based on Bayesian network was constructed, and the risk quantification classification method was proposed. The risk level of vehicle operation was determined, and the sensitivity of the model was analyzed. Results show that the Bayesian network model based on vehicle control and eye movement characterization could effectively conduct quantitative evaluation of driving risk in the driving process. The research results can provide theoretical and technical support for driving risk assessment and early warning in the natural driving process.
Key words: traffic engineering driving risk Bayesian network quantification classification natural driving
马艳丽, 范璐洋, 吕天玲, 郭琳. 车辆运行风险贝叶斯网络量化分级方法[J]. 哈尔滨工业大学学报, 2020, 52(3): 33-37. DOI: 10.11918/201810126.
MA Yanli, FAN Luyang, Lü Tianling, GUO Lin. Quantification classification method for driving risk quantization using Bayesian network[J]. Journal of Harbin Institute of Technology, 2020, 52(3): 33-37. DOI: 10.11918/201810126.
基金项目 国家重点基础研究发展计划(2017YFC0803901);国家自然科学基金(51108136) 作者简介 马艳丽(1974—), 女，博士，副教授，硕士生导师 通信作者 马艳丽，mayanli@hit.edu.cn 文章历史 收稿日期: 2018-10-24
Abstract Full text Figures/Tables PDF
车辆运行风险贝叶斯网络量化分级方法
马艳丽1
, 范璐洋1,2, 吕天玲3, 郭琳3 1. 哈尔滨工业大学 交通科学与工程学院, 哈尔滨 150090;
2. 中国电建集团成都勘测设计研究院有限公司, 成都 610072;
3. 黑龙江省劳动安全科学技术研究中心, 哈尔滨 150040
收稿日期: 2018-10-24
基金项目: 国家重点基础研究发展计划(2017YFC0803901);国家自然科学基金(51108136)
作者简介: 马艳丽(1974—), 女，博士，副教授，硕士生导师
通信作者: 马艳丽，mayanli@hit.edu.cn
摘要: 为评估自然驾驶过程中车辆运行存在的交通风险，采用贝叶斯网络对车辆运行风险进行量化研究.首先开展自然驾驶试验，获取车辆距离控制指标、加速度、方向盘转向熵车辆控制数据及驾驶人视线转移时间、扫视速度、眨眼频率眼动数据.然后，分析了各项指标的风险概率，确定各项指标阈值对应风险等级.最后，构建了基于贝叶斯网络的车辆运行风险评估模型，给出了风险量化分级方法，确定了车辆运行风险等级，并对模型进行了敏感性分析.结果表明:基于车辆控制和眼动表征的贝叶斯网络模型能够有效地对驾驶过程中车辆运行风险进行定量评估.研究结果可评估自然驾驶过程中的车辆运行风险，并为运行风险进行量化分级.
关键词: 交通工程 运行风险 贝叶斯网络 量化分级 自然驾驶
Quantification classification method for driving risk quantization using Bayesian network
MA Yanli1
, FAN Luyang1,2, Lü Tianling3, GUO Lin3 1. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090, China;
2. Power China Chengdu Engineering Corporation Limited, Chengdu 610072, China;
3. Heilongjiang Administration of Work Safety, Harbin 150040, China
Abstract: In order to evaluate the risk in the process of natural driving, Bayesian network was used to carry out quantitative research on driving risk. First, natural driving test was conducted to obtain the vehicle control data of vehicle spacing, acceleration, and steering entropy, as well as the eye movement data, including the driver's sight transfer time, saccade speed, and blink frequency. Then, the risk rule of each index data was analyzed, and the risk level threshold of each index was determined. Finally, a vehicle operation risk assessment model based on Bayesian network was constructed, and the risk quantification classification method was proposed. The risk level of vehicle operation was determined, and the sensitivity of the model was analyzed. Results show that the Bayesian network model based on vehicle control and eye movement characterization could effectively conduct quantitative evaluation of driving risk in the driving process. The research results can provide theoretical and technical support for driving risk assessment and early warning in the natural driving process.
Keywords: traffic engineering driving risk Bayesian network quantification classification natural driving
近十年来，尽管中国道路交通事故发生次数、受伤及死亡人数大幅度降低，但与发达国家相比，各指标仍处于较高水平[1].对车辆运行过程进行早期评估，及早发现驾驶过程中存在的风险，对驾驶人提供风险预警，为驾驶人提供足够的反应与操作时间，进而研究如何减少甚至避免发生道路交通事故显得十分重要.
关于车辆运行风险评估指标，文献[2]认为个体驾驶人车辆运行风险与事故率、年龄、人格特征有关；文献[3]发现车辆横向转动行为与驾驶人状态相关，当驾驶人处于疲劳状态时，车道位置会变得不稳定；文献[4]分析了次任务对驾驶人的扫视行为影响关系，认为驾驶人扫视行为对交通安全有影响；文献[5]采集驾驶人的眼动数据，包括换道行为以及超车行为，提出眼动行为比操作行为发生较早，可用于预测驾驶行为；文献[6]分析车载信息设备操作对驾驶绩效影响的显著性，将驾驶人视点转移时长、行驶速度、加速度、横向位移、方向盘转速、车辆横向位置等指标作为判定驾驶人是否分心的指标；文献[7]对交通流与风险的相关性进行了分析，评估不同交通流状态下的车辆运行风险；文献[8]对年轻人自然驾驶数据进行研究，获得风险因素各因素之间的相互关系.风险评估方法研究中，文献[9]基于GIS技术，将聚类分析和回归分析法应用于交通事故的风险评估中；文献[10]提出了一种基于马尔可夫链的驾驶风险状态预测算法；文献[11]将贝叶斯网络应用于交通危急状况下的警告系统，贝叶斯网络在概率分析方面具有强大优势；文献[12]通过道路驾驶测试来确定不同的驾驶相关风险评估指标，建立了基于动态贝叶斯网络的驾驶相关风险评价模型.
目前的评价方法主要针对多指标的宏观交通运行状况进行评价.风险影响因素上，认为与驾驶人个体特征、眼动行为、扫视行为、交通流、车辆控制行为及运行状态等因素有关，忽视了车辆运行风险影响因素之间的关联性.贝叶斯网络被广泛应用于辅助智能决策、模式识别等领域，通过参数学习和概率推理来获取结果分布信息的贝叶斯网络已广泛应用于对核工业操作员的工作环境进行评价[13]、搜索营救可靠性[14]以及分析航空系统存在的风险[15]等方面.基于上述背景，本文将贝叶斯网络应用到车辆运行风险评估研究.
1 车辆运行风险指标确定车辆运行风险不可能由单一的指标界定，因此，应选择有效、可靠和敏感的风险指标[6-8].结合车辆控制及驾驶人行为对车辆运行风险影响的显著性，确定车辆运行风险判定变量，选取车辆控制指标、驾驶人眼动指标作为风险评价指标.
1.1 车辆控制指标 1.1.1 车辆距离控制指标为保证车辆行驶安全，驾驶人必须与前车保持一定的距离.由车辆制动过程位移变化情况可以推导车辆间最小间距.车辆制动过程中行驶的距离为
${D_i} = {v_i}(t)\tau + \frac{{{v_i}(t)}}{{2{\alpha _i}(t)}} - \frac{{{{\left[ {{v_{i - 1}}(t)} \right]}^2}}}{{2{\alpha _{i - 1}}(t)}} + {d_0}.$ (1)
式中：vi为制动开始前第i辆车的行驶速度，τ为驾驶人反应时间和制动起效时间之和，αi为第i辆车的最大制动减速度，d0为停止后两辆车之间需满足的最小距离.
假设制动过程前，前后两辆车保持速度一致且制动效果一致，则行驶过程中车辆需保持的最小间距为
${D_{\min }}(t) = {v_i}(t)\tau + {d_0}.$ (2)
车辆距离控制指标
1.1.2 加速度加速度体现了一辆车速度变化的情况，驾驶员对加速度的控制情况可以间接地体现车辆运行风险问题.正常驾驶过程中加速度应维持稳定变化，保持在合理的范围内，加速度过大会导致行驶过程中存在一些驾驶隐患，故应对行驶过程中驾驶员操作下的加速度进行分析.
1.1.3 方向盘转向熵转向熵是驾驶人对车辆转向运动操作的稳定性和对环境信息采取预判断能力的评价指标.驾驶人在驾驶过程中需要不间断地对环境信息进行判断，对风险进行评估，实时对车辆进行转向控制.文献[16]提出采用转向熵来量化驾驶人的转向控制能力.在每个时间点t利用二阶Taylor公式，预测下一时刻转向角θp(t)，即
$\begin{array}{l}{\theta _p}(t) = \theta (t - 1) + (\theta (t - 1) - \theta (t - 2)) + \\\;\;\;\;\;\;\;\;\;\;\;\frac{1}{2}\{ [\theta (t - 1) - \theta (t - 2)] - [(\theta (t - 2) - \\\;\;\;\;\;\;\;\;\;\;\;\theta (t - 3)]\} , \end{array}$ (3)
预测误差为
$e(t) = \theta (t) - {\theta _p}(t).$ (4)
计算驾驶人对转向预判断错误频率分布的90百分位值α.驾驶人转向控制越平稳，α值越小，转向控制越激烈，α值越大.将驾驶人对方向判断上产生的偏差进行划分，将区间划分为9个.统计每个区间内驾驶人对方向盘控制产生的转角值的频数，获得转向熵公式为
${S_{\rm{E}}} = \sum\limits_{i = 1}^9 - {p_i}{\log _9}\left( {{p_i}} \right).$ (5)
式中SE为方向盘转向熵，pi为预测误差落在误差区间的分布概率.
1.2 眼动表征指标1) 视线转移时间.驾驶人视线离开前方视野是对驾驶存在风险的驾驶行为，其转移时间是受很多因素影响，如行人、前车等因素.
2) 扫视速度.扫视产生于两次注视之间，又称为眼跳.扫视阶段的视点移动速度即为扫视速度，在驾驶过程中驾驶人为收集环境信息会产较快的扫视行为.
3) 眨眼频率.驾驶人眨眼频率可以体现驾驶人对驾驶环境信息的采集能力和敏感性及驾驶人的精神状态.驾驶人精神状态不同，眨眼频率也会有所不同.正常驾驶过程中驾驶人的眨眼频率集中在1.5次/s左右.
2 试验方案 2.1 试验设计1) 试验人员.选取不同年龄(20~55岁)，驾龄为2~15 a的驾驶人20人(10名男性、10名女性)作为被试对象，被试者身体状态正常，在进行试验前24 h内，禁止摄入对神经存在刺激性作用的食物或药品.记录试验过程中出现的驾驶事件.
2) 试验设备.试验所采用的设备有小轿车、距离测量仪、加速度传感器、方向盘传感器、眼动仪、行车记录仪、摄像机等.各测量仪器布设如图 1所示.
Fig. 1
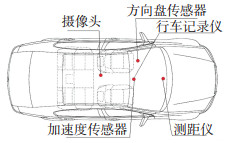图 1 车内仪器布设 Fig. 1 Layout of instruments inside the vehicle 3) 试验地点.本研究选取稳定流、道路条件理想且交通干扰较小的路段.试验路线为哈尔滨市和谐大道与城乡路交叉口至安发桥与新阳路交叉口，全长6 km.城乡路至乡政街为主干路，长度3 km；乡政街至安发桥为次干路，长度3 km.试验时段为天气良好的非高峰时段.
2.2 试验步骤具体试验步骤：1)采集驾驶人基本信息、试验时间. 2)驾驶人佩戴眼动仪，工作人员检测并同步所有设备，驾驶人进行预试验. 3)试验进行过程中实时采集交通环境、驾驶人及车辆的相关试验数据.驾驶人依据环境信息采取起步、停车、转弯、换道、跟驰、超车等驾驶操作. 4)试验结束后，收集驾驶过程中所采集的数据，对数据进行整理分析，对视频数据进行分类.
2.3 实验结果分析 2.3.1 车辆距离控制指标通过驾驶数据计算车辆距离控制指标，对车辆距离控制指标风险发生概率统计分析，获得风险等级.
当ξ(t)≤0.8时，为低风险；当0.8 < ξ(t)≤0.85时，为一般风险；当0.85 < ξ(t)≤1时，为较高风险；当ξ(t)>1时，为高风险.
2.3.2 加速度根据不同的驾驶阶段，当加速度百分位数为5%、10%、20%、30%、40%、50%、60%、70%、75%、80%、90%、95%时，对应的加速度分别为-1.143 0、-0.647 0、-0.278 5、-0.136 9、-0.050 7、0.022 0、0.088 0、0.175 1、0.235 4、0.292 9、0.722 6、0.951 3 m/s2.
根据百分位数可知，加速度小于-0.647 0 m/s2和大于0.722 6 m/s2时的概率很小，概率为10%，此范围内存在驾驶风险.
当|a| < 0.3 m/s2时，为低风险；当0.3 m/s2≤|a| < 0.7 m/s2时，为一般风险；当0.7 m/s2≤|a| < 1.3 m/s2时，为较高风险；当|a|≥1.3 m/s2时，为高风险.
2.3.3 方向盘转向熵试验中10名驾驶人正常驾驶和风险驾驶的转向熵如图 2所示.
Fig. 2
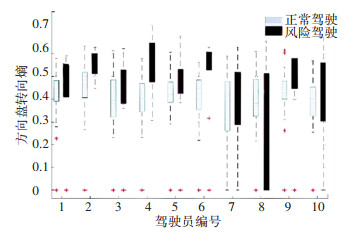图 2 正常驾驶和风险驾驶转向熵 Fig. 2 Steering entropy of normal and risky driving 所有驾驶人转向熵明显增加，可见转向熵与驾驶风险成正比.由于实验过程中实验数据提取过程可能存在误差，排除第8位驾驶人数据.车辆方向盘转向熵对应风险等级如下：当SE≤0.5时，为低风险；当0.5 < SE≤0.6时，为一般风险；当0.6 < SE≤0.7时，为较高风险；当SE>0.7时，为高风险.
2.3.4 视线转移时间驾驶人视线离开前方视野时间如图 3所示.
Fig. 3
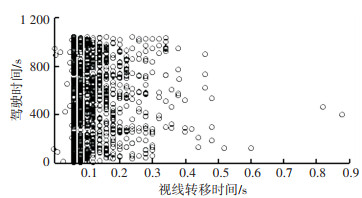图 3 驾驶人视线离开前方视野时间散点图 Fig. 3 Scatter diagram of driver's sight deviation time 统计数据显示90%的驾驶人视线转移时间小于0.24 s，且最大时间为0.88 s.当驾驶人视线离开前方视野时间超过1 s，则认为是不安全的眼动行为.根据视线转移时间DT划定风险等级，具体分级如下：当DT < 0.2 s时，为低风险；当0.2 s≤DT < 0.4 s时，为一般风险；当0.4 s≤DT < 1.0 s时，为较高风险；当DT≥1.0 s时，为高风险.
2.3.5 扫视速度驾驶人眼动的扫视速度如图 4所示.当出现重要信息时，眼睛的扫视为速度会有很大的变化.根据扫视速度GS划定风险等级，具体分级如下：当GS ＜440 °/s时，为低风险；当440 °/s≤GS < 1 000 °/s时，为一般风险；当1 000 °/s≤GS < 2 000 °/s时，为较高风险；当G≥2 000 °/s时，为高风险.
Fig. 4
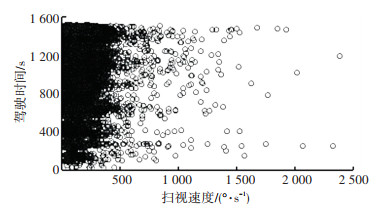图 4 扫视速度散点图 Fig. 4 Scatter diagram of driver's saccade speed 2.3.6 眨眼频率驾驶人眨眼频率疲劳时较正常状态明显降低，正常状态下眨眼次数大于0.5次/s，瞌睡状态下眨眼次数为0.2~0.5次/s，入睡状态下眨眼次数小于0.2次/s.
眨眼频率BF划分风险等级如下:当BF＞1次/s时，为低风险；当0.5次/s≤BF < 1次/s时，为一般风险；当0.2次/s≤BF < 0.5次/s时，为较高风险；当BF≤0.2次/s时，为高风险.
3 贝叶斯网络风险评估 3.1 贝叶斯网络模型车辆运行风险评估贝叶斯网络结构，如图 5所示.
Fig. 5
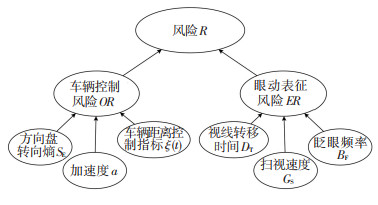图 5 车辆运行风险贝叶斯网络结构 Fig. 5 Bayesian network structure of vehicle operation risk 根据图 5可知变量DT、GS、BF、SE、a、ξ(t)是观测节点，用Yj表示，可以直接获取；R、OR、ER是隐含节点，用Xi表示，通过计算得到，隐含节点有“Y”、“N”两种状态.
$\begin{array}{l}\;\;\;P\left( {{X_1}, {X_2}, {X_3}|{Y_1}, {Y_2}, \cdots , {Y_6}} \right) = \\\frac{{\prod\nolimits_i P \left( {{X_i}|{\rm{ parent }}\left( {{X_i}} \right)} \right)\prod\nolimits_j P \left( {{Y_j}|{\rm{ parent }}\left( {{Y_j}} \right)} \right)}}{{\prod\nolimits_j P \left( {{Y_j}} \right)}}, \end{array}$ (6)
由式(6)可得
$\begin{array}{l}\;\;\;\;P\left( {{X_1}|{X_2}, {X_3}, {Y_1}, {Y_2}, \cdots , {Y_6}} \right) = \\\frac{{P\left( {{X_1}, {X_2}, {X_2}|{Y_1}, {Y_2}, \cdots , {Y_6}} \right)\prod\nolimits_j P \left( {{Y_j}} \right)}}{{\prod\nolimits_m P \left( {{X_m}} \right)\prod\nolimits_j P \left( {{Y_j}|{\rm{ parent }}\left( {{Y_j}} \right)} \right)}}.\end{array}$ (7)
其中: i∈[1, 2], j∈[1, 6], m∈[2, 3].
3.2 模型推理1) 指标风险条件概率.观测节点推理的条件概率见表 1.
表 1
表 1 风险的条件概率 Tab. 1 Conditional probability of risk 指标 指标取值 概率/% ξ(t) [1, +∞)
[0.85, 1)
[0.8, 0.85)
(0, 0.8) 60
25
10
5
|a| [1.3, +∞)
[0.7, 1.3)
[0.3, 0.7)
[0, 0.3) 50
30
15
5
SE [0.7, +∞)
[0.6, 0.7)
[0.5, 0.6)
[0, 0.5) 60
30
8
2
DT [1, +∞)
[0.4, 1)
[0.2, 0.4)
(0, 0.2) 50
25
20
5
GS [2 000, +∞)
[1 000, 2 000)
[440, 1 000)
[0, 440) 40
30
25
5
BF [1, +∞)
[0.5, 1)
[0.2, 0.5)
[0, 0.2) 10
20
30
40
表 1 风险的条件概率 Tab. 1 Conditional probability of risk
2) 车辆运行风险等级划分.依据《国家突发公共事件总体应急预案》[17]分类方法.跟据车辆运行风险发生概率，将风险等级划分为低、一般、较高、高4级，见表 2.
表 2
表 2 风险等级表 Tab. 2 Risk levels 风险等级 风险结果 风险概率/% Ⅳ级 低 0~25
Ⅲ级 一般 25~50
Ⅱ级 较高 50~75
Ⅰ级 高 75~100
表 2 风险等级表 Tab. 2 Risk levels
3) Netica推理.选取Netica软件对贝叶斯网络进行推理计算，量化风险等级，输入节点参数并计算节点风险概率.根据贝叶斯网络结构，进一步推导出车辆控制风险和眼动表征风险的条件概率，以及相关因素影响的风险值.建立Netica贝叶斯网络评价模型，对车辆运行风险进行量化分级.
3.3 有效性验证选取驾驶试验数据中正常驾驶与存在风险路段进行对比分析，风险会随自然驾驶过程中事件的变化而发生改变.如图 6所示，一般在驾驶过程中风险概率处于较低值，主要在20%上下波动，属于较低风险.而在风险路段的驾驶过程中发生风险的概率大于正常路段的值，风险概率处于35%~70%之间，认为具有较高的风险.可以看出时间点3的风险概率随交通事件的发生突然增加至70%，而驾驶人采取相应操作后，风险逐渐降低至40%左右；对于时间点7，由于驾驶过程中不同路段事件发生不同，正常路段驾驶过程中突发性事件导致驾驶风险短时增加，也可说明模型对风险驾驶事件也可以量化分析.数据表明模型对车辆运行风险分析有效.
Fig. 6
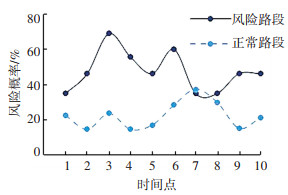图 6 不同时段车辆运行风险 Fig. 6 Driving risks at different time periods 4 结论1) 通过驾驶试验，获取驾驶人眼动规律与操作车辆行为的数据，分析了各指标数据可能存在的风险规律，确定了各个指标的风险阈值.
2) 考虑车辆控制和驾驶人眼动指标，建立了基于贝叶斯网络的车辆运行风险评估模型，标定了模型参数范围，给出了车辆运行风险量化分级方法.
3) 通过Netica软件对车辆运行风险模型进行推理分析，通过不同路段车辆运行风险变化规律的分析验证了模型的有效性.
参考文献
[1] 中华人民共和国国家统计局. 中国统计年鉴2017[M]. 北京: 中国统计出版社, 2018.
The National Bureau of Statistics of the People's Republic of China. China statistical yearbook 2017[M]. Beijing: China Statistics Press, 2018.
[2] GUO Feng, FANG Youjia. Individual driver risk assessment using naturalistic driving data[J]. Accident Analysis and Prevention, 2013, 61(61): 3.
[3] ROSEY F, AUBERLET J M. Driving simulator configuration impacts drivers' behavior and control performance: an example with studies of a rural intersection[J]. Transportation Research: Part F Traffic Psychology and Behavior, 2014, 27: 99. DOI:10.1016/j.trf.2014.09.009
[4] BARGMAN J, LISOVSKAJA V, VICTOR T, et al. How does glance behavior influence crash and injury risk? A 'what-if' counterfactual simulation using crashes and near-crashes from SHRP2[J]. Transportation Research: Part F Traffic Psychology and Behavior, 2015, 35: 152. DOI:10.1016/j.trf.2015.10.011
[5] LETHAUSL F, RATAJ J. Do eye movements reflect driving maneuvers[J]. IET Intelligent Transport Systems, 2007, 1(3): 199. DOI:10.1049/iet-its:20060058
[6] 马艳丽, 顾高峰, 高月娥, 等. 基于驾驶绩效的车载信息系统操作分心判定模型[J]. 中国公路学报, 2016, 29(4): 123.
MA Yanli, GU Gaofeng, GAO Yuee, et al. Based on the driving performance of the vehicle information system operating distracted judgment model[J]. China Journal of Highway and Transport, 2016, 29(4): 123. DOI:10.3969/j.issn.1001-7372.2016.04.015
[7] XU Chengcheng, LIU Pan, WANG Wei, et al. Evaluation of the impacts of traffic states on crash risks on freeways[J]. Accident Analysis & Prevention, 2012, 47(1): 162.
[8] GERSHON P, EHSANI J, ZHU Chunming, et al. Vehicle ownership and other predictors of teenager's risky driving behavior: evidence from a naturalistic driving study[J]. Accident analysis and prevention, 2018, 118(1): 96.
[9] NG K, HUNG W, WONG W. An algorithm for assessing the risk of traffic accident[J]. Journal of Safety Research, 2002, 33(3): 387. DOI:10.1016/S0022-4375(02)00033-6
[10] XIONG Xiaoxia, CHEN Long, LIANG Jun. Vehicle driving risk prediction based on Markov chain model[J]. Discrete Dynamics in Nature and Society, 2018, 2018(8): 1.
[11] OH C, OH J, RITCHIE S G. Real-time hazardous traffic condition warning system: framework and evaluation[J]. IEEE Transaction on Intelligent Transportation System, 2005, 6(3): 265. DOI:10.1109/TITS.2005.853693
[12] MA Y, QI S, FAN L, et al. Dynamic Bayesian network approach to evaluate vehicle driving risk based on on-road experiment driving data[J]. IEEE Access, 2019, 2019(7): 135050.
[13] KIM M C, SEONG P H. An analytic model for situation assessment of nuclear power plant operators based on Bayesian inference[J]. Reliability Engineering and System Safety, 2006, 91(13): 270.
[14] NORRINGTON L, QUIGLEY J, RUSSELL A. Modeling the reliability of search and rescue operations with Bayesian belief networks[J]. Reliability Engineering and System Safety, 2008, 93(7): 940. DOI:10.1016/j.ress.2007.03.006
[15] LUXHOJ J T. Probabilistic causal analysis for system safety risk assessments in commercial air transport[C]//Second Workshop on Investigating and Reporting of Incidents and Accidents.Williamsburg: National Aeronautics and Space Administration, 2003: 17
[16] PAVELKA M. Indication of driver fatigue with help of steering wheel movement[C]//IEEE 7th International Conference on Automatic Control, Modeling and Simulation.Zhengzhou: World Scientific and Engineering Academy and Society, 2005: 162
[17] 中华人民共和国国务院. 国家突发公共事件总体应急预案[M]. 北京: 中国法制出版社, 2006.
The State Council of the People's Republic of China. National overall emergency plan for public emergencies[M]. Beijing: China Legal Publishing House, 2006.
