邓志平, 陈浩, 陈三凤


中国农业大学农业生物技术国家重点实验室, 北京 100193
收稿日期:2015-11-10;修回日期:2016-02-01;网络出版日期:2016-03-04
*通信作者:Sanfeng Chen, Tel:+86-10-62731551;Fax:+86-10-62732746;E-mail:sanfeng_chen@126.com
摘要: [目的]固氮类芽孢杆菌Paenibacillus sp.1-49是本实验室分离的具有潜在生物肥料价值的微生物菌剂。该菌在常见的培养基中不能高效生长(OD600≤1)。本文拟优化发酵培养基成分以获得最大菌体生物量。[方法]运用响应面分析中的因素筛选实验设计和最陡爬坡实验以及中心复合设计法,对菌株的发酵培养基进行了响应面优化。[结果]利用响应面优化法最终确定了菌株最佳培养基:蔗糖36.22g/L,Tryptone 5.31 g/L,Yeast Extract 10.92 g/L,MgSO4 0.51 g/L,NaCl 3.5 g/L,Na2MoO4 0.02 g/L,FeSO4 0.02 g/L。通过摇瓶发酵后菌体OD600=10.280,达到预测值的94.6%。[结论]利用响应面法成功地对Paenibacillus sp. 1-49的发酵培养基进行了优化,为该菌株和其他类芽孢杆菌的大规模发酵提供了参考。
关键词: Paenibacillus sp.1-49 中心复合设计 响应面优化
Medium optimization for nitrogen fixer Paenibacillus sp. 1-49
Zhiping Deng, Hao Chen, Sanfeng Chen


State Key Laboratory for Agrobiotechnology and College of Biological Sciences, China Agricultural University, Beijing 100193, China
Received 10 November 2015; Revised 01 February 2016; Published online 04 March 2016
*Corresponding author: Sanfeng Chen, Tel:+86-10-62731551;Fax:+86-10-62732746;E-mail:sanfeng_chen@126.com
Supported by the National High Technology Research and Development Program of China (2013AA102802-04)
Abstract: [Objective]Paenibacillus sp. 1-49 is a nitrogen-fixing bacterium that has the potential as a fertilizer. However, it grows poorly (OD600≤1) in both mineral medium and rich medium. To achieve high-yield biomass, we optimized fermentation medium for Paenibacillus sp. 1-49.[Methods]Plackett-Burman Design and Central Composite Design in response surface methodology were used to optimize medium composition.[Results]The optimal fermentation medium contained:(per liter) 36.22 g Sucrose, 5.31 g Tryptone, 10.92 g Yeast Extract, 0.51 g MgSO4, 3.5 g NaCl, 0.02 g Na2MoO4 and 0.02 g FeSO4. The maximum OD600 of 10.280±0.009 was obtained in shake flask fermentation, reached 94.6% of the predicted value.[Conclusion]We succeeded in using a response surface methodology to optimize the fermentation medium for Paenibacillus sp. 1-49. Our results will be useful for largescale fermentation of this strain and other Paenibacillus spp..
Key words: Paenibacillus sp. 1-49 central composite design response surface methodology
Paenibacillus is a genus of facultative anaerobic, endospore-forming bacteria within the Firmicute division. The genus Paenibacillus was originally included within the genus Bacillus and then reclassified as a separate genus in 1993 [1]. At that time, it encompassed 11 species, including the 3 N2-fixing species P. polymyxa, P. macerans and P. azotofixan. Paenibacillus currently comprises more than 120 named species, more than 20 of which have nitrogen fixation ability, including the following 8 novel species described by our laboratory: P. sabinae [2], P. zanthoxyli [3], P. forsythia [4], P. sonchi [5], P. sophorae [6], P. jilunlii [7], P. taohuashanense [8] and P. beijingensis [9]. Some nitrogen-fixing Paenibacillus, such as P. polymyxa, are used in agriculture and horticulture [10]. However, many members of these Paenibacillus strains grow poorly in both mineral medium and in rich medium such as LB medium. It is generally accepted that bacterial growth is greatly affected by culture medium components, such as carbon, nitrogen and salt sources, and the fermentation conditions [11]. In conventional method, the medium is optimized by changing one factor at a time while keeping others at a constant level, which is laborious and often leads to wrong conclusions. Multivariate experiments are designed not only to reduce the number of necessary experiments in the optimization process, but also to produce more defined results than those available by univariate strategies. Plackett-Burman (P-B) and response-surface methodology (RSM) are multivariate analyzing tools comprising of mathematical and statistical techniques for generating empirical models that obtained importance for optimizing production conditions of industrially high value products such as chemicals, enzymes, and for studying enzyme kinetics. The statistical tool has been used in many biotechnological processes namely optimization of culture conditions, enzyme production, ethanol production, and biomass production [12-14]. In this study, RSM was used to optimize the culture medium for obtaining the greatest bacterial growth rate during flask fermentation process of Paenibacillus sp. 1-49.
1 Materials and Methods 1.1 Organism and culture conditions The nitrogen-fixing bacterium Paenibacillus sp. 1-49 was isolated by our laboratory from the soil samples collected from Shaanxi Province, China. And this strain was maintained on LD medium (per liter) containing 10 g Tryptone, 5 g Yeast Extract and 2.5 g NaCl with agar at pH 7.0 at 4 ℃ and-70 ℃ for short and long term storage, respectively. The seed culture was prepared by inoculating single colony from the LD medium plate. In order to obtain fresh and stable strains, the clones were transferred into a new plate by streak culture for several times. After incubation for 2 or 3 days at 30 ℃, the single colony from the flat plate was transferred to 50 mL LD seed medium in a 250 mL shake flask and incubated at 30 ℃ for 18 hours on a rotary shaker (200 r/min). The cells growth was monitored by absorbance measurement at 600 nm with a UV-visible spectrophotometer. For shake flask culture, the liquid medium was sterilized in the autoclave at 121 ℃ for 20 min, and pH was adjusted to 7.0 before autoclaving.
1.2 Screening of critical media components using a Plackett-Burman design The Plackett-Burman factorial design was used to select significant medium components affecting the growth of Paenibacillus sp. 1-49. Flask-shaking fermentation condition was designed by Minitab 16 statistical software (State College, PA, USA). Previous studies showed that Sucrose, Tryptone, Yeast Extract, Magnesium Sulfate, Ferric Sulfate, Potassium Nitrate, Sodium Molybdate were effective medial components for process modeling. A total of fifteen process variables comprising of seven medial components (Sucrose, Tryptone, Yeast Extract, Magnesium Sulfate, Ferric Sulfate, Potassium Nitrate, Sodium Molybdate) and inoculum size were studied in Plackett-Burman screening experiments.
Each variable was represented at 2 levels, upper (high, +), and lower (low, -) levels of the range covered by each variable and the response (Table 1). Experimental responses were analyzed by first order model by the following equation Y=β0 + Σβixi (i=1......k) where y is the response for OD600, β0 is the model intercept and βi is the linear coefficient, and xi is the level of the independent variable. A first-order model could be obtained from the regression results of fractional factorial experiment. This model describes the interaction among factors and it is used to screen and evaluate important factors that influence the response. From the regression analysis of the variables, the factors having significant effect on the biomass were further optimized by RSM.
Table 1. Range of different factors investigated with Plackett-Burman
| Variables | Fermentation factors | Low level (–) | High level (+) |
| X1 | Sucrose /(g/L) | 15.00 | 30.00 |
| X2 | Na2MoO4 /(g/L) | 0.02 | 0.06 |
| X3 | KNO3 /(g/L) | 1.00 | 3.00 |
| X4 | MgSO4 /(g/L) | 0.20 | 0.60 |
| X5 | Inoculum size (%) | 4.00 | 5.00 |
| X6 | FeSO4 /(g/L) | 0.02 | 0.06 |
| X7 | Tryptone /(g/L) | 5.00 | 10.00 |
| X8 | Yeast Extract /(g/L) | 0 | 5.00 |
表选项
1.3 Method of steepest ascent Because the operating conditions are normally far from the optimum response settings, the experiment needs to move from the current operating conditions to the optimum region in the most efficient way. In order to establish an effective fitting equation, steepest ascent design was conducted to obtain the optimum region of the maximum OD600. Step size was designed separately according to the effect of significant factors which were screened by the Plackett-Burman method while the other factors were maintained at the low (-) level.
1.4 Optimization of medium with the response surface method Central composite design (CCD) and response methodology (RSM) were employed for random experimental design. The second-order model used to fit the response to the independent variables is shown in Equation (1).
 | (1) |
2 Results and Discussion 2.1 Screening of significant factors by Plackett-Burman design Eight factors, including seven medial components (Sucrose, Tryptone, Yeast Extract, Magnesium Sulfate, Ferric Sulfate, Potassium Nitrate and Sodium Molybdate) and inoculum size, as listed in Table 1 in the Plackett-Burman model, were used to test on the influence of bacterial growth rate during shaking flask fermentation process. The results from fifteen experiments revealed that the combination of Sucrose, Tryptone, Yeast Extract and inoculum size produced the highest bacterial growth rate. Furthermore, regression coefficients and standard error coefficient were determined by using the software of Minitab (Table 2). The P value was less than 0.1 implied that model terms were significant. From the experimental data, five of these variables could distinctly affect the OD600 of the culture and these were taken as the main factor affecting the density of bacterial strains by significant analysis. Among them, Sucrose (P=0.014), Magnesium Sulfate (P=0.026), Yeast Extract (P=0.003), and inoculum size (P=0.020) exerted positive effect, whereas the amount of Tryptone (P=0.084) exerted negative effects on the OD600. After screening of the influence factors, the linear regression equation which took the OD600 as the response values was obtained and the model was given in Equation (2).
 | (2) |
| Factor | Regression coefficient | Standard error coefficient | t-value | P-value |
| Constant | 4.7198 | 0.1813 | 26.04 | 0.000 |
| X1 | 0.6761 | 0.1981 | 3.41 | 0.014 |
| X2 | -0.1465 | 0.1981 | -0.74 | 0.488 |
| X3 | -0.2113 | 0.1981 | -1.07 | 0.327 |
| X4 | 0.5821 | 0.1981 | 2.94 | 0.026 |
| X5 | 0.6224 | 0.1981 | 3.14 | 0.020 |
| X6 | -0.1056 | 0.1981 | -0.53 | 0.610 |
| X7 | -0.4105 | 0.1981 | -2.07 | 0.084 |
| X8 | 1.1968 | 0.2417 | 4.95 | 0.003 |
表选项
As shown in the analysis of variance, the values of Prob (P) > F was 0.003 in variance analysis model. This implied that the regression equation reached a very significant level. The R2 coefficient obtained, of 94.3%, suggests that it is a reliable model and is attributed to a high correlation. The relatively high-adjusted determination coefficient (RAdj2=0.8680) indicates that 86.8% of the variability from experimental data can be explained by this regression model. Considering the inoculation amount of bacteria in a single system could not affect the highest density, the four remaining optimum variables (Sucrose, Magnesium Sulfate, Yeast Extract and Tryptone) were further evaluated by a method of steepest ascent design.
2.2 Method of steepest ascent Based on the model equation obtained, the path of steepest ascent experiment was conducted to find the more accuracy domain towards the optimum region. According to the effect of the significant factors screened from the Plackett-Burman experiment, compensation was designed for steepest ascent to search for the maximum value of OD600, while the rest was maintained at “-” level. Results are shown in Table 3.
Table 3. Experimental results of steepest ascent method
| No. | c(sucrose)/(g/L) | c(yeast eXtract)/(g/L) | c(tryptone)/(g/L) | c(MgSO4·7H2O)/(g/L) | OD600 |
| 1 | 18 | 1 | 7.2 | 0.2 | 4.684±0.012 |
| 2 | 22 | 3 | 6.4 | 0.4 | 6.040±0.009 |
| 3 | 26 | 5 | 5.8 | 0.6 | 8.045±0.010 |
| 4 | 30 | 7 | 5 | 0.8 | 10.060±0.006 |
| 5 | 34 | 9 | 4.2 | 1.0 | 9.540±0.003 |
| The central point for this Central Composite Design (CCD) experiment was reallocated as follow: Sucrose 30 g/L, Tryptone 5 g/L, Yeast Extract 7 g/L, MgSO4 0.8 g/L. | |||||
表选项
2.3 Optimization of fermentation medium for Paenibacillus sp. 1-49 using RSM To search for the optimum combination of these components in the culture medium, a Central Composite Design (CCD) experimental plan was carried out. Their suitable concentration ranges were preliminarily determined. Table 4 shows various combinations used and the corresponding OD600. The experimental results revealed that this mathematical tool could satisfactorily explain the effects of the variables concentration (Sucrose, Yeast Extract, Tryptone and Magnesium Sulfate) in biomass of Paenibacillus sp. 1-49 in shake-flask cultures. The P-value blew 0.05 indicated that test parameter was significant at 5% level of significance. The regression coefficients, t and P values for all linear, interaction and quadratic effects of the variables were shown in Table 5. It was shown that Tryptone (X7) and Yeast Extract (X8) were significant in linear effect of bacterial density, Sucrose (X1) and MgSO4 (X4) were not significant. All of the four factors were significant in surface effect of bacterial density. As for in interaction effect, both Sucrose (X1) Tryptone (X7) and Sucrose (X1) Yeast Extract (X8) were significant but not the rest. Analysis of variance (ANOVA) for the Quadratic model was shown in Table 6. Value of “Model Prob (P) > F” was 0.001 implied that the model was high significant. In this case X1, X7, X8 and X4 are significant model terms. The “Lack of Fit Prob > F value” of 0.002 showed that the lack of fit is insignificant. The R2 coefficient obtained, of 0.8791, suggests that it is a reliable model and that 87.91% of the sample variation of biomass is attributed to a high correlation between the independent variables. Only 12.09% of the total variation of biomass was not explained by the model. The relatively high-adjusted determination coefficient (RAdj2=0.7662) accounts for significance of the model. This revealed that the equation is a suitable model to describe the response of experiment pertaining to cell density (OD600). Data were analyzed by linear multiple regression using Minnitab 16 software (State College, PA, USA) and the Equation (3) was obtained.
 | (3) |
| Run | Variables | OD600 | |||
| X1 (Sucrose) | X7 (Tryptone) | X8 (Yeast Extract) | X4 (MgSO4) | ||
| 1 | -2 | 0 | 0 | 0 | 9.066 |
| 2 | 0 | 0 | -2 | 0 | 6.987 |
| 3 | 0 | 2 | 0 | 0 | 7.910 |
| 4 | 2 | 0 | 0 | 0 | 8.645 |
| 5 | 0 | -2 | 0 | 0 | 6.487 |
| 6 | 0 | 0 | 0 | 2 | 7.531 |
| 7 | 0 | 0 | 0 | 0 | 9.685 |
| 8 | 0 | 0 | 0 | -2 | 9.868 |
| 9 | 0 | 0 | 2 | 0 | 10.397 |
| 10 | 0 | 0 | 0 | 0 | 10.000 |
| 11 | 0 | 0 | 0 | 0 | 9.988 |
| 12 | -1 | -1 | 1 | 1 | 7.454 |
| 13 | 1 | -1 | -1 | -1 | 7.130 |
| 14 | -1 | -1 | -1 | -1 | 6.424 |
| 15 | 1 | 1 | -1 | -1 | 7.790 |
| 16 | -1 | 1 | 1 | -1 | 9.177 |
| 17 | 1 | -1 | 1 | -1 | 10.210 |
| 18 | 1 | 1 | 1 | 1 | 9.470 |
| 19 | 0 | 0 | 0 | 0 | 9.871 |
| 20 | 1 | -1 | 1 | 1 | 9.970 |
| 21 | 1 | 1 | 1 | -1 | 8.990 |
| 22 | 0 | 0 | 0 | 0 | 9.821 |
| 23 | -1 | -1 | 1 | -1 | 7.583 |
| 24 | -1 | 1 | 1 | 1 | 9.620 |
| 25 | 1 | -1 | -1 | 1 | 7.180 |
| 26 | 1 | 1 | -1 | 1 | 8.100 |
| 27 | 0 | 0 | 0 | 0 | 10.124 |
| 28 | -1 | 1 | -1 | -1 | 7.965 |
| 29 | -1 | -1 | -1 | 1 | 7.273 |
| 30 | -1 | 1 | -1 | 1 | 8.129 |
表选项
Table 5. Coefficient estimates by the regression quadratic model
| Source of variation | Regression coefficient | Standard error coefficient | t-value | P-value |
| Constant | 9.9148 | 0.2473 | 40.090 | 0.000 |
| X1 | 0.3644 | 0.2473 | 1.474 | 0.161 |
| X7 | 0.7386 | 0.2473 | 2.986 | 0.009 |
| X8 | 1.6086 | 0.2473 | 6.504 | 0.000 |
| X4 | -0.2289 | 0.2473 | -0.926 | 0.369 |
| X1X1 | -1.1142 | 0.4627 | -2.408 | 0.029 |
| X7X7 | -2.7712 | 0.4627 | -5.989 | 0.000 |
| X8X8 | -1.2777 | 0.4627 | -2.762 | 0.015 |
| X4X4 | -1.2702 | 0.4627 | -2.745 | 0.015 |
| X1X7 | -1.5742 | 0.6058 | -2.599 | 0.020 |
| X1X8 | 1.0993 | 0.6058 | 1.815 | 0.009 |
| X1X4 | -0.1818 | 0.6058 | -0.300 | 0.768 |
| X7X8 | -0.4843 | 0.6058 | -0.799 | 0.437 |
| X7X4 | 0.2168 | 0.6058 | 0.358 | 0.725 |
| X8X4 | -0.2047 | 0.6058 | -0.338 | 0.740 |
| S=0.605790, PRESS=31.1892, R2=0. 8791, RAdj2=76.62% | ||||
表选项
Table 6. Analysis of variance for the quadratic model of CCD design
| Source | DF | Seq SS | Adj SS | Adj MS | F-value | P-value |
| Model | 14 | 40.0090 | 40.0090 | 2.8578 | 7.79 | 0.001 |
| Linear | 4 | 19.9095 | 19.9095 | 4.9774 | 13.56 | 0.001 |
| Square | 4 | 16.0565 | 16.0565 | 4.0141 | 10.94 | 0.000 |
| Interaction | 6 | 4.0430 | 4.0430 | 0.6738 | 1.84 | 0.159 |
| Residual error | 15 | 5.5047 | 5.5047 | 0.3670 | – | – |
| Lack of fit | 10 | 5.3848 | 5.3848 | 5.385 | 22.45 | 0.002 |
| Pure error | 5 | 0.1199 | 0.1199 | 0.0240 | – | – |
| Total | 29 | 45.5137 | – | – | – | – |
| S=0.605790, PRESS=31.1892, R2=0. 8791, RAdj2=76.62%. | ||||||
表选项
Where Y is the predicted response (OD600), X1, X7, X8 and X4 are the symbols of concentration of Sucrose, Yeast Extract, Tryptone and Magnesium Sulfate respectively.
The response surfaces of fermentation medium for maximum OD600 of Paenibacillus sp. 1-49 have been established according to the model.
Figure 1 shows the mutual influences of Sucrose and Tryptone on OD600 of Paenibacillus sp. 1-49 when the concentration of Yeast Extract and MgSO4 were under optimal condition.
 |
| Figure 1. Response surface and contour line of the influence of sucrose and tryptone on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: Response surface graph of mutual-influence for sucrose and tryptone on OD600; B: The contour plot between sucrose and tryptone on OD600. |
| 图选项 |
Figure 2 shows the mutual influences of Sucrose and Yeast Extract on OD600 when the concentration of Tryptone and MgSO4 were under optimal condition.
 |
| Figure 2. Response surface and contour line of the influence of sucrose and yeast extract on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: Response surface graph of mutual-influence for sucrose and yeast extract on OD600; B: The contour plot between sucrose and yeast extract on OD600. |
| 图选项 |
Figure 3 shows the mutual influences of Sucrose and MgSO4 on OD600 when the concentration of Tryptone and Yeast Extract were under optimal condition.
 |
| Figure 3. Response surface and contour line of the influence of sucrose and MgSO4 on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: response surface graph of mutual-influence for sucrose and MgSO4 on OD600; B: The contour plot between sucrose and MgSO4 on OD600. |
| 图选项 |
Figure 4 shows the mutual influences of Tryptone and Yeast Extract on OD600 when the concentration of Sucrose and MgSO4 were under optimal condition.
 |
| Figure 4. Response surface and contour line of the influence of tryptone and yeast extract on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: response surface graph of mutual-influence for tryptone and yeast extract on OD600; B: the contour plot between tryptone and yeast extract on OD600. |
| 图选项 |
Figure 5 shows the mutual influences of Tryptone and MgSO4 on OD600 when the concentration of Sucrose and Yeast Extract were under optimal condition.
 |
| Figure 5. Response surface and contour line of the influence of tryptone and MgSO4 on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: response surface graph of mutual-influence for tryptone and MgSO4 on OD600; B: the contour plot between tryptone and MgSO4 on OD600. |
| 图选项 |
Figure 6 shows the mutual influences of MgSO4 and Yeast Extract on OD600 when the concentration of Sucrose and Tryptone were under optimal condition.
 |
| Figure 6. Response surface and contour line of the influence of yeast extract and MgSO4 on cell growth rate (OD600) of Paenibacillus sp. 1-49. A: response surface graph of mutual-influence for yeast extract and MgSO4 on OD600; B: the contour plot between yeast extract and MgSO4 on OD600. |
| 图选项 |
On the basis of these response surfaces, the optimal fermentation medium for the maximal maximum bacterial density is composed of 33.62 g/L Sucrose, 5.31 g/L Tryptone, 10.92 g/L Yeast Extract and 0.51 g/L MgSO4. The maximal OD600 of 10.867 is predicted.
2.4 Optimization and model verification From the study of plots, the maximum OD600 of Paenibacillus sp. 1-49 was obtained when the optimal concentrations of 33.62 g/L Sucrose, 5.31 g/L Tryptone, 10.92 g/L Yeast Extract and 0.51 g/L MgSO4 were used for flask fermentation at 30 ℃, 200 r/min for 18 hours. To verify the predicted results, the triplicate verification experiments were performed under the optimized nutrients levels. The maximum OD600 was obtained to 10.280±0.009, which reached 94.6% of the predicted value. As a result, the models developed were considered to be accurate and reliable for predicting the biomass of OD600 for Paenibacillus sp. 1-49. Figure 7 described the bacterial growth curve.
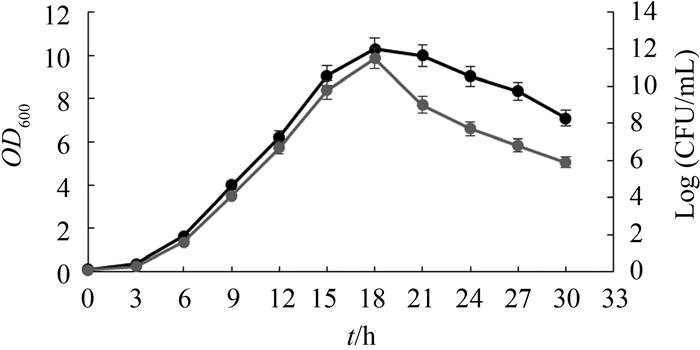 |
| Figure 7. Growth of Paenibacillus sp. 1-49 in optimized medium by flask fermentation at 30 ℃, 200 r/min, for 30 hours. Each point represents the mean of three independent experiments±1 SEM. The black dot: values of OD600; the gray dot: log colony-forming units (CFU)/mL. |
| 图选项 |
As well known, many strains of bacilli, mainly species of the genera Bacillus and Paenibacillus, displaying important plant growth promoting (PGP) characteristics were isolated and identified in the past decades [15]. At the same time, numerous Bacillus and Paenibacillus strains express plant growth promoting activities and a number of these strains have already been commercially developed as biological fungicides, insecticides, and nematicides or generic plant growth promoters [16]. Nitrogen-fixing Paenibacillus species have the potential use as biofertilizer in agriculture. It is a genus of gram-positive, facultative anaerobic, endospore-forming bacterium. They can survive in strict environmental conditions and are easy to be stored. So, the use of these strains in agriculture has been viewed as promising prospects in the future. A nitrogen-fixing bacterium Paenibacillus sp. 1-49 was newly isolated from soil samples had relatively high nitrogenase activity. It can be used as a kind of potential microbial fertilizer.
In order to obtain large biomass production as bacterial agents, fermentation is a general method for industrial biological processes. Many medium experiments include group factors such as culture media components and the fermentation conditions [17]. The present study shows that the RSM based on CCD established an efficient model to describe the shake flask fermentation process of Paenibacillus sp. 1-49. The high similarity between the observed value and the predicted ones implied that the RSM was an accurate tool to optimize the culture medium for biomass production of Paenibacillus sp. 1-49 in fermentation industry. By utilizing the statistical methodology, the optimum OD600 was obtained to 10.280±0.009. Under optimized culture conditions, the OD600 was dramatically increased, almost 10-fold than in both mineral medium and rich medium. In particularly, the culture temperature and time was both decreased too. This process will show the direction to find the optimum condition in further experimentation.
参考文献
| [1] | Ash C, Priest FG, Collins MD. Molecular identification of rRNA group 3 bacilli (Ash, Farrow, Wallbanks and Collins) using a PCR probe test.Proposal for the creation of a new genus Paenibacillus.Antonie Van Leeuwenhoek, 1993, 64(3/4): 253–260. |
| [2] | Ma YC, Xia ZQ, Liu XM, Chen SF. Paenibacillus sabinae sp.nov., a nitrogen-fixing species isolated from the rhizosphere soils of shrubs.International Journal of Systematic and Evolutionary Microbiology, 2007, 57(1): 6–11DOI:10.1099/ijs.0.64519-0. |
| [3] | Ma YC, Zhang J, Chen SF. Paenibacillus zanthoxyli sp.nov., a novel nitrogen-fixing species isolated from the rhizosphere of Zanthoxylum simulans.International Journal of Systematic and Evolutionary Microbiology, 2007, 57(4): 873–877DOI:10.1099/ijs.0.64652-0. |
| [4] | Ma YC, Chen SF. Paenibacillus forsythiae sp.nov., a nitrogen-fixing species isolated from rhizosphere soil of Forsythia mira.International Journal of Systematic and Evolutionary Microbiology, 2008, 58(2): 319–323DOI:10.1099/ijs.0.65238-0. |
| [5] | Hong YY, Ma YC, Zhou YG, Gao F, Liu HC, Chen SF. Paenibacillus sonchi sp.nov., a nitrogen-fixing species isolated from the rhizosphere of Sonchus oleraceus.International Journal of Systematic and Evolutionary Microbiology, 2009, 59(11): 2656–2661DOI:10.1099/ijs.0.009308-0. |
| [6] | Jin H, Lv J, Chen SF. Paenibacillus sophorae sp.nov., a nitrogen-fixing species isolated from the rhizosphere of Sophora japonica.International Journal of Systematic and Evolutionary Microbiology, 2011, 61(4): 767–771DOI:10.1099/ijs.0.021709-0. |
| [7] | Jin HJ, Zhou YG, Liu HG, Chen SF. Paenibacillus jilunlii sp.nov., a nitrogen-fixing species isolated from the rhizosphere of Begonia semperflorens.International Journal of Systematic and Evolutionary Microbiology, 2011, 61(6): 1350–1355DOI:10.1099/ijs.0.025056-0. |
| [8] | Xie JB, Zhang LH, Zhou YG, Liu HC, Chen SF. Paenibacillus taohuashanense sp.nov., a nitrogen-fixing species isolated from rhizosphere soil of the root of Caragana kansuensis Pojark.Antonie van Leeuwenhoek, 2012, 102(4): 735–741DOI:10.1007/s10482-012-9773-4. |
| [9] | Wang LY, Li J, Li QX, Chen SF. Paenibacillus beijingensis sp.nov., a nitrogen-fixing species isolated from wheat rhizosphere soil.Antonie van Leeuwenhoek, 2013, 104(5): 675–683DOI:10.1007/s10482-013-9974-5. |
| [10] | Lal S, Tabacchioni S. Ecology and biotechnological potential of Paenibacillus polymyxa:a minireview.Indian Journal of Microbiology, 2009, 49(1): 2–10DOI:10.1007/s12088-009-0008-y. |
| [11] | Vine AE, Lewis SM, Dean AM, Brunson D. A critical assessment of two-stage group screening through industrial experimentation.Technometrics, 2008, 50(1): 15–25DOI:10.1198/004017007000000489. |
| [12] | Théodore K, Panda T. Application of response surface methodology to evaluate the influence of temperature and initial pH on the production of β-1, 3-glucanase and carboxymethylcellulase from Trichoderma harzianum.Enzyme and Microbial Technology, 1995, 17(12): 1043–1049DOI:10.1016/0141-0229(94)00029-8. |
| [13] | Steinberg DM, Bursztyn D. Response surface methodology in biotechnology.Quality Engineering, 2010, 22(2): 78–87DOI:10.1080/08982110903510388. |
| [14] | Ghomshe SMT, Aminzadeh R, Abarzani M. Use of response surface methodology to study the combined effect of various parameters on hexavalent chromium adsorption.Chemical Engineering Communications, 2014, 201(2): 191–208DOI:10.1080/00986445.2013.766602. |
| [15] | Beneduzi A, Peres D, Vargas LK, Bodanese-Zanettini MH, Passaglia LMP. Evaluation of genetic diversity and plant growth promoting activities of nitrogen-fixing bacilli isolated from rice fields in South Brazil.Applied Soil Ecology, 2008, 39(3): 311–320DOI:10.1016/j.apsoil.2008.01.006. |
| [16] | McSpadden Gardener BB. Ecology of bacillus and Paenibacillus spp.in agricultural systems..Phytopathology, 2004, 94(11): 1552–1258. |
| [17] | Vine AE, Lewis SM, Dean AM, Brunson D. A critical assessment of two-stage group screening through industrial experimentation.Technometrics, 2008, 50(1): 15–25DOI:10.1198/004017007000000489. |
