 , 傅月芸, 蔡润龙, 蒋靖坤
, 傅月芸, 蔡润龙, 蒋靖坤
 , 郝吉明
, 郝吉明清华大学环境学院, 环境模拟与污染控制国家重点联合实验室, 北京 100084
收稿日期: 2019-02-25; 修回日期: 2019-03-19; 录用日期: 2019-03-19
基金项目: 国家自然科学基金面上项目(No.21896094)
作者简介: 薛墨(1993-), 男, E-mail:xuem16@mails.tsinghua.edu.cn
通讯作者(责任作者): 蒋靖坤, E-mail:jiangjk@tsinghua.edu.cn
摘要: 基于二甘醇的扫描电迁移率粒径谱仪(DEG-SMPS)是常用的1~3 nm颗粒物粒径分布测量系统.目前对1~3 nm颗粒物在该系统中通过效率的量化不够准确,这给大气颗粒物粒径分布的测量带来了较大的不确定性.本文研究了1~3 nm颗粒物和离子在直管、弯管以及气溶胶中和器等系统组件中的通过效率,并使用等效管长法来量化颗粒物在这些组件单元中的通过效率.研究表明,1~3 nm颗粒物在直管内的通过效率不受颗粒物电性影响,且可以由Gormley-Kennedy(G-K)方程估算.当采样流量为2.5 L·min-1时,DEG-SMPS系统中总等效管长约为433 cm,其中气溶胶中和器的等效管长为160 cm,弯头的等效管长为33 cm.
关键词:1~3 nm颗粒物通过效率扫描电迁移率粒径谱仪等效管长
Penetration of 1~3 nm particles through a diethylene glycol scanning mobility particle spectrometer (DEG-SMPS)
XUE Mo
 , FU Yueyun, CAI Runlong, JIANG Jingkun
, FU Yueyun, CAI Runlong, JIANG Jingkun
 , HAO Jiming
, HAO Jiming State Key Joint Laboratory of Environment Simulation and Pollution Control, School of Environment, Tsinghua University, Beijing 100084
Received 25 February 2019; received in revised from 19 March 2019; accepted 19 March 2019
Abstract: Diethylene glycol scanning mobility particle spectrometer (DEG-SMPS) system has been used for measuring the size distribution of 1~3 nm particles. However, penetration efficiency of 1~3 nm particles in DEG-SMPS is not accurately calculated, which increases the uncertainty of the measured 1~3 nm particle size distributions. In this study, the penetration efficiencies of 1~3 nm tungsten oxide particles and ions through different devices before entering the detector, including straight tubes, elbows, and an aerosol neutralizer are calibrated and the equivalent length method is used to describe particle penetration through these devices. The penetration efficiency through a straight tube can be estimated using the Gormley-Kennedy formula and it is negligibly affected by the charging polarity. At the sampling flow rate of 2.5 L·min-1, the equivalent length for the whole DEG-SMPS system is 433 cm, and for aerosol neutralizer and elbows are 160 cm and 33 cm, respectively.
Keywords: 1~3 nm particlespenetration efficiencyscanning mobility particle spectrometerequivalent length
1 引言(Introduction)1~3 nm是大气新粒子生成的关键粒径尺度.对1~3 nm颗粒物的有效检测是研究大气新粒子生成现象的重要基础.由于颗粒物粒径越小, 扩散效应越显著, 在测量系统中的扩散损失也就越高, 所以1~3 nm颗粒物在测量系统中的通过效率问题不可忽视.基于二甘醇的扫描电迁移率粒径谱仪(DEG-SMPS)是常用的1~3 nm颗粒物测量系统(Jiang et al., 2011).在测量过程中, 颗粒物需经采样、荷电、筛分和检测等单元, 高比例的颗粒物会损失在系统组件中, 所以量化1~3 nm颗粒物在系统中的扩散损失规律有利于降低由通过效率计算引入的不确定性, 从而实现大气颗粒物的浓度和粒径分布的更准确测量.
已有研究表明, 颗粒物在理想直管中的通过效率可以由Gormley-Kennedy (G-K)方程计算(Gormley et al., 1948; Alonso et al., 1997).对于更为复杂的结构(如中和器等)和非直管件(如弯头或弯管等), 通常采用等效管长(Equivalent length)方法来表征颗粒物的通过效率, 即使用一段等效的直管来间接量化颗粒物在复杂结构中的通过效率.Wang等(2002)对5~15 nm颗粒物在弯头中的通过效率进行了研究;Covert等(1997)研究了3 nm以上颗粒物在3种基于放射源的气溶胶中和器中的通过效率, 但缺乏3 nm以下的研究结果.此外, 国内通常使用以软X射线为电离源的气溶胶中和器, 同已报道的气溶胶中和器的气路结构不同, 所以颗粒物在基于放射源的气溶胶中和器中的通过效率不应直接应用于DEG-SMPS系统中.
本文首先通过实验验证了G-K方程对3 nm以下具有不同电性颗粒物的适用性, 研究了1~3 nm颗粒物在气溶胶中和器和主要管件(直管、弯头、90°弯管和120°弯管)中的通过效率, 并使用等效管长法量化了颗粒物在各部分管件中的通过效率.
2 材料与方法(Materials and methods)2.1 DEG-SMPS系统的通过效率计算方法DEG-SMPS系统如图 1所示, 其工作原理是:1~3 nm颗粒物经采样后, 进入以软X射线为电离源的气溶胶中和器进行荷电, 进而由差分电迁移率粒径分析仪(DMA)(Cai et al., 2017)筛分得到特定粒径的单分散颗粒物, 再由以二甘醇为工作液的冷凝生长器(DEG-UCPC)激活长大, 激活后的颗粒物进入以正丁醇为工作液的颗粒物冷凝生长计数器(CPC)进行计数.系统中总的通过效率(ηpene)为:
图 1(Fig. 1)
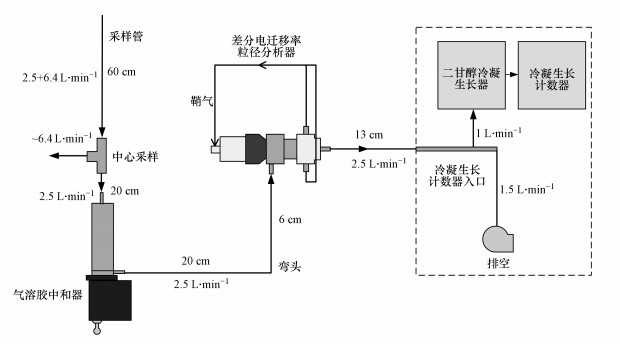 |
| 图 1 基于二甘醇的扫描电迁移率粒径谱仪各部件和管路示意图(DEG-SMPS) Fig. 1Schematics of the Diethylene glycol scanning mobility particle sizer (DEG-SMPS) system |
 | (1) |
直管中颗粒物的通过效率ηpene可以由G-K方程计算, 如公式(2)和(3)所示:
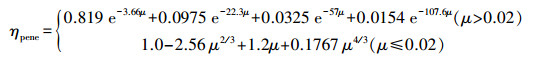 | (2) |
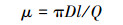 | (3) |
 | (4) |
其他管件和结构(如中和器、弯头等)的通过效率由实验测得, 再通过G-K方程反算, 得到相应的等效管长.
计算系统中总通过效率的方法如下:将系统中所有部件的等效管长(包括中和器等效管长lNeu、DMA等效管长lDMA、系统管路管长lTube和修正参数的等效管长lcorr累加起来后得到总等效长度ltot, 再使用G-K方程计算总通过效率ηltot.这种计算方法同各部件通过效率的直接连乘结果近似相等, 如公式(5)所示:
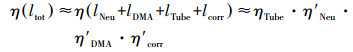 | (5) |
2.2 颗粒物通过效率标定颗粒物的发生和标定装置如图 2a所示, 颗粒物由钨丝发生器或电喷雾颗粒物发生器产生, 入口流量为20 L·min-1.颗粒物钨丝发生器主要由一根直径为0.4 mm、长为12 cm的钨丝和两个电极构成, 接入120 W直流电并在氮气气氛中运行, 能产生粒径约为1~10 nm的氧化钨颗粒物.电喷雾颗粒物发生器使用四庚基溴化铵的甲醇溶液生成电迁移率粒径为1.47 nm及更大粒径的离子(Ude et al., 2005).产生的颗粒物和离子首先通过高分辨率差分电迁移率粒径分析器(Half-min DMA)(De la Mora et al., 2013)实现不同粒径的筛分, 之后经由气溶胶分流器分成两路, 一路进入参比气溶胶静电计1(TSI, Inc., 3068B), 另一路通过待测部件进入气溶胶静电计2(TSI, Inc., 3068B), 两路流量保持相等, 并根据实验条件同时改变.为保证进入待测部件和参比仪器的颗粒物浓度分布相对稳定, 在二者进口处均设置一段长为36 cm的直管.颗粒物在待测部件中的通过效率由两台静电计的信号计算, 进而根据G-K方程反算出待测管件的等效管长.如公式(6)所示, 通过待测组件的静电计数浓度(NEM2)和上游静电计的数浓度(NEM1)的比值与由G-K方程计算的上游36 cm管长的通过效率(η(36))和下游通过效率(η(36+x))相等.解得的x即为该待测管件的等效管长.
图 2(Fig. 2)
 |
| 图 2 颗粒物扩散损失测量系统(a)和待标测部件(b) Fig. 2Schematics of the calibration system(a) and schematics of structures to be calibrated (b) |
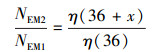 | (6) |
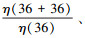

待测量颗粒物通过效率的部件如图 2b所示, 分别是56 cm和38 cm直管, 气溶胶中和器(TSI, Inc., 3088)、90°弯头(Swagelok, 1/4英寸)、90°弯管(20 cm, 1/4英寸)和120°弯管(20 cm, 1/4英寸).测量中和器的通过效率时, 中和器处于关闭状态, 这是由于中和器产生的离子会干扰静电计对颗粒物的检测.中和器内部的流道长度为28 cm.90°弯头安装方式是直管直接插入弯头内部, 其增加的流道长度不足2.5 cm, 可以忽略不计.90°和120°弯管均是由20 cm长度的不锈钢直管弯折而成, 所以在考虑管路弯曲带来的颗粒物损失之外, 增加的20 cm的管道长度不可忽略.
两台气溶胶静电计中的流量由皂膜流量计(Sensidyne, Inc., Gilibrator 2)进行标定.发生颗粒物的氮气流量由质量流量控制器(MFC, Sevenstar, Inc., D07-9E)控制.为保证标定数据的准确性, 在分流器出口后的所有管路和接头都使用不锈钢制卡套连接, 管材使用线切割处理以保证管口无毛刺.标定过程中, 气溶胶静电计2的摆放方向均与管路的实际方向相一致, 以保证管路都是直线连接.
3 结果与讨论(Result and discussion)3.1 颗粒物在直管中的通过效率不同化学组分颗粒物在直管中的通过效率如图 3a所示.氧化钨颗粒物的通过效率在同样的流量条件下, 随粒径的增大而增大;而在一定的粒径下, 通过效率随流量的增加而提高.56 cm直管下的通过效率与G-K方程计算结果所呈现趋势相对一致.电迁移率粒经为1.47 nm的四庚基溴化铵离子的通过效率与56 cm管长G-K方程计算的结果较为接近, 在1 L·min-1和2.5 L·min-1流量条件下相对偏差分别为8%和3%.这说明直管内颗粒物的通过效率可以使用理论公式—G-K方程来计算.
图 3(Fig. 3)
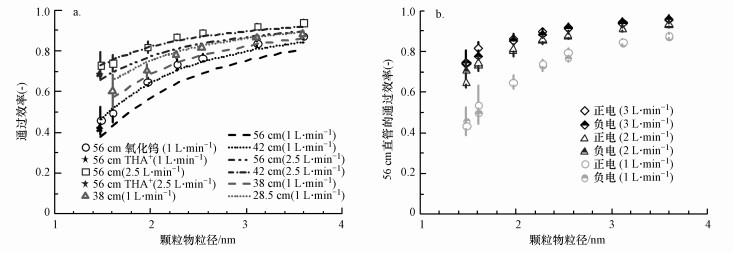 |
| 图 3 不同化学组分颗粒物在直管中的通过效率(a)及不同电性氧化钨颗粒物在56 cm直管中的通过效率(b) Fig. 3Penetration of particles of different chemical composition through straight tubes (a) and penetration of positive and negative charged tungsten oxide particles through a 56 cm straight tube (b) |
氧化钨颗粒物测量值和G-K方程计算值存在一定偏差(最大相对偏差为19%), 这可能是由于基于电迁移率粒径计算的颗粒物扩散系数同实际颗粒物的扩散系数略有不同.由于颗粒物的粒径过小, 且不同化学组分的颗粒物具有不同的结构, 故电迁移率直径同其真实直径有一定的不同(Tammet, 1995; Li et al., 2003; Ku et al., 2009; Wang, 2010; Tammet, 2012).目前小粒径颗粒物的扩散系数与电迁移率直径之间的关系尚不明确, 会带来一定偏差.为定量这种偏差带来的不确定性, 我们将氧化钨在56 cm直管中的实际通过效率根据公式(6)反算出等效管长, 为42 cm, 即等效管长与真实管长间具有25%的偏差.对于38 cm直管, 氧化钨颗粒物的通过效率正好在28.5 cm和38 cm等效管长计算值之间, 等效管长的偏差同样为25%.
此外, 1、2和3 L·min-1的流量条件下, 实验测得的带正电和带负电颗粒物在直管中的通过效率几乎相同(最大相对偏差8%), 如图 3b所示, 这表明在直管段下的1~3 nm颗粒物的扩散损失不受颗粒物电性影响.
3.2 气溶胶中和器通过效率氧化钨颗粒物在气溶胶中和器中的通过效率随粒径和流量的增大而增大, 变化规律与直管中类似, 如图 4所示.在1、2.5和3.5 L·min-1 3个流量条件下, 1.48 nm颗粒物的通过效率分别为22%、43%和53%, 这表明小颗粒物在中和器中的损失十分显著.在以上3个流量条件下, 由氧化钨颗粒物测得的等效管长分别为90、120和130 cm, 考虑25%的偏差后等效管长为120、160和170 cm, 远远大于其流道的物理长度(28 cm), 这可能是因为其内部结构导致的流场变化造成了颗粒物的额外损失.
图 4(Fig. 4)
 |
| 图 4 颗粒物在气溶胶中和器中的通过效率 Fig. 4Penetration of particles through aerosol neutralizer |
3.3 弯头和弯管的通过效率研究弯头的通过效率如图 5a所示, 在1 L·min-1条件下, 弯头的等效管长约为20 cm;当流量条件改为2.5 L·min-1和3.5 L·min-1时, 弯头的等效管长约为25 cm.对于弯头来说, 管件本身的流道长度可以忽略不计, 实验评测通过效率较低的原因是弯头结构带来的额外损失.已有研究表明, 弯头会改变流体原本的层流状态, 造成截面上的涡流从而增大颗粒物的损失(Pui et al., 1987; Wilson et al., 2011).
图 5(Fig. 5)
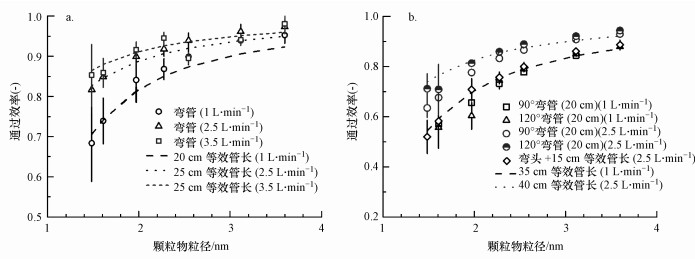 |
| 图 5 颗粒物在弯头中的通过效率(a)及颗粒物在90°弯管、120°弯管和弯头加20 cm等效管长合成的通过效率(b) Fig. 5Penetration of particles through elbow (a) and Penetration of particles through 90 ° bend, 120° bend and calculated elbow + 20 cm tube(b) |
对于弯管来说, 除了管路弯曲带来的损失之外, 还需要考虑弯管本身的长度(20 cm), 对于氧化钨颗粒物修正后的长度为15 cm.弯头和弯管通过效率的对比如图 5b所示, 在1 L·min-1流量下, 弯头的通过效率(图 5a中获得)与20 cm管路通过效率(计算时使用15 cm修正后的长度)的乘积, 同弯管的通过效率一致, 并与35 cm总长的等效管长的通过效率一致.在2.5 L·min-1条件下, 弯管(弯头+20 cm管长)的通过效率与40 cm(弯管等效管长25 cm+修正后的15 cm直管长)等效管长一致.这表明由于管路弯曲造成的颗粒物损失可以用等效管长描述, 并可以在计算时直接进行累加.对比120°转角和90°转角下的通过效率表明, 这两种角度的管路弯曲导致的颗粒物损失相近.综上, 在1 L·min-1条件下, 通过氧化钨颗粒物测得, 弯头的等效管长约为20 cm, 修正后为27 cm, 当流量条件改为2.5 L·min-1和3.5 L·min-1时, 弯头的等效管长约为25 cm, 修正后为33 cm.
3.4 颗粒物在检测系统中总的通过效率DEG-SMPS中各管段的长度如表 1所示, 从中心采样装置到进入冷凝生长计数器之前的流量均为2.5 L·min-1(图 1), 通过实验标定和计算, 并根据实际流量选取的中和器和弯头的等效管长分别为160 cm和33 cm.DMA的等效管长根据Cai等的结果(Cai et al., 2017), 为181 cm.整套系统总的等效管长约为433 cm.其中DMA、中和器的等效管长最大、颗粒物损失最多.
表 1(Table 1)
| 表 1 DEG-SMPS系统中主要管件的管长或等效管长 Table 1 Equivalent length of the structures in DEG-SMPS system | ||||||||||||||||
表 1 DEG-SMPS系统中主要管件的管长或等效管长 Table 1 Equivalent length of the structures in DEG-SMPS system
| ||||||||||||||||
DEG-SMPS系统中总的等效管长为433 cm, 1~5 nm颗粒物在其中的通过效率如图 6所示.小粒径颗粒物在系统中的通过效率极低, 例如, 1.5 nm的颗粒物通过效率不足5%、1.2 nm颗粒物的通过效率仅有1%.由颗粒物化学组分不同造成的25%等效管长的偏差如阴影部分所示, 越小的颗粒物对应的偏差范围越大.
图 6(Fig. 6)
 |
| 图 6 颗粒物在DEG-SMPS系统中的通过效率 Fig. 6Penetration of particles through the DEG-SMPS system |
为了提高颗粒物的检测比例, 同时减小偏差对通过效率计算的影响, 应进一步优化系统构型、减小管路长度、少使用会带来额外损失的管件.在不改变DMA结构的前提下, 若能通过优化中和器结构, 即在不改变28 cm流道长度的基础上使中和器内部管路变直, 同时改变整台仪器内部部件的布局, 可实现约100 cm等效管长的缩减, 即可大幅提高小颗粒物的通过效率.例如, 1.5 nm颗粒物在333 cm管长的通过效率约是现有系统的2倍, 而1.2 nm颗粒物约为2.86倍.
4 结论(Conclusions)1) 标定了1~3 nm氧化钨颗粒物在直管中的扩散损失, 证明其通过效率可用G-K方程计算, 且不受颗粒物电性影响.
2) 通过1~3 nm氧化钨颗粒物扩散损失的标定实验得到中和器、弯头和弯管的等效扩散管长;给出了DEG-SMPS的整体等效管长, 为433 cm;并由此计算了颗粒物在DEG-SMPS系统中的通过效率.
致谢:感谢中国气象科学研究院孙俊英老师提供的气溶胶静电计支持!
参考文献
| Alonso M, Kousaka Y, Hashimoto T, et al. 1997. Penetration of nanometer-sized aerosol particles through wire screen and laminar flow tube[J]. Aerosol Science and Technology, 27(4): 471–480.DOI:10.1080/02786829708965487 |
| Cai R, Chen D R, Hao J, et al. 2017. A miniature cylindrical differential mobility analyzer for sub-3 nm particle sizing[J]. Journal of Aerosol Science, 106: 111–119.DOI:10.1016/j.jaerosci.2017.01.004 |
| Covert D, Wiedensohler A, Russell L. 1997. Particle charging and transmission efficiencies of aerosol charge neutralizes[J]. Aerosol Science and Technology, 27(2): 206–214.DOI:10.1080/02786829708965467 |
| De la Moja J F, Kozlowski J. 2013. Hand-held differential mobility analyzers of high resolution for 1~30 nm particles:design and fabrication considerations[J]. Journal of Aerosol Science, 57(2): 45–53. |
| Fu Y, Xue M, Cai R, et al. 2019. Theoretical and experimental analysis of the core sampling method:Reducing diffusional losses in aerosol sampling line[J]. Aerosol Science and Technology, 53(7): 793–801.DOI:10.1080/02786826.2019.1608354 |
| Gormley P G, Kennedy M. 1948. Diffusion from a stream flowing through a cylindrical tube[J]. Procroyirish Acada, 52: 163–169. |
| Jiang J, Chen M, Kuang C, et al. 2011. Electrical mobility spectrometer using a diethylene glycol condensation particle counter for measurement of aerosol size distributions down to 1 nm[J]. Aerosol Science and Technology, 45(4): 510–521. |
| Kangasluoma J, Franchin A, Duplissy J, et al. 2016. Operation of the airmodus A11 nano condensation nucleus counter at various inlet pressures and various operation temperatures, and design of a new inlet system[J]. Atmospheric Measurement Techniques, 9(7): 2977–2988.DOI:10.5194/amt-9-2977-2016 |
| Ku B K, Mora J F D L. 2009. Relation between electrical mobility, mass, and size for nanodrops 1~6.5 nm in diameter in air[J]. Aerosol Science and Technology, 43(3): 241–249.DOI:10.1080/02786820802590510 |
| Li Z, Wang H. 2003. Drag force, diffusion coefficient, and electric mobility of small particles. Ⅰ. Theory applicable to the free-molecule regime[J]. Physical Review E, 68(6): 061206.DOI:10.1103/PhysRevE.68.061206 |
| Pui D Y H, Romay-Novas F, Liu B Y H. 1987. Experimental study of particle deposition in bends of circular cross section[J]. Aerosol Science and Technology, 7(3): 301–315.DOI:10.1080/02786828708959166 |
| Tammet H. 1995. Size and mobility of nanometer particles, clusters and ions[J]. Journal of Aerosol Science, 26(3): 459–475.DOI:10.1016/0021-8502(94)00121-E |
| Tammet H. 2012. The function-updated millikan model:a tool for nanometer particle size-mobility conversions[J]. Aerosol Science and Technology, 46(10): ⅰ–ⅳ. |
| Ude S, Mora J F D L. 2005. Molecular monodisperse mobility and mass standards from electrosprays of tetra-alkyl ammonium halides[J]. Journal of Aerosol Science, 36(10): 1224–1237.DOI:10.1016/j.jaerosci.2005.02.009 |
| Wang H. 2010. Transport properties of small spherical particles[J]. Annals of the New York Academy of Sciences, 1161(1): 484–493. |
| Wang J, Flagan R C, Seinfeld J H. 2002. Diffusional losses in particle sampling systems containing bends and elbows[J]. Journal of Aerosol Science, 33: 843–857.DOI:10.1016/S0021-8502(02)00042-3 |
| Wilson S R, Liu Y, Matida E A, et al. 2011. Aerosol deposition measurements as a function of reynolds number for turbulent flow in a ninety-degree pipe bend[J]. Aerosol Science and Technology, 45(3): 364–375.DOI:10.1080/02786826.2010.538092 |
