 , 郭熙1,2
, 郭熙1,2

1. 江西农业大学, 江西省鄱阳湖流域农业资源与生态重点实验室, 南昌 330045;
2. 江西农业大学, 国土资源与环境学院, 南昌 330045
收稿日期: 2018-09-03; 修回日期: 2018-09-29; 录用日期: 2018-09-29
基金项目: 国家重点研发项目(No.2017YFD0301603)
作者简介: 江叶枫(1994-), 男, E-mail:jiangyf0308@163.com
通讯作者(责任作者): 郭熙, E-mail:guoxi@jxau.edu.cn
摘要: 合适的方法和多源的辅助数据对于准确预测土壤重金属的空间分布具有重要意义.该研究提出一种径向基函数神经网络结合普通克里格法的模型(RBFNN_OK),由主成分分析(PCA)提取的地形因子、遥感数据和邻近信息等多源辅助数据作为自变量,预测江西省都昌县稻田土壤砷空间分布.为验证RBFNN_OK的可行性:首先在全县范围内采集144个稻田表层(0~20 cm)土壤样品,运用ArcGIS地统计模块随机抽取115个(80%)采样点作为测试集,29个(20%)采样点作为验证集.其次多源辅助数据包括地形因子、遥感数据和邻近信息等14个定量因子作为预测变量,将预测变量进行主成分分析,得到前10个主成分的累积贡献率达到97.62%.再次一个特定的RBFNN_OK被用来预测土壤砷空间分布.最后将RBFNN_OK模型的预测结果与径向基神经网络模型(RBFNN)、回归克里格模型(RK)和多元逐步线性回归模型(MSLR)进行比较.结果表明,RBFNN_OK的测量值标准偏差与均方根误差的比值(RPD)较其它3种方法分别提高了14.92%、35.71%和44.67%.此外,RBFNN_OK还提供了更加真实且有关土壤砷空间分布的细节信息.RBFNN_OK取得最优效果可能归因于引入多源辅助数据,考虑多源辅助数据和土壤砷之间的多重共线性和非线性关系.该方法可为稻田土壤砷调查与环境保护提供更为精准的信息.
关键词:稻田土壤径向基神经网络模型砷污染多源数据主成分分析
Prediction of spatial distribution of soil arsenic in paddy fields based on multi-source auxiliary data and neural network model
JIANG Yefeng1,2
 , GUO Xi1,2
, GUO Xi1,2

1. Key Laboratory of Poyang Lake Watershed Agricultural Resources and Ecology of Jiangxi Province, Jiangxi Agricultural University, Nanchang 330045;
2. Academy of Land Resource and Environment, Jiangxi Agricultural University, Nanchang 330045
Received 3 September 2018; received in revised from 29 September 2018; accepted 29 September 2018
Abstract: A suitable method and appropriate auxiliary data are important for accurately predicting heavy metal distribution in soils. Here we propose a radial basis function neural network combined with ordinary kriging (RBFNN_OK), multi-source auxiliary data such as topographic factors, remote sensing data, and neighboring information extracted by principal component analysis (PCA) as independent variables for predicting the spatial distribution of arsenic in paddy soils in Duchang County, Jiangxi Province, China. First, surface (0~20 cm) soil samples were collected from 144 sampling points in paddy fields across the study area; 115 (80%) of the sampling points were selected at random as the calibration set and 29 (20%) were selected as the validation set using ArcGIS Geostatistical Analyst. Next, multi-source auxiliary data includes 14 quantitative factors such as the topographic factors, remote sensing data, and neighboring information were selected as auxiliary variables, these variables were used for PCA and the cumulative contribution of the first 10 principal components to the total variance reached 97.62%. Then, a particular RBFNN_OK model was adapted to predict the spatial distribution of soil arsenic using the first 10 principal components. Finally, the predictions of RBFNN_OK were compared with those of radial basis function neural network (RBFNN), regression kriging (RK), and multiple stepwose linear regression (MSLR) for assessment of prediction accuracy. Results showed that the ratio of standard deviation of measured values to root mean square error of predictions was 2.85 for RBFNN_OK and 1.97~2.48 for the other three models, RBFNN_OK was increased by 14.92%, 35.71% and 44.67%, respectively, compared with the others. In addition, RBFNN_OK provides more detailed information about the spatial distribution of soil arsenic. The improved performance of RBFNN_OK can be attributed to the introduction of multi-source auxiliary data, to consider the multicollinearity and nonlinear relationship between multi-source auxiliary data and soil arsenic. This method may provide more accurate information for the investigation of arsenic in the paddy soil and environmental protection.
Keywords: paddy soilsradial basis function neural networkarsenic contaminationauxiliary dataprincipal component analysis
1 引言(Introduction)土壤是有限且不可再生的自然资源, 是人类可持续发展的重要基础(Mcbratney et al., 2014).因此, 为维护自然资源对未来的可持续发展, 我们需要改善和维护土壤的生态系统服务功能(Guo et al., 2018).然而土壤重金属污染使其成为一个实质性挑战(Dai et al., 2018).重金属可在土壤中长时间累积且难以降解, 快速准确的掌握区域土壤重金属空间分布是进行土壤重金属污染防治的关键和前提(Geen et al., 2008).田间采样可为采样点提供高精度的土壤重金属数据, 但由于费时的取样过程和昂贵的土壤样品分析导致采样点一般较少, 这极大的限制了环境管理和风险控制者对土壤重金属空间分布的需求(Li et al., 2017a).因此, 需要在有限采样点的基础上, 结合更加精确的模型来获取土壤重金属空间分布.
前人研究表明(Mcbratney et al. 2003; Li et al. 2017b), 预测土壤重金属空间分布的模型大致可以分为3种类型.第一种被称为纯空间模型, 比如普通克里格(Ordinary Kriging, OK)(Lv et al., 2015), 它充分考虑区域化变量的空间自相关性且能够对预测误差进行理论估计, 但该方法没有考虑环境因素对土壤重金属空间分布的影响(Goovaerts, 1997), 往往会存在平滑效应, 导致对未采样点处产生较大误差.第二种类型称为“Scorpan”模型(Li et al., 2017b; Jiang et al., 2018), 这种模型基于土壤重金属与辅助变量(如地形、遥感数据和邻近信息等)的映射关系, 从而实现对土壤重金属空间分布进行预测.比如多元逐步线性回归(Multiple Stepwise Linear Regression, MSLR), 该模型拥有操作简单, 计算效率高和直接插值的优点(Zhao et al., 2012).第3种类型, 例如回归克里格(Regression Kriging, RK)(Odeha et al., 1994; Hengl et al., 2004; Jiang et al., 2018), 是一种基于辅助数据与土壤重金属之间的回归趋势项, 同时叠加由纯空间方法来描述Scorpan模型预测残差的残差项.该模型的前提是由辅助变量引起的目标土壤变量可以用“Scorpan”方程解释(Li et al., 2017b; Jiang et al., 2018).在土壤重金属空间分布预测的3种模型中, 引入相关环境要素作为多源辅助数据, 特别是考虑土壤重金属空间分布的确定性与非确定性两个部分的第3种模型, 已经被许多研究证明对于改进土壤重金属空间分布预测精度是有效的(Kumar et al., 2012; Zhang et al., 2012; Dai et al., 2014; Jiang et al., 2018), 越来越受到关注.
然而要恰当地引入合适的辅助数据并结合第三类模型对土壤重金属空间分布进行预测, 应考虑两个问题(Li et al. 2017b).首先根据McBratney等(2003)总结并提出土壤形成过程中的7种因素, 接近80%的研究只使用过一种或者两种类型的因素, 很少有研究考虑过3种及3种以上的因素(Mcbratney et al., 2003; Li et al., 2017b).其次本质上来讲, 我们不应该假设土壤重金属与辅助数据之间的关系是线性的(Mcbratney et al., 2003), 即使MSLR已经成功运用于捕捉土壤属性和辅助数据的关系(Grunwald. 2009; Mishra et al., 2010).为此, 我们试着尝试解决这两个问题.第一, 考虑3种类型的辅助数据, 包括地形要素、遥感数据和邻近信息.在小区域内地形控制着土壤重金属的蓄积和运移过程(Li et al., 2017a);遥感数据可以反映土壤表面作物生长与土壤重金属含量的关系(史舟等, 2014; Mishra et al., 2016);邻近信息则在预测时会增加土壤重金属与辅助数据的映射关系(李启权等, 2008; 江叶枫等, 2017), 因为根据地理学第一定律, 相邻的比远处的更相关(Miller, 2004).第二, 为了克服线性模型难以捕捉复杂条件下土壤重金属与多源辅助数据的映射关系, 非线性模型常常被用来捕捉这种关系(Li et al., 2013a; Dai et al., 2014).最近, 径向基函数神经网络(Radial Basis Function Neural Network, RBFNN)方法在土壤重金属空间分布中表现较好(Li et al., 2013a; Li et al., 2017a; Li et al., 2017b), 因为它可以通过学习自动捕捉多源辅助变量与土壤重金属之间的非线性关系.
稻田土壤砷含量关系到稻田质量与人类的生命安全, 严重威胁着土壤环境与农业可持续发展(Ahmed et al., 2011; Hu et al., 2016), 掌握稻田土壤砷空间分布特征是有效防止土壤砷污染和保护稻田质量的基础与前提(Rogan et al., 2010; Feng et al., 2012).为此, 本文以江西省都昌县为案例区, 稻田土壤砷为研究对象, 采用RBFNN结合OK的模型(Radial Basis Function Neural Network combined with OK, RBFNN_OK)对稻田土壤砷空间分布进行模拟, 并与RBFNN、RK和MSLR进行比较, 以期为区域高精度土壤重金属空间分布预测提供方法参考.
2 材料与方法(Materials and methods)2.1 研究区概况研究区为都昌县, 该区位于江西省北部, 地理坐标介于28°50′N~29°38′N, 116°2′E ~116°36′E之间, 总面积为2669.53 km2, 其中陆地面积1279.22 km2, 水域面积为1390.31 km2, 水域面积约占鄱阳湖水域总面积的1/3.都昌县辖24个乡镇, 259个村委会, 总人口83万.地形地貌以丘陵和滨湖平原为主, 海拔高度范围从11~599 m, 东北部和中部海拔较高, 东南部和西北部较低.年平均气温16~17 ℃, 雨量充沛, 年均降水量1391~1728 mm;全年无霜期约227~300 d.土壤类型主要有水稻土、红壤、黄棕壤、紫色土和石灰土等.耕地面积4.38×104 hm2, 其中稻田3.05×104 hm2, 旱地1.33×104 hm2, 粮食作物以水稻为主, 水稻种植面积约占全县耕地总面积的69.63%.研究区pH处于5.5~6.5之间.
2.2 田间采样与样品分析在参考村级行政区、地形条件、土壤类型、人为源与自然源的基础上, 在都昌县选取具有代表性的稻田作为采样区, 共采集144个采样点(图 1a, 2016年2月).每个样点在同一田块内随机钻取4~5个采样点形成一个混合样, 土壤样品充分混合后选取1 kg装入塑料袋并运用GPS记录经纬度, 土壤样品经过自然风干后带回实验室.将采集的土壤样品于阴凉通风处风干、磨细混合均匀后过80目尼龙筛.准确量取0.5~1.0 g土壤样品, 用H2SO4-HNO3-HCLO4消解, 用二乙基二硫代氨基甲酸银分光光度法测定(GB/T 17134-1997), 使用仪器为UV-2550PC紫外分光光度计(Li et al., 2013b).实验全过程采样国家土壤标准参比物质(GBW-07401)进行分析质量控制.
图 1(Fig. 1)
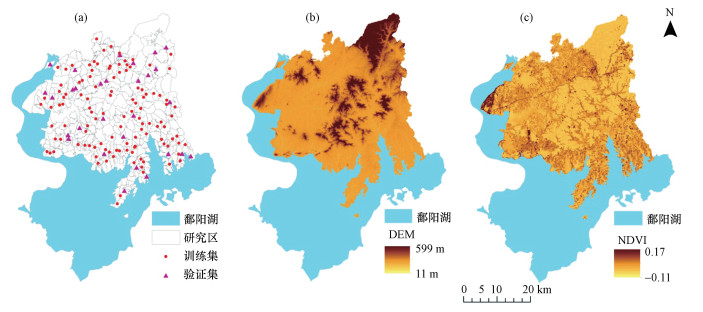 |
| 图 1 土壤采样点(a), 数字高程模型(b)和归一化植被指数(c) Fig. 1Soil sampling sites (a), Digital elevation model (DEM) (b), and Normalized Difference Vegetation Index (NDVI) (c) |
2.3 多源辅助数据2.3.1 地形因子和遥感数据在考虑成本低廉和数据可获取性原则的基础上, 选取高程(DEM)、坡度(S)、坡向(AS)、曲率(C)、坡度变率(SOS)、坡向变率(SOA)、地形起伏度(QFD)7个地形因素作为影响土壤砷空间分布的地形因子.地形因子可通过ArcGIS空间分析从DEM数据获取(图 1b).各地形因子的计算公式见参考文献(Grunwald, 2009; Li et al., 2013a).遥感数据包括植被覆盖指数(NDVI)和与土壤砷含量显著相关的波段1和波段2(表 1)(Mirzaee et al., 2016), 其中植被覆盖指数由Landsat 8 OLI影像(拍摄日期为2015年10月11日, 空间分辨率30 m)的第4波段和第5波段在ArcGIS10.2中进行栅格计算获取(图 1c).DEM数据与Landsat 8 OLI影像来源于地理空间数据云(http://www.gscloud.cn/).
表 1(Table 1)
| 表 1 土壤砷与遥感影像波段的Pearson相关性分析 Table 1 Pearson correlation coefficients of soil arsenic with remote sensing data band | ||||||||||||||||||||||||||||||
表 1 土壤砷与遥感影像波段的Pearson相关性分析 Table 1 Pearson correlation coefficients of soil arsenic with remote sensing data band
| ||||||||||||||||||||||||||||||
2.3.2 邻近信息四方位搜索法(The four-direction search method)(江叶枫等, 2017)被用来获取采样点附近土壤砷含量.四方位搜索法是基于地理学第一定律(Miller, 2004)和空间自相关理论(Biswas et al., 2017), 根据采样点之间的距离越近影响越大, 距离越远影响越小的思想, 以采样点为坐标原点, 土壤砷变程为半径, 在每个象限内选择一个邻近点土壤砷含量值Pi(i=1、2、3、4).四方位搜索法步骤:
1) 在Matlab中新建一个mat文件, 导入所有采样点地理坐标(x, y)和土壤砷含量(z);
2) 从文件中随机抽取一个点, 赋值给Fi;
3) 在mat文件剩余点中随机抽取一个点, 赋值给Gi;
4) 计算M、N两点之间的欧氏距离, 设为d, 令Temp1=Temp2=Temp3=Temp4=a, 若d>a, 则回到步骤3);
5) 若Gi(x)>Fi(x), Gi(y)≥Fi(y)且d≤Temp1, 则Temp1=d, P1=Gi(z);
6) 若Gi(x)≤Fi(x), Gi(y)>Fi(y)且d≤Temp2, 则Temp2=d, P2=Gi(z);
7) 若Gi(x) < Fi(x), Gi(y)≤Fi(y)且d≤Temp3, 则Temp3=d, P3=Gi(z);
8) 若Gi(x)≥Fi(x), Gi(y) < Fi(y)且d≤Temp4, 则Temp4=d, P4=Gi(z);
9) 重复步骤2)~ 8), 直至遍历mat文件中所有点, 将P1、P2、P3、P4存放在文本中.
9) 重复步骤2)~ 8), 直至遍历mat文件中所有点, 将P1、P2、P3、P4存放在文本中.
四方位搜索法在Matlab R2014a中实现, 出现的空值由其他象限的平均值进行计算.其中P1、P2、P3、P4分别代表以采样点为坐标原点, 四个象限内与采样点最近点的土壤砷含量值;Fi和Gi表示采样点的地理坐标, Fi(x)和Gi(x)表示经度, Fi(y)和Gi(y)表示纬度.
2.4 预测模型2.4.1 RBFNNRBFNN是由输入层, 隐层和输出层构成的三层前向网络(Li et al., 2013a; Li et al., 2017a; Li et al., 2017b).第一层为输入层, 节点个数等于输入维数;第二层为隐藏层, 节点个数视问题的复杂度而定.第三层为输出层, 节点个数等于输出维数.其中隐含层是非线性的, 将输入向量空间转换到隐含层空间, 使原来线性不可分的问题变得线性可分, 而在高维空间中的输出层中实现加权线性组合.使用高斯激活函数作为隐藏层的基函数, 由式(1)给出.
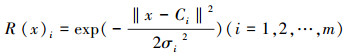 | (1) |
输入层是从x到R(x)i非线性映射,输出层实现从R(x)i到y的线性映射,由式(2)给出:
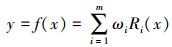 | (2) |
因此,RBFNN预测土壤砷空间分布的表达式可以由式(3)表示:
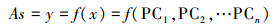 | (3) |
2.4.2 MSLR在回归分析中, 因变量受许多自变量的影响, 如果有两个或两个以上的自变量, 则称为多元回归(Zhao et al., 2012; 江叶枫等, 2017).通过多变量的最优组合来预测或估计因变量, 与仅用单变量预测或估计更有效.当自变量和因变量的数量是线性关系时, 我们一般使用多元逐步线性回归(MSLR), 进而剔除一些对土壤砷含量影响不显著的变量, 由式(4)给出:
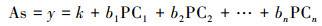 | (4) |
2.4.3 RKRK考虑地理现象的空间分布及其影响因素, 即模拟其空间分布的确定性趋势也模拟其不确定性(Odeha et al., 1994; Hengl et al., 2004; Kumar et al., 2012).RK:通过SPSS软件中多元逐步回归方程拟合土壤砷含量与由主成分分析提取的多源辅助变量PC1、PC2、PC3···PCn之间的MSLR方程, 得到代表确定性部分的趋势项和代表随机性部分的预测残差, 然后把趋势项的预测结果导入ArcGIS中转成栅格文件, 同时利用OK对预测残差进行插值, 最后将两者的结果在ArcGIS中运用栅格计算器进行叠加, 其过程可表示为:
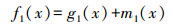 | (5) |
2.4.4 RBFNN_OKRBFNN_OK(图 2):通过RBFNN建立土壤砷含量与由主成分分析提取的多源辅助变量PC1、PC2、PC3···PCn之间的非线性映射关系, 得到代表确定性部分的趋势项和代表随机性部分的残差项, 然后把趋势项的预测结果导入ArcGIS中转成栅格文件, 同时利用OK对残差项进行插值, 最后将两者的结果在ArcGIS中运用栅格计算器进行叠加, 其过程可表示为:
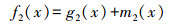 | (6) |
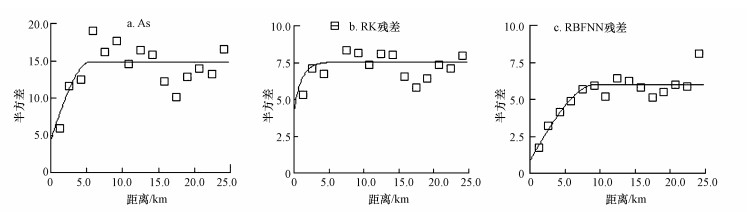 |
| 图 2 半变异函数关于土壤砷(a)、RK残差(b)和RBFNN残差(c) Fig. 2Semivariograms (points) and fitted models (lines) ofsoil arsenic concentration (a), regression kriging residuals (b) and radial basis function neural network residuals (c) |
式中, f2(x)为RBFNN_OK在x处的插值结果, g2(x)为RBFNN在x处的趋势项, m2(x)为RBFNN残差在x处的OK插值结果.
2.5 精度评价为验证以上4种方法的性能, 通过ArcGIS10.2中地统计模块生成样本数据子集:其中随机均匀选取80%(115)土壤样点进入测试集;剩下20%(29)土壤样点进入验证集用于验证预测精度.以均方根误差(RMSE)、平均绝对误差(MAE)、平均相对误差(MRE)和测量值标准偏差与均方根误差的比值(RPD)对测试集和验证集预测值与实际测量值进行对比分析, 得出精度评价结果.其公式分别为:
 | (7) |
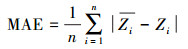 | (8) |
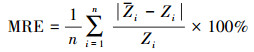 | (9) |
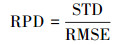 | (10) |
3 结果(Results)3.1 描述性统计从土壤砷的描述性统计分析结果可以看出(表 2), 土壤砷含量平均值为8.49 mg·kg-1, 低于鄱阳湖及周边地区的背景值(10.2 mg·kg-1);值域范围为2.61~32.40 mg·kg-1.根据中国土壤环境标准(GB15618—1995)土壤砷含量超过国家一级标准和二级标准的样点数分别为138、5;存在1个样点的土壤砷含量高于国家土壤环境二级标准, 达到32.4 mg·kg-1.从变异系数来看, 土壤砷属于中等变异性.
表 2(Table 2)
| 表 2 土壤砷的描述性统计分析结果 Table 2 Descriptive statistics analysis result of soil arsenic | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 土壤砷的描述性统计分析结果 Table 2 Descriptive statistics analysis result of soil arsenic
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.2 主成分分析主成分分析法能将原来的多个指标组合成相互独立的少数几个能够充分反映总体信息的指标.运用SPSS软件中主成分分析法, 对14个(DEM, S, AS, C, SOS, AOS, QFD, P1, P2, P3, P4, Band1, Band2, NDVI)用来映射土壤砷含量的多源辅助变量转换成14个主成分.第1主成分包括P1、P2、P3、P4, Band 1和Band 2, 主要代表邻近信息和部分遥感影像信息;第2, 4, 5, 6主成分主要代表地形因子.第3主成分主要代表遥感影像信息.如表 3所示, 得到的前10个主成分可解释总方差的97.62%, 因此可以选择前10个主成分作为RK和RBFNN模型的预测变量.
表 3(Table 3)
| 表 3 主成分分析结果 Table 3 Results of principal component analysis | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3 主成分分析结果 Table 3 Results of principal component analysis
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.3 RBFNN与RK在本研究中, 前10个主成分被用作RBFNN输入节点进行网络的训练, 以土壤砷含量为网络的输出层, 通过不断改变网络参数来优化网络.本质上来讲, 最优网络主要取决于验证样点的预测精度.为了克服过度拟合问题, 本文以RMSE最小为约束条件, 隐含层节点数从1开始每次增加1个节点, 扩展常数从0开始每次增加0.05, 使得均方根误差最小的2个参数组合即为预测研究区土壤砷空间分布的最优RBFNN模型参数.最后得到网络的最优结构为12-0.8-4:输入层节点数为12(包括经纬度), 扩展常数为0.8, 最大神经元个数为4.与RBFNN模型一样, 运用前10个主成分作为自变量, 借助SPSS中多元逐步回归方法完成自变量筛选, 直至模型方程与各解释变量均显著.表 5是土壤砷的多元逐步回归预测过程.
表 5(Table 5)
| 表 5 土壤砷多元回归逐步方程过程 Table 5 Stepwise process of multiple regression equations for soil arsenic | |||||||||||||||
表 5 土壤砷多元回归逐步方程过程 Table 5 Stepwise process of multiple regression equations for soil arsenic
| |||||||||||||||
3.4 半方差函数分析运用GS+对土壤砷、RK残差和RBFNN残差进行半方差函数拟合, 用半方差函数描述三者的空间变异性.从图 3可以看出, 土壤砷、RK残差和RBFNN残差的最优模型分别为球状模型、指数模型和球状模型.从模型的参数来看(表 4), 土壤砷、RK残差和RBFNN残差的块金效应(随机性因素引起的空间变异占系统总空间变异的比值)分别为29.23%、55.63%和13.98%.根据Cambardella(1994)关于块金效应的划分(< 25%, 强空间变异;25%~75%, 中等空间变异性;75%, 弱空间变异), 表明土壤砷和RK残差呈中等空间变异而RBFNN残差呈强空间变异.土壤砷、RK残差和RBFNN残差的变程分别为5.52、3.30和9.45 km, 表明3者的空间自相关范围较小.RK残差和RBFNN残差的半方差模型参数与土壤砷变化较小, 基本保留了土壤砷的空间结构特征.
图 3(Fig. 3)
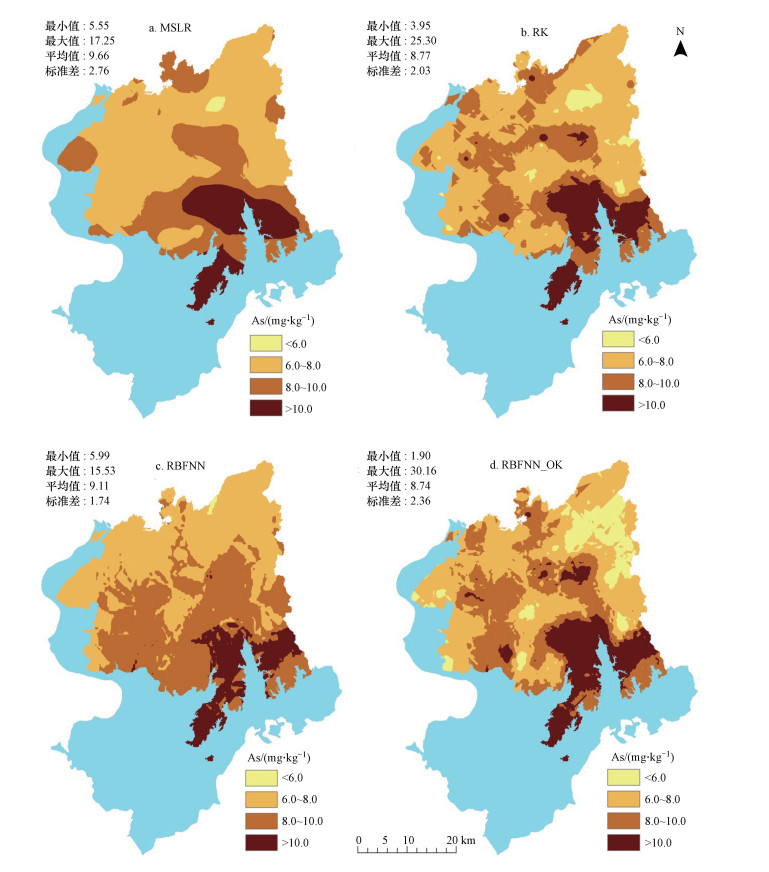 |
| 图 3 土壤砷空间分布图通过使用多元逐步线性回归(a), 回归克里格(b), 径向基函数神经网络(c)和径向基函数神经网络结合普通克里格(d) Fig. 3Predicted soil arsenic concentration maps using multiple stepwise linear regression (a), regression kriging (b), radial basis function neural network (c) and radial basis function neural network combined with ordinary kriging (d) |
表 4(Table 4)
| 表 4 土壤砷、RK残差和RBFNN残差的半方差函数参数 Table 4 Semivariogram model parameters for soil arsenic, RK residuals and RBFNN residuals | ||||||||||||||||||||||||||||||||
表 4 土壤砷、RK残差和RBFNN残差的半方差函数参数 Table 4 Semivariogram model parameters for soil arsenic, RK residuals and RBFNN residuals
| ||||||||||||||||||||||||||||||||
3.5 预测精度对比分析为验证本文使用4种方法的模拟效果, 将4种方法预测的土壤砷空间分布均以30 m分辨率在ArcGIS中显示(图4).首先, 从验证集预测效果可以看出(表 6), RBFNN_OK的RPD为2.85, 表明RBFNN_OK模型具有很好的预测能力;RK与RBFNN模型的RPD为2.45与2.10, 表明两者具有较好的预测能力;而MSLR的RPD为1.97, 表明MSLR只能粗略估计土壤砷污染物的空间分布.RBFNN_OK较RBFNN模型的RMSE、MAE和MRE分别降低了13.00%、5.66%和43.03%;较RK分别降低了26.27%、24.24%和62.00%;较MSLR模型分别降低了30.95%、39.02%和68.65%;RBFNN_OK的RPD较后3种模型分别提高了14.92%、35.71%和44.67%.从测试集预测效果可以看出(表 6), RBFNN的RPD仅为1.37, 对测试集的训练效果较差, 这可能是因为本文以验证集的RMSE最小为约束条件来寻找最优参数, 而较少考虑测试集的训练效果.MSLR的RPD仅为1.08, 对测试集的训练效果最差, 表明单个线性模型难以捕捉多源辅助变量与土壤砷的复杂关系.RBFNN_OK和RK的RPD分别为3.78和2.55, 较RBFNN与MSLR有较为明显的提高.作为RBFNN_OK和RK的一部分, OK对根据RBFNN与MSLR预测残差的空间自相关性程度进行预测, 由于RBFNN与MSLR预测残差空间自相关性较强且自相关范围小, OK能够在训练集预测的基础上充分反映“Scorpan”模型预测残差的变化, 考虑了稻田土壤砷空间分布的确定性和随机性模拟.
表 6(Table 6)
| 表 6 4种方法的精度评估 Table 6 Assessment of the four methods for predicting soil arsenic | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 6 4种方法的精度评估 Table 6 Assessment of the four methods for predicting soil arsenic
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
其次从空间分布图可以看出, 通过4种方法模拟的土壤砷含量空间分布图表现出相似的空间格局, 表明土壤砷含量较高的区域在东南部;其中MSLR与RBFNN预测的空间分布图更为相似, RK与RBFNN_OK预测的空间分布高低值变化更为相似.然而4种方法预测的空间局部特征差异明显.首先MSLR模型模拟的结果在整体上能表达一定的空间异质性信息, 在局部描写异质性信息不够, 预测图具有一定的平滑效应, 且预测土壤砷含量范围为5.55~17.25 mg·kg-1, 预测范围较小且与统计分析值有一定差距;RBFNN模拟结果高低值区域明显但也较为平滑, 预测范围大部分在5.99~15.53 mg·kg-1之间, 与采样点的算术平均值较为接近.其次, RK与RBFNN_OK模拟的结果高低值之间的变化较为突兀, 高低值斑块多且分布离散, 突出了数据的波动性, 能够在尊重原始观测数据情况下更加客观地描述土壤砷空间分布的异质性.但RBFNN_OK的预测范围(1.90~30.16 mg·kg-1)较RK的预测范围(3.95~25.30 mg·kg-1)更加接近统计分析值(2.61~32.40 mg·kg-1).因此, RBFNN_OK对土壤砷模拟结果与实际分布最为接近, 取得了最优效果.
4 讨论(Discussion)4.1 多源辅助数据预测土壤砷空间分布的有效性土壤是在成土过程和环境因素综合作用下形成的.由于各种原因, 土壤重金属含量可能发生显著变化, 即使是在较小尺度或者距离只发生微小变化的区域(Li et al., 2017a).在没有辅助数据的情况下, 很难真实有效的反映出土壤重金属空间分布特征.许多研究已经证明了辅助数据可以提高对土壤重金属(或土壤属性)预测的准确性(Mcbratney et al., 2003; Hengl et al., 2004).因此, 为了得到精确的土壤重金属空间分布, 应充分考虑影响土壤重金属空间分布的各种因素及土壤重金属的空间自相关性, 提取一些成本低廉、高效和获取简单的多源辅助数据, 运用一种成本有效且技术可行的方法预测土壤重金属的空间分布(Kumar et al., 2012).
地形因素, 作为一种常见的环境协变量, 能够明显的影响土壤重金属空间分布(Odeha et al., 1994).Kim等(2009)研究表明, 土壤砷蓄积与运移过程受地形因子的影响较大.一般而言, 高程越高, 受到降雨冲刷作用越强烈, 导致土壤砷易随地表径流向下流动.都昌县东南部地势较低, 而西北部较高, 一些含砷的硫化物或氧化物岩石经风化或鄱阳湖水流冲刷等过程将砷释放到土壤中, 并在地势低洼处累积(图 1b).而不同地形拥有不同的水热条件和物质运移与堆积特点, 造成了土壤水体中氧化还原环境和沉积物释放的差异, 通过地下水的氧化还原环境间接影响到砷的释放、迁移与富集过程.根据江西省鄱阳湖及周边经济区农业地质调查系列成果(2009)显示, 都昌县鄱阳湖入湖口处土壤砷表层含量较高而深层偏低, 这表明都昌县土壤砷累积受到自然形成的地形地貌和植被覆盖等因素影响, 同时西北部由于土壤砷受植被覆盖的影响固化程度较深(图 1c), 土壤砷空间分布较为均匀.
遥感数据能够监测土壤表面作物的生长状况.研究表明(史舟等, 2014; Mirzaee et al., 2016), 遥感影像波段, 尤其是植被覆盖指数, 与土壤重金属污染水平存在联系.当作物受砷污染时, 会造成土壤环境的变化, 从而影响作物的生理、生态指标发生规律性的变化, 植被的反射会发生较为显著地变化.而邻近信息, 能够在稀疏采样的基础上充分挖掘土壤砷的空间自相关性, 根据地理学第一定律选取邻近采样点的土壤砷信息, 进而增强多源辅助数据与土壤砷的映射关系(李启权等, 2008; 江叶枫等, 2017).江叶枫等(2017)研究表明, 邻近信息在土壤相关属性的数字制图中有着极其重要的影响, 其运用四方位搜索法获取插值点附近的4个邻近信息值, 并与未运用邻近信息的插值方法进行比较, 其结果表明引入邻近信息的插值结果能更好地揭示土壤属性的局部变化特征, 能在提高精度的同时更加真实地反映土壤属性空间变异的全局与局部特征.李启权等(2008)根据空间距离衰减规律, 选取离插值点最近的3个土壤属性值, 在不同土壤属性间较其它模型误差降低达到显著水平.因此, 在缺乏连续监测系统以及考虑数据可获取的基础上, 应在土壤砷空间分布预测中引入邻近信息.
4.2 RBFNN_OK预测土壤砷空间分布的可行性在本研究中, RBFNN_OK在预测土壤砷空间分布中取得了最佳模拟效果.这可以归因于3点:首先RBFNN的非线性映射能力, 能以任意精度逼近任意连续函数(Li et al., 2013a).一些****发现基于多源辅助数据的MSLR模型可能不适合模拟土壤属性, MSLR模型可能会破坏目标土壤属性的空间结构(Li, 2010).因为本质上来讲, 我们不能假设土壤重金属与多源辅助数据之间的关系是线性的(Mcbratney et al., 2003).在本研究乃至其它许多研究区域中, 土壤重金属与多源辅助变量间的关系并非是线性的(Dai et al., 2014; Li et al., 2017a), 这表明人工神经网络可能更适合捕捉这种映射关系.其次多源辅助数据用于土壤重金属的映射关系, 同时运用主成分分析消除多源辅助数据间的多重共线性(Li et al., 2017b).第一主成分代表邻近信息和部分影像数据, 贡献率达到28.40%(表 3), 表明土壤砷在空间上表现为强空间相关性(表 4), 邻近信息可在局部范围内刻画土壤砷的空间分布特征(江叶枫等, 2017).通常来自高污染风险区域的土壤重金属含量是局部空间异常值, 而基于邻近信息的RBFNN_OK可以更好的捕捉这种异常值(Li et al., 2017a).最后, 运用OK法对RBFNN残差进行空间插值, 考虑了确定性因素与随机性因素的空间模拟(江叶枫等, 2017).而RBFNN模型由于仅考虑采样点的确定性模拟, 而忽略了有关随机性部分的残差模拟(Dai et al., 2014).在本研究中, 若不将代表随机部分的残差表示为随机变量, 很难在整个研究区中用已有方法精确地描述土壤砷含量的空间变化特征(Li et al., 2013a).为了克服这个问题, OK模拟的随机性部分被用来减轻一些限制, 作为RBFNN_OK和RK的一部分, 可以根据空间自相关性的水平预测RBFNN和RK残差空间分布.从半方差函数参数可知(表 4), RBFNN残差具有高度的空间依赖性, OK法可以把神经网络模型模拟的不确定性部分进行预测, 能够在尊重原始数据的基础上较好地反映土壤砷含量空间变化, 因此, RBFNN_OK估测土壤砷含量与统计分析值较RBFNN更为接近.RK也取得了比MSLR更好的模拟效果.
尽管本文提出的RBFNN_OK法取得了最佳模拟效果, 但RBFNN_OK无法像地统计学那样定量描述土壤砷的空间自相关性, 不能解释多源辅助数据与土壤砷的变化关系, 这也是其不足之处.因此, 在后续研究中需要考虑以下两点:①在残差存在高度空间自相关性充分运用地统计学方法(或纯空间方法)对残差进行空间插值.②为了更大范围地扩大模型的适应度, 应引入一些代表人为活动的指标(如灌溉方式、施肥量和与养殖场的距离)以及更多的辅助变量(如土壤类型、土壤质地和土地利用方式)还可以更加精确地描述土壤砷空间分布特征.
4.3 土壤砷空间分布模拟的意义近年来稻田中土壤砷的累积是客观存在的事实, 这种现象在集约化程度较高、农业投入品用量大的稻田中尤为明显.曾希柏等(2013)研究结果表明, 在中国其他农业主产区, 由于使用砷含量较高的磷肥、复合肥、污泥及畜禽粪便等, 稻田表层中土壤砷的累积速度较快, 部分稻田砷含量已经超标, 必须引起足够重视.为防止稻田土壤和鄱阳湖水域砷含量的继续上升, 十分有必要采取一定措施对稻田土壤中的砷进行调控, 降低农作物对砷的吸收量和收获物中砷的含量, 减轻其环境风险, 保障农产品质量安全和农业环境安全.一方面, 通过深翻、化学还原技术、植物与微生物调控等改变作物对表层土壤砷的吸收量以及降低砷的有效性(Geen et al., 2008; Dai et al., 2018).更重要的是, 快速准确的掌握稻田土壤砷空间分布以及识别砷的污染源, 研究制定源头污染控制技术措施及相应的管理法规等, 有效降低含砷物质向农田生态系统的输入, 实现源头阻控目标(Lv et al., 2015; Li et al., 2017a; Jiang et al., 2018).该文提出的方法为快速、成本有效和精准获取研究区土壤砷空间分布提供了方法参考.
5 结论(Conclusions)本文提出的RBFNN_OK被用来建立土壤砷含量与多源辅助数据的映射关系, 对土壤砷空间分布进行模拟, 并与RBFNN、RK和MSLR模型进行比较, 对29个验证样点的误差分析结果表明RBFNN_OK预测结果的RMSE、MAE和MRE较RBFNN、RK和MSLR分别降低了13.00%, 5.66%, 43.03%;26.27%, 24.24%, 62.00%;30.95%, 39.02%, 68.65%;RBFNN_OK预测结果的RPD较后3种模型分别提高了14.92%、35.71%和44.67%.结果表明在稀疏采样的基础上, 充分挖掘土壤砷含量与多源辅助数据的内在联系可为精准获取土壤砷空间分布提供方法参考.
参考文献
| Ahmed Z U, Panaullah G M, Degloria S D, et al. 2011. Factors affecting paddy soil arsenic concentration in Bangladesh:prediction and uncertainty of geostatistical risk mapping[J]. Science of the Total Environment, 412(412/413): 324–335. |
| Biswas S R, Macdonald R L, Chen H Y H. 2017. Disturbance increases negative spatial autocorrelation in speciesdiversity[J]. Landscape Ecology, 32(4): 823–834.DOI:10.1007/s10980-017-0488-9 |
| Cambardella C A. 1994. Field-scale variability of soil properties in central Iowa soils[J]. Soilence Society of America Journal, 58(5): 1501–1511.DOI:10.2136/sssaj1994.03615995005800050033x |
| Dai F, Zhou Q, Lv Z, et al. 2014. Spatial prediction of soil organic matter content integrating artificial neural network and ordinary kriging in Tibetan Plateau[J]. Ecological Indicators, 45(5): 184–194. |
| Dai L, Wang L, Li L, et al. 2018. Multivariate geostatistical analysis and source identification of heavy metals in the sediment of Poyang Lake in China[J]. Science of the Total Environment, 621: 1433–1444.DOI:10.1016/j.scitotenv.2017.10.085 |
| Feng J, Zhao J, Bian X, et al. 2012. Spatial distribution and controlling factors of heavy metals contents in paddy soil and crop grains of rice-wheat cropping system along highway in East China[J]. Environmental Geochemistry and Health, 34(5): 605–614.DOI:10.1007/s10653-012-9454-2 |
| Goovaerts P. 1997. Geostatistics for Natural Resources Evaluation[M]. USA: Oxford University Press. |
| Geen A V, Zheng Y S, Goodbred J, et al. 2008. Flushing history as a hydrogeological control on the regional distribution of arsenic in shallow groundwater of the Bengal Basin[J]. Environmental Science & Technology, 42(7): 2283–2288. |
| Grunwald S. 2009. Multi-criteria characterization of recent digital soil mapping and modeling approaches[J]. Geoderma, 152: 195–207.DOI:10.1016/j.geoderma.2009.06.003 |
| Guo X, Li H Y, Yu H M, et al. 2018. Drivers of spatio-temporal changes in paddy soil pH in Jiangxi Province, China from 1980 to 2010[J]. Scientific Reports.DOI:10.1038/s41598-018-20873-5 |
| Hengl T, Heuvelink G B M, Stein A. 2004. A generic framework for spatial prediction of soil variables based on regression-kriging[J]. Geoderma, 120(1/2): 75–93. |
| Hu Y, Jia Z, Cheng J, et al. 2016. Spatial variability of soil arsenic and its association with soil nitrogen in intensive farming systems[J]. Journal of Soils and Sediments, 16(1): 169–176.DOI:10.1007/s11368-015-1182-7 |
| 江西省地质调查研究院. 2009. 鄱阳湖地球化学图集[M]. 南昌: 江西科学技术出版社: 106–107. |
| 江叶枫, 孙凯, 郭熙, 等. 2017. 基于环境因子和邻近信息的土壤属性空间分布预测[J]. 环境科学研究, 2017, 30(7): 1059–1068. |
| Jiang Y F, Rao L, Sun K, et al. 2018. Spatio-temporal distribution of soil nitrogen in Poyang Lake ecological economic zone (South-China)[J]. Science of the Total Environment, 626: 235–243.DOI:10.1016/j.scitotenv.2018.01.087 |
| Kim K, Moon J T, Kim S H, et al. 2009. Importance of surface geologic condition in regulating As concentration of groundwater in the alluvial plain[J]. Chemosphere, 77(4): 478–484.DOI:10.1016/j.chemosphere.2009.07.053 |
| Kumar S, Lal R, Liu D. 2012. A geographically weighted regression kriging approach for mapping soil organic carbon stock[J]. Geoderma, 189-190(6): 627–634. |
| 李启权, 王昌全, 岳天祥, 等. 2008. 不同输入方式下RBF神经网络对土壤性质空间插值的误差分析[J]. 土壤学报, 2008, 45(2): 360–365.DOI:10.3321/j.issn:0564-3929.2008.02.024 |
| Li Y. 2010. Can the spatial prediction of soil organic matter contents at various sampling scales be improved by using regressionkriging with auxiliary information?[J]. Geoderma, 159(1): 63–75. |
| Li Q Q, Yue T X, Wang C Q, et al. 2013a. Spatially distributed modeling of soil organic matter across China:An application of artificial neural network approach[J]. Catena, 104(2): 210–218. |
| Li X Y, Liu L J, Wang Y G, et al. 2013b. Heavy metal contamination of urban soil in an old industrial city(Shenyang) in Northeast China[J]. Geoderma, 192(1): 50–58. |
| Lv J, Liu Y, Zhang Z, et al. 2015. Identifying the origins and spatial distributions of heavy metals in soils of Ju country (Eastern China) using multivariate and geostatistical approach[J]. Journal of Soils & Sediments, 15(1): 163–178. |
| Li QQ, Wang C Q, Dai T F, et al. 2017a. Prediction of soil cadmium distribution across a typical area of Chengdu Plain, China[J]. Scientific Reports.DOI:10.1038/s41598-017-07690-y |
| Li QQ, Zhang H, Jiang X Y, et al. 2017b. Spatially distributed modeling of soil organic carbon across China with improved accuracy[J]. Journal of Advances in Modeling Earth Systems.DOI:10.1002/2016MS000827 |
| Mcbratney A B, Santos M L M, Minasny B. 2003. On digital soil mapping[J]. Geoderma, 117(1): 3–52. |
| Miller H J. 2004. Tobler's First Law and Spatial Analysis[J]. Annals of the Association of American Geographers, 94(2): 284–289.DOI:10.1111/j.1467-8306.2004.09402005.x |
| Mishra U, Lal R, Liu D S, et al. 2010. Predicting the spatial variation of the soil organic carbon pool at a regional scale[J]. Soil Science Society of America Journal, 74(3): 906–914.DOI:10.2136/sssaj2009.0158 |
| Mcbratney A, Field D J, Koch A. 2014. The dimensions of soil security[J]. Geoderma, 213(1): 203–213. |
| Mirzaee S, Ghorbani-Dashtaki S, Mohammadi J, et al. 2016. Spatial variability of soil organic matter using remote sensing data[J]. Catena, 145: 118–127.DOI:10.1016/j.catena.2016.05.023 |
| Odeha I O A, Mcbratney A B, Chittleborough D J. 1994. Spatial prediction of soil properties from landform attributes derived from a digital elevation model[J]. Geoderma, 63(3/4): 197–214. |
| Rogan N, Dolenec T, Serafimovski T, et al. 2010. Distribution and mobility of heavy metals in paddy soils of the Ko?ani Field in Macedonia[J]. Environmental Earth Sciences, 61(5): 899–907.DOI:10.1007/s12665-009-0405-x |
| Razakamanarivo R H, Grinand C. 2011. Mapping organic carbon stocks in eucalyptus plantations of the central highlands of Madagascar:A multiple regression approach[J]. Geoderma, 162(3/4): 335–346. |
| 史舟, 王乾龙, 彭杰, 等. 2014. 中国主要土壤高光谱反射特性分类与有机质光谱预测模型[J]. 中国科学:地球科学, 2014, 44(5): 978–988. |
| Zhang S, Huang Y, Shen C, et al. 2012. Spatial prediction of soil organic matter using terrain indices and categorical variables as auxiliary information[J]. Geoderma, 171-172(2): 35–43. |
| Zhao H, Xia B, Fan C, et al. 2012. Human health risk from soil heavy metal contamination under different land uses near Dabaoshan Mine, Southern China[J]. Science of the Total Environment, 417-418(7385): 45–54. |
| 曾希柏, 徐建明, 黄巧云, 等. 2013. 中国农田重金属问题的若干思考[J]. 土壤学报, 2013, 50(1): 186–194. |
