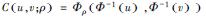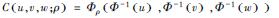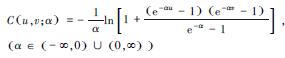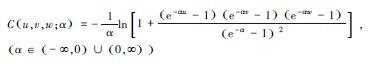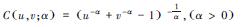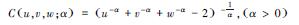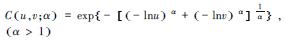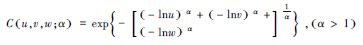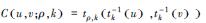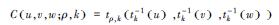, 窦明1
, 窦明1
 , 李桂秋1
, 李桂秋11. 郑州大学水利与环境学院, 郑州 450001;
2. 中国农业科学院农田灌溉研究所, 新乡 453002
收稿日期: 2018-04-10; 修回日期: 2018-05-14; 录用日期: 2018-05-14
基金项目: 国家自然科学基金(No.51679218,51879239);河南省高校科技创新人才支持计划项目(No.17HASTIT031);郑州大学优秀青年教师发展基金(No.1521323001)
作者简介: 张彦(1989-), 男, E-mail:15136479128@163.com
通讯作者(责任作者): 窦明(1975—),男,教授,郑州大学水利与环境学院,长期从事水资源与水环境研究,发表论文140余篇.E-mail:douming@zzu.edu.cn
摘要: 为了分析小型人工湖水体富营养化指标联合风险发生的概率,基于Copula函数的基本原理,结合眉湖水体富营养化模型模拟结果,建立了水体富营养化指标的边缘分布及Copula函数联合概率分布.通过Copula函数拟合检验和拟合优度评价筛选出不同组合方式下最优的Copula函数,并根据最优的Copula函数计算出水体富营养化指标的二维和三维联合风险概率.结果表明,不同组合方式下水体富营养化指标达到不同富营养化状态时的联合风险概率区别较大;当Chl-a和COD都为轻度富营养时,二维联合风险概率最大为62.29%,说明这种组合方式下眉湖水体极易发生轻度富营养;当Chl-a和COD都为轻度富营养、TN为中度富营养时,三维联合风险概率最大为45.46%,说明这种组合方式下眉湖水体极易发生中度富营养;由于受到水体富营养化指标监测系列的影响,部分二维和三维联合风险概率较小甚至为零.
关键词:Copula函数富营养化联合风险概率
The analysis of joint risk probability of eutrophication based on copula function
ZHANG Yan1,2
 , DOU Ming1
, DOU Ming1
 , LI Guiqiu1
, LI Guiqiu1 1. College of Water Conservancy and Environment, Zhengzhou University, Zhengzhou 450001;
2. Farmland Irrigation Research Institute, Chinese Academy of Agricultural Sciences, Xinxiang 453002
Received 10 April 2018; received in revised from 14 May 2018; accepted 14 May 2018
Supported by the National Natural Science Foundation of China(No.51679218, 51879239), the Program for Science & Technology Innovation Talents in Universities of Henan Province(No.17HASTIT031) and the Outstanding Young Talent Research Fund of Zhengzhou University(No.1521323001)
Biography: ZHANG Yan(1989—), male, E-mail:15136479128@163.com
*Corresponding author: DOU Ming, E-mail:douming@zzu.edu.cn
Abstract: In order to analyze the joint risk probability of eutrophication indexes in a small artificial lake, a marginal distribution of eutrophication indexes and a joint probability distribution of the copula function are established based on the basic principle of the copula function combined with the simulation results of a eutrophication model in Meihu Lake. The optimal copula functions were selected under different combinations by the fit test of copula function and the goodness of fit evaluation. The two-dimensional and three-dimensional joint risk probability of eutrophication indexes were calculated using the optimal copula functions. Results show that the joint risk probability varies substantially when the eutrophication indexes reach different states of eutrophication under different combinations; the maximum two-dimensional joint risk probability is 62.29% when the chlorophyll a and chemical oxygen demand (COD) reached the light eutropher, which indicates that this combination is likely to cause light eutropher in the Meihu Lake; the maximum three-dimensional joint risk probability is 45.46% when the chlorophyll a and COD reached the light eutropher, and the total nitrogen reached the middle eutropher, which indicates that this combination is likely to cause middle eutropher in the Meihu Lake; some two-dimensional and three-dimensional joint risk probability are small or even zero due to the impact of the monitoring series of the eutrophication indexes.
Keywords: copula functioneutrophicationjoint risk probability
1 引言(Introduction)富营养化是指生物生长所需营养物质大量进入水体中,以致水质严重恶化的一种现象(秦伯强等,2013).国内外对水体富营养化的形成、危害、评价及治理进行了一定的研究(Smith et al., 1999; Koelmans et al., 2001; Xu et al., 2001;Hullebusch et al., 2002),而水体富营养化评价主要是以相应的评价方法确定营养级别来说明水体的富营养化程度(王明翠等,2002;任黎等,2004;Lee et al., 2009;李如忠等,2014;尚佰晓等,2014),对于水体富营养化的组合风险概率问题的研究还相对较少.一些****利用累计概率密度模型对富营养化风险进行了预测分析(Biggs et al., 2000; Fitzpatrick et al., 2009; Azevedo et al., 2015;武暕等,2017);王霞等(2006)利用频率和累计频率分布对松花湖富营养化发生的概率进行了分析;范敏等(2010)提出来基于概率关系模型的水体富营养化风险分析建模方法;杨龙等(2010)运用水质模型模拟富营养化过程构建了富营养化风险评价方法体系;王起峰等(2010)利用Copula函数对太湖不同分区富营养化风险进行了评估;陈晶等(2011)建立了Copula函数的水体富营养化评价模型并得到各评价样本的综合评价指标值;王保栋等(2012)建立了一种以压力-状态-响应模式为基本框架、以富营养化症状为主的第2代近岸海域富营养化评价体系;Wang等(2012)利用Copula法分析了叶绿素a与环境变量之间的内在关系;以上研究主要以富营养化评价为基础,对评价整体结果或单个富营养化指标进行风险分析.Copula函数作为连接两变量或多变量分布的连接函数,可以将富营养化指标联合进行风险分析,其在洪水频率分析计算(肖义等,2007;冯平等,2013)、干旱特征分析(闫宝伟等,2007;陆桂华等,2010)、降雨频率分析计算(高超等,2013)、水质水量联合分析(张翔等,2011)及水生态环境稳态关系(李胜朋等,2009)等方面已有应用,总体上前期研究采用不同的方法对富营养化进行了分析评价,但利用Copula函数对富营养化风险概率方面的研究成果相对较少.本文以郑州大学人工湖-眉湖为研究对象,在富营养化模型模拟的基础上建立了水体富营养化指标的边缘分布函数和Copula函数联合分布,定量分析水体富营养化指标二维和三维的联合风险概率,为湖泊富营养化治理工作提供一定的依据.
2 研究方法(Research methods)本文首先在已建立眉湖水体富营养化模型的基础上(张彦等,2017),通过模拟得到眉湖水体富营养化指标(SD、Chl-a、TN、TP和COD)的模拟序列;其次利用模拟序列建立各指标相应的边缘分布,得到各水体富营养化指标标准限值的模拟频率,进而根据边缘分布函数计算水体富营养化指标二维和三维的联合分布概率;最后通过建立Copula联合概率分布,结合Copula函数拟合检验和拟合优度评价筛选出二维和三维联合概率分布最优的Copula函数,再依据最优的Copula函数定量分析水体富营养化指标二维和三维的联合风险概率.
2.1 边缘分布建立根据眉湖水体富营养化模型模拟的结果,得到水体富营养化指标的模拟序列{xn︱n=1, 2, …, N},N是模拟序列的个数.对于模拟序列{xn}中的任意一个样本值xm,如果模拟序列{xn}中小于xm的数目为Nm,那么可以把xm对应的累积频率表示为:
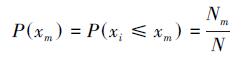 | (1) |
对于水质污染物来说,如果该污染物的状态变量为{xn},如给定的水体富营养化等级的控制限值为xk,则该污染物的超标风险可以表示为:
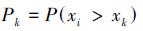 | (2) |
2.2 联合概率分布假设X、Y和Z分别表示水体富营养化事件中具有相互关系的指标序列,其边缘分布函数分别为u=F(x), v=F(y), w=F(z),则其二维和三维联合分布概率的表达式如下所示(宋松柏等,2012).
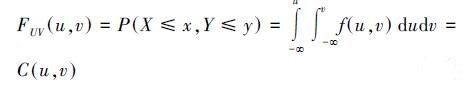 | (3) |
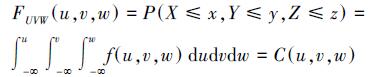 | (4) |
表 1(Table 1)
| 表 1 二维和三维Copula函数联合分布模型 Table 1 Two-dimensional and three-dimensional joint distribution models of the copula function | ||||||||||||||||||
表 1 二维和三维Copula函数联合分布模型 Table 1 Two-dimensional and three-dimensional joint distribution models of the copula function
| ||||||||||||||||||
其中,α为Frank Copula、Clayton Copula和Gumbel Copula函数中描述2个和3个变量相互关系的参数.ρ是对角线上的元素全为1的2阶和3阶对称正定矩阵,Φρ表示相关系数矩阵为ρ的二元和三元标准正态分布的分布函数,Φ-1表示标准正态分布的分布函数的逆函数;tρ, k表示相关系数矩阵为ρ,自由度为k的标准二元和三元t分布的分布函数,tk-1表示自由度为k的二元和三元t分布的分布函数的逆函数.
2.4 Copula函数拟合检验和拟合优度评价Copula函数的拟合度检验主要分析所选用的Copula函数是否合适,能不能恰当地描述变量之间的相关性.通过拟合检验的Copula函数可以根据拟合优度评价指标进行下一步的优选Copula模型,本文主要运用K-S检验统计量D进行Copula函数的拟合度检验.拟合优度评价是筛选Copula函数联合分布概率的重要的标准,常用的拟合优度评价方法主要有图形评价分析法、均方根误差法(RMSE)、赤池信息量准则法(AIC准则法)和贝叶斯信息准则法(BIC法),这些方法的原理和求解过程可参考相关文献(谢中华,2010;宋松柏等,2012),在此不再赘述.
3 应用研究(Application research)本文以郑州大学新校区人工湖——眉湖为研究对象,该湖是一个典型的人工景观湖泊,湖泊水面宽度30~60 m,湖长约为500 m,湖面面积约为2.2×104 m2.眉湖中配置了水循环系统,包括局部喷泉和上扬式曝气管循环和整体的南北循环.供水水源包括地下水和雨水两部分,并以地下水补给为主,雨水则来自处理过的贮存雨水.湖水分为北、中、南3段,中段较长且水流缓慢,北端地势较高,南端设有高低阶梯.2015年4—7月,在眉湖共进行了10次系统监测,采集了21个水样,监测指标包括光照强度、透明度(SD)、浊度、溶解氧(DO)、水温、叶绿素a(Chl-a)、藻类(PYT)、水深和流速,水样检测指标主要有化学需氧量(COD)、总磷(TP)、总氮(TN)、氨氮(NH3-N)和硝氮(NO3-N).同时水体富营养化模型的建立主要是以水动力模型和水质模型为基础,其结果主要是对水体富营养化指标(SD、Chl-a、TN、TP和COD)进行模拟分析(张彦等,2017).
3.1 边缘分布的建立通过已建立的水体富营养化模型模拟出水体富营养化指标(SD、Chl-a、TN、TP和COD)的模拟序列,得到水体富营养化指标模拟序列的经验频率分布,即5个水体富营养化指标模拟序列的理论频率分布.将5个频率分布作为水体富营养化指标的边缘分布,运用Copula函数建立5个水体富营养化指标的概率联合分布模型.水体富营养化指标的经验频率分布与计算频率分布的点拟合情况如图 1所示.
图 1(Fig. 1)
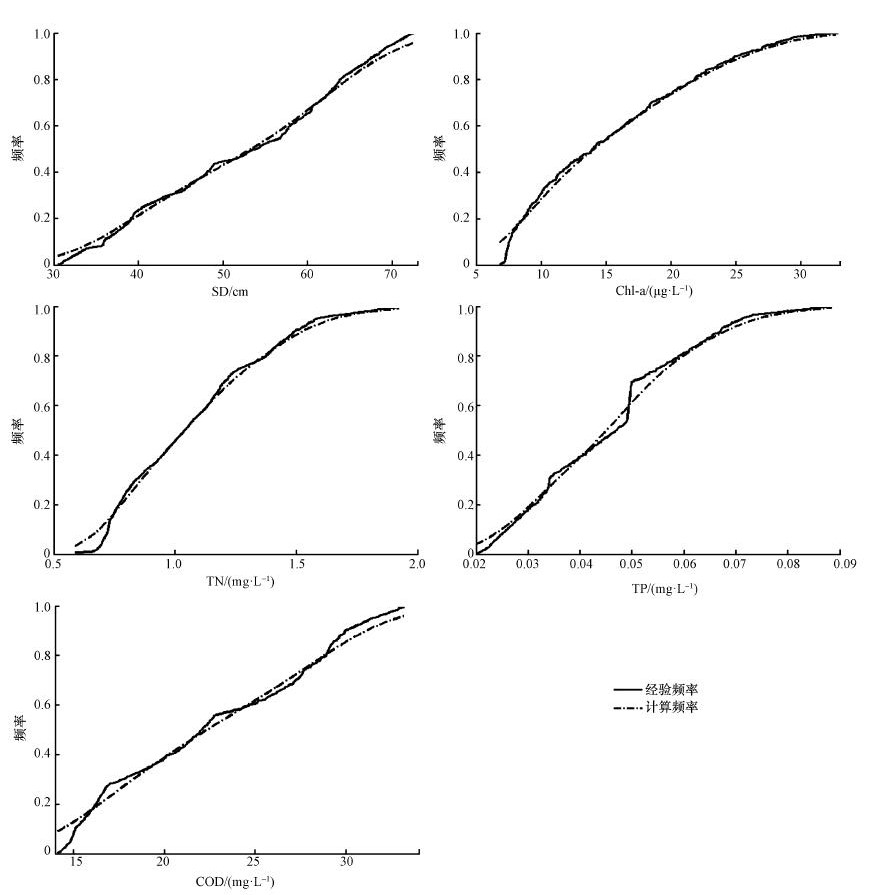 |
| 图 1 水体富营养化指标经验频率与计算频率的拟合情况 Fig. 1The fitting situations of the empirical frequency and calculated frequency of the eutrophication indexes |
结合目前我国湖泊各指标对应的营养状态分级标准的限值情况(表 2),依据水体富营养化指标的边缘频率分布情况,得到各水体富营养化指标标准限值的模拟频率如表 3所示,其中Chl-a、TP、TN和COD为累积频率,而SD为超越频率.
表 2(Table 2)
| 表 2 湖泊水质指标营养等级限值 Table 2 The limiting value of nutritional level for the water quality index of the lake | |||||||||||||||||||||||||||||||||||||||||
表 2 湖泊水质指标营养等级限值 Table 2 The limiting value of nutritional level for the water quality index of the lake
| |||||||||||||||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 湖泊水质指标营养等级的限值对应的累计频率 Table 3 The accumulative frequency of the limiting value of nutritional level for the water quality index of the lake | |||||||||||||||||||||||||||||||||||||||||
表 3 湖泊水质指标营养等级的限值对应的累计频率 Table 3 The accumulative frequency of the limiting value of nutritional level for the water quality index of the lake
| |||||||||||||||||||||||||||||||||||||||||
3.2 Copula函数的选择对眉湖水体富营养化指标SD、Chl-a、TN、TP和COD进行二维和三维组合,都有10种组合方式.由于Chl-a是体现水体中藻类生长的主要指标,TN和TP是藻类生长的主要营养物质,为了分析水体富营养化指标联合风险概率,本文选择对(TP, TN)、(Chl-a, SD)、(Chl-a, TP)和(Chl-a, COD)4种二维组合方式以及(Chl-a, TP, TN)、(Chl-a, TP, SD)、(Chl-a, TN, COD)和(TP, TN, COD)4种三维组合方式进行分析.同时首先利用Gaussian、Frank、Clayton和Gumbel 4种Copula函数对二维组合方式及利用Gaussian Copula和t-Copula函数对三维组合方式进行拟合检验,其次通过拟合优度评价筛选各组合方式适用的Copula函数.
3.2.1 拟合检验根据二维和三维Copula函数联合分布模型和水体富营养化指标模拟系列所得到的模拟频率,同时计算出各组合方式下不同Copula函数联合分布的统计量D,具体情况如表 4所示.取K-S检验的显著性水平α=0.02,n=350对应的分位点值为0.8178,从表 4中可以看出各组合方式下不同Copula函数联合分布的统计量D均小于0.8178,因此各组合方式均可运用对应的Copula函数模型进行计算.为了选择出各组合方式下最适合的Copula函数类型,故需要进行下一步的拟合优度评价.
表 4(Table 4)
| 表 4 各组合方式下不同Copula函数联合概率分布拟合检验统计量D Table 4 The fitting test statistics D of the joint probability distribution of the different copula functions under different combinations | ||||||||||||||||||||||||||||||||||||||||||||
表 4 各组合方式下不同Copula函数联合概率分布拟合检验统计量D Table 4 The fitting test statistics D of the joint probability distribution of the different copula functions under different combinations
| ||||||||||||||||||||||||||||||||||||||||||||
3.2.2 拟合优度评价根据二维和三维联合经验频率分布计算出各组合方式的经验联合频率值,结合二维和三维Copula函数联合分布模型计算各组合方式下的理论联合频率值,将二者绘制成散点图,如图 2和图 3所示.
图 2(Fig. 2)
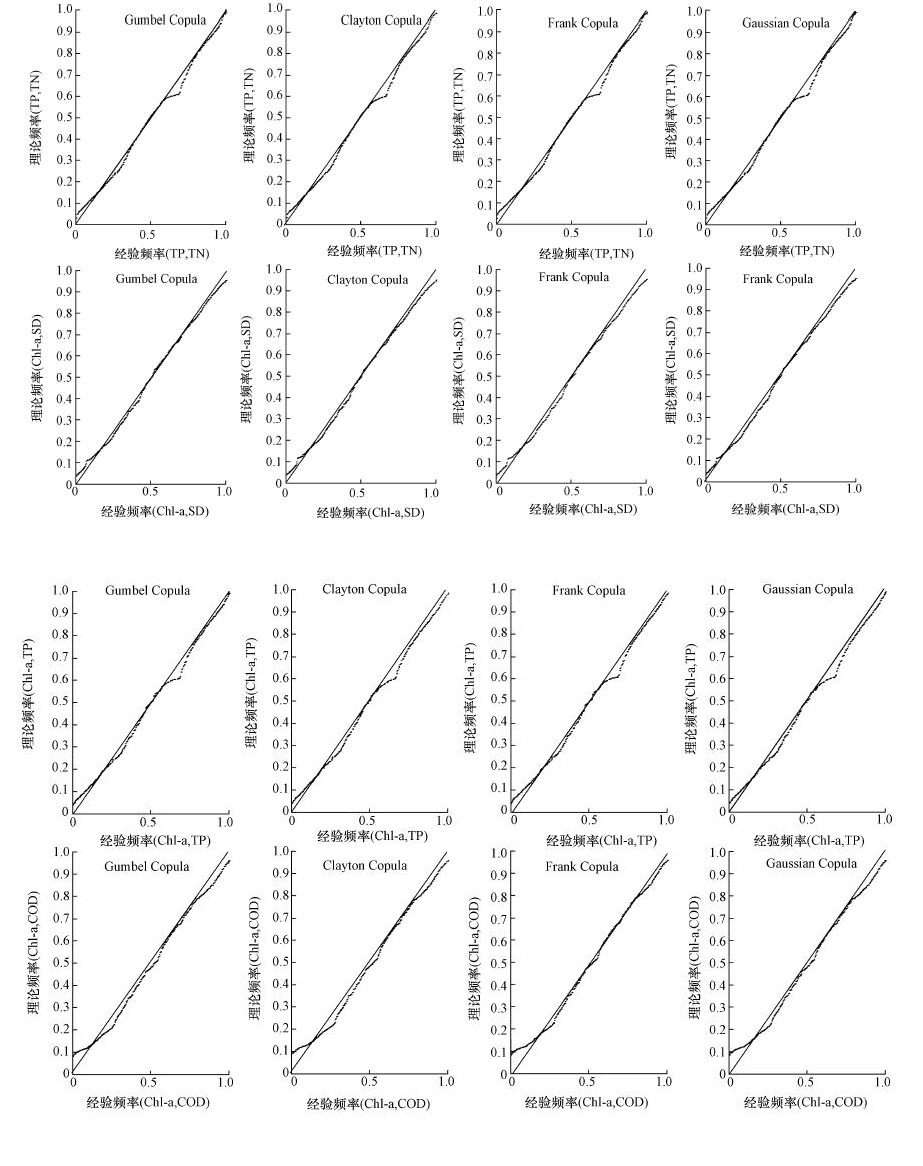 |
| 图 2 二维组合方式下理论联合频率与经验联合频率的拟合图 Fig. 2The fitting figure of the theoretic and empirical joint frequency under the two-dimensional combinations |
图 3(Fig. 3)
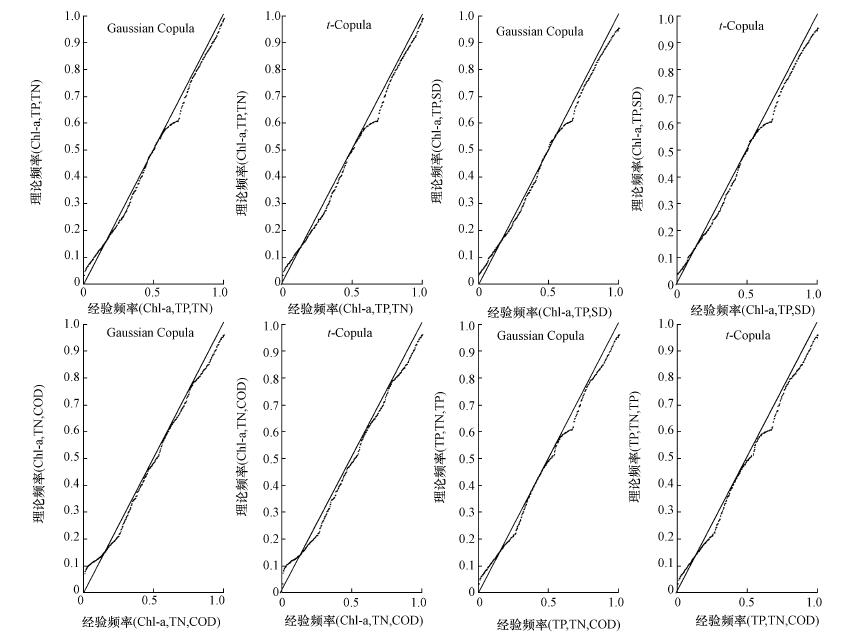 |
| 图 3 三维组合方式下理论联合频率与经验联合频率的拟合图 Fig. 3The fitting figure of the theoretic and empirical joint frequency under the three-dimensional combinations |
从图 2和图 3中可以看出,各组合方式下Copula函数的拟合效果均较好,单从直观上不易区分出各种Copula函数拟合效果的明显差别,为了定量的分析Copula函数理论联合频率值与经验联合频率值的拟合优劣程度,再利用均方根误差法(RMSE)、AIC准则法及BIC法对各Copula函数进行进一步的拟合优度评价,以确定各组合方式最优的Copula函数,其计算结果如表 5所示.
表 5(Table 5)
| 表 5 各种组合方式下不同Copula函数联合概率分布的拟合优度评价 Table 5 The goodness of fit evaluation of the joint probability distribution of the different copula functions under different combinations | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 5 各种组合方式下不同Copula函数联合概率分布的拟合优度评价 Table 5 The goodness of fit evaluation of the joint probability distribution of the different copula functions under different combinations
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
根据RMSE、AIC和BIC值越小,则Copula联合概率分布函数拟合的就越好的准则.从表 5中可以看出,对于二维组合方式(TP, TN)、(Chl-a, SD)和(Chl-a, TP),3种组合方式在Clayton Copula函数下,RMSE最小分别为0.0216、0.0176和0.0208,AIC最小分别为-2674.74、-2817.85和-2701.45,BIC最小分别为-2663.16、-2806.28和-2689.87,故这3种组合方式拟合效果最好的Copula函数为Clayton Copula函数;(Chl-a, COD)在Gumbel Copula函数下,RMSE最小为0.0278,AIC最小为-2499.26,BIC最小为-2487.68,(Chl-a, COD)拟合效果最好的Copula函数为Gumbel Copula函数.对于三维组合方式(Chl-a, TP, TN)、(Chl-a, TP, SD)、(Chl-a, TN, COD)和(TP, TN, COD),4种组合方式在Gaussian Copula函数下,RMSE最小分别为0.0217、0.0178、0.0253和0.0234,AIC最小分别为-2669.83、-2806.60、-2561.67和-2601.33,BIC最小分别为-2654.40、-2791.16、-2546.24和-2601.33,故这4种组合方式拟合效果最好的Copula函数为Gaussian Copula函数.因此选用拟合优度最好的Clayton Copula、Gumbel Copula和Gaussian Copula函数分别计算二维和三维水体富营养化指标的联合风险概率.
3.3 联合风险概率分析3.3.1 水体富营养化指标二维联合风险概率根据选取二维组合方式下拟合效果最好的Copula函数模型,对4种组合方式进行分析得到对应的组合方式下的联合分布函数,如图 4所示.
图 4(Fig. 4)
 |
| 图 4 各组合方式下二维Copula函数联合概率分布 Fig. 4The joint probability distribution of the two-dimensional copula functions under different combinations |
基于建立的Clayton Copula函数联合分布模型,对眉湖水体富营养化指标二维组合超标风险概率进行研究,选取4种组合方式的组合超标风险进行分析,具体的二维联合风险概率如表 6所示.
表 6(Table 6)
| 表 6 水体富营养化指标二维联合风险概率 Table 6 The two-dimensional joint risk probability of the eutrophication indexes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 6 水体富营养化指标二维联合风险概率 Table 6 The two-dimensional joint risk probability of the eutrophication indexes
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 6可知,当Chl-a和COD均为轻度富营养时二者的联合风险概率为62.29%,当TP为中营养、TN为中度富营养时二者的联合风险概率为51.76%,这两种状态下二者的联合风险概率均较大,说明眉湖水质在这两种状态下受到的影响较大;其次当Chl-a和SD均为轻度富营养时二者的联合风险概率为48.58%,当TP为中营养、Chl-a为轻度富营养时二者的联合风险概率为38.51%;而有些情况下二维联合风险概率较小,当TP为中营养、Chl-a为中度富营养时二者的联合风险概率为0.06%,当Chl-a轻度富营养、COD为中营养时二者的联合风险概率为0.02%,当Chl-a为中营养、SD为轻度富营养时二者的联合风险概率为0.01%,说明眉湖水质在这些状态下受到的影响较小.
3.3.2 水体富营养化指标三维联合风险概率基于建立的Gaussian Copula函数联合分布模型,对眉湖水体富营养化指标三维组合超标风险概率进行研究,选取4种组合方式的组合超标风险进行分析,具体的三维联合风险概率如表 7所示.
表 7(Table 7)
| 表 7 水体富营养化指标三维联合风险概率 Table 7 The three-dimensional joint risk probability of the eutrophication indexes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 7 水体富营养化指标三维联合风险概率 Table 7 The three-dimensional joint risk probability of the eutrophication indexes
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 7可知,当COD和Chl-a都为轻度富营养、TN为中度富营养时三者的联合风险概率为45.46%,当COD为轻度富营养、TN为中度富营养、TP为中营养时三者的联合风险概率为39.21%,这两种状态下三者的联合风险概率相对较大,说明眉湖水质在这两种状态下受到的影响较大;其次当Chl-a为轻度富营养、TP为中营养、TN为中度富营养时三者的联合风险概率为28.87%,当Chl-a和SD都为轻度富营养、TP为中营养时三者的联合风险概率为24.83%;而有些情况下三维联合风险概率较小,当Chl-a为中度富营养、TP和TN都为轻度富营养时三者的联合风险概率为2.71%,当COD为中度富营养、TN和TP都为轻度富营养时三者的联合风险概率为1.54%,当COD和Chl-a为中度富营养、TN为轻度富营养时三者的联合风险概率较小为1.54%,当Chl-a和TP都为中营养、SD为轻度富营养时三者的联合风险概率较小为0.02%,说明眉湖水质在这些状态下受到的影响较小.
综上所述,眉湖水体富营养化受到多种因素的多重影响,对于4种二维组合方式,当Chl-a和COD都为轻度富营养时联合概率最大为62.29%,说明这种组合方式下眉湖水体极易发生轻度富营养;对于组合(TP, TN),当TP富营养化程度一定时随着TN富营养化程度的增加二者的联合概率增大,而当TN富营养化程度一定时随着TP富营养化程度的增加二者的联合概率减小,说明组合(TP, TN)联合概率受到TN影响较大;对于组合(Chl-a, SD),当Chl-a为中营养时随着SD富营养化程度的增加二者的联合概率增大,而Chl-a为轻度富营养时随着SD富营养化程度的增加二者的联合概率减小,且SD出现了重度富营养状态.对于4种三维组合方式,当Chl-a和COD都为轻度富营养、TN为中度富营养时联合概率最大为45.46%,说明这种组合方式下眉湖水体极易发生中度富营养;对于组合(Chl-a, TP, TN),当Chl-a和TP富营养化程度一定时随着TN富营养化程度的增加三者的联合概率增大,当Chl-a和TN富营养化程度一定时随着TP富营养化程度的增加三者的联合概率减小;对于组合(TP, TN, COD),当TP和COD富营养化程度一定时随着TN富营养化程度的增加三者的联合概率增大,当COD为中营养或轻度富营养、TN富营养化程度一定时随着TP富营养化程度的增加三者的联合概率减小;对于组合(Chl-a, TN, COD),当Chl-a和COD富营养化程度一定时随着TN富营养化程度的增加三者的联合概率增大.而各种组合方式的联合概率较小甚至出现了联合概率为0的情况,这主要是因为监测数据系列相对较短,一些指标的监测数据过度的集中在一个富营养化状态范围内,故出现了以上的情况;为了更加精确合理的分析眉湖水体富营养化发生的联合风险概率,需要进一步的对眉湖进行监测增加数据系列.
4 结论(Conclusions)1) 结合眉湖水体富营养化模型模拟结果,在Copula函数基本原理下建立了水体富营养化指标的边缘分布和Copula函数的二维和三维联合概率分布.
2) 通过Copula函数拟合检验和拟合优度评价筛选出不同组合方式下最优的Copula函数,得到二维组合方式(TP, TN)、(Chl-a, SD)和(Chl-a, TP)拟合效果最好的Copula函数为Clayton Copula函数,(Chl-a, COD)拟合效果最好的Copula函数为Gumbel Copula函数;三维组合方式(Chl-a, TP, TN)、(Chl-a, TP, SD)、(Chl-a, TN, COD)和(TP, TN, COD)拟合效果最好的Copula函数为Gaussian Copula.
3) 根据计算出的不同组合方式下的二维和三维联合风险概率可知,不同组合方式下各水体富营养化指标达到不同富营养化状态时的联合风险概率区别较大,当Chl-a和COD都为轻度富营养时二维联合风险概率最大为62.29%,当Chl-a和COD都为轻度富营养、TN为中度富营养时三维联合风险概率最大为45.46%,受到监测系列的影响一些二维和三维联合风险概率较小甚至为零.
参考文献
| Azevedo L B, Zelm R V, Leuven R S E W, et al. 2015. Combined ecological risks of nitrogen and phosphorus in European freshwaters[J]. Environmental Pollution, 200(5): 85–92. |
| Biggs B J F. 2000. Eutrophication of streams and rivers:Dissolved nutrient-chlorophyll relationships for benthic algae[J]. Journal of the North American Benthological Society, 19(1): 17–31.DOI:10.2307/1468279 |
| 陈晶, 王文圣, 李跃清. 2011. Copula评价法及其在湖泊水质富营养化评价中的应用[J]. 四川大学学报(工程科学版), 2011, 43(增刊1): 39–42, 66. |
| 范敏, 石为人. 2010. 基于PRM的水体富营养化风险分析建模[J]. 计算机工程, 2010, 36(24): 261–263, 266.DOI:10.3969/j.issn.1000-3428.2010.24.094 |
| 冯平, 李新. 2013. 基于Copula函数的非一致性洪水峰量联合分析[J]. 水利学报, 2013, 44(10): 1137–1147. |
| Fitzpatrick J J. 2009. Assessing skill of estuarine and coastal eutrophication models for water quality managers[J]. Journal of Marine Systems, 76(1/2): 195–211. |
| 高超, 梅亚东, 涂新军. 2013. 基于Copula函数的区域降水联合分布与特征分析[J]. 水电能源科学, 2013, 31(6): 1–5. |
| Hullebusch E V, Deluchat V, Chazal P M, et al. 2002. Environmental impact of two successive chemical treatments in a small shallow eutrophied lake:Part Ⅱ Case of copper sulfate[J]. Environmental Pollution, 120: 627–634.DOI:10.1016/S0269-7491(02)00191-4 |
| 侯芸芸.2010.基于Copula函数的多变量洪水频率计算研究[D].杨凌: 西北农林科技大学http://cdmd.cnki.com.cn/Article/CDMD-10712-2010149892.htm |
| Koelmans A A, Van der Heijde A, Knijff L M, et al. 2001. Integrated modelling of eutrophication and organic contaminant fate and effects in aquatic ecosystems[J]. Water Research, 35(15): 3517–3536.DOI:10.1016/S0043-1354(01)00095-1 |
| Lee Y G, An K G, Ha P T, et al. 2009. Decadal and seasonal scale changes of an artificial lake environment after blocking tidal flows in the Yeongsan Estuary region, Korea[J]. Science of the Total Environment, 407: 6063–6072.DOI:10.1016/j.scitotenv.2009.08.031 |
| 李如忠, 刘科峰, 钱靖, 等. 2014. 合肥市区典型景观水体氮磷污染特征及富营养化评价[J]. 环境科学, 2014, 35(5): 1718–1726. |
| 李胜朋, 冯剑丰, 王洪礼. 2009. 基于Copula函数的海洋生态系统的稳态转换[J]. 天津大学学报, 2009, 42(6): 533–538. |
| 陆桂华, 闫桂霞, 吴志勇, 等. 2010. 基于copula函数的区域干旱分析方法[J]. 水科学进展, 2010, 21(2): 188–193. |
| 牛军宜.2010.供水枢纽工程水环境系统安全管理问题的研究[D].天津: 天津大学http://cdmd.cnki.com.cn/Article/CDMD-10056-1011266466.htm |
| 秦伯强, 高光, 朱广伟, 等. 2013. 湖泊富营养化及其生态系统响应[J]. 科学通报, 2013, 58(10): 855–864. |
| 任黎, 董增川, 李少华. 2004. 人工神经网络模型在太湖富营养化评价中的应用[J]. 河海大学学报, 2004, 32(2): 147–150.DOI:10.3321/j.issn:1000-1980.2004.02.006 |
| Smith V H, Tilman G D, Nekola J C. 1999. Eutrophication:impacts of excess nutrient inputs on freshwater marine and terrestrial ecosystems[J]. Environmental Polution, 100: 179–196.DOI:10.1016/S0269-7491(99)00091-3 |
| 尚佰晓, 王莉, 王爽, 等. 2014. 铁岭莲花湖水体富营养化评价[J]. 湿地科学, 2014, 12(1): 97–101. |
| 宋松柏, 蔡焕杰, 金菊良, 等. 2012. Copula函数及其在水文中的应用[M]. 北京: 科学出版社. |
| 王保栋, 孙霞, 韦钦胜, 等. 2012. 我国近岸海域富营养化评价新方法及应用[J]. 海洋学报, 2012, 34(4): 61–66. |
| 王明翠, 刘雪芹, 张建辉. 2002. 湖泊富营养化评价方法及分级标准[J]. 中国环境监测, 2002, 18(5): 47–49.DOI:10.3969/j.issn.1002-6002.2002.05.018 |
| 王起峰, 王春阳, 王勇. 2010. 基于Copula函数与经验频率曲线的富营养化风险分析[J]. 安徽农业科学, 2010, 38(30): 17037–17039.DOI:10.3969/j.issn.0517-6611.2010.30.122 |
| 王霞, 吕宪国, 白淑英, 等. 2006. 松花湖富营养化发生的阈值判定和概率分析[J]. 生态学报, 2006, 26(12): 3989–3997.DOI:10.3321/j.issn:1000-0933.2006.12.009 |
| Wang Y K, Ma H Q, Sheng D, et al. 2012. Assessing the interactions between chlorophyll a and environmental variables using Copula method[J]. Journal of Hydrologic Engineering, 17(4): 495–506.DOI:10.1061/(ASCE)HE.1943-5584.0000387 |
| 武暕, 冯承莲, 李延东, 等. 2017. 桓仁水库富营养化风险预测预警[J]. 环境工程, 2017, 35(4): 125–128. |
| Xu F L, Tao S, Dawson R W, et al. 2001. Lake ecosystem health assessment:Indicators and methods[J]. Water Research, 35(13): 3157–3167.DOI:10.1016/S0043-1354(01)00040-9 |
| 肖义, 郭生练, 刘攀, 等. 2007. 基于Copula函数的设计洪水过程线方法[J]. 武汉大学学报(工学版), 2007, 40(4): 13–17. |
| 谢中华. 2010. MATLAB统计分析与应用:40个案例分析[M]. 北京: 北京航空航天大学出版社: 187–213. |
| 闫宝伟, 郭生练, 肖义, 等. 2007. 基于两变量联合分布的干旱特征分析[J]. 干旱区研究, 2007, 24(4): 537–542. |
| 杨龙, 王晓燕, 王子健, 等. 2010. 基于磷阈值的富营养化风险评价体系[J]. 中国环境科学, 2010, 30(Suppl.): 29–34. |
| 张翔, 冉啟香, 夏军, 等. 2011. 基于Copula函数的水量水质联合分布函数[J]. 水利学报, 2011, 42(4): 483–489. |
| 张彦, 窦明, 李桂秋, 等. 2017. 考虑光盐交互作用的湖泊富营养化数学模型[J]. 中国环境科学, 2017, 37(11): 4312–4322.DOI:10.3969/j.issn.1000-6923.2017.11.037 |