,1,2, 王武,1,*, 姜金荣,1, 赵莲,1Implementation of Parallel FMM Based on Charm++
Ding Lei,1,2, Wang Wu,1,*, Jiang Jinrong,1, Zhao Lian,1通讯作者: 王武（E-mail：wangwu@sccas.cn）
收稿日期:2020-02-19网络出版日期:2020-06-20
| 基金资助: |
Received:2020-02-19Online:2020-06-20
作者简介 About authors
丁磊,中国科学院计算机网络信息中心,硕士研究生,主要研究方向为高性能计算、并行计算。
本文承担工作为：移植与负载均衡方案设计,代码实现,结果测试。
Ding Lei is a master student at Computer Network Information Center of Chinese Academy of Sciences. His main research interests are high performance computing and parallel computing.
In this paper he undertakes the following tasks: design, implementation and test of the load balance strategy.
E-mail:
王武,中国科学院计算机网络信息中心,博士,副研究员,研究方向为并行算法,高性能计算。
本文承担工作为：FMM与N-body开发指导。
Wang Wu, Ph.D., is an associate research fellow at Computer Network Information Center, Chinese Academy of Sciences. His main research interests are parallel algorithm and high performance computing.
In this paper, he is the execution director of implementation of FMM and N-body simulation.
E-mail:
姜金荣,中国科学院计算机网络信息中心,博士,研究员,主要研究方向为并行算法与框架软件、计算地球科学。
本文承担工作为：整体方案设计指导。
Jiang Jinrong is the research fellow at Computer Network Information Center of Chinese Academy of Sciences. His main research interests are parallel computing algorithms and frameworks.
In this paper he undertakes the following tasks: design of general implementation.
E-mail:
赵莲,中国科学院计算机网络信息中心,助理研究员,博士,主要研究方向为高性能计算、并行计算。
本文承担工作为：Charm++开发指导。
Zhao Lian, Ph.D., is an assistant research fellow at Computer Network Information Center of Chinese Academy of Sciences. Her main research interests are high performance computing and parallel computing.
In this paper she directed the code implementation of Charm++.
E-mail:
摘要
【目的】为了利用Charm++的过分解与运行时迁移特性,提高FMM的并行执行效率,本文在Charm++上完成了FMM的并行实现。【方法】通过分析通信、并行任务分解、异步调用转化,采用SDAG实现了基本通信函数,并利用LPT近似策略达到了负载均衡,最终实现了并行FMM。【结果】测试结果表明,FMM的Charm++实现的计算精度与MPI实现完全相同,在千核规模上的执行速度优于MPI实现。过分解与负载均衡策略在粒子分布不均的情况下减少了10%的运行时间。【局限】目前的实现没有利用Charm++共享内存的结构,仍有优化的空间,负载均衡策略较为简单。【结论】本文给出了一个较为通用的MPI风格程序向Charm++转化的策略,并证明了Charm++的过分解与负载均衡策略对FMM有加速效果。
关键词：
Abstract
[Objective] This paper has implemented a parallel FMM based on Charm++ to take advantage of its over-decomposition and migratability. [Methods] It is achieved by analyzing communication, separating parallel tasks, and converting synchronous communication to asynchronous communication. Also, the SDAG was used to implement the basic communication calls and the LPT approximation strategy was adopted for dynamic load balancing. [Results] The results show that the implementation of parallel FMM based on Charm++ has the same accuracy as that of MPI implementation, and its execution speed on the thousand-core scale is better than that of MPI implementation. Over-decomposition and load-balancing strategy contribute to the execution time reduction by 10% in the unbalance particle distribution. [Limitations] The current implementation does not use the shared memory structure of Charm++ and needs further optimizations. Besides, the load balancing strategy is simple. [Conclusions] This paper gives a relatively general method to convert the MPI style programs to Charm++ style ones and proves that over-decomposition and load-balancing strategy can accelerate FMM execution.
Keywords：
PDF (8609KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
丁磊, 王武, 姜金荣, 赵莲. 基于Charm++的并行FMM实现. 数据与计算发展前沿[J], 2020, 2(3): 101-112 doi:10.11871/jfdc.issn.2096-742X.2020.03.009
Ding Lei, Wang Wu, Jiang Jinrong, Zhao Lian.
引言
N体问题[1]（N-body problem）是已知多个粒子的初始位置、速度和质量,求解出其在经典力学下的后续运动的问题,属于高性能数值计算的七类典型应用之一[2],在宇宙学模拟[3]、分子动力学研究[4]等诸多领域有十分重要的应用。常用的N体求解方法有直接法[5]（Particle-Particle, PP）、粒子-网格法[5]（Particle-Mesh, PM）、树方法[6]（Barnes-Hut, BH）、快速多极子方法[7]（Fast Multipole Method, FMM）等。FMM采用长程力近似计算方式,基于树结构的多层递归盒子划分策略,使用核心函数的级数展开,将远程力的作用近似为粒子与盒子的作用及盒子间的作用,极大降低了场中粒子相互作用的计算复杂度。由于可以指定划分的层数和展开阶数,FMM能有效平衡执行时间与计算误差[8]。与BH相比,FMM基于高阶展开,因此精度可以达到更高,同时可以控制计算量。
近年来,国内外有许多FMM相关研究与应用成果。如曹小林[9]等基于JASMIN框架实现了FMM的求解器;Cruz[10]等基于PETSc框架实现了PetFMM 软件;Winkel[11]等基于MPI实现了N体计算软件PEPC。随着异构系统的不断发展,****开始针对特定体系结构进行研究。Lashuk[12]等使用256块GPU在NCSA Lincoln cluster上对KIFMM进行加速;Yokota[13]等在TSUBAME 2.0系统上使用4096块GPU来计算各向同性湍流;王武[14]等基于申威众核处理器进行FMM优化。此外,还有基于FMM-PM方法在GPU上进行N体模拟实现[15]等。
Charm++是一种基于消息驱动的编程框架,具有过分解（Over-decomposition）、可迁移（Migratability）、
异步消息驱动（Asynchronous Message-Driven Execution）等特点,可以提供运行时的动态负载均衡与容错机制[16]。近年来,有许多工作利用Charm++的动态负载均衡特性,取得了不错的效果。如中国科学院计算机网络信息中心研发的并行框架SC_Tangram[17]、基于Charm++的非结构网格[18]等。本文中,我们将基于Charm++实现FMM程序的并行化,并与MPI版本的并行实现进行对比分析,结果表明整体性能有10%左右的提升。
1 并行FMM介绍
1.1 FMM的计算流程
FMM是一种区域划分的计算方法,其核心思路在于对位势函数在远场进行多极展开,再将多极展开转化为近场的局部展开,继而通过位势计算出粒子在引力场所受到的作用力。FMM使用球坐标的多极展开来近似多个粒子形成的引力场对外界的作用,用局部展开来近似外界引力场对区域内粒子的作用,包括P2M、M2M、M2L、L2L、L2P、P2P六个计算步骤。
下列公式中,$\alpha $、$\beta $、$\rho $分别表示球坐标的极角、方位角与径向距离,${{\text{m}}_{i}}$为粒子质量。P为展开阶数,球谐展开中的系数m、n与P正相关。
（1）P2M (Particle to Multipole Expansion)
P2M操作只发生在计算区域的最底层,也就是最小的盒子区域内。主要的思想是根据盒子里面的粒子位置,计算出这个盒子的多极展开系数。
P2M的计算方法如下[19]：
$M_{n}^{m}=\sum\limits_{i=1}^{k}{{{m}_{i}}\cdot \rho _{i}^{n}\cdot Y_{n}^{-m}({{\alpha }_{i}},{{\beta }_{i}})}$
其中,k为盒子中的粒子数, $M_{n}^{m}$是多极展开系数,$Y_{n}^{m}(\theta ,\phi )$是球谐函数,计算公式为：
$Y_{\text{n}}^{m}\left( \theta ,\varphi \right)=\sqrt{\frac{\left( n-\left| m \right| \right)\ !}{\left( n+\left| m \right| \right)\ !}}P_{n}^{\left| m \right|}\left( \cos \theta \right){{e}^{im\varphi }}$
式中$P_{\text{n}}^{{}}\left( x \right)$为Legendre多项式。
（2）M2M (Multipole Expansion to Multipole Expansion)
M2M操作的计算方法如下[19]：
其中,$M_{j}^{k}$是转移中心之后的多极展开系数,$O_{j}^{k}$是下一层盒子的多极展开系数。
M2M是一个自下向上的过程,不断地收集下层的多极展开系数,计算本层的多极展开系数,再到更高一层进行计算。
（3）M2L (Multipole Expansion to Local Expansion)
P2M操作与M2M只进行多极展开系数的计算,目的是计算出盒子对空间的作用效果。而M2L操作是计算相互作用。
M2L是一个多极展开转化为局部展开的过程,计算方法如下[19]：
$L_{j}^{k}=\sum\limits_{n=0}^{\infty }{\sum\limits_{m=-n}^{n}{\frac{O_{n}^{m}\cdot {{i}^{\left| k-m \right|-\left| k \right|-\left| m \right|}}\cdot A_{n}^{m}\cdot A_{j}^{k}\cdot Y_{j+n}^{m-k}(\alpha ,\beta )}{{{(-1)}^{n}}A_{j+n}^{m-k}\cdot {{\rho }^{j+n+1}}}}}$
其中,$L_{j}^{k}$为局部展开系数,$O_{n}^{m}$为多极展开系数。
在计算M2L的过程中,需要找到当前盒子的次相邻盒子,即与当前盒子不相邻,但是父盒子与当前盒子的父盒子相邻的盒子。根据这些盒子的多极展开系数,计算出局部展开系数。
（4）L2L (Local Expansion to Local Expansion)
L2L的计算公式如下[19]：
$L_{j}^{k}=\sum\limits_{n=j}^{P}{\sum\limits_{m=-n}^{n}{\frac{{\mathrm O}_{n}^{m}\cdot {{i}^{\left| m \right|-\left| m-k \right|-\left| k \right|}}\cdot A_{n-j}^{m-k}\cdot A_{j}^{k}\cdot Y_{n-j}^{m-k}(\alpha ,\beta )\cdot {{\rho }^{n-j}}}{{{(-1)}^{n+j}}\cdot A_{n}^{m}}}}$
其中,$L_{j}^{k}$为局部展开系数,$O_{n}^{m}$为局部展开系数。
L2L是一个与M2M相反的过程,完成了相互作用的中心转移。在M2L中只考虑了本层的相互作用,那些来自父盒子的作用力是通过L2L来计算。这样,就可以计算出来自非邻居盒子的作用。
（5）L2P (Local Expansion to Particle)
L2P是P2M的逆过程。经过L2L操作后,已经在最底层盒子中获取来自非邻居盒子的作用,而L2P就是把这些局部展开系数转为盒子中粒子所受到的作用力。
L2P的计算公式如下[19]：
$\Phi (P)=\sum\limits_{j=0}^{P}{\sum\limits_{k=-j}^{j}{L_{j}^{k}\cdot Y_{j}^{k}(\theta ,\varphi )\cdot {{r}^{j}}}}$
（6）P2P (Particle to Particle)
由于近似计算需要两个区域有一定的距离,无法使用近似的方式求解出最底层盒子来自邻居盒子的作用力。因此,只能依照万有引力公式,求解出邻居盒子中粒子的作用力。
1.2 并行FMM算法
FMM的并行分解即为空间分解。如算法1所示,每个并行单元负责一个区域,在区域中按照预定分布初始化全局粒子的位置,通过partition操作将粒子划分给处理区域,并依照希尔伯特编码建立树。此后执行粒子到盒子以及盒子到盒子的P2M和M2M操作,获得多极展开系数。算法1
算法1并行FMM
 |
新窗口打开|下载CSV
鉴于P2P操作和M2L操作需要了解相邻和次相邻盒子的信息,需要进行一次全局通信,将这些信息保存在本地关建树（local essential tree）中。最终执行树的自上而下的遍历,完成L2L与L2P操作。因此,在并行FMM中需要进行两次全局通信,分别发生在partition和local essential tree处。
2 Charm++介绍
Charm++是基于C++的面向对象并行编程框架,由UIUC并行编程实验室开发,具有过分解、可迁移、异步消息驱动的特点[20]。过分解指并行计算对象的数量多于实际的处理器数量。可迁移指并行计算对象可以在处理器间移动,完成动态负载均衡。异步消息驱动指每个处理器上的并行对象的执行流由消息驱动,计算对象间的消息传递采用异步方式,不阻塞执行流。Chare是Charm++的基本计算单元,其本质是分布在不同的处理器上的C++对象。代理（Proxy）是一种特殊的C++对象,用以表示一个远程的Chare。Chare间的通信通过调用代理的特殊成员方法来实现,由Runtime负责将本次调用的参数封装成消息,并发送到对应的远程Chare,该过程通常被称为远程调用。
Charm++提供了Chare array、group、node group等并行数据结构。其中,Chare array提供一个统一的代理,每个array的成员Chare都有一个thisIndex,可以通过proxy[someIndex]来调用编号为someIndex的Chare上的方法。
PUP (Pack and Unpack) 框架是Charm++提供的序列化框架,负责远程调用和Chare迁移时的序列化工作。
PE (Processing Element) 和Node是Charm++的抽象概念。其中PE是Chare的执行实体,其上有许多Chare和消息。Node由多个PE组成,是一种共享内存的抽象表达。Node上的不同Chare共享Node的地址空间。在实现上,PE一般对应线程,而Node对应于进程。
Charm++的各种实体概念如图1所示。
图1
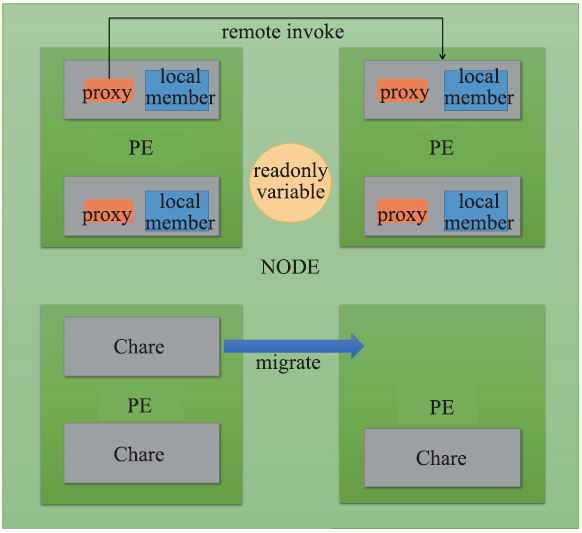新窗口打开|下载原图ZIP|生成PPT图1Charm++ 概念示意图
Fig.1Charm++ concept diagram
Charm++的项目由ci (Charm++ interface) 文件和C++源码构成。其中ci文件定义了Charm++中的Chare、message、module等实体。预处理系统解析ci文件后生成对应头文件和实现文件,使用者需要在C++源码中引入这些文件。
Charm++不支持全局可变变量,但支持全局只读变量。只读变量在ci文件中使用readonly关键字引入,在mainChare的构造函数中进行初始化。
每个PE上都有一个消息队列。以PE的视角看,有一个执行流不断从队列中取出消息。如果消息是种子,将创建新的Chare。如果消息是远程调用,则找到PE上对应的Chare,将消息解包并调用。在调用过程中可能会产生新的种子和远程调用,由Runtime决定新消息对应的PE。
因此,Chare间的消息传递是异步的方式。调用者只知道消息在队列里,但不清楚消息是否已被执行,即调用者无法立即获得执行的结果。使用者可以定义一个远程方法供接收方调用,并在这个远程方法中获取通信结果,执行后续操作。这种风格使代码杂乱且易错。为了方便表示执行流的依赖关系,Charm++提供了SDAG[21] (structure dagger) 表示方法。
SDAG的语法采用 <keyword> { } 模式,其中<keyword>有when、serial等。serial用于表示一段完整执行的不被抢占的代码。when表示等待消息,如 when method (arg) {serial {do_something (arg) }} 表示当前执行流等待远程方法method被调用,并在该条件触发后执行do_something操作。
Charm++预处理器会分析ci文件中的SDAG语法,并生成对应的代码,将SDAG语句块拆分成许多continuation函数,即多个阶段。以when语句为例,Runtime会在method被触发后,调用下一个阶段对应的continuation。这样使用者无需自行编写等待、判断以及跳转的远程方法。
3 并行实现
3.1 任务分解与预处理
在本文中,我们定义一个名为master的mainChare作为并行任务的发起者和规约消息的接收者,定义一个名为slave的一维Chare array,作为基本的并行计算单元。鉴于Chare需要在PE上执行,而且存在运行时迁移的情况,我们将原始的全局变量保存在slave 的成员中,并以参数的方式传递进去。
对于计算开始前已知且只读的全局变量,使用Charm++提供的readonly变量表示,并在master中进行初始化。
3.2 异步通信转化
Charm++采用异步通信的方式,这使得通信的发起方无法了解到消息是否被接收。在MPI中,我们可以在一个函数中发起多次通信。对于阻塞通信,操作系统会将函数的实参和局部变量保存在栈中,等到通信结束后再进行调度;对于非阻塞通信,程序中有循环代码对通信结束条件进行判断,控制流始终在该函数中。在Charm++中,用户只能通过消息驱动来触发后续操作,这意味着通信发起时,我们就失去了局部变量和实参的内存分配。为了恢复状态,需要将跨越通信的实参和局部变量保存到Chare的成员中。
针对通信函数XXmethod,我们引入结构体XXmethod_param来保存这些信息。考虑到实参的初始化有传值和传引用的方式,我们只在结构体里保存变量地址。对于传值的方式,需要引入init_XX_by_value来动态分配内存并保存;对于传引用的方式,引入init_XX_by_ref,来保存已有变量的值,并提供一个release方法用于释放值初始化时分配的空间。
另一方面,某个通信函数可能被调用多次,结束后跳转到不同的执行流。为了保证通信结束后函数的正常驱动,我们需要保存通信结束后的下一步执行的位置。
本文中,我们将需要通信的函数设置为slave的成员函数,并根据通信将程序划分为多个state。在slave的成员变量中,使用一个栈来保存通信结束后下一步执行的函数指针以及state值。通过set_continuation来将函数指针和state压栈,do_continuation来将函数指针和state出栈,并调用该函数。在每个state开始时,我们取出函数中需要用到的局部变量和实参。在第一个state的时候对局部变量进行初始化。实参的初始化发生在函数的调用处。
图2是一个MPI风格的通信函数示例,在Some-Method函数中,有全局通信global_communication。其中有实参parameter,有局部变量local_variable,这些变量都要跨越通信的。
图2
新窗口打开|下载原图ZIP|生成PPT图2MPI 风格示例通信函数
Fig.2Example of communication in MPI style
图3是对应的Charm++表达方式。全局通信将SomeMethod分成了两个部分。state是Chare array的成员变量,用于标识当前处理的状态。CharmSome-Method_param是我们针对通信函数CharmSome-Method引入的结构体,其中保存了该函数执行时需要的实参parameter、局部变量local_variable。
图3
新窗口打开|下载原图ZIP|生成PPT图3Charm++风格示例通信函数
Fig.3Example of communication in Charm++ style
在state为0的时候,我们调用set_continuation函数来指定在本次通信后需要执行的函数为Charm-SomeMethod的下一个state,并调用init_XX_by_value来为局部变量分配内存。实参parameter的初始化发生在CharmSomeMethod被调用处。此后,我们通过CharmSomeMethod_param获得parameter和local_variable,并执行串行操作do_some_serial_job_1。鉴于通信函数global communication需要传入local_variable的引用,这里我们对global_communication_param使用init_XX_by_ref进行初始化,记录local_variable的地址。在执行完global_communication通信后,执行流到了CharmSomeMethod的state1,再一次从CharmSomeMethod_param中获得parameter和local_variable变量,执行串行操作do_some_serial_job_2。由于该函数已经执行到最后,可以释放CharmSome-Method_param中的空间,并调用do_continuation,获取之前保存的下一步执行的函数和state。global_communication内部实现与CharmSomeMethod类似。
本文只对最基本的通信函数使用SDAG。这样对于调用层数较深处发生的通信,只需要提供基本通信的实现,无需将所有包含通信的函数都改写成SDAG风格,可以较大程度减少代码修改量。至此,除基本通信函数外,所有的MPI风格的同步通信逻辑都可以转化为Charm++异步通信的表示,且用户修改部分较少。
基本通信函数的实现将在下一节中介绍。
3.3 基本通信的实现
并行FMM的通信发生在partition 和local essential tree操作中,包括基本通信Alltoallv与Allreduce。Alltoallv需要每个并行计算单元向其它并行计算单元发送不等长的消息,同时从其它并行计算单元中接收这些不等长的消息。Allreduce需要对所有并行单元的某个参数进行规约。
在Charm++中,使用message比参数序列化快[22],而且用户无需过多了解序列化知识。我们针对不同的类型,定义了对应的message类型,如图4所示。其中,data保存信息的本体,size表示消息的大小,from表示消息的发送者。
图4
新窗口打开|下载原图ZIP|生成PPT图4message 类型的定义
Fig.4Defination of message
在实现Alltoallv时,我们使用结构体来保存整个通信过程需要用到的变量。在serial语句块中,每个Chare构造消息并发送,同时触发等待消息的when语句块,从消息中取出数据,放到缓冲区中。Alltoallv的实现如伪代码1所示,其中param保存了alltoalv调用时的参数,thisProxy指Chare array的代理,通过这个代理向自己发送消息。
伪代码 1
伪代码 1Alltoallv 的 Charm++实现
 |
新窗口打开|下载CSV
Allreduce的实现包括规约和广播。首先在slave上获取到所有的规约数据,指定master 的处理函数来做规约。在规约结束后,master 发布广播消息,触发slave的when语句,master和slave的实现过程见伪代码2与伪代码3。
伪代码2
伪代码2Allreduce在slave上的实现
 |
新窗口打开|下载CSV
伪代码3
伪代码3Allreduce在master上的实现
 |
新窗口打开|下载CSV
3.4 负载均衡与迁移策略
大规模分布式并行系统上动态负载均衡,可以分成分布式、集中式和层次式三种[23]。分布式策略只考虑相邻处理器,如Cybenko[24]等给出了扩散算法的一般化形式,处理器从高负载处理器中获取负载,并把负载给低负载处理器。Hui[25]等提出了基于水动力学的负载均衡,利用水的连通性特性来控制负载均衡。
集中式策略考虑全局负载,将信息集中到一个处理器上进行计算。如全局随机指派[26],贪心方法[26]等。
层次式负载均衡策略根据拓扑结构建立层次树。如HBM[27]根据网络结构将处理器划分成多个组,在层次结构的每一层都执行负载均衡迁移,直到根节点为止。
Charm++提供了在运行时移动Chare的方法,使得处理器上的负载可以进行动态调节。本文中,我们利用MigrateMe函数,使用集中式负载均衡策略,在运行时对slave的Chare进行迁移。
图5是负载均衡的实现时序图。slave在某个阶段将自己包含的粒子信息发送到master上。master负责对这些信息进行分析,经由负载均衡策略给出一个Chare的重新分布,并依次通知相应的Chare。这些Chare调用MigrateMe函数来移动到新的PE上,并向master汇报迁移的结束。master收到所有的迁移结束消息后,向slave发起一个广播,使其继续执行计算。
图5
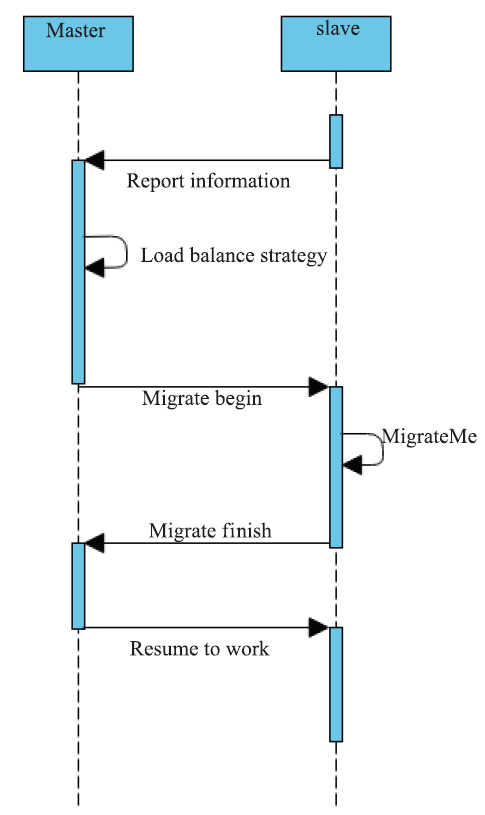新窗口打开|下载原图ZIP|生成PPT图5负载均衡时序图
Fig.5Sequence Diagram of load balance
本文中,负载均衡的执行时期为partition结束时,此时所有的Chare都已经拿到自己负责处理的粒子。为了简化负载均衡的实现逻辑,我们假设所有的处理器都是相同性能,仅考虑PE的计算负载,并用PE上的总粒子数来近似。
该负载均衡问题被称为相同并行机调度（Identical Parallel-Machine Scheduling）问题,属于NP-hard问题[28]。本文中,我们采用最长处理时优先策略（Longest Processing Time,LPT）来求解,简述如下：
(1)将Chare按照粒子数量从大到小排序
(2)依次将Chare指派到当前粒子总数最少的PE上。
该策略可以达到4/3近似[28],即对于该问题的所有情况,近似策略都能给出最优解4/3倍以内的可行解。
3.5 实现技术
上述message、Alltoallv、Allreduce等需要针对不同类型实现。此外,对于每个通信函数,都需实现一个XX_param的结构体,其成员函数需要覆盖到在通信中使用到的变量,且应当区分by_value和by_ref。在通信函数的最开始部分,都需要获得全部的XX_param结构体成员。这些代码都是相似的,可以使用脚本语言生成。本文将需要生成的类型参数写成json的格式,通过Python脚本解析,基于模板自动生成了message、基础通信函数、XX_param结构体的C++代码片段和宏定义。在并行FMM源码中只需在对应的地方引入这些宏定义即可,无需大量修改源码。
主要的实现流程包括：
(1)全局变量局部化;
(2)基于通信划分state;
(3) Python脚本生成C++代码片段;
(4)调整通信函数内部风格;
(5)在通信函数中引入XX_param等代码。
4 数值结果
以下测试均在中国科学院计算机网络信息中心超级计算机“元”上进行测试。每台刀片计算节点配置 2 颗 Intel E5-2680 V2（Ivy Bridge | 10C | 2.8GHz）处理器,64 GB DDR3 ECC 1866MHz 内存。编译环境为Intel Composer XE 2013编译器,Charm++ 版本为6.6.1,编译时使用-O3优化选项和C++0x标准。4.1 正确性检验
为了验证FMM的Charm++实现正确性,我们选择了不同分布与参数进行测试,比较了Charm++与MPI下每个粒子的受力值,结果完全一致,这表明我们的计算精度和已有的MPI实现的精度相同。4.2 性能检验
以16384万个粒子为例,采用均匀的立方体分布作为粒子的初值分布,分别对MPI和Charm++实现进行测试,保证Chare数量和PE数量相等（即不使用过分解）,结果如图6所示。可以看出,随着处理器规模从32核增加到1024核,两种实现的速度基本接近,Charm++实现相比MPI实现在千核规模上有提升。图6
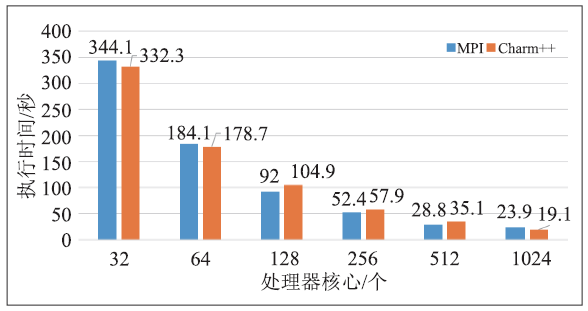新窗口打开|下载原图ZIP|生成PPT图616384 万粒子的执行时间
Fig.6Execution time of 163,840,000 particles
在上述测试中,以32核规模的执行时间作为基准,计算了Charm++和MPI版本的加速比,结果如图7所示。可以看出,与理想情况相比,FMM的Charm++实现在256核以下的强扩展性能较好。随着核数增加到千核规模,全局通信会扩大,扩展性有一些下降。与MPI实现相比,Charm++实现在1024核规模的加速效果较好,但在64核至512核规模的加速效果较为逊色。这一现象是因为千核规模下,通信占比增大,而MPI实现使用全局通信,在partition阶段的通信时间远大于使用点对点通信的Charm++实现。
图7
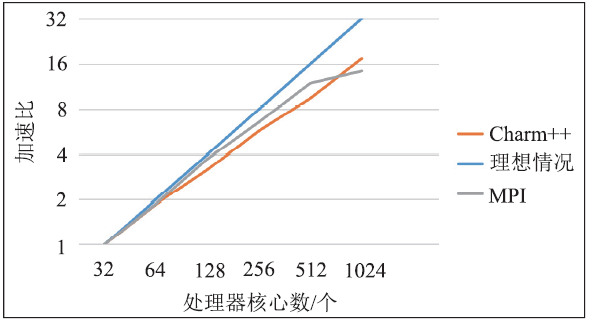新窗口打开|下载原图ZIP|生成PPT图7并行 FMM 的加速比
Fig.7Speedup ratio of different implementations
为了验证过分解对负载不均衡情况的优化效果,本文针对65536万粒子的球壳状不均匀分布,固定处理器数量为64,调整每个处理器上的Chare数量,从64增加到512,进行了测试。我们统计了每个处理器上的总粒子数Ni,并计算了所有处理器上的极差($N_{\max}-N_{\min}$)和标准差($\sqrt{\frac{1}{n}\sum\limits_{i=1}^{n}(N_{i}-\bar{N})^{2}}$)。
测试结果如表1所示,在不使用过分解的情况下,可以看出粒子分布的标准差和极差较大。随着Chare数量增加,LPT负载均衡策略降低了标准差和极差的数量级,也减少了计算时间。最优情况在使用256个Chare时取得,与不采用过分解的情况相比,减少了10%的计算时间。上述结果表明,过分解和负载均衡策略对粒子分布不均匀下的FMM计算有一定优化效果,可以平衡不同处理器上的计算负载。
Table 1
表1
表1过分解测试结果
Table 1
| Chare 总数量 | 时间/秒 | 标准差 | 极差 | 均值 |
|---|---|---|---|---|
| 64 | 640.53 | 527032 | 2755781 | 10240000 |
| 128 | 591.73 | 85038 | 432258 | 10240000 |
| 256 | 576.40 | 112005 | 563038 | 10240000 |
| 512 | 585.27 | 164129 | 593829 | 10240000 |
新窗口打开|下载CSV
5 总结与展望
本文基于Charm++并行编程框架,实现了并行FMM程序。首先分析了FMM的并行实现关键和主要通信,介绍了Charm++并行编程环境。在并行实现的过程中,本文讨论了MPI编程模型和Charm++编程模型的异同,引入了用异步模型表示同步计算的一般性方法,给出了一个通用的MPI并行程序向Charm++转化的流程,并针对基本通信函数给出了SDAG的实现方案。最终,本文在“元”超级计算机上对FMM的Charm++实现进行了检验与测试。结果表明,基于Charm++实现的FMM具有较好的扩展性,针对负载不均衡的情况,过分解和LPT负载均衡策略可以减少10%的执行时间。文本中实现中只利用了Charm++提供的Chare array类型,即把每个Chare看作一个独立且内存不共享的个体。如何使用Charm++提供的逻辑节点与本地存储来减少通信量,提高并行效率,将是未来的一个尝试方向。另一方面,本文在负载均衡时仅考虑了PE上的总粒子数,且假定计算负载与粒子数成正相关,不一定反映了真实的负载情况。因此,使用更贴近FMM的负载均衡指标也是一个可以考虑的方向。
针对目前高性能计算系统广泛使用异构计算的情况[29],本文提供的Charm++实现也具有一定适应性。只需声明一组绑定PE的Charm group,在其中执行耗时的P2P与M2L操作。异构加速与具体体系结构有关,涉及内容较多,故本文仅提供接口。
利益冲突声明
所有作者声明不存在利益冲突关系参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
[D].
[本文引用: 1]
[EB/OL]. [
URL [本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[D].
[本文引用: 2]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
DOI:10.1002/nme.v85.4URL [本文引用: 1]
[J].
DOI:10.1016/j.cpc.2011.12.013URL [本文引用: 1]
The efficient parallelization of fast multipole-based algorithms for the N-body problem is one of the most challenging topics in high performance scientific computing. The emergence of non-local, irregular communication patterns generated by these algorithms can easily create an insurmountable bottleneck on supercomputers with hundreds of thousands of cores. To overcome this obstacle we have developed an innovative parallelization strategy for Barnes-Hut tree codes on present and upcoming HPC multicore architectures. This scheme, based on a combined MPI-Pthreads approach, permits an efficient overlap of computation and data exchange. We highlight the capabilities of this method on the full IBM Blue Gene/P system JUGENE at inch Supercomputing Centre and demonstrate scaling across 299,912 cores with up to 2,048,000,000 particles. Applying our implementation PEPC to laser-plasma interaction and vortex particle methods close to the continuum limit, we demonstrate its potential for ground-breaking advances in large-scale particle simulations. (C) 2011 Elsevier B.V.
[C]//
[本文引用: 1]
[J].
DOI:10.1016/j.cpc.2012.09.011URL [本文引用: 1]
This paper reports large-scale direct numerical simulations of homogeneous-isotropic fluid turbulence, achieving sustained performance of 1.08 petaflop/s on GPU hardware using single precision. The simulations use a vortex particle method to solve the Navier-Stokes equations, with a highly parallel fast multipole method (FMM) as numerical engine, and match the current record in mesh size for this application, a cube of 4096(3) computational points solved with a spectral method. The standard numerical approach used in this field is the pseudo-spectral method, relying on the FFT algorithm as the numerical engine. The particle-based simulations presented in this paper quantitatively match the kinetic energy spectrum obtained with a pseudo-spectral method, using a trusted code. In terms of parallel performance, weak scaling results show the FMM-based vortex method achieving 74% parallel efficiency on 4096 processes (one GPU per MPI process, 3 GPUS per node of the TSUBAME-2.0 system). The FFT-based spectral method is able to achieve just 14% parallel efficiency on the same number of MPI processes (using only CPU cores), due to the all-to-all communication pattern of the FFT algorithm. The calculation time for one time step was 108 s for the vortex method and 154 s for the spectral method, under these conditions. Computing with 69 billion particles, this work exceeds by an order of magnitude the largest vortex-method calculations to date. (c) 2012 Elsevier B.V.
[J].
[本文引用: 1]
[J].
[本文引用: 1]
[J].
DOI:10.1145/167962URL [本文引用: 1]
[J].
[本文引用: 1]
[C]//
[本文引用: 1]
[D].
[本文引用: 5]
[C]//
[本文引用: 1]
[C]//
[本文引用: 1]
[EB/OL]. [
URL [本文引用: 1]
[J].
URL [本文引用: 1]
动态负载均衡(Dynamic Load Balancing,DLB)是提高动态和非规则问题计算效率与规模的一个挑战问题.阐述了DLB的一般性问题,根据DLB策略的主要特征给出了一个综合分类方法,按分类对近30年提出的各种主要DLB策略做了细致的分析和深入的比较,并做了策略有效性分析.在总结现有研究成果基础上,分析了该领域的最新发展趋势,为下一步的研究提出了新的问题和思路.
[J].
DOI:10.1016/0743-7315(89)90021-XURL [本文引用: 1]
[J].
DOI:10.1109/71.809572URL [本文引用: 1]
[R].
[本文引用: 2]
[J].
DOI:10.1109/71.243526URL [本文引用: 1]
[C]//
[本文引用: 2]
[J].
[本文引用: 1]
