Ji-Wei Cui¹, Xian-Rong Zhou^,21School of Physics and Optoelectronic Engineering, Xidian University, Xi'an 710071, China
²Department of Physics, East China Normal University, Shanghai 200241, China

Received:2021-03-27Revised:2021-05-25Accepted:2021-06-1Online:2021-09-17


Abstract
Based on the beyond-mean-field Skyrme–Hartree–Fock model, impurity effects of the Λhyperon in the hypernuclear systems ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si are investigated, respectively. Four cases, in which the Λhyperon occupies the single-particle orbitals ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$, ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$, are focused. In each case, the potential energy surface and the energy curves projected on certain angular momenta are employed to show the influence of the Λhyperon on the nuclear core. Beside the shrinkage effect that is induced by the Λhyperon occupying the s_Λ orbital, it is found that the Λhyperon on the p_Λ orbital, ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$, drives the nuclear core toward a prolate shape, while the ones on the other two p_Λ orbitals, ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$, drive the nuclear core toward an oblate shape. The energy spectra and the corresponding intra-band E2 transition rates for the rotational bands are given as a prediction for future experiments.
Keywords： Λ hypernuclei;Skyrme–Hartree–Fock model;angular momentum projection;generator coordinate method


PDF (638KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Ji-Wei Cui, Xian-Rong Zhou. Impurity effects of the Λhyperon in the hypernuclear systems ${}_{{\rm{\Lambda }}}^{25}\mathrm{Mg}$ and ${}_{{\rm{\Lambda }}}^{29}\mathrm{Si}$. Communications in Theoretical Physics, 2021, 73(11): 115301- doi:10.1088/1572-9494/ac06bd

1. Introduction

In the past several decades, experimental technologies for Λhypernuclear systems have been well developed [1–3]. By (K⁻, π⁻) and (π⁺, K⁺) reactions, excited energy levels corresponding to various hypernuclear configurations were obtained [1–3]. Most of hypernuclear configurations are constructed by a nuclear core coupled with a Λhyperon occupying the s_Λ or p_Λ orbital, and these configurations lead to various impurity effects. However, high-resolution energy levels for the p_Λ-orbital hyperon are rare except that the ones for the configuration [¹²C $\bigotimes {{\rm{\Lambda }}}_{p}$] were observed [4, 5]. In recent years, due to the (e, e^′K⁺) reaction [6] and the Ge detector array (Hyperball) [7, 8], high qualitative information on Λhypernuclear structure is available and these provide a good opportunity to precisely study the transitions that involve the Λhyperon exited onto the p_Λ orbital. For the observed light hypernuclei lighter than ${}_{{\rm{\Lambda }}}^{13}$ C, most of the p_Λ states are unbound. Therefore, it is needed to study the impurity effects of the p_Λ hyperon in heavier systems. The hypernuclear systems with a nuclear core in sd-shell region become good choices. There are also experimental plans for medium and heavy Λhypernuclei [9].

On the other hand, theoretical studies about Λhypernuclei also achieve great progress. For light Λhypernuclei, the shell model [10–13] and the microscopic cluster model [14–17] are the most promising ones that can give very precise predictions for the energy spectra and transition rates. And recently, the abinitio calculation has also been extended to the hypernuclear regime [18]. However, for the hypernuclei beyond the p-shell mass region, those three kinds of models are bothered by the rapidly increasing computational burden. For sd-shell Λhypernuclei, the antisymmetrized molecular dynamics (AMD) seems to be a suitable model that gives very detailed predictions about the energy spectra and E2 transitions [19–22], which is waiting for the testification of experimental observations in future.

Among all the existing theoretical models, only the mean-field models, i.e. the Skyrme–Hartree–Fock (SHF) model [23–31] and the relativistic mean-field (RMF) model [32–37], are able to study all the hypernuclei from light ones to heavy ones, with an acceptable computational burden. And furthermore, the mean-field calculations treat the nucleons and the Λhyperon on equal footing. In the last 5 years, beyond SHF [38–41] calculations and beyond RMF [42–44] calculations are, respectively, implemented to study the Λhypernuclear systems. In these beyond-mean-field calculations, the angular momentum projection (AMP) techniques give the rotational energy levels, and the generator coordinate method takes the configuration-mixing effect into consideration. Based on the mean-field calculations, five-dimensional collective Hamiltonian model (5DCH) [45, 46] and the particle-rotor model [47–49] are also used to investigate the energy spectra or impurity effects of the Λhypernuclei, although the two models are not totally microscopic.

In the sd-shell mass region, ²⁴Mg and ²⁸Si are two typical nuclei that are prolately deformed and oblately deformed, respectively, which are testified by the observed static quadrupole moments [50]. Therefore, contrastive investigations of ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si are helpful to clarify the impurity effects of the Λhyperon that occupies the s_Λ or p_Λ orbital. In this paper, the beyond SHF model is employed to give the energy spectra and intra-band E2 transitions of ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si. On one hand, the energy spectra and E2 transitions give reliable clues about the impurity effects; and on the other hand, the theoretical predictions in this paper will shed some light on the future experiments.

This paper is organized as follows. In section 2, the formalism of the beyond-mean-field calculation is introduced. Section 3 presents the results and discussions. Finally, a conclusion is given in section 4.

2. Model and method

In the SHF model, the energy density functional (EDF) of the Λhypernuclear system is given as [30](1)$\begin{eqnarray}\varepsilon ={\varepsilon }_{N}^{\mathrm{Skyrme}}+{\varepsilon }_{{\rm{\Lambda }}}+{\varepsilon }_{{\rm{s}}.{\rm{o}}.}^{{\rm{\Lambda }}},\end{eqnarray}$where ${\varepsilon }_{N}^{\mathrm{Skyrme}}$ represents the Skyrme-type NN interaction for the nuclear core and ${\varepsilon }_{{\rm{\Lambda }}}$ accounts for the Skyrme-type $N{\rm{\Lambda }}$ interaction. The last term, ${\varepsilon }_{{\rm{s}}.{\rm{o}}.}^{{\rm{\Lambda }}}$, is for the hyperonic spin–orbit interaction that is always neglected in the former researches for its smallness, but kept in this current calculation as [29, 51](2)$\begin{eqnarray}{\varepsilon }_{{\rm{s}}.{\rm{o}}.}^{{\rm{\Lambda }}}=-\displaystyle \frac{1}{2}{W}_{{\rm{\Lambda }}}({\rho }_{{\rm{\Lambda }}}{\rm{\nabla }}\cdot {{\boldsymbol{J}}}_{N}+{\rho }_{N}{\rm{\nabla }}\cdot {{\boldsymbol{J}}}_{{\rm{\Lambda }}}).\end{eqnarray}$

Single-particle states are obtained by the variation of the EDF. It must be emphasized that an additional quadrupole constraint is included in the variational procedure, which ensures the axiality of the whole system. The variational procedure is a self-consistent one, and in each iteration, the pairing force between nucleons are included. It takes the form of a density-dependent delta interaction [52](3)$\begin{eqnarray}G({\boldsymbol{r}})={V}_{0}\left[1-\displaystyle \frac{\rho ({\boldsymbol{r}})}{{\rho }_{0}}\right],\end{eqnarray}$where ρ₀ is the saturation density and V₀ is the strength of the pairing force. The BCS method is employed to deal with the pairing force.

The wave function of the Λhypernuclear system in the body-fixed frame of reference is given in the form of a direct product as(4)$\begin{eqnarray}\left|{{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,(\beta )\right\rangle =\left|{{\rm{\Phi }}}^{N}(\beta )\right\rangle \otimes \left|{{\rm{\Phi }}}^{{\rm{\Lambda }}}\right\rangle ,\end{eqnarray}$where $\left|{{\rm{\Phi }}}^{N}(\beta )\right\rangle $ and $\left|{{\rm{\Phi }}}^{{\rm{\Lambda }}}\right\rangle $ are intrinsic wave functions of the nuclear core with quadrupole deformation β and the Λhyperon, respectively.

In the lab-fixed frame of reference, the eigen state of a Λhypernuclear system is represented by a superposition of different configurations(5)$\begin{eqnarray}\left|{{\rm{\Psi }}}_{\alpha }^{{JM}}\right\rangle =\sum _{\beta }{F}_{\alpha }^{J}(\beta ){\hat{P}}_{{MK}}^{J}\left|{{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,(\beta )\right\rangle ,\end{eqnarray}$where the deformation parameter, β, plays the role of generator coordinate, and the AMP operator, ${\hat{P}}_{{MK}}^{J}$, restores the rotational symmetry. The third component of angular momentum in the body-fixed frame of reference, K, is a sum of two parts(6)$\begin{eqnarray}K={K}_{c}+{K}_{{\rm{\Lambda }}},\end{eqnarray}$in which K_c and ${K}_{{\rm{\Lambda }}}$ are for the nuclear core and the Λhyperon, respectively. With the assumption of time-reversal symmetry for the nuclear core, K_c=0 and K is totally determined by ${K}_{{\rm{\Lambda }}}$.

The weight function ${F}_{\alpha }^{J}(\beta )$ in equation (5) and the eigen energies are determined by the Hill–Wheeler–Griffin equation [53](7)$\begin{eqnarray}\sum _{{\beta }^{{\prime} }}\left[{H}_{{KK}}^{{\prime} J}(\beta ,{\beta }^{{\prime} })-{E}_{\alpha }^{J}{N}_{{KK}}^{J}(\beta ,{\beta }^{{\prime} })\right]{F}_{\alpha }^{J}({\beta }^{{\prime} })=0,\end{eqnarray}$where the Hamiltonian and norm elements are given by(8)$\begin{eqnarray}{H}_{{KK}}^{{\prime} J}(\beta ,{\beta }^{{\prime} })=\left\langle {{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,({\beta }^{{\prime} })\right|\hat{{H}^{{\prime} }}{\hat{P}}_{{KK}}^{J}\left|{{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,(\beta )\right\rangle ,\end{eqnarray}$(9)$\begin{eqnarray}{N}_{{KK}}^{J}(\beta ,{\beta }^{{\prime} })=\left\langle {{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,({\beta }^{{\prime} })\right|{\hat{P}}_{{KK}}^{J}\left|{{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,(\beta )\right\rangle .\end{eqnarray}$The corrected Hamiltonians $\hat{{H}^{{\prime} }}$ is(10)$\begin{eqnarray}\hat{{H}^{{\prime} }}=\hat{H}-{\lambda }_{p}({\hat{N}}_{p}-Z)-{\lambda }_{n}({\hat{N}}_{n}-N),\end{eqnarray}$where the last two terms on the right-hand side account for the fact that the projected wave function does not provide the correct number of particles on average [54–56] and $\hat{H}$ is determined by the EDF in equation (1).

The reduced E2 transition rate is derived as(11)$\begin{eqnarray}B\left(E2,J\alpha \to {J}^{{\prime} }{\alpha }^{{\prime} }\right)=\displaystyle \frac{1}{2J+1}{\left|\langle {\alpha }^{{\prime} };{J}^{{\prime} }\parallel {\hat{Q}}_{2}\parallel \alpha ;J\rangle \right|}^{2},\end{eqnarray}$where(12)$\begin{eqnarray}\begin{array}{l}\langle {\alpha }^{{\prime} };{J}^{{\prime} }\parallel {\hat{Q}}_{2}\parallel \alpha ;J\rangle =\sqrt{2{J}^{{\prime} }+1}\sum _{M\mu \beta {\beta }^{{\prime} }}{{F}_{{\alpha }^{{\prime} }}^{{J}^{{\prime} }}}^{* }({\beta }^{{\prime} }){F}_{\alpha }^{J}(\beta )\\ \ \ \times \ {C}_{{JM}2\mu }^{{J}^{{\prime} }{K}^{{\prime} }}\left\langle {{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,({\beta }^{{\prime} })\right|{\hat{Q}}_{2\mu }{\hat{P}}_{{MK}}^{J}\left|{{\rm{\Phi }}}^{(N{\rm{\Lambda }})}\,(\beta )\right\rangle .\end{array}\end{eqnarray}$In the equation above, ${\hat{Q}}_{2\mu }={r}^{2}{Y}_{2\mu }(\varphi ,\theta )$ is the electric quadrupole operator [57], and ${C}_{{JM}2\mu }^{{J}^{{\prime} }{K}^{{\prime} }}$ denotes the Clebsh–Gordon coefficients.

Notations: In this paper, single-particle orbitals of the Λhyperon are denoted by the Nilsson quantum numbers [Nn₃m_l]Ω^π, and the same notation is also adopted in [36]. Then, a certain configuration of the Λhypernuclear system is given as ${}^{A-1}$ Z $\otimes {\rm{\Lambda }}[{{Nn}}_{3}{m}_{l}]{{\rm{\Omega }}}^{\pi }$, in which ${}^{A-1}{Z}$ is the nuclear core and ${\rm{\Lambda }}[{{Nn}}_{3}{m}_{l}]{{\rm{\Omega }}}^{\pi }$ represents a Λhyperon occupying the orbital [Nn₃m_l]Ω^π.

Parameters: In the current calculation, the SLy4 [58] and SLL4 [31] parameters are adopted for the NN interaction and for the $N{\rm{\Lambda }}$ interaction, respectively. The strength of the pairing force is set to V₀=−1000 MeV fm³ for both protons and neutrons [59], and a smooth pairing energy cutoff of 5 MeV around the Fermi level is used as in [29, 39].

3. Results and discussions

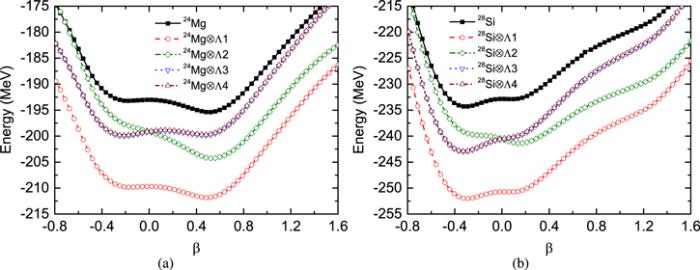
To investigate the impurity effects of Λhyperon occupying different orbitals, it is helpful to show the results of ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si contrastingly, because the deformations of the core nuclei ²⁴Mg and ²⁸Si are prolate and oblate, respectively.

Figure 1 gives the potential energy surfaces (PES) of ²⁴Mg, ${}_{\,{\rm{\Lambda }}}^{25}$ Mg, ²⁸Si, and ${}_{\,{\rm{\Lambda }}}^{29}$ Si. In Panel (a), it is shown that the PES of ²⁴Mg has two minima, and the prolate one is deeper than the oblate one. The addition of one Λhyperon onto the s_Λ orbital, ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, makes the two energy minima a little shallower and drives the two minima toward the spherical shape, which is due to the shrinkage effect. For the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, the Λbinding energy is B_Λ = 16.5 MeV in the mean-field calculation, which is very close to the results of AMD calculation [21]. Actually, the shrinkage effect of the s_Λ-orbital hyperon is not obvious in the sd-shell region, while the impurity effects of the p_Λ-orbital hyperon is remarkable. In panel (a), we can see that the Λhyperon on the orbital ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ eliminates the oblate energy minimum and makes the prolate one much deeper. On the other hand, the Λhyperon occupying the orbital ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ or ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ makes the prolate energy minimum shallower and enhances the oblate one. This phenomenon is due to the fact that the Λhyperon on ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ is prolately distributed, and its coupling to a prolate nuclear core leads to a lower total energy. Due to the same guide line, the Λhyperon on ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ or ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ prefers an oblate nuclear core. It must be emphasized that the $N{\rm{\Lambda }}$ spin–orbit coupling term is very small, so the two single-particle orbitals ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ coincide with each other and have nearly the same density distribution.

Figure 1.

New window|Download| PPT slide
Figure 1.Potential energy surfaces as functions of deformation parameter β, derived from mean-field calculation, for ²⁴Mg and ${}_{\,{\rm{\Lambda }}}^{25}$ Mg (panel (a)), and for ²⁸Si and ${}_{\,{\rm{\Lambda }}}^{29}$ Si (panel (b)). ${\rm{\Lambda }}1$, ${\rm{\Lambda }}2$, ${\rm{\Lambda }}3$ and ${\rm{\Lambda }}4$ represent different hyperonic orbitals and correspond to ${\rm{\Lambda }}[000]1/{2}^{+}$, ${\rm{\Lambda }}[110]1/{2}^{-}$, ${\rm{\Lambda }}[101]3/{2}^{-}$ and Λ[101]1/2⁻, respectively.


Panel (b) of figure 1 shows that ²⁸Si is oblately deformed and the Λhyperon occupying the s_Λ orbital, ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, also drives the energy minimum toward the spherical shape. The calculated Λbinding energy of the ${s}_{{\rm{\Lambda }}}$ orbital is B_Λ = 17.7 MeV, which is 0.8 MeV larger than the one given by the YBZ6 interaction [24, 29] and about 2 Mev smaller than the one given by the RMF calculation [32]. Because ²⁸Si is oblately deformed, it is found that energy minima of the configurations ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ are lower than the one of ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$.

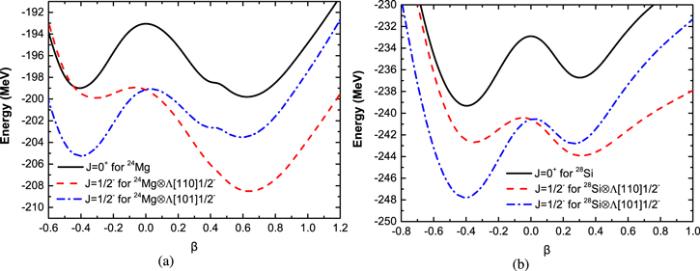
It is known that the rotational symmetry of a nuclear or hypernuclear system is not conserved in the mean-field calculation, so the mean-field states in the intrinsic frame of reference are not exact eigenstates with good angular momenta. In this paper, the AMP are used technically to restore the rotational symmetry and the energy curve $E(\beta ,J,K)=\tfrac{{H}_{{KK}}^{{\prime} J}(\beta ,\beta )}{{N}_{{KK}}^{J}(\beta ,\beta )}$ is much better to demonstrate the impurity effect of the Λhyperon on ${p}_{{\rm{\Lambda }}}$ orbital. Panels (a) and (b) of figure 2 show the E(β, J=0, K=0) for the core nuclei ²⁴Mg and ²⁸Si, respectively. It is found that both the oblate and prolate energy minimum of E(β, J=0, K=0) are more obvious than those of the mean-field PES shown in figure 1. If the energy of the core nucleus with a spherical shape, E_spherical, is chosen as the reference point, we can see that the prolate energy minimum of ²⁴Mg and the oblate energy minimum of ²⁸Si are 2–3 MeV lower than E_spherical, respectively, as in figure 1. On the other hand, for the the energy curve E(β, J=0, K=0) in figure 2, prolate energy minimum of ²⁴Mg and the oblate energy minimum of ²⁸Si are both 6–7 MeV lower than E_spherical, which indicates the more obvious energy gains compared to the mean-field PES. For the same kind of energy curve, E(β, J=0, K=0), the oblate minimum of ²⁴Mg and the prolate one of ²⁸Si are also deepened by the AMP. It must be mentioned that the two minima of E(β, J=0, K=0) for ²⁴Mg are probably saddle points in the γ direction [60]. Figure 2 also shows $E(\beta ,J=\tfrac{1}{2},K=\tfrac{1}{2})$ for the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ and ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ in Panel (a), and for the configuration ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ and ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ in panel (b). In both panels we can see that the Λhyperon occupying the orbital ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ enhances the prolate energy minimum and reduces the oblate one, while the one occupying the orbital ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ leads to opposite impurity effects. As is mentioned above, the Λhyperons occupying orbital ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ have nearly the same impurity effects to the nuclear core, so $E(\beta ,J=\tfrac{3}{2},K=\tfrac{3}{2})$ for the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ are not shown in figure 2 for simplification.

Figure 2.

New window|Download| PPT slide
Figure 2.Energy curve E(β, J, K) for ²⁴Mg and ${}_{\,{\rm{\Lambda }}}^{25}$ Mg (panel (a)), and for ²⁸Si and ${}_{\,{\rm{\Lambda }}}^{29}$ Si (panel (b)). The configurations and corresponding angular momenta are shown in each panel.


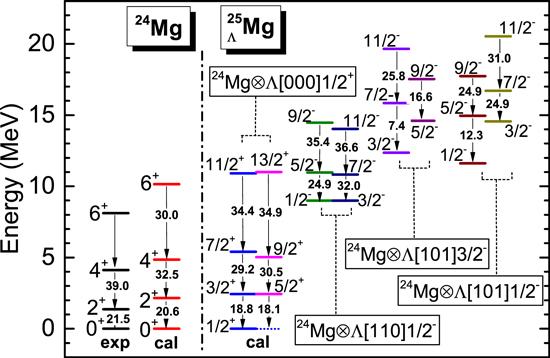
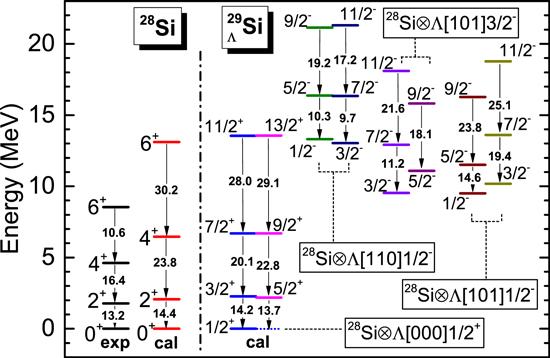
The comprehensive energy spectra which are composed by the rotational bands corresponding to various hypernuclear configurations are given in figures 3 and 4 for ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si, respectively. In each figure, the experimental and theoretical ground-state bands of the core nuclei are also shown for comparison.

Figure 3.

New window|Download| PPT slide
Figure 3.Energy spectra for ²⁴Mg and ${}_{\,{\rm{\Lambda }}}^{25}$ Mg. The observed data and calculated ones are labeled by ‘exp' and ‘cal', respectively. The reduced E2 transition rates are indicated by solid arrows and the configurations of the rotational bands are indicated by dashed lines. The experimental data are taken from [61] for ²⁴Mg.

Figure 4.

New window|Download| PPT slide
Figure 4.Same as figure 3, but for ²⁸Si and ${}_{\,{\rm{\Lambda }}}^{29}$ Si.


According to figure 3, it is indicated that for the ground-state band of ²⁴Mg, the current model gives reasonable energy levels and E2 transition rates in comparison with the observed ones. The addition of a Λhyperon onto the s_Λ orbital forms a positive-parity band with the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, and this rotational band is slightly stretched compared to the calculated ground-state band of ²⁴Mg, which indicates the shrinkage effect of the Λhyperon. It must be emphasized that, the similar results have been obtained in the 5DCH model [45] and AMD [21]. In addition, there are three negative-parity bands with the band heads at 9.0 MeV, 12.4 MeV and 11.6 MeV for the configurations ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$, ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$, respectively. The band of the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ is obviously lower than the ones of other two configurations, because the Λhyperon on the orbital ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ is prolately distributed and so is the core nucleus ²⁴Mg, which leads to a comparatively stronger attraction.

Figure 4 gives the energy spectra of ²⁸Si and ${}_{\,{\rm{\Lambda }}}^{29}$ Si in a similar way as figure 3 does. The calculated energies of 4⁺ and 6⁺ states in the ground-state band of ²⁸Si are obviously larger than the corresponding observed ones, and this may be due to the softness of the shape in γ direction which is not taken into consideration in this current work. Nevertheless, the calculated 2⁺ energy level and the E2 transition rates fit the observed ones well. Similar to the case of ${}_{\,{\rm{\Lambda }}}^{25}$ Mg, beside the positive-parity rotational band of ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$, the configurations ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$, ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ give three negative-parity rotational bands with the band heads at 13.3 MeV, 9.5 MeV and 9.5 MeV, respectively. In contrast to the case of ${}_{\,{\rm{\Lambda }}}^{25}$ Mg, band heads of configuration ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ are lower than that of ²⁸Si $\bigotimes $ ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$, which is due to the fact that the core nucleus ²⁸Si is oblately deformed and the coupling with the oblately distributed Λhyperons leads to lower energy.

Beside the energy bands, the intra-band E2 transition rates are also presented in figures 3 and 4 waiting for testification by future experiments. In earlier researches such as the 5DCH model [45] and the AMD model [21], E2 transition rates of nuclear cores, denoted by cB(E2), are given to show the shrinkage effect of the configuration ²⁴Mg $\bigotimes $ ${\rm{\Lambda }}$[000]${\tfrac{1}{2}}^{+}$. The 5DCH model shows that, for the E2 transition from ${2}_{1}^{+}$ state to ${0}_{1}^{+}$ state, cB(E2) is reduced by about 9% compared to B(E2) of ²⁴Mg[45], while the AMD model shows such reduction is about 6%[21]. In our current work, cB(E2) is also calculated and it is reduced by about 9%, which indicates that the beyond SHF model is as reliable as the other models available on the market.

It is worth mentioning that impurity effects of the Λhyperon on the nuclear core with octupole deformation (a pear-like shape) is very interesting. The RMF calculation has shown that, in ${}_{{\rm{\Lambda }}}^{21}$ Ne, the ${{\rm{\Lambda }}}_{s}$ (${{\rm{\Lambda }}}_{p}$) becomes more and more concentrated around the bottom (top) of the ‘pear' with the increase of octupole deformation [44]. ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si may also have nuclear cores with octupole deformations due to the clustering structure. To investigate impurity effects under such conditions, constraints on octupole moments and parity projection techniques will be introduced into the beyond SHF model in our future work.

4. Conclusions

In this paper, sd-shell Λhypernuclei, ${}_{\,{\rm{\Lambda }}}^{25}$ Mg and ${}_{\,{\rm{\Lambda }}}^{29}$ Si, are studied by the beyond-mean-field SHF model with SLy4 and SLL4 parameter sets for NN interaction and $N{\rm{\Lambda }}$ interaction, respectively. Mean-field calculation shows that the PES of a Λhypernuclear system is determined jointly by the orbital that the Λhyperon occupies and the shape of nuclear core. Beside the shrinkage effect of the ${s}_{{\rm{\Lambda }}}$-orbital hyperon, it is found that the Λhyperon occupying the orbital ${\rm{\Lambda }}$[110]${\tfrac{1}{2}}^{-}$ pulls the shape of the nuclear core toward the prolate side, while Λhyperon on the orbitals ${\rm{\Lambda }}$[101]${\tfrac{3}{2}}^{-}$ and ${\rm{\Lambda }}$[101]${\tfrac{1}{2}}^{-}$ make the nuclear core more oblate. From the perspective of beyond-mean-field calculation, the current model gives the positive- and negative-parity rotational bands for various configurations separately. The impurity effects of different configurations mentioned above are also shown by the relative positions of the energy bands and the E2 transition rates, which wait for further testification by future experiments.

Acknowledgments

One of the authors thanks X Y Wu for helpful discussions. This work was supported by the National Natural Science Foundation of China (Nos. 11905165, 11775081 and 11547044) and the Fundamental Research Funds for the Central Universities (Nos. JB160510 and XJS18020).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Hashimoto O Tamura H 2006 Prog. Part. Nucl. Phys. 57 564
DOI:10.1016/j.ppnp.2005.07.001 [Cited within: 2]

[2]Botta E Bressani T Garbarino G 2012 Eur. Phys. J. A 48 41
DOI:10.1140/epja/i2012-12041-6

[3]Gal A Hungerford E V Millener D J 2016 Rev. Mod. Phys. 88 035004
DOI:10.1103/RevModPhys.88.035004 [Cited within: 2]

[4]Ajimura S et al. 2001 Phys. Rev. Lett. 86 4255
DOI:10.1103/PhysRevLett.86.4255 [Cited within: 1]

[5]Kohri H et al. 2002 Phys. Rev. C 65 034607
DOI:10.1103/PhysRevC.65.034607 [Cited within: 1]

[6]Gogami T et al. (HKS (JLab E05-115) Collaboration) 2015 Phys. Rev. C 94 021302(R)
DOI:10.1103/PhysRevC.94.021302 [Cited within: 1]

[7]Tamura H et al. 2000 Phys. Rev. Lett. 84 5963
DOI:10.1103/PhysRevLett.84.5963 [Cited within: 1]

[8]Tanida K et al. 2001 Phys. Rev. Lett. 86 1982
DOI:10.1103/PhysRevLett.86.1982 [Cited within: 1]

[9]Tamura H 2012 Prog. Theor. Exp. Phys. 2012 02B012
DOI:10.1093/ptep/pts056 [Cited within: 1]

[10]Gal A Soper J M Dalitz R H 1971 Ann. Phys. 63 53
DOI:10.1016/0003-4916(71)90297-1 [Cited within: 1]

[11]Gal A Soper J M Dalitz R H 1972 Ann. Phys. 72 455
DOI:10.1016/0003-4916(72)90222-9

[12]Gal A 2005 Nucl. Phys. A 754 91c
DOI:10.1016/j.nuclphysa.2005.01.021

[13]Gal A Millener D J 2011 Phys. Lett. B 701 342
DOI:10.1016/j.physletb.2011.05.069 [Cited within: 1]

[14]Hiyama E Kamimura M Motoba T Yamada T Yamamoto Y 2000 Phys. Rev. Lett. 85 270
DOI:10.1103/PhysRevLett.85.270 [Cited within: 1]

[15]Hiyama E Kamimura M Motoba T Yamada T Yamamoto Y 2002 Phys. Rev. C 66 024007
DOI:10.1103/PhysRevC.66.024007

[16]Hiyama E Yamamoto Y Motoba T Kamimura M 2009 Phys. Rev. C 80 054321
DOI:10.1103/PhysRevC.80.054321

[17]Hiyama E Kamimura M Yamamoto Y Motoba T 2010 Phys. Rev. Lett. 104 212502
DOI:10.1103/PhysRevLett.104.212502 [Cited within: 1]

[18]Wirth R Gazda D Navratil P Calci A Langhammer J Roth R 2014 Phys. Rev. Lett. 113 192502
DOI:10.1103/PhysRevLett.113.192502 [Cited within: 1]

[19]En'yo Y K Horiuchi H Ono A 1995 Phys. Rev. C 52 628
DOI:10.1103/PhysRevC.52.628 [Cited within: 1]

[20]Isaka M Kimura M Dote A Onishi A 2011 Phys. Rev. C 83 044323 54304
DOI:10.1103/PhysRevC.83.044323

[21]Isaka M Homma H Kimura M Dote A Onishi A 2012 Phys. Rev. C 85 034303
DOI:10.1103/PhysRevC.85.034303 [Cited within: 4]

[22]Isaka M Kimura M Dote A Onishi A 2013 Phys. Rev. C 87 021304(R)
DOI:10.1103/PhysRevC.87.021304 [Cited within: 1]

[23]Rayet M 1981 Nucl. Phys. A 367 381
DOI:10.1016/0375-9474(81)90655-2 [Cited within: 1]

[24]Yamamoto Y Bandō H Žofka J 1988 Prog. Theor. Phys. 80 757
DOI:10.1143/PTP.80.757 [Cited within: 1]

[25]Cugnon J Lejeune A Schulze H-J 2000 Phys. Rev. C 62 064308
DOI:10.1103/PhysRevC.62.064308

[26]Vidaña I Polls A Ramos A Schulze H-J 2001 Phys. Rev. C 64 044301
DOI:10.1103/PhysRevC.64.044301

[27]Zhou X-R Schulze H-J Sagawa H Wu C-X Zhao E-G 2007 Phys. Rev. C 76 034312
DOI:10.1103/PhysRevC.76.034312

[28]Zhou X-R Polls A Schulze H-J Vidaña I 2008 Phys. Rev. C 78 054306
DOI:10.1103/PhysRevC.78.054306

[29]Win M-T Hagino K Koike T 2011 Phys. Rev. C 83 014301
DOI:10.1103/PhysRevC.83.014301 [Cited within: 3]

[30]Schulze H-J Rijken T 2013 Phys. Rev. C 88 024322
DOI:10.1103/PhysRevC.88.024322 [Cited within: 1]

[31]Zhou X-R Hiyama E Sagawa H 2016 Phys. Rev. C 94 024331
DOI:10.1103/PhysRevC.94.024331 [Cited within: 2]

[32]Win M-T Hagino K 2008 Phys. Rev. C 78 054311
DOI:10.1103/PhysRevC.78.054311 [Cited within: 2]

[33]Song C Y Yao J M Lü H F Meng J 2010 Int. J. Mod. Phys. E 19 2538
DOI:10.1142/S0218301310017058

[34]Lu B-N Zhao E-G Zhou S-G 2011 Phys. Rev. C 84 014328
DOI:10.1103/PhysRevC.84.014328

[35]Tanimura Y Hagino K 2012 Phys. Rev. C 85 014306
DOI:10.1103/PhysRevC.85.014306

[36]Lu B-N Hiyama E Sagawa H Zhou S-G 2014 Phys. Rev. C 89 044307
DOI:10.1103/PhysRevC.89.044307 [Cited within: 1]

[37]Xu R Wu C Ren Z 2015 Nucl. Phys. A 933 82
DOI:10.1016/j.nuclphysa.2014.09.093 [Cited within: 1]

[38]Cui J-W Zhou X-R Schulze H-J 2015 Phys. Rev. C 91 054306
DOI:10.1103/PhysRevC.91.054306 [Cited within: 1]

[39]Cui J-W Zhou X-R Guo L-X Schulze H-J 2017 Phys. Rev. C 95 024323
DOI:10.1103/PhysRevC.95.024323 [Cited within: 1]

[40]Cui J-W Zhou X-R 2017 Prog. Theor. Exp. Phys. 2017 093D04
DOI:10.1093/ptep/ptx120

[41]Li W-Y Cui J-W Zhou X-R 2018 Phys. Rev. C 97 034302
DOI:10.1103/PhysRevC.97.034302 [Cited within: 1]

[42]Mei H Hagino K Yao J M 2016 Phys. Rev. C 93 011301(R)
DOI:10.1103/PhysRevC.93.011301 [Cited within: 1]

[43]Wu X Y Mei H Yao J M Zhou X-R 2017 Phys. Rev. C 95 034309
DOI:10.1103/PhysRevC.95.034309

[44]Xia H J Wu X Y Mei H Yao J M 2019 Sci. China-Phys. Mech. Astron. 62 42011
DOI:10.1007/s11433-018-9308-0 [Cited within: 2]

[45]Yao J M Li Z P Hagino K Win M-T Zhang Y Meng J 2011 Nucl. Phys. A 868 12
DOI:10.1016/j.nuclphysa.2011.08.006 [Cited within: 4]

[46]Xue W X Yao J M Hagino K Li Z P Mei H Tanimura Y 2015 Phys. Rev. C 91 024327
DOI:10.1103/PhysRevC.91.024327 [Cited within: 1]

[47]Mei H Hagino K Yao J M Motoba T 2014 Phys. Rev. C 90 064302
DOI:10.1103/PhysRevC.90.064302 [Cited within: 1]

[48]Mei H Hagino K Yao J M Motoba T 2015 Phys. Rev. C 91 064305
DOI:10.1103/PhysRevC.91.064305

[49]Mei H Hagino K Yao J M Motoba T 2016 Phys. Rev. C 93 044307
DOI:10.1103/PhysRevC.93.011301 [Cited within: 1]

[50]Stone N J 2016 At. Data Nucl. Data Tables 111–112 1
DOI:10.1016/j.adt.2015.12.002 [Cited within: 1]

[51]Schulze H-J Hiyama E 2014 Phys. Rev. C 90 047301
DOI:10.1103/PhysRevC.90.047301 [Cited within: 1]

[52]Bender M Rutz K Reinhard P-G Maruhn J A 2000 Eur. Phys. J. A 8 59
DOI:10.1007/s10050-000-4504-z [Cited within: 1]

[53]Ring P Schuck P 1980 The Nuclear Many-Body Problem Berlin Springer
[Cited within: 1]

[54]Rodriguez-Guzman R Egido J L Robledo L M 2000 Phys. Lett. B 474 15
DOI:10.1016/S0370-2693(00)00015-0 [Cited within: 1]

[55]Bonche P Dobaczewski J Flocard H Henneen P-H Mayer J 1990 Nucl. Phys. A 510 466
DOI:10.1016/0375-9474(90)90062-Q

[56]Yao J M 2009 Covariant density functional theory for nuclear spectroscopy
PhD ThesisPeking University, Beijing
[Cited within: 1]

[57]Dobaczewski J et al. 2009 Comput. Phys. Commun. 180 2361
DOI:10.1016/j.cpc.2009.08.009 [Cited within: 1]

[58]Chabanat E Bonche P Haensel P Meyer J Schaeffer R 1998 Nucl. Phys. A 635 231
DOI:10.1016/S0375-9474(98)00180-8 [Cited within: 1]

[59]Valor A Heenen P-H Bonche P 2000 Nucl. Phys. A 671 145
DOI:10.1016/S0375-9474(99)00830-1 [Cited within: 1]

[60]Bender M Heenen P-H 2008 Phys. Rev. C 78 044309
DOI:10.1103/PhysRevC.78.044309 [Cited within: 1]

[61]National Nuclear Data Center, http://nndc.bnl.gov/
[Cited within: 1]