Mingwen Zhang, Li Li^,, Zhezhen Zhao, Jinlan Nie, Xiaotao Zu, Hongxiang DengSchool of Physics, University of Electronic Science and Technology, Chengdu 610054, China

Received:2020-10-29Revised:2021-02-12Accepted:2021-02-16Online:2021-03-22

Fund supported:

National Natural Science Foundation of China.11804046

Abstract
Although rare-earth metals have increasingly received attention for use in the storage and transportation of the tritium used in nuclear fusion reactions, they still face great challenges, such as the effect of helium on the mechanical properties of different erbium hydrides. In this work, first principles are used to study the mechanical properties (elastic constants, Young’s modulus, transverse shear modulus and bulk modulus) of different erbium hydrides exposed to helium. The Young’s modulus, the transverse shear modulus and the bulk modulus are given based on the elastic constants calculated according to first principles. It is found that the mechanical properties of all three erbium hydrides decrease in the presence of helium, and the decline of the mechanical properties of ErH₃ is the most serious. To explain the reason for the decrease in the mechanical properties, the densities of the states of erbium hydrides are calculated. During the calculations, helium embrittlement is not found and the ductility of the erbium hydrides improves following the production of helium at the helium concentrations considered in this work.
Keywords： ab initio calculation;Er hydrides;helium;mechanical properties


PDF (702KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Mingwen Zhang, Li Li, Zhezhen Zhao, Jinlan Nie, Xiaotao Zu, Hongxiang Deng. Ab initio study of the effects of helium on the mechanical properties of different erbium hydrides. Communications in Theoretical Physics, 2021, 73(5): 055701- doi:10.1088/1572-9494/abe699

1. Introduction

Nuclear energy production is perceived as a means of satisfying national energy demands while contributing to a potentially sustainable energy transition. Tritium is used to fuel the neutron tubes in a nuclear fusion reaction and is a reaction product of molten salt reactors. However, tritium is radioactive. It would extremely valuable to solve the problem of safe tritium storage and transportation to support the practical use of nuclear energy [1, 2].

Because of their high tritium storage densities, metals have been widely considered as possible storage materials for tritium. Up until now, depleted uranium is the only metal that has actually been used to store tritium. However, depleted uranium is not only radioactive but also combustible [3]. Therefore, the identification of a new suitable tritium storage metal has become an important research direction.

Rare-earth metals can absorb a lot of hydrogen and hydrogen isotopes. The number of tritium atoms that can be stored in a rare-earth metal can be several times greater than the number of metal atoms. At the same time, the equilibrium pressure in a rare-earth metal that has absorbed tritium atoms is very low. Because of the above advantages, rare-earth metals are considered to be excellent tritium storage materials. Among the rare-earth metals, erbium is considered a significant tritium storage material.

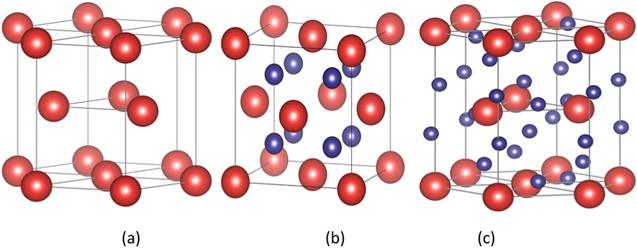
After erbium absorbs tritium, erbium tritides of different phases are formed according to the different ratios of tritium absorption. There are three kinds of stable structure in the Er-T binary system: HCP α - Er, FCC β- ErT₂, and triclinic γ- ErT₃, as shown in figure 1. Their structures are similar to Mg, CaF₂ and HoH₃, respectively [4].

Figure 1.

New window|Download| PPT slide
Figure 1.Schematic representation of the different erbium hydride configurations (a) Er, (b) ErT₂, (c) ErT₃.


In metal tritium storage systems, tritium decays to ³He through β decay. Since ³He does not react, but accumulates in metals, helium bubbles eventually form. The helium bubbles do not grow in an unrestricted manner; when they break, they cause surface damage. From a macroscopic point of view, helium leads to a decrease in the mechanical properties of materials, and makes materials brittle—helium embrittlement, which affects the lifetime and properties of materials [5–9].

Over the years, many researchers have studied He behavior in the Er-H system. Wixom et al calculated the migration of H, O, and He in β-ErH₂ using first principles [10]. Snow observed the growth of He bubbles in ErT₂ thin films using transmission electron microscope (TEM) [11], and Knapp observed the evolution of mechanical properties of ErT₂ thin films [12]. Dai and Schultz studied the mechanical properties of ErH₂ using first principles [13, 14].

However, since most current studies only focus on ErH₂, there is a lack of research into α-Er and γ-ErH₃. Also, the effects of He on the mechanical properties of erbium hydrides have not been considered when helium is in different interstitial positions. In particular, there are no reports comparing the three phases (α-Er, β-ErT₂ and γ-ErT₃). Therefore, it is necessary to study the effects of He on the mechanical properties of Er–T in different phases.

It should be noted that tritium is an isotope of hydrogen and has the same electronic number as hydrogen. Relevant studies have shown that erbium tritide and erbium hydride have similar properties [15]. Therefore, tritium is replaced by hydrogen in the calculations of this paper.

2. Simulation method

The calculation is based on density functional theory (DFT) theory, and the Vienna ab initio simulation package (VASP) is employed in our calculation. The projector augmented wave method is used to determine the interaction between ions and electrons, while the exchange and correlation interactions are described by the generalized gradient approximation (GGA) proposed by Perdew and Wang [16]. The pseudo-potentials used in the calculations are all derived from the pseudo-potential library of the VASP software package. Brillouin zone sample points are generated using the Monkhorst–Pack method. First, the unit cell size and atomic positions are both optimized. The pseudo-potentials and the cutoff energy are all tested, and the cutoff energy is set to 500 eV. The accuracy and convergence of the calculation results are relatively good. Based on the unit cell, a super cell is built to calculate the physical parameters.

To compare the effect of He on different erbium hydrides, supercells are built for three erbium hydrides with the same number of atoms (24). For α-Er, the cell used in the calculation is 3×2×2 and 5×5×5 k-points are used; for β-ErH₂, the cell used in the calculation is 2×2×1, and 7×7×7 k-points are used; for γ- ErH₃, the cell used in the calculation is 1×1×1, and 7×7×7 k-points are used.

There are tetrahedral vacancies (T) and octahedral vacancies (O) in α-Er. Therefore, a He atom is put in the tetrahedral vacancy or the octahedral vacancy for α-Er to calculate the elastic constants and the density of state. ErH₂ has an face center cubic (fcc) metallic sub-structure and all the tetrahedral positions are occupied by H atoms. Two conditions are considered for ErH₂, the first condition is that the H atom at a T position is replaced by a He atom, and the second condition is that H is deleted at the T position and a He atom is placed at the O position. ErH₃ has an hexagonal close packed (hcp) sub-structure whereby all the tetrahedral positions and octahedral positions are occupied by H atoms. Two conditions are considered for ErH₃. The first condition is that a H atom at a T position is replaced by a He atom, and the second condition that a H atom at an O position is replaced by a He atom.

The number of independent elastic constants are different for different crystal systems. α-Er belongs to the hexagonal system and there are five independent elastic constants, which are (${C}_{11},{C}_{12},{C}_{13},{C}_{33},{C}_{44}$). β-ErH₂ belongs to the cubic system with the highest symmetry and there are only three independent elastic constants, which are (${C}_{11},{C}_{12},{C}_{44}$). γ-ErH₃ belongs to the trigonal system and there are six independent elastic constants, which are (${C}_{11},{C}_{12},{C}_{13},{C}_{14},{C}_{33},{C}_{44}$).

3. Results and discussion

In this section, a VASP calculation is employed to obtain the elastic constants and the densities of state of erbium hydrides. The elastic constant calculation is based on the stress–strain method which is embedded in VASP [17]. The elastic moduli are obtained based on the calculated elastic constants according the equation for elastic constants and elastic modulus. The effects of He on the mechanical properties are analyzed and compared in detail for the three erbium hydrides.

3.1. Lattice constants

First, both the lattice sizes and internal atomic coordinates of the three phases are fully relaxed. The lattice constants obtained are listed in table 1. From the data listed in the table, it can be seen that the results in this work are agreement with both the calculated and experimental results in the literature [18, 19], indicating that our calculation methods and calculation parameter settings are all reasonable.


Table 1.
Table 1.The calculated lattice constants (Å) of three erbium hydrides.

	α-Er	β-ErH2	γ-ErH3
This work	a 3.575	abc 5.125	a 6.272
	c 5.556		c 6.526
References	a 3.559	abc 5.123	a 6.235
	c 5.587		c 6.496

New window|CSV

3.2. Elastic constants

The data in brackets in table 2 are from published results [14, 20]. It can be seen from table 2 that the errors between the calculation results in this paper and the results from the literature are within 3%, which shows that our calculation results are reasonable and reliable. It also can be seen that the elastic constant changed after He was produced. Further analysis according our calculation results shows that the production of He inevitably leads to a certain degree of lattice distortion. However, the lattice distortion is less than 0.05%, as the doping concentration of He in this work is relatively low. So the small change of the elastic constant matrix caused by lattice distortion is ignored in this work.


Table 2.
Table 2.Calculated and reference values (Gpa) of elastic constants.

	α-Er			β-ErH2			γ-ErH3
	No He	He-tetra	He-octa	No He	He-tetra	He-octa	No He	He-tetra	He-octa
C11	83.53	78.14	78.80	145.48	117.02	129.29	196.33	186.74	180.03
	(86.15)			(142.3)
C12	24.06	24.36	24.04	61.09	73.60	64.51	56.59	63.39	57.56
	(23.86)			(64.1)
C13	25.51 (28.37)	25.88	25.42				21.27	23.26	26.81
C14							1.34	0.45	1.12
C33	87.78	85.19	85.49				171.99	169.32	172.45
	(91.28)
C44	27.92	27.69	27.94	74.37	66.20	67.83	41.79	33.41	32.41
	(24.13)			(75.0)

New window|CSV

We now calculate the elastic modulus using the elastic constants and the effect of He on the mechanical parameters is analyzed.

3.3. Elastic modulus

Elastic moduli are physical quantities that describe the elasticity of materials, which include Young’s modulus (Y), the shear modulus (G), the bulk modulus (B), etc. They represent the changes of stress with strain in the elastic deformation stage. The elastic modulus is an important performance parameter of engineering materials. From the macroscopic point of view, the elastic modulus measures the ability of materials to resist elastic deformation. From the microscopic point of view, the elastic modulus reflects the bonding strengths between atoms, ions, or molecules.

Using the elastic constants in section 3.2 and the Voigt–Reuss–Hill approximation [21], Young’s modulus, the shear modulus, the bulk modulus, and the value of B/G can be calculated.(1)$\begin{eqnarray}{B}_{\mathrm{Voigt}}=\left({C}_{11}+{C}_{22}+{C}_{33}\right)/9+2\left({C}_{12}+{C}_{13}+{C}_{23}\right)/9,\end{eqnarray}$(2)$\begin{eqnarray}{B}_{\mathrm{Re}\mathrm{uss}}={\left[\left({S}_{11}+{S}_{22}+{S}_{33}\right)+2\left({S}_{12}+{S}_{13}+{S}_{23}\right)\right]}^{-1},\end{eqnarray}$(3)$\begin{eqnarray}B=\left({B}_{\mathrm{Voigt}}+{B}_{\mathrm{Re}\mathrm{uss}}\right)/2,\end{eqnarray}$(4)$\begin{eqnarray}\begin{array}{lll}{G}_{\mathrm{Voigt}} & = & \left[\left({C}_{11}+{C}_{22}+{C}_{33}\right)-\left({C}_{12}+{C}_{13}+{C}_{23}\right)\right]/15\\ & & +\,\left({C}_{44}+{C}_{55}+{C}_{66}\right)/5,\end{array}\end{eqnarray}$(5)$\begin{eqnarray}\begin{array}{lll}{G}_{\mathrm{Re}\mathrm{uss}} & = & 15\left[4\left({S}_{11}+{S}_{22}+{S}_{33}\right)-4\left({S}_{12}+{S}_{13}+{S}_{23}\right)\right.\\ & & {\left.+3\left({S}_{44}+{S}_{55}+{S}_{66}\right)\right]}^{-1},\end{array}\end{eqnarray}$(6)$\begin{eqnarray}G=\left({G}_{\mathrm{Voigt}}+{G}_{\mathrm{Re}\mathrm{uss}}\right)/2,\end{eqnarray}$(7)$\begin{eqnarray}Y=\left[9{B}_{\mathrm{Hill}}{G}_{\mathrm{Hill}}\right]/\left[3{B}_{\mathrm{Hill}}+{G}_{\mathrm{Hill}}\right],\end{eqnarray}$(8)$\begin{eqnarray}v=\left(3{B}_{\mathrm{Hill}}-Y\right)/6{B}_{\mathrm{Hill}}.\end{eqnarray}$

It can be seen from table 3 that the Y, G, and B of Er are smaller than those of ErH₂ and ErH₃, which indicates that Er has the weakest deformation resistance. The mechanical properties are closely related to the bonding strength. On the one hand, the distance between atoms of Er is large and the interaction distance is long. On the other hand, the Er–H bond is absent in Er, compared with the ErH₂ and ErH₃ which contain hydrogen. This could be the reason for the weak deformation resistance of Er.


Table 3.
Table 3.Calculated values (Gpa) for the elastic modulus.

	α-Er			β-ErH2			γ-ErH3
	No He	He-tetra	He-octa	No He	He-tetra	He-octa	No He	He-tetra	He-octa
Y	70.77	67.27	68.00	144.07	142.65	134.14	140.93	125.72	104.64
G	29.07	27.47	27.86	59.24	58.35	54.32	59.12	51.18	43.49
B	41.67	40.71	40.56	84.53	84.29	84.26	76.23	77.14	58.70
B/G	1.43	1.48	1.46	1.43	1.44	1.55	1.28	1.50	1.34

New window|CSV

Also, it can be observed from table 3 that all the elastic moduli of the three phases decrease after He is produced. This is consistent with the experiment described in [22]. For α-Er, the maximum reduction rate of the elastic modulus is from 2.66% to 5.50%. For β-ErH₂, the maximum reduction rate is from 3.19% to 8.29%. For γ-ErH₃, the maximum reduction rate is from 22.72% to 26.44%. Therefore, the influence of He is the greatest on the mechanical properties of ErH₃. This result means that the damage of He to different phases is different and the damage to ErH₃ is the most serious.

It can be seen from table 3 that with the generation of He, the value of B/G increases. The ductility and brittleness of materials can be judged by their B/G value [23]. In general, the larger the value of B/G, the better the ductility of the material. The critical value of B/G for brittleness and ductility is 1.75. From table 3, it can be noticed that when there is no He, the ratio of B/G is less than 1.75, showing that the materials are brittle. With the generation of He, the ductility of the material increases. However, the value of B/G is still less than 1.75, which means that the materials are still brittle.

While the ductility of the material increases with the generation of He, no helium embrittlement appears under the condition described in this work. It can be inferred that helium embrittlement is produced only when the helium concentration reaches a certain level.

3.4. Electronic structural analysis

The mechanical strength of the material can be reflected by the elastic modulus from the macroscopic point of view, and it can be reflected by the bonding strength from the microscopic point of view. The bonding strength can be a reflection of the electronic structure. To further investigate the effect of He on metal hydrides, the density of states of each phase of erbium hydrides are calculated.

3.4.1. The effect of He on α-Er

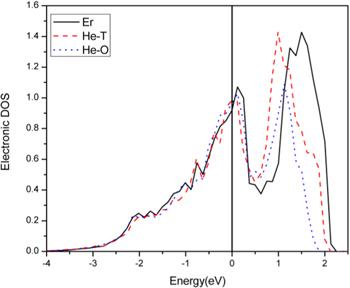
Figure 2 is a density of states diagram of the d orbital of the Er atom nearest to He. In figure 2, the black curve is the density of states diagram of the d orbital of the Er atom, as there is no He introduced into the Er. The red curve is the density of states diagram of the d orbital of the Er atom when the He atom is in a tetrahedral site. It should be mentioned that the density of states of the Er atom is the average of the four Er atoms nearest to the He. The blue curve is the density of states diagram of the d orbital of an Er atom when the He atom is in an octahedral site. Here, the density of states of the Er atom is the average of the six Er atoms nearest the He.

Figure 2.

New window|Download| PPT slide
Figure 2.Density of states diagram of the d orbital of an Er atom.


From figure 2, it can be seen that the density of states changes greatly following He generation. The change is expected to be caused by the production of an Er–He bond. When He is in the octahedral position, the change to the density of states is larger. This indicates that the interaction between the He and Er atoms is stronger when the He is in the octahedral position. Because He is a closed-shell atom, the stronger the interaction with the surrounding atoms, the more unstable the material. In other words, α-Er is more unstable when He is in the tetrahedral position than when He is in the octahedral position. This conclusion is consistent with table 3.

3.4.2. The effect of He on β-ErH₂

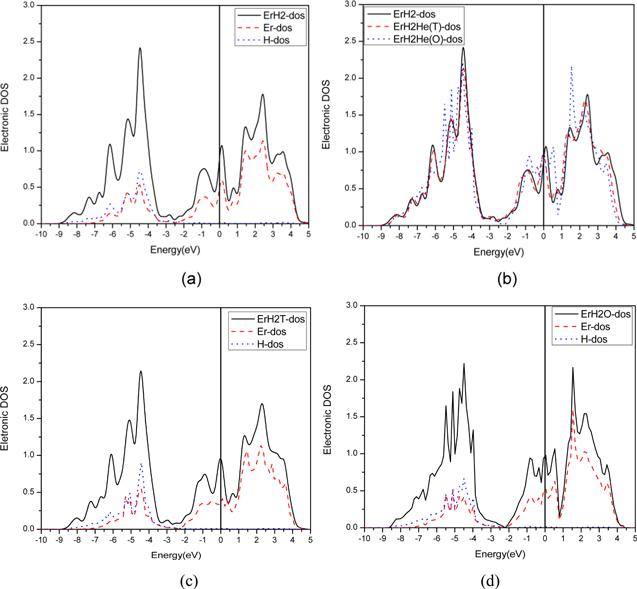
It can be seen from figure 3(a) that the density of states of ErH₂ is mainly contributed by the s orbitals of H and the d orbitals of Er at low energy levels. In the range of −5.5 eV∼−4.5 eV, the density of states of H-s and Er-d overlap and hybrid peaks appear, showing that the H–Er bond is strong. At high energy levels, the density of states is mainly contributed by the d orbitals of Er.

Figure 3.

New window|Download| PPT slide
Figure 3.Density of states diagram of ErH_2. (a) The total density of states (TDOS) of ErH₂ and the (density of states (DOS) of the d orbital of Er and the s orbital of H, (b) TDOS of pure ErH₂, ErH₂ with He in the octahedral site, and the tetrahedral site. (c) TDOS of ErH₂ with He in the T site and the DOS of the d orbital of Er and the s orbital of H. (c) TDOS of ErH₂ with He in the O site and the DOS of the d orbital of Er and the s orbital of H.


From figure 3(b), it can be observed that the total density of states at the Fermi level increases slightly after He production, showing that the interaction of He and Er increases. The stronger the interaction between the He and the metal, the more unfavorable it is to the stability of the system, and the mechanical properties decrease.

Figures 3(c) and (d) show the TDOS and the DOS of the d orbital of Er and the s orbital of H in ErH2 with He in the T and O sites. It can be observed that the hybridization of H and Er is slightly weaker after the generation of He. This obviously leads to a decrease in the mechanical properties.

At the same time, we note that the density of states of He in an octahedron is significantly higher than that in a tetrahedron (as shown by figure 3(b)), which indicates that the interaction between He and Er in the octahedral position is stronger than that with Er in the tetrahedral position. Therefore, when He is in an octahedron, the mechanical properties decrease more noticeably.

According to the van’t Hoff equation, the higher the stability of the system, the lower the equilibrium pressure. Through the above analysis, we know that the production of He leads to a decline in the stability of the system [24]. Therefore, the equilibrium pressure of the system increases after He is produced. The increase of equilibrium pressure means that the tritium storage performance of the material decreases. Therefore, the hydrogen storage capacity decreases following He generation.

3.4.3. The effect of He on γ-ErH₃

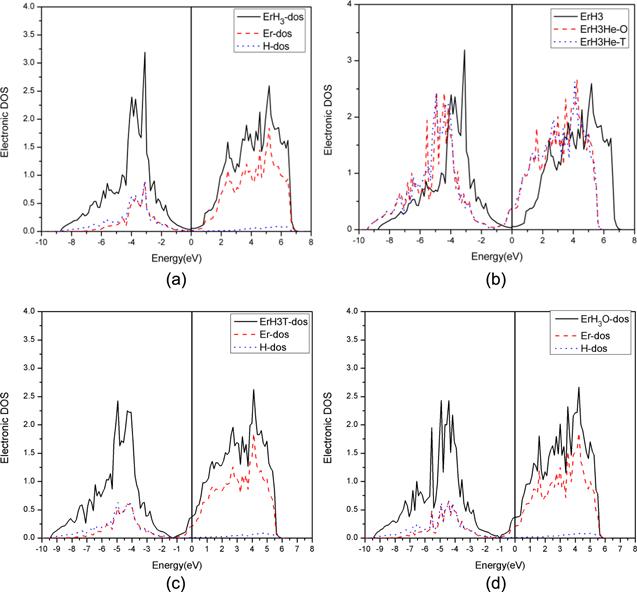
From figure 4(a), it can be seen that Er and H have strong hybridization at low energy levels. The density of states is contributed by both the s orbital of H and the d orbit of Er at low energy levels, and by the d orbital of Er at high energy levels. At the same time, it can be observed from figure 4(a) that the density of states at the Fermi level of ErH₃ (as the most H-containing phase) is close to zero. The result indicates that ErH₃ shows a nonmetallic property.

Figure 4.

New window|Download| PPT slide
Figure 4.Density of states diagram of ErH₃ (a) TDOS of ErH₃ and the DOS of the d orbital of Er and the s orbital of H, (b) TDOS of pure ErH₃, ErH₃ with He in the octahedral site and the tetrahedral site. (c) TDOS of ErH₃ with He in the T site and the DOS of the d orbital of Er and the s orbital of H. (c) TDOS of ErH₃ with He in the O site and the DOS of the d orbital of Er and the s orbital of H.


Figure 4(b) shows that the density of states at the Fermi level increases after He generation. This indicates that the stability of the structure is decreased. At the same time, it can be observed that the density of states changes more obviously when He is in the octahedral site. This shows that the interaction between the He and Er atoms is stronger when He is in the octahedral site, which may explain why the octahedral site is less stable than the tetrahedral site.

Figures 4(c) and (d) are the TDOS and the DOS of the d orbital of Er and the s orbital of the H of ErH₃ with He in the T site and the O site. It can be observed that the hybridization of H and Er is weaker following the generation of He, and that the DOS shifts to a lower energy level. This obviously leads to a reduction in the mechanical properties.

Similarly to the analysis of ErH₂, the hydrogen storage capacity of ErH₃ will decrease following He generation.

4. Conclusions

Using ab initio calculations based on DFT, the influences of He on the mechanical properties of different erbium hydrides was systematically studied. The calculations of the relative elastic modulus and the DOS showed that:(1) The mechanical properties of all three erbium hydrides decreased due to the production of He. He has the biggest impact on the mechanical properties of ErH₃ and the decrease of the elastic modulus (a mechanical property of ErH₃) can be more than 20%.
(2) The calculated results for the densities of states were consistent with those of the mechanical parameters. The results for the densities of states showed that the destruction of the Er–H bond and the establishment of an Er–He bond led to a reduction in the mechanical properties.
(3) Research also shows that the materials were still ductile and that no helium embrittlement appeared under the conditions described in this work. This indicates that helium embrittlement takes place at a specific He density in erbium hydrides.


This work helps in the exploration of the hydrogen storage capacity of rare-earth metals from a microscopic point of view.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant No. 11804046 and No. 61505023).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Pravalie R, Bandoc G 2018 Nuclear energy: between global electricity demand, worldwide decarbonisation imperativeness, and planetary environmental implications
J. Environ. Manage. 209 81 92
DOI:10.1016/j.jenvman.2017.12.043 [Cited within: 1]

[2]Taylor N et al. 2017 Materials-related issues in the safety and licensing of nuclear fusion facilities
Nucl. Fusion 57 092003
DOI:10.1088/1741-4326/57/9/092003 [Cited within: 1]

[3]Yun S H, Chang M H, Kang H G, Chung D Y, Oh Y H, Jung K J, Chung H, Koo D, Sohn S H, Song K M 2015 Key technologies for tritium storage bed development
Fusion Sci. Technol. 67 671 676
DOI:10.13182/FST14-T107 [Cited within: 1]

[4]Zhou X S, Zhang L, Wang W D, Liu Q, Peng S M, Ding W, Long X G, Cheng G J, Liang J H, Fu Y Q 2015 3He retention and structural evolution in erbium tritides: phase and aging effects
J. Nucl. Mater. 461 157 163
DOI:10.1016/j.jnucmat.2015.03.012 [Cited within: 1]

[5]Li S H, Li J T, Han W Z 2019 Radiation-Induced Helium Bubbles in Metals
Materials (Basel) 12 1036
DOI:10.3390/ma12071036 [Cited within: 1]

[6]Lin W, Liu S, Chen D, Dang C, Niu H, Zhao Y, Han B, Lu Y, Kai J-J 2019 Interaction between recrystallization and helium behavior in cold-rolled nickel
Mater. Lett. 250 68 71
DOI:10.1016/j.matlet.2019.04.111

[7]Han W-Z, Ding M-S, Shan Z-W 2018 Cracking behavior of helium-irradiated small-volume copper
Scr. Mater. 147 1 5
DOI:10.1016/j.scriptamat.2017.12.029

[8]Torres E, Pencer J 2018 Molecular dynamics study of the role of symmetric tilt grain boundaries on the helium distribution in nickel
J. Nucl. Mater. 502 86 94
DOI:10.1016/j.jnucmat.2018.01.046

[9]Huang H F, Zhang W, De Los Reyes M, Zhou X L, Yang C, Xie R, Zhou X T, Huai P, Xu H J 2016 Mitigation of He embrittlement and swelling in nickel by dispersed SiC nanoparticles
Mater. Des. 90 359 363
DOI:10.1016/j.matdes.2015.10.147 [Cited within: 1]

[10]Wixom R R, Browning J F, Snow C S, Schultz P A, Jennison D R 2008 First principles site occupation and migration of hydrogen, helium, and oxygen in β-phase erbium hydride
J. Appl. Phys. 103 123708
DOI:10.1063/1.2940134 [Cited within: 1]

[11]Snow C S, Browning J F, Bond G M, Rodriguez M A, Knapp J A 2014 ³He bubble evolution in ErT₂: a survey of experimental results
J. Nucl. Mater. 453 296 306
DOI:10.1016/j.jnucmat.2014.07.032 [Cited within: 1]

[12]Knapp J A, Browning J F, Bond G M 2009 Evolution of mechanical properties in ErT₂ thin films
J. Appl. Phys. 105 053501
DOI:10.1063/1.3082011 [Cited within: 1]

[13]Schultz P A, Snow C S 2016 Mechanical properties of metal dihydrides
Modell. Simul. Mater. Sci. Eng. 24 035005
DOI:10.1088/0965-0393/24/3/035005 [Cited within: 1]

[14]Yun-Ya D, Peng Shu-Ming Y L, Xing-Gui L, Xiao-Song Z, Xiao-Tao Z 2012 First-principles calculation for mechanical properties of metal dihydrides
Acta Phys. Sin. 61 108801
DOI:10.7498/aps.61.108801 [Cited within: 2]

[15]Bhattacharyya R, Mohan S 2015 Solid state storage of hydrogen and its isotopes: an engineering overview
Renew. Sustain. Energy Rev. 41 872 883
DOI:10.1016/j.rser.2014.09.004 [Cited within: 1]

[16]Feng S, Wang N, Li M-L, Xiao H-Y, Liu Z-J, Zu X-T, Qiao L 2021 The thermal and electrical transport properties of layered LaCuOSe under high pressure
J. Alloys and Compounds 861 157984
DOI:10.1016/j.jallcom.2020.157984 [Cited within: 1]

[17]Holec D, Friák M, Neugebauer J, Mayrhofer P H 2012 Trends in the elastic response of binary early transition metal nitrides
Phys. Rev. B 85 064101
DOI:10.1103/PhysRevB.85.064101 [Cited within: 1]

[18]Mascaro A, Toffolon-Masclet C, Raepsaet C, Joubert J-M 2013 Experimental study and thermodynamic assessment of the erbium–hydrogen binary system
Calphad 41 50 59
DOI:10.1016/j.calphad.2013.01.004 [Cited within: 1]

[19]Liang J H, Dai Y Y, Yang L, Peng S M, Fan K M, Long X G, Zhou X S, Zu X T, Gao F 2013 Ab initio study of helium behavior in titanium tritides
Comput. Mater. Sci. 69 107 112
DOI:10.1016/j.commatsci.2012.11.033 [Cited within: 1]

[20]Fan K-M, Yang L, Sun Q-Q, Dai Y-Y, Peng S-M, Long X-G, Zhou X-S, Zu X-T 2013 First-principles study on elastic properties of hexagonal phase ErAx (A H, He)
Acta Phys. Sin. 62 116201
DOI:10.7498/aps.62.116201 [Cited within: 1]

[21]Hill R 1952 The-elastic-behaviour-of-a-crystall
Proc. Phys. Soc. A 65 5
DOI:10.1088/0370-1298/65/5/307 [Cited within: 1]

[22]Yang L, Peng S M, Long X G, Gao F, Heinisch H L, Kurtz R J, Zu X T 2010 Ab initio study of intrinsic, H, and He point defects in hcp-Er
J. Appl. Phys. 107 054903
DOI:10.1063/1.3309834 [Cited within: 1]

[23]Pollnow D, Penelle R, Lacombe P 1975 Relations between the plastic properties and the microstructure of iron single crystals deformed in tension at room temperature
Mem. Sci. Rev. Metall. 72 491 503
[Cited within: 1]

[24]Blaschko O, Pleschiutschnig J, Glas R, Weinzierl P J P R B 1991 Helium damage in metal-tritium systems
Phys.Rev. B 44 9164
DOI:10.1103/PhysRevB.44.9164 [Cited within: 1]