Mian Peng, Li-Hua Bai^,, Zhen GuoDepartment of Physics, College of Sciences, Shanghai University, Shanghai 200444, China

Received:2021-03-15Revised:2021-04-23Accepted:2021-04-26Online:2021-06-04


Abstract
We investigate the nonsequential double ionization (NSDI) of linear triatomic molecules by the counter-rotating two-color circularly polarized (CRTC) laser fields with a classical ensemble method. The results of the simulation reveal that NSDI yield strongly connected with the relative phase. The trajectory tracking method shows that the return time of the electron is controlled by the relative phase. In addition, when we change the CRTC laser wavelengths, the relative phase of the maximum and minimum yield of NSDI also changes. This shows that the influence of the Coulomb potential in the triatomic molecules on the electron return process cannot be ignored. This work will effectively promote the electronic dynamics study of NSDI for the triatomic molecule.
Keywords： linear triatomic molecules;relative phase;two-color laser fields;nonsequential double ionization


PDF (1486KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Mian Peng, Li-Hua Bai, Zhen Guo. Influence of relative phase on the nonsequential double ionization process of CO₂ molecules by counter-rotating two-color circularly polarized laser fields. Communications in Theoretical Physics, 2021, 73(7): 075501- doi:10.1088/1572-9494/abfb60

1. Introduction

The nonsequential double ionization (NSDI) indicates an unusual electron−electron correlation process, where the first ionized electron will return, affecting the ionization dynamics of the second electron. When the energy of the first electron (return electron) returned is greater than the ionization potential of the second electron (bound electron), the bound electron will be ionized directly. This type of ionization is called recollision-impact ionization (RII) [1, 2]. The bound electron cannot be ionized directly if the energy of the returning electron is less than the ionization potential of the bound electron, then the type of ionization is defined as the recollision-induced excitation with subsequent ionization (RESI) [3, 4]. The recollision (RC) process between the first electron and second electron resulting in two electrons ionized in NSDI are strongly correlated [5–7]. The correlation behavior had attracted a lot of experimental [8–11] and theoretical research [12–15] in the past few decades.

In recent years, two-color laser fields have been widely concerned [16–18]. The electric field curve can be regulated by adjusting the parameters [19], which induces the change of dynamic process for electrons in the two-dimensional plane. Recently, the counter-rotating two-color circularly polarized (CRTC) laser fields are used to enhance and suppress high-order harmonic generation of ${{\rm{H}}}_{2}^{+},$ [20]. In the CRTC laser field, the yield of NSDI strongly depends on the amplitude ratio of the electric field [21]. Very recently, studies have discussed that in the CRTC laser fields with a frequency ratio of 1:3 the NSDI events of O₂ molecules have been significantly increased [22]. In the study of two-electron emission dynamics process of NSDI, the interference of the relative phase on the angular distributions and RC is a hot topic. As the relative phase decreases, the triangular structure of the negative vector potential changes significantly, resulting in a change in the ion momentum distribution [23, 24]. Emission direction of the electrons changes with the relative phase, which is causes of RC time and the return angle of the first electron is determined by relative phase of the CRTC laser fields [25]. It is well known that the curve of the CRTC laser fields will rotate in the two-dimensional plane with the varying relative phase, which can greatly affect the return time of the electrons. For aligned molecules the relative phase change will obviously affect the movement of electrons and causes changes in NSDI yield. However, for atoms, because of their spherically symmetry, the relative phase change will not affect the yield. In the above studies [23–25], the dependence of NSDI yield on the relative phase for simple diatomic molecules in CRTC laser fields has been discussed. But the influence of the relative phase on NSDI yield for linear triatomic molecules by CRTC laser fields has not been specifically concerned.

In our paper, we investigate the relative phase influence of the NSDI for CO₂ irradiated by CRTC laser fields with a classical ensemble method. We find that NSDI yield of CO₂ sensitively depends on the relative phase of the CRTC laser fields. For example, the maximum and minimum yield of NSDI are at the relative phase $3\pi /16$ and $7\pi /16.$ The trajectory analysis shows that single ionization and RC time sensitively connected with the relative phase of the CRTC laser fields. In addition, when we change the CRTC laser wavelengths, the maximum and minimum yield of NSDI corresponding to the relative phase also changes. The RC process could be effectively driven by varying the relative phase.

2. Method

In this work, we have used the classical ensemble method [26, 27] to explore the ionization dynamics of CO₂ molecules in CRTC laser fields. This method has been widely used in the research field of intense laser field electron dynamics [28–30]. The classical ensemble method to study the NSDI of linear triatomic molecules in the CRTC laser fields with different relative phase is also used in this paper.

In our calculation, the CO₂ molecular is arranged on the x-axis. The two oxygen atoms are placed at coordinates (−R,0) and (R,0) respectively. Here, the internuclear R=2.19 a.u. the Hamiltonian of a two-electron for linear triatomic molecules without an electric field can be written as (in atomic units)(1)$\begin{eqnarray}{H}_{{e}}=T({{\boldsymbol{p}}}_{i}\,)+V({{\boldsymbol{r}}}_{i}),\end{eqnarray}$where the CO₂ molecular kinetic energy T are given by:(2)$\begin{eqnarray}T({{\boldsymbol{p}}}_{i})=\displaystyle \displaystyle \sum _{i=1,2}\displaystyle \frac{{{\boldsymbol{p}}}_{i}^{2}}{2},\end{eqnarray}$the CO₂ molecular potential energy V are given:(3)$\begin{eqnarray}\begin{array}{lll}V({{\boldsymbol{r}}}_{i}) & = & {V}_{{\rm{n}}{e}}({{\boldsymbol{r}}}_{i})+{V}_{{ee}}({{\boldsymbol{r}}}_{{\boldsymbol{i}}}),\\ {V}_{{\rm{n}}{e}}({{\boldsymbol{r}}}_{i}) & = & -\displaystyle \displaystyle \sum _{i=1,2}\displaystyle \frac{{Z}_{{\rm{c}}}}{\sqrt{{x}_{i}^{2}+{y}_{i}^{2}+{{a}_{{\rm{c}}}}^{2}}}\\ & & -\displaystyle \displaystyle \sum _{i=1,2}\displaystyle \frac{{Z}_{{\rm{o}}}}{\sqrt{{({x}_{i}-R)}^{2}+{y}_{i}^{2}+{{a}_{{\rm{o}}}}^{2}}}\\ & & -\displaystyle \displaystyle \sum _{i=1,2}\displaystyle \frac{{Z}_{{\rm{o}}}}{\sqrt{{({x}_{i}+R)}^{2}+{y}_{i}^{2}+{{a}_{{\rm{o}}}}^{2}}},\\ {V}_{{ee}}({{\boldsymbol{r}}}_{i}) & = & \displaystyle \frac{1}{\sqrt{{({x}_{1}-{x}_{2})}^{2}+{({y}_{1}-{y}_{2})}^{2}+{b}^{2}}},\end{array}\end{eqnarray}$where it is usually the sum of the first ionization potential and the second ionization potential, and where r_i and p_i represent the position and momentum ($i=1,2$) of the electron, respectively. ${Z}_{{\rm{c}}}=2/3$ and ${Z}_{{\rm{o}}}=2/3$ are effective nuclear charge. The potential ${V}_{{\rm{ne}}}({{\boldsymbol{r}}}_{i})$ represents the ion-electron Coulomb interactions, the potential ${V}_{{ee}}({{\boldsymbol{r}}}_{i})$ represents the electron-electron Coulomb interactions. Here, ${a}_{{\rm{c}}}=1,$ ${a}_{{\rm{o}}}=0.8$ and $b=0.05$ are called softening parameters, ${a}_{{\rm{c}}},$ ${a}_{{\rm{o}}}$ is the soft core coefficient used to adjust the bond potential of the atom, shielding the attraction of the atomic nucleus to electrons, and b is the soft core coefficient used to adjust the Coulomb potential between electrons, that is, the Coulomb repulsion of electrons to electrons. Next, we turn on the external laser field. The Hamiltonian of two electrons linear triatomic molecules in the laser field is expressed by(4)$\begin{eqnarray}H={H}_{{e}}+({{\boldsymbol{r}}}_{1}+{{\boldsymbol{r}}}_{2})\cdot {\boldsymbol{E}}(t),\end{eqnarray}$where ${\boldsymbol{E}}(t)={{\boldsymbol{E}}}_{x}(t)+{{\boldsymbol{E}}}_{y}(t)$ is the electric field of the CRTC laser fields. It can be written as(5)$\begin{eqnarray}\begin{array}{lll}{E}_{x}(t) & = & \displaystyle \frac{{E}_{0}}{\sqrt{2}(1+{\gamma }_{E})}f(t)[\,\cos ({\omega }_{1}t+\phi )]\\ & & +\,\displaystyle \frac{{\gamma }_{E}{E}_{0}}{\sqrt{2}(1+{\gamma }_{E})}f(t)[\,\cos ({\omega }_{2}t)],\end{array}\end{eqnarray}$(6)$\begin{eqnarray}\begin{array}{lll}{E}_{y}(t) & = & \displaystyle \frac{{E}_{0}}{\sqrt{2}(1+{\gamma }_{E})}f(t)[\,\sin ({\omega }_{1}t+\phi )]\\ & & -\,\displaystyle \frac{{\gamma }_{E}{E}_{0}}{\sqrt{2}(1+{\gamma }_{E})}f(t)[\,\sin ({\omega }_{2}t)],\end{array}\end{eqnarray}$here, ${E}_{0}$ is the combined electric field amplitude, respectively. In this paper, ${\omega }_{1}=0.057{\rm{a}}.{\rm{u}}.$ (Corresponding wavelength is 800 nm) and ${\omega }_{2}=0.114{\rm{a}}.{\rm{u}}.$ (Corresponding wavelength is 400 nm). φ is the relative phase of CRTC laser fields. $f(t)={\sin }^{2}(\pi t/NT)$ is the pulse envelope function, where N is the number of optical cycles and T is the period of the 1600 nm laser field. In our simulation, N is equal to 16, ${\gamma }_{E}$ is equal to 1, which means the laser intensities of two laser pulses are the same. In our calculations, the two electric field intensities of the CRTC laser field are the same value $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The motion of two electrons is governed by Newton's equations of motion as follows:(7)$\begin{eqnarray}\displaystyle \frac{{\rm{d}}{{\boldsymbol{r}}}_{i}}{{\rm{d}}t}=\displaystyle \frac{\partial H}{\partial {{\boldsymbol{p}}}_{i}},\displaystyle \frac{{\rm{d}}{{\boldsymbol{p}}}_{i}}{{\rm{d}}t}=-\displaystyle \frac{\partial H}{\partial {{\boldsymbol{r}}}_{i}}.\end{eqnarray}$

This equation can be solved with the standard fourth to fifth Runge–Kutta algorithm. The initial position and momentum distribution of the two electrons satisfy the Gaussian random distribution, that ensures the total kinetic energy is positive. Then the electrons are allowed to evolve freely for a long time (100 a.u.) where the position and momentum distribution of the electrons is stable. After getting a stable initial ensemble through screening, the laser field is added, and all electrons begin to evolve under the collective effect of Coulomb potential and electric field until the end of the pulse. When the total energy of both electrons is greater than zero at the end of the pulse, it is recorded as a double ionization event.

3. Results and discussion

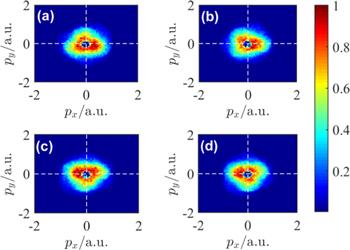
Figure 1 demonstrates the momentum distribution of the two electrons for four relative phases in CRTC laser fields. In the simple-man model [31], we ignore the influence of the initial momentum and Coulomb potential at the moment of ionization, at this time, the final momentum of the electron is the same as the negative vector potential $-{\boldsymbol{A}}(t).$ But in our calculations, the final momentum distribution of the electron is not completely distributed along the negative vector potential triangle. This is because the triatomic molecules have a large Coulomb potential than diatomic molecules, which leads to no obvious triangular structure in the final momentum distribution diagram. In figure 1(a) for $\phi =0,$ more electrons are distributed in the fourth quadrant. For $\phi =3\pi /16$ (figure 1(b)), the distribution of electrons in the first quadrant is the same as that in the second quadrant. For $\phi =7\pi /16$ (figure 1(c)), the electrons are mainly distributed in the second quadrant. For $\phi =\pi /2$ (figure 1(d)), the number of electrons in the third quadrant increases compared to that in figure 1(c). As a whole, the momentum distribution of electrons tends to rotate anticlockwise. This is because the negative vector potential affects the emission direction of electrons. When the relative phase increases, the curve of the negative vector potential rotates clockwise. The information about the momentum distributions of electron in CRTC laser field has been controlled by varying the relative phase.

Figure 1.

New window|Download| PPT slide
Figure 1.Momentum distributions of electrons in CRTC laser fields. The relative phase is: (a) $\phi =0,$ (b) $\phi =3\pi /16,$ (c) $\phi =7\pi /16,$ (d) $\phi =\pi /2,$ respectively.


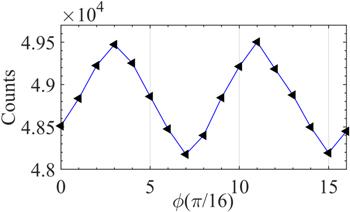
In order to explore the influence of relative phase on NSDI probability, we calculate the change of NSDI probability with relative phases. As shown in figure 2, the NSDI yield is strongly relative to the relative phase. With the change of relative phase, it shows a periodic evolution with the period $\pi /2.$ We can find the NSDI yield achieves its maximum at $\phi =3\pi /16,\,11\pi /16$ and its minimum at $\phi =7\pi /16,15\pi /16.$ When the relative phase changes, the electric field will rotate in the polarization plane. We find that the electric field when the relative phase is $0\sim \pi /2$ and the electric field when the relative phase is $\pi /2\sim \pi $ show symmetry, and when the relative phase is changed by π/2, the electric field is symmetrical with the original; when the relative phase is changed by π, the electric field returns to its original state. Considering that linear triatomic molecules are evenly symmetrical when fixed on the x-axis, the angle of the electron emission and the return angle of the electron are constant with respect to the molecular axis in the case of symmetry. Therefore, the yield of NSDI change periodically with period π/2. Because the yield changes periodically, we mainly focus on the yield of the first half of the cycle. According to the principle of maximum, minimum and boundary conditions, we select four representative phases to discuss.

Figure 2.

New window|Download| PPT slide
Figure 2.The evolution of NSDI yield with relative phase. The CRTC laser wavelength is 800 nm and 400 nm. The division value of relative phase is π/16.


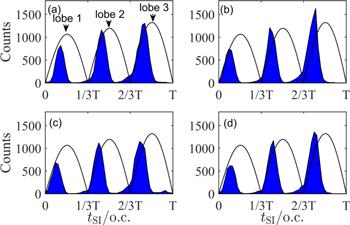
According to the classical electron trajectories analysis method, we investigate the ultrafast dynamics of NSDI in CRTC laser fields. We count the distributions of the single ionization (SI) time ${t}_{{\rm{SI}}}$ and the recollision (RC) time ${t}_{{\rm{RC}}},$ as shown in the figures 3 and 4, respectively. The SI time is defined as the time when the first electron has non-zero energy. The RC time is defined as the time when the returning electron is closest to the second electron. Figures 3(a)–(d) show the SI time distributions for $\phi =0,$ $3\pi /16,$ $7\pi /16$ and π/2 respectively. It is clear that SI mainly occurs before each electric field peak. By comparing the distribution of SI time for different relative phases, it can be known that the yields of SI at the lobe 1 and lobe 2 is approximately the same. The main contribution to the difference of NSDI yield is from the SI at lobe 3. For $\phi =3\pi /16,$ the SI yield at lobe 3 achieves its maximum. For $\phi =7\pi /16,$ the SI yield at lobe 3 achieves its minimum, and for $\phi =0$ and π/2, the SI yield at lobe 3 is roughly the same. From figures 4(a)–(d), one can observe that the RC at lobe 1 varies significantly with the relative phase, and the RC time as a whole increase with the increase of the relative phase. When $\phi =3\pi /16,$ there is the maximum for RC yield. This is because RC occurs at the minimum value of the electric field, when the suppressed potential barrier is lower, RC events is more likely to occur. For $\phi =7\pi /16,$ the situation is the opposite. RC occurs at the maximum value of the electric field, which results in a height of the suppressed potential barrier, reducing RC events. And NSDI yield reach its minimum. So the relative phase is in the range of $(0,\pi /2),$ the NSDI yield reach its maximum at $\phi =3\pi /16,$ its minimum at $\phi =7\pi /16.$ The main reason for this phenomenon is that the yield of NSDI is affected by the angle between the electric field and the molecular axis [24]. As the relative phase increases the three-lobed structure of electric field begins to rotate, which will cause the angle between each lobe of the electric field and the molecular axis increase and decrease periodically. When the angle between the electric field and the molecular axis increases, the suppressed potential barrier becomes higher, thereby inhibiting the dynamic process of electrons. In contrast, it promotes the dynamics of electrons.

Figure 3.

New window|Download| PPT slide
Figure 3.The distributions of SI time in any nth period for (a) $\phi =0,$ (b) $3\pi /16,$ (c) $7\pi /16$ and (d) $\pi /2.$ The CRTC laser wavelength is 800 nm and 400 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The black curve represents the three lobes of the two-color laser electric field in one cycle. The three peaks represent the three maximums in one cycle of the CRTC laser fields.

Figure 4.

New window|Download| PPT slide
Figure 4.The distributions of RC time in any nth period for (a) $\phi =0,$ (b) $3\pi /16,$ (c) $7\pi /16$ and (d) $\pi /2.$ The CRTC laser wavelength is 800 nm and 400 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The black curve represents the three lobes of the two-color laser electric field in one cycle. The first three lobes represent the three maximum of the electric field in one period, and the last lobe represents the first maximum of the electric field in the next period.


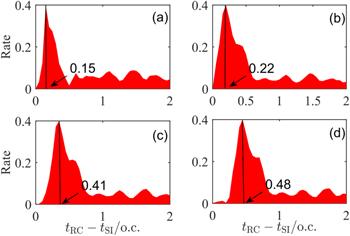
Figures 5(a)–(d) show the traveling time (${t}_{{\rm{R}}}-{t}_{{\rm{SI}}}$) distributions for different relative phases $\phi =0,$ $3\pi /16,$ $7\pi /16$ and $\pi /2$ respectively. The traveling time is the interval between the RC time and the SI time. We can see that as the relative phase increases, the traveling time gradually increases. When the relative phase is $\phi =3\pi /16$ (figure 5(b)), the traveling time is mainly distributed in 0.22 o.c., since the SI time is mainly distributed in 0.085 o.c., 0.385 o.c. and 0.685 o.c. The RC occurs at about 0.3o.c., 0.6 o.c. and 0.9 o.c., corresponding to the trough of electric fields. For $\phi =7\pi /16$ (figure 5(c)), SI time is the same as before, the traveling time is mainly distributed in 0.41 o.c. The RC at about 0.5 o.c., 0.83 o.c. and 1.16 o.c., corresponding to the peak of electric fields. The electron returns at the maximum of the electric field, causing the low energy of the return electrons, thereby suppressing the occurrence of recollision and reducing the yield of NSDI. In contrast, at the minimum electric field, the return electron's energy is higher, which increases the yield of NSDI.

Figure 5.

New window|Download| PPT slide
Figure 5.The distributions of traveling time (${t}_{{\rm{R}}}-{t}_{{\rm{SI}}}$) for (a) $\phi =0,$ (b) $3\pi /16,$ (c) $7\pi /16$ and (d) $\pi /2.$ The CRTC laser wavelength is 800 nm and 400 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The numbers with arrows indicate the main distribution of travel time.


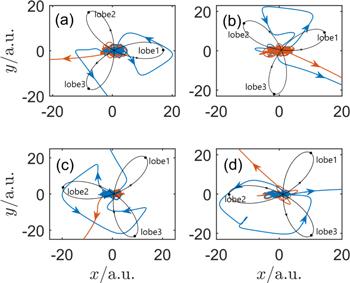
In order to deeply study the position of the electrons of NSDI in CRTC laser fields when they return, we obtain the trajectory of the two electrons in the two-dimensional plane by the trajectory tracking method, as shown in figure 6. It can be seen from the trajectory diagram that for different relative phase, the first electron is ionized near the maximum of lobe 1. As the relative phase changes, the return angle (The return angle is defined as the angle between the electron return direction and the x-axis.) of electrons changes. When the relative phases are $0$ (figure 6(a)) or $\pi /2$ (figure 6(d)), both the electrons return after the maximum value of the electric field. For $\phi =3\pi /16$ (figure 6(b)), the electrons return at minimum of electric field. At this time, the electric field is in the same direction, so the suppressed potential barrier is reduced, which is beneficial to the ionization of the second electron. For $\phi =7\pi /16$ (figure 6(c)), the electrons return at maximum of electric field, at the moment, the electric field will change its direction immediately after the maximum electric field, which will increase the suppressed potential barrier and inhibit the ionization of the second electron.

Figure 6.

New window|Download| PPT slide
Figure 6.The trajectory of the two electrons in the two-dimensional plane for (a) $\phi =0,$ (b) $3\pi /16,$ (c) $7\pi /16$ and (d) $\pi /2.$ The CRTC laser wavelength is 800 nm and 400 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The blue curve represents the trajectory of returning electrons, and the red curve represents the trajectory of bound electrons. The black curve represents the three-lobed structure of the electric field. The point on each lobe represents the maximum value of the electric field.


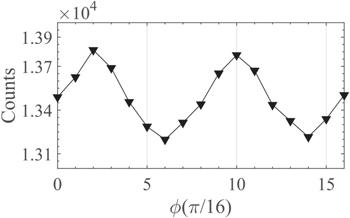
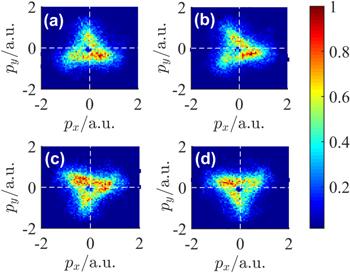
We change the frequency of the CRTC laser fields to ${\omega }_{1}=0.0285\,{\rm{a}}.{\rm{u}}.$ (1600 nm) and ${\omega }_{2}=0.057{\rm{a}}.{\rm{u}}.$ (800 nm). The change of NSDI yield with relative phase is shown in figure 7. The figure shows that the NSDI probabilities reaches its maximum when $\phi =\pi /8,$ and has a minimum when $\phi =3\pi /8.$ We can also see the period is $\pi /2,$ which indicates that we change the wavelength of the CRTC laser field, the yield of NSDI remains periodic with the change of relative phase. However, the peak value of NSDI yield shifts backward, it is different from the laser wavelength 800 nm and 400 nm. This is because when the wavelength of the CRTC laser field increases, the trajectory of the returning electrons becomes longer, resulting in a longer return time. Compared with diatomic molecules, triatomic molecules have a larger Coulomb potential, which will slow down the first electron ionization process and return process. Therefore, the return time of the electrons is prolonged, and the maximum of NSDI yield is shifted. In order to explore the influence of relative phase on the two electrons of NSDI momentum distribution in the long-wavelength laser field, we calculate the final momentum distribution of the two electrons in the NSDI for $\phi =0,$ $\pi /8,$ $3\pi /8$ and $\pi /2,$ with the laser wavelength 1600 nm and 800 nm, as shown in figure 8. It can be seen from figures 8(a)–(d) that the red area where the electron momentum is concentrated changes with the relative phase. Previous studies have shown that the final momentum distribution of the returning electrons is related to the RC time [24]. The momentum distributions of electrons show a phenomenon of counterclockwise rotation, which indicate that the relative phase can also control the RC time in a long-wavelength laser field well. Compared with the momentum distribution of short-wavelength CRTC laser fields, this phenomenon is more obvious. This shows that the wavelength change can also effectively control the electronic recollision process.

Figure 7.

New window|Download| PPT slide
Figure 7.The evolution of NSDI yield with relative phase for CRTC laser fields. The wavelength is 1600 nm and 800 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The division value of relative phase is $\pi /16.$

Figure 8.

New window|Download| PPT slide
Figure 8.Momentum distributions of electrons in the CRTC laser field. The wavelength is 1600 nm and 800 nm, and the laser intensities $2\times {10}^{14}\,{\rm{W}}\,{{\rm{cm}}}^{-2}.$ The relative phase for (a) $\phi =0,$ (b) $\phi =\pi /8,$ (c) $\phi =3\pi /8,$ (d) $\phi =\pi /2.$

4. Conclusions

In summary, we investigated the NSDI of CO₂ molecules by CRTC laser fields with wavelength of 800 nm+400 nm for different relative phases by using the 2D classical ensemble method. The numerical result shows that NSDI yield strongly depends on the relative phase, which reach its maximum at the relative phase $\phi =3\pi /16$ and minimum at $\phi =7\pi /16.$ By analyzing the NSDI trajectories, we find that the electron returns at the minimum of the electric field, which can increase the RC events in $\phi =3\pi /16.$ For $\phi =7\pi /16,$ the situation is the opposite. Furthermore, when the wavelength of CRTC laser fields is 1600 nm+800 nm, the maximum and minimum yield of NSDI corresponding to the relative phase also changes. This is because triatomic molecules have a larger Coulomb potential, which prolongs the return time of electrons. This shows that the influence of the Coulomb potential on the electron return process in triatomic molecules cannot be ignored. Our research provides valuable help for exploring the dynamics of the NSDI process of triatomic molecules.

Acknowledgments

This work was supported by the Natural Science Foundation of Shanghai (Grant No. 18ZR1413600).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Ye D Li M Fu L B Liu J Gong Q H Liu Y Q Ullrich J 2015 Phys. Rev. Lett. 115 123001
DOI:10.1103/PhysRevLett.115.123001 [Cited within: 1]

[2]Maxwell A S Figueira de Morisson F C 2016 Phys. Rev. Lett 116 143001
DOI:10.1103/PhysRevLett.116.143001 [Cited within: 1]

[3]Liu Y Q Fu L B Ye D F Liu J Li M Wu C Y Gong Q H Moshammer R Ullrich J 2014 Phys. Rev. Lett. 112 013003
DOI:10.1103/PhysRevLett.112.013003 [Cited within: 1]

[4]Huang C Guo W L Zhou Y M Wu Z M 2016 Phys. Rev. A 93 013416
DOI:10.1103/PhysRevA.93.013416 [Cited within: 1]

[5]Zhou Y M Liao Q Lu P X 2009 Phys. Rev. A 80 023412
DOI:10.1103/PhysRevA.80.023412 [Cited within: 1]

[6]Kulander K C Cooper J Schafer K J 1995 Phys. Rev. A51 561
DOI:10.1103/PhysRevA.51.561

[7]Corkum P B 1993 Phys. Rev. Lett. 71 1994
DOI:10.1103/PhysRevLett.71.1994 [Cited within: 1]

[8]Weber Th et al. 2000 Nature 405 658
DOI:10.1038/35015033 [Cited within: 1]

[9]WangY L Xu S P Quan W Gong C Lai X Y Hu S L Liu M Q Chen J Liu X J 2016 Phys. Rev. A 94 053412
DOI:10.1103/PhysRevA.94.053412

[10]Eckart S et al. 2016 Phys. Rev. Lett. 117 133202
DOI:10.1103/PhysRevLett.117.133202

[11]Emmanouilidou A Staudte A 2009 Phys. Rev. A 80 053415
DOI:10.1103/PhysRevA.80.053415 [Cited within: 1]

[12]Becker W Liu X Jo Ho P Eberly J H 2012 Rev. Mod. Phys. 84 031011
DOI:10.1103/RevModPhys.84.1011 [Cited within: 1]

[13]Zhang Z L Bai L H Zhang J T 2014 Phys. Rev. A 90 023410
DOI:10.1103/PhysRevA.90.023410

[14]Xu T T Zhu Q Y Chen J H Ben S Zhang J Liu X S 2018 Opt. Express 26 001645
DOI:10.1364/OE.26.001645

[15]Tong A Li Q Ma X Zhou Y Lu P 2019 Opt. Express 27 006415
DOI:10.1364/OE.27.006415 [Cited within: 1]

[16]Mancuso C A et al. 2016 Phys. Rev. Lett. 117 133201
DOI:10.1103/PhysRevLett.117.133201 [Cited within: 1]

[17]Fleischer A Kfir O Diskin T Sidorenko P Cohen O 2014 Nat. Photonics 8 543
DOI:10.1038/nphoton.2014.108

[18]Wu D Guo F M Wang J Chen J G Yang Y J 2020 Communications in Theoretical Physics 72 055503
DOI:10.1088/1572-9494/ab7eca [Cited within: 1]

[19]Chen A Kling M F Emmanouilidou A 2017 Phys. Rev. A 96 033404
DOI:10.1103/PhysRevA.96.033404 [Cited within: 1]

[20]Li H R Zhang H D Zhang J Pan X F Guo P Y Liu X S 2019 Opt. Communications 436 121
DOI:10.1016/j.optcom.2018.12.010 [Cited within: 1]

[21]Eckart S et al. 2016 Phys. Rev. Lett. 117 133202
DOI:10.1103/PhysRevLett.117.133202 [Cited within: 1]

[22]Li B Yang X Ren X Zhang J 2019 Opt. Express 27 032700
DOI:10.1364/OE.27.032700 [Cited within: 1]

[23]Feng F Z Bai L H 2018 Chin. Opt. Lett. 16 063201
DOI:10.3788/COL201816.063201 [Cited within: 2]

[24]Chen J H Xu T T Han T Sun Y Xu Q Y Liu X S 2020 Chin. Phys. B 29 013203
DOI:10.1088/1674-1056/ab5d03 [Cited within: 3]

[25]Huang C Pang H L Huang X F Zhong M M Wu Z M 2020 Opt. Express 28 10505
DOI:10.1364/OE.390281 [Cited within: 2]

[26]Panfili R Eberly J H Haan S L 2001 Opt. Express 8 431
DOI:10.1364/OE.8.000431 [Cited within: 1]

[27]Haan S L Breen L Karim A Eberly J H 2006 Phys. Rev. Lett. 97 103008
DOI:10.1103/PhysRevLett.97.103008 [Cited within: 1]

[28]Peng M Bai L H 2020 Chin. Opt. Lett. 18 110201
DOI:10.3788/COL202018.110201 [Cited within: 1]

[29]Ma X M Zhou Y M Chen Y B Li M Li Y Zhang Q B Lu P X 2019 Opt. Express 27 001825
DOI:10.1364/OE.27.001825

[30]Luo S Q Ma X M Xie H Li M Zhou Y M Cao W Lu P X 2018 Opt. Express 26 13666
DOI:10.1364/OE.26.013666 [Cited within: 1]

[31]L'Huillier A Lompre L A Mainfray G Manus C 1983 Phys. Rev. A 27 2503
DOI:10.1103/PhysRevA.27.2503 [Cited within: 1]