Zihan Wang, Jianxin Zhang^,, Pan Li, Youjian Zhang, Huixin Jin, Wenyang ZhangKey Laboratory for Liquid-Solid Structural Evolution & Processing of Materials (Ministry of Education), School of Materials Science and Engineering, Shandong University, Jinan 250061, China

Received:2020-08-26Revised:2020-11-23Accepted:2020-12-06Online:2021-01-25


Abstract
In this work, the equilibrium structure, electronic and elastic properties of L1₂-ordered Co-Al-W and Co-Al-W-X (X=Ti and Nb) phase were calculated, using first-principles calculations. Among six nonequivalent sites (Al₁, Al₂, Co₃, Co₄, W₅, W₆), Ti and Nb prefer to occupy the W₆ site, since the formation enthalpy of the system is lowest when Ti and Nb occupy the W₆ site. Both Ti and Nb most affect the density of states of Al atoms. Compared with the Al₂ site, which is the sub-preference site of Ti and Nb, the density of states of Al atoms is higher with the addition of Ti and Nb in the W₆ site, which means that the latter system is more stable. According to the bulk modulus B, shear modulus G, Young’s modulus E, hardness H_V and Poisson’s ratio σ, for Co₃(Al, W) alloy, the addition of Ti and Nb in the W₆ site decreases its hardness but increases its ductility. This work confirms that Ti and Nb can stabilize the Co₃(Al, W) alloy and have a positive effect in solving the relatively poor ductility of this alloy, which has important implications for the development of cobalt-based alloys.
Keywords： Co-Al-W phase;equilibrium structure;electronic and elastic properties;first-principles study


PDF (897KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Zihan Wang, Jianxin Zhang, Pan Li, Youjian Zhang, Huixin Jin, Wenyang Zhang. Site preference of Ti and Nb in L1₂-ordered Co-Al-W phase and their effect on the properties of the alloy: first-principles study. Communications in Theoretical Physics, 2021, 73(2): 025702- doi:10.1088/1572-9494/abd0e6

1. Introduction

Superalloys are a special type of high-temperature-resistant material that can work in complex stress and corrosive environments at temperatures above 800 °C. In this class, the successful application is the nickel-based superalloys, which are widely used in turbine blades and engines [1, 2]. As a stable microstructure that contains cuboidal L1₂-ordered γ′-Ni₃Al coherent precipitates appearing in a face-centered cubic (fcc) γ-Ni matrix, these alloys possess sustained high-temperature strength [3]. However, for high-temperature alloys, high-temperature strength is not enough, and hot corrosion resistance is also required, since hot corrosion and oxidation are an important cause of material loss and performance degradation [4]. In order to deal with the problem of hot corrosion, special coatings are used on nickel-based alloys, but such coatings are expensive and require high stability in long-term use [5, 6]. Therefore, an alloy with both high-temperature strength and hot corrosion resistance is required.

Cobalt-based superalloys have excellent resistance to hot corrosion. They can form dense oxide scales to protect the internal metal from corrosion [7-9]. However, the mechanical strength of nickel-based alloys is higher than that of cobalt-based alloys, which limits the application of cobalt-based alloys. The mechanical properties of cobalt-based alloys can be improved by adding solid solution elements and carbides to the alloys [10, 11]. The Co₃Al phase does not exist in the binary Co-Al phase diagram [12]. However, Sato et al discovered the L1₂-ordered Co-Al-W phase, which is similar to the γ′ phase in the nickel-based alloy in the cobalt-based superalloy, which sets the goal of studying the cobalt-based superalloy [11]. The thermodynamic stability of γ′-Co₃₍Al, W) with the addition of Ta and Hf was studied, and it was found that an addition of up to 2.2 at.% Ta does not change the phase equilibria in the Co-Al-W ternary system, but a small addition of Hf stabilizes the γ′ phase [13]. Elemental partitioning and mechanical properties of Ti- and Ta-containing Co-Al-W-based superalloys was studied by atom probe tomography and nanoindentation [14]. In cobalt-based superalloys, Ti, Ta, Nb, Mo and V tend to enter the γ′ phase and increase the solvus temperature of the γ′ phase, whereas Cr, Mn, Fe and Re tend to enter the γ phase and lower the solvus temperature [15-19]. In some cases, the strength of the cobalt-based superalloy is close to the strength of the existing nickel-based superalloy [12].

In the past decade, the first-principles method has become an important method for studying the phase stability, mechanical and thermodynamic properties of crystalline materials [20-22]. Some properties of L1₂γ′-Co₃(M, W) (M=Al, Ge, Ga) have been studied through the first-principles method, which indicates that the γ′ precipitate has a positive significance for improving the performance of cobalt-based alloys [21-24]. Ti and Nb are often added to the γ′ precipitate. They are found to be the most effective in improving the γ′ solvus temperature of Co-Al-W based alloys and are γ′-forming elements which enhance the volume fraction of the γ′ phase [15-17]. The current Co-Al-W based alloy has a main deficiency, which is relatively poorer ductility compared to a nickel-based superalloy [25, 26]. Ti and Nb have an effect on its mechanical properties and probably solve this problem. In addition, the site preference behavior of Ti and Nb in γ′ precipitates and the interaction with their nearby atoms play an important role in improving the performance of γ′ precipitates, so we perform a first-principles study on the phase stability, elastic and electronic properties and site preference of the L1₂-ordered Co₃(Al, W) precipitate doped with Ti and Nb in this work.

2. Theoretical methods

2.1. Computational details

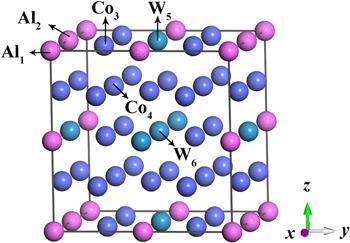
In the unit cell of A₃B compound with the cubic L1₂ structure whose space group is Pm3m, A atoms are located at face centers and B atoms are at cube corners [27]. In this work, the chemical formula is assumed as Co₂₄(Al₄, W₄), which has six nonequivalent positions (Al₁, Al₂, Co₃, Co₄, W₅, W₆) for the substitution by Ti and Nb, as shown in figure 1. The composition of Co₂₄(Al₄, W₄) is similar to the value of γ′ precipitates measured in the experiment [11, 13, 14].

Figure 1.

New window|Download| PPT slide
Figure 1.Crystal structure of L1₂-ordered Co3(Al, W) phase.


In this work, the first-principles method, which is based on the density functional theory (DFT) [28], was applied. The Cambridge Serial Total Energy Package (CASTEP) [28] program was used to perform all the calculations. The generalized gradient approximation (GGA) with Wang parameterization (PW91) and ultra-soft pseudopotential of Vanderbily-type were adopted. The plane wave cut-off energy and k-point were 400 eV and 3×3×3, respectively. The Broyden Fletcher Goldfarb Shanno (BFGS) method [29] was applied to relax the structures. The geometry optimizations were considered to be converged when the energy change per atom, maximum force, maximum stress and maximum atomic displacement were less than $1.0\times {10}^{-5}$ eV, 0.03 eV Å⁻¹, 0.05 GPa and 0.001 Å, respectively. The specific parameters in elastic constant calculation are energy $2.0\times {10}^{-6}$ eV/atom, maximum force 0.006 eV Å⁻¹, maximum atomic displacement 0.0002 Å and maximum strain amplitude 0.003. The spin polarization is considered.

2.2. Elastic properties

The elastic constants can reflect the deformation resistance of a material caused by external stress and express some mechanical properties. The Young’s modulus E, shear modulus G, Poisson’s ratio σ and bulk modulus B can be acquired by the Voigt-Reuss-Hill method [30], which is considered to be a good method to evaluate the theoretical polycrystalline elastic modulus.(1)$\begin{eqnarray}\begin{array}{c}B=\displaystyle \frac{{B}_{V+}{B}_{R}}{2},\end{array}\end{eqnarray}$(2)$\begin{eqnarray}\begin{array}{c}G=\displaystyle \frac{{G}_{V}+{G}_{R}}{2},\end{array}\end{eqnarray}$(3)$\begin{eqnarray}\begin{array}{c}E=\displaystyle \frac{9BG}{3B+G},\end{array}\end{eqnarray}$(4)$\begin{eqnarray}\begin{array}{c}\sigma =\displaystyle \frac{3B-2G}{2\left(3B+G\right)}.\end{array}\end{eqnarray}$

The upper and lower limits of the polycrystalline constants are the values obtained by the Voigt and Reuss equations [31]. Thence, the shear and bulk moduli are estimated by the arithmetic mean values of the Voigt and Reuss moduli [31].

For cubic [32]:(5)$\begin{eqnarray}\begin{array}{c}{B}_{V}=\displaystyle \frac{{C}_{11}+2{C}_{12}}{3},\end{array}\end{eqnarray}$(6)$\begin{eqnarray}\begin{array}{c}{G}_{V}=\displaystyle \frac{{C}_{11}-{C}_{12}+3{C}_{44}}{5},\end{array}\end{eqnarray}$(7)$\begin{eqnarray}\begin{array}{c}{B}_{R}=\displaystyle \frac{1}{3{S}_{11}+6{S}_{12}},\end{array}\end{eqnarray}$(8)$\begin{eqnarray}\begin{array}{c}{G}_{R}=\displaystyle \frac{5}{4{S}_{11}-4{S}_{12}+3{S}_{44}}.\end{array}\end{eqnarray}$

The hardness of materials can be correlated with the product of the squared Pugh’s modulus ratio (k = G/B) and the shear modulus [33]:(9)$\begin{eqnarray}\begin{array}{c}{H}_{V}=2{\left({k}^{2}G\right)}^{0.585}-3.\end{array}\end{eqnarray}$

3. Results and discussion

3.1. Structural properties

In order to analyze the stability of the pure system and doped system, the formation enthalpy (H), which is equal to the energy of formation at 0 K temperature and 0 GPa pressure when the zero-vibration contribution is much smaller than the formation energy, was calculated. A negative H value indicates that the system is stable. The lower formation enthalpy demonstrates a more stable system, which can be applied to assess site replacement behavior of Ti and Nb in Co-Al-W phase. The formation enthalpy can be assessed by the following equation [34-36]:(10)$\begin{eqnarray}\begin{array}{c}H=\displaystyle \frac{{E}_{{\rm{tot}}}-\displaystyle \sum {n}_{i}{E}_{{\rm{atom}}\left(i\right)}}{32},\end{array}\end{eqnarray}$where E_tot is the total energy of the supercell, n_i is the number of i atom in the supercell, and E_atom(i) is the energy per atom of bulk i. Here, the hexagonal close packed (hcp) structure for Co and Ti, face-centered cubic (fcc) structure for Al, and body-centered cubic (bcc) structure for W and Nb are considered as their most stable elemental phases.

The lattice constants (a and c) and formation enthalpy (H) of the pure system and doped system are shown in table 1. Our calculation results are similar to others’ calculation results and experimental results, which shows that our calculation results are credible [11, 37]. It can be seen that Co₃(Al, W) with Ti and Nb replacing any atom in six sites is stable, since their formation enthalpy are all negative. However, compared with the pure system, only when Ti is in the site of Al₁, Al₂, Co₃, W₅ and W₆, and Nb is in the site of Al₂, W₅ and W₆, is the value of formation enthalpy lower. This shows that doping in these sites can make the original system more stable. Ti and Nb show the strongest preference for the W₆ site, followed by the Al₂ site, since the system has the lowest formation enthalpy when Ti and Nb occupy the W₆ site. Among the six substituted sites, the lattice constants of the system with the Co₃ and Co₄ site replaced change more than that of others, as Ti and Nb at these two sites make the symmetry of the system slightly worse. However, the lattice constants change very little, before and after doping, which signifies that the addition of Ti and Nb has little effect on the structure of the system.


Table 1.
Table 1.Calculated structural properties of Co₃(Al, W) phase, including lattice constants a and c, formation enthalpy H.

Materials	site	a (Å)	c (Å)	H (eV/atom)
Co3(Al, W)	\	3.580	3.580	−0.2201
Co3(Al, W) Cal. [37]	\	3.565	3.565	−0.1659
Co3(Al, W) Exp. [11]	\	3.599	3.599	\
Ti doped into Co3(Al, W)	Al1	3.584	3.584	−0.2255
	Al2	3.589	3.574	−0.2398
	Co3	3.621	3.552	−0.2374
	Co4	3.642	3.526	−0.2175
	W5	3.586	3.565	−0.2392
	W6	3.578	3.578	−0.2403
Nb doped into Co3(Al, W)	Al1	3.593	3.593	−0.2080
	Al2	3.598	3.578	−0.2260
	Co3	3.628	3.565	−0.2144
	Co4	3.649	3.539	−0.1901
	W5	3.587	3.585	−0.2239
	W6	3.585	3.585	−0.2269

New window|CSV

3.2. Electronic structures

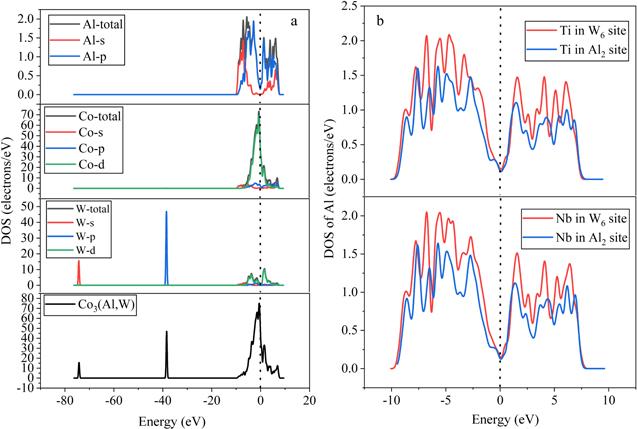
The density of states (DOS) and partial density of states (PDOS) of the L1₂ Co-Al-W and Co-Al-W-X (X=Ti and Nb) phases were calculated, providing information on the physical basis for the phase stability. The DOS of the pure system and the most stable (Ti or Nb is in the W₆ site) and second stable (Ti or Nb is in the Al₂ site) doping systems are shown in figure 2. The level at zero energy is the Fermi energy level (E_F), which is described by the dotted line and is defined to be the highest energy level occupied by the valence electrons at 0 K. The density of states corresponding to the Fermi surface is not zero, indicating that both pure and doped systems are conductive phases [38]. The pseudogap that is the deep valley close to E_F appears in both the pure system and the systems with Ti or Nb occupying the W₆ or Al₂ site, which means that these alloys show a little covalent feature [39]. What is more, their E_F locates in the valley or the left of the pseudogap, demonstrating that both pure and doped systems are stable [38]. According to the partial density of states, this shows that the major valence electron contributions to the bonding electrons in the whole regions are Co (3d), Al (3p), W (5d), Ti (3d) and Nb (4d). The hybridization of Al and W mainly occurs at −7.5 eV ∼ −5 eV and −5 eV ∼ −2.5 eV. Co and W mainly hybridize around −1.5 eV. Doping Ti and Nb has little effect on Co and W atoms, but has a great effect on Al atoms, for the density of states. In figure 2(b), the DOS value of Al atoms in the system with Ti occupying the W₆ site is greater than that in the system with Ti doped in the Al₂ site, indicating that the former system is more stable [40], which is consistent with the previous result that is acquired from the formation enthalpy. In addition, the pseudogap of the former is narrower than that of the latter, which reveals that the bond of the former is more metallic than the latter [38]. The effects of Nb on the Co-Al-W phase are the same as Ti since their DOS are similar.

Figure 2.

New window|Download| PPT slide
Figure 2.The DOS of pure Co₃(Al, W) and doped Co₃(Al, W): (a) the pure Co₃(Al, W); (b) the DOS of Al with addition of Ti or Nb in the Al₂ or W₆ site; (c) Ti in the W₆ site; (d) Ti in the Al₂ site; (e) Nb in the W₆ site; (f) Nb in the Al₂ site.

3.3. Elastic properties

As the most stable structure is when Ti and Nb occupy the W₆ site, followed by the Al₂ site, this section studies the mechanical properties in these two cases. The structures of the Co-Al-W and Co-Al-W-X (X=Ti, Nb) phases are cubic. Table 2 shows the elastic stiffness constants and elastic compliance matrix of them. The corresponding mechanical stability conditions are [41]:(11)$\begin{eqnarray}\begin{array}{c}{C}_{44}\gt 0,{C}_{11}\gt \left|{C}_{12}\right|,{C}_{11}+2{C}_{12}\gt 0.\end{array}\end{eqnarray}$


Table 2.
Table 2.Calculated elastic stiffness constants C_ij (GPa) and elastic compliance matrix S_ij (1/GPa) of Co₃(Al, W) and Co₃(Al, W) with Ti or Nb doping.

Materials	C11	C12	C44	S11	S12	S44
Co3(Al, W)	346.2	191.7	184.0	0.00477	−0.00170	0.00543
Ti in W6 site	322.6	190.6	178.4	0.00552	−0.00205	0.00561
Ti in Al2 site	360.8	184.9	185.2	0.00428	−0.00140	0.00540
Nb in W6 site	324.6	192.2	178.3	0.00551	−0.00205	0.00561
Nb in Al2 site	369.4	182.9	184.8	0.00407	−0.00139	0.00541

New window|CSV

It is obvious that the Co-Al-W and Co-Al-W-X (X= Ti, Nb) phases satisfy the above conditions, indicating that they are all mechanically stable. As the value of C₁₁ is larger than that of C₁₂ and C₄₄, for both the pure system and doped system, they are all very incompressible under uniaxial stress along x axis [31].

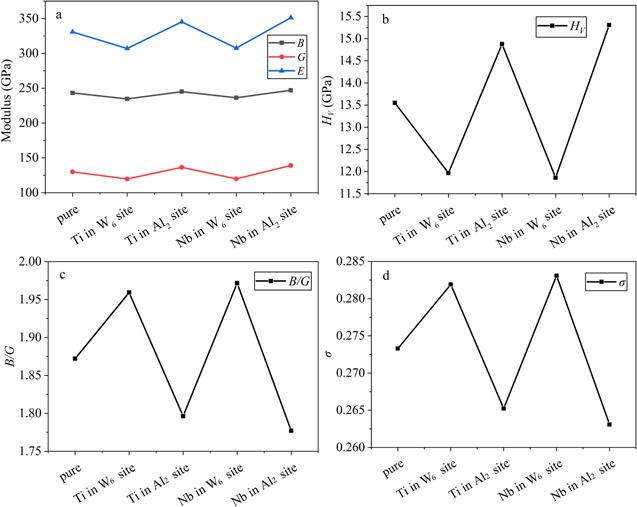
The bulk modulus B and shear modulus G reflect the ability to withstand the volume change under pressure and shear deformation under shear pressure, respectively [42]. In figure 3(a), the values of B and G decline (increase), with the occupation of Ti and Nb in the W₆ (Al₂) site, which means that the resistance ability to volume change and shape change by applied pressure is reduced (improved). Young’s modulus E can be used as a qualitative indicator to reflect the hardness of a material, and a large value of E indicates that the solid is hard [43]. It shows that with adding Ti and Nb in the W₆ site, the values of E decline, which clarifies that the hardness of the doped system decreases. This is consistent with the content in figure 3(b), which is that the H_V value reduces with the addition of Ti and Nb in the W₆ site. However, the change of E and H_V value in the system of the Al₂ site occupied by Ti and Nb is the opposite. The hardness of a metal is generally expressed by its resistance to local deformation [44]. It is obvious that Ti and Nb occupying the W₆ site weaken the ability of the alloy to resist deformation, compared to the Al₂ site. The ratios between bulk modulus and shear modulus B/G and Poisson’s ratio σ reflect the brittleness and ductility of a material [42]. A high (low) B/G value signifies a tendency for ductility (brittleness), and 1.75 is a key value to assess ductility and brittleness [42]. In figure 3(c), all the B/G values are larger than 1.75, which indicates that both the pure system and doped system are ductile. Poisson’s ratio σ (−1< σ < 0.5) can represent the shear resistance of a material [45]. A high Poisson’s ratio σ means that the material has good plasticity [45]. Figure 3(d) shows that Ti and Nb occupying the W₆ (Al₂) site are able to enhance (decrease) the plasticity of the alloy, probably since the system doped in the W₆ site is more metallic than that in the Al₂ site, which is stated in the section on electronic structures. The ductility is closely related to the fracture mechanisms and embrittlement, and generally, achieving high σ is regarded as an approach to improve the toughness [46-48]. It is obvious that Ti and Nb occupying the W₆ site result in less likelihood of fracture and embrittlement, which provides the direction of the design of the Co-based alloy.

Figure 3.

New window|Download| PPT slide
Figure 3.The elastic properties of pure Co₃(Al, W) and doped Co₃(Al, W) with Ti and Nb occupying the Al₂ and W₆ site: (a) the bulk modulus B, shear modulus G and Young’s modulus E; (b) the hardness H_V; (c) the ratios between bulk modulus and shear modulus B/G; (d) Poisson’s ratio σ.

4. Conclusions

The present work was carried out for the equilibrium structure, electronic and elastic properties of the L1₂-ordered Co-Al-W and Co-Al-W-X (X=Ti and Nb) phases, using first-principles calculations. It is found that in doping Ti and Nb to any of six nonequivalent sites, the formation enthalpy of these systems are negative. However, compared with the pure system, the doped system with Ti and Nb occupying the W₆ site is the most stable, followed by the Al₂ site, as the formation enthalpy are most negative. Therefore, Ti and Nb prefer to occupy the W₆ site in the Co-Al-W phase. Ti and Nb most affect the DOS of Al atoms and the DOS shows that the system with the W₆ site doped is most stable. The addition of Ti and Nb in the W₆ (Al₂) site declines (increases) the hardness and the resistance to volume change and shape change of the alloy and improves (reduces) the ductility of the alloy.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (Grant Numbers 51971118, 51771102, 51471098).

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Pollock T M Tin S 2006 J. Propul. Power 22 361
DOI:10.2514/1.18239 [Cited within: 1]

[2]Reed R C Tao T Warnken N 2009 Acta Mater. 57 5898
DOI:10.1016/j.actamat.2009.08.018 [Cited within: 1]

[3]Nembach E Neite G 1985 Prog. Mater Sci. 29 177
DOI:10.1016/0079-6425(85)90001-5 [Cited within: 1]

[4]Eliaz N Shemesh G Latanision R M 2002 Eng. Failure Anal. 9 31
DOI:10.1016/S1350-6307(00)00035-2 [Cited within: 1]

[5]Nicholls J R 2003 MRS Bull. 28 659
DOI:10.1557/mrs2003.194 [Cited within: 1]

[6]Zhu S L Wang F H Lou H Y Wu W T 1995 Surf. Coat. Technol. 71 9
DOI:10.1016/0257-8972(94)02289-3 [Cited within: 1]

[7]Tzvetkoff T Girginov A Bojinov M 1995 J. Mater. Sci. 30 5561
DOI:10.1007/BF00356688 [Cited within: 1]

[8]Douglass D L Bhide V S Vineberg E 1981 Oxid. Met. 16 29
DOI:10.1007/BF00603744

[9]Misra A K 1986 Oxid. Met. 25 373
DOI:10.1007/BF01072916 [Cited within: 1]

[10]Jiang W H Yao X D Guan H R Hu Z Q 1999 J. Mater. Sci. 34 2859
DOI:10.1023/A:1004683301816 [Cited within: 1]

[11]Sato J Omori T Oikawa K Ohnuma I Kainuma R Ishida K 2006 Science 312 91
DOI:10.1126/science.1121738 [Cited within: 5]

[12]Makineni S K Nithin B Chattopadhyay K 2015 Acta Mater. 85 85
DOI:10.1016/j.actamat.2014.11.016 [Cited within: 2]

[13]Kobayashi S Tsukamoto Y Takasugi T 2012 Intermetallics 31 94
DOI:10.1016/j.intermet.2012.06.006 [Cited within: 2]

[14]Povstugar I Choi P P Neumeier S Bauer A Zenk C H Göken M Raabe D 2014 Acta Mater. 78 78
DOI:10.1016/j.actamat.2014.06.020 [Cited within: 2]

[15]Ooshima M Tanaka K Okamoto N L Kishida K Inui H 2010 J. Alloys Compd. 508 71
DOI:10.1016/j.jallcom.2010.08.050 [Cited within: 2]

[16]Bauer A Neumeier S Pyczak F Göken M 2010 Scripta Mater. 63 1197
DOI:10.1016/j.scriptamat.2010.08.036

[17]Cui C Y Ping D H Gu Y F Harada H 2006 Mater. Trans. 47 2099
DOI:10.2320/matertrans.47.2099 [Cited within: 1]

[18]Omori T Oikawa K Sato J Ohnuma I Kattner U R Kainuma R Ishida K 2013 Intermetallics 32 274
DOI:10.1016/j.intermet.2012.07.033

[19]Meher S Yan H Y Nag S Dye D Banerjee R 2012 Scripta Mater. 67 850
DOI:10.1016/j.scriptamat.2012.08.006 [Cited within: 1]

[20]Baghmar D Gaur N K Gupta D C 2010 Phys. B 405 133
DOI:10.1016/j.physb.2009.08.044 [Cited within: 1]

[21]Guédou J Y Joshi S R Vamsi K V Karthikeyan S Choné J 2014 MATEC Web Conf. 14 18001
DOI:10.1051/matecconf/20141400001 [Cited within: 1]

[22]Xu W W Han J J Wang Z W Wang C P Wen Y H Liua X J Zhu Z Z 2013 Intermetallics 32 303
DOI:10.1016/j.intermet.2012.08.022 [Cited within: 1]

[23]Yao Q Zhu Y H Wang Y 2011 Phys. B 406 1542
DOI:10.1016/j.physb.2011.01.065

[24]Chen M Wang C Y 2009 Scripta Mater. 60 659
DOI:10.1016/j.scriptamat.2008.12.040 [Cited within: 1]

[25]Makineni S K Nithin B Chattopadhyay K 2015 Scripta Mater. 98 36
DOI:10.1016/j.scriptamat.2014.11.009 [Cited within: 1]

[26]Feng G Li H Li S S Sha J B 2012 Scripta Mater. 67 499
DOI:10.1016/j.scriptamat.2012.06.013 [Cited within: 1]

[27]Yao Q Shang S L Hu Y J Wang Y Wang Y Zhu Y H Liu Z K 2016 Intermetallics 78 1
DOI:10.1016/j.intermet.2016.08.002 [Cited within: 1]

[28]Segall M D Lindan P J D Probert M J Pickard C J Hasnip P J Clark S J Payne M C 2002 J. Phys. Condens. Matter 14 2717
DOI:10.1088/0953-8984/14/11/301 [Cited within: 2]

[29]Head J D Zerner M C 1985 Chem. Phys. Lett. 122 264
DOI:10.1016/0009-2614(85)80574-1 [Cited within: 1]

[30]Hill R 1952 Proc. Phys. Soc. Sect. A 65 349
DOI:10.1088/0370-1298/65/5/307 [Cited within: 1]

[31]Liu S Zhan Y Z Wu J Y Chen X X Ye H M 2016 Comp. Mater. Sci. 117 1
DOI:10.1016/j.commatsci.2016.01.019 [Cited within: 3]

[32]Duan Y H Sun Y Peng M J Guo Z Z Zhu P X 2012 J. Wuhan Univ. Technol. Mater. Sci. Ed. 27 377
DOI:10.1007/s11595-012-0469-4 [Cited within: 1]

[33]Chen X Q Niu H Y Li D Z Li Y Y 2011 Intermetallics 19 1275
DOI:10.1016/j.intermet.2011.03.026 [Cited within: 1]

[34]Freysoldt C Grabowski B Hickel T Neugebauer J Kresse G Janotti A Van de Walle C G 2014 Rev. Mod. Phys. 86 253
DOI:10.1103/RevModPhys.86.253 [Cited within: 1]

[35]Jiang C 2007 Acta Mater. 55 4799
DOI:10.1016/j.actamat.2007.04.049

[36]Huang S Zhang C H Li R Z Shen J Chen N X 2014 Intermetallics 51 24
DOI:10.1016/j.intermet.2014.02.020 [Cited within: 1]

[37]Yao Q Xing H Sun J 2006 Appl. Phys. Lett. 89 161906
DOI:10.1063/1.2362574 [Cited within: 2]

[38]Du J Wen B Melnik R Kawazoe Y 2014 Intermetallics 54 110
DOI:10.1016/j.intermet.2014.05.021 [Cited within: 3]

[39]Liu Q J Zhang N C Liu F S Liu Z T 2014 J. Alloys Compd. 589 278
DOI:10.1016/j.jallcom.2013.11.215 [Cited within: 1]

[40]Li H S Cao Y Zhou S G Zhu P X Zhu J C 2016 Mod. Phys. Lett. B 30 1650133
DOI:10.1142/S0217984916501335 [Cited within: 1]

[41]Mouhat F Coudert F X 2014 Phys. Rev. B 90 224104
DOI:10.1103/PhysRevB.90.224104 [Cited within: 1]

[42]Pugh S F 1954 Philos. Mag. 45 823
DOI:10.1080/14786440808520496 [Cited within: 3]

[43]Hu W C Liu Y Li D J Li K Jin H L Xu Y X Xu C S Zeng X Q 2014 Philos. Mag. 94 3945
DOI:10.1080/14786435.2014.971903 [Cited within: 1]

[44]Tabor D 1970 Rev. Phys. Technol. 1 145
DOI:10.1088/0034-6683/1/3/I01 [Cited within: 1]

[45]Cao Y Zhu J C Liu Y Nong Z S Lai Z H 2013 Comp. Mater. Sci. 69 40
DOI:10.1016/j.commatsci.2012.11.037 [Cited within: 2]

[46]Hao Y L Li S J Sun B B Sui M L Yang R 2007 Phys. Rev. Lett. 98 216405
DOI:10.1103/PhysRevLett.98.216405 [Cited within: 1]

[47]Greaves G N Greer A L Lakes R S Rouxel T 2011 Nat. Mater. 10 823
DOI:10.1038/nmat3134

[48]Ngai K L Wang L M Liu R Wang W H 2014 J. Chem. Phys. 140 044511
DOI:10.1063/1.4862822 [Cited within: 1]