,?, B. Mirza,?, H. Nadi,§, M. Rostami,?Department of Physics, Isfahan University of Technology, Isfahan, 84156-83111, IranCorresponding authors: ?E-mail:z.sherekat@ph.iut.ac.ir?E-mail:b.Mirza@cc.iut.ac.ir§E-mail:h.nadi@ph.iut.ac.ir?E-mail:mojtaba.rostami@ph.iut.ac.ir
Received:2018-08-31Online:2019-05-1
| Fund supported: |
Abstract
Keywords：
PDF (365KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Z. Sherkatghanad, B. Mirza, H. Nadi, M. Rostami. Extended Phase Space in the Framework of Holography. [J], 2019, 71(5): 590-598 doi:10.1088/0253-6102/71/5/590
1 Introduction
Black holes as thermodynamic objects that can be described by a physical temperature and an entropy has been studied for many years.[1] Hawking and Page explained the instabilities of anti-de Sitter (AdS) black holes and investigated the existence of a specific phase transition in the phase space of the Schwarzschild anti-de Sitter black hole.[2] Black hole thermodynamics with a negative cosmological constant has attracted a lot of attention.[3-4] The properties and critical behaviors of black holes in the AdS space-time are different from those of the black holes in an asymptotically flat space-time.[5-11] The discovery of the first and second order phase transition in the charged Reissner-Nordstrom-anti-de Sitter (RN-AdS) black hole space-time is of particular interest.[12] This transition describes the classical critical behavior and is similar to a liquid-gas phase transition.The Anti-de-Sitter/Conformal field theory (AdS/ CFT) correspondence admits a gauge duality description, where a weak coupling gravity theory in a $d$-dimensional AdS space-time is dual to a strong CFT on the $(d-1)$-dimensional on the boundary. The first attempt to describe duality between the superconductor and gravity theory was reported in Ref. [13]. In order to describe these phenomena within the framework of field theory, we may consider non-local observables such as a two-point correlation function, Wilson loop, which are dual to the geodesic length and minimal area surface, respectively.[14-21]
Some studies have been devoted to the probe of the phase transition of a Van der Waals-like behavior in the framework of holography.[22-25] In Ref. [26], the entanglement entropy and the critical behavior of the heat capacity were calculated close to the critical point for RN-AdS black holes in the background in a fixed charge ensemble. In this condition, the change of entanglement entropy with respect to the reverse of temperature was plotted. We should note that the entanglement entropy is derived by using Ryu and Takayanagi (RT) method and temperature is the black hole temperature (Hawking temperature). Since this temperature is not correspond to the entanglement temperature presented in the first law of entanglement entropy, naturally the black hole temperature is not conjugate with the entanglement entropy. Also, the phase structure of the BI-AdS black holes was considered by using the two-point correlation function and holographic entanglement entropy in Ref. [27]. The results show that the phase transitions and critical behaviors in the framework of holography are similar to the thermal behavior of a charged-AdS black hole. The critical behaviors of black holes in the AdS space in the extended phase space have been studied where the cosmological constant behaves as a thermodynamic parameter, pressure, in the first law of thermodynamics.[28-32] In this approach, the black hole mass $M$ is replaced with enthalpy instead of internal energy. The analogy between AdS charged black holes in an extended phase space and the Van der Waals fluid have been shown in Ref. [33]. Also, the phase diagrams of rotating black holes with single and multiple spinnings have been shown to be similar to those of Reentrant phase transition and triple point phenomena, respectively.[34-38] Thus, treating the cosmological constant as a variable in an extended phase space, can be significant from the holographic viewpoint.
We should note that the thermodynamic quantities in the framework of holography ``probes" the phase transition that black hole thermodynamics tells us. However, because the ``first law" employed in these works is not actually a valid first law, such a construction generically predicts the wrong temperatures for the phase transitions. Many of these issues have recently been nicely discussed in Ref. [39].
Recently, there are two conjectures for the holographic calculation of the complexity. One of them is called the ``complexity=volume'' proposal and refereed by CV. The other one is called ``complexity=action'' and refereed by CA.
For CV proposal, Susskind proposed the ideas of geometric holographic duals of complexity of a quantum system as volumes in an AdS space-time.[40] A maximal volume spacelike slice in the bulk, anchored at the boundary, gives the complexity of the boundary state at a given time-slice.[41-43] In CA proposal, it was suggested that the complexity is indicated by the gravitational action evaluated on a bulk region known as the Wheeler-DeWitt (WDW) patch.[44] An appropriate prescription for calculating the action for a region of spacetime bounded by null surfaces was obtained in Refs. [45-48]. In Ref. [49], an investigation towards understanding circuit complexity in quantum field theory is accomplished. We should note that both conjectures (CV and CA) have competence, as well as shortcomings.
One can consider the CV proposal with a natural generalization which concerns generic mixed states, which is described by what is well known as the reduced density matrix. For such a state, the volume is enclosed by the minimal area appearing in the computation of the holographic entanglement entropy and the corresponding subregion in the boundary theory.[50] The holographic subregion complexity is defined as
where, volume, $V (\gamma)$ is the part in the bulk geometry that is enclosed by the minimal hyper-surface; $R$ is the radius of the curvature of the space-time, (e.g. that of AdS radius); and $G$ is the Newton's constant. We build upon this assumption to probe an extended phase space thermodynamic of black holes for the holographic system using the subregion complexity and fidelity susceptibility as the holographic volumes and the cosmological constant (pressure) as the thermodynamic variables. In our set up, we search the pseudo phase srtucture in the background of RN-AdS and BI-AdS black holes in the holographic framework.
In Ref. [51], the gravity dual of fidelity susceptibility was proposed based on a volume of maximal time slice in an AdS space-time. Also, a quantum information metric was investigated with respect to a small perturbation within conformal field theories using a primary operator. Thus, for an asymptotically AdS$_{d+1}$ solution, fidelity susceptibility is holographically defined by
where, $n_d$ is a constant of order one and $R$ is the AdS radius.
We study the diagram of the pressure with respect to volumes associated to minimal surface and fidelity susceptibility for the RN-AdS black hole in background. There exists a critical point where one can observe a second order phase transition. For the pressures smaller than the critical value, there is a first order phase transition; however, when its values exceed the critical value, there is no phase transition and the system is stable. This critical behavior in the holographic extended phase space is reminiscent of the Van der Waals liquid-gas system. We should note that, since there is not the possibility to define the first law of thermodynamic conjugate to the second law, the phase transitions in the framework of holography are not real and we call them pseudo phase transition. Also, we take the Born-Infeld-AdS black holes in the bulk as a nonlinear electrodynamic solution of the Einstein-Born-Infeld action. We calculate the volume enclosed by the minimal area appearing in the computation of the entanglement entropy.
The rest of the paper is organized as follows. In Sec. 2, we review the phase structure of four-dimensional-RN-AdS black holes in the extended phase space. In Sec. 3, we assume the cosmological constant as pressure and and volume as the codimension one-time slice in the bulk geometry enclosed by the minimal area appearing in the computation of the holographic entanglement entropy in the background of RN-AdS black holes. In this condition we probe the pseudo phase structure of the corresponding thermodynamic system. Also, the pseudo phase structure of the holographic thermodynamic system is described where the fidelity susceptibility is taken as the volume and RN-AdS black holes is in the background. In Sec. 4, the calculations are extended to the BI-AdS black holes to explore the pseudo phase transition.
2 Phase Structure of Four-Dimensional RN-AdS Black Holes in the Extended Phase Space
We start this section with a review of some of the basic thermodynamic properties and phase transitions of the spherical RN-AdS black hole.[12,33] The Einstein-Maxwell action in 4 dimensions reads as follows:The RN-AdS metric which is a solution of this action and the U(1) field are given by:
where $d\Omega_2^2$ is the standard element on $S^2$. Here, the parameter $M$ represents the ADM mass of the black hole, which is associated with the enthalpy of the system in the extended phase space and $Q$ represents the total charge. The event horizon of the black hole is located in the larger root of $f(r_+) = 0$. The thermodynamic quantities of the RN-AdS black hole are[33]
The first law of black hole thermodynamics in an extended phase space; when it includes $P$ as the thermodynamic variables , it turns to the following form:
The equation of state for a fixed charge $Q$ from Eqs. (6) can now be written as
where, $v=2 r_+$ is the specific volume. The critical point is estimated by the following conditions,
Using the above conditions and Eq. (9), we can plot the corresponding $ "P - r_+$ diagram" in Fig. 1 for fixed values of $Q$ and $T$. Clearly, there is an inflection point for the isotherm $T<T_c$ and a critical isotherm at $T=T_c$, which is similar to the Van der Waals behavior.
Fig. 1
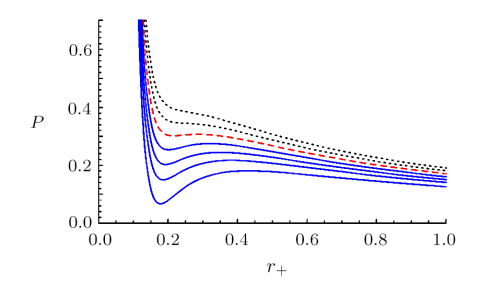New window|Download| PPT slideFig. 1(Color online) The $P-r_+$ diagram of RN-AdS black hole for $d=4$ and $Q=0.1$. The temperatures of the isotherms increase from bottom to top. The upper dotted (black) lines correspond to the ideal gas, we have one phase for $T > Tc$ and the critical isotherm $T = Tc=0.44$ is denoted by the dashed (red) line. The lower (blue) solid lines correspond to temperatures smaller than the critical one $T <Tc$.
The phase transitions and the swallowtail behavior can be explicitly shown in the $G-T$ plane, where $G=M-TS$ is the Gibbs free energy. Using the first law of black hole thermodynamics in Eq. (8) one can obtain:
Evaluation of the constant value of $G(T_0)$ should be based on the fact that the Gibbs free energy vanishes for the zero value of horizon. The diagram of $G-T$ is depicted in Fig. 2. It may be noted that there is a first order phase transition for $P<P_c$ and that a second order phase transition occurs at the critical point $P=P_c$. Therefore, the system shows a first order small/large black hole phase transition similar to the liquid/gas phase in fluids.
Fig. 2
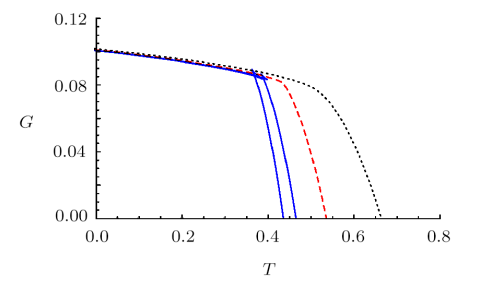New window|Download| PPT slideFig. 2(Color online) Gibbs free energy of the RN-AdS black hole with respect to temperature for $d=4$, $Q=0.1$. Pressure $P$ increases from bottom to top. The dashed (red) line corresponds to the critical pressure $P=P_c= 0.3315$.
3 Holographic Extended Phase Space for RN-AdS Black Holes in 4 Dimensions
The entanglement entropy can be given by the area of a minimal surface in the following form,[52]by replacing Eq. (4) and the definition of the area into Eq. (12), we have
where, $\theta_0$ is the boundary of the entangling region in the $\theta$ direction. Considering the Euler-Lagrange equation, the equation of motion for $r(\theta)$ is given by
It is not easy to solve $r(\theta)$ analytically, thus, we try to solve it numerically using the boundary conditions
where, $\epsilon$ is a small parameter in the order of $10^{-6}$. Since the entanglement entropy is divergent at the boundary, we regularize it by subtracting the entanglement entropy from the pure AdS one, $\delta S_{\rm Reg}=S-S_{\rm AdS}$.
In order to describe the pseudo phase transition in the holographic system, we need to consider anpressure and volume corresponding to the minimal surface. The pressure can be described as follows:
The Volume related to the bulk geometry enclosed by the minimal hyper-surface in the calculation of entanglement entropy for a subsystem $A$ in the boundary theory is
Thus, the volume for the pure AdS from Eq. (17) read as
here
and $\theta_0$ is the boundary in which $r(\theta_0)=\infty$. We regulate the volume by taking into account $r(\theta_0)={l^2}/{\epsilon}$ in our calculations.[26] Now, the volume enclosed by the minimal area for RN-AdS black hole can be evaluated as follows:
By replacing the numerical calculations of $r(\theta$) from the Euler-Lagrange equation in Eq. (14), we can obtain the volume enclosed by the minimal area. Since this quantity is divergent at the boundary, $\theta=\theta_0$, it should be regularized by subtracting off the volume of the pure AdS in Eq. (18). The regularized volume is denoted by $\delta V_{\rm Reg}=V-V_{\rm AdS}$. In the numerical calculation, we consider the size of the boundary region to be $\theta_0 = 0.16$ and we take the UV cutoff in the dual field theory equal to $r(0.159)$.
We can depict the isocharges on the pressure-volume plane, $P-\delta V_{ \rm Reg}$, on the boundary in Fig. 3 for fixed values of $Q$. We observe that there is an inflection point for the isotherm at $T<T_c$ and a critical isotherm at $T=T_c$. We may conclude that the thermodynamic behavior associated with the minimal surface in the background of a four-dimensional RN-AdS black hole, corresponds to that of the Van der Waals fluid. So we call this Van der Waals-like behaviour.
Fig. 3
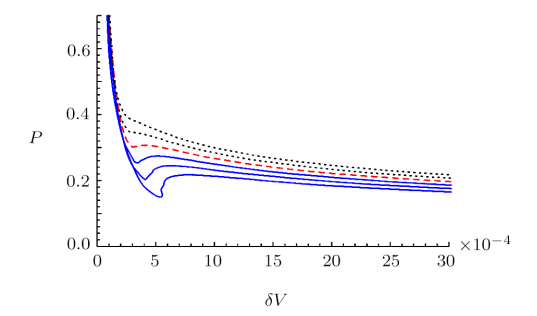New window|Download| PPT slideFig. 3(Color online) The $P-\delta V_{\rm Reg}$ diagram for $d=4$ and $Q=0.1$. The temperature of the isotherms increase from bottom to top. The upper dotted (black) line corresponds to the ideal gas. We have one phase for $T > Tc$. The critical isotherm $T = Tc=0.44$ is denoted by the dashed (red) line. The lower (blue) solid lines correspond to temperatures smaller than the critical one $T <Tc$.
Now we propose a new quantity, $G =-\int SdT|_{Q,P}$ where $S$ is entanglement entropy and $T$ is Hawking temperature. We call this quantity, $G$, the pesudo Gibbs free energy. It may be noticed that $G$ is proportional to the entanglement entropy. Therefore, it is divergent at the boundary, $\theta=\theta_0$, and the entanglement entropy should be regularized by subtracting off one in the pure AdS, which is then designated by $\delta G$. We should note that the definition of $\delta G$ is not based on first law of entanglement entropy and $S-S_{\rm AdS}$ and $T$ are not conjugate. So the argument of $dS > 0 =>dG < 0$ does not follow. In this condition, we consider $\delta G$ for fixed values of $Q$ and $P$ as
The critical behavior of $\delta G$ with respect to temperature on the boundary is depicted for $d = 4$ in Fig. 4. The pseudo phase transitions and the swallowtail behavior can be explicitly shown in this diagram. The novel and interesting result is that we see a behavior similar to a first order phase transition for $P<P_c$ and a pseudo second order phase transition occurs at the critical point $P=P_c$. Also, we observe one phase for $P>P_c$. Thus, when the volume (subregion complexity) is taken as the variable, the phase structure in the extended phase space of this holographic system follows the Van der Waals behavior. The critical behavior of $\delta G$ with respect to temperature is similar to that of RN-AdS black holes and that is why we call this quantity the pesudo Gibbs free energy.
Fig. 4
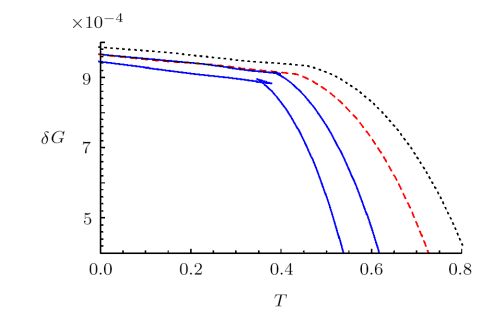New window|Download| PPT slideFig. 4(Color online) The $\delta G-T$ diagram for $d=4$ and $Q=0.1$. The pressure $P$ increases from bottom to top. The dashed (red) line corresponds to the critical pressure $P=P_c= 0.3315$.
3.1 Phase Structure of Fidelity Susceptibility
As the gravity dual of fidelity susceptibility is represented by a volume of maximal time slice in an AdS spacetime,[51] it is plausible to follow the phase structure of black hole in the holographic framework provided that we get the fidelity susceptibility as the volume in the extended phase space. The geometric holographic duals of fidelity susceptibility of a quantum system as volume in AdS space-time is investigated in Ref. [51].It is not out of place at this juncture to extend our arguments so far to other volumes that might exhibit a critical behavior similar to that of Van der waals system. Consider the quantum state $|\Psi(\lambda)>$ and perturb it with $\lambda$ infinitesimally $\lambda \to \lambda+\delta\lambda$ while $\lambda$ is an external excitation parameter. If the two states are close to each other, then it is possible to define the inner product between them as follows
where, $G_{\lambda \lambda}$ represents fidelity susceptibility defined by Eq. (2). Also, the volume ${\rm Vol}(\sum_{\max})$ can be evaluated in the following form
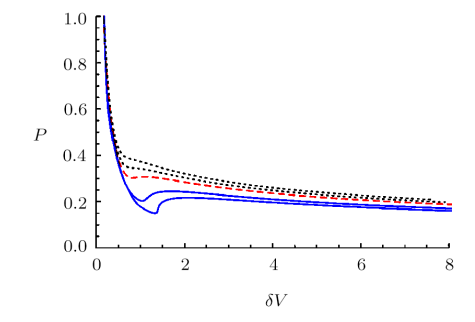
where, $r_\infty$ is a cutoff parameter and we set $r_{\infty}={1}/{\epsilon}$, while $\epsilon \ll 0.01$ in our numerical calculation. The volume that comes from the fidelity susceptibility is divergent at the boundary, $r_\infty$, and it should be subtracted from the volume in the pure AdS. The regularized volume was previously designated by $\delta V_{\rm Reg}=V-V_{\rm AdS}$. We depict the isocharges on the pressure-volume, $P-\delta V$, plane, on the boundary in Fig. 5. Therefore, when the volume is related to the fidelity susceptibility, the critical behavior of the holographic system in the extended phase space exhibits a behavior similar to that of RN-AdS black holes for fixed values of $Q$. The novel result is that the two proposed $P-V$ system where volumes represent the subregion complexity and fidelity susceptibility have the same critical behavior while the critical temperatures $T_c$ are also equal.
Fig. 5
New window|Download| PPT slideFig. 5(Color online) The $P-\delta V_{\rm Reg}$ diagram from the ``fidelity susceptibility" in $d=4$ and $Q=0.1$. The temperatures of the isotherms increase from bottom to top. The upper dotted (black) line corresponds to the ideal gas; we have one phase for $T > Tc$ and the critical isotherm $T = Tc=0.44$ is denoted by the dashed (red) line. The lower (blue) solid lines correspond to temperatures smaller than the critical one $T <Tc$.
4 Holographic Extended Phase Space for Born-Infeld-AdS Black Holes in 4 Dimensions
In this subsection, we study the black hole solution of Einstein-Born-Infeld action in the 4-dimensional extended phase space. The Enistein-Born-Infeld action in the AdS space-time is of the following form[30]where
and $\beta$ is known as the Born-Infeld parameter, which represents the maximal electromagnetic field strength. In the Schwarzschild-like coordinates, the metric and the electromagnetic field of the spherically symmetric solution reads as follows:
here, $d\Omega_2^2$ denotes the metric of a unit $2$ sphere. The metric function is given by:
in which, ${_2 F}_1({1}/{4},{1}/{2};{5}/{4};{Q^2}/{\beta^2 r^4})$ is the hypergeometric function. For the first law of thermodynamics, we have[33]
In the extended phase space, the thermodynamic quantities such as the black hole temperature $T$, entropy $S$, volume $V$ and the corresponding pressure $P$ are given by:
The corresponding phase transitions and critical exponents of the Born-Infeld-AdS black holes in the extended phase space have been investigated in the canonical ensemble.[33] The equation of state from Eq. (29) for the Born-Infeld-AdS black hole with a fixed charge $Q$ and a Born-Infeld parameter $\beta$ translates into:
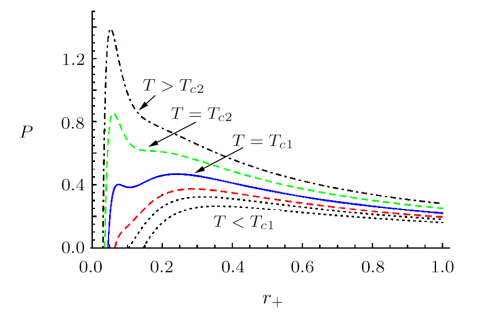
One can show that the $P-r_{+}$ diagram of the BI-AdS black hole for $d=4$, $Q=0.16$ and $\beta=5$ is similar to that of the Van der Waals gas (Fig. 1). The associated isotherms in the $P-r_+$ diagrams are displayed in Fig. 6 for a charge values of $Q=0.08$ and Born-Infeld parameter of $\beta=5$. The critical behavior depends on values of charge, Q, and a Born-Infeld parameter, $\beta$. For $\beta Q > 1/2$, the behavior is qualitatively similar to that of the Van der Waals gas. For $\beta Q <1/2$, the phase transitions are different from those of the Van der Waals fluid. In this regime, there are two critical points at $T=T_{c1}=0.5$ and $T=T_{c2}=0.58$. Therefore, the system undergoes a Reentrant phase transition while a monotonic variation of one thermodynamic quantity results in two (or more) phase transitions such that the final state is macroscopically similar to the initial state, for $\beta Q <1/2$.[33]
Fig. 6
New window|Download| PPT slideFig. 6(Color online) The $P-r_+$ diagram of the BI-AdS black hole for $d=4$, $Q=0.08$, and $\beta=5$. The temperatures of the isotherms increase from bottom to top. We have two critical points a $T=T_{c1}=0.5$ and $T=T_{c2}=0.58$.
4.1 Holographic Phase Structure
Now let us probe the phase transitions represented by BI-AdS black hole thermodynamic in the framework of holography by using the volume associated with the minimal area appearing in the computation of the holographic entanglement entropy in the presence of BI-AdS black hole,where
Similar to the previous calculations we can obtain the numerical solutions of $r(\theta$) from the Euler-Lagrange equation expressed by Eq. (14). It is, then, possible to obtain the volume enclosed by the minimal area. Since this quantity is divergent at the boundary, $\theta=\theta_0$, it should be regularized by subtracting off the area in the pure AdS with the same entangling surface on the boundary.The regularized volume was designated by $\delta V_{\rm Reg}=V-V_{\rm AdS}$. The sizes of the boundary region and the UV cutoff in the dual field theory are taken to be equal $\theta_0 = 0.16$ and $r(0.159)$, respectively.
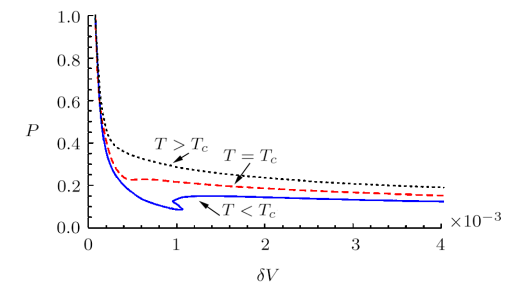
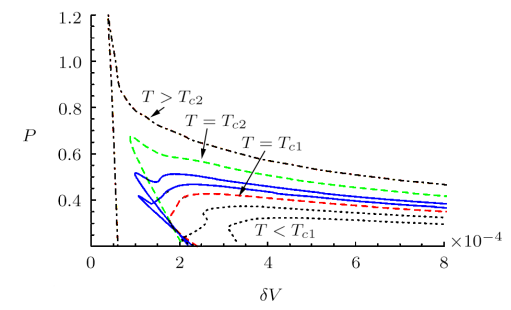
The isocharges for the pressure-volume plane, $P$-$\delta V$, on the boundary are depicted in Figs. 7 and 8. Clearly, the critical behavior is similar to that of BI-AdS black holes and the results depend on the two parameters of $Q$ and $\beta$. For $\beta Q>{1}/{2}$, we find an inflection point for the isotherm at $T<T_c$ and a critical isotherm at $T=T_c$. We may conclude that the critical behavior of the holographic surface for $\beta Q>{1}/{2}$ is similar to those of a Van der Waals fluid. Also, for $\beta Q<{1}/{2}$ we have two critical points at $T = T_{c1}$ and $T = T_{c2}$ corresponding to a Reentrant phase transition (Fig. 8). Results show that the phase structure of this holographic extended phase space in the background of BI-AdS black hole mimic the phase transition of BI-AdS black hole.
Fig. 7
New window|Download| PPT slideFig. 7(Color online) The $P-\delta V_{\rm Reg}$ diagram of BI-AdS black hole for $d=4$, $Q=0.16$, and $\beta=5$. The temperature of isotherms increase from bottom to top. The upper dotted (black) line corresponds to the ideal gas, for $T > Tc$ and the critical isotherm $T = T_c=0.36$ is denoted by the dashed (red) line. The lower (blue) solid line corresponds to temperatures smaller than the critical one $T <Tc$.
Fig. 8
New window|Download| PPT slideFig. 8(Color online) The $P$-$\delta V_{\rm Reg}$ diagram of a BI-AdS black hole for $d=4$, $Q=0.08$, and $\beta=5$. The temperatures of the isotherms increase from bottom to top. We have two critical points at $T = T_{c1}$ and $T = T_{c2}$.
5 Conclusion
Recently, holographic dual volumes have been proposed as related to the subregion complexity and fidelity susceptibility of a quantum system on the boundary of the AdS space time. Considering the cosmological constant (pressure) as variable and the volumes associated to the minimal hyper-surface (entanglement entropy) or fidelity susceptibility in the background of RN-AdS and BI-AdS black holes leads to an extended phase space. In order to explore the phase transitions in the framework of this extended phase space, we studied the isocharges on the pressure and volume plane. We then calculated the volume related to a codimension one-time slice in the bulk geometry enclosed by the minimal area appearing in the computation of the holographic entanglement entropy. Also, the isocharges on the pressure-volume plane for both volumes (the subregion complexity and fidelity susceptibility) were found to a Van der Waals-like structure for the RN-AdS in background. We observed a analogy between this system and the Van der Waals liquid-gas. We should note that, since the pressure and volume are not conjugate, we have not a valid first law. The results only suggest these quantities can serve as probes of the underlying phase transition dictated by black hole thermodynamics, but do not describe different structures. That is, no special meaning can be given to crossing points of the pseudo-Gibbs free energy. In this condition, there are not strong reasons to describe the observed phase transitions as different structure. This interesting observation needs to be more investigated in the future studies. We hope that this research initiates some more investigation about this interesting subject. It was also found the Van der Waals and Reentrant phase transition for four-dimensional BI-AdS black holes depended on the values of the Born-Infeld parameter $\beta$ and charge $Q$. For $\beta Q>{1}/{2}$, we obtain an inflection point for the isotherm at $T<T_c$ and a critical isotherm at $T=T_c$. This led to conclusion that the critical behavior of the minimal hyper surface for $\beta Q>{1}/{2}$ is similar to that of a Van der Waals fluid. Also, for $\beta Q<{1}/{2}$, we noticed two critical points at $T = T_{c1}$ and $T = T_{c2}$ corresponding to a Reentrant phase transition. Results showed that the phase structure from holographic point of view is analogous to that of the four-dimensional BI-AdS black hole in the extended phase space. Meanwhile, it was understood that the holographic extended phase space exhibits similar phase structures for both volumes related to the subregion complexity and fidelity susceptibility. It would be interesting to explore the phase structure and critical behavior at the dual boundary within the framework of the field theory and to investigate the thermodynamic behavior of subregion complexity and fidelity susceptibility on the boundary of the AdS space time.Acknowledgments
We would like to thank M. Alishahiha for useful discussions.Reference By original order
By published year
By cited within times
By Impact factor
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 2]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 6]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 1]
[Cited within: 3]
[Cited within: 1]
