Caiyun Xiong¹, Xiaolin Nie², Yixue Peng¹, Xun Zhou², Yangtao Fan^,3,∗∗, Hu Chen^,4,∗∗, Yanhui Liu^,1,5,∗∗1College of Physics, Guizhou University, Guiyang 550025, China
²School of Physics and Electronic Science, Guizhou Normal University, Guiyang 550025, China
³Collaborative Innovation Center for Optoelectronic Semiconductors and Efficient Devices, PenTung Sah Institute of Micro-Nano Science and Technology, Xiamen University, Xiamen, 361005, China
⁴Research Institute for Biomimetics and Soft Matter, Fujian Provincial Key Lab for Soft Functional Materials Research, Department of Physics, Xiamen University, Xiamen, 361005, China
⁵Breeding and Reproduction in The Plateau Mountainous Region, Ministry of Education (Guizhou University), Guizhou Guiyang, 550025, China

First author contact: ^∗∗Authors to whom any correspondence should be addressed.
Received:2021-02-18Revised:2021-04-24Accepted:2021-04-29Online:2021-06-04

Fund supported:

National Natural Science Foundation of China under Grant Nos.11464004.11864006.11564015 Guizhou Scientific and Technological Program.20185781.20185781-15 Foundation of Key Laboratory of Animal Genetics, Breeding and Reproduction in The Plateau Mountainous Region, Ministry of Education (Guizhou University).KY2020243

Abstract
Knots are discovered in biophysical systems, such as DNA and proteins. Knotted portions in knotted DNA are significantly bent and their corresponding bending angles are comparable with or larger than the sharp bending angle resulting in flexible defects. The role of flexible defects in the interplay of supercoiling and knotting of circular DNA were predicted by a Monte Carlo simulation. In knotted DNA with a particular knot type, a flexible defect noticeably enhances the supercoiling of the knotted DNA and the decreasing excitation energy makes the knotted portion more compact. A reduction in twist rigidity and unwinding of flexible defects are incorporated into the numerical simulations, so that interplay of supercoiling and knotting of circular DNA is studied under torsional conditions. Increasing unwinding not only results in a wider linking number distribution, but also leads to a drift of the distribution to lower values. A flexible defect has obvious effects on knotting probability. The summation of equilibrium distribution probability for nontrivial knotted DNA with different contour length does not change with excitation energy monotonically and has a maximum at an intermediate value of excitation energy around 5k_BT. In the phase space of knot length and gyration radius of knotted DNA, knot length does not anticorrelate with its gyration radius, which is attributed to the flexible defect in the knotted portion, which leads to the release of bending energy and inhibited the competition between entropy and bending energy.
Keywords： knot; flexible defect;DNA topology;knotted DNA;Monte-Carlo simulation


PDF (1087KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Caiyun Xiong, Xiaolin Nie, Yixue Peng, Xun Zhou, Yangtao Fan, Hu Chen, Yanhui Liu. Influences of flexible defect on the interplay of supercoiling and knotting of circular DNA^*. Communications in Theoretical Physics, 2021, 73(7): 075602- doi:10.1088/1572-9494/abfcb7

1. Introduction

Circular DNA can develop into physical knots with different complexity facilitated by DNA topoisomerases and knots have been discovered in a wide range of systems, from biopolymers, such as DNA and proteins, to macroscopic objects, such as umbilical cords and catheters [1–3]. Over the past decades, significant advances in experiments and the theory of knots have been made [4–9]. In experiments, knots in DNA or other biopolymers can be tied manually [10], formed spontaneously [11] or by compression [12]; the knot in DNA under tension [13] or in nanochannel can be identified as a bright spot diffusing along DNA via fluorescent labeling [14]. And knots in DNA can also be identified directly via Atomic-force microscopy imaging [15] or nanopore translocation experiment [16].

Theoretical works concentrated on knot behaviors under various conditions, such as in a free space [17], in spatial confinement [18], under pulling forces [19], in a crowded environment [20] and with different bending stiffness [21, 22]. Related molecular dynamics simulations were performed on a model of diblock flexible-stiff polymer ring hosting a knot to address a question of how the stiffness of polymer could affect topological properties, such as the position and size of knots within a circular knotted polymer. When both blocks are long enough to accommodate a knot, raising temperature could drive a knot shift from the flexible part to the stiffer one [23].

The dependence of equilibrium knotting properties on the bending rigidity was detected by Monte Carlo simulations. Knotting probability is non-monotonically dependent on knot length of semi-flexible rings, which are taken from rigidity to fully-flexible limit [24]. Effects of intra-chain interactions on knots have been systematically investigated, the results indicated that knots could be tightened by long-range repulsions [25], which could be applied to trap a knot into tight conformations by Langevin dynamics simulations. The strength of intra-chain repulsion was tuned to weakly trap a knot, so that the knot weakly trapped could escape from the trap and was then re-trapped by thermal fluctuations; its switching between tight and loose conformations was referred to as ‘knot breathing' [26].

A tightly knotted portion makes it a preferred substrate for binding and unknotting by type II DNA topoisomerases [27]. Recent Brownian dynamics simulations [28] found that knotted portions in circular DNA could be tightened by supercoiling and became significantly more bent than the remaining portions. The dominant bending angles are around 80°–90° [28], which are comparable with the sharp bending angle resulting in flexible defect and hence the reduction of bending rigidity, twist rigidity and the unwinding of DNA [29–32]. In current works, effects of flexible defect on the interplay of supercoiling and knotting of circular DNA will be detected. Effects of flexible defect on topological states of chiral knotted DNA are first looked at, and then the reduction of twist rigidity and the unwinding of flexible defect are incorporated into the numerical simulations, so that the interplay of supercoiling and knotting of circular DNA can be studied under torsional conditions. At last, the question of how flexible defect affects the knotting probability is addressed by the phase diagram constructed in the phase space of knot length and gyration radius of knotted DNA.

2. Methods of calculations

2.1. DNA model and Monte Carlo simulation procedure

Worm-like chain (WLC) model of DNA has been widely used to predict the linking number distributions in good agreement with those measured in experiments of circular DNAs of 250–10 000 bp size in a wide temperature range of 4 °C–37 °C [33–35]. However, the above experiments and simulations do not rule out the possibility that WLC may fail to describe DNA elasticity at sharper bending conditions, resulting in melted base pairs or base pairs that lose their stacking interactions with its neighboring base pairs. The possibility of excitation of such defect was first pointed out by Crick and Klug [36], recently observed in ≤ 65 bp minicircles, and furthermore proved by molecular-dynamics simulation [37], where the defect is an unstacked base-pair step that allows formation of ≥90° of bending at the defect site [38].

In WLC model, a DNA was considered as a discredited chain consisting of N straight segments with segment length b. While the defect resulted from the sharp bending is considered, its total bending energy (E) including the persistence length of B-DNA α and the flexible kink $\alpha ^{\prime} $, and the energy required to excite one flexible defect μ (in k_BT unit) can be expressed as the summation of all the vertex energies, $\tfrac{E}{{k}_{{\rm{B}}}T}={\sum }_{i=1}^{N}{E}_{i}({\hat{t}}_{i},{\hat{t}}_{i+1})$, and a single vertex energy E_i connecting two adjacent tangent vectors ${\hat{t}}_{i}$ and ${\hat{t}}_{i+1}$ can be generalized as(1)$\begin{eqnarray}{E}_{i}({\hat{t}}_{i},{\hat{t}}_{i+1})=\displaystyle \frac{{\delta }_{{n}_{i},0}a+{\delta }_{{n}_{i},1}a^{\prime} }{2}{\left({\hat{t}}_{i+1}-{\hat{t}}_{i}\right)}^{2}+\mu {\delta }_{{n}_{i},1},\end{eqnarray}$where the two-state variable n_i indicates whether the segment i is either in B-DNA form (n_i = 0) or in flexible defect state (n_i = 1), $a=\tfrac{\alpha }{b}$ and $a^{\prime} =\tfrac{\alpha ^{\prime} }{b}$ indicate the bending rigidity of B-DNA site and the defect site, respectively. In current simulation, α, $\alpha ^{\prime} $ and b are chosen to be 50 nm, 1 nm and 1 nm, respectively, and μ is scanned from 4k_BT to ∞. Obviously, the Ising freedom degree {n₁, n₂, n₃, …..,n_N} is independent of the conformational freedom degree $\{{\hat{t}}_{1},{\hat{t}}_{2},{\hat{t}}_{3},\ldots ..,{\hat{t}}_{N}\}$, by summarizing over the Ising freedom degree, an effective vertex energy that only depends on the conformation can be derived as(2)$\begin{eqnarray}{E}_{i}=-\mathrm{ln}[{{\rm{e}}}^{-\tfrac{a}{2}{\left({\hat{t}}_{i+1}-{\hat{t}}_{i}\right)}^{2}}+{{\rm{e}}}^{-\mu -\tfrac{a^{\prime} }{2}{\left({\hat{t}}_{i+1}-{\hat{t}}_{i}\right)}^{2}}],\end{eqnarray}$which is conveniently used to carry out Monte Carlo simulation for writhe distribution of knotted DNA. During simulation process, if the bending angle at a vertex in a knotted DNA conformation exceeds the critical bending angle ${\theta }_{c}=\arccos (1-\tfrac{\mu }{a-a^{\prime} })$, this vertex will be defected [29].

Based on equation (2), Monte Carlo simulation is applied to sample the conformations of knotted DNA. To update the conformation, a subchain is rotated by a random angle around the straight line connecting two randomly chosen nonadjacent vertices. Metropolis criterion is applied to determine whether the new conformation is accepted [29].

2.2. Topology variables of knotted DNA

Generally, two important variables are used to describe the topology states of closed circular DNA. One is the linking number, Lk, which describes the winding of the complementary strand of DNA about each other, but it is more convenient to use the difference between linking number Lk and that of relaxed DNA (Lk₀), ΔLk = Lk − Lk₀, than Lk itself. Since both Lk₀ and ΔLk are not integer, however, ΔLk can only be differed by integer number.

The other is the knot type, K, formed by the double helix axis. The knot type can be identified according to Alexander polynomial Δ(t) at t = −1 and t = −2. During simulation, the change of knot type is prevented by rejecting the trial conformation for which the values of Δ(− 1) and Δ(− 2) have changed [39]. The writhe number of a knotted conformation with a particular knot type can be calculated by ${Wr}=\tfrac{{b}^{2}}{4\pi }{\sum }_{i,j=1,i\ne j}^{N}\tfrac{{\hat{t}}_{j}\times {\hat{e}}_{{ij}}\cdot {\hat{t}}_{i}}{{d}_{{ij}}^{2}}$, where ${\hat{e}}_{{ij}}$ is the unit vector pointing from the jth vertex to the ith vertex and d_ij is the distance between two vertices [40, 41]. And its corresponding writhe distribution ρ(Wr∣K) can be obtained directly from simulations. The twist of DNA, ΔTw, the difference between the actual twist and relaxed twist of the same circular DNA, which is combined with the writhe distribution with a particular knot type ρ(Wr∣K) by the White's equation, which puts a constraint on the linking number, the writhe and twist of a knotted DNA as ΔLk = Wr + ΔTw. Due to this constraint, the linking number distribution of knotted DNA with a particular knot type ρ(ΔLk∣K) can be obtained from the convolution(3)$\begin{eqnarray}\begin{array}{l}\rho ({\rm{\Delta }}{Lk}| K)=\int \rho ({Wr}| K)\rho ({\rm{\Delta }}{Tw}){\rm{d}}{Wr}\\ \quad =\ \int \rho ({Wr}| K)\rho ({\rm{\Delta }}{Lk}-{Wr}){\rm{d}}{Wr},\end{array}\end{eqnarray}$where this convolution is based on an assumption that ρ(Wr∣K) and ρ(ΔTw) are independent to a good approximation [42]. The torsional energy of closed knotted DNA, approximated as ${E}_{t}=(\tfrac{2{\pi }^{2}C}{L}){\left({\rm{\Delta }}{Tw}\right)}^{2}$, results in a Gaussian distribution of the twist, ρ(ΔTw), with a variance ${\sigma }_{{Tw}}^{2}=\tfrac{L}{4{\pi }^{2}C}$. L is the DNA contour length and C is the twist persistence length and its canonical value is about 75 nm.

While the chain segments are allowed to pass through each other in simulation procedure, the knot type of the chain changes during successive deformations. By calculating the value of the Alexander polynomial Δ(t) at t = −1 and t = −2, different knot type in the equilibrium set of chain conformations can be distinguished, and their corresponding probability ρ(K) can be specified. Combing the probability ρ(K) with the linking number distribution of a particular knot type ρ(ΔLk∣K), an important derivative distributions ρ(ΔLk, K) and the general distribution ρ(ΔLk) can be obtained as the following(4)$\begin{eqnarray}\rho ({\rm{\Delta }}{Lk},K)=\rho ({\rm{\Delta }}{Lk}| K)\rho (K),\end{eqnarray}$(5)$\begin{eqnarray}\rho ({\rm{\Delta }}{Lk})=\sum _{K}\rho ({\rm{\Delta }}{Lk},K),\end{eqnarray}$through which, effects of flexible defect on the the interplay of supercoiling and knotting of circular DNA can be investigated thoroughly.

To clarify the interplay of supercoiling and knotting of circular DNA and characterize the different degree of compactness and hence of geometrical complexity, a bottom-up method [28, 43] is applied to define the knot length L_knot. Namely, a smaller contour length ℓ is first selected from the knot ring at will. After closing this arc ℓ, its topology is still the same as the overall knot. Moreover, its complementary arc on the knot ring is different from the whole knot topology. Thus, ℓ is identified as the knot length L_knot. Otherwise, ℓ is increased by one segment and the search for a knotted arc starts again. Clearly, the search stops when the knot length is identified.

3. Results and discussions

3.1. Effects of flexible defect on topological states of chiral knotted DNA

In current simulations, three simplest knots, 3₁, 4₁ and 5₁ are generated, in which knots 3₁ and 5₁ are chiral and knot 4₁ is achiral, R and L are used to indicate right-handed chirality and left-handed chirality, respectively. Their corresponding writhe distribution based on energy equation (1) is obtained by the normalized histogram of the recorded writhe numbers using a bin size of 0.01. The normalized frequency is then divided by the bin size to obtain the density distribution function ρ(Wr∣K). Figures 1(a)–(d) show ρ(Wr∣K) for knotted DNA with two different sizes 80 and 160 nm and knot type 5₁ and 3₁. The writhe distribution of chiral knot, such as R5₁ and L5₁, R3₁ and L3₁, symmetrically locates at both sides of the one of trivial knot 0₁, and is subject to various excitation energies. Clearly, the excitations in general lead to larger fluctuations of Wr in the range of excited energies studied. Different from achirality of knotted DNA, such as nontrivial knot type 4₁ and trivial knot type 0₁, their mean of the writhe number distribution is not zero.

Figure 1.

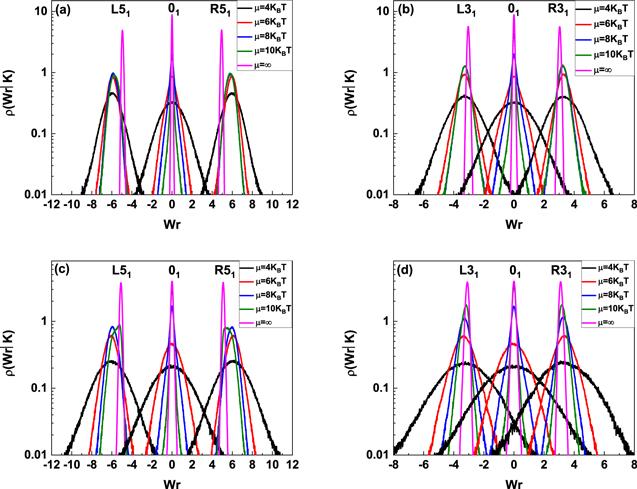New window|Download| PPT slide
Figure 1.Writhe number distributions of knotted DNA with chirality. (a) 80 nm, L5₁, 0₁ and R5₁ knotted DNA; (b) 80 nm, L3₁, 0₁ and R3₁ knotted DNA, (c) 160 nm, L5₁, 0₁ and R5₁ knotted DNA; (d) 160 nm, L3₁, 0₁ and R3₁ knotted DNA. In each figure, from outside to inside, the excitation energies are 4k_BT, 6k_BT, 8k_BT, 10k_BT and ∞ (B-DNA), respectively.


Once the writhe distribution ρ(Wr∣K) is obtained by simulation, the linking number distribution can be obtained by equation (3) through the numerical convolution of ρ(Wr∣K) and ρ(ΔTw), and their corresponding results summarized in figure 2, the widths of linking number distributions are noticeably increased by the excitations of flexible defects. At the same time, the decreasing excitation energy μ enhances the negative supercoiling of knotted DNA with left-handed chirality, which seems to affect the results of topoisomerase action, such as effectively favouring knot formation in the presence of type II DNA topoisomerase.

Figure 2.

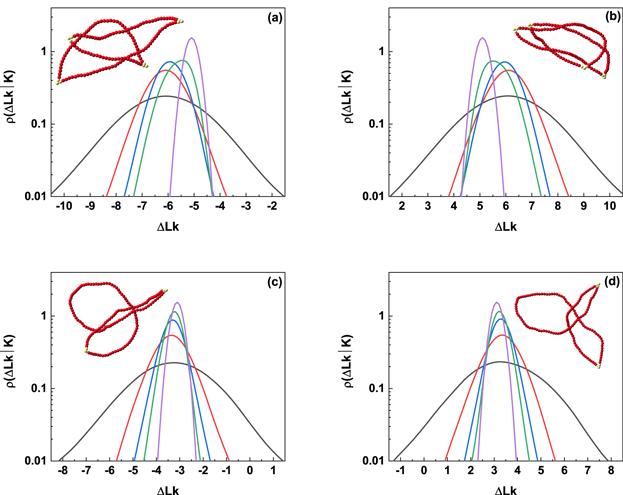New window|Download| PPT slide
Figure 2.Linking number distributions of knotted DNA with chirality. (a) 160 nm, L5₁ DNA knot; (b) 160 nm, R5₁ DNA knot; (c) 160 nm, L3₁ DNA knot; (d) 160 nm, R3₁ DNA knot. In each figure, from outside to inside, the excitation energies are 4k_BT, 6k_BT, 8k_BT, 10k_BT, and ∞ (B-DNA), respectively. Typical conformations are illustrated in inset of each figure and the excitation energy corresponding to each conformation is 10k_BT.


The insets in figure 2 show the typical knotted conformations with a few flexible defects, and the average number of flexible defects in knotted DNA with different knot type as a function of the excitation energy μ is demonstrated in figure 3. Figures 3(a)–(c) indicate that the average number of flexible defect decreases with the increasing excited energy, but the generation of flexible defect is dependent on the counter length of knotted DNA. For knotted DNA with small contour length, when the excited energy is larger than 4k_BT, the generation of flexible defect was enhanced by knotting in compared with that of trivial knot 0₁. With the increasing contour length, knotting can only enhance the generation of flexible defect at relatively large excited energies, at the same time, current simulations indicate that the average number of flexible defect increases with the growing complexity of knotted DNA, but not obviously depend on the chirality of knotted DNA. Figure 3(d) shows the average number of flexible defects for R5₁ knotted DNA from 80 nm to 200 nm. For excitation energy μ > 8k_BT, the average number of flexible defect is inversely proportional to contour length of knotted DNA. When excitation energy μ decreases to 6k_BT or even 4k_BT, the average number of flexible defects begins to increase with increasing contour length of knotted DNA. At 4k_BT, there are about 100 flexible defects in knotted DNA with contour length 200 nm, namely, about half of the knotted DNA is melted. Figures 4(a)–(d) demonstrate the scaled knot length for knotted portion changing with the excited energy μ. For knotted DNA with different contour length ranging from 80 to 200 nm, the scaled knot length reduced with the decreasing excitation energy μ, which indicates that the decreasing excited energy μ enhances the tightness of knot portion in knotted DNA, which generally facilitates the binding of the type IIA DNA topoisomerase to unknot the knotted DNA. The scaled knot length does not obviously depend on the chirality, and even overlaps together for complex knotted DNA with different chirality. At a fixed excitation energy μ, the scaled knot length of knotted DNA increases sharply as the knot complexity grows.

Figure 3.

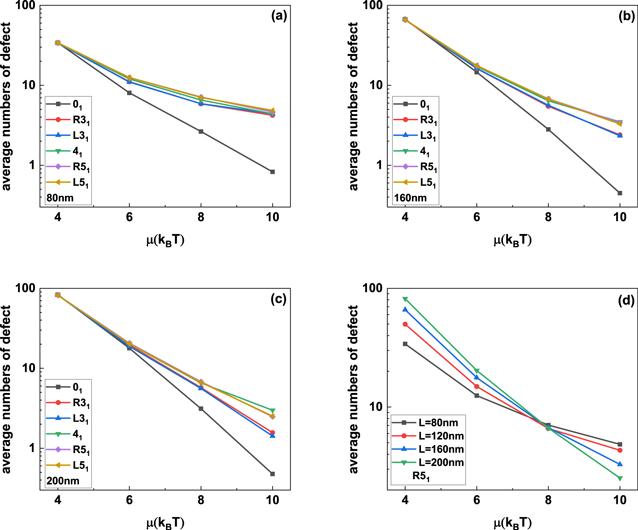New window|Download| PPT slide
Figure 3.(a)–(c) Average numbers of flexible defects in knotted DNA with different knot type changing with excitation energy μ. (d) The average number of defects in R5₁ DNA knot as a function of the excitation energy μ.

Figure 4.

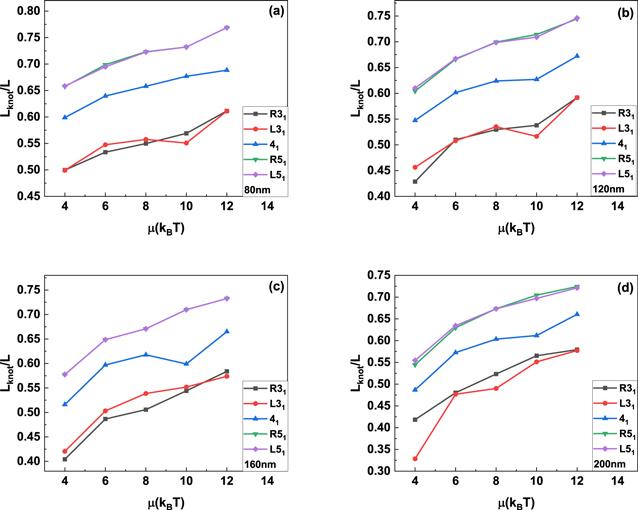New window|Download| PPT slide
Figure 4.The average knot length scaled by contour length of knotted DNA changing with the excitation energy μ. The DNA knot types are R3₁, L3₁, 4₁, R5₁ and L5₁, respectively.

3.2. Effects of reduced twist rigidity and unwinding of the flexible defect

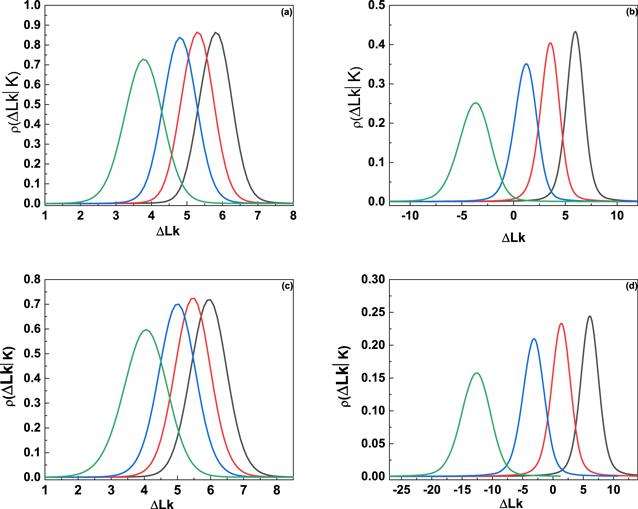
The aforementioned discussions clearly addressed that the flexibility of flexible defects increases the withes of the writhe distribution, and hence those of the linking number distribution. In addition to reduction of bending rigidity, the flexible defect also leads to the reduced twist rigidity and the unwinding of DNA, which will further increase the variances of linking number distribution. Generally, the conditional twist distribution in the presence of n flexible defects ρ_n(ΔTw) is still a Gaussian distribution [29] with variances(6)$\begin{eqnarray}{\sigma }_{{\rm{\Delta }}{Tw}}^{2}=\displaystyle \frac{1}{4{\pi }^{2}}(\displaystyle \frac{(N-n)b}{C}+\displaystyle \frac{{nb}}{C^{\prime} }),\end{eqnarray}$where n is the number of flexible defect in a knotted conformation and $C^{\prime} $ is the reduced twist rigidity, $C^{\prime} =\tfrac{C}{4}$. The kink structure also destroys the local geometry constraint of twist and result in unwinding by an angle φ , so that the twist angle per segment in defected area is about $\tfrac{6\pi }{10.5}-\phi $, where $\tfrac{6\pi }{10.5}$ corresponds to twist angle per segment of 1 nm(3 bp) in B-form DNA. Their combined effects make ρ_n(Wr∣K) and ρ_n(ΔTw) no longer independent from each other, so that the linking number distribution of a particular knot type ρ(ΔLk∣K) can be obtained by(7)$\begin{eqnarray}\begin{array}{l}\rho ({\rm{\Delta }}{Lk}| K)=\sum _{n}{P}_{n}{\rho }_{n}({\rm{\Delta }}{Lk}| K)\\ \quad =\ \sum _{n}{P}_{n}\int {\rm{d}}{Wr}{\rho }_{n}({Wr}| K){\rho }_{n}({\rm{\Delta }}{Lk}-{Wr}),\end{array}\end{eqnarray}$where P_n is the probability of knotted DNA with n flexible defects. And the numerical calculation of equation (7) could be obtained directly from current simulations and expressed as(8)$\begin{eqnarray}\rho ({\rm{\Delta }}{Lk}| K)=\displaystyle \frac{1}{M}\sum _{i=1}^{M}{\rho }_{{n}_{i}}({\rm{\Delta }}{Lk}-{{Wr}}_{i}),\end{eqnarray}$where ${\rho }_{{n}_{i}}({\rm{\Delta }}{Lk}-{{Wr}}_{i})$ is a Gaussian function and its variance is determined by equation (6) and average value −n_iφ, where n_i is the number of flexible defects in the ith conformation. Wr_i and M are the writhe number of a sampled conformation in simulation and the total number of sampled conformations, respectively.

The numerical linking number distributions ρ(ΔLk∣K) obtained according to equation (8) are shown in figure 5, in each figure, from right to left, the unwinding angle φ is 0°, 26°, 51°, and 103°, respectively, and the reduced twist rigidity $C^{\prime} $ is 18.75 nm. Where the dependence of linking number distributions on unwinding angle and reduction of twist rigidity is identified separably. Except the twist rigidity reduced from 75 to 18.75 nm, the linking number distribution with unwinding angle 0° in figure 5(c) and that with excited energy μ = 8k_BT in figure 2(b) have the same parameters $\alpha ^{\prime} $=1 nm, unwinding angle φ = 0° and excited energy μ = 8k_BT, and the reduced twist rigidity does not result in significant increase in the variance of the linking number distribution. Different from effects of reduced twist rigidity on the linking number distribution, increasing unwinding angle not only results in a linking number distribution with large variance, but also leads to the drift of linking number distribution to the left. At the same time, the larger number of flexible defects caused by the lower excitation energy μ = 4k_BT also leads to the average linking number drifts to much lower values.

Figure 5.

New window|Download| PPT slide
Figure 5.Effects of unwinding angle on the linking number distributions of L5₁ DNA knot. (a) 80 nm, μ = 8k_BT; (b) 80 nm, μ = 4k_BT; (c) 160 nm, μ = 8k_BT; (d) 160 nm, μ = 4k_BT. In each figure, from right to left, the unwinding angle per defect is φ = 0°, 26°, 51°, and 103°.$C^{\prime} $ = $\tfrac{C}{4}=18.75\,\mathrm{nm}$ was used in the calculation.

3.3. Effects of flexible defect on the knotting of circular DNA

In the aforementioned section, our discussions concentrate on effects of flexible defects on the knotted DNA with particular knot type, namely, the change of knot type was prevented during simulations. In this section, the chain segments are allowed to pass through each other during successive conformations transition in simulations, so that the equilibrium distributions probability of knots, ρ(K), can be specified from the constructed equilibrium set of chain conformations and partial data is summarized in table 1. The equilibrium distributions probability for trivial knot (0₁) is dominant over that of nontrivial knots. At a fixed excited energy, the equilibrium distributions probability decrease sharply when the knot complexity grows.


Table 1.
Table 1.The equilibrium distribution probability of knots with 800 nm in length at different excited energy μ. ∑ indicates the summation of the equilibrium distribution probability of the nontrivial knotted DNA at different excitation energy μ.

knot type K	μ = 4	μ = 6	μ = 8	μ = 10	μ = ∞
01	0.993 452	0.982 434	0.992 174	0.996 545	0.997 500
31	0.005 723	0.015 284	0.007 259	0.003 257	0.002 444
41	0.000 049	0.001 439	0.000 336	0.000 099	0.000 056
51	0.000 000	0.000 298	0.000 142	0.000 000	0.000 000
52	0.000 776	0.000 248	0.000 089	0.000 000	0.000 016
∑	0.006 548	0.017 566	0.007 826	0.003 355	0.002 500

New window|CSV

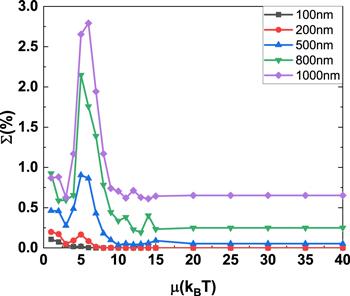
The summation (Σ) of equilibrium distributions probability (ρ(K)) for nontrivial knotted DNA with different contour length changing with excitation energy μ is demonstrated in figure 6 and does not change with excitation energy μ monotonically. Specifically, Σ has a maximum for an intermediate value of excitation energy μ around 5k_BT as the contour length for knotted DNA is increased from 100 to 1000 nm. The maximum value of Σ grows rapidly with the contour length for knotted DNA.

Figure 6.

New window|Download| PPT slide
Figure 6.The summation of the equilibrium distributions of the nontrivial knotted DNA changing with excitation energy μ.


According to equation (4), the equilibrium distribution ρ(ΔLk, K) can be calculated based on the simulated distribution of ρ(ΔLk∣K) and ρ(K), as the same time, the general linking number distribution ρ(ΔLk) also can be specified according to equation (5) by summarizing ρ(ΔLk, K) over K. Figures 7(a), (b) demonstrate the simulated distribution of ρ(△Lk, K) and the general linking number distribution ρ(△Lk) for knotted DNA with 800 nm in length at excited energy 8k_BT and ∞. When the excited energy μ ranges from 8k_BT to ∞, four separate peaks corresponding to nontrivial knot 5₁, 5₂ disappear.

Figure 7.

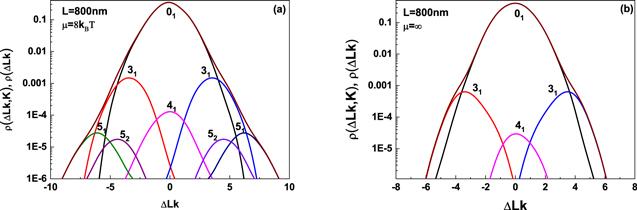
New window|Download| PPT slide
Figure 7.Simulated distribution of ρ(△Lk, K) and ρ(△Lk), these simulations are carried out for circular DNA with 800 nm in length at excited energy 8k_BT and ∞. The distribution ρ(ΔLk, K) corresponding to different knots is indicated by separate peaks and the distribution ρ(ΔLk), the summation of ρ(ΔLk, K) over K, is represented by wine line.


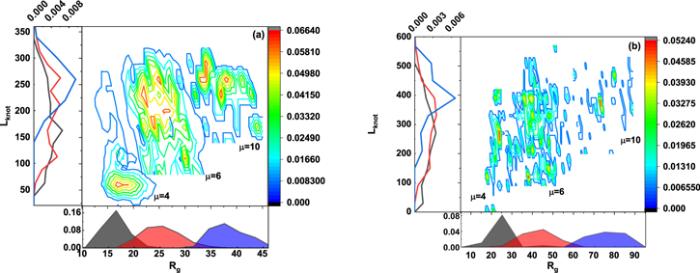
Three characteristic parameters, namely gyration radius (R_g), knot length (L_knot) and excitation ennergy μ of flexible defect are used to further describe the supercoiling and knotting of circular DNA, and their interplay for knotted DNA with contour length 500 nm and 800 nm is summarized in the phase diagram shown in figure 8(a)∼(b), respectively, which are constructed in phase space of gyration radius (R_g) and knot length (L_knot). Their corresponding distributions are shown in the side panels and the distribution probability ρ(L_knot, R_g) for different excitation energy is demonstrated in the central panel.

Figure 8.

New window|Download| PPT slide
Figure 8.The central panel corresponds to the contour maps of the probability distribution ρ(R_g, L_knot) of knotted DNA for three different excitation energies 4k_BT, 6k_BT and 10k_BT. The side panels show the marginal distribution of R_g and L_knot. The contour length for knotted DNA in (a) and (b) is 500 nm and 800 nm, respectively.


A recent work [24] also reported similar phase diagram based on the control of bending rigidity ranging from the rigid to the fully-flexible limit, and its results indicated that knot length (L_knot) anticorrelated with gyration radius (R_g), and their anticorrelation was particularly evident for the smallest bending rigidity shown in their results. This property was rationalized by the competition between entropy and bending energy, namely, reducing the knot length is equivalent to increasing the length of the complementary unknotted arc and, because this enjoys a larger conformational freedom, it ultimately reflects in a larger gyration radius of the ring.

In comparison with the findings mentioned by the recent work [24], the phase diagrams in figures 8(a), (b) do not indicate obvious anticorrelation between knot length (L_knot) and gyration radius (R_g), and contour length of knotted DNA ranging from 500 to 800 nm has strong influences on the phase diagrams. The absence of anticorrelation and the dependence of phase diagrams on contour length of knotted DNA could attribute to the local generation of flexible defect in knotted DNA, which has a remarkably high probability to be within the knot portion [23], so that the bending energy could be released and the competition between bending energy and entropy is inhibited. With the increasing contour length, few flexible defects are excited, so that the bending rigidity recover to the canonical one, at which knot length (L_knot) anticorrelate with gyration radius (R_g) as reported by [24].

4. Conclusions

In the current work, a Monte Carlo simulation is applied based on flexible defect excitations to predict the roles of flexible defects in the interplay of supercoiling and knotting of circular DNA. Flexible defects obviously enhance the fluctuation of linking number distribution of knotted DNA and hence its supercoiling. The decreasing excitation energy makes the knotted portion more compact. The reduction of twist rigidity has no obvious influence on the distribution ρ(ΔLk∣K), by contrast, the increasing unwinding angle not only enhances the variance of this distribution, but also leads to a drift of linking number distribution to lower values. The summation of equilibrium distribution probability for nontrivial knotted DNA with different contour length does not change with excitation energy monotonically and has a maximum at an intermediate value of excitation energy around 5k_BT, the maximum value increases with the increasing contour length of knotted DNA. A phase diagram in phase space of knot length and gyration radius of knotted DNA is constructed and the phase diagrams for knotted DNA with different contour length indicated that knot length did not anticorrelate with the gyration radius of knotted DNA, which could be attributed to the flexible defect in the knot portion. The flexible defect results in a reduction of bending rigidity and hence the release of bending energy, so that the competition between entropy and bending energy is inhibited.

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Meluzzi D Smith D Arya G 2010 Annu. Rev. Biophys. 39 349
DOI:10.1146/annurev.biophys.093008.131412 [Cited within: 1]

[2]Rybenkov V V Cozzarelli N R Vologodskii A V 1993 Proc. Natl Acad. Sci. USA 90 5307
DOI:10.1073/pnas.90.11.5307

[3]Valentin R Ullsperger V 1997 Science 277 690
DOI:10.1126/science.277.5326.690 [Cited within: 1]

[4]Arsuaga J Vazquez M Trigueros S Sumners D W Roca J 2002 Proc. Natl Acad. Sci. USA 99 5373
DOI:10.1073/pnas.032095099 [Cited within: 1]

[5]Arsuaga J Vazquez M McGuirk P Trigueros S Sumners D W Roca J 2005 Proc. Natl Acad. Sci. USA 102 9165
DOI:10.1073/pnas.0409323102

[6]Marenduzzo D Orlandini E Stasiak A Sumners D W Tubiana L Micheletti C 2009 Proc. Natl Acad. Sci. USA 106 22269
DOI:10.1073/pnas.0907524106

[7]Taylor W R 2000 Nature 406 916
DOI:10.1038/35022623

[8]Virnau P Mirny L A Kardar M 2006 PLoS Comput. Biol. 2 e122


[9]Dai L Zhou Y 2011 J. Mol. Biol. 408 585
DOI:10.1016/j.jmb.2011.02.056 [Cited within: 1]

[10]Bao X R Lee H J Quake S R 2004 Phys. Rev. Lett. 91 265506
DOI:10.1103/PhysRevLett.91.265506 [Cited within: 1]

[11]Metzler R Reisner W Riehn R Austin R Tegenfeldt J O Sokolov I M 2007 Eur. Phys. Lett. 76 696
DOI:10.1209/epl/i2006-10312-5 [Cited within: 1]

[12]Tang J Du N Doyle P S 2011 Proc. Natl Acad. Sci. USA 108 16153
DOI:10.1073/pnas.1105547108 [Cited within: 1]

[13]Bao X R Lee H J Quake S R 2003 Phys. Rev. Lett. 91 265506
DOI:10.1103/PhysRevLett.91.265506 [Cited within: 1]

[14]Grosberg A Y 2016 Polym. Sci. Ser. 58 864 872
DOI:10.1134/S0965545X16060079 [Cited within: 1]

[15]Ercolini E Valle F Adamcik J Witz G Metzler R Paolo D L R Roca J Dietler G 2007 Phys. Rev. Lett. 98 058102
DOI:10.1103/PhysRevLett.98.058102 [Cited within: 1]

[16]Plesa C Verschueren D Pud S Jaco V D T Ruitenberg J W Witteveen M J Jonsson M P Grosberg A Y Rabin Y Dekker C 2016 Nat. Nanotechnol. 11 1093
DOI:10.1038/nnano.2016.153 [Cited within: 1]

[17]Orlandini E Whittington S G 2007 Rev. Mod. Phys. 79 611
DOI:10.1103/RevModPhys.79.611 [Cited within: 1]

[18]Dai L Renner C B Doyle P S 2015 Macromolecules 48 2812 2818
DOI:10.1021/acs.macromol.5b00280 [Cited within: 1]

[19]Huang L Makarov D E 2007 J. Phys. Chem. A 111 10338
DOI:10.1021/jp071940+ [Cited within: 1]

[20]D'Adamo G Micheletti C 2015 Macromolecules 48 6337
DOI:10.1021/acs.macromol.5b01323 [Cited within: 1]

[21]Poier C M R Likos P 2014 Macromolecules 47 3394
DOI:10.1021/ma5006414 [Cited within: 1]

[22]Matthews R Louis A A Likos C N Likos N 2012 ACS Macro Lett. 1 1352
DOI:10.1021/mz300493d [Cited within: 1]

[23]Orlandini E Baiesi M Zonta F 2016 Macromolecules 49 4656
DOI:10.1021/acs.macromol.6b00712 [Cited within: 2]

[24]Coronel L Orlandini E Micheletti C 2017 Soft Matter 13 4260
DOI:10.1039/C7SM00643H [Cited within: 4]

[25]Dai L Doyle P S 2016 Macromolecules 49 7581
DOI:10.1021/acs.macromol.6b01653 [Cited within: 1]

[26]Liang D Patrick D 2017 Polymers 9 57
DOI:10.3390/polym9020057 [Cited within: 1]

[27]Dong K C Berger J M 2007 Nature 450 1201
DOI:10.1038/nature06396 [Cited within: 1]

[28]Witz G Dietler G Stasiak A 2011 Proc. Natl Acad. Sci. USA 108 3608
DOI:10.1073/pnas.1016150108 [Cited within: 3]

[29]Chen H Liu Y Zhou Z Hu L Ou-Yang Z-C Yan J 2009 Phys. Rev. E 79 041926
DOI:10.1103/PhysRevE.79.041926 [Cited within: 4]

[30]Liebl K Zacharias M 2017 J. Phys. Chem. B 121 11019
DOI:10.1021/acs.jpcb.7b07701

[31]Cloutier T E Widom J 2004 Mol. Cell 4 355
DOI:10.1016/S1097-2765(04)00210-2

[32]Zhang X Bao L Wu Y Y 2017 J. Chem. Phys. 147 054901
DOI:10.1063/1.4991689 [Cited within: 1]

[33]Horowitz D Wang J C 1984 J. Mol. Biol. 173 75
DOI:10.1016/0022-2836(84)90404-2 [Cited within: 1]

[34]Depew E Wang J C 1975 Proc. Natl Acad. Sci. USA 72 4275
DOI:10.1073/pnas.72.11.4275

[35]Rybenkov V R Vologodskii A V Cozzarelli N R 1997 Nucleic Acids Res. 25 1412
DOI:10.1093/nar/25.7.1412 [Cited within: 1]

[36]Crick F H C Klug A 1975 Nature 255 530
DOI:10.1038/255530a0 [Cited within: 1]

[37]Lankas F Lavery R Maddocks J H 2006 Structure 14 1527
DOI:10.1016/j.str.2006.08.004 [Cited within: 1]

[38]Du Q Kotlyar A Vologodskii A 2008 Nucleic Acids Res. 36 1120
DOI:10.1093/nar/gkm1125 [Cited within: 1]

[39]Podtelezhnikov A A Cozzarelli N R Vologodskii A V 1999 Proc. Natl Acad. Sci. USA 96 12974
DOI:10.1073/pnas.96.23.12974 [Cited within: 1]

[40]Fenley M O Olson W K Tobias I Manning G S 1994 Biophys. Chem. 50 255
DOI:10.1016/0301-4622(93)E0094-L [Cited within: 1]

[41]Sucato C A Rangel D P Aspleaf D Fujimoto B S Schurr J M 2004 Biophys. J. 85 3079
DOI:10.1016/S0006-3495(04)74357-X [Cited within: 1]

[42]Vologodskii A V Cozzarelli N R 1993 J. Mol. Biol. 232 1130
DOI:10.1006/jmbi.1993.1465 [Cited within: 1]

[43]Tubiana L Orlandini E Micheletti C 2011 Prog. Theor. Phys. Suppl. 191 192
DOI:10.1143/PTPS.191.192 [Cited within: 1]