Zhang Xie¹, Zheng Li², Gang Lou¹, Qing Liang¹, Jiang-Xing Chen³, Jianlong Kou^,,1,∗, Gui-Na Wei^,41Institute of Condensed Matter Physics, Zhejiang Normal University, Jinhua 321004, China
²School of Petroleum Engineering, China University of Petroleum (East China), Qingdao 266580, China
³Department of Physics, Hanghzou Dianzi University, Hangzhou 310018, China
⁴Division of Nephrology, The Second Affiliated Hospital of Zhejiang University, School of Medicine, Hangzhou 310009, China

First author contact: ^∗Author to whom any correspondence should be addressed.
Received:2021-01-8Revised:2021-02-20Accepted:2021-02-20Online:2021-03-22

Fund supported:

Natural Science Foundation of Zhejiang Province.LR21A020001 National Natural Science Foundation of China.11774313

Abstract
The folding and unfolding of the carbon chain, which is the basic constitutional unit of polymers, are important to the performance of the material. However, it is difficult to regulate conformational transition of the carbon chain, especially in an aqueous environment. In this paper, we propose a strategy to regulate the conformational transition of the carbon chain in water based on the all-atom molecular dynamics simulations. It is shown that the unfolded carbon chain will spontaneously collapse into the folded state, while the folded carbon chain will unfold with an external electric field. The regulation ability of the electric field is attributed to the electric field-induced redistribution of interface water molecules near the carbon chain. The demonstrated method of regulating conformational transition of the carbon chain in water in this study provides an insight into regulating hydrophobic molecules in water, and has great potential in drug molecule design and new polymer material development.
Keywords： carbon chain unfolding;electric field;interface water;molecular dynamics simulations


PDF (6398KB)MetadataMetricsRelated articlesExportEndNote|Ris|BibtexFavorite
Cite this article
Zhang Xie, Zheng Li, Gang Lou, Qing Liang, Jiang-Xing Chen, Jianlong Kou, Gui-Na Wei. Interface water-induced hydrophobic carbon chain unfolding in water. Communications in Theoretical Physics, 2021, 73(5): 055602- doi:10.1088/1572-9494/abe84e

1. Introduction

The regulation of conformational transition of the carbon chain in aqueous solutions is of fundamental importance in various fields such as biology, chemistry and physical processes, [1–5] because whether the carbon chain is folded or unfolded can greatly influence the properties of complex carbon products [6–9]. Understanding the mechanism behind this regulation behavior is a prerequisite for its application and popularization [10–15].

As the simplest hydrophobic molecules and the constitutional unit of many complex soft matters, like the polymer chain, [16] the carbon chain can largely affect the molecule performance by folding or unfolding [17, 18]. Generally, the preparation of macromolecules containing carbon chains is conducted in aqueous solutions [19, 20]. In aqueous solutions, the carbon chain usually has low solubility because carbon atoms are usually regarded as hydrophobic [21, 22]. The unfolded carbon chain will spontaneously collapse into the folded state [21, 22]. The driving force provided by the hydrophobic interaction has been considered to be one of the main reasons for the self-assembly of the carbon chain [23]. Similarly, some proteins and DNAs will also be folded driven by the interaction between its internal hydrophobic groups [24–26]. To obtain an unfolded carbon chain, different methods were proposed. [27–34] P. Leuenberger et al [27] systematically analyzed the sensitivity of the protein, indicating that higher temperature can make the protein unfolded. S. N. Innes-Gold et al [28] found that a charged polymer would change shape continuously by increasing ion concentrations in the solution. R. Zangi et al [29] showed by molecular dynamics (MD) simulations that a urea solution can change the folded carbon chain into an unfolded one. R. Godawat et al [30] found that adding guanidine chloride to the aqueous solution could overcome the hydrophobic interaction of the carbon chain, and the conformation would change. However, the introduced molecules are difficult to recycle after the system reaches stability, so they will affect the properties of the soft matter.

Electric field is an effective and controllable method to control the properties of materials [35–43]. Water confined in a nanochannel can freeze with a weak electric field, [35] and it will melt with a strong electric field [36]. A gradient electric field could drive nonpolar nanoparticles in water motion in one direction [39] The orientation of graphene and carbon nanotubes in water can be controlled by an electric field [40, 41]. Based on these insights, here we study conformational transition of the carbon chain in water using molecular dynamics simulations. We demonstrate that the conformational transition of the carbon chain in water can be regulated by applying an external electric field, i.e., the carbon chain in water can spontaneously collapse into the folded conformation, while the folded carbon chain will unfold with an external electric field.

2. Methodology and simulation methods

It has been reported that the carbon chain is the basic unit of polymer materials [16]. Here, various carbon chains are prepared, i.e., 40 carbon atoms with/without hydrogen atoms, and 50 carbon atoms with/without hydrogen atoms. For the carbon chains without hydrogen atoms, carbon atoms are like beads that string them together in a chain. For the carbon chains with hydrogen atoms, the chain is like a saturated hydrocarbon molecule with hydrogen atoms on each carbon atom. Figure 1 shows the simulation framework, which consists of one carbon chain of 40 carbon atoms without hydrogen atoms and 7121 water molecules. Two typical initial conformations, i.e., folding topology and unfolding topology, were prepared, as shown in figures 1(a) and (b). To investigate the conformational transition of the carbon chain, we chose an electric field with strength below 2.5V nm^-1, which is based on the previous reports that water molecules could be instantaneously dissociated when the electric field strength was greater than 3.5 V nm^-1 [44]. In addition, the selected electric field strength is comparable to that of water molecules near the surfaces of biopolymers or in the cracks of amino acid crystals [45, 46]. Similar electric field strengths have been used successfully for studying water transportation, biological gating and DNA detection [35–41, 43].

Figure 1.

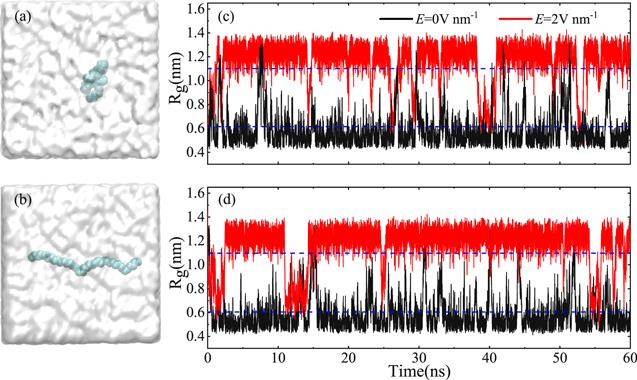New window|Download| PPT slide
Figure 1.Two typical initial conformations without hydrogen atoms at carbon chain end, (a) the folded state and (b) the unfolded state. The carbon atoms are depicted by spheres in cyan. The water molecules are shown as cloud-like. Gyration radius (R_g) of the hydrophobic carbon chain as a function of simulation time without (black) and with (red) electric field for using (c) initial conformation (a), and (d) initial conformation (b), respectively. The dashed blue lines are the critical R_g of the unfolded and folded carbon chain.


In our simulations, the OPLS-AA force field was used. For the carbon chain without hydrogen atoms, the carbon atoms in the chain are thought to be uncharged. The uncharged carbon atoms were modeled as Lennard-Jones(L-J) particles with ϵ_CC = 0.276 kJ mol^-1 and σ_CC = 0.35 nm. The two-carbon bond was 0.153 nm and the three-carbon angle was 112.7° before relaxation, which were maintained by harmonic potentials with spring constants of 224 262.4 kJ mol^-1 nm⁻² and 488.273 kJ mol^1- deg⁻², respectively. For the carbon chain with hydrogen atoms, the carbon atoms in the chain are thought to be charged and the whole chain is electrically neutral. The detailed force-field parameters can be found in our paper [47]. The van der Waals interactions were described with L-J potential with a cut-off distance of 1.4 nm, and particle mesh Ewald method was used to calculate the electrostatic interaction, in which the mesh spacing of fast fourier transform was 0.12 nm. All simulations were carried out by using the Gromacs-5.1.5 molecular dynamics program in the NPT ensemble [48]. The TIP4P water model was used, [49] which has been used successfully to study phase transition of water with an electric field, [36, 50, 51] and the TIP3P water model was also tested [52]. The pressure was controlled by Parrinello-Rahman scheme to 1.0 bar with a compressibility coefficient of 4.5 × 10⁻⁵ bar^-1 [53]. The V-rescale thermostat was used to keep the temperature of the system at 300 K [54]. The periodic boundary conditions were employed in all directions. For each simulation, a total of 60 ns was performed, and the data of the last 40 ns were collected for analysis. For each condition, three independent simulations were performed.

The free energy landscape can be determined by calculating the probability distribution of carbon chain conformation [55] P(x) = exp[−RT G(x)]/Z, where x is the conformation of the carbon chain and Z is the partition function. The relative free energy can be expressed as ${\rm{\Delta }}G=G({x}_{2})-G({x}_{1})=-{RT}\mathrm{ln}[P({x}_{2})/P({x}_{1})]$. Here, we used the gyration radius (R_g) and root mean square deviation (RMSD) to describe the conformation of the carbon chain.

3. Results and discussion

We performed molecular dynamics to study conformational transition of the carbon chain. In order to reduce the effect of charge of the carbon chain on the conformational transition of the carbon chain with an electric field, we first selected the carbon chain model of 40 carbon atoms without hydrogen atoms. For the convenience of discussion, the gyration radius (R_g) of the carbon chain is defined as the average distance between the coordinates of all atoms and the center of mass. When the R_g is smaller than 0.6 nm, the conformation is considered to be in a folded state, as shown in figure 1(a). The conformation is regarded as an unfolded state when the R_g is greater than 1.1 nm, as shown in figure 1(b). The dashed blue lines in figures 1(c) and (d) point out the critical R_g of the unfolded and folded carbon chain.

Figures 1(c) and (d) show the R_g of the carbon chain as a function of time in water without and with an electric field for different initial conformations. When a folded carbon chain is used as initial conformation (see figure 1(a)), the R_g is almost unchanged without electric field, as shown in figure 1(c) (black line) or movie 1 in the Supporting Information (stacks.iop.org/CTP/73/055602/mmedia). This indicates that the folded carbon chain is still in a folded state, which is consistent with previous findings [29]. This is a result of the competing balance of the carbon-carbon interaction, the rigidity of the carbon chain and the carbon-water interaction [29]. When an electric field is applied to the system, the R_g of the carbon chain increases rapidly, exceeding the critical value of 1.1nm, as shown in figure 1(c) (red line) or movie 2 in the Supporting Information (stacks.iop.org/CTP/73/055602/mmedia). This means that the folded carbon chain is unfolded. A longer simulation time of 200 ns was also performed, as shown in figure S1 of the Supporting Information. The trend of folding and unfolding will not change with increasing simulation time. This confirms that the folded carbon chain is still in the folded state without electric field, and the folded carbon chain can be unfolded with electric field. To check the reliability of the initial conformation of the carbon chain, an initially unfolded carbon chain (figure 1(b)) is used in the molecular dynamics simulations. In the absence of the electric field, the unfolded carbon chain turns into the folded state spontaneously. When an electric field is applied to the system, the unfolded carbon chain will remain unfolded, as shown in figure 1(d). Moreover, we performed the molecular dynamics simulations with the TIP3P water model [52]. The carbon chain exhibits similar behaviors of folding and unfolding, as shown in figure S2. This suggests that the electric field can unfold the carbon chain in water.

We calculated the radial distribution, g(r), of the oxygen atom in water molecules around the proximal carbon atoms of the carbon chain, as shown in figure S3. Water molecules exhibit a layer-like distribution along the perpendicular direction to the carbon chain. At 0.5 nm from the carbon chain, there is a highest-density water layer. The region from the carbon chain to 0.5 nm is named the interface-region. Other regions are named as bulk-region. We calculated the number of water molecules in the interface-region with varying electric field strengths, as shown in figure 2(a). With increasing electric strength, more water molecules appeared in the interface-region. This indicates that water molecules in the interface-region redistribute with an electric field and the surface of the carbon chain becomes hydrophilic.

Figure 2.

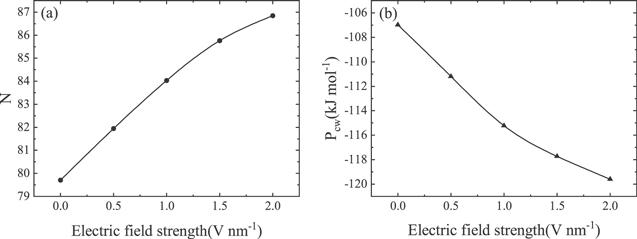New window|Download| PPT slide
Figure 2.Electric field dependence of (a) the average number (N) of water molecules in the interface-region, and (b) the average energy (P_cw) of the carbon-water interaction.


The average energies of carbon-water interactions, carbon-carbon interactions and the rigidity of the carbon chain are important to conformation transition of the carbon chain [24, 25]. We fixed the configuration of the carbon chain and calculated the carbon-water interaction energy for the folded carbon chain under different electric field strengths, and the results are illustrated in figure 2(b). In the absence of an electric field, the carbon-carbon interaction is greater than the sum of the rigidity of the carbon chain and the carbon-water interaction, leading to the folding of the carbon chain. When an electric field is applied to the system, the carbon-water interaction increases [41]. This means that the surface of carbon-water becomes more hydrophilic, and the folded chain will be opened to ensure maximum contact area between the water molecules and the surface of the hydrophilic chain. In particular, the sum of rigidity of the carbon chain and the carbon-water interaction is greater than the carbon-carbon interaction, and the carbon chain will break away from self-restraint to open.

We calculated the average number of hydrogen bonds of a water molecule (N_Hbond) in the interface-region, as shown in figure 3(a). A hydrogen bond is formed when the distance of O-O is less than 0.35 nm and the angle O-H-O is less than 30° between two water molecules [58]. It can be see that the N_Hbond increases with increasing electric field strength. In the absence of an electric field, the application of a hydrophobic carbon chain destroys the hydrogen bond network between water molecules. The hydrophobic carbon chain will collapse to reduce the interface area between the water molecules and carbon chain and the destruction of the hydrogen bond [56, 57]. When an electric field is applied, the arrangement of water molecules in the interface-region will change, resulting in the change of the hydrogen bond network in the interface-region. The increase of hydrogen bonds from figure 3(a) indicates that the hydrophobic interaction is weakened, which means that the surface of the carbon chain is more hydrophilic. Therefore, the carbon chain will be open to obtain a larger carbon-water interface area, which is consistent with the above discussion. We calculated the solvent accessible surface area (SASA) of the folded carbon chain without and with the electric field, as shown in figure S4 of the Supporting Information. We can see that the SASA keeps a small value without the electric field, while the SASA keeps a large value with an electric field.

Figure 3.

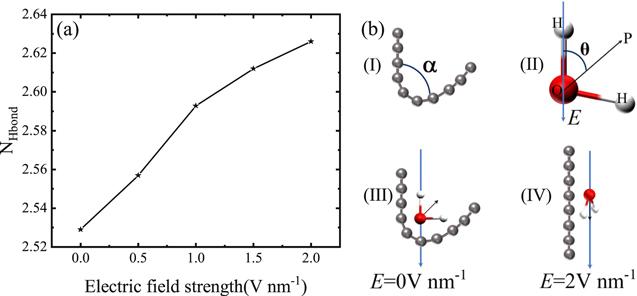New window|Download| PPT slide
Figure 3.(a) Electric field dependence of the average number of hydrogen bonds of water molecules in interface-region. (b) Schematic diagrams of (I) a bending carbon chain with an angle α, (II) spatial orientation of a water molecule and the electric field, a water molecule on the surface of carbon chain (III) without electric field and (IV) with an electric field.


To find out why the carbon chain breaks away from self-restraint to an open chain with direction and what happens to the interaction between water molecules and the carbon chain with the electric field, we select one part of the carbon chain with specific bending angle θ for analysis, as shown in figure 3(b)(I). We define the dipole (θ) as the angle formed by the dipole moment of the water molecule and the reverse direction of the electric field, as shown in figure 3(b)(II). The direction of the carbon chain is defined as the direction of the connection between the first and the last carbon atoms. For the electric field-free case at the bend location, the oxygen atom of the water molecule is toward the carbon atom of the chain, while the hydrogen atoms of the water molecule are far away from the carbon atom, as shown in figure 3(b)(III). When an electric field is applied, the water molecule will obtain a torque as, M = E × P, [40, 62] where P is the dipole moment of water molecule and E is the applied electric field. The torque can be rewritten as, M = −P Esinθ. The dipole direction of the water molecule will turn to the direction of the electric field [40, 41, 59, 62]. In addition, the electrostatic energy of the dipole moment is calculated as W = − P · E. The electrostatic energy of the dipole moment can be rewritten as, W=P E cosθ. When the angle θ is 180°, the electrostatic energy is the minimum, as shown in figure 3(b)(IV). In other words, when the direction of the dipole moment is along the direction of the electric field, the water molecule is the most stable. Applying an electric field will cause the rotation of the water molecule dipole, which induces a torque, resulting in the extension of the carbon chain.

To understand unfolding carbon chain with an electric field in water, we calculated the dipole of water molecules. A folded carbon chain and an unfolded carbon chain are selected and kept in initial state, as shown in figure 4(a). Figures 4(b) and (c) show the dipole distribution of water molecules both the bulk-region and the interface-region in different electric fields. It is well known that water molecules flip along the direction of the electric field [40, 41, 59–62]. We can see from the half height width of figures 4(b) and (c) that the dipole direction of water molecule is closer to the direction of electric field with a larger electric field strength (or see figure 4(a)), which is consistent with the discussion in the previous paragraph. For the bulk-region, whether the carbon chain is folded or not, the water molecules keep the same dipole distribution, as shown in figure 4(b). This indicates that carbon chain can not affect the dipole distribution of water molecules in the bulk-region, only the dipole direction of water molecule is induced by the electric field. For the interface-region, the dipole distribution of water molecules of the folded carbon chain is different from the unfolded carbon chain, as shown in figure 4(c). When the electric field strength is equal to zero, the dipole distribution of water molecules in folded carbon chain is higher than that of unfolded carbon chain. Therefore, there is a tendency that the dipole distribution of water molecules in the unfolded carbon chain system changes to that of the folded carbon chain system. As a result, the unfolded carbon chain is folded spontaneously. When the electric field is applied, the dipole distribution of water molecules of the unfolded carbon chain is higher than that of the folded carbon chain, as shown in figure 4(c). Comparing figures 4(b) and (c), we also see that the dipole distribution of the unfolded carbon chain in the interface-region is closer to that of the bulk-region. Based on the previous knowledge, the electric field can unfold the carbon chain in water, i.e., the unfolded carbon chain is more stable. In other words, there is a tendency that the dipole distribution of water molecules in the folded carbon chain changes to that of the unfolded carbon chain. In this way, rotating the dipole direction of the water molecules will apply a force on the folded carbon chain to make it turn, so that the conformational transition of the carbon chain will take place from the folded state to the unfolded state.

Figure 4.

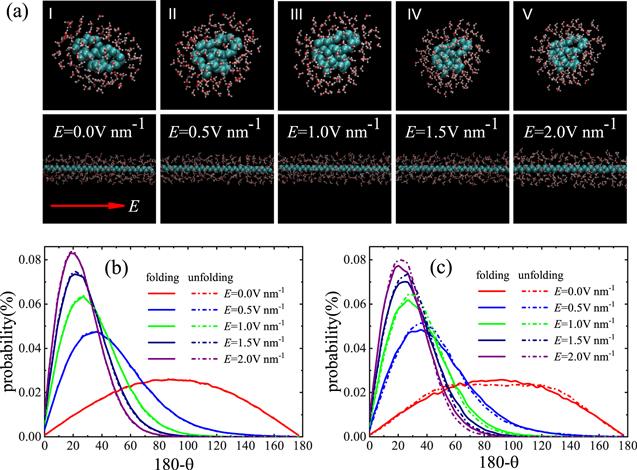New window|Download| PPT slide
Figure 4.Dynamics of water molecules under different electric field strengths. (a) The snapshots of distribution of water molecules of unfolded carbon chain and folded carbon chain in the interface region. Inset arrow indicates the direction of the electric field. The average probability distribution of the dipole of water molecules in (b) the bulk-region, and (c) the interface-region.


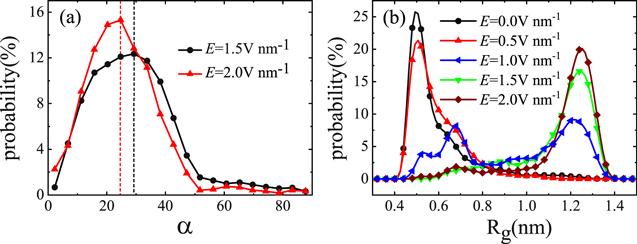
Furthermore, we investigate the relationship between the electric field direction and the carbon chain direction. The probability distribution of the angle between the carbon chain and the electric field is calculated, as shown in figure 5(a). The angle between the carbon chain and the electric field is defined as the angle between the direction of the connection between the first and the last carbon atoms and the electric field. We find that the angle between the carbon chain and the electric field is not completely the same under an electric field. There is a small angle between the carbon chain and the electric field. This means that the extended carbon chain will be folded at some time, which is consistent with figure 1 in that there are some fluctuations in the gyration radius spectrum, indicating that the extended carbon chain folds occasionally, or the folded carbon chain extends occasionally. This shows that the carbon chain in the water is not stable. When a larger electric field is applied, the angle will decrease, but is still not zero. To clarify the stability, we calculated the probability distribution of the gyration radii of the carbon chain with varying electric field strength, as shown in figure 5(b). It can be seen that when the electric field strength is lower than 0.5 V nm^-1, the effect of the electric field on the carbon chain is almost negligible and the carbon chain will remain folded as for that without an electric field. When the electric field strength increases, the R_g will be enlarged. In particular, when the electric field strength is higher than 1.5 V nm^-1, the R_g is almost greater than 1.1 nm corresponding to the unfolded carbon chain. It can be understood that a larger electric field can more easily control the dipole orientation of water molecules and provide a higher torque. When the electric field strength is between 0.5 V nm^-1 and 1.5 V nm^-1, the unstable carbon chain exhibits two maximum probabilities at the gyration radius of 0.50 nm and 1.25 nm, respectively. In such an electric field, the folded state and the unfolded state will transform to each other continuously.

Figure 5.

New window|Download| PPT slide
Figure 5.The probability distribution of (a) the average angle between the direction of the electric field and the direction of carbon chain, (b) the gyration radius of the carbon chain with different electric field strength.


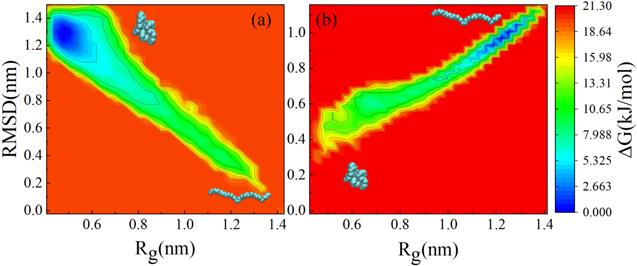
To probe the physical forces governing the conformational transition of the carbon chain, we computed the free energy in the process of the transition. Although we have defined the gyration radius which can quantitatively describe the folding degree of the carbon chain, there are different conformations with the same gyration radius (R_g). We calculated root mean square deviation (RMSD) at a given gyration radius, as shown in figure S5 of the Supporting Information. Initial states of the unfolded conformation and folded conformation are taken as the references for figures S5(a) and (b), respectively. Figure 6 shows the free energy landscape of the carbon chain in different gyration radii corresponding to the RMSD without and with applied electric fields. To observe the spontaneous transformation process of the carbon chain, an unfolded carbon chain is used without electric field (inset in the lower-right corner of figure 6(a)), while a folded carbon chain is used with electric field (inset in the lower-left corner of figure 6(b)), and the initial state is taken as the reference in calculating RMSD and free energies. One gyration radius can correspond to different conformations with different free energies. It can be seen that the free energies display the opposite trend with variation of the gyration radius, as shown in figure 6. This is consistent with the discussion above that the extended carbon chain will be folded, while the folded carbon chain will be unfolded under the effect of the electric field. It is noted that without electric field (see figure 6(a)), the folded carbon chain has a lower free energy than that of the unfolded carbon chain. This means that the unfolded carbon chain prefers to be folded. Therefore, the unfolded carbon chain will change to the folded carbon chain spontaneously, which is consistent with the previous findings [29]. On the contrary, when an electric field is applied to the folded carbon chain with low free energy (without electric field) (see figure 6(b)), the free energy of the folded carbon chain increases, while the free energy of the unfolded carbon chain decreases. As a result, the free energy of the folded carbon chain is higher than that of the unfolded carbon chain with an electric field. The relatively lower free energy of the unfolded carbon chain will allow it to remain unfolded. This is the reason why the folded carbon chain can be converted into the unfolded carbon chain by the electric field in water.

Figure 6.

New window|Download| PPT slide
Figure 6.Free energy landscape of the carbon chain as a function of R_g and RMSD (a) without electric field and (b) with an electric field. Insets in the lower-right corner of figure 6(a) and inset in the lower-left corner of figure 6(b) are the initial conformations.


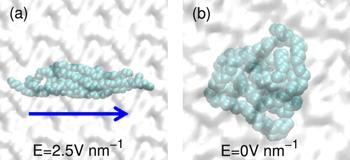
Generally, a polymer material is usually composed of many carbon chains. Here, we also constructed five carbon chains, each of which is consistent with the above carbon chain. Initially, the five carbon chains are arranged side by side in the water. When the electric field is applied to the system, the five carbon chains will be arranged closely and keep the same direction as the electric field, as shown in figure 7(a). With the increase of the electric field strength, the carbon chains will unfold and gradually extend completely. Note that in the absence of an electric field, five carbon chains will fold spontaneously and become a ball, as shown in figure 7(b). If an electric field is applied to the system with folded conformation, all carbon chains will be unfolded again. This expected fast change of carbon chain conformation under electric field may be exploited to develop new rapid response materials.

Figure 7.

New window|Download| PPT slide
Figure 7.Snapshots of five carbon chains suspended in water in various field strengths. (a) Unfolded carbon chain conformation with electric field. (b) Folded carbon chain conformation without electric field.


Finally, it is significant to explore the universality of the electric field-induced carbon chain unfolding, which may bridge the connection with various applications. We have chosen the various conformations, e.g. the longer carbon chain with 50 carbon atoms, and the carbon chain with hydrogen atoms, as shown in figure S6. With increasing length of the carbon chain, the carbon chain is more stable with folding or unfolding; meanwhile, the carbon chain unfolding with an electric field and the carbon chain folding spontaneously can still be observed. The existence of hydrogen atoms on the carbon chain will increase its rigidity, resulting in a difference in the spontaneous carbon chain folding. These studies indicate that the electric field-induced carbon chain unfolding in water is rather universal.

4. Conclusions

In summary, we have investigated the conformational transition of the carbon chain in water by molecular dynamics simulations. It is found that the unfolded carbon chain can spontaneously collapse into the folded state, while the folded carbon chain can be unfolded by an external electric field. Different analyses are given to understand the mechanism of folding and unfolding of the carbon chain. The electric field can enhance the interaction between carbon and water, and reduce the free energy at the unfolded state of the carbon chain. This work presents a new method to regulate the carbon chain conformation, which has applications in the design of ordered materials, and can provide new insights into understanding the conformational transition of the hydrophobic molecule chain. The method with the electric field is safe for the conformational transition of the carbon chain. It does not introduce chemicals and avoids the permanent destruction of the polymer structure. In addition, if the applied electric field is removed, the unfolded polymer will recover to the folded state.

Acknowledgments

This work was partially supported by the Zhejiang Provincial Natural Science Foundation of China (No. LR21A020001) and the National Natural Science Foundation of China (No. 11 774 313). J.K. was supported by the Start-up fund of Zhejiang Normal University.

Supporting Information

Long simulation time (figure S1), water model test (figure S2), radial distribution function (figure S3), solvent accessible surface area (figure S4), root mean square deviation (figure S5), and the reliability of the carbon chain length and hydrogen on carbon chain (figure S6). Movies of conformational transition of the carbon chain without the electric field (movie 1) and with the electric field (movie 2).

ORCID iDs

Jianlong Kou https://orcid.org/0000-0001-7839-7384

Reference View Option By original order
By published year
By cited within times
By Impact factor

[1]Berne B J, Weeks J D, Zhou R 2009 Dewetting and hydrophobic interaction in physical and biological systems
Annu. Rev. Phys. Chem. 60 85 103
DOI:10.1146/annurev.physchem.58.032806.104445 [Cited within: 1]

[2]Ashbaugh H S, Pratt L R 2006 Scaled particle theory and the length scales of hydrophobicity
Rev. Mod. Phys. 78 159 178
DOI:10.1103/RevModPhys.78.159

[3]Djikaev Y S, Ruckenstein E 2016 Recent developments in the theoretical, simulational, and experimental studies of the role of water hydrogen bonding in hydrophobic phenomena
Adv. In Colloid Int. Sci. 235 23 45
DOI:10.1016/j.cis.2016.05.006

[4]Fusco D, Charbonneau P 2016 Soft matter perspective on protein crystal assembly
Colloid. Surface. B-Bioint. 137 22 31
DOI:10.1016/j.colsurfb.2015.07.023

[5]Kang J, Yuan S C, Hong Y L, Chen W, Kamimura A, Otsubo A, Miyoshi T 2016 Unfolding of isotactic polypropylene under uniaxial stretching
ACS Macro Lett. 5 70 73
DOI:10.1021/acsmacrolett.5b00727 [Cited within: 1]

[6]Andreas M, Nikolaus P, Wolfgang V 2000 Protein unfolding by mitochondria
EMBO Rep. 1 404 410
DOI:10.1093/embo-reports/kvd093 [Cited within: 1]

[7]Hansoge N K, Keten S 2019 Effect of polymer chemistry on chain conformations in hairy nanoparticle assemblies
ACS Macro Lett. 8 1209 1215
DOI:10.1021/acsmacrolett.9b00526

[8]Wang Y, Zheng M, Wang X, Li S, Sun J 2018 Polymers with a coiled conformation enable healing of wide and deep damages in polymeric films
ACS Appl. Mater. Inter. 10 30716 30722
DOI:10.1021/acsami.8b10277

[9]Carlson T M, Lam K W, Lam C W, He J Z, Maynard J H, Cavagnero S 2017 Naked-Eye detection of reversible protein folding and unfolding in aqueous solution
J. Chem. Educ. 94 350 355
DOI:10.1021/acs.jchemed.6b00507 [Cited within: 1]

[10]Stuart M A C et al. 2010 Emerging applications of stimuli-responsive polymer materials
Nat. Mate. 9 101 113
DOI:10.1038/nmat2614 [Cited within: 1]

[11]Liu S, Jamali S, Liu Q, Maia J, Baek J B, Jiang N, Xu M, Dai L 2016 Conformational transitions of polymer brushes for reversibly switching graphene transistors
Macromolecules 49 7434 7441
DOI:10.1021/acs.macromol.6b01011

[12]Churchfield L A, Tezcan F A 2019 Design and construction of functional supramolecular metalloprotein assemblies
Accounts Chem. Res. 52 345 355
DOI:10.1021/acs.accounts.8b00617

[13]Yu Y, Hu C, Xia L, Wang J 2018 Artificial metalloenzyme design with unnatural amino acids and non-native cofactors
ACS Catal. 8 1851 1863
DOI:10.1021/acscatal.7b03754

[14]Hernandez N E et al. 2019 Stimulus-responsive self-assembly of protein-based fractals by computational design
Nature Chem. 11 605 614
DOI:10.1038/s41557-019-0277-y

[15]Wang H D, Tan L S 2019 Origami-inspired fabrication: self-folding or self-unfolding of cross-linked-polyimide objects in extremely hot ambience
ACS Macro Lett. 8 546 552
DOI:10.1021/acsmacrolett.9b00198 [Cited within: 1]

[16]Gandini A 2008 Polymers from renewable resources: a challenge for the future of macromolecular materials
Macromolecules 41 9491 9504
DOI:10.1021/ma801735u [Cited within: 2]

[17]Li H, Linke W A, Oberhauser A F, Carrion-Vazquez M, Kerkvliet J G, Lu H, Marszalek P E, Fernandez J M 2002 Reverse engineering of the giant muscle protein titin
Nature 418 998 1002
DOI:10.1038/nature00938 [Cited within: 1]

[18]Azzaroni O, Moya S, Farhan T, Brown A A, Huck W T S 2005 Switching the properties of polyelectrolyte brushes via hydrophobic collapse
Macromolecules 38 10192 10199
DOI:10.1021/ma051549r [Cited within: 1]

[19]Maeda Y, Makhlynets O V, Matsui H, Korendovych I V 2016 Design of catalytic peptides and proteins through rational and combinatorial approaches
Annu. Rev. Biomed. Eng. 18 311 328
DOI:10.1146/annurev-bioeng-111215-024421 [Cited within: 1]

[20]Maity B, Ueno T 2017 Design of bioinorganic materials at the interface of coordination and biosupramolecular chemistry
Chem. Rec. 17 383 398
DOI:10.1002/tcr.201600122 [Cited within: 1]

[21]Hummer G 2007 Water pulls the strings in hydrophobic polymer collapse
Proc. Natl. Acad. Sci. USA 104 14883 14884
DOI:10.1073/pnas.0706633104 [Cited within: 2]

[22]Athawale M V, Goel G, Ghosh T, Truskett T M, Garde S 2007 Effects of lengthscales and attractions on the collapse of hydrophobic polymers in water
Proc. Natl. Acad. Sci. USA 104 733 738
DOI:10.1073/pnas.0605139104 [Cited within: 2]

[23]ten Wolde P R, Chandler D 2002 Drying-induced hydrophobic polymer collapse
Proc. Natl. Acad. Sci. USA 99 6539 6543
DOI:10.1073/pnas.052153299 [Cited within: 1]

[24]Dill K A 1985 Theory for the folding and stability of globular proteins
Biochemistry 24 1501 1509
DOI:10.1021/bi00327a032 [Cited within: 2]

[25]Gerstman B S, Chapagain P P 2005 Self-organization in protein folding and the hydrophobic interaction
J. Chem. Phys. 123 054901
DOI:10.1063/1.1990110 [Cited within: 1]

[26]Torres-Sanchez A, Vanegas J M, Purohit P K, Arroyo M 2019 Combined molecular/continuum modeling reveals the role of friction during fast unfolding of coiled-coil proteins
Soft Matter 15 4961 4975
DOI:10.1039/C9SM00117D [Cited within: 1]

[27]Leuenberger P, Ganscha S, Kahraman A, Cappelletti V, Boersema P J, von Mering C, Claassen M, Picotti P 2017 Cell-wide analysis of protein thermal unfolding reveals determinants of thermostability
Science 355 eaai7825
DOI:10.1126/science.aai7825 [Cited within: 2]

[28]Innes-Gold S N, Pincus P A, Stevens M J, Saleh O A 2019 Polyelectrolyte conformation controlled by a trivalent-rich ion jacket
Phys. Rev. Lett. 123 187801
DOI:10.1103/PhysRevLett.123.187801 [Cited within: 1]

[29]Zangi R, Zhou R, Berne B J 2009 Urea’s action on hydrophobic interactions
J. Am. Chem. Sol. 131 1535 1541
DOI:10.1021/ja807887g [Cited within: 4]

[30]Godawat R, Jamadagni S N, Garde S 2010 Unfolding of hydrophobic polymers in guanidinium chloride solutions
J. Phys. Chem. B. 114 2246 2254
DOI:10.1021/jp906976q [Cited within: 1]

[31]Watson M D, Monroe J, Raleigh D P 2018 Size-dependent relationships between protein stability and thermal unfolding temperature have important implications for analysis of protein energetics and high-throughput assays of protein
J. Phys. Chem. B 122 5278 5285
DOI:10.1021/acs.jpcb.7b05684

[32]Canchi D R, Paschek D, Garc A E 2010 Equilibrium study of protein denaturation by urea
J. Am. Chem. Soc. 132 2338 2344
DOI:10.1021/ja909348c

[33]Das P, Xia Z, Zhou R H 2013 Collapse of a hydrophobic polymer in a mixture of denaturants
Langmuir 103 4877 4882
DOI:10.1021/la3046252

[34]Khan S H, Prakashb A, Pandey P, Lynn A M, Islam A, Hassan M I, Ahmad F 2019 Protein folding: molecular dynamics simulations and in vitro studies for probing mechanism of urea- and guanidinium chloride-induced unfolding of horse cytochrome-c
Int. J. Biol. Macromol. 122 695 704
DOI:10.1016/j.ijbiomac.2018.10.186 [Cited within: 1]

[35]Zangi R, Mark A E 2004 Electrofreezing of confined water
J. Chem. Phys. 120 7123 1130
DOI:10.1063/1.1687315 [Cited within: 3]

[36]Qiu H, Guo W 2013 Electromelting of confined monolayer ice
Phys. Phys. Lett. 110 195701
DOI:10.1103/PhysRevLett.110.195701 [Cited within: 2]

[37]Farimani A B, Min K, Aluru N R, Base D N A 2014 Detection using a single-layer MoS2
ACS Nano 8 7914 7922
DOI:10.1021/nn5029295

[38]Su J Y, Guo H X 2011 Control of unidirectional transport of single-file water molecules through carbon nanotubes in an electric field
ACS Nano 5 351 359
DOI:10.1021/nn1014616

[39]Xu Z, Wang C, Sheng N, Hu G, Zhou Z, Fang H 2016 Manipulation of a neutral and nonpolar nanoparticle in water using a nonuniform electric field
J. Chem. Phys. 144 014302
DOI:10.1063/1.4939151 [Cited within: 1]

[40]Daub C D, Bratko D, Ali T, Luzar A 2009 Microscopic dynamics of the orientation of a hydrated nanoparticle in an electric field
Phys. Phys. Lett. 29 207801
DOI:10.1103/PhysRevLett.103.207801 [Cited within: 4]

[41]Guo X, Su J, Guo H 2012 Electric field induced orientation and self-assembly of carbon nanotubes in water
Soft Matter 8 1010 1016
DOI:10.1039/C1SM06509B [Cited within: 5]

[42]Jiang Z, You L, Dou W, Sun T, Xu P 2019 Effects of an electric field on the conformational transition of the protein: a molecular dynamics simulation study
Polymers 11 282
DOI:10.3390/polym11020282

[43]Xie Z, Li Z, Li J, Kou J, Yao J, Fan J 2021 Electric field-induced gas dissolving in aqueous solutions
J. Chem. Phys. 154 024705
DOI:10.1063/5.0037387 [Cited within: 2]

[44]Saitta A M, Saija F, Giaquinta P V 2012 Ab initio molecular dynamics study of dissociation of water under an electric field
Phys. Rev. Lett. 108 207801
DOI:10.1103/PhysRevLett.108.207801 [Cited within: 1]

[45]Gavish M, Wang J L, Eisenstein M, Lahav M, Leiserowitz L 1992 The role of crystal polarity in alphaamino acid crystals for induced nucleation of ice
Science 256 815
DOI:10.1126/science.1589763 [Cited within: 1]

[46]Drost-Hansen W, Singleton J L 1992 Fundamentals of Medical Cell Biology (JAI, Greenwich, CT) 3a 157
[Cited within: 1]

[47]Li Z, Yao J, Kou J L 2019 Mixture composition effect on hydrocarbon-water transport in shale organic nanochannels
J. Phys. Chem. Lett. 10 4291 4296
DOI:10.1021/acs.jpclett.9b01576 [Cited within: 1]

[48]Hess B, Kutzner C, Spoel D V D, Lindahl E 2008 GROMACS 4: algorithms for highly ecient, load-balanced, and scalable molecular simulation
J. Chem. Theory. Comput. 4 435
DOI:10.1021/ct700301q [Cited within: 1]

[49]Lawrence C P, Skinner J L 2003 Flexible TIP4P model for molecular dynamics simulation of liquid water
Chem. Phys. Lett. 372 842 847
DOI:10.1016/S0009-2614(03)00526-8 [Cited within: 1]

[50]Svishchev I M, Kusalik P G 1996 Electrofreezing of liquid water: a microscopic perspective
J. Am. Chem. Soc. 118 649 654
DOI:10.1021/ja951624l [Cited within: 1]

[51]Yan J Y, Patey G N 2011 Heterogeneous ice nucleation induced by electric fields
J. Phys. Chem. Lett. 2 2555 2559
DOI:10.1021/jz201113m [Cited within: 1]

[52]Jorgensen W L, Chandrasekhar J, Madura J D 1983 Comparison of simple potential functions for simulating liquid water
J. Chem. Phys. 79 926
DOI:10.1063/1.445869 [Cited within: 2]

[53]Nose S, Klein M L 1983 Constant pressure molecular dynamics for molecular systems
Mol. Phys. 50 1055 1076
DOI:10.1080/00268978300102851 [Cited within: 1]

[54]Bussi G, Donadio D, Parrinello M 2007 Canonical sampling through velocity rescaling
J. Chem. Phys. 126 014101
DOI:10.1063/1.2408420 [Cited within: 1]

[55]Dinner A R, Lazaridis T, Karplus M 1999 Understanding β-hairpin formation
Proc. Natl. Acad. Sci. USA 96 9068
DOI:10.1073/pnas.96.16.9068 [Cited within: 1]

[56]Huang X, Margulis C J, Berne B J 2003 Dewetting-induced collapse of hydrophobic particles
Proc. Natl. Acad. Sci. USA 100 11955 11958
DOI:10.1073/pnas.1934837100 [Cited within: 1]

[57]Mondal J, Morrone J A, Berne B J 2013 How hydrophobic drying forces impact the kinetics of molecular recognition
Proc. Natl. Acad. Sci. USA 110 13277 13282
DOI:10.1073/pnas.1312529110 [Cited within: 1]

[58]Xu H, Berne B 2001 Hydrogen-bond kinetics in the solvation shell of a polypeptide
J. Phys. Chem. B 105 11929 11932
DOI:10.1021/jp012749h [Cited within: 1]

[59]Rinne K F, Gekle S, Bonthuis D J, Netz R R 2012 Nanoscale pumping of water by AC electric fields
Nano Lett. 12 1780 1783
DOI:10.1021/nl203614t [Cited within: 2]

[60]Kou J, Lu H, Wu F, Fan J, Yao J 2014 Electricity resonance-induced fast transport of water through nanochannels
Nano Lett. 14 4931 4936
DOI:10.1021/nl500664y

[61]Kou J, Yao J, Lu H, Zhang B, Li A, Sun Z, Zhang J, Fang Y, Wu F, Fan J 2015 Electromanipulating water flow in nanochannels
Angew. Chem. Int. Ed. 54 2351 2355
DOI:10.1002/anie.201408633

[62]Zhu Z, Chang C, Shu Y, Song B 2020 Transition to a superpermeation phase of confined water induced by a terahertz electromagnetic wave
J. Phys. Chem. Lett. 11 256 262
DOI:10.1021/acs.jpclett.9b03228 [Cited within: 3]