摘要:电压调控磁各向异性磁隧道结(voltage controlled magnetic anisotropy magnetic tunnel junction, VCMA-MTJ)作为磁随机存储器(magnetic random access memory, MRAM)的核心器件, 具有读写速度快、功耗低、与CMOS工艺相兼容等优点, 现已得到国内外****的广泛关注. 然而随着VCMA-MTJ尺寸不断缩小、MRAM存储容量不断增大, 工艺偏差对MTJ性能的影响变得越来越显著, 甚至会引起VCMA-MTJ电路的读写错误. 本文在充分考虑磁控溅射薄膜生长工艺中自由层厚度偏差(γ_tf)、氧化势垒层厚度偏差(γ_tox)以及离子束刻蚀工艺中由侧壁再沉积层引入的刻蚀工艺稳定因子(α)偏差影响的情况下, 给出了基于工艺偏差的VCMA-MTJ电学模型, 并将该模型应用到VCMA-MTJ读写电路中, 研究了工艺偏差对上述电路读写错误率的影响. 结果表明: 当γ_tf ≥ 13%, γ_tox ≥ 11%时, VCMA-MTJ将无法实现磁化状态的有效切换; 当α ≤ 0.7时, VCMA-MTJ磁化方向的进动过程变得不稳定. 进一步地, VCMA-MTJ电路的读错误率和写错误率也将随着工艺偏差的增大而增大. 研究表明, 通过增大外加电压(V_b)和减小外加电压脉冲宽度(t_pw)可有效降低VCMA-MTJ电路的写错误率, 增大电路的读驱动电压(V_dd)可有效降低VCMA-MTJ电路的读错误率.
关键词: 磁隧道结/
电压调控磁各向异性/
工艺偏差/
读写电路

English Abstract

全文HTML

--> --> -->

物联网、5G通信和人工智能技术的飞速发展以及大数据云时代的来临, 对计算机体系结构中随机储存器(random access memory, RAM)的速度、功耗、集成度和可靠性均提出了更高要求^[1]. 对于传统的基于互补金属氧化物半导体(complementary metal oxide semiconductor, CMOS)工艺的易失性RAM而言, 随着器件特征尺寸的不断缩小, 漏电流的增加以及处理器与存储器的互连延迟都将制约存储器性能提升^[2]. 为了解决上述问题, 国内外****对包括相变存储器(phase change random access memory, PCRAM)、阻变存储器(resistive random access memory, RRAM)以及自旋转移力矩磁随机存储器(spin-transfer torque magnetoresistive random access memory, STT-MRAM)和自旋轨道转矩磁随机存储器(spin–orbit torque magnetoresistive random access memory, SOT-MRAM)在内的以磁随机存储器(magnetic random access memory, MRAM)为代表的非易失性RAM进行了广泛研究^[3-5]. 上述非易失性RAM使系统在断电情况下不丢失数据, 可用以消除漏电流和静态功耗, 同时采用后道工艺可减小互连延迟. 其中, STT-MRAM以其高速、小尺寸且与CMOS工艺相兼容等优点, 已进入商业化初始阶段^[6-8]. 然而STT-MRAM写入数据时需要较大的写入电流, 动态功耗较高^[9,10].
不同于STT-MRAM通过改变电流来引入自旋力矩和磁场, 电压调控磁各向异性磁随机存储器(voltage controlled magnetic anisotropy magnetic random access memory, VCMA-MRAM)通过改变外加电压即电场来快速调控磁化方向, 从而有效减小由电流引起的欧姆损耗, 因此具有写入速度快且写入功耗低的显著特点, 有望成为下一代的主流非易失性存储器^[11-13]. 而作为构成VCMA-MRAM基本存储单元的磁隧道结(magnetic tunnel junction, MTJ), 现已受到国内外****的广泛关注^[14-16]. 近年来, 随着VCMA-MTJ理论的不断深入, 有关****基于VCMA效应建立了VCMA-MTJ的电学模型^[17,18], 通过电压来调控MTJ自由层磁化方向, 从而实现数据存储. 然而随着VCMA-MTJ尺寸的不断缩小, 工艺偏差对MTJ性能的影响变得越来越严重, 甚至对VCMA-MTJ电路的读写功能产生了较大影响. 本文在充分考虑磁控溅射(magnetron sputtering)薄膜生长工艺和离子束刻蚀(ion beam etching)工艺会引入工艺偏差的情况下, 给出基于工艺偏差的VCMA-MTJ电学模型, 并研究工艺偏差对VCMA-MTJ自由层磁化方向翻转的影响. 在此基础上, 进一步研究工艺偏差对VCMA-MTJ读写电路中写错误率和读错误率的影响. 本文的研究工作对于VCMA-MTJ器件及其应用电路的设计具有重要的理论和指导意义.

图1为VCMA-MTJ结构示意图, 其中氧化势垒层由氧化镁(MgO)材料构成; 参考层和自由层作为VCMA-MTJ的两个电极, 均由钴铁硼(CoFeB)材料构成. 参考层磁化方向固定不变, 当外加电压(V_b)变化时, 自由层磁化方向会发生翻转^[19]. 当自由层磁化方向与参考层磁化方向平行时称为平行态(P态), 器件呈低阻特性; 当自由层磁化方向与参考层磁化方向反平行时称为反平行态(AP态), 器件呈高阻特性.
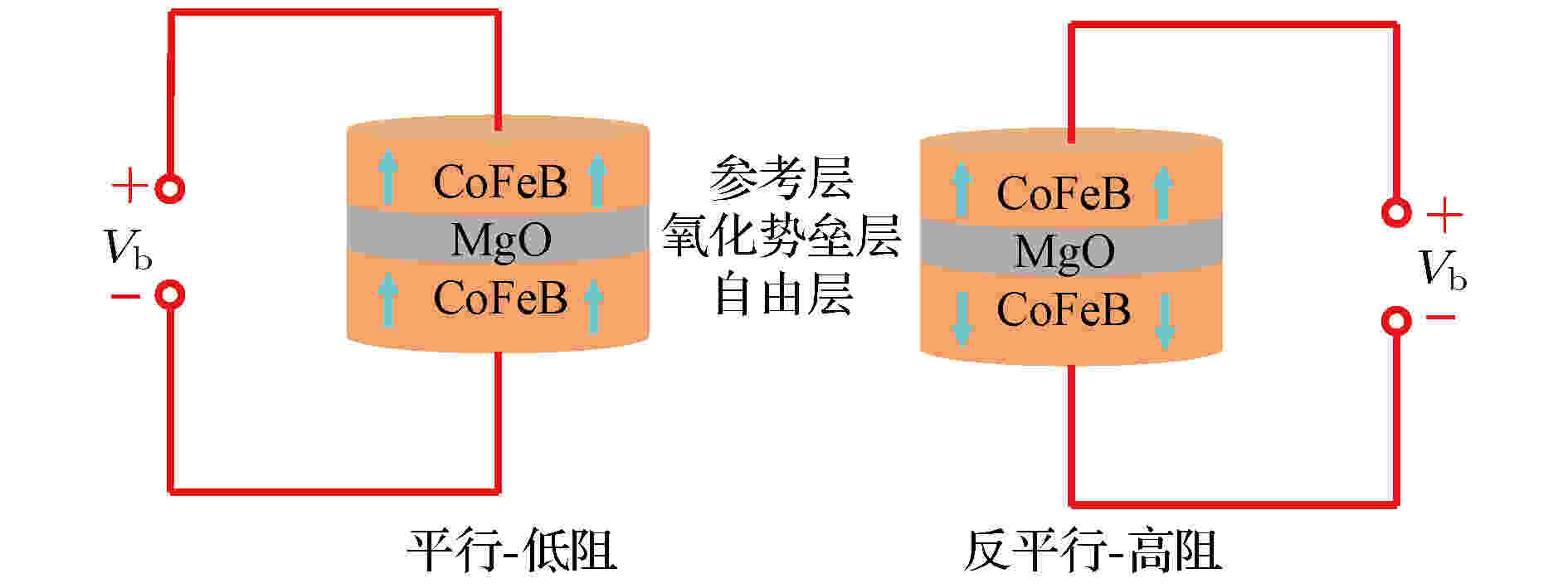图 1 VCMA-MTJ结构示意图
Figure1. Schematic structure of the VCMA-MTJ device.

进一步地, VCMA-MTJ在P态和AP态之间的切换与V_b的大小和加载时间密切相关, 下面将结合图2给出的VCMA-MTJ磁化动力学示意图进行分析.
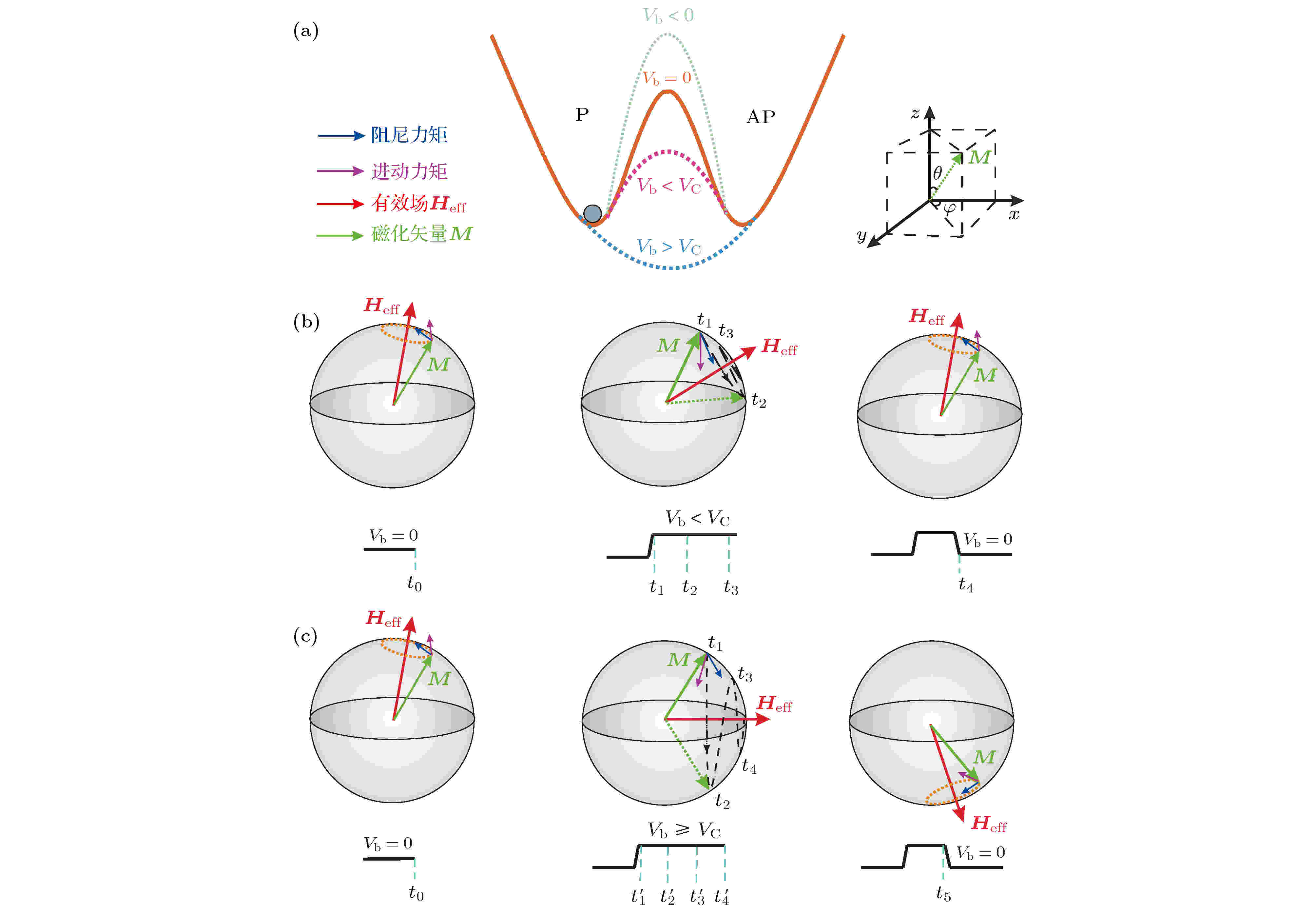图 2 VCMA-MTJ的磁化动力学示意图　(a)不同电压对MTJ磁化状态能量势垒的影响; (b)V_b < V_C的情况; (c)V_b > V_C的情况
Figure2. Illustration of magnetization dynamics for the VCMA-MTJ device: (a) The impacts of different voltages on the energy barrier of MTJ; (b) at a relatively low voltage (V_b < V_C); (c) at a high positive voltage (V_b > V_C).

从图2(a)中可以看出, VCMA-MTJ在两个稳定磁化状态(P态和AP态)切换时需要克服一定的能量势垒. 该势垒大小受V_b的影响, 当V_b增大时, P态与AP态之间的能量势垒会随之降低, 这有利于VCMA-MTJ的状态切换. 从能量势垒角度来看, 当能量势垒完全消除时, 对应的外加电压称为临界电压(V_C).
在图2(b)中, 设参考层磁化方向为z轴正方向且固定不变, 当V_b = 0 V时, 自由层的磁化矢量(M)将围绕有效场(H_eff)做强度不变而方向改变的拉莫尔进动, M末端的运动轨迹为一个圆周. 由于自由层M在z轴分量为正, 即与参考层磁化方向平行, 因此VCMA-MTJ将处于P态. 当在t₁时刻加载V_b且0 < V_b < V_C时, 电荷会在自由层与氧化势垒层接触界面处聚集, 使得垂直磁各向异性发生变化, 导致H_eff向x-y平面偏转, 此现象即为电压调控磁各向异性(VCMA)效应^[20]. 此时, M将围绕新的H_eff方向进动, 并随着时间从t₁→t₂→t₃的增加, M将不断靠近H_eff. 由于M在z轴分量始终为正, VCMA-MTJ仍然处于P态, 无法实现VCMA-MTJ状态的切换. 在t₄时刻撤除外加电压(V_b = 0 V)后, H_eff和M都将返回初始状态, M仍将围绕H_eff做强度不变而方向改变的拉莫尔进动, VCMA-MT仍将处于P态.
在图2(c)中, 设参考层磁化方向为z轴正方向且固定不变, 当在t₁’时刻加载V_b且V_b ≥ V_C时, H_eff方向偏转并与x-y平面重合, M将围绕新的H_eff方向进动. 在t₁’时刻M在z轴的分量为正, VCMA-MTJ处于P态. 在t₂’时刻M在z轴的分量变为负, 此时VCMA-MTJ将由P态切换到AP态. 进一步, 随着时间从$t_1' \to t_2' \to t_3' \to t_4'$的增加, VCMA-MTJ将在P态→AP态→P态→AP态之间循环切换, 同时M不断靠近H_eff方向. 当在t₅’时刻撤除外加电压(V_b = 0 V)时, H_eff将向-z轴偏转, 且M仍将围绕H_eff做强度不变而方向发生改变的拉莫尔进动, 此时VCMA-MTJ将处于AP态. 可见, VCMA-MTJ切换状态不仅与V_b的大小有关, 还与V_b的加载时间即外加电压脉冲宽度密切相关.

由于VCMA-MTJ中自由层的磁化矢量M是在空间中呈连续分布的, 其动态特性可采用LLG(Landau-Lifshitz-Gilbert)方程^[21]进行描述,

$\dfrac{{{\rm{d}}{{M}}}}{{{\rm{d}}t}} = - \gamma {{M}} \times {{{H}}_{{\rm{eff}}}} + \dfrac{{{\alpha _{\rm{d}}}}}{{{M_{\rm{s}}}}}\left( {{{M}} \times \dfrac{{{\rm{d}}{{M}}}}{{{\rm{d}}t}}} \right),$

其中, $ \gamma $为简化的旋磁比, $ {\alpha }_{\rm{d}} $为与自由层材料相关的Gilbert阻尼因子, M_S为饱和磁化强度. 等式右侧第一项表示为M围绕H_eff进行的拉莫尔进动; 第二项为Gilbert阻尼力矩. 可以看出, 若不考虑阻尼力矩的影响, M和H_eff的夹角将保持不变; 若考虑阻尼力矩的影响, 在进动过程中, M的方向会越来越靠近H_eff, 并最终与H_eff的磁化方向重合.
设m为自由层磁化矢量方向上的单位向量, 则有M = M_S·m, 且m在直角坐标系中可表示为

${{m}} = {m_x}{{{e}}_{{x}}} + {m_y}{{{e}}_y} + {m_z}{{{e}}_z},$

其中, m_x, m_y, m_z分别为m在x, y, z轴上的分量, e_x, e_y, e_z分别为x, y, z轴上的单位向量.
当考虑外加电压V_b对有效磁场H_eff的影响时, H_eff可具体表示为^[22]

${{{H}}_{{\rm{eff}}}}\left( {{V_{\rm{b}}}} \right) = {{{H}}_{{\rm{ext}}}} + {{{H}}_{{\rm{dem}}}} + {{{H}}_{{\rm{th}}}} + {{{H}}_{\rm{k}}}\left( {{V_{\rm{b}}}} \right),$

其中, H_ext为外加磁场, H_dem为退磁化场, H_th为热噪声场, H_k(V_b)为垂直磁各向异性场.
可以看出, H_k与外加电压V_b有关, 可进一步表示^[23]为

${{{H}}_{\rm{k}}}\left( {{V_{\rm{b}}}} \right) = \left( {\dfrac{{2{K_{\rm{i}}}{t_{{\rm{ox}}}} - 2\xi {V_{\rm{b}}}}}{{{\mu _0}{{{M}}_{\rm{s}}}{t_{\rm{f}}}{t_{{\rm{ox}}}}}}} \right){m_z}{{{e}}_z},$

其中, K_i为垂直磁各向异性系数, ξ为电压调控磁各向异性系数, t_ox为氧化势垒层厚度标准值, t_f为自由层厚度标准值, μ₀为磁导率, M_s为饱和磁化强度, m_z为m在z轴上的分量.
同时, 设参考层磁化方向为z轴正方向且固定不变, 则m还可表示为

${{m}} = {\rm{sin}}\theta {\rm{cos}}\varphi {{{e}}_x} + {\rm{sin}}\theta {\rm{sin}}\varphi {{{e}}_y} + {\rm{cos}}\theta {{{e}}_z},$

其中, θ为m与z轴的夹角, φ为m在x-y平面上投影向量与x轴的夹角. 可以看出, m的动态可由θ和φ随时间的变化来描述, 而VCMA-MTJ状态的切换可由m_z(即m_z = cosθ)来确定.
将(2)—(5)式带入(1)式, 求解得到

$\begin{split}& \dfrac{{{\rm{d}}\theta }}{{{\rm d}t}} =\dfrac{\gamma }{{1 + {\alpha _d}^2}}\\ & \times \big[ {({H_x} - {N_x}{M_{\rm{S}}}{\rm{sin}}\theta {\rm{cos}}\varphi )\left( {{\alpha _{\rm{d}}}\cos \theta \cos \varphi - \sin \varphi } \right)}\\& { + ({H_y} - {N_y}{M_{\rm{S}}}{\rm{sin}}\theta {\rm{sin}}\varphi )\left( {{\alpha _{\rm{d}}}\cos \theta \sin \varphi + \cos \varphi } \right)}\\& - ({H_z} + \left( {{H_{\rm{k}}}\left( {{{\rm{V}}_{\rm{b}}}} \right) - {N_z}{M_{\rm{S}}}} \right){\rm{cos}}\theta ){\alpha _{\rm{d}}}\sin \theta \big],\\[-12pt] \end{split}$

其中, H_x, H_y, H_z分别为H_ext在x, y, z轴上的分量, 且H_y = H_z = 0; N_x, N_y, N_z分别为H_dem在x, y, z轴上的退磁因子.
进一步地, 通过求解θ即m_z = cosθ来确定VCMA-MTJ的磁化状态. 本文中VCMA-MTJ模型用到的部分参数^[17,18]如表1所示.

参数	符号	数值	单位
氧化势垒层厚度标准值	tox	1.4	nm
垂直磁各向异性系数	Ki	0.32	mJ/m2
电压调控磁各项异性系数	ξ	60	fJ/(V·m)
自由层厚度标准值	tf	1.1	nm
简化的旋磁比	γ	2.21 × 105	m/(A·s)
磁导率	μ0	1.256 × 10–6	H/m
吉尔伯特阻尼因子	αd	0.05
饱和磁化强度	Ms	0.625 × 106	A/m
x, y 轴退磁因子	Nx, y	0.0168
z 轴退磁因子	Nz	0.966
外加磁场在 x 轴分量	Hx	31830	A/m

表1VCMA-MTJ模型参数列表
Table1.Parameters of the VCMA-MTJ model.

图3给出了VCMA-MTJ自由层磁化矢量在z轴分量(即m_z)随时间的变化曲线, 并分析了V_b对磁化状态切换的影响. 从图3可以看出, 在恒定的外加电压脉冲宽度(t_pw = 0.4 ns)下, 当V_b ≤ 0.9 V时, m_z始终为正, VCMA-MTJ磁化状态保持不变, 始终处于初始态P态; 当V_b ≥ 1.0 V时, 随着时间的增加, m_z将由正变负, 即磁化状态发生改变, VCMA-MTJ将由初始的P态切换为AP态. 同时, 将m_z首次经由1降低至–0.95所持续的时间定义为VCMA-MTJ的切换速度(t_sw), 则V_b = 1.0 V, t_pw = 0.4 ns时对应的t_sw为1.25 ns.
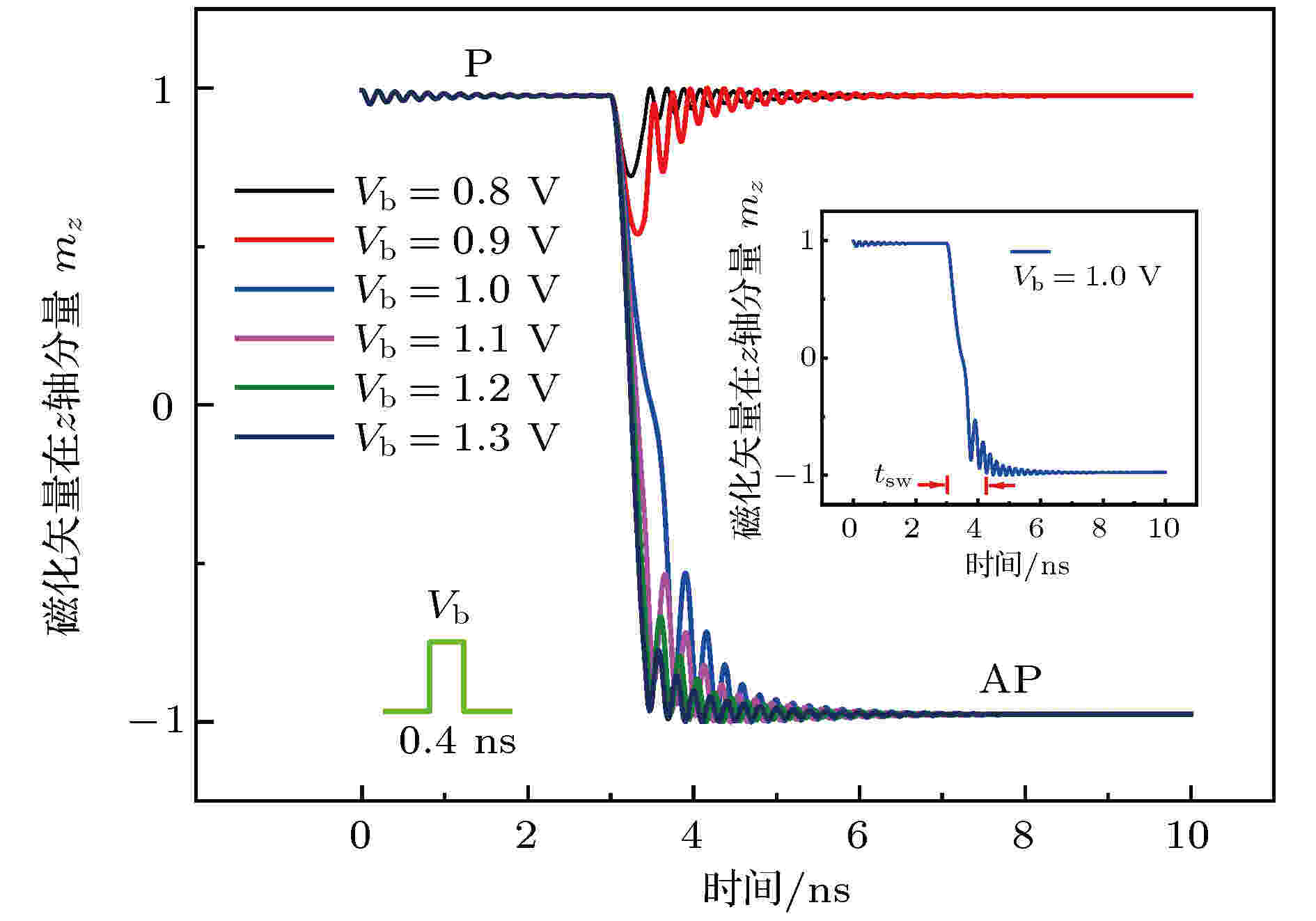图 3 VCMA-MTJ磁化状态随时间的变化曲线, 其中插图是切换速度的定义
Figure3. Magnetization state versus time of VCMA-MTJ, the inset represents the definition of the switching speed.

图4进一步给出了t_sw随V_b的变化曲线. 从图4可以看出, 在t_pw = 0.4 ns时, 当V_b ≤ 1.3 V时, t_sw随V_b的增加呈显著下降趋势; 当V_b > 1.3 V时, V_b对t_sw的影响不大, t_sw几乎保持不变. 通过拟合可以看出, t_sw与V_b近似呈e指数关系.
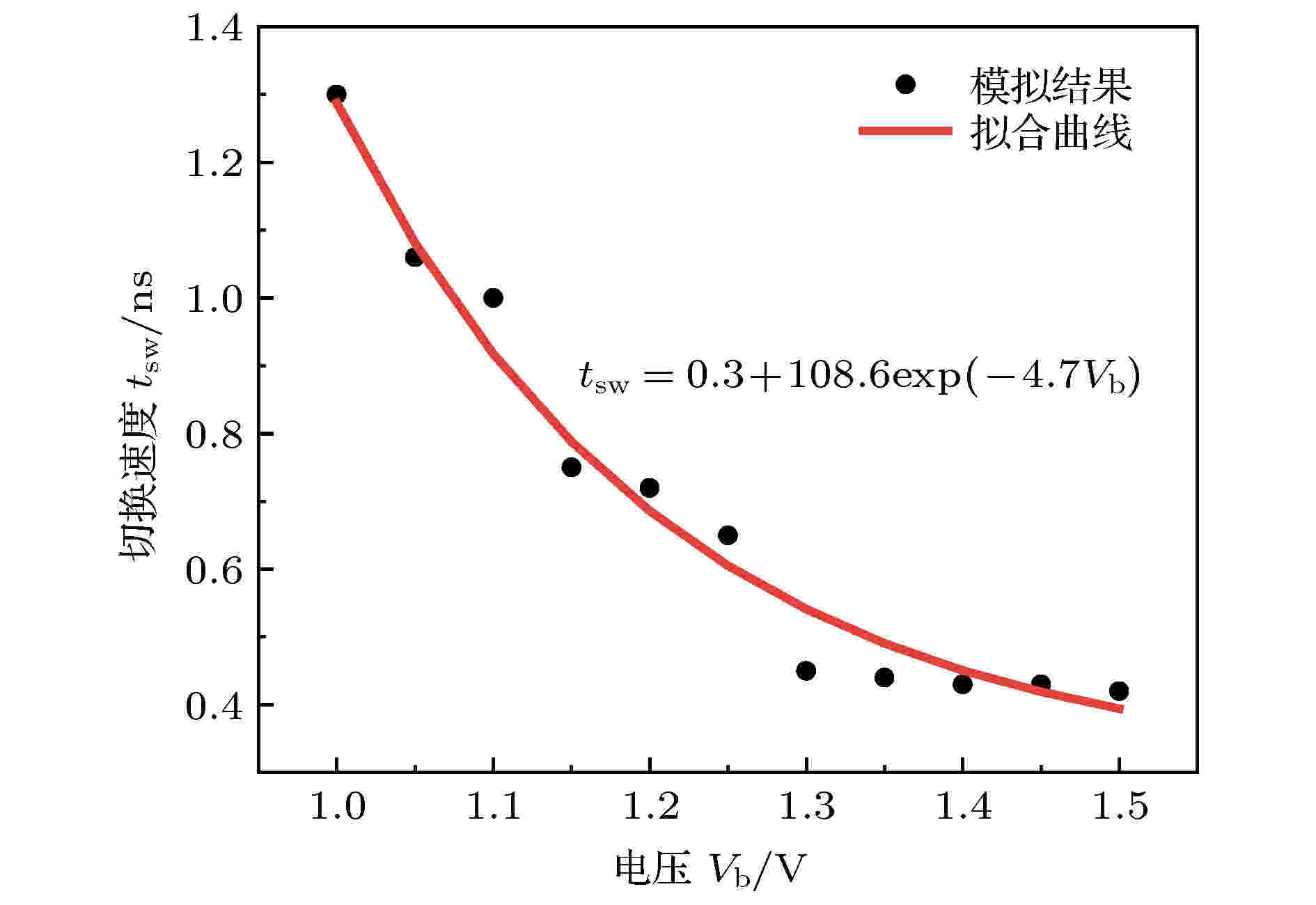图 4 不同V_b对VCMA-MTJ磁化状态切换速度的影响, 其中t_pw = 0.4 ns
Figure4. Effect of V_b on the magnetization direction switching speed of VCMA-MTJ at t_pw = 0.4 ns.

图5给出了t_pw对VCMA-MTJ磁化状态切换的影响. 从图5可以看出, 在恒定的外加电压(V_b = 1.2 V)下, 当t_pw ≤ 0.1 ns时, m_z始终为正, VCMA-MTJ磁化状态保持不变, 始终处于初始态P态; 当0.2 ns ≤ t_pw ≤ 0.6 ns时, 随着时间的增加, m_z将由正变负, 即磁化状态发生改变, VCMA-MTJ将由初始的P态切换为AP态. 当t_pw进一步增大(例如t_pw = 0.8 ns)时, 在拉莫尔进动过程中随着时间从$ t_1' \to t_2' \to t_3' $的增加, VCMA-MTJ将经由P态到AP态后, 再次切换为P态.
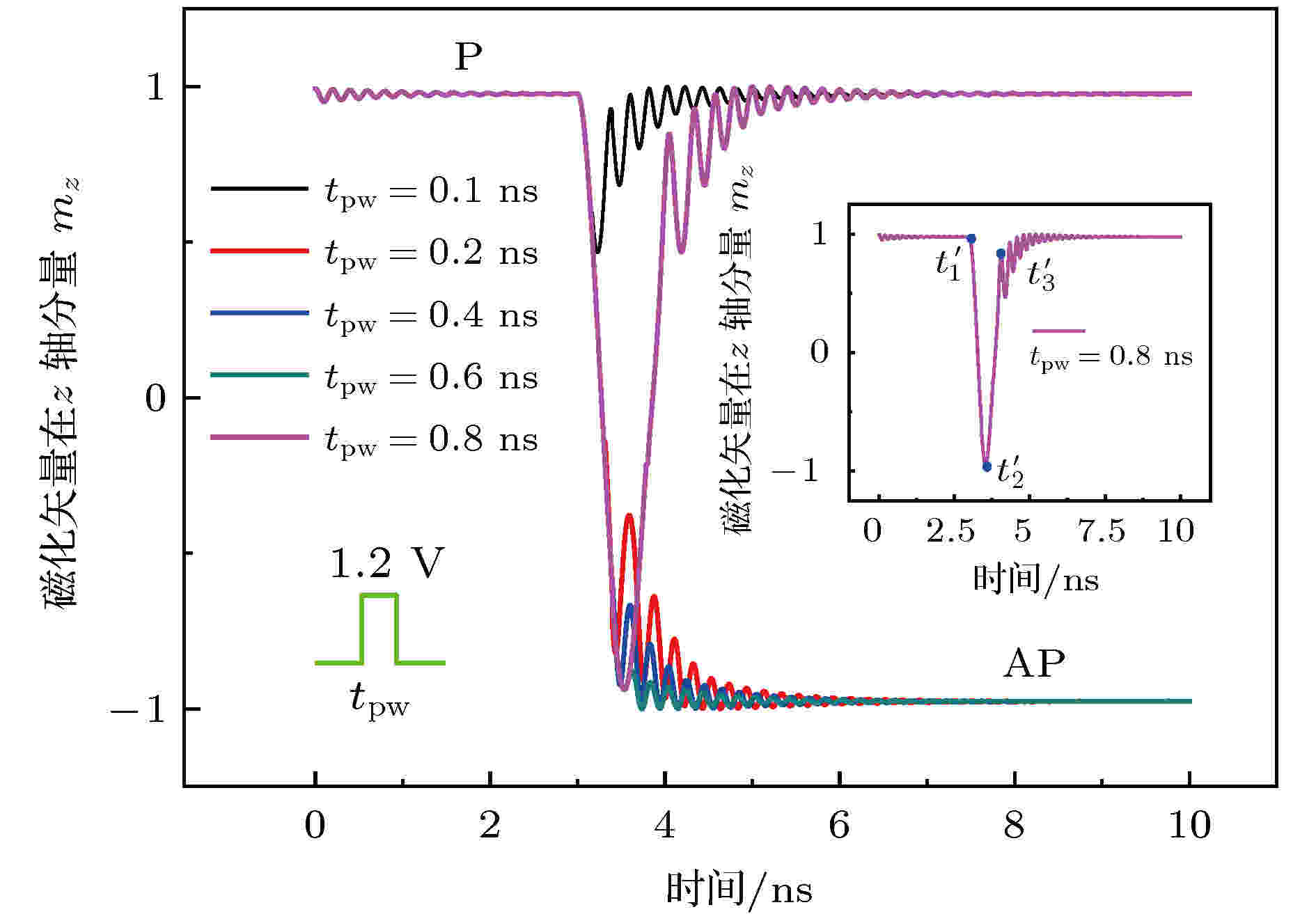图 5 不同t_pw对VCMA-MTJ磁化状态切换的影响, 插图为与图2(c)相对应的m_z变化情况
Figure5. Effect of t_pw on the magnetization direction switching of VCMA-MTJ, the inset shows the precession of m_z corresponding to Fig. 2(c).

2

-->

3.1.薄膜生长工艺偏差的影响

VCMA-MTJ的典型制备工艺主要包括薄膜生长、热退火及刻蚀工艺. 其中VCMA-MTJ中自由层、氧化势垒层和参考层大都是采用磁控溅射法^[24,25]制备得到, 该方法具有薄膜沉积速度快、适用于多种材料混合溅射、可实现大批量生产等优点. 然而在薄膜生长过程中, 薄膜厚度会不可避免地存在几个原子层厚度范围内的微小偏差^[26,27], 如图6所示, 其中t_ox0和t_ox1分别为氧化势垒层厚度的最大值和最小值, t_f0和t_f1分别为自由层厚度的最大值和最小值, t_oxm和t_fm分别为考虑薄膜厚度偏差情况下氧化势垒层厚度和自由层厚度的等效均值. 随着VCMA-MTJ尺寸的不断缩小, 上述薄膜厚度偏差将会对器件的磁化翻转产生重要的影响.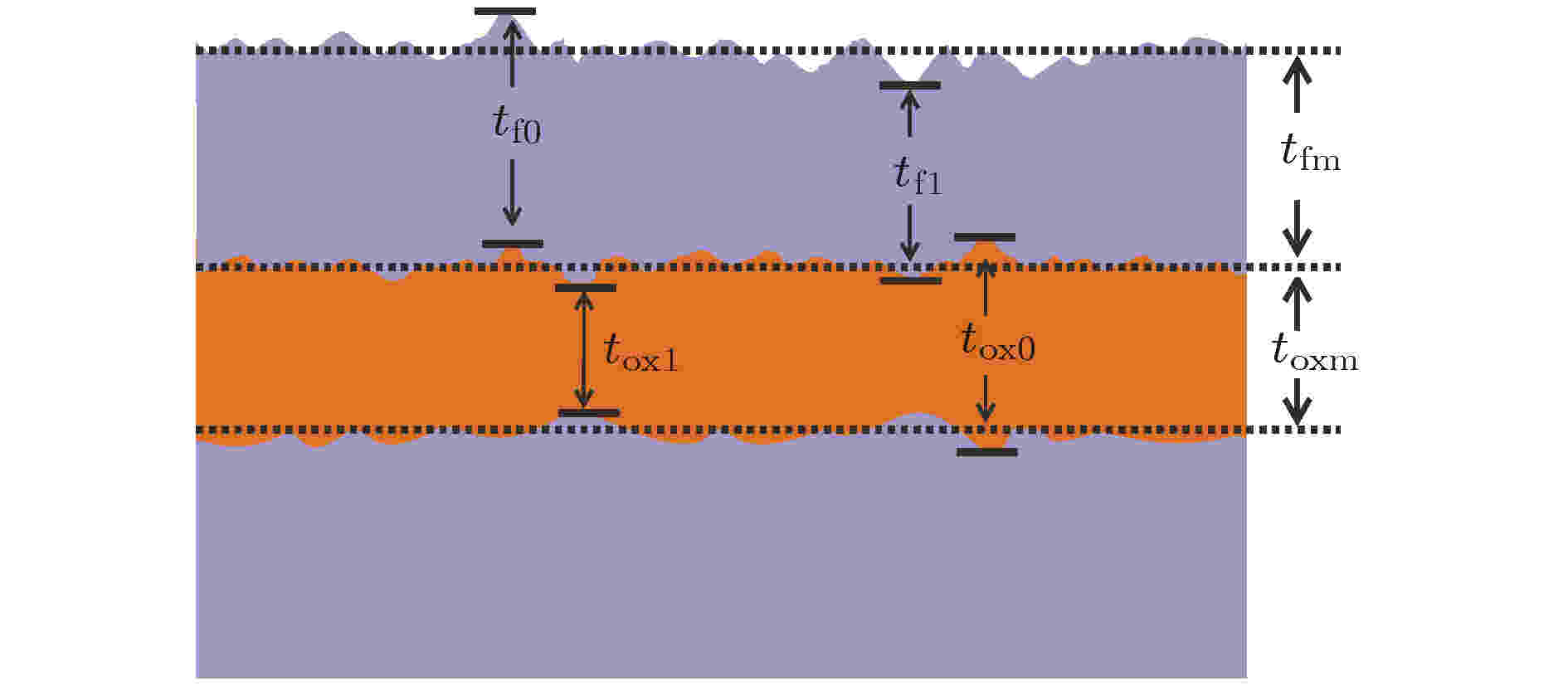
图 6 薄膜生长工艺产生的厚度偏差示意图
Figure6. Schematic illustration of thickness deviation caused by the thin film growth process.

考虑到垂直磁各向异性主要来源于自由层和氧化势垒层之间的界面相互作用, 垂直磁各向异性对自由层厚度和氧化势垒层厚度的变化更为敏感^[28]. 本文采用自由层厚度偏差(γ_tf)和氧化势垒层厚度偏差(γ_tox)来具体表征在磁控溅射工艺生长薄膜中产生的厚度偏差. 此时, 可分别表示为

${\gamma _{{\rm{tf}}}} = \dfrac{{{t_{{\rm{fm}}}} - {t_{\rm{f}}}}}{{{t_{\rm{f}}}}},$

${\gamma _{{\rm{tox}}}} = \frac{{{t_{{\rm{oxm}}}} - {t_{{\rm{ox}}}}}}{{{t_{{\rm{ox}}}}}},$

其中t_f和t_ox为不考虑薄膜生长工艺偏差的理想情况下自由层厚度和氧化势垒层厚度的标准值.
此时, 垂直磁各向异性场H_k可表示为

${{{H}}_{\rm{k}}} = \left[ {\frac{{2{K_{\rm{i}}}{t_{{\rm{ox}}}}\left( {1 + {\gamma _{{\rm{tox}}}}} \right) - 2\xi {V_{\rm{b}}}}}{{{\mu _0}{{{M}}_{\rm{s}}}{t_{\rm{f}}}\left( {1 + {\gamma _{{\rm{tf}}}}} \right){t_{{\rm{ox}}}}\left( {1 + {\gamma _{{\rm{tox}}}}} \right)}}} \right]{m_z}{{{e}}_z}.$

将(9)式代入(3)式并令H_eff在z轴分量为零, 此时的外加电压即为临界电压V_C, 可表示为

$\begin{split}{V_{\rm{C}}} =& \dfrac{{{K_{\rm{i}}}{t_{{\rm{ox}}}}\left( {1 + {\gamma _{{\rm{tox}}}}} \right)}}{\xi } \\&- \dfrac{{{\mu _0}M_{\rm{s}}^2{t_{\rm{f}}}\left( {1 + {\gamma _{{\rm{tf}}}}} \right){t_{{\rm{ox}}}}\left( {1 + {\gamma _{{\rm{tox}}}}} \right){N_z}}}{{2\xi }}.\end{split}$

其中(10)式中等式右侧第二项远小于第一项, 可忽略不计, 即γ_tox与V_C呈正比关系.
图7给出了不同γ_tf对VCMA-MTJ磁化状态切换的影响, 其中V_b = 1.2 V, t_pw = 0.4 ns. 当γ_tf ≤ 12%时, MTJ自由层的磁化方向能够实现从P态到AP态的切换; 当γ_tf ≥ 13%时, MTJ不能实现从P态到AP态的切换. 这是因为, 从(9)式可知, 随着γ_tf的增加, H_k将减小, 从而导致MTJ的H_eff向x-y平面偏转, 这不利于磁化方向的有效翻转.
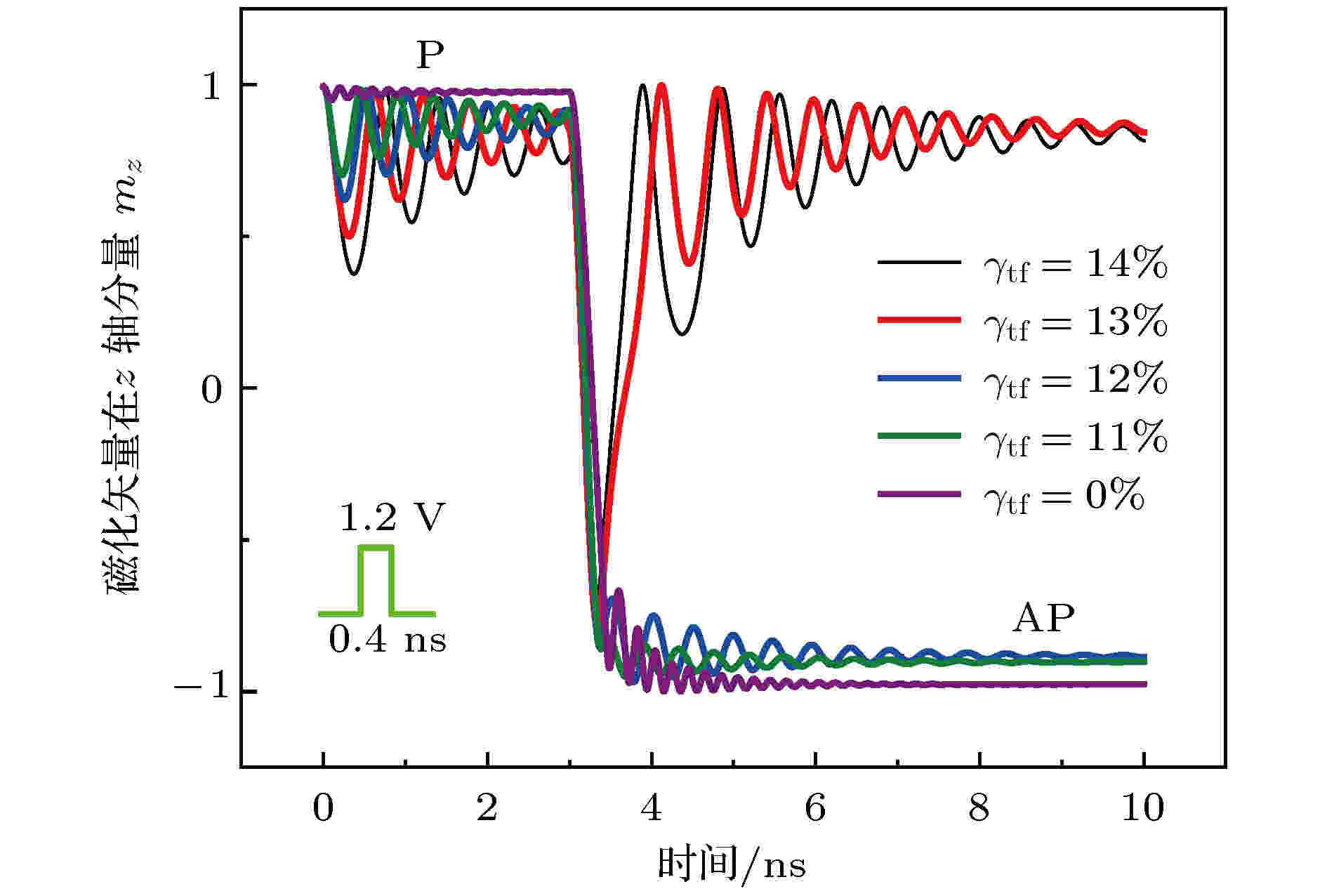图 7 γ_tf对VCMA-MTJ磁化方向切换的影响, 其中V_b = 1.2 V, t_pw = 0.4 ns
Figure7. Effect of γ_tf on the magnetization direction switchingof VCMA-MTJ at V_b = 1.2 V, t_pw = 0.4 ns.

图8给出了不同γ_tox对VCMA-MTJ磁化状态切换的影响. 当γ_tox ≤ 10%时, 自由层的磁化矢量能够发生翻转, VCMA-MTJ将由初始的P态切换为AP态; 当γ_tox ≥ 11%时, VCMA-MTJ将无法实现磁化状态的切换. 这是因为, 从(10)式可知, 当γ_tox较大时, 临界电压V_C增大, 进而影响了自由层磁化矢量的进动, 从而导致切换错误.
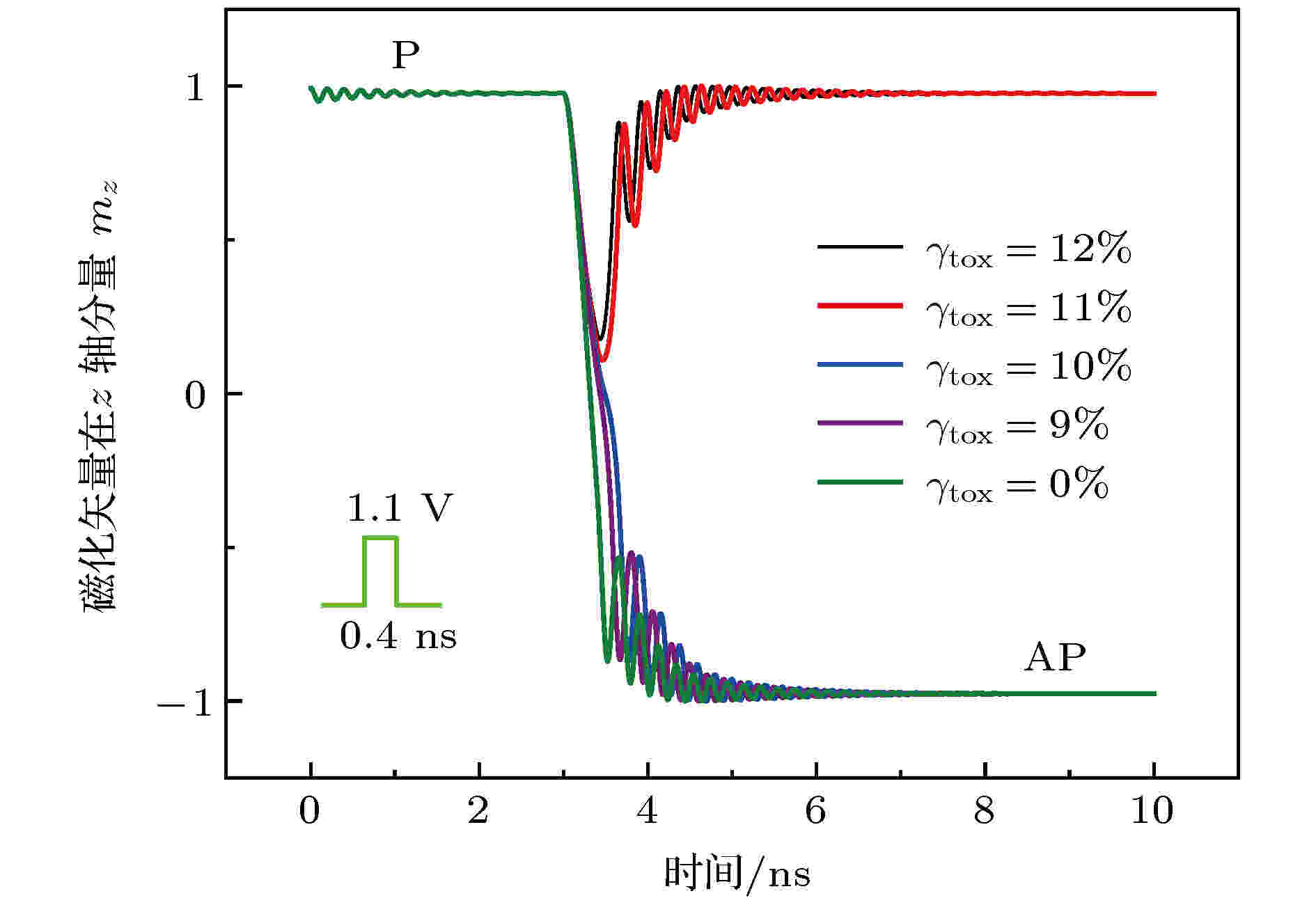图 8 不同γ_tox对VCMA-MTJ磁化状态切换的影响, 其中V_b = 1.1 V, t_pw = 0.4 ns
Figure8. Effect of γ_tox on magnetization direction switching of VCMA-MTJ at V_b = 1.1 V and t_pw = 0.4 ns.

2 -->

3.2.刻蚀工艺

离子束刻蚀技术具有刻蚀速率快、图形精度高、工艺参数可控性好等优势, 因此成为MTJ刻蚀的主流工具^[29-31]. 但离子束刻蚀不可避免地会产生具有磁性的非挥发刻蚀产物, 如果沟槽深度较大或者沟槽宽度较小, 则粒子不能全部飞出槽外, 导致部分粒子附着在侧壁上, 形成再沉积层^[32,33](图9).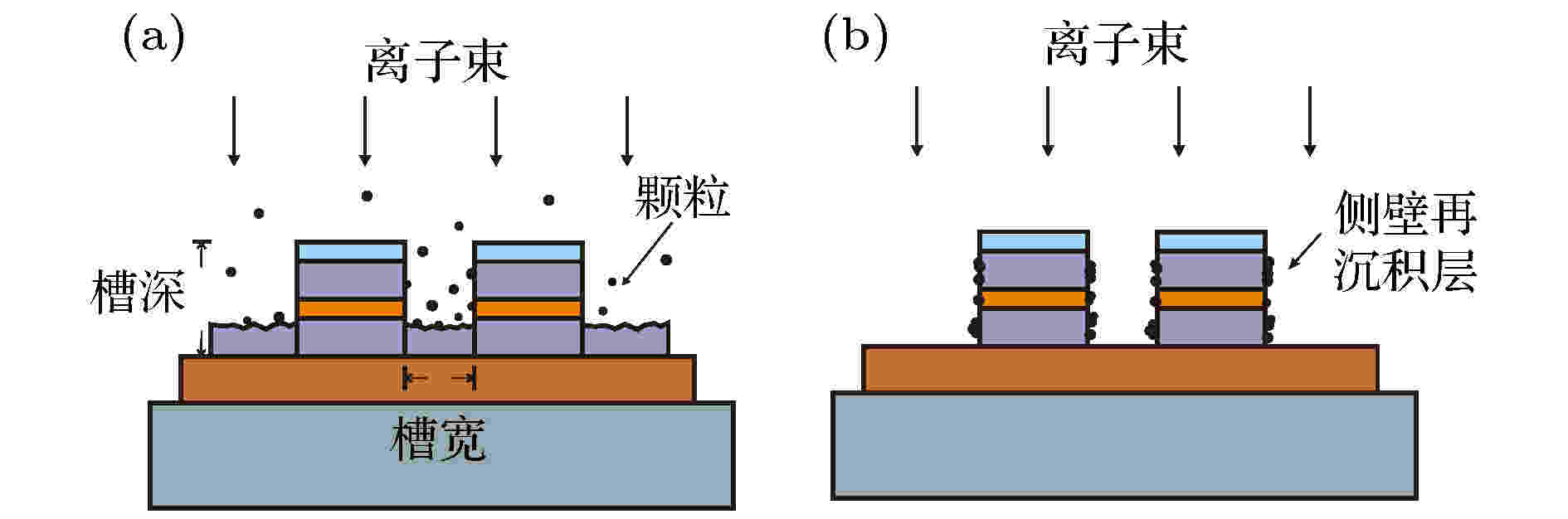
图 9 离子束刻蚀产生侧壁再沉积层示意图　(a)刻蚀产生磁性粒子; (b)粒子聚集形成再沉积层
Figure9. Illustration of the formation of the sidewall re-deposited layer with ion beam etching: (a) Producing of magnetic particleses with etching process; (b) formation of the re-deposition layer with magnetic particleses.

由于侧壁再沉积层引入的磁性会干扰自由层的垂直磁各向异性场^[34], 因而需要考虑再沉积层对自由层磁性的影响. 此时, 有效的垂直磁各向异性场可表示为

${{{H}}_{\rm{k}}} = \left[ {{a^{\rm{\beta }}}\left( {\frac{{2{K_{\rm{i}}}}}{{{\mu _0}{M_{\rm{s}}}{t_{\rm{f}}}}}} \right) - \frac{{2\xi {{\rm{V}}_{\rm{b}}}}}{{{\mu _0}{M_{\rm{s}}}{t_{\rm{f}}}{t_{{\rm{ox}}}}}}} \right]{m_z}{{{e}}_z},$

其中, α为刻蚀工艺稳定因子(0 ≤ α ≤ 1), 主要取决于刻蚀角度、刻蚀时间和温度等; β为常数(β = 0.3).
图10给出了不同α对VCMA-MTJ磁化状态切换的影响. 当0.8 ≤ α ≤ 1时, 自由层的磁化方向可以实现稳定的翻转; 当α ≤ 0.7时, 磁化方向的进动过程变得紊乱. 这是因为随着α的减小, H_k将呈指数式减小, 即再沉积层的存在显著降低了垂直磁各向异性, 使得有效磁场的垂直方向发生偏移, 稳定性降低, 此时VCMA-MTJ的自由层磁化方向在翻转的过程中更易受到温度相关因素的干扰.
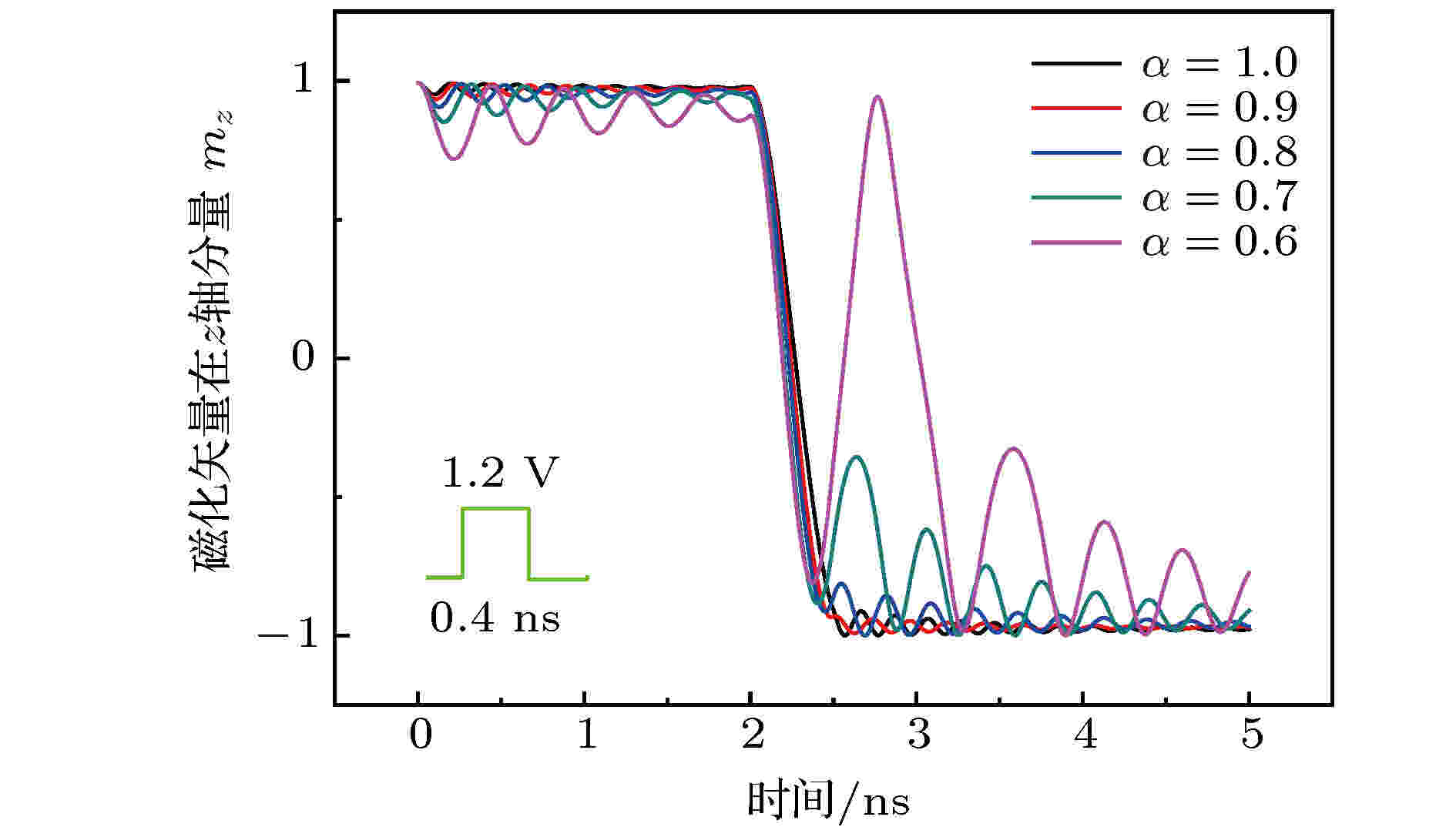图 10 不同α对VCMA-MTJ磁化方向切换的影响
Figure10. Effect of α on magnetization direction switching of VCMA-MTJ.

综上所述, 工艺偏差的存在使得VCMA-MTJ自由层磁化方向的翻转变得不确定, 从而影响到VCMA-MTJ读写电路数据存储的正确性. 下面将采用上述电学模型来分析工艺偏差对VCMA-MTJ读写电路错误率的影响.

图11给出了典型的VCMA-MTJ读写电路结构^[35], 它由2个VCMA-MTJ(MTJ0, MTJ), 5个PMOS(P₀, P₁, P₂, P₃, P₄)和6个NMOS(N₀, N₁, N₂, N₃, N₄, N₅)组成, V_dd为电路的读驱动电压, CLK为时钟脉冲控制信号, 高电平时开启电路. 其中, MTJ1为工作单元, 当电路写信号(Write)有效时, 可通过MTJ1高低阻态的改变来存储数据“1”和“0”; MTJ0为参考单元, 当电路读信号(Read)有效时, 可用于辅助读出MTJ1存储的数据. VCMA-MTJ读写电路的仿真波形如图12所示, 假设初始MTJ1为P态. 结合图11和图12可以看出, 当时钟脉冲信号(CLK)为低电平“0”时, N₄, N₅关断, MTJ1的阻态保持不变, 读写电路不工作, MTJ1保持P态不变.
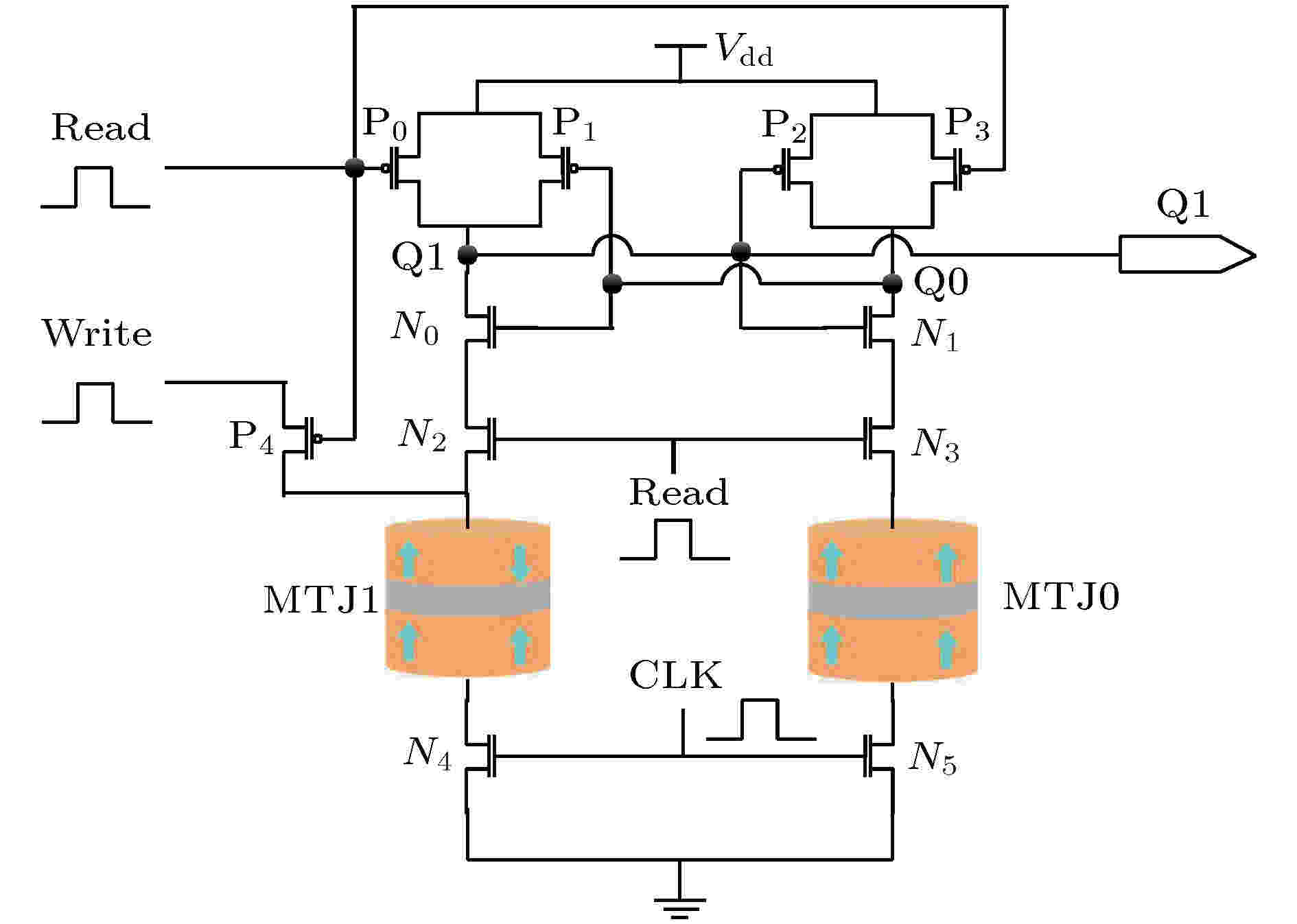图 11 VCMA-MTJ读写电路
Figure11. Reading and writing circuit of VCMA-MTJ.

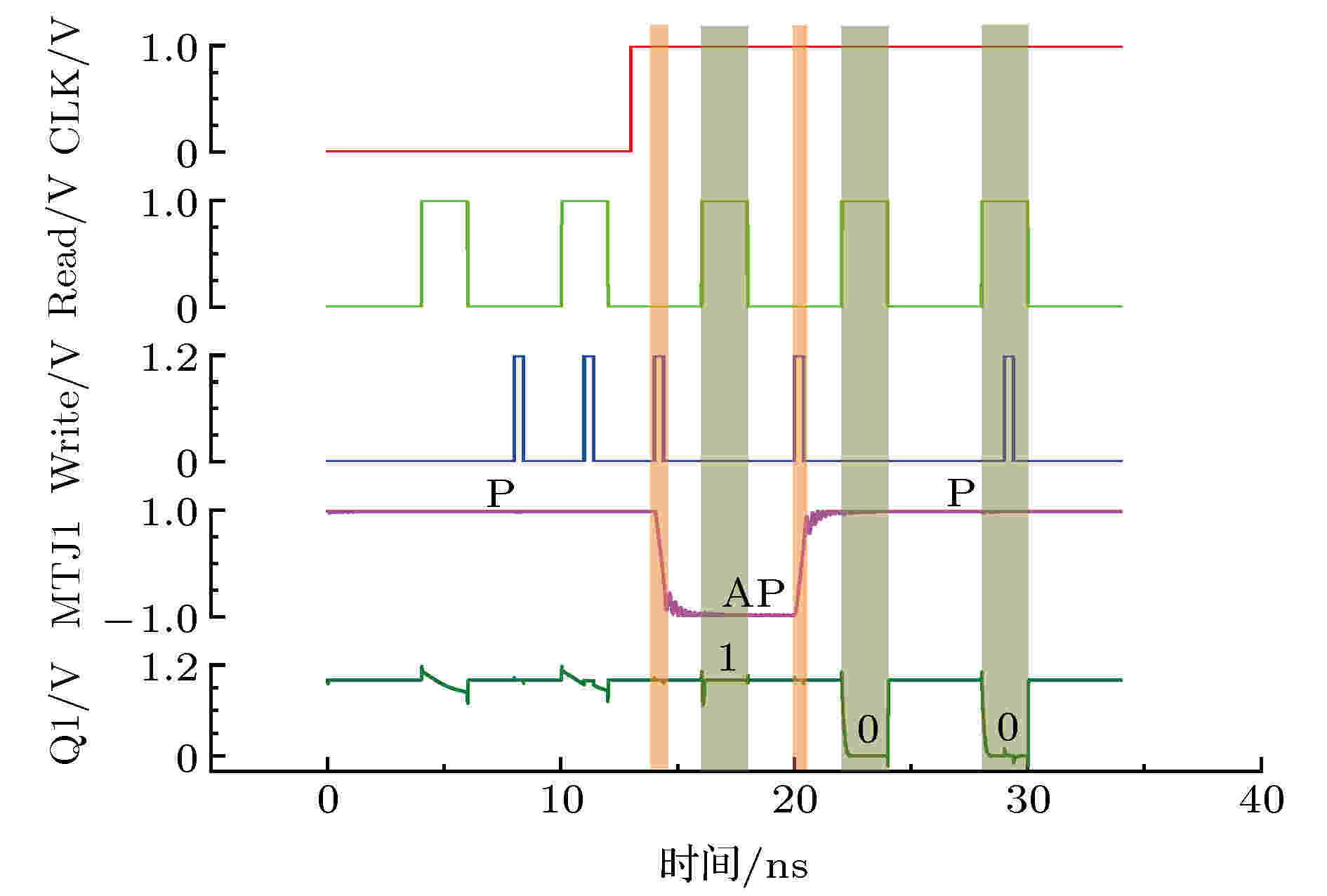图 12 VCMA-MTJ读写电路的仿真波形
Figure12. Simulation waveform of the reading and writing circuit of VCMA-MTJ.

当CLK为高电平“1”时, N₄, N₅导通. 若Read为“0”, 则N₂, N₃关断, N₄导通. 此时当Write为“1”时, 进行写操作, MTJ1从P态变为AP态, 存入数据“1”.
由于Read为“0”, P₀, P₁, P₂和P₃导通, 且N₂, N₃关断, V_dd将Q0, Q1上拉到高电平, N₀, N₁导通. 若此时Read变为“1”, 则P₀, P₃关断, N₂, N₃导通, 上述电路通过比较MTJ1和MTJ0的阻值来进行读操作, 共有两种情况: 1)当MTJ1存储数据为“1”时, 呈AP态, 其电阻(R1)大于MTJ0的电阻(R0), 此时Q0电位下降速度快于Q1, 相应地, P₁早于P₂导通, Q1将由V_dd上拉到高电平, 输出“1”, 实现读操作; 2)当MTJ1存储数据为“0”时, 呈P态, 即R1小于R0, 此时Q1电位下降速度快于Q0, 相应地, P₂早于P₁导通, Q0将由V_dd上拉到高电平, N₀持续导通, 使得Q1输出“0”, 实现读操作.
现今, 基于自旋转移力矩磁隧道结(spin-transfer torque-magnetic tunnel junction, STT-MTJ)的MRAM存储容量已高达1 GB^[36], 此时工艺偏差对MTJ的影响将变得越来越严重. 本文以VCMA-MTJ为研究对象, 重点研究了工艺偏差对器件几何参数(包括t_f, t_ox, α)及其所在读写电路特性的影响. 通常在考虑工艺偏差影响的情况下, 可认为MRAM中VCMA-MTJ的t_f, t_ox和α遵循高斯分布^[37], 即

$P\left( x \right) = \frac{1}{{\sigma \sqrt {2{\rm{\pi }}} }}{e^{ - \textstyle\frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}},$

$\sigma = \sqrt {\frac{1}{N}\sum\nolimits_{i = 1}^N {{\left( {{x_i} - \mu } \right)}^2}} ,$

其中, x可分别代表t_f, t_ox, α; μ为参数平均值; σ为标准偏差; N为MRAM中包含的VCMA-MTJ个数; x_i为第i个MTJ对应的几何参数(分别为t_fi, t_oxi, α_i). 下文将使用3σ/μ来表征工艺偏差对MRAM中VCMA-MTJ读写电路工作状态的影响, 并采用蒙特卡洛仿真研究工艺偏差对VCMA-MTJ电路数据读写错误率的影响.
2

-->

4.1.写错误率

图13给出了VCMA-MTJ读写电路在进行写“1”操作时的蒙特卡洛仿真波形, 其中N = 100, 3σ/μ = 0.03, V_b = 1.2 V, t_pw = 0.4 ns. 结果表明, 由于工艺误差的影响, 4%的VCMA-MTJ未能实现磁化方向的翻转而出现写错误, 即写错误率为4%.
图 13 VCMA-MTJ写电路的蒙特卡洛仿真波形, 其中N = 100, 3σ/μ = 0.03, V_b = 1.2 V, t_pw = 0.4 ns
Figure13. Monte Carlo simulation waveform of the writing circuit of VCMA-MTJ at N = 100, 3σ/μ = 0.03, V_b = 1.2 V, t_pw = 0.4 ns.

图14给出了不同V_b下写错误率随3σ/μ的变化关系曲线. 从图14可以看出, 写错误率均随着3σ/μ的增大而增大, 适当增大V_b可显著降低写错误率. 当V_b = 1.3 V, 3σ/μ增大为0.05时, 写错误率为0%, 远低于V_b = 1.15 V, 3σ/μ = 0.05时的写错误率(30%).
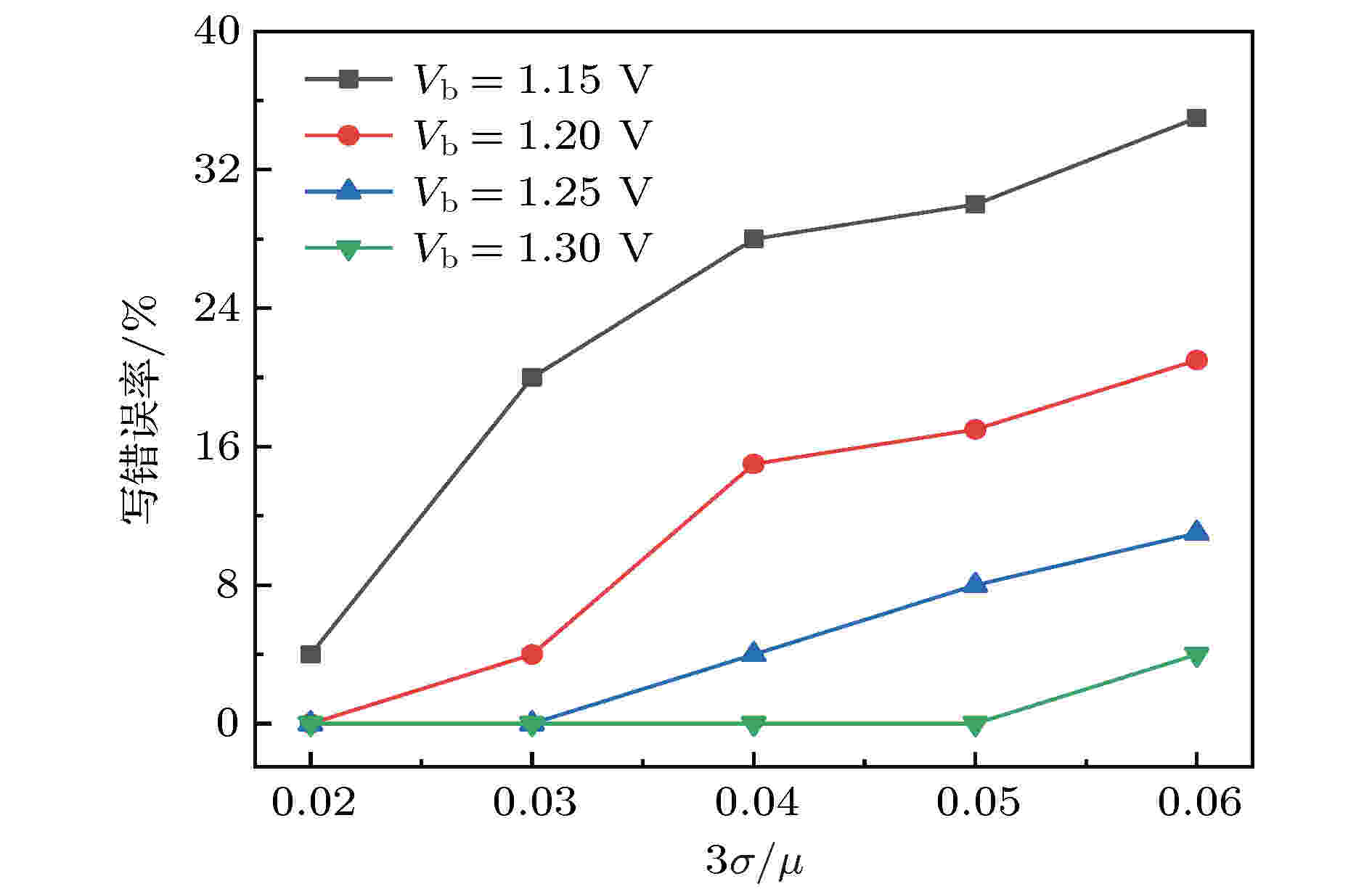图 14 不同V_b下写错误率随3σ/μ的变化关系
Figure14. Writing error rate versus 3σ/μ at different V_b

图15给出了不同t_pw下写错误率随3σ/μ的变化关系曲线. 从图15可以看出, 写错误率均随着3σ/μ的增大而增大, 适当减小t_pw可显著降低写错误率. 当t_pw = 0.5 ns, 3σ/μ = 0.05时, 写错误率仅为15%, 远低于t_pw = 0.8 ns, 3σ/μ = 0.05时的写错误率(42%).
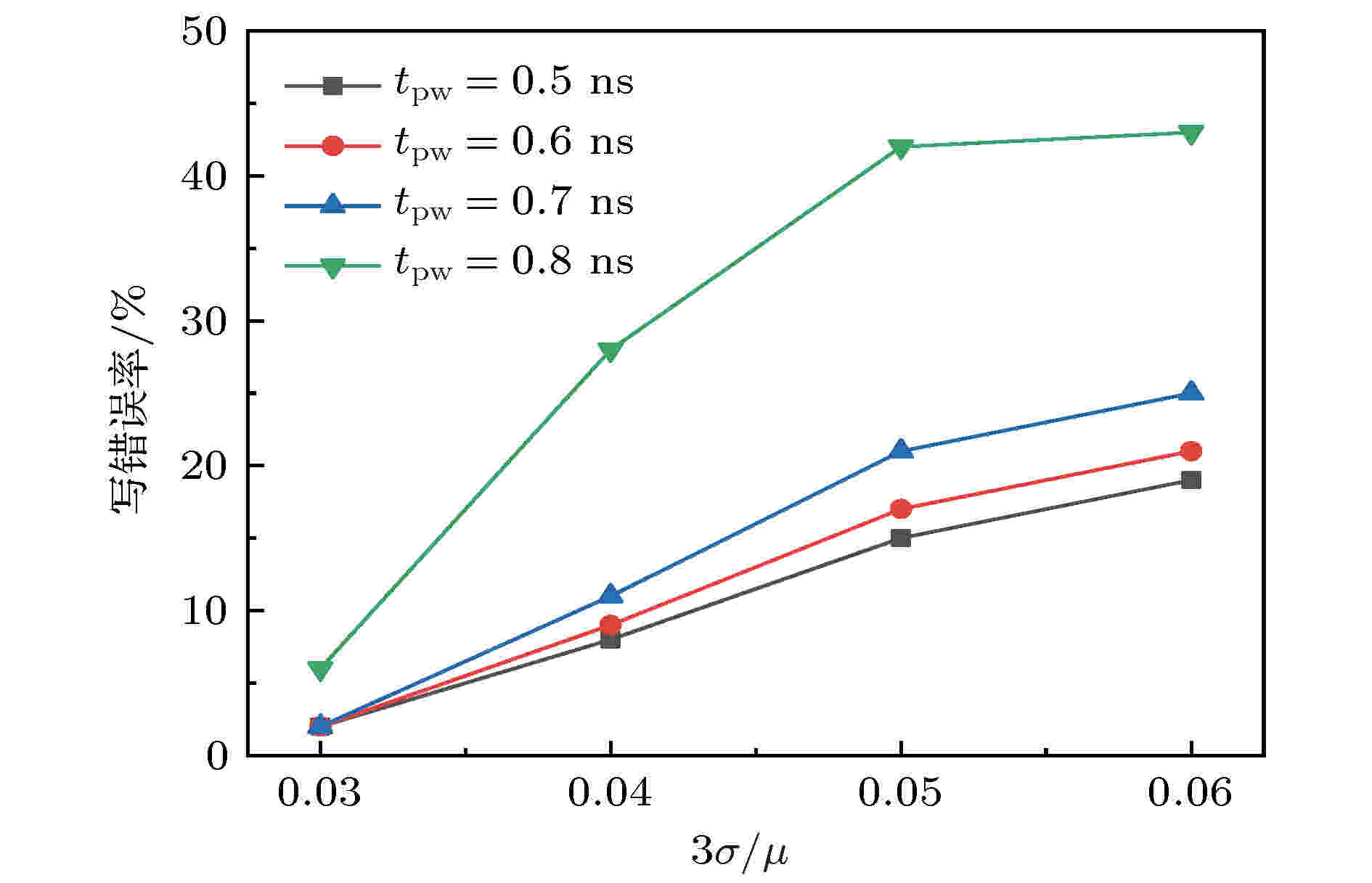图 15 不同t_pw下写错误率随3σ/μ的变化关系
Figure15. Writing error rate versus 3σ/μ at different t_pw.

2 -->

4.2.读错误率

图16给出了VCMA-MTJ读写电路在进行读“0”操作时的蒙特卡洛仿真波形, 其中N = 100, 3σ/μ = 0.07, V_dd = 0.8 V. 结果表明, 由于工艺误差的影响, 读错误率为2%.
图 16 VCMA-MTJ读电路的蒙特卡洛仿真波形, 其中N = 100, 3σ/μ = 0.07, V_dd = 0.8 V
Figure16. Monte Carlo simulation waveform of the reading circuit of VCMA-MTJ at N = 100, 3σ/μ = 0.07, V_dd = 0.8 V

图17给出了不同V_dd下VCMA-MTJ读写电路发生读操作错误时读错误率随3σ/μ变化的关系曲线, 上述读写电路中N = 100. 从图17可以看出, 读错误率均随着3σ/μ的增大而增大, 适当增大V_dd可显著降低读错误率. 在相同3σ/μ = 0.07下, 当V_dd = 0.9 V时, 读错误率为0%, 远低于V_dd = 0.6 V时的读错误率(31%). 然而增大V_dd会增加读写电路的功耗, 需要折中考虑.
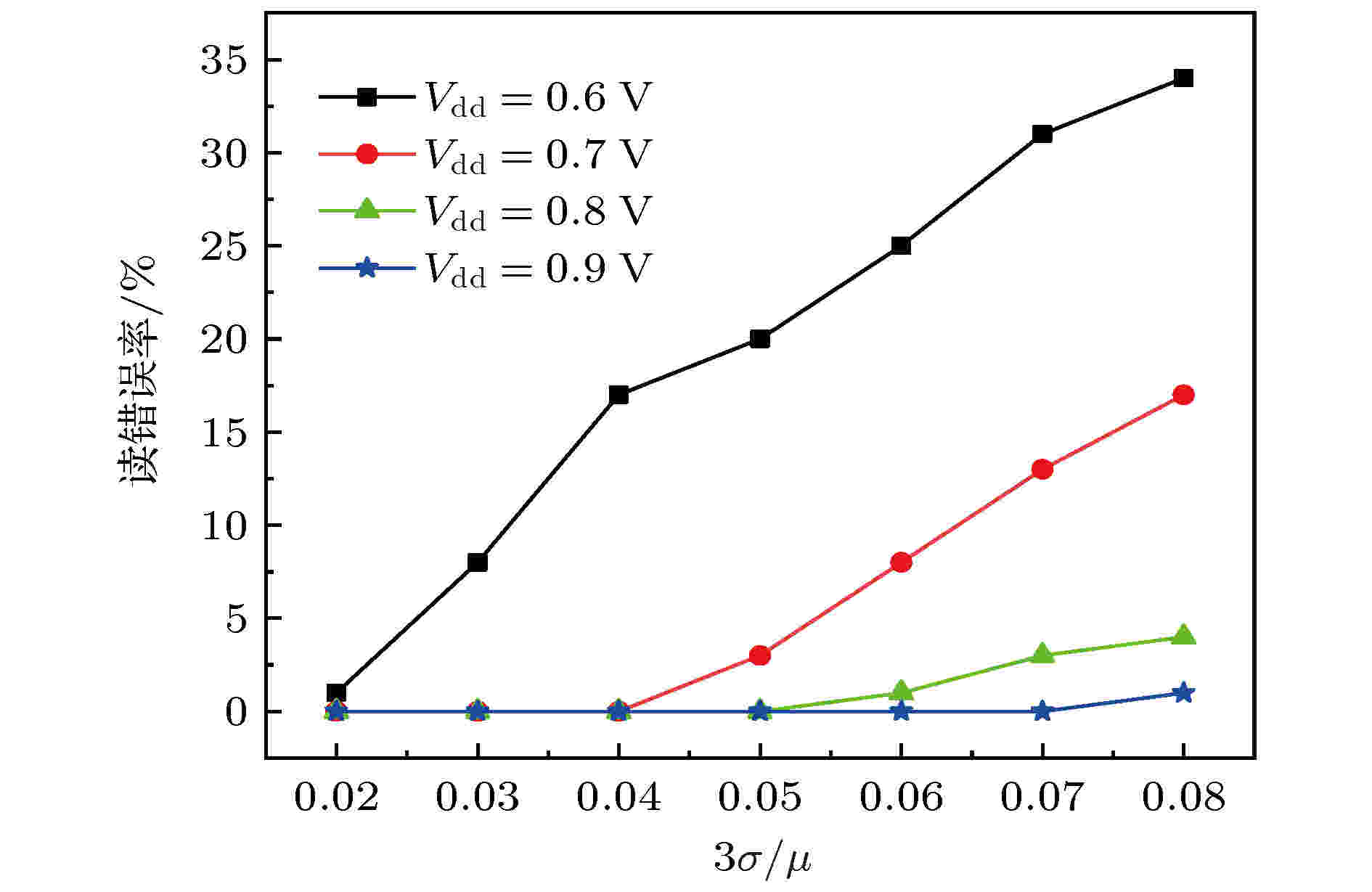图 17 不同V_dd下读错误率随3σ/μ的变化关系
Figure17. Reading error rate versus 3σ/μ at different V_dd.

随着MRAM存储容量的不断增大以及VCMA-MTJ尺寸的不断缩小, 在制备VCMA-MTJ电路时的工艺偏差会对MTJ性能产生重要影响, 甚至会引起上述电路的读写错误. 本文在充分考虑磁控溅射薄膜生长工艺中自由层厚度偏差(γ_tf)、氧化势垒层厚度偏差(γ_tox)以及离子束刻蚀工艺中由侧壁再沉积层引入的刻蚀工艺稳定因子(α)偏差影响的情况下, 给出了基于工艺偏差的VCMA-MTJ电学模型, 研究了上述工艺偏差对VCMA-MTJ磁化方向翻转的影响. 结果表明, 垂直磁各向异性场(H_k)随着γ_tf的增加而减小, 临界电压(V_C)随着γ_tox的增加而增大, 当γ_tox ≥ 11%, γ_tf ≥ 13%时, VCMA-MTJ将无法实现磁化方向的有效翻转. 同时, H_k随着α的减小呈指数式减小, 当α ≤ 0.7时, VCMA-MTJ磁化方向的进动过程将变得紊乱而不稳定. 进一步地, 本文将上述模型应用到VCMA-MTJ读写电路中, 使用3σ/μ来表征工艺偏差(γ_tf, t_ox和α), 并采用蒙特卡洛仿真方法进行研究. 可以看出, 在VCMA-MTJ电路中, 当3σ/μ = 0.05, 外加电压V_b = 1.15 V时, 写错误率高达30%; 当3σ/μ = 0.05, 读驱动电压V_dd = 0.6 V时, 读错误率为20%. 通过适当增大V_b和减小外加电压脉冲宽度(t_pw)均可有效降低VCMA-MTJ电路的写错误率; 适当增大V_dd会有利于VCMA-MTJ电路读错误率的显著改善. 本文的研究工作将会对VCMA-MTJ器件及其应用电路的设计和可靠性分析提供有益指导.