摘要: 利用有限温度场论和平均场近似的方法, 在考虑夸克真空涨落的情况下, 研究了两个夸克味的夸克介子模型的量子色动力学相变的相图结构, 得到了当夸克化学势密度较小时, 量子色动力学相变是过渡相变, 而当夸克化学势密度较大的时候, 量子色动力学相变是一级相变. 对于一级相变的区域, 基于薄壁近似, 给出了当温度等于临界温度
$ {T_{\rm{c}}}$ 时, 强子相表面张力随夸克化学势密度的变化关系. 本研究为相对论重离子对撞实验和中子星早期结构演化提供必要的参考.
关键词: 夸克介子模型 /
手征相变 /
有限温度场论 /
表面张力 English Abstract Phase structure and surface tension in quark meson model Shen Wan-Ping You Shi-Jia Mao Hong Department of Physics, Hangzhou Normal University, Hangzhou 311121, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant No. 11675048)Received Date: 24 May 2019Accepted Date: 12 July 2019Available Online: 01 September 2019Published Online: 20 September 2019Abstract: In a mean-field approximation, we study the in-medium effective potential of the two-flavor quark meson model in the presence of a fermionic vacuum term at a finite temperature and density. There exists a crossover phase transition in the low-density region, and also there is a first-order phase transition in the high-density region accompanied by a critical end point. For the first-order phase transition, when the temperature is close to the critical temperature, the values of surface tension are calculated at various chemical potentials and we find that our results are very close to the results recently found in other chiral models with two flavors. Some consequences and possible applications of our results are also pointed out for the experiments on heavy ion collisions and the evolutions of the compact stars in their early stages.Keywords: quark-meson model /chiral phase transition /thermal field theory /surface tension 全文HTML --> --> --> 1.引 言 量子色动力学是描述强相互作用的基本理论, 可以用来描述夸克强子相变的动力学, 特别是与量子色动力学相变紧密相关的手征对称性恢复和退禁闭等问题. 此外, 量子色动力学相变的研究与目前正在进行的相对论重离子对撞实验和致密星体的内部结构研究密切相关, 它可以帮助人们深入理解和洞察夸克胶子等离子体的物理性质和揭示夸克强子相变的动力学机制[1 —3 ] . 但是, 量子色动力学是非阿贝尔的规范场论, 由于理论存在渐近自由的性质和夸克幽禁的效应, 使得在低能非微扰区域量子色动力学的直接理论和数值计算受到了极大的限制[4 ,5 ] . 为了克服这一问题, 在低能非微扰能区, 人们通常采用有效模型或者有效理论来研究量子色动力学真空的非微扰性质. 比较常见的模型有Nambu-Jona-Lasinio (NJL) 模型[6 —11 ] , 夸克介子模型(the quark-meson model)[12 ,13 ] 和相对论平均场模型(the relativistic mean-field mode)[14 —16 ] 等.17 ]研究了相对论重离子对撞实验中一级相变的动力学, 讨论了一级相变的相变表面张力、一级相变的临界半径和相变的成核率等问题. 不过, 该文献在模型的计算中选取了一个非常大的夸克介子耦合常数g , 使得模型在整个相变区域都是一级相变, 与目前格点量子色动力学和其他模型的理论预言不一致. 另外, 模型在具体的计算过程中, 没有考虑夸克的真空涨落和重整化效应, 使得理论的预言缺乏实际可参考的价值和意义. 为了解决上述两个问题, 本文选取与实验相一致的理论参数, 在考虑夸克的真空涨落和重整化效应的基础上, 重新计算了两个味道的夸克介子模型的相图和一级相变区域的表面张力, 为今后相对论重离子对撞实验和天体物理中致密星体结构的研究提供参考依据.2.夸克介子模型的有效势能 首先, 考虑介子与夸克耦合的两个味道的夸克介子模型, 其拉氏密度为[13 ] $q = \left( {u,d} \right)$ 为组分夸克场. 这里, σ介子和π介子具有对称性自发破缺特征的势能表达式为σ 和三个赝标量场${{\pi}} = \left( {{{\textit{π}}_1},{{\textit{π}}_2},{{\textit{π}}_3}} \right)$ 一起构成一个四分量的手征性场, 定义其为$\varPhi = \left( {\sigma,{{\pi}}} \right)$ . 在手征极限的情况下(不考虑夸克质量), H 为零, 该拉氏量在${\rm{SU}}{\left( {\rm{2}} \right)_{\rm{L}}} \times {\rm{SU}}{\left( {\rm{2}} \right)_{\rm{R}}}$ 的手征变换下具有不变性. 在真空态, 模型满足手征对称性自发破缺的要求, 此时介子场的真空期望值取为$\left\langle \sigma \right\rangle = {f_{\text{π}}}$ , $\left\langle{{\pi}} \right\rangle = {\rm{0}}$ , 其中${f_{\text{π}}} = $ 93 MeV为介子衰变常数. 如果考虑夸克的质量贡献, 那么模型具备手征对称明显破缺的特征, 由PCAC (部分轴矢流守恒)关系可知: $H = {f_{\text{π}}}m_{\text{π}}^2$ , 其中${m_{\text{π}}} = $ 138 MeV是π介子的质量. 耦合常数λ 由σ介子的质量确定: $m_{\text{σ}} ^2 = 2\lambda f_{\text{π}}^2 +$ $ m_{\text{π}} ^2 $ , 对于σ介子的质量, 通过查阅粒子数据组的最新结果可知, 其取值在400 MeV到550 MeV之间, 本文取${m_{\text{σ}} } = $ 500 MeV, 对应有$\lambda \approx {\rm{13}}$ . 常数${\upsilon ^2}$ 满足${\upsilon ^2} = f_{\text{π}} ^2 - {{m_{\text{π}} ^2} / \lambda }$ . 最后, 模型的参数耦合常数g 由真空中的组分夸克质量决定, ${M_q} = g {f_{\text{π}}}$ , 约为核子质量的${{\rm{1}} / {\rm{3}}}$ , 本文取$g \approx 3.3$ .T 和夸克化学势$\mu \equiv {{{\mu _{\rm{B}}}} / 3}$ 下处于热力学平衡的热力学巨正则体系, 其巨正则配分函数为$\int_x \equiv \,{\rm{i}}\int_0^{{1 / T}} {{\rm{d}} t} \int_V {{{\rm{d}}^3}x} $ , V 为系统的体积.${\cal Z}$ 的对数, 可以得到热力学有效势能的具体形式是:${v_q} = 2{N_{\rm{c}}}{N_{\rm{f}}} = 12$ 是夸克的内部自由度, ${E_q} = \sqrt {{{{p}}^2} + M_q^2} $ 是夸克和反夸克的能量, 组分夸克(反夸克)的质量${M_q}$ 被定义为${M_q} = g\sigma $ .7 )式中第一项表示的是夸克的真空单圈贡献, 由于该积分是发散的, 理论计算需要通过重整化来消除发散项, 为了计算方便, 在很多文献中$\varOmega _{\bar qq}^{\rm{V}}$ 项经常被忽略. 为了理论的完整性和计算的可靠性, 在接下来的讨论中, 我们将考虑$\varOmega _{\bar qq}^{\rm{V}}$ 项的贡献, 即在模型的计算中加入真空的涨落和模型的重整化效应. 利用维数正规化方法进行重整化, 费米子真空单圈的重整贡献为[18 ] Λ 是任意重整化标度. 值得注意的是, 热力学势和所有的物理观测值都不依赖于Λ 的选择, 通过重新定义模型中的参数可以很好地消除Λ 的依赖性. 故等式(7 )右边的第一项真空贡献可以用等式(8 )中给出的适当的重整化费米子真空贡献代替.7 )右边的第二项中, $g_q^ + $ 和$g_q^ - $ 为$\varOmega \left( {T,\mu } \right)$ 对σ 求导, 可以得到体系关于σ 场的运动方程, 求解该运动方程即可得到σ 场随温度和密度的变化关系, 进而可以计算研究系统的压强、热力学熵密度、系统的能量密度和状态方程等体系的其他全部热力学性质.3.夸克介子模型的相图结构 在考虑了重整化效应和夸克真空涨落贡献的前提下, 通过求解关于σ 场的运动方程: $\dfrac{{\partial \varOmega \left( {\sigma,T,\mu } \right)}}{{\partial \sigma }} = 0$ , 可以得到在不同夸克化学势密度条件下, σ 场的真空期望值随温度的演化行为.图1 给出了在不同夸克化学势密度下, σ 场的真空期望值随温度的变化关系. 从图1 可以发现在$\mu < $ 299 MeV的情况下, σ 场的真空期望值随温度的演化行为是连续变化的, 只是当系统温度接近手征相变临界温度${T_{\rm{c}}}$ 时, σ 场的真空期望值变化才比较明显, 且当温度很大时, σ 场只是趋向于零, 而不等于零, 可以判断此时的量子色动力学手征相变是过渡相变. 而对于$\mu > $ 299 MeV的情况, 当温度接近手征相变临界温度${T_{\rm{c}}}$ 时, 由于σ 场的真空期望值随温度的变化有一个明显的跃变, 即从一个相对大的数值直接跳到一个相对小的数值, 表明此时的量子色动力学手征相变是一级相变.图 1 在不同夸克化学势密度条件下, σ 场的真空期望值随温度的演化行为Figure1. Chiral condensate σ as a function of temperature at various chemical potential.σ 场的真空期望值与有效势能$\varOmega \left( {\sigma,T,\mu } \right)$ 直接的对应关系. 对于0 MeV$ \leqslant \mu < $ 299 MeV时的过渡相变, 以$\mu = $ 0 MeV为例: 如图2(a) 所示, 当温度较小时, 势能曲线有两个极小值和一个极大值, 一个极小值位于σ 较小的位置, 另外一个极小值位于σ 较大的位置, 中间有一个局域的极大值, 也就是在两个极值之间有一个势垒, σ 场的真空期望值由势能最小时所对应的σ 值决定; 当温度逐渐升高时, 两个势能极小值所对应的σ 逐渐靠拢, 当$T = $ 127 MeV时, 两个极小值之间的势垒消失, 此时模型的有效势能只有一个极小值, 此时的温度称为亚稳态分解温度(spinodal temperature). 由于对于过渡相变, 严格来说两相之间没有一个严格的界限, 所以此时的温度还不能被定义成相变温度, 通常人们选择图1 中σ 场的真空期望值对温度T 的一阶导数的峰值作为相变温度, 也就是σ 场的真空期望值随温度变化最快的那个温度作为过渡相变的临界温度, 也就是$T = 152.6$ MeV.图 2 (a) $\mu = 0$ MeV和(b) $\mu = 310$ MeV时, 有效势能随σ 场的演化行为Figure2. Effective potential as a function of the chiral condensate σ for (a) $\mu = 0$ MeV and (b) $\mu = 310$ MeV.$ \leqslant \mu \leqslant $ 324 MeV时, 可以观察到一级相变的特征, 以$\mu = $ 310 MeV为例: 如图2(b) 所示, 当温度小于临界温度时, 系统的有效势能有两个极小值, 并且在这两个极小值之间还存在一个势垒, 与过渡相变的情况类似, 一个极小值位于σ 较小的位置, 另外一个极小值位于σ 较大的位置; 当系统温度逐渐升高时, 这两个势能极小值的高度差开始变得越来越小, 等温度达到临界温度时, 两个势能极小值相等, 临界温度${T_{\rm{c}}}$ 下势能极小值均为–1.45 MeV, 对应σ 场的真空期望值分别为32.16和89.63 MeV, 与过渡相变不同的是, 此时两个极小值之间的势垒还存在, 并没有消失, 这个就是一级相变和过渡相变的本质区别; 当温度大于临界温度${T_{\rm{c}}}$ 时, σ 场的真空期望值从一个相对较大的数值越变到相对较小的数值, 从而实现从假真空到真真空的翻转.$\mu = {\mu _{\rm{c}}} = $ 299 MeV时, 系统从过渡相变演化到一级相变. 当温度等于临界温度${T_{\rm{c}}}$ 时, 一级相变中的势垒消失(这个条件作为一级相变消失的判据), 势能变成一个很平坦“U”形, 并且, 此时势能曲线同时具有过渡相变和二级相变的部分相变特征.图3 给出了量子色动力学相图结构, 对于夸克化学势密度在0 MeV$ \leqslant \mu < $ 299 MeV区域, 可以观察到过渡相变, 对于夸克化学势密度在299 MeV$ \leqslant$ $ \mu \leqslant$ 324 MeV区域, 可以观察到一级相变. 在两个相变的交界处就是量子色动力学相变的相变临界点(critical end point). 如何从相对论重离子对撞实验上寻找该相变临界点和确认该相变临界点的位置是当前高能核物理理论和实验研究的热点问题[19 ] .图 3 量子色动力学相图结构Figure3. The $T \text{-} \mu $ phase diagram in the quark meson model4.强子夸克相变的表面张力 对于一级相变, 当体系的温度达到相变临界温度时, 模型的热力学势能具有两个相等的极小值, 并且这两个极小值被一个势垒分开. 此外, 由图1 可知, 这两个极小值所对应的σ 场的真空期望值分别对应一个大的数值和一个小的数值. 如果体系的温度进一步降低, 那么σ 期望值较小的那个真空势能将大于σ 期望值大的那个真空势能, 此时我们把前面那个真空称为亚稳态真空(通常称为伪真空), 而把后面那个真空称为稳定真空(通常称为真真空). 在经典物理中, 虽然伪真空的能量高于真真空, 但是由于两个真空之间还有一个势垒, 故伪真空无法回到真真空. 但是, 对于一个量子体系, 由于存在量子隧穿效应, 伪真空还有一定的概率可以回到真真空, 从而发生一级相变, 并把多余的能量以相变潜热的形式释放出来. 为了准确地描述该一级相变的相变动力学过程, 我们借助液滴核合成唯象模型来描述夸克强子的一级相变[20 —24 ] .${r^3}$ 成正比, 表面自由能与${r^2}$ 成正比, 故存在一个临界半径${r_{\rm{c}}}$ , 当$r < {r_{\rm{c}}}$ 时, 表面自由能占主导地位, 泡泡会最终收缩为伪真空, 从而消失; 而对于$r > {r_{\rm{c}}}$ , 体积自由能占主导地位, 泡泡会一直膨胀直至占据整个系统, 从而完成夸克相到强子相的完全转变.r 的球形泡泡, 那么体系总自由能的改变为ε 为伪真空与真真空的单位体积自由能密度之差; Σ 是泡壁的表面能量密度, 即两相界面的表面张力.[24 ] T 为系统温度. 因子${\cal P} $ 通常比较难计算, 为了计算方便通常采用简单的量纲分析, 用${T^4}$ 近似代替${\cal P} $ .${V_{{\rm{eff}}}}(\sigma ) = \varOmega \left( {\sigma,T,\mu } \right)$ . 则体系的自由能表示为${F_{\rm{b}}}$ 对σ 进行变分, 可以得到一个非线性微分方程,${\sigma _{ {\rm{f}}}}$ 为伪真空下的σ 场的真空期望值. 也就是说, 远离真真空泡泡的中心, 体系处于亚稳态, 相当于真真空的泡泡在伪真空中产生并膨胀.${V_{{\rm{eff}}}}$ , 在边界条件(16 )式下, 通常不能通过解析方法得到(15 )式的解析解, 只能求助计算机得到该方程的数值解. 但是, 如果考虑真真空泡泡的尺寸比壁厚大得多的情况, 或者伪真空与真真空的势能差与介于两个真空之间的势垒相比小得多的情况, 该情况也称为薄壁(thin-wall)近似, 则方程式(15 )中的第二项与第一项相比可以被忽略, 即方程进一步简化为17 )可以解析地求解出来, 得到$\dfrac{{{\rm{d}}\sigma }}{{{\rm{d}}r}} = \sqrt {2{V_{{\rm{eff}}}}(\sigma )} $ . 把$\dfrac{{{\rm{d}}\sigma }}{{{\rm{d}}r}}$ 代入到泡泡的表面张力的表达式中, 可以得到11 )和(18 ), 泡泡的临界半径${r_{\rm{c}}}$ 等于$\varepsilon = V(\sigma ) - V({\sigma _{\rm{f}}})$ . 将(19 )式代入方程(11 ), 可得${F_{\rm{b}}}$ 以ε 和Σ 为变量的形式:${F_{\rm{b}}}$ , 就可以很容易估算出夸克强子一级相变的成核率Γ .图4 给出了当$T = {T_{\rm c}}$ 时, 夸克强子一级相变的表面张力随夸克化学势的变化. 可知在一级相变区域, 当化学势增大时, 强子相的表面张力也随着化学势增大. 当温度接近零时, 强子夸克相变的表面张力约为12.6 MeV/fm2 . 在$T \to 0$ 的情况, 本文理论预言与文献[25 ]一致, 但该文献只是考虑$T = 0$ 的冷夸克物质的夸克强子一级相变.图 4 $T = {T_{\rm{c}}}$ 时表面张力与夸克化学势的演化关系Figure4. Surface tension as a function of a quark chemical potential when $T = {T_{\rm{c}}}$ 5.结 论 利用两个夸克味的夸克介子模型, 在有限温度、有限夸克化学势密度条件下, 本文计算了模型热力学有效势能, 通过求解该热力学有效势能对σ 场的变分, 得到σ 介子场的运动方程, 求解该运动方程得到σ 场的真空期望值随温度和密度的变化关系. 我们发现, 在高温低密度区域, 量子色动力学的相变是过渡相变, 而在低温高密度区域, 量子色动力学的相变是一级相变, 在过渡相变和一级相变的交界处存在一个相变的临界点, 我们称之为CEP (critical end point). 为了提供更加完整的理论结果, 不同于其他文献, 我们在模型的计算中考虑夸克场的真空涨落和重整化效应, 并且我们采用了一套广泛应用并被实验认可的模型参数来计算. 特别是夸克场的真空涨落效应, 通常会使得一级相变的相变区域变得很小, 从而进一步推低夸克强子相变的强子相的表面张力的数值, 而很小的表面张力数值, 使得中子星在早期演化过程中产生更加复杂的中子星结构, 比如中子星的混合相的出现, 夸克星硬层的出现等物理现象[26 ] .[27 —30 ] . 由于考虑了Polyakov圈拓展, 需要在模型中引入另外两个序参量, 因此PQM模型具有三个序参量, 在计算夸克强子相变表面张力时, 需要同时求解三个非线性微分方程组[31 ] , 理论和数值计算将变得非常复杂和困难, 特别是在这种情况下, 薄壁近似将不再有效, 只能采用数值计算来获得表面张力的数值信息. 目前, 该方向的研究正在进行中. 






































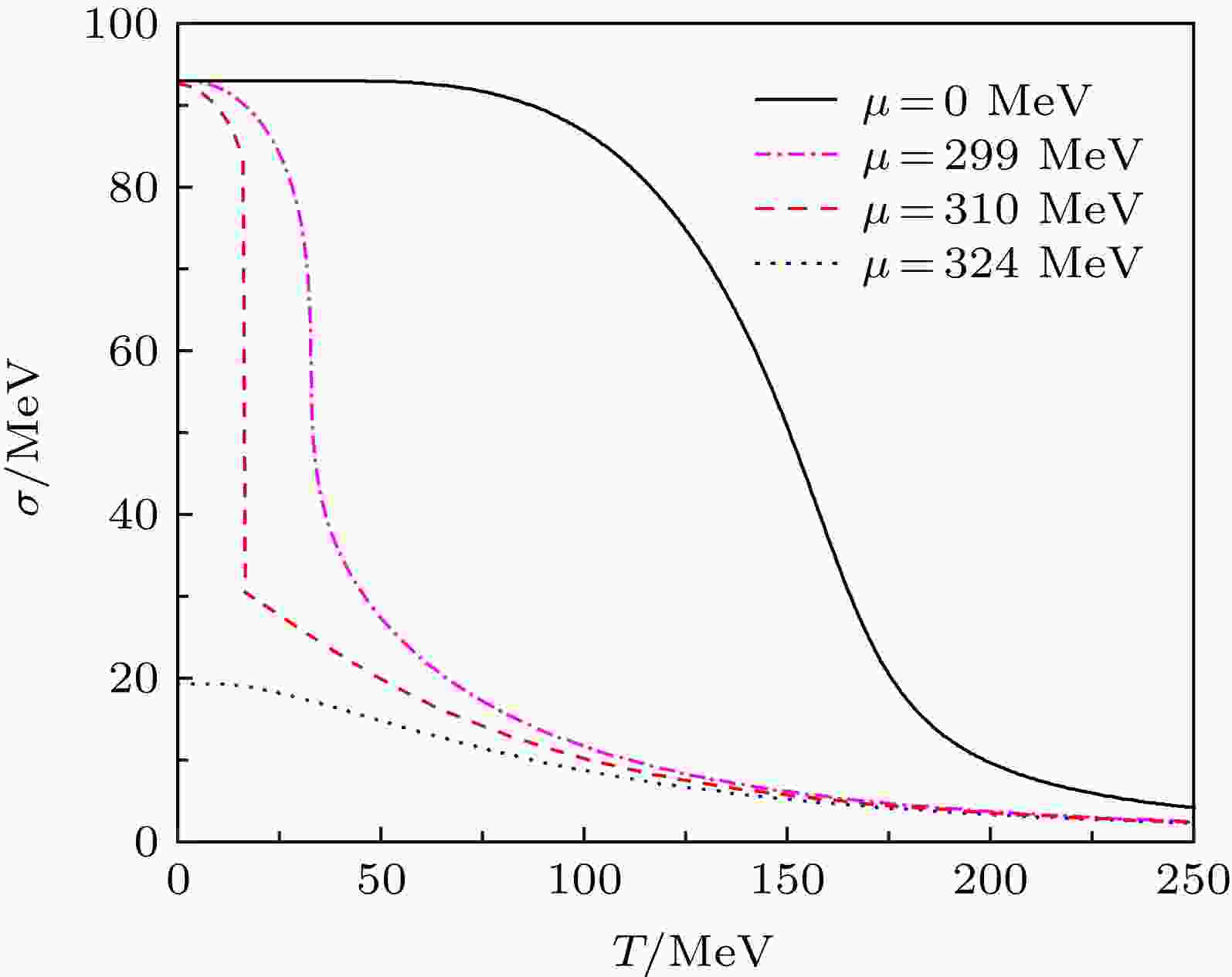 图 1 在不同夸克化学势密度条件下, σ场的真空期望值随温度的演化行为
图 1 在不同夸克化学势密度条件下, σ场的真空期望值随温度的演化行为




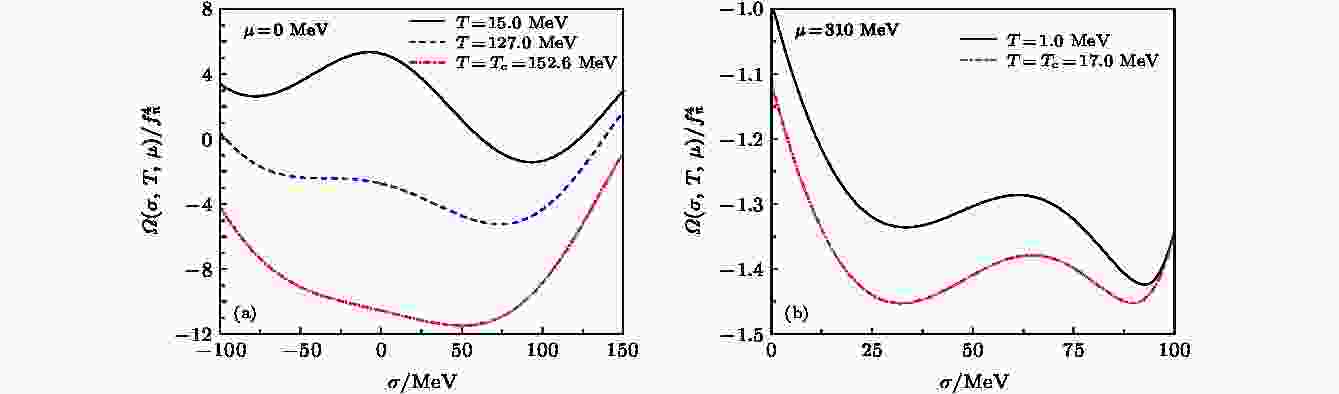 图 2 (a)
图 2 (a) 














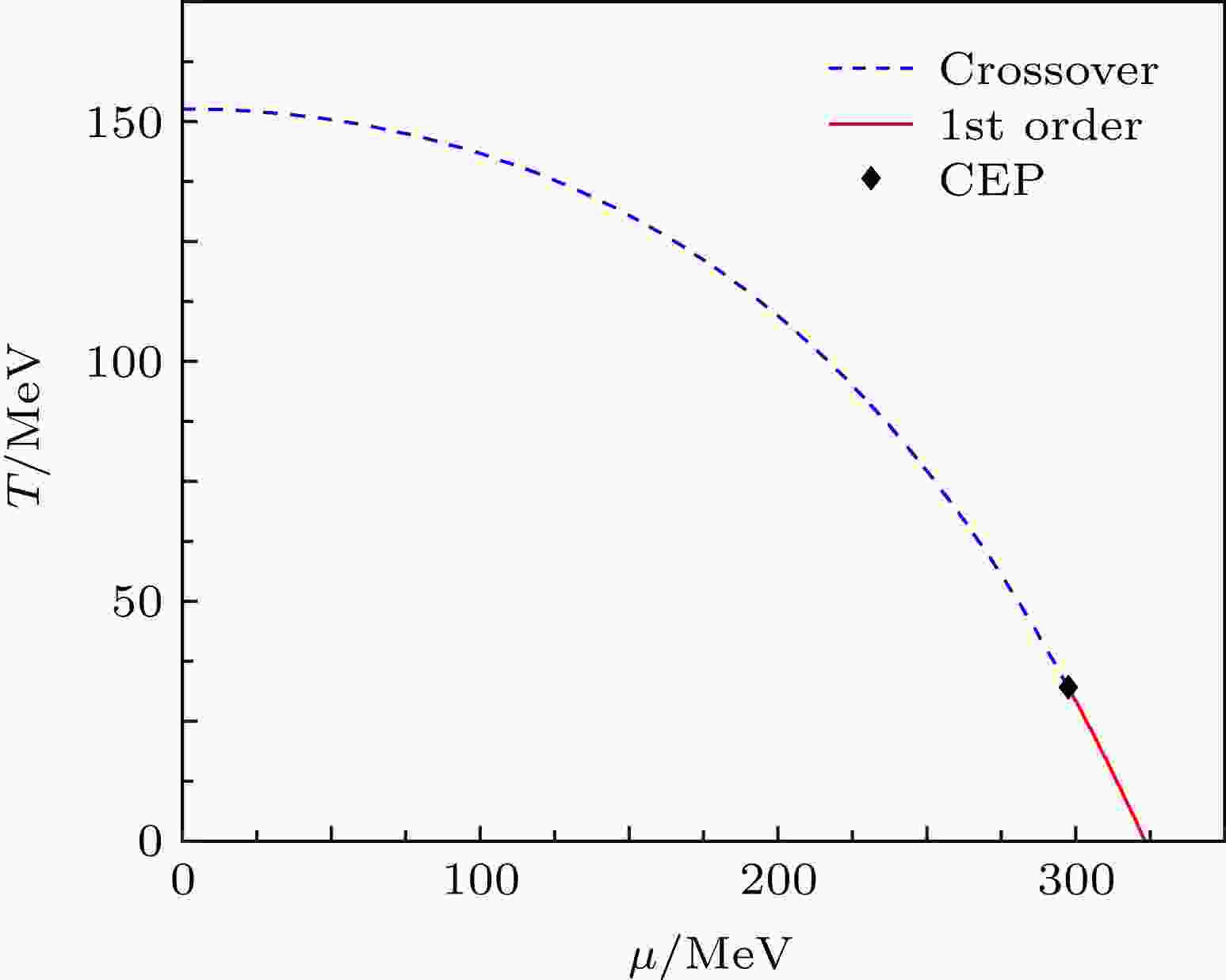 图 3 量子色动力学相图结构
图 3 量子色动力学相图结构























 图 4
图 4 


