摘要:针对锂离子电池硅及其复合电极材料, 采用Cahn-Hilliard型扩散方程与有限变形理论全耦合的电化学-力模型来描述其在循环锂化过程中的扩散和力学相关性问题, 构造高效的数值算法, 在商用有限元软件平台上实现对该理论的数值求解. 在此基础上, 研究了硅电极恒流锂化和脱锂过程, 基于界面反应动力学, 得到电压响应曲线, 计算结果整体趋势与实验结果吻合较好, 同时预测的应力响应也与实验结果一致, 验证了本方法的有效性. 其次, 研究了中空碳包覆硅负极锂化过程中的电化学与力学行为, 计算结果表明, 锂化期间中空碳包覆硅负极应力水平明显低于实心硅负极, 随锂化的进行, 应力差值越来越大, 锂化结束时应力值降低约27%, 这种应力的缓解提高了整个电极内化学势水平, 使得锂离子浓度水平显著提高, 更易达到完全锂化状态. 同时, 数值研究表明应力水平的缓解延缓了中空碳包覆硅负极的容量衰减(容量提升74%), 充分显示出该电极良好的电化学性能. 本研究揭示了应力对硅复合电极容量影响的作用机制, 为将连续介质电化学-力耦合理论应用于实验预测提供了途径并为电极材料设计提供了理论依据.
关键词: 电化学-力耦合/
中空碳包覆硅负极/
有限元数值计算/
循环稳定性

English Abstract

全文HTML

--> --> -->

可充电锂离子电池已成为当今社会中各种便携式电子产品的主要电源, 包括智能手机、笔记本电脑和可携带电子产品, 且在电动工具、电动汽车和电网存储中得到了广泛应用^[1,2]. 硅因其具有高达4200 mAh·g^–1的理论比容量而被认为是应用于锂离子电池最有前景的负极材料. 然而, 硅锂化过程中高于300%的体积膨胀导致硅极易粉碎且具有极差的容量保持率、不稳定的固体电解质层(SEI)和较差的导电性, 阻碍了硅基负极在锂离子电池中的实际应用^[3]. 理论和实验已经证明纳米尺度硅基材料表现出锂化诱导应力的缓解和断裂抗性的增强^[4,5]. 尽管如此, 其体积变化仍然会导致活性材料从集电器剥离以及不稳定的SEI层形成, 这些问题严重限制了电池的循环寿命且降低了商业应用的可行性^[6]. 因此, 如何设计硅基微纳米颗粒以增强电极电化学性能成为当前研究的热点.
最近几年的研究集中在如何缓解应力诱导的电极电化学性能降解, 其中中空纳米结构的构建被认为是适应过量体积膨胀最可行的策略, 因此受到广泛关注. 理论计算结果表明空心硅颗粒的应力水平明显低于实心硅颗粒^[7,8]. 此外, 还提出了许多理论模型来研究空心圆柱体的扩散诱导断裂机制和应力演化^[9,10]. 北京大学Zhang等^[11]观察到a-Si/c-Si界面处的各向异性体积膨胀以及裂纹萌生、渗透、偏转和分层的整个过程, 实验结果表明新颖的空心和非等轴几何设计显示出大幅提高硅电极抗断裂行为的能力, 这意味着通过几何设计可极大地提高应力释放能力. Cho^[12]合成的介孔硅纳米粒子具有均匀且规则分布的孔隙, 均匀的孔隙结构确保了电极表面与电解质的均匀接触以及在循环过程中均匀的体积变化, 有助于降低循环锂化过程中电极内的应力水平. 然而, SEI薄膜不稳定、库仑效率低及电导率差等问题无法通过单独优化硅纳米结构来解决. 碳材料与纳米硅的结合已被广泛开发并被认为是改善电极电化学性能的有效方法. 柔性、轻质、高导电和热稳定的碳材料不仅可以提高导电性, 还可以限制硅的体积膨胀并缓解SEI层的断裂^[13,14], 同时, 碳包覆层还用作防止活性颗粒在充放电循环过程中聚集的物理屏障. 清华大学Hao和Fang^[15]开发了一个由碳壳包覆的球形电极模型以研究核-壳纳米结构的扩散诱导应力, 结果表明应力在很大程度上取决于碳层的厚度和杨氏模量. 尽管核-壳结构有助于改善锂离子电池的电化学性能, 但在100次循环后几乎所有固体核-壳结构的电极容量均小于1000 mAh·g^{–1[16—18]}, 仍然面临表面破裂和界面剥离等问题. 与实心核-壳结构形成鲜明对比的是, 中空核-壳结构通过在核-壳结构的中心提供工程空隙来有效地解决硅的大体积膨胀问题, 该中心空隙允许硅核在锂化期间向内膨胀, 因此, 在锂化和脱锂过程中外壳上的应变最小, 有助于颗粒和导电添加剂之间的界面稳定. 此外, 多孔硅碳复合结构和硅碳Yolk-Shell结构均显示出长循环寿命、高可逆比容量和高倍率容量等优异的电化学性能^[19—22]. Ashuri等^[23,24]实验制备的中空碳包覆硅纳米球(HSi@C)表现出比微纳米尺寸硅负极更好的电化学稳定性. 尽管在理论方面国内外****已做了相应的研究^[25—28], 但硅锂化过程中伴随大的体积变形所涉及的几何非线性问题及循环锂化过程中对电极电化学性能的数值预测尚不足, 需同时发展高性能的数值计算方法, 特别是对复合和中空结构电极的电化学性能研究目前尚止于实验阶段. 如何构筑集理论与计算于一体的数值仿真平台是研究锂电问题的一大瓶颈, 该工作有助于理解在整个电化学过程中的应力演化对电极材料电化学性能及循环稳定性的重要作用.
本文采用Cahn-Hilliard型扩散理论和有限变形理论全耦合的扩散-应力模型来描述锂离子电池硅负极材料在循环锂化过程中的电化学-力学耦合机制. 采用有限元数值积分方案, 对该理论进行求解, 并在有限元软件Abaqus计算平台上, 通过用户单元子程序(UEL)构建了该理论的数值预测模块, 利用该理论和数值计算工具研究了硅电极循环锂化过程中扩散-应力耦合作用机制对电极容量的影响规律. 基于界面反应动力学, 计算电压响应, 得到与实验测量整体趋势较一致的结果, 验证了本方法的有效性. 在此基础上, 数值研究了中空碳包覆硅负极充放电过程中的浓度场和应力场. 探究了新结构对应力的缓解效果, 并从力学角度解释了中空碳包覆硅负极优异的循环稳定性背后的作用机理. 该项研究为锂离子电池电极材料的结构设计提供了理论依据和优化策略.

这里采用Cahn-Hillard型扩散理论与有限变形理论全耦合的化学-力模型来描述锂离子电池硅电极在循环锂化过程中的扩散和力学相关性问题.
2

-->

2.1.本构方程

3 -->

2.1.1.变形分析

由变形梯度的乘法分解有^[29]

${F} = {{F}^{\rm{e}}}{{F}^{\rm{s}}},$

式中, F表示变形梯度; ${{F}^{\rm{e}} }$表示弹性变形; ${{F}^{\rm{s}} }$表示膨胀变形,

${{F}^{\rm{s}}} = {({J^{\rm{s}}})^{1/3}}{I},$

其中,

${J^{\rm{s}}} = 1 + \varOmega ({c_{\rm{R}}} - {c_0}), $

Ω为扩散原子的摩尔体积, ${c_{\rm{R}} }$为参考构形下单位体积的摩尔浓度, ${c_0}$表示电极内的初始锂离子浓度.
3 -->

2.1.2.自由能

考虑一个可分离的参考构形下的单位体积自由能形式^[30]:

${\varPsi _{\rm{R}}} = \varPsi _{\rm{R}}^{{\rm{chemical}}} + \varPsi _{\rm{R}}^{{\rm{elastic}}}.$

$\varPsi _{\rm{R}}^{{\rm{chemical}}}$是由于锂离子同电极材料混合而引起的化学自由能变化,

$\begin{split}\varPsi _{\rm{R}}^{{\rm{chemical}}} =\;& {\mu ^0}{c_{\rm{R}}} + R\vartheta {c_{\max }}[ {\bar c\ln \bar c } \\&+{(1 - \bar c)\ln (1 - \bar c) + \chi \bar c(1 - \bar c)} ],\end{split}$

其中$\bar c = c{\rm{/}}{c_{\max }}$是归一化锂离子浓度, ${c_{\max }}$表示电极内的最大锂离子浓度, ${\mu ^0}$是化学势参考值, R是通用气体常数, $\vartheta $是绝对温度(假定为恒定), $\chi $表示扩散物质和电极材料的能量相互作用因子.
$\varPsi _{\rm{R}}^{{\rm{elastic}}}$是由于电极材料弹性变形而对自由能变化的贡献,

$\begin{split}\varPsi _{\rm{R}}^{{\rm{elastic}}} =\; & {J^{\rm{s}}}\left( {\frac{1}{2}{{E}^{\rm{e}}}:\mathbb{C}(\bar c)[{{E}^{\rm{e}}}]} \right),\\\mathbb{C}(\bar c) =\; &2G(\bar c)\mathbb{I} + (K(\bar c) - \frac{2}{3}G(\bar c)){\pmb{\it 1}} \otimes {\pmb{\it 1}},\end{split}$

其中, $\mathbb{C}({\bar c})$表示依赖于浓度的弹性张量, $G(\bar c)$和$K({\bar c})$分别表示依赖于浓度的剪切模量和体积模量, $\mathbb{I}$和$\pmb{\it 1}$分别表示四阶和二阶单位张量.
结合方程(5)和(6), 一个简单的用以解释混合、膨胀和有限应变的自由能函数如下:

$\begin{split}{\varPsi _{\rm{R}}} =\;& {\mu ^0}{c_{\rm{R}}} + R\vartheta {c_{\max }}[ {\bar c\ln \bar c + (1 - \bar c)\ln (1 - \bar c) }\\&+{\chi \bar c(1 - \bar c)} ] + {J^{\rm{e}}}\left( {\frac{1}{2}{{E}^{\rm{e}}}:\mathbb{C}(\bar c)[{{E}^{\rm{e}}}]} \right).\end{split}$

3 -->

2.1.3.应力

Mandel应力和Cauchy应力分别由下式给出:

${{M}^{\rm{e}}} = {{J}^{s - 1}}\frac{{\partial {\varPsi _{\rm{R}}}}}{{\partial {{E}^{\rm{e}}}}} = 2G{{E}^{\rm{e}}} + \left(K - \frac{2}{3}G\right)\!({\rm{tr}}{{E}^{\rm{e}}}){\pmb{\it 1}},$

$\begin{split}{T} \;&= {J^{e - 1}}{{R}^{\rm{e}}}{{M}^{\rm{e}}}{{R}^{{\rm{eT}}}} \\&= {J^{e - 1}}\left[2G{E}_{\rm{H}}^{\rm{e}} + \left(K - \frac{2}{3}G\right)({\rm{tr}}{E}_{\rm{H}}^{\rm{e}}){\pmb{\it 1}}\right],\end{split}$

其中, ${{E}^{\rm{e}} }$表示参考构形下的弹性对数应变, ${E}_{\rm{H}} ^{\rm{e}} $表示空间弹性对数应变.
3 -->

2.1.4.化学势

锂离子嵌入电极材料后产生的化学势由下式给出:

$\begin{split}\;& \mu = \frac{{\partial {\varPsi _{\rm{R}}}}}{{\partial {c_{\rm{R}}}}} - \varOmega \frac{1}{3}{\rm{tr}}{{M}^{\rm{e}}}\\ = & \; R\vartheta \left(\ln \left(\frac{{\bar c}}{{1 - \bar c}}\right) - 2\chi \right) - \varOmega \frac{1}{3}{\rm{tr}}{{M}^{\rm{e}}} \\&+ \frac{{{J^{\rm{c}}}}}{{{c_{\max }}}}\left(\frac{1}{2}{{E}^{\rm{e}}}\!:\!\frac{{\partial \mathbb{C}(\bar c)}}{{\partial \bar c}}[{{E}^{\rm{e}}}]\right) \!+\! \varOmega \!\left(\frac{1}{2}{{E}^{\rm{e}}}\!:\!\mathbb{C}(\bar c)[{{E}^{\rm{e}}}]\right).\end{split}$

引进“应力化学势”:

$\begin{split}{\mu _\sigma } =\; & - \varOmega \frac{1}{3}{\rm{tr}}{{M}^{\rm{e}}} + \frac{{{J^{\rm{c}}}}}{{{c_{\max }}}}\left(\frac{1}{2}{{E}^{\rm{e}}}:\frac{{\partial \mathbb{C}(\bar c)}}{{\partial \bar c}}[{{E}^{\rm{e}}}]\right) \\&+\varOmega \left(\frac{1}{2}{{E}^{\rm{e}}}:\mathbb{C}(\bar c)[{{E}^{\rm{e}}}]\right),\end{split}$

以此量化变形对化学势的影响. 由于在数值计算过程中, 后两项相比于第一项要小得多, 由此将应力化学势近似地简化为

${\mu _\sigma } = - \varOmega \frac{1}{3}{\rm{tr}}{{M}^{\rm{e}}}.$

3 -->

2.1.5.粒子流通量

锂离子嵌入电极材料的空间通量j依赖于化学势的空间梯度:

${j} = - m \cdot {\rm{grad}}\mu ,$

式中, m为运动系数,

$m = \frac{{{D_0}}}{{R\vartheta }}c(1 - \bar c),$

其中${D_0}$表示锂离子扩散系数.
2 -->

2.2.控制方程、边界条件和初始条件

3 -->

2.2.1.控制方程

1)局部力平衡

${\rm{div}}{T} = 0, $

这里, 柯西应力T由方程(9)给出.
2)粒子浓度守恒方程

${\dot c_{\rm{R}}} = - J{\rm{div}}{j}.$

3 -->

2.2.2.边界条件

本处边界条件分为两类: 弹性场边界条件和化学边界条件. 其中, 弹性场边界边界条件又分为位移已知的位移边界条件和面力已知的力边界条件, 如下:

$\begin{split}& {u} = \tilde{ u},\\& {{T}_{\rm{n}}} = \tilde{ t}.\end{split}$

化学边界条件也分为两类, 一类是化学势已知的边界条件, 一类是粒子流量已知的边界条件, 如下:

$\begin{split}&\mu = \tilde \mu ,\\&{j} \cdot {n} = \tilde j.\end{split}$

3 -->

2.2.3.初始条件

$\begin{split}& {u}({X},0) = 0,\\& \mu ({X},0) = {\mu _0}({X}).\end{split}$

第2节给出了扩散-力耦合理论和相应的边界条件、初值, 该理论具有强非线性性质, 需要采用有效的数值积分方法来求解. 首先, 采用有限元数值积分方案对上述理论进行求解, 构造相应的数值方法, 然后将其通过ABAQUS UEL补充到商用有限元软件中, 以实现对该理论的数值求解.
2

-->

3.1.残 差

采用标准的有限元求解方法求解2.2节中的方程组, 得到相应的位移残差和化学势残差如下:

$\begin{split}&R_u^A = \int_{{{B}^{\rm{e}}}} {(T{\rm{grad}}{N^A}} ){\rm{d}}v - \int_{{S}_{\rm{t}}^{\rm{e}}} {({N^A}\tilde t} ){\rm{d}}a,\\&R_\mu ^A = \int_{{{B}^{\rm{e}}}} {\big({N^A}{{\dot c}_{\rm{R}}}} ({J^{ - 1}}) \!-\! {\rm{grad}}{N^A} (m{\rm{grad}}\mu )\big){\rm{d}}v \\&\qquad \quad + \int_{{B}_{\rm{j}}^{\rm{e}}} {{N^A}\tilde j} {\rm{d}}a.\end{split}$

这里$ N^A$为形函数.
2 -->

3.2.切线刚度

基于残差方程(20), 便可知有限元数值求解时所需的切线刚度矩阵, 如下:

${({{K}_{uu}})^{{AB}}} = - \frac{{\partial {{({{R}_{{u}}})}^{{A}}}}}{{\partial {{u}^{{B}}}}},$

${({{K}_{u\mu }})^{{AB}}} = - \frac{{\partial {{({{R}_{{u}}})}^{{A}}}}}{{\partial {\mu ^{{B}}}}}, $

${({{K}_{\mu u}})^{{AB}}} = - \frac{{\partial {{({{R}_\mu })}^{{A}}}}}{{\partial {{u}^{{B}}}}},$

${({{K}_{\mu \mu }})^{{AB}}} = - \frac{{\partial {{({{R}_\mu })}^{{A}}}}}{{\partial {\mu ^{{B}}}}}.$

位移残差相对于位移自由度的切线刚度以指标形式表示为

$\begin{split}K_{{u_i}{u_k}}^{AB} =\; & - \int_{{B^{\rm{e}}}} {\frac{{\partial {N^A}}}{{{x_j}}}({\mathbb{M}_{ijkl}})\frac{{\partial {N^B}}}{{\partial {x_l}}}} {\rm{d}}v \\&+ \int_{s_{\rm{t}}^{\rm{e}}} {\left({N^A}{N^B}\frac{{\partial {{\tilde t}_i}}}{{\partial {u_k}}}\;\right)} {\rm{d}}a,\end{split}$

在数值计算中, 将空间切线模量近似简化为弹性张量, 即

$\mathbb{M} \approx \mathbb{C} = 2G\mathbb{I} + \left(K - \frac{2}{3}G\right){\pmb{\it 1}} \otimes {\pmb{\it 1}}, $

位移残差相对于化学势自由度的切线刚度:

$K_{{{u}_i}\mu }^{AB} = - \int_{{{B}^{\rm{e}}}} {\frac{{\partial {N^A}}}{{\partial {x_j}}}} \frac{{\partial {{T}_{ij}}}}{{\partial \mu }}{N^B}{\rm{d}}v + \int_{{S}_{\rm{t}}^{\rm{e}}} {{N^A}{N^B}\frac{{\partial \tilde t}}{{\partial \mu }}} {\rm{d}}a.$

这里做近似:

$\frac{{\partial {T}}}{{\partial \mu }} \approx {J^{e - 1}}\frac{{\partial {{M}^{{\rm e}}}}}{{\partial \mu }}.$

由方程及(8)及${\rm{tr}}{{E}^{\rm{e}}} = \ln (J{\rm{/}}{J^{\rm{s}}})$得

${{M}^{\rm{e}}} = 2G{{E}^{\rm{e}}} + K\ln (J{\rm{/}}{J^{\rm{s}}}){\pmb{\it 1}},$

最终得

$\frac{{\partial {{M}^{\rm{e}}}}}{{\partial \mu }} = - \frac{{{{K}}\varOmega }}{{{J^{\rm{s}}}}}\frac{{\partial {c_{\rm{R}}}}}{{\partial \mu }}{\pmb{\it 1}},$

其中, $\partial {c_{\rm{R}} }/\partial \mu $使用有限差分法进行数值计算.
化学势残差相对于化学势自由度的切线刚度为

$\begin{split}K_{\mu \mu }^{AB} \!= &\!\int_{{{B}^{\rm{e}}}} \!\! \left(\!\! - {J^{ - 1}}{N^A}{N^B}\frac{{\partial {{\dot c}_R}}}{{\partial \mu }} \!+\! \frac{{\partial m}}{{\partial \mu }}{N^B}\frac{{\partial {N^A}}}{{\partial {x_i}}}\frac{{\partial \mu }}{{\partial {x_i}}} \right.\\&\left. +\; m\frac{{\partial {N^A}}}{{\partial {x_i}}}\frac{{{N^B}}}{{\partial {x_i}}} \right)\! {\rm{d}}v - \int_{{S}_j^{\rm{e}}} {{N^A}{N^B}} \frac{{\partial \tilde j}}{{\partial \mu }}{\rm{d}}{a_{\rm{R}}}.\end{split}$

同样, $\partial {\dot c_{\rm{R}}}/\partial \mu $使用有限差分法进行数值计算, 使用(14)式, 得

$\frac{{\partial m}}{{\partial \mu }} = \frac{{\partial m}}{{\partial {c_{\rm{R}}}}}\frac{{\partial {c_{\rm{R}}}}}{{\partial \mu }} = \frac{{{D_0}}}{{R\vartheta }}{J^{ - 1}}(1 - 2\bar c)\frac{{\partial {c_{\rm{R}}}}}{{\partial \mu }}.$

化学势残差相对于位移自由度的切线刚度为

$\begin{split}K_{\mu {{u}_{{k}}}}^{AB} =\;& - \int_{{{B}^{\rm{e}}}} {\frac{{\partial {N^A}}}{{\partial {x_i}}}} \left(m\frac{{\partial \mu }}{{{x_k}}}{\delta _{il}}\right)\frac{{\partial {N^B}}}{{\partial {x_l}}}{\rm{d}}v \\&- \int_{{S}_{\rm{j}}^{\rm{e}}} {{N^A}{N^B}} \frac{{\partial \tilde j}}{{\partial {u_i}}}{\rm{d}}{a_{\rm{R}}}.\end{split}$

在数值应用中, 将(33)式简化为0, 即$K_{\mu {{u}_{{k}}}}^{AB} = 0$, 虽然这将影响收敛速度, 但并不影响数值求解的准确性.
在数值求解过程中需要计算每一增量步的锂离子浓度${c_{\rm{R}} }$以便评估本构响应函数和残差, 以无量纲形式表示:

$\begin{split}&\frac{{{\mu ^0} - \mu }}{{R\vartheta }} + \ln \left(\frac{{\bar c}}{{1 - \bar c}}\right) \\&- \frac{{\varOmega K}}{{R\vartheta }}\ln \left(\frac{J}{{1 + \varOmega (\bar c - {c_0}){c_{{\rm{R}}.\max }}}}\right) = 0 .\end{split}$

这是关于${\bar c}$的隐函数方程, 给定任意时刻的变形梯度F和化学势$\mu $可求解相应的归一化锂离子浓度(SOC)值.

2

-->

4.1.模型参数

本部分以无定形硅薄膜电极为研究对象, 长宽均为100 nm, 其材料参数如表1所列.

参数	单位	值
${E_{\rm{a} {\text -} {\rm{Si}}}}$	GPa	80[31]
${v_{\rm{a} {\text -} {\rm{Si}}}}$	—	0.22[31]
${c_{\max }}$	mol/m3	$2.95 \times {10^5}$[32]
$\varOmega $	m3/mol	$8.89 \times {10^{ - 6}}$[32]
${c_0}$	—	0.005
$\vartheta $	K	298
${D_0}$	m2/s	$1 \times {10^{ - 16}}$[33]
${k_0}$	mol/s	$3.25 \times {10^{ - 7}}$[34]

表1材料参数
Table1.Material parameters.

2 -->

4.2.电极/电解质界面反应动力学: Butler-Volmer方程

本节讨论了控制电极/电解质界面处的电化学反应动力学.
当锂离子电池充电或放电时, 在电极表面上, 通量$\tilde j$与外部施加电流I具有如下关系:

$I = - F \cdot \tilde j,$

其中, F为法拉第常数. 以${\mu ^{{\rm{surface}}}}$表示电极表面化学势, 它与平衡电位U有如下关系:

$U = {V_0} - \frac{{{\mu ^{{\rm{surface}}}}}}{F},$

其中, ${V_0}$是参考电位.
以V表示施加的外电路电压, 电化学反应的驱动力由下式给出:

$\eta = V - U,$

这里, $\eta $是用以驱动锂离子进入负极的过电位. 通过唯像Butler-Volmer方程量化该电化学反应的速率, 该方程将电流密度I与电极/电解质界面处的过电位相关联, 由下式给出^[35]:

$I = {I_0}\left(\exp \left( - \alpha \frac{{F\eta }}{{R\vartheta }}\right) - \exp \left(1 - \alpha \frac{{F\eta }}{{R\vartheta }}\right)\right),$

其中, $0 < \alpha < 1$是对称因子; ${I_0}$是依赖于浓度的交换电流, 由下式给出^[34]

${I_0} = F{k_0}{(1 - \bar c)^\alpha }{(\bar c)^\alpha },$

参数${k_0}$是由实验测定的速率常数. 在数值模拟中, 取$\alpha = 0.5$, 这种情况下, 方程(37)可转换成下式:

$\eta = 2\frac{{R\vartheta }}{F}{\sinh ^{ - 1}}\left( - \frac{1}{2}\frac{I}{{{I_0}}}\right).$

然后, 结合方程(35), (36)和(39), 由下式计算电压V:

$V = {V_0} - \frac{{{\mu ^{{\rm{surface}}}}}}{F} + 2\frac{{R\vartheta }}{F}{\sinh ^{ - 1}}\left( - \frac{1}{2}\frac{I}{{{I_0}}}\right).$

2 -->

4.3.理论验证

近年来, 带基底的薄膜电极常用来研究锂电体系在充放电过程中应力对电化学过程的影响. 如实验方面, Pharr等^[34]利用基底曲率技术, 以恒定倍率对玻璃基底上的无定形硅薄膜电极进行锂化和脱锂, 原位测量了电极充放电过程中的电压和应力响应. 故这里首先利用本文发展的方法, 数值研究硅薄膜电极的锂化-脱锂过程, 来验证本方法的可行性和有效性. 这里, 取电流为0.5 A, 图1给出了第一次充放电循环期间实验测量的电压与应力响应, 如图中虚线^[34]所示, 数值计算结果如图中实线所示.
图 1 锂化-脱锂过程中的(a)电压与(b)应力验证
Figure1. (a) Voltage and (b) stress verification during lithiation-delithiation.

从图1可看出, 基于界面反应动力学, 计算得到的电压响应曲线与实验结果整体趋势吻合较好, 同时, 应力响应定量地再现了实验结果的主要特征, 但理论和实验之间仍存在一些差异. 首先, 本模型低估了锂化时电压的瞬态下降和脱锂循环结束时电压的快速上升; 其次, 完全充电后的容量高于实验测量值且能完全脱锂; 最后, 该模型预测锂化过程中应力的增加比实验观测到得更快. 这些差异可归因于模型中忽略了充放电循环期间在硅电极表面形成的SEI层. 此外, 电压在充电和放电之间存在偏差, 给定SOC下的锂化电位低于该状态下的脱锂电位, 锂化-脱锂之间的电压滞后现象被认为是由应力对发生在硅表面电化学反应的影响造成的. 仿真模拟与实验结果之间的有力比较证明了本模型对中空碳包覆硅负极理论预测的适用性和可行性.

如引言所述, 为了缓解SEI层的断裂, 各研究组已经提出使用新型硅纳米结构以限制循环锂化期间SEI层的变形. Ashuri等^[24]实验制备了中空碳包覆硅颗粒(HSi@C), 其外壳被碳层包裹, 内部保持中空, 参见图2(a)的透射电子显微镜(TEM)图像, HSi@C结构示意图如图2(b)所示. 为了最大限度地减少计算工作量, 本文只考虑1/4区域.
这里, 边界条件如图2(c)所示.
力边界条件: 沿边缘AB的节点被约束为具有零水平位移, 而沿边缘CD的节点被约束为在垂直方向上具有零位移.
化学边界条件: 边AB和CD规定为具有零通量, ${j} \cdot {n} = 0$. 而在外部边界AD上, 通量由如下边界条件控制:

${j} \cdot {n} = \mu _{{\rm{Li}}}^{({\rm{electrodesurf}})} - {\mu _{{\rm{ext}}}},$

其中, $\mu _{{\rm{Li}}}^{{\rm{(electrode surf)}}}$表示电极颗粒边界处的化学势, 它取决于边界处的浓度和应力, 由方程(10)给定; 而${\mu _{{\rm{ext}}}}$表示外部施加的化学势, 通过控制${\mu _{{\rm{ext}}}}$以模拟嵌锂($\mu _{{\rm{Li}}}^{{\rm{(electrode surf)}}} < {\mu _{{\rm{ext}}}}$)和脱锂($ \mu _{{\rm{Li}}}^{{\rm{(electrode surf)}}} >$$ {\mu _{{\rm{ext}}}}$)过程, 数值模拟中设定单次充放电时间为3600 s.
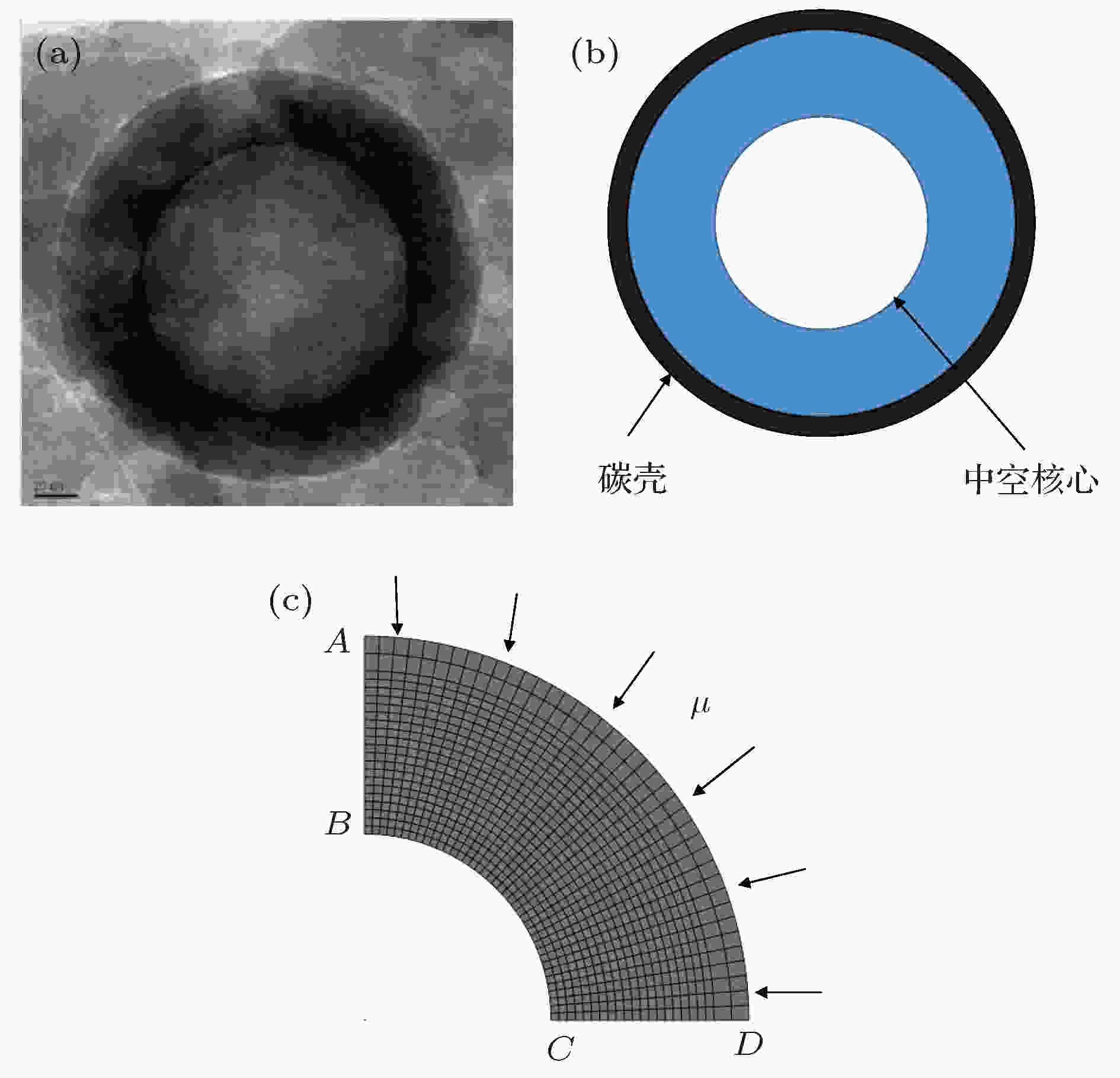图 2 中空碳包覆硅结构的建模　(a) Ashuri等^[24]实验制备的中空碳包覆硅颗粒TEM图像; (b)中空核-壳结构有限元模型示意图; (c)中空核-壳结构有限元网格划分示意图
Figure2. Modeling of hollow carbon coated silicon structure: (a) TEM image of hollow carbon coated silicon particles reproduced by Ashuri et al.^[24]; (b) finite element model of hollow core-shell structure; (c) schematic diagram of finite element meshing of hollow core-shell structure.

2

-->

5.1.实心硅和中空碳包覆硅负极的浓度场和应力场分析

本节主要研究实心硅电极和中空碳包覆硅电极锂化期间的应力演化及锂化状态. 对于中空碳包覆硅结构, 考虑空心硅材料内半径为a, 外半径为b, 碳层厚度为t, 计算中取a/b = 0.54, t/b = 0.1.
图3为实心硅和中空碳包覆硅电极在整个锂化-脱锂阶段应力随时间的演化规律, 可以看到, 在整个锂化-脱锂期间中空碳包覆硅电极应力水平明显低于实心硅电极, 且随着锂化的进行, 应力差值越来越大, 表明应力缓解效应越来越显著, 锂化结束时应力值降低约27%, 充分显示出碳层和内部孔隙对于应力缓解和释放的双重效应.
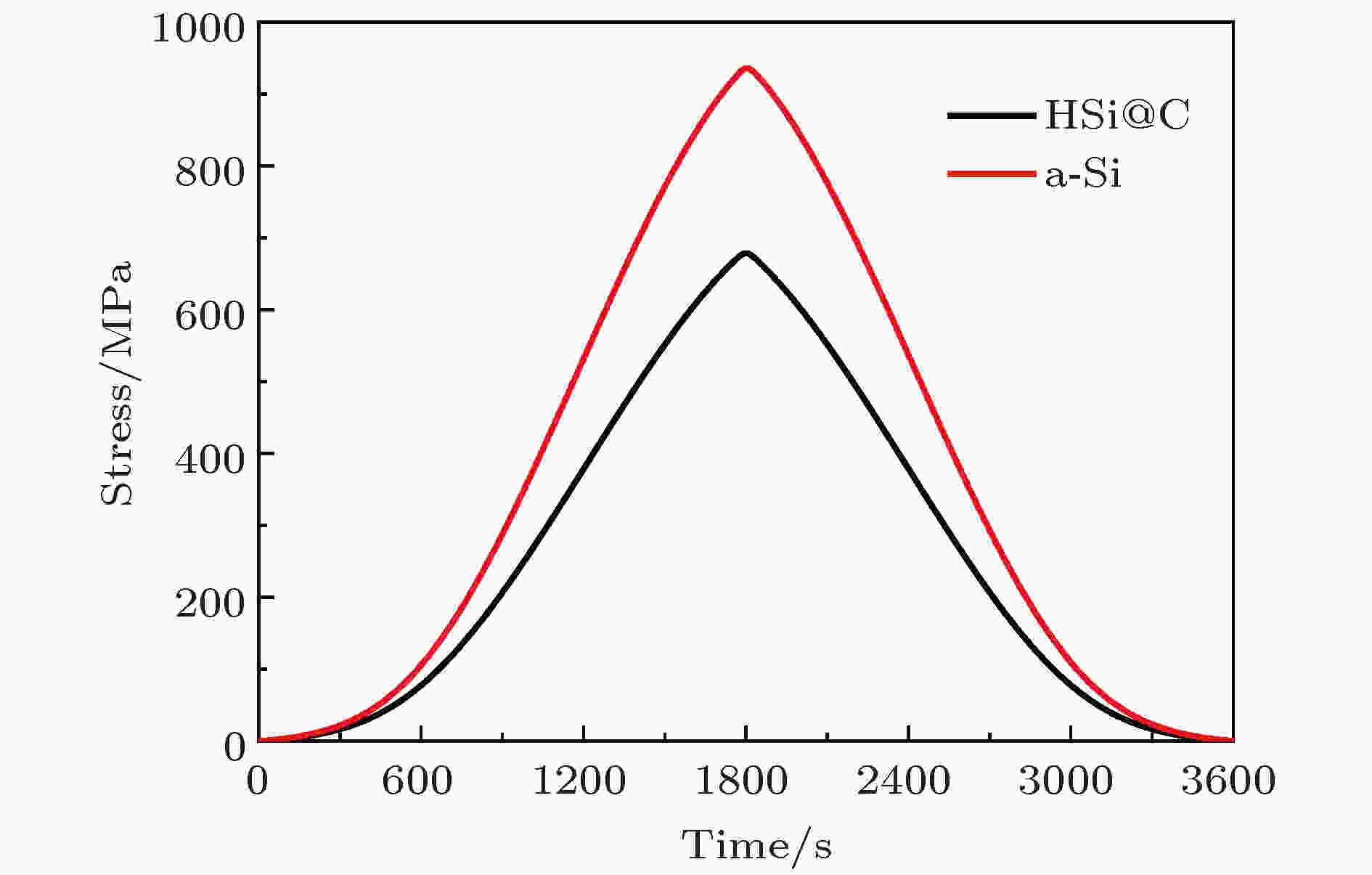图 3 实心硅电极和中空碳包覆硅电极在整个锂化-脱锂阶段应力随时间的演化
Figure3. Evolution of stress over time in lithiation-delithiation stage with solid silicon electrode and hollow carbon-coated silicon electrode.

图4为不同时刻实心硅电极和中空碳包覆硅电极内的锂离子浓度分布云图. 从图4可知, 对于实心硅电极, 嵌入的锂离子浓度呈“带”状分布, 高浓度区域位于颗粒表面, 随着外部区域的硅不断锂化至饱和, 内层材料渐渐锂化并逐渐向心部推进, 表明外部区域在内部区域之前完全锂化. 而对于中空碳包覆硅颗粒, 锂化期间内部锂离子浓度水平整体明显高于实心硅颗粒, 且更趋向于均匀分布, 这有助于缓解电极降解. 同时, 中空碳包覆硅电极更早地达到完全锂化状态, 表明中空核-壳结构优异的电化学性能. 由此看来, 由于中空碳包覆硅电极内部在锂化过程中, 更有利于锂离子浓度的均匀分布, 从而从另一方面缓解应力, 即均匀分布的锂离子浓度有利于降低电极内部的整体应力水平.
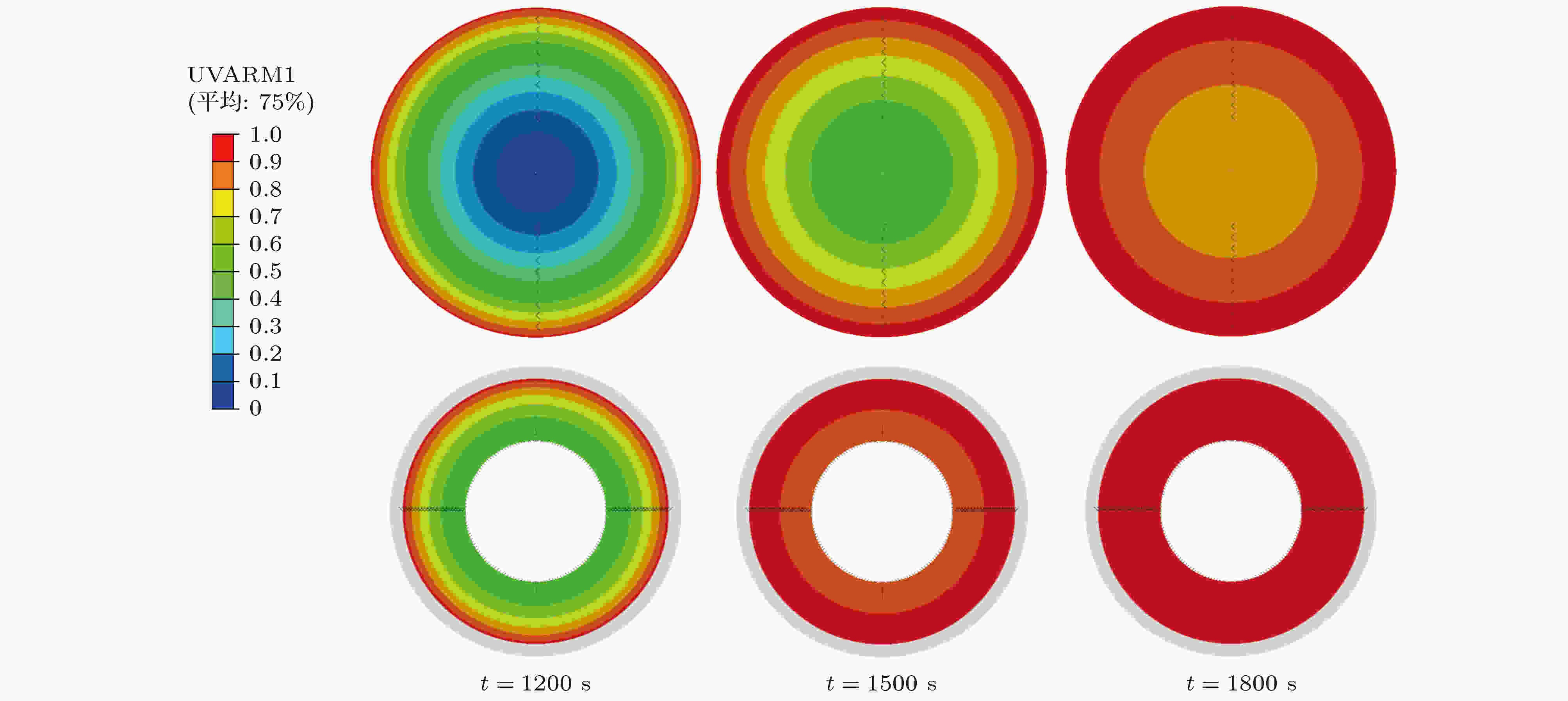图 4 t = 1200, 1500, 1800 s时实心硅电极和中空碳包覆硅电极内锂离子浓度分布云图
Figure4. Cloud distribution of lithium ion concentration in solid silicon electrode and hollow carbon coated silicon electrode at t = 1200, 1500, 1800 s.

为了进一步研究电化学过程中的应力响应, 图5给出了实心硅和中空碳包覆硅电极在锂化后期, 锂离子浓度(a)、应力(b)、化学势(c)沿径向的分布图. 从图5(a)可看出, 靠近外表面处两者锂离子浓度差异偏低, 而电极内部两者浓度差异较大, 最大值达0.06. 两电极内部锂离子浓度最小和最大差值分别为0.04和0.1, 较大的浓度差异将导致较高的浓度梯度, 从而在电极内产生较大的应力. 其对应的沿径向方向应力值如图5(b)所示, 可以看出, 中空碳包覆硅电极相较于实心硅电极应力水平明显降低. 由(10)式可知化学势可分解为由锂离子浓度主导的化学势和由应力支配的应力化学势, 从图5(b)和图5(c)可看出, 应力水平地缓解通过改变应力化学势提高了与锂离子浓度近似线性相关的化学势, 且两电极内化学势差值从表面到内部逐渐增加, 由此解释了实心硅电极和中空碳包覆硅电极内部锂离子浓度水平及分布的不同.
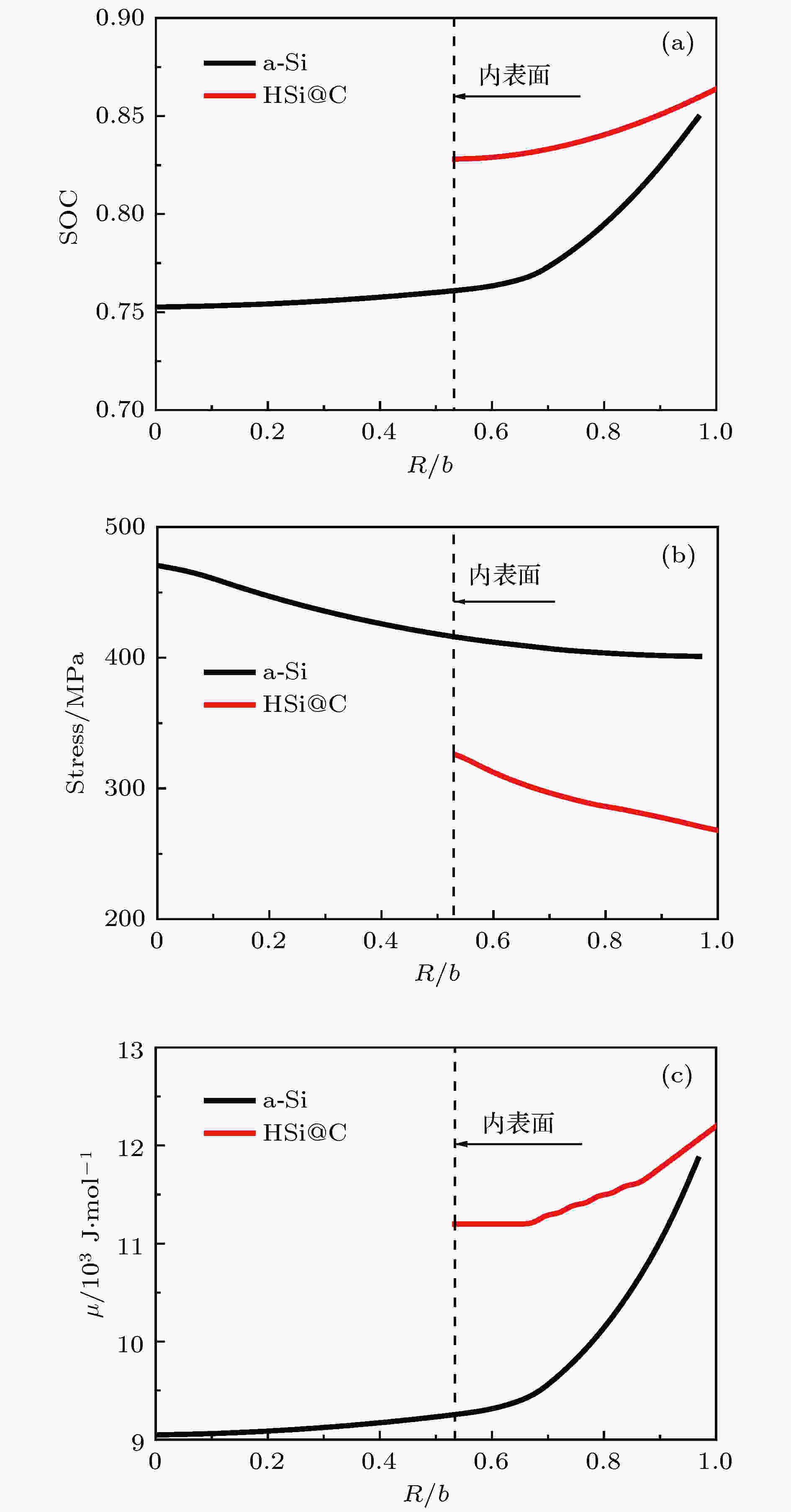图 5 实心硅和中空碳包覆硅电极在锂化后期沿径向方向的(a)锂离子浓度、(b)应力和(c)化学势
Figure5. Distribution of (a) the lithium ion concentration, (b) stress, and (c) chemical potential of solid silicon and hollow carbon coated silicon electrode in the radial direction at the late stage of lithiation.

2 -->

5.2.循环锂化容量与应力演化规律

本节主要研究中空碳包覆硅电极在充放电循环过程中的容量衰减及锂化诱导应力演化过程, 意在从力学角度出发揭示锂化诱导应力演变对电极容量的影响. Ashuri等^[24]研究了中空碳包覆硅电极经历20次脱嵌锂循环过程中不同倍率下容量的衰减情况, 这里对该实验结果进行数值模拟, 考虑其在0.5 A电流下(1C-rate)进行充放电循环, 并与实验进行对比.
图6给出了中空碳包覆硅电极在20次充放电循环过程中理论预测和实验测量电极容量对比曲线, 并给出了应力随时间的变化. 从图6(a)可看出, 数值计算所表现出的容量衰减情况与Ashuri等^[24]实验测量所得结果具有比较好的符合度. 但模拟结果整体相对于实验测量值偏高, 主要原因包括: 为了简化计算, 模型已做了大量简化, 以及忽略了一些其他的化学反应; 此外, 模拟的容量发生了衰减, 这是由于放电截止时活性材料中的锂残留量增多. 电化学循环期间中空碳包覆硅电极的应力演化如图6(b)所示, 前四次循环下应力急剧下降, 应力峰值从680 MPa降低至350 MPa, 在随后的循环过程中应力峰值下降相对变缓, 基本维持在270—350 MPa区间内. 应力峰值的变化及波动, 既与容量变化有关, 又与这里模型的简化有关, 对于硅电极由于充放电过程中产生较大变形和应力, 不可避免地会产生黏塑性变形, 这里没有考虑, 是未来需要重点考虑的方向. 结构调控下应力水平的缓解延缓了中空碳包覆硅负极容量的衰减, 应力水平的降低通过调节化学势表现出相对于实心硅电极容量的提升, 容量提高74%, 良好的循环稳定性能归因于碳包覆层和内部孔隙对体积膨胀和应力缓解的双重效应.
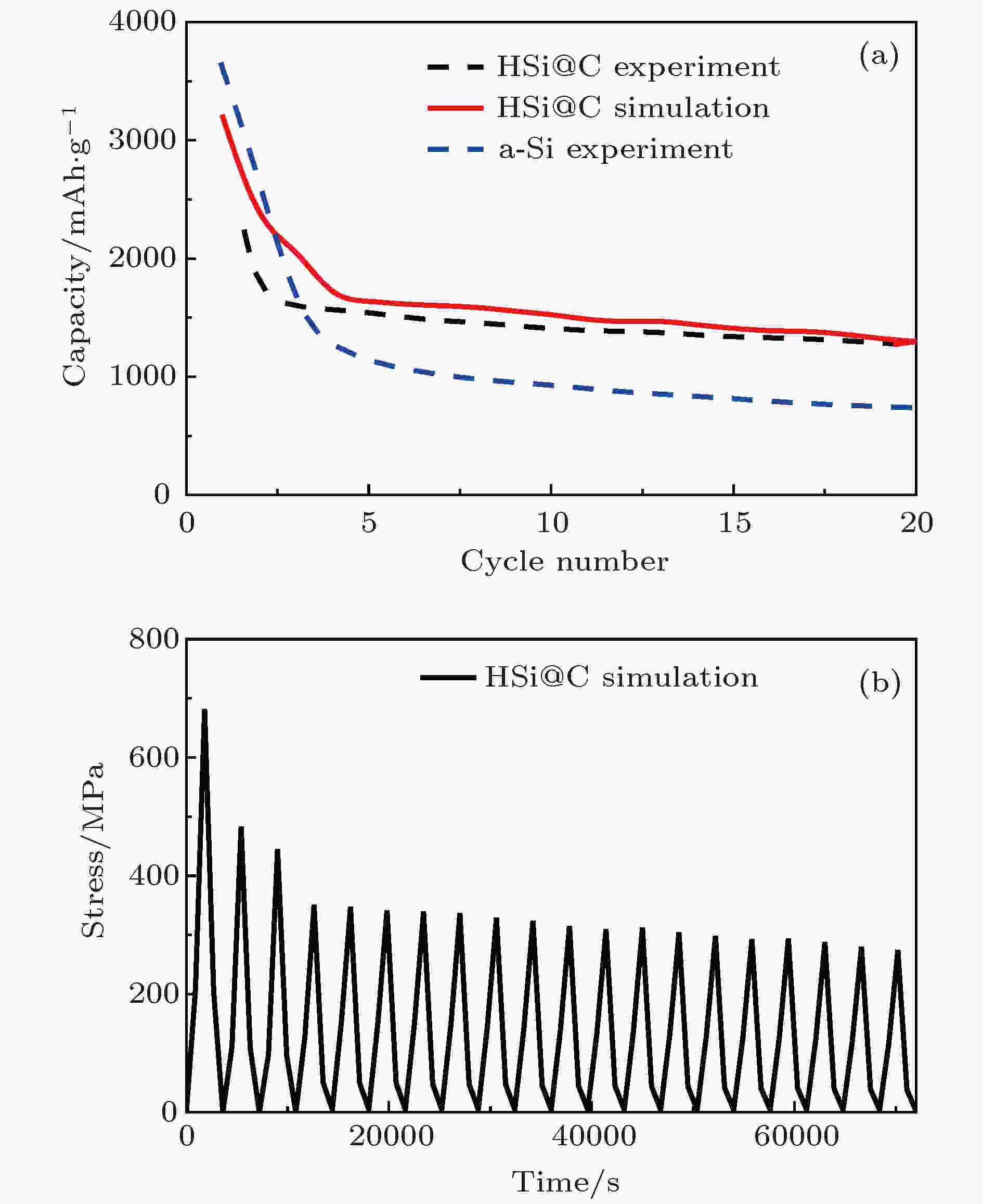图 6 20次充放电循环过程　(a)理论预测和实验测量容量值的对比; (b)应力随时间的演化
Figure6. Twenty times charge and discharge cycles: (a) Comparison of theoretical prediction and experimental measurement capacity values; (b) evolution of cauchy stress over time.

本文采用有限变形理论和Cahn-Hilliard扩散理论全耦合的化学-力模型来描述锂离子电池硅负极锂化-脱锂过程中的扩散及由此产生的变形和应力问题, 构造了相应的有限元数值求解方案, 并将其通过ABAQUS UEL补充到商用有限元软件中, 在此计算平台上数值研究了中空碳包覆硅复合电极的应力作用机制, 进而研究了锂化-脱锂循环过程中的容量衰减和应力演化规律, 为提高和设计硅复合电极提供有效途径和理论依据.
首先, 研究了硅电极恒流锂化和脱锂过程, 基于界面反应动力学, 计算得到电压响应曲线, 与实验结果吻合较好, 验证了本文所发展方法的可行性和有效性. 在此基础上, 对比研究了实心硅负极和中空碳包覆硅复合负极的电化学性质. 研究发现, 在锂化过程中, 相比于实心硅负极, 由于碳包覆层和内部孔隙对体积膨胀缓解的双重效应, 中空碳包覆硅负极应力水平明显降低, 且随锂化的进行, 应力缓解效应越发显著. 锂化期间, 中空碳包覆硅颗粒内部应力水平的缓解通过改变化学势而提高了锂离子浓度水平, 且趋向于均匀分布, 更早地达到完全锂化状态, 充分显示出其优异的电化学性能. 此外, 利用本文的方法研究了中空碳包覆硅电极20次充放电过程, 计算得到的容量变化趋势与实验测量结果符合得很好, 并从应力的角度探究了应力在电化学过程中的变化规律, 研究发现充放电循环过程中应力水平的缓解延缓了中空碳包覆硅负极的容量衰减.