摘要: 提出一种高效产生任意矢量光场的方法. 利用两个光束偏移器分别对两个正交线偏振分量进行分束与合束, 将传统激光模式转化为任意矢量光场. 所产生矢量光场的偏振态和相位分布通过相位型空间光调制器(SLM) 加载相应的相位实时调控. 由于光路系统中不涉及任何衍射光学元件和振幅分光元件, 光场转换效率高, 仅取决于SLM的反射率, 并且光路系统结构紧凑、稳定, 同轴性易于调节. 实验结果显示, 采用反射率为79%的相位型SLM产生矢量光场的转换效率可达到58%.
关键词: 偏振态 /
空间光调制器 /
矢量光场 English Abstract A method of efficiently generating arbitrary vector beams Qi Shu-Xia Liu Sheng Li Peng Han Lei Cheng Hua-Chao Wu Dong-Jing Zhao Jian-Lin Shaanxi Key Laboratory of Optical Information Technology, School of Science, Northwestern Polytechnical University, Xi'an 710072, China Fund Project: Project supported by the National Natural Science Foundation of China (Grant Nos. 11634010, 61675168, 11774289), the National Key Research and Development Program of China (Grant No. 2017YFA0303800), the Joint Fund of the National Natural Science Foundation of China and China Academy of Engineering Physics (Grant No. U1630125), the Basic Research Plan of the Natural Science Research Project of Shaanxi Province, China (Grant No. 2018JM1057), and the Seed Foundation of Innovation and Creation for Graduate Students in Northwestern Polytechnical University, China (Grant No. ZZ2018177).Received Date: 08 October 2018Accepted Date: 25 October 2018Available Online: 01 January 2019Published Online: 20 January 2019Abstract: Vector beams have been used in scientific and engineering researches due to their unique focusing properties. In recent years, many methods of generating the vector beams have been proposed, among which the spatial light modulator (SLM) is widely used based on the superposition principle with using orthogonally polarized beams. However, the energy waste is generally associated with these superposition methods. How to efficiently generate vector beams is still a hot topic. Recently, we proposed an efficient method to generate tunable vector beams by using two triangular common-path interferometers (TCPIs) as the beam splitting and combining system. However, due to the complex structure of the TCPI, the system is difficult to adjust and unstable. In addition, the optical system brings about a long optical path, and the vector beams consisting of non-eigen modes will be distorted obviously with a long distance propagation. In this paper, an improved method is proposed. We replace the TCPIs with a pair of beam displacers, which act as a beam splitter and combiner, respectively. In this setup, we can arbitrarily manipulate the polarization states and phase distributions of vector beams in real time by managing the phase diagrams load on the SLM. The whole optical system does not involve any diffractive optical elements, and has a higher conversion efficiency. The improved optical system is compact and stable, and makes the adjustment of coaxiality easier. The light energy utilization depends mainly on the reflectivity of SLM. The efficiency of generating vector beams is increased to 58% by using an SLM with a reflectivity value of 79%. Several typical vector beams with phases and tunable amplitude, including cylindrical vector beams, fractional vector beams, and vector beams with double singularities, double-mode, radially variant polarization distribution, and azimuthally and radially variant polarization distribution, are generated and verified well experimentally. This method is also expected to create high-power vector beams and play an important role in laser processing and light trapping.Keywords: polarization /space light modulator /vector beam 全文HTML --> --> --> 1.引 言 根据偏振态在横向空间的分布, 一般可将光场分为标量和矢量光场. 标量光场的偏振态在横向空间均匀分布, 如线偏振、圆偏振和椭圆偏振光场等; 矢量光场的偏振态随横向空间位置变化, 如径向偏振、角向偏振等柱矢量光场. 柱矢量光场是应用最广泛的一类矢量光场, 其特点是偏振态呈柱对称分布[1 ] . 径向偏振柱矢量光场经高数值孔径透镜紧聚焦时, 可产生超衍射极限的焦斑[2 ,3 ] , 并且经特殊光学元件进一步调制后会形成诸多具有奇异结构的焦场, 如光针、光笼、光链等[4 ?7 ] . 此外, 通过调控矢量光场偏振态的空间分布, 可实现自旋相关传输[8 ?11 ] 、自旋-轨道相互作用[12 ?15 ] 等特殊物理过程. 此外, 矢量光场独特的偏振和紧聚焦特性, 使其在飞秒激光加工[16 ] 、超分辨成像[17 ] 、光学微操控[18 ,19 ] 及光通信[20 ] 等领域具有广阔的应用前景.[21 ?23 ] , 其优点是产生效率高, 但缺乏灵活性, 并且特定设计的谐振腔只能产生具有特定偏振态分布的矢量光场. 被动法是指在激光器外光路中插入特殊设计的光学元件或某种装置以改变常规激光的偏振态, 从而形成矢量光场[24 ?28 ] . 该类方法的灵活性很强, 可以通过调节光路或元件方便地获得不同结构的矢量光场. 在研究矢量光场特性及应用过程中, 通常需要对光场的各个参数进行调节, 因而采用被动法更合适. 特别地, 借助相位型空间光调制器(SLM)可实时调控矢量光场的偏振态和相位分布, 更加突出了被动法的灵活性. 目前, 利用SLM生成矢量光场最为普遍, 由于主要是将两个正交偏振光场同轴叠加而构成矢量光场, 因此又被称为干涉法[29 ?32 ] .[33 ] , 该方法利用两个三角共路干涉装置分别作为分束和合束系统, 从而有效降低了光路的能量损耗. 但是, 双三角共路干涉光路结构复杂, 难以调节且不易稳定. 此外, 光束在该光路中经历的光程较长, 导致所产生的一些非本征模式的矢量光场会随传输距离的增加而发生畸变. 为此, 本文提出一种改进的光路结构, 利用两个光束偏移器代替三角共路干涉光路分别作为光束分束器与合束器, 这样便可以在不降低产生效率的前提下, 使得整个光路系统结构更加紧凑、稳定, 同轴性调节更容易, 从而更方便、高效地实现任意矢量光场的产生. 同时, 采用反射率更高的SLM, 可以进一步提高矢量光场的产生效率, 拓展矢量光场在激光加工及光学捕获等方面的应用.2.实验装置 图1 为改进的实验光路. 自He-Ne激光器输出的波长为632.8 nm的线偏振高斯光束经半波片(HWP1 )调制后, 其偏振方向转至与水平方向成45°夹角, 再经过第一个光束偏移器(BD1 )后, 被分成偏振方向正交的两束线偏振光(即水平偏振的p-分量和垂直偏振的s-分量), 并以一定距离平行分开. p-分量和s-分量经直角反射棱镜(RAPM)一侧的反射面分别反射至分屏SLM左右两部分. 由于SLM只对水平偏振态响应, 因此p-分量直接照射至SLM的左半部分, 而s-分量需先经过半波片(HWP2 )转化为水平偏振后再照射至SLM的右半部分. 经SLM左右两部分加载的相位调制后, 原s-分量保持水平偏振, 而p-分量经HWP2 转化为垂直偏振. 两个分量由第二个光束偏移器(BD2 )实现同轴叠加, 然后通过1/4波片(QWP, 光轴与水平方向成45°夹角)分别转化为左、右旋圆偏振分量, 最终叠加生成矢量光场. 为准确探测所生成的矢量光场, 采用透镜(L)(焦距f = 15 cm)将SLM清晰成像在电荷耦合器件(CCD)靶面上, 并利用检偏器(P)对所产生的矢量光场做进一步分析. 另外, 在实际应用中, 可以在QWP后通过4f 系统使SLM平面共轭成像在后焦平面处. 此时矢量光场的输出平面位于4f 系统的后焦平面.1 可改变s-分量和p-分量的强度比, 从而使生成的矢量光场的局域偏振态具有不同椭圆度, 可以生成高阶庞加莱球矢量光场[33 ] , 并且可以利用几何相位法测量其偏振态分布[34 ] . 本文为简化讨论, 实验中设定HWP1 与水平方向成22.5°的夹角, 此时p-分量和s-分量等强度, 所产生的矢量光场为局域线偏振. 经过QWP转化的左、右旋圆偏振分量, 其琼斯矢量分别为(1, i)T 和(1, ?i)T . 假设自SLM左右两部分获得的调制相位分别为$ \delta_1$ (x , y )和$\delta $ 2 (x , y ), 则两分量的电场强度矢量分别表示为E 1 = E 0 exp(i$ \delta$ 1 ) (1, i)T , E 2 = E 0 exp(i$ \delta$ 2 ) (1, ?i)T , 其中, E 0 表示入射光场复振幅分布. 于是, 叠加光场的电场强度矢量表示为$ \alpha$ = ($\delta $ 1 ?$\delta $ 2 )/2, $ \beta$ = ($\delta $ 1 + $\delta $ 2 )/2. (1 )式描述了一个携带相位$ \beta$ 、偏振方向为$\alpha $ 的矢量光场. 通过设置SLM左右两部分加载的相位结构$ \delta$ 1 (x , y )和$\delta $ 2 (x , y ), 可构成任意偏振态及相位分布的矢量光场.图 1 可产生任意矢量光场的实验光路 HWP, 半波片; BD, 光束偏移器; RAPM, 直角反射棱镜; SLM, 空间光调制器; QWP, 1/4波片; L, 透镜; P, 检偏器; CCD, 电荷耦合器件; 插图表示±1阶相位Figure1. Experimental setup for generating arbitrary vector beams. HWP, half-wave plate; BD, beam displacer; RAPM, right-angle prism mirror; SLM, spatial light modulator; QWP, quarter-wave plate; L, lens; P, polarizer; CCD, charge-coupled device; the inset shows the first-order helix phase map.图1 所示, 线偏振光进入BD1 后发生双折射, 其中水平偏振(红线表示)分量沿原入射方向通过, 而竖直偏振(绿线表示)分量倾斜通过. 因此, 两正交分量经过BD1 后会存在一定光程差. 但由于利用两个相同的光束偏移器BD1 和BD2 分别实现分束与合束, 整个光路系统对称, 保证了最终合成时两束光的光程延迟相等, 因此其具有良好的稳定性.1, 2 , 型号为Thorlabs BD40, 光束间隔为4.0 mm, 偏向角为5.75°)以及反射率为79%的相位型SLM (型号为Hamamatsu X11840-07, 像素为792 × 600, 像元尺寸为20 μm). 当SLM上加载的相位$\delta $ 1 和$\delta $ 2 分别为$\pm \,1$ 阶螺旋相位时, 产生一阶矢量光场的效率为58%. 所加载的相位图如图1 中插图所示. 如果不考虑光场的本征模式在传输过程中的衍射效应, 该光路生成其他矢量光场的效率不会有变化.3.实验结果与讨论 23.1.柱矢量光场的产生 3.1.柱矢量光场的产生 SLM上加载的相位结构$\delta$ 1 (x , y ), $ \delta$ 2 (x , y )决定了所合成矢量光场的偏振态和相位分布. 在柱坐标系(r , $ \phi$ )下, 若取$\delta $ 1 = ?$ \delta$ 2 = m $\phi $ + $\phi $ 0 , 可产生柱矢量光场, 其中整数m 表示拓扑荷, $\phi $ 0 为初始相位. 例如, 当m = 1, $\phi $ 0 = 0时, 得到典型的柱矢量光场—径向偏振矢量光场. 由于SLM具有非线性的相位响应特性, 需要对其进行相位校正[29 ] . 但校正后仍然不可避免地存在相位误差, 这将导致所生成矢量光场在0—2$\text{π} $ 的相位阶跃处出现一条暗线. 为消除此暗线, 需对调制相位$\delta $ 1 和$\delta $ 2 附加相同的相位光栅$\phi $ g = k x x (k x $ \phi$ g 会提高所合成矢量光场的质量, 但也会由于光栅衍射降低光场的转换效率, 此时得到的径向偏振矢量光场的转换效率约为56%.$ \delta$ 1 = ?$\delta $ 2 = m $\phi $ + $ \phi$ 0 , 即(1 )式中$ \alpha$ ≠ 0, $\beta $ = 0时, 所得到的柱矢量光场不携带涡旋相位, 其电场强度矢量分布可表示为图2 给出了实验得到的几种柱矢量光场, 其中图(a)—(d)分别为径向、角向偏振光场和二阶、五阶矢量光场. 图中第一行为矢量光场强度和偏振态分布(短线表示线偏振方向), 第二、三行为矢量光场分别经水平和竖直方向检偏后的强度分布. 可以看出, 柱矢量光场的强度分布中心均存在一个暗核, 其为偏振奇点. 且拓扑荷m 越大, 暗核尺寸越大. 由矢量光场经检偏器检偏后的强度分布可进一步判断其偏振态分布. 如图2(a) , (b) 所示, 径向矢量光场与角向矢量光场存在$ \text{π}$ /2的相位差, 经过检偏器后, 两种光场的消光位置正交. 同理, 如图2(c) , (d) 所示, 高阶柱矢量光场(即m > 1)经过检偏器后, 光场分布为多个对称光斑, 并且其数目为2m .图 2 柱矢量光场的实验产生结果 (a) m = 1, $ \phi$ 0 = 0; (b) m = 1, $ \phi$ 0 = $ \text{π}$ /2; (c) m = 2, $ \phi$ 0 = 0; (d) m = 5, $ \phi$ 0 = 0; 第一行为光场强度分布和偏振态分布(由短线表示);第二、三行为分别经水平和竖直方向检偏后的光场强度分布Figure2. Experiment results of cylindrical vector beams: (a) m = 1, $ \phi$ 0 = 0; (b) m = 1, $ \phi$ 0 = $ \phi$ /2; (c) m = 2, $ \phi$ 0 = 0; (d) m = 5, $ \phi$ 0 = 0. The first column: intensity distributions of light fields with polarizations marked with short lines; the second and third columns: intensity distributions of light fields passing through the horizontal and vertical polarizers, respectively.$ \delta$ 1 和$\delta $ 2 分别为$ \delta$ 1 = m 1 $\phi $ + $ \phi$ 0 , $\delta $ 2 = m 2 $\phi $ + $ \phi$ 0 , 且|m 1 | ≠ |m 2 |时, 即(1 )式中$\alpha $ ≠ 0, $ \beta$ ≠ 0时, 得到的柱矢量光场同时携带涡旋相位. 图3(a) 和图3(b) 分别给出了m 1 = 2, m 2 = 0, $\phi_0$ = 0和m 1 = 5, m 2 = ?1, $ \phi$ 0 = 0时, 所得到的矢量涡旋光场. 图中第一列为矢量光场强度和偏振态分布, 第二、三列为矢量光场分别通过水平和竖直方向检偏后的强度分布. 当SLM左右两部分加载的相位拓扑荷数分别为m 1 , m 2 时, 则产生的矢量光场的偏振阶数为(m 1 ? m 2 )/2, 相位拓扑荷为(m 1 + m 2 )/2. 因此, 图3(a) 所示为拓扑荷等于1的一阶柱矢量涡旋光场; 图3(b) 所示为拓扑荷等于2的三阶柱矢量光场. 从图中可明显看出, 携带与不携带涡旋相位的柱矢量光场经过检偏器后的强度分布相同.图 3 携带涡旋相位的柱矢量光场的实验结果 (a) m 1 = 2, m 2 = 0, $\phi $ 0 = 0; (b) m 1 = 5, m 2 = ?1, $\phi $ 0 = 0. 第一列为光场强度分布和偏振态分布;第二、三列为分别经水平和竖直方向检偏后的光场强度分布Figure3. Experiment results of cylindrical vector beams with vortex phase: (a) m 1 = 2, m 2 = 0, $\phi $ 0 = 0; (b) m 1 = 5, m 2 = ?1, $\phi $ 0 = 0. The first column: intensity and polarizations distributions of light fields; the second and third columns: intensity distributions of light field passing through the horizontal and vertical polarizers, respectively.3.2.分数阶矢量光场的产生 -->3.2.分数阶矢量光场的产生 当SLM加载相位满足$\phi $ 1 = ?$ \phi$ 2 = m $\phi $ + $ \phi_0$ , 且m 为分数时, 可产生分数阶矢量光场. 图4(a) 和图4(b) 分别对应m = 1/2, $\phi $ 0 = 0和m = 3/2, $ \phi$ 0 = 0时得到的实验结果. 图中第一列为光场强度和偏振态分布, 第二、三列分别为经水平和竖直方向检偏后的光场强度分布. 与整数拓扑荷相比, 分数拓扑荷导致所产生的矢量光场发生柱对称破缺. 未加检偏器的矢量光场强度图中, 除中心存在奇点外还存在一条暗线, 可理解为暗线上下两侧光场在该处存在相位差而发生相消干涉. 分数阶矢量光场分别经水平和竖直方向检偏后, 当m = 1/2时, 出现一个消光位置, 如图4(a) 所示; m = 3/2时, 出现3个消光位置, 如图4(b) 所示.图 4 分数阶矢量光场的实验结果 (a) m = 1/2, $\phi $ 0 = 0; (b) m = 3/2, $\phi $ 0 = 0. 第一列为光场强度和偏振态分布; 第二、三列为分别经水平和竖直方向检偏后的光场强度分布Figure4. Experiment results of fractional vector beams: (a) m = 1/2, $\phi $ 0 = 0; (b) m = 3/2, $\phi $ 0 = 0. The first column: intensity and polarizations distributions of light fields; the second and third columns: intensity distributions of light field passing through the horizontal and vertical polarizers, respectively.3.3.多奇点矢量光场的产生 -->3.3.多奇点矢量光场的产生 令SLM加载相位满足${\delta _1} = - {\delta _2} =\sum\nolimits_{j = 1}^N$ $ {{m_j}{\phi _j}} + {\phi _0}$ , 其中m j j 个相位奇点的拓扑荷, (x j y j j 个相位奇点的横向位置, 且${\phi _j} =$ $ {\rm{ta}}{{\rm{n}}^{ - 1}}\left[ {{{\left( {y - {y_j}} \right)}/{\left( {x - {x_j}} \right)}}} \right]$ , 则可以得到多奇点矢量光场. 图5 给出了两种典型的双奇点矢量光场的实验结果. 第一列为光场强度和偏振态分布, 第二、三列为分别经水平和竖直方向检偏后的光场强度分布. 从图中可看出, 未加检偏器时, 两种双奇点矢量光场的总强度分布相同, 且均存在两个暗核. 但由于其偏振态分布不同, 通过检偏器后光场强度分布也各不相同. 当m 1 = m 2 = 1时, 如图5(a) 所示, 光场经水平方向检偏后, 竖直方向的亮斑连为一体; 当经竖直方向检偏后, 其光场分布类似于二阶柱矢量光场. 当m 1 = ?m 2 = 1时, 如图5(b) 所示, 由于相反拓扑荷间的相互作用, 经水平方向检偏后, 光场中出现一个暗环; 经竖直方向检偏后, 在水平方向出现一条暗线, 并且其上下的亮斑对称.图 5 双奇点矢量光场的实验结果 (a) m 1 = m 2 = 1, $\phi $ 0 = 0; (b) m 1 = ?m 2 = 1, $\phi $ 0 = 0. 第一列为光场强度和偏振态分布, 第二、三列为分别经水平和竖直方向检偏后的光场强度分布Figure5. Experiment results of vector beams with double singularities: (a) m 1 = m 2 = 1, $\phi $ 0 = 0; (b) m 1 = ?m 2 = 1, $\phi $ 0 = 0. The first column: intensity and polarizations distributions of light fields; the second and third columns: intensity distributions of light field passing through the horizontal and vertical polarizers, respectively.3.4.其他矢量光场的产生 -->3.4.其他矢量光场的产生 进一步, 将加载的相位沿径向进行分割, 使内外环相位分别满足$ \delta$ 1 = ? $\delta $ 2 = $\phi $ , $\delta $ 1 = ?$ \delta$ 2 =$\delta $ + $\text{π} $ /2, 则可以得到图6(a) 所示的双模矢量光场. 当SLM加载的相位满足$\delta $ 1 = ?$\delta $ 2 = 2$\text{π} $ r /r 0 时, 得到图6(b) 所示的偏振态沿径向变化的矢量光场, 其总强度分布类似于高斯光场, 通过检偏器后其消光位置为不同半径的同心圆环. 然而, 当SLM左右两部分加载的相位满足$\delta $ 1 = $\phi $ , $ \delta$ 2 = ?2πr /r 0 时, 则得到图6(c) 所示的偏振态沿角向和径向同时变化的矢量光场, 其总强度分布与图6(b) 类似, 但通过检偏器后其消光位置呈现出一条螺旋线.图 6 其他几种矢量光场的实验结果 (a) 双模矢量光场; (b) 偏振态沿径向变化矢量光场; (c) 偏振态沿角向与径向同时变化矢量光场. 第一行为光场强度分布和偏振态分布; 第二、三行为分别经水平和竖直方向检偏后的光场强度分布Figure6. Experiment results of other vector beams: (a) Double-mode vector beam; (b) vector beam with radially variant polarization distribution; (c) vector beam with azimuthally and radially variant polarization distribution. The first column: intensity distributions and polarizations of light fields; the second and third columns: intensity distributions of light fields passing through the horizontal and vertical polarizers, respectively.4.结 论 提出了一种改进的高效产生任意矢量光场的方法. 利用两个光束偏移器分别作为光束分束器与合束器, 通过在SLM上加载的调制相位实时调控光场的偏振态和相位分布, 实现了任意矢量光场的产生. 所设计的光路系统不涉及任何衍射光学元件和振幅分光元件, 因而光场转换效率高(仅取决于所用相位型SLM的反射率), 并且光路系统结构紧凑、稳定, 同轴性易于调节. 实验中, 采用反射率为79%的SLM, 使矢量光场的产生效率达到58%. 利用该方法实验产生了柱矢量光场、分数阶矢量光场、多奇点矢量光场、双模矢量光场, 以及偏振态沿径向变化和角向与径向同时变化矢量光场, 并且光束质量高. 利用这种高效产生的任意矢量光场, 可进一步拓展矢量光场在激光加工及光学捕获等方面的应用. 





































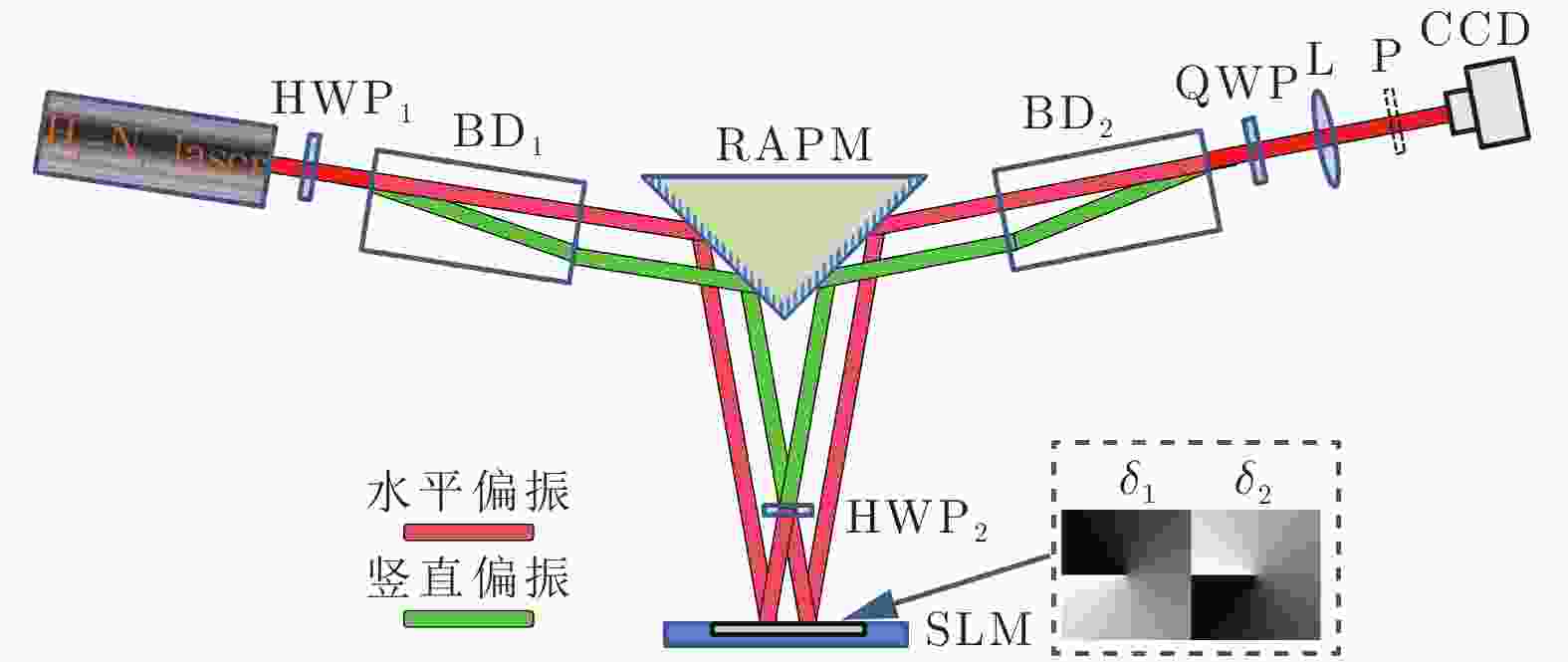 图 1 可产生任意矢量光场的实验光路 HWP, 半波片; BD, 光束偏移器; RAPM, 直角反射棱镜; SLM, 空间光调制器; QWP, 1/4波片; L, 透镜; P, 检偏器; CCD, 电荷耦合器件; 插图表示±1阶相位
图 1 可产生任意矢量光场的实验光路 HWP, 半波片; BD, 光束偏移器; RAPM, 直角反射棱镜; SLM, 空间光调制器; QWP, 1/4波片; L, 透镜; P, 检偏器; CCD, 电荷耦合器件; 插图表示±1阶相位























































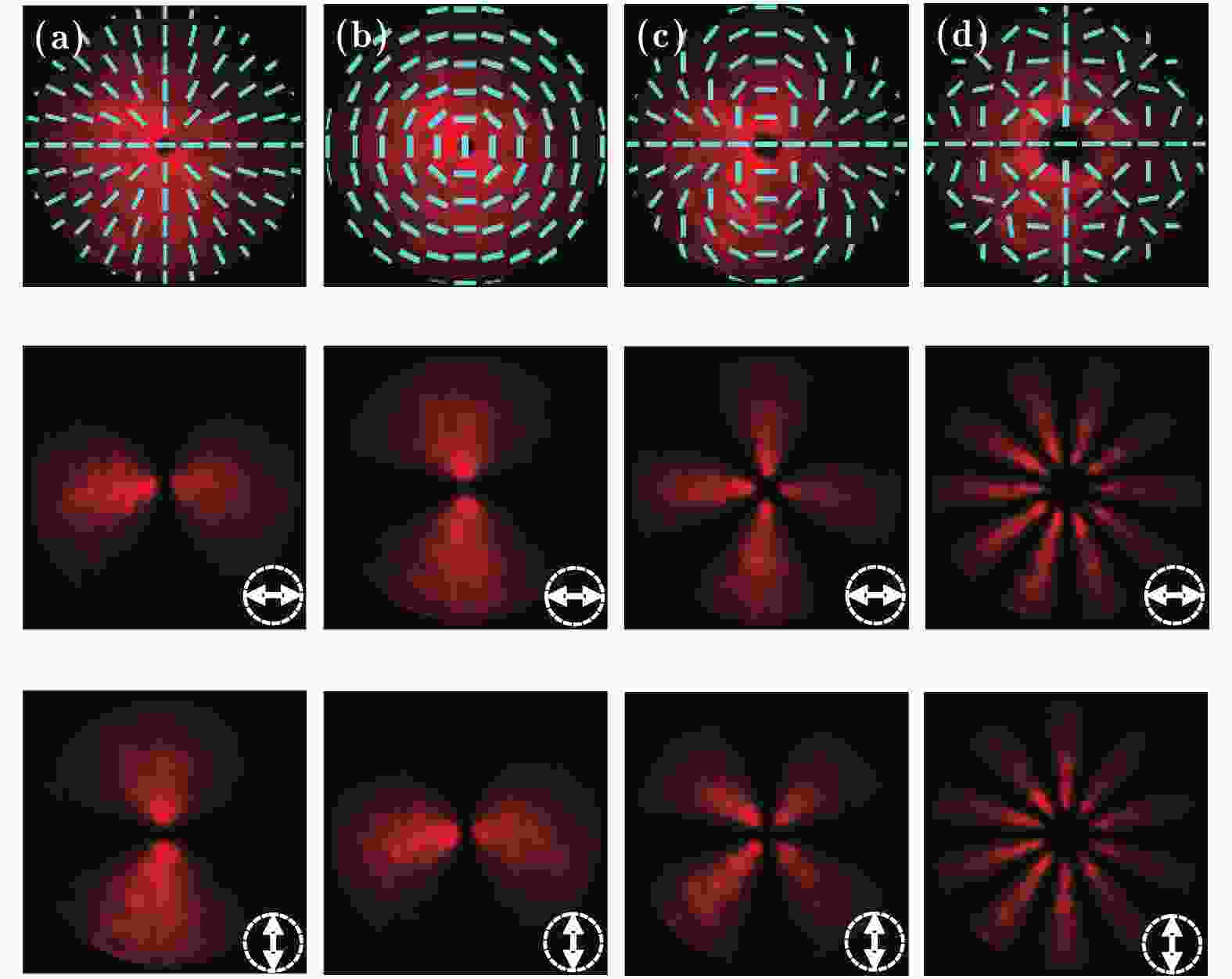 图 2 柱矢量光场的实验产生结果 (a) m = 1,
图 2 柱矢量光场的实验产生结果 (a) m = 1, 

































































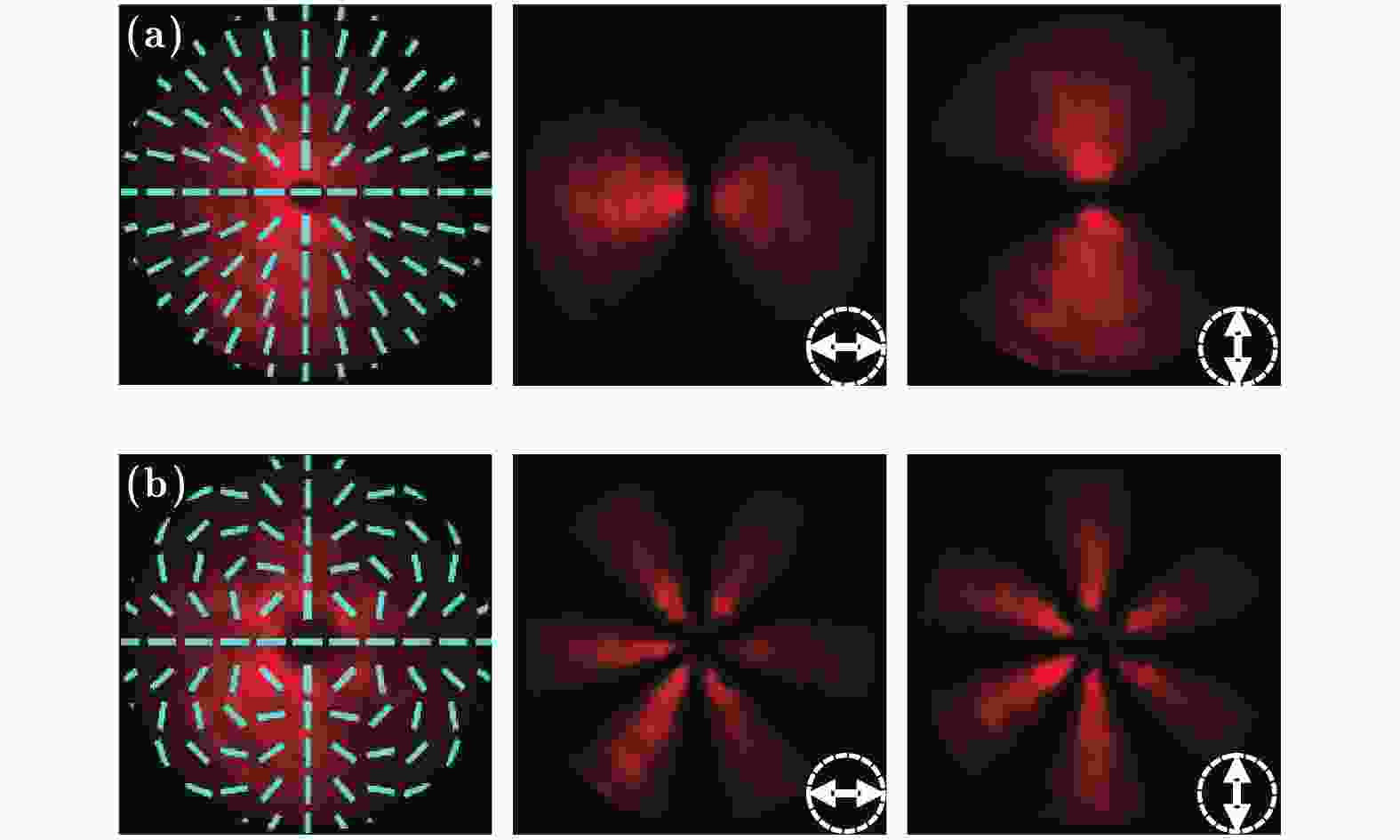 图 3 携带涡旋相位的柱矢量光场的实验结果 (a) m1 = 2, m2 = 0,
图 3 携带涡旋相位的柱矢量光场的实验结果 (a) m1 = 2, m2 = 0, 





















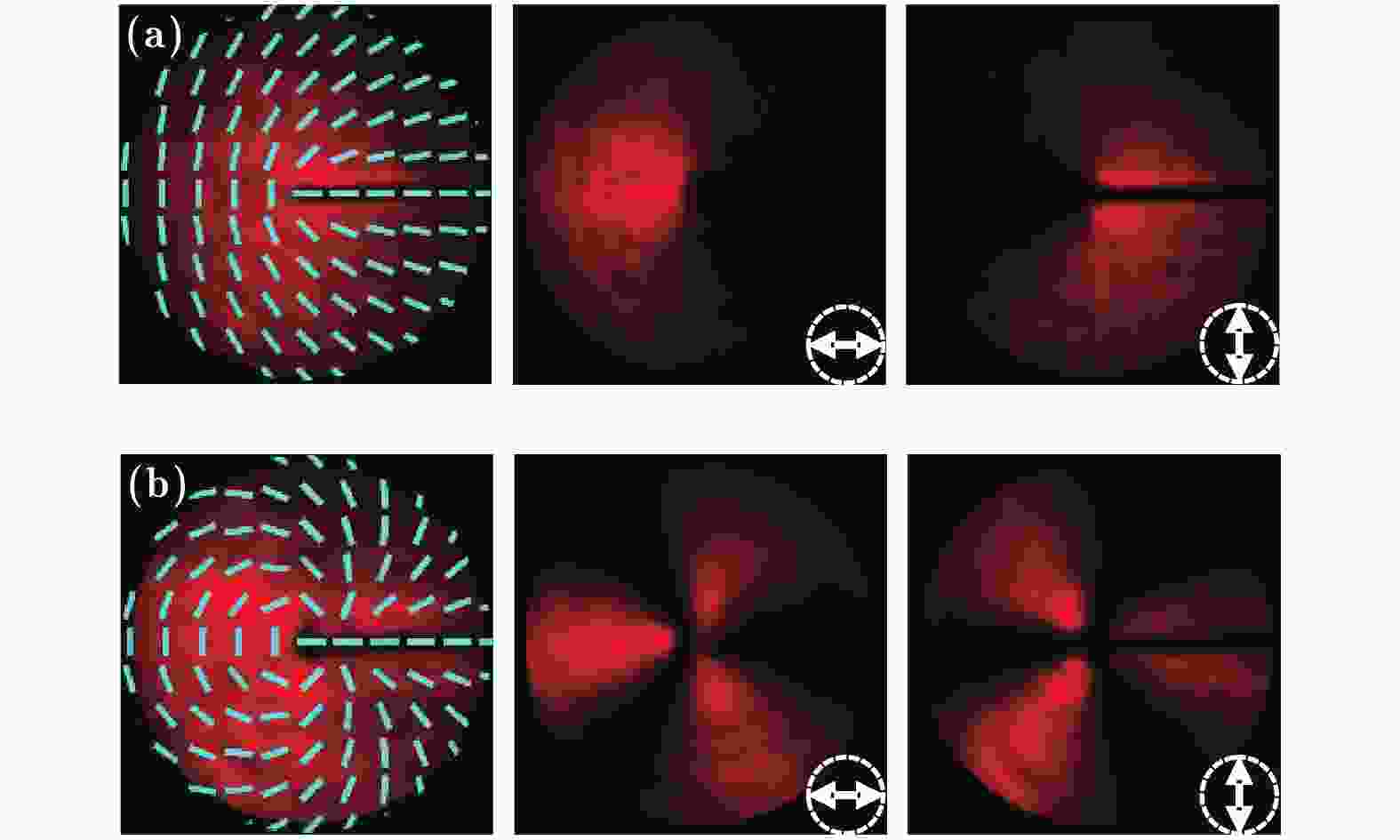 图 4 分数阶矢量光场的实验结果 (a) m = 1/2,
图 4 分数阶矢量光场的实验结果 (a) m = 1/2, 











 图 5 双奇点矢量光场的实验结果 (a) m1 = m2 = 1,
图 5 双奇点矢量光场的实验结果 (a) m1 = m2 = 1, 




























































 图 6 其他几种矢量光场的实验结果 (a) 双模矢量光场; (b) 偏振态沿径向变化矢量光场; (c) 偏振态沿角向与径向同时变化矢量光场. 第一行为光场强度分布和偏振态分布; 第二、三行为分别经水平和竖直方向检偏后的光场强度分布
图 6 其他几种矢量光场的实验结果 (a) 双模矢量光场; (b) 偏振态沿径向变化矢量光场; (c) 偏振态沿角向与径向同时变化矢量光场. 第一行为光场强度分布和偏振态分布; 第二、三行为分别经水平和竖直方向检偏后的光场强度分布