
 , 张伟2, 崔焘1
, 张伟2, 崔焘11. 河北工业大学 电子信息工程学院, 天津 300401;
2. 河北工业大学医院, 天津 300401
2018-09-10 收稿, 2018-10-15 录用
国家自然科学基金(61401307)、河北省科学技术研究与发展项目(11213565)和河北省引进留学人员资助项目(CL201707)资助
*通讯作者: 池越, E-mail: chiyueliuxin@126.com
摘要: 基于非局部自相似性块组学习的图像去噪(PGPD)算法去除高斯噪声效果优异,但是对于磁共振(MR)图像中Rician噪声的去除效果不理想。为此本文提出一种结合方差稳定变换和PGPD的新去噪算法FPGPD。该算法首先对含有Rician噪声的MR图像进行方差稳定变换,使噪声在变换域中近似服从高斯分布。用PGPD算法在变换域中去噪,最后经过方差稳定逆变换得到无偏去噪图像。理论分析和实验结果表明,FPGPD算法在去除MR图像中Rician噪声时比PGPD算法去噪性能好,具体体现为对图像细节和轮廓边缘保护得更好。
关键词: 磁共振图像去噪方差稳定变换PGPD
Combining Variance Stable Transform and PGPD to Remove Rician Noise from Magnetic Resonance Images
ZHANG Ruonan1, CHI Yue1

 , ZHANG Wei2, CUI Tao1
, ZHANG Wei2, CUI Tao11. School of Electronics and Information Engineering, Hebei University of Technology, Tianjin 300401, P. R. China;
2. Hebei University of Technology Hospital, Tianjin 300401, P. R. China
*Corresponding author: CHI Yue, E-mail: chiyueliuxin@126.com
Abstract: The patch group based non-local self-similarity prior learning for image denosing (PGPD) algorithm has excellent effect of removing Gaussian noise, but the removal effect of Rician noise in MR images is not ideal. In this paper, a new algorithm FPGPD combining variance stable transform and PGPD is proposed. Firstly, the algorithm performs the variance-stable transformation on the MR image with Rician noise, so that the noise approximation obeys the Gaussian distribution in the transform domain. Then, using the PGPD algorithm to denoise in the transform domain, and finally obtains the unbiased denoising image through the inverse variance transform. Theoretical analysis and experimental results indicate that the FPGPD algorithm has significantly improved denoising performance compared to the PGPD algorithm when removing Rician noise in MR images, which is better for image detail and contour edges.
Key words: MR imagedigital image denoisingvariance stable transformationPGPD
磁共振(MR)因具有功能强大、对人体伤害小的特点,目前广泛应用于医疗诊断。但MR成像过程复杂,硬件电路和人体散热等因素容易产生Rician噪声[1],噪声存在使得MR图像细节模糊,组织边界难以识别,对医学诊断造成困难,因此去噪处理很有必要。
传统MR图像去噪方法主要有滤波法[2]、变换域法[3]和统计法[4],这些方法在去除高斯噪声时效果显著,但对于MR图像中Rician噪声则去噪效果一般,尤其对医学MR图像细节边缘保护不好,容易丢失有用信息。目前小波变换和基于非局部滤波等方法已被广泛用于MR图像Rician噪声的去除。2008年程巧翠[5]在小波变换的基础上结合SURE硬阈值滤波和维纳滤波对MR图像去噪,但重建时易造成相位失真;2011年Foi[6]首次将方差稳定变换用于MR图像Rician噪声去除,取得良好效果;2015年陈创泉提出一种改进的非局部滤波算法[7]用于MR图像中Rician噪声的去除,算法结构复杂,不宜寻找最优参数[8]。2016年黄学优等[9]提出一种双数复小波域的MR图像去噪算法,该算法结合双边滤波器和基于Stein无偏误差估计[10]的领域收缩法,在去除MR图像Rician噪声方面取得突破性进展。
对于MR图像中的Rician噪声,利用方差稳定变换将Rician噪声变换成类加性高斯白噪声,减小噪声与原始图像依赖性,实验效果显著[11, 12]。方差稳定变换作为一种数学变换,可将异方差数据变为同方差数据,方便解决实际中的复杂问题。PGPD算法[13]采用非局部自相似性(non-local self-similarity,NSS)原理,将一幅图像划分成多个局部块,根据块组之间相似性,提取多个非局部块,两者结合构成新块组,进行NSS模型[14]学习。该算法与其它算法相比,在去除高斯噪声方面展现出很大优势。
PGPD算法学习阶段通过高斯混合模型学习原始图像先验NSS,去噪阶段选择高斯分量,都是针对方差恒定的高斯分布而言。而MR图像中的Rician噪声在信噪比低的部分服从瑞利分布,在信噪比高的部分服从高斯分布,因此传统PGPD去噪算法对于MR图像Rician噪声的去除无优势。
本文提出一种结合方差稳定变换和PGPD的新去噪算法。首先对含有Rician噪声的MR图像进行方差稳定变换,在变换域中使得噪声与图像独立,Rician噪声近似转化为加性高斯噪声。然后采用去除高斯噪声效果优异的PGPD算法去噪,最后经过方差稳定逆变换得到无偏去噪图像。
1 MR图像所含噪声分析MR因成像迅速、危害小等特点广泛用于医疗诊断中,但成像过程中常会引入噪声。检测对象和电路元件是产生磁共振图像噪声的两大主要来源。MR原始数据采集于K空间,K空间的数据由实部和虚部两部分信号构成,相位相差90度[15]。MR图像所含噪声在复数域呈高斯分布[16],通过应用计算机辅助图形分析,得到MR图像所含噪声整体服从Rician分布,实部和虚部分别含有均值为0、方差相同且相互独立的加性高斯噪声,具体为信噪比低强度区域呈瑞利分布,信噪比高强度区域服从高斯分布[17]。
对K空间数据进行傅里叶变换[18],得到变换图像。由于傅里叶变换只是将图像变换到频域中,噪声形式不会发生变化,因此得到的变换图像是复数信号,表达式如下:
 | (1) |
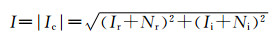 | (2) |
 | (3) |
2 结合方差稳定变换和PGPD的新去噪算法FPGPD2.1 经典PGPD算法原理基于块的图像去噪算法因其具有良好的去噪性能,近几年受到越来越多关注。2015年PGPD算法首次被提出,利用图像的非局部自相似性,将图像分成一定数量的局部块,其中任意局部块可提取出多个与此局部块相似的非局部块,它们共同组成新的块组,用于学习明确的NSS模型,利用此模型对含噪图像进行处理。PGPD算法在抑制高斯噪声方面较其它算法性能大幅提升。
PGPD算法包括学习阶段和去噪阶段。在学习阶段提取非局部相似块组,通过高斯混合模型的块组(PG-GMM)学习原始图像的先验NSS。在去噪阶段先进行高斯分量选择,再经加权稀疏编码去除噪声,最后将处理后的块组重建,得到去噪后的图像。
2.2 FPGPD去噪新算法MR图像噪声类型主要为Rician噪声,在信噪比低的部分Rician噪声呈瑞利分布,在信噪比较高的区域Rician噪声呈高斯分布。传统去除高斯噪声优异的PGPD算法对于MR图像中Rician噪声已不再适用。因此本文提出结合方差稳定变化和PGPD的一种新去噪算法,简称FPGPD。
2.2.1 方差稳定变换研究某一噪声的具体分布,需要分析其方差统计模型,一般情况下总是假定以下3点:(1)观测对象呈正态分布;(2)样本之间相互独立;(3)总体方差满足方差齐性,即方差为常数。当非常数的方差出现,可借助方差稳定变换,将异方差数据转变为同方差数据,使问题更容易解决。
方差稳定变换是一种常用的数学变换方法,在2009年由Foi首次提出,并于2011年用于医学图像去噪[6]。其基本原理如下:
假设图像的均值和方差为:
 | (4) |
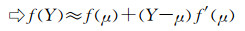 | (5) |
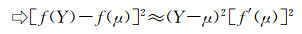 | (6) |
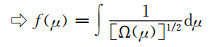 | (7) |
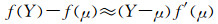 | (8) |
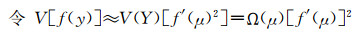 | (9) |
 | (10) |
MR图像中Rician噪声在低信噪比处趋近瑞利分布,在高信噪比处趋近高斯分布,概率密度图如图 1所示。
图 1
Fig. 1
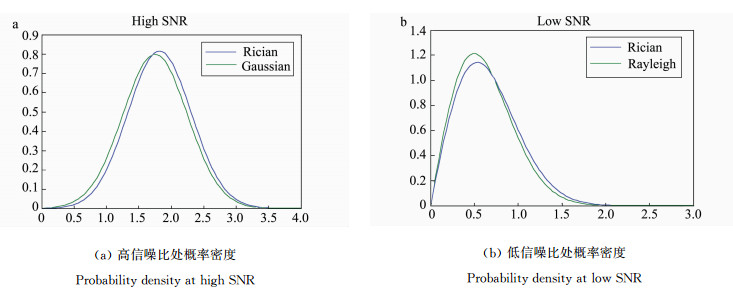 | 图 1 不同信噪比处的概率密度图Fig.1 Probability density map at different SNR |
对于原始MR图像,分别加入9%的Rician噪声和9%的高斯噪声,作为参考对象。加入Rician噪声经过方差稳定变换得到的图像与参考对象做对比。
如图 2所示,(a)为原始MR图片,分别在原始图片上叠加相同噪声含噪的Rician噪声与高斯噪声,加噪后的图像分别为(b)和(c),对叠加有Rician噪声的图像进行方差稳定变换得到图(d), 变换后的图像从视觉角度看与加入高斯噪声的图像相似,与理论推导结果相同。
图 2
Fig. 2
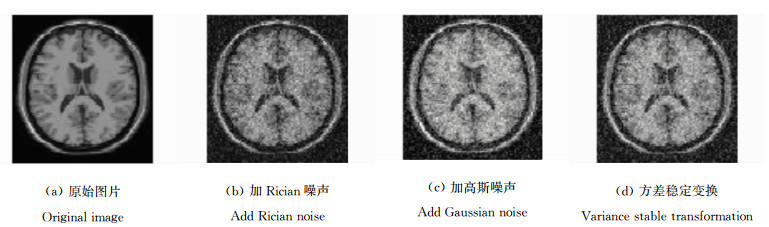 | 图 2 加入不同噪声的对比图Fig.2 Add different noise comparison pictures |
综上所述,首先将含Rician噪声的MR图像进行方差稳定变换,在变换域中噪声与图像之间依赖关系被解除,噪声和图像近似独立,同时噪声由原来的Rician分布近似转化为高斯分布,方差由变量转化为常数1。
2.2.2 去噪处理经方差稳定变换后,Rician分布的噪声近似转换为加性高斯噪声。叠加有Rician噪声的MR图像经过方差稳定变换后作为PGPD算法的输入,对输入图像进行块组分割,提取非局部相似块组,通过高斯混合模型块组(PG-GMM)学习原始图像的先验NSS。完成学习阶段后,进行高斯分量选择和加权稀疏编码抑制噪声,最后经方差稳定逆变换得到无偏去噪图像。
学习阶段,寻找非局部相似快组是关键。第一步选定任一局部块x0,以其为中心构建一大小适宜的局域窗,用欧式距离公式计算窗内块与块的间距,取最小距离的M块作为局域块的相似块,这M个相似块构成一集合,作为新的块分量,将其定义为xm=xm-μ,新的块组均值分量为μ=
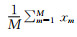
去噪阶段,高斯分量选择直接影响去噪结果,对于每一X, 对其加入噪声V,构成新的含噪块组Y=X+V,从训练好的PG-GMM模型中选择最优高斯分量,假设噪声服从高斯分布,方差为σ2,则第k个块组的协方差为∑k+σ2I, 其中I为单位矩阵。通过后验概率对k个高斯分量进行选择。在PG-GMM中,相似块发生变化,变化的趋势相同均呈高斯分布。对块组Y中的每一个相似块ym稀疏编码,可得
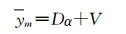 | (11) |
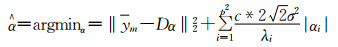 | (12) |
由于去噪处理是在变换域中进行,最后得到的图像值会有偏差,所以最后一步要进行方差稳定逆变换,得到无偏去噪图像。
综上所述,本文提出的FPGPD算法实现流程如下:
第一步:输入原始MR图像;
第二步:对MR图像叠加不同含量的Rician噪声;
第三步:对叠加有噪声的MR图像进行方差稳定变换;
第四步:计算每个局域块与中心块的欧氏距离,构建搜索窗,寻找非局部相似块;
第五步:块组采样、抽取,构建新块组;
第六步:新块组进行高斯分量选择;
第七步:加权稀疏变编码;
第八步:重建得到去噪MR图像;
第九步:方差稳定逆变换,得到无偏MR图像;
第十步:输出无偏去噪MR图像。
3 MR图像去噪实验为验证FPGPD去噪算法的有效性,特做以下实验。实验在内存8 GB、CPU主频2.50 GHz、MATLAB(R2014a)的64位Windows7版个人笔记本电脑上运行。图片来源为BrainWeb及MR图像数据库(http://brainweb.bic.mni.mcgill.ca/cgi/brainweb)。
本文以3张不同大脑切片和3张身体其它部位的MR图像为例进行去噪实验。分别在图像实部、虚部中叠加均值μ=0、均方差σ=1、2、3、4、5、6、7、8、9的Rician噪声来研究MR图像去噪效果,从峰值信噪比(PSNR)、结构相似度(SSIM)和视觉角度这3个方面分析去噪效果。
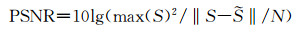 | (13) |
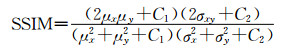 | (14) |
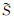
SSIM表示结构相似度,X、Y代表原始图像和去噪图像的像素集,μx是X的平均值,σx2是X的方差,μy是Y的平均值,μy2是Y的方差,σxy是XY的协方差,C1、C2为常数。SSIM作为衡量两幅图像相似度的指标,取值范围为-1~1,分别从亮度、结构和对比度这3方面评价图像的相似性,其值越接近于1,代表去噪后图像与原始图像越相似。
3.1 加噪实验原始MR图像由MR模拟滤波器生成,并非实际采集的人体MR图像,其生成原理与医学MR设备相同,除做特殊处理不含噪声外,其他数据均相同。研究中为尽可能还原实际MR图像,对原始无噪MR图像叠加不同量级的Rician噪声,结果如图 3所示。其中图 3(a)为原始不含噪的MR图像,图 3(b)~(j)分别为叠加不同含量Rician噪声的MR图像,噪声含量设置为1%、2%、3%、4%、5%、6%、7%、8%和9%。实际MR图像所含噪声不会太大,为便于实验分析,对原始MR图像叠加噪声范围取值为1%~9%。
图 3
Fig. 3
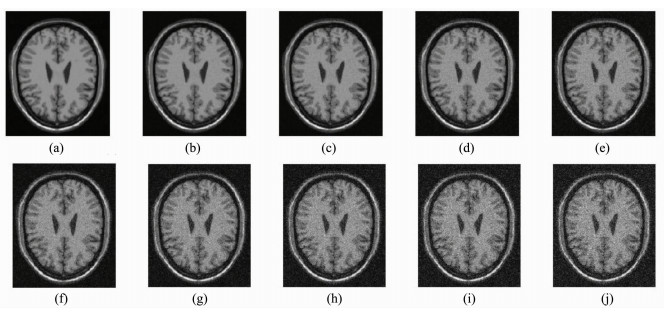 | 图 3 噪声含量不同的MR图像Fig.3 MR images with different noise levels |
3.2 去噪实验3.2.1 同一组织的不同切片选用3组大脑切片MR图像,分别叠加5%的Rician噪声,用原PGPD算法和本文提出的FPGPD算法分别去噪,结果展示如图 4所示。
图 4
Fig. 4
 | 图 4 不同切片值的大脑MR图像处理Fig.4 Brain MR image processing with different slice values |
通过上述3组大脑不同切片值的MR图像加噪去噪实验,从视觉角度分析如下:原PGPD算法去噪后图像过于平滑,比较模糊,视觉感较差。本文提出的FPGPD算法去除噪声干净,图像清晰,细节和轮廓保护好。对比PGPD算法,本文提出的FPGPD算法从视觉角度分析效果更好。
为进一步比较两种算法去噪性能,分别计算PSNR和SSIM两值,定量分析两种去噪算法性能,实验结果如图 5所示。图 5(a)为两种去噪算法对叠加有不同噪声含量的9幅图像去噪后的PSNR值,蓝色表示原PGPD算法去噪后的PSNR值,红色表示FPGPD算法去噪后的PSNR值。在噪声含量低的时候,FPGPD算法PSNR值要远远高于PGPD算法,随着噪声含量的增加,FPGPD算法的优势逐渐减少,当噪声含量大于7%后,两种去噪算法性能相差不大,说明在噪声含量较低时,本文提出的FPGPD算法对图像的保真度要高于原PGPD算法。
图 5
Fig. 5
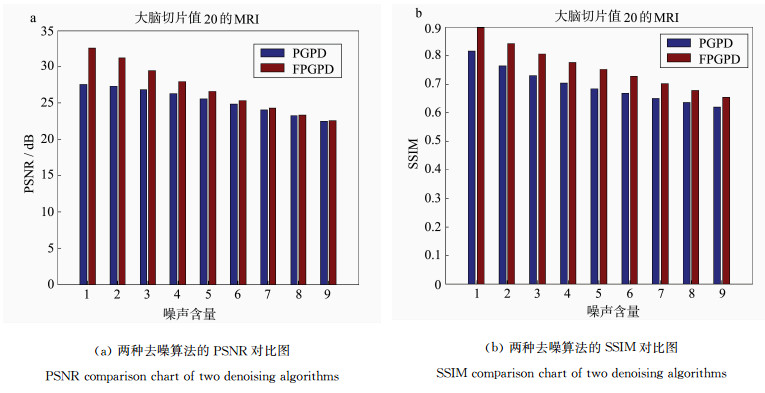 | 图 5 两种去噪算性能比较Fig.5 Comparison of two denoising performances |
图 5(b)为两种去噪算法对叠加有不同噪声含量的9幅图像去噪后的SSIM值,蓝色表示原PGPD算法去噪后的SSIM值,红色表示FPGPD算法去噪后的SSIM值,FPGPD算法去噪后的SSIM值总是比PGPD算法更接近于1,说明从亮度、结构和对比度3个方面衡量两幅图像的相似度时,FPGPD算法优于PGPD算法,去噪后的图像更接近原始图像。
如表 1所示,大脑切片值为50时的MR图像用PGPD算法和FPGPD算法去噪,并对两种算法从PSNR值和SSIM值两方面分析对比:噪声含量较低时,FPGPD算法PSNR值提高较多;随着噪声含量增加,PSNR值提高的百分比逐渐下降,当噪声大于7%时,PSNR值不再提高甚至下降。FPGPD算法的SSIM值始终高于PGPD算法,尽管随着噪声含量的增加,SSIM提高的百分比稍有下降,但依旧高于PGPD算法。
表1
Table 1
| 表 1 大脑切片值为50时用两种算法去噪后的结果对比 Table 1 Comparison of results after denoising by two algorithms when the brain slice value is 50 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由于MR图像所含Rician分布的噪声,信噪比低的部分服从瑞利分布,信噪比高的部分服从高斯分布,方差稳定变换将Rician分布的噪声近似变为加性高斯噪声,对图像信噪比低的部分变换较明显,而对图像信噪比较高的部分变换相对不明显,体现为随着噪声含量增加,FPGPD算法去噪后的PSNR值和SSIM值提高的百分比逐渐降低。经过方差稳定变换后的图像发生偏差,需要乘以相应的系数恢复原始图像,表中所列变换系数为大量实验寻优所得结果。
3.2.2 不同组织的MR图像去噪实验为验证本文提出的FPGPD算法针对不同MR图像的去噪效果,分别选取不同组织的含噪MR图像进行去噪实验,选取的图像为:细节含量丰富的肝脏MR图像、细节含量中等的人体脊椎MR图像和细节含量较少的人体膝盖MR图像。分别叠加5%的Rician噪声,用原PGPD算法和本文提出的FPGPD算法分别去噪,结果展示如图 6所示。
图 6
Fig. 6
 | 图 6 两种去噪算法对不同部位的MR图像处理Fig.6 Two kinds of denoising algorithms for MR image processing in different parts |
根据实验结果,从视觉角度看,图 6(a)为人体肝脏MR图像,人体肝脏结构复杂,内部含有多个腔室和丰富的血管结构。经FPGPD去噪后图像稍有模糊,但依旧能够清晰看到腔室和血管组织结构,细节轮廓清晰,而PGPD去噪后图像模糊,内部结构几乎无法辨认。
图 6(b)为人体脊椎MR图像,人体脊椎含有较为丰富的骨骼结构,但不如肝脏结构细节丰富。经FPGPD去噪后,去除噪声干净,脊椎骨骼结构清晰可见,而PGPD算法去噪后,脊椎骨骼难以识别,图像比较模糊。
图 6(c)为人体膝盖MR图像,人体膝盖结构简单,细节含量少,轮廓清晰。经FPGPD算法去噪后,噪声去除干净,结构清晰,细节丢失少,与原始图像差别较小。PGPD算法去噪后,噪声去除干净,清晰度比FPGPD稍差,但整体效果良好,图像较为清晰。
综上所述,从视觉角度看,本文所提出的FPGPD算法对于MR图像去噪处理效果优于原PGPD算法。
为了更好的验证两种去噪算法性能,分别用PSNR和SSIM两个指标来定量分析,对比实验如图 7所示。
图 7
Fig. 7
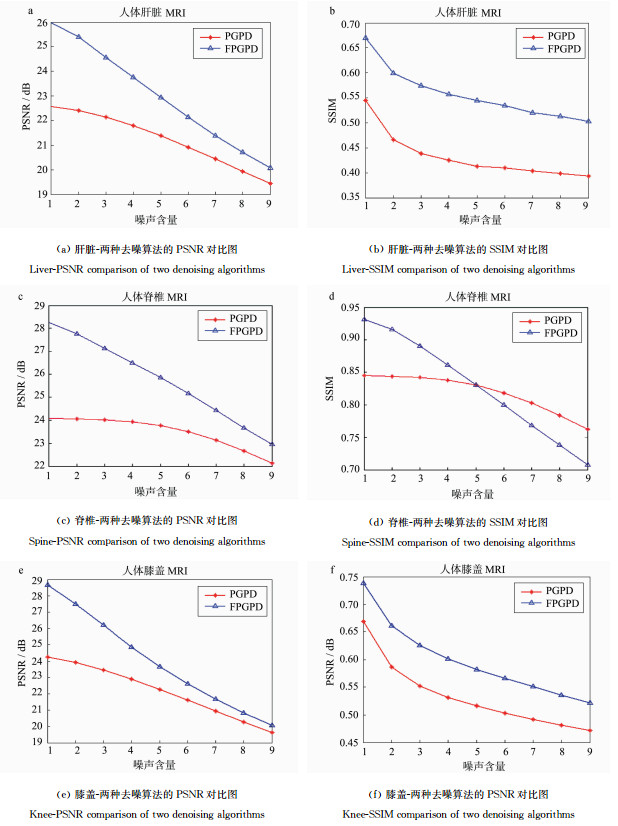 | 图 7 两种去噪算法对不同部位去噪性能分析Fig.7 Denoising performance analysis of different parts by two denoising algorithms |
图 7(a)、(b)为人体肝脏MR图像经过两种去噪算法对叠加有不同噪声含量的9幅图像去噪后的PSNR值和SSIM值的分析比较,红色代表PGPD算法,蓝色代表FPGPD算法。从图(a)中看出,FPGPD算法的PSNR值始终高于PGPD算法。从图(b)中可以发现,FPGPD算法的SSIM值始终高于PGPD算法,且提高值保持0.1以上。
图 7(c)、(d)为人体脊椎MR图像经过两种去噪算法对叠加有不同噪声含量的9幅图像去噪后的PSNR值和SSIM值的分析比较。从图(c)中看出,FPGPD算法的PSNR值始终高于PGPD算法。从图(d)中可以发现,在噪声含量低于5%时,FPGPD算法的SSIM值高于PGPD算法,但是在噪声含量大于5%以后,FPGPD算法的SSIM值低于PGPD算法,原因是有用图像相对于背景区域而言所占比例较小,导致图像整体细节含量减少。
图 7(e)、(f)为人体膝盖MR图像经过两种去噪算法对叠加有不同噪声含量的9幅图像去噪后的PSNR值和SSIM值的分析比较。从图(e)中看出,FPGPD算法的PSNR值始终高于PGPD算法。从图(f)中可以发现,FPGPD算法的SSIM值始终高于PGPD算法,且提高值保持0.1左右。
通过多组实验对比,在噪声含量较低时,FPGPD算法去噪性能明显优于PGPD算法。从视觉角度看,FPGPD算法去噪后的图像细节清晰、图像保真度高、SSIM值高。在噪声含量较高时,两种去噪算法的PSNR值相当,图像细节含量越丰富,FPGPD算法去噪后的SSIM值越高于PGPD算法。在噪声含量较低时,本文所提出的FPGPD算法去噪性能明显高于PGPD算法。
4 结论本文提出一种结合方差稳定变换和PGPD的新算法FPGPD。由于MR图像中所含噪声为Rician分布的随机噪声,Rician噪声在信噪比较低时服从瑞利分布,在信噪比较高时服从高斯分布。首先将含噪MR图像经过方差稳定变换,在变换域中,服从Rician分布的噪声近似转化为高斯噪声,通过PGPD算法进行去噪,重建得到变换域中的去噪图像,最后经过方差稳定逆变换,得到无偏去噪图像。理论分析和实验结果表明,FPGPD算法在噪声含量较低时,能够有效去除MR图像中Rician噪声,更好的保护图像细节和边缘信息。对比PGPD算法,FPGPD算法的PSNR值和SSIM值均明显提高,从视觉角度观察效果更好。此结果证实,在处理医学MR图像中的Rician噪声方面,FPGPD算法优势明显。
参考文献
| [1] | Jacobus F J, Walter H B, Klaas N, Kooi M E. 1HMR spectroscopy of the brain:absolute quantification of metabolites[J]. Radiology, 2006, 240(2): 318–322.DOI:10.1148/radiol.2402050314 |
| [2] | 吴建华, 李迟生, 周卫星. 中值滤波与均值滤波的去噪性能比较[J]. 南昌大学学报(工科版), 1998, 20(1): 33–36+62. Wu J H, Li C S, Zhou W X. Comparison of denoising performance between median filter and mean filter[J]. Journal of Nanchang University (Engineering Edition), 1998, 20(1): 33–36+62. |
| [3] | 石满红, 刘卫. 一种新的平移不变Shearlet变换域图像去噪算法[J]. 红外技术, 2016, 38(1): 33–40. Shi M H, Liu W. A new translation invariant shearlet transform domain image denoising algorithm[J]. Infrared Technology Journal, 2016, 38(1): 33–40. |
| [4] | 陈晓钢.基于统计分析的图像去模糊与图像去噪新方法研究[D].上海: 上海交通大学, 2013. Chen X G. Research on image deblurring and image denoising based on statistical analysis[D]. Shanghai: Shanghai Jiaotong University, 2013.http://cdmd.cnki.com.cn/Article/CDMD-10248-1014077486.htm |
| [5] | 程巧翠.磁共振复数图像小波去噪研究[D].湖南: 湘潭大学, 2008. Cheng Q C. Research on wavelet denoising of magnetic resonance complex image[D].Hunan: Xiangtan University, 2008.http://cdmd.cnki.com.cn/Article/CDMD-10530-2008180557.htm |
| [6] | Foi A. Noise estimation and removal in MR imaging: the variance-stabilization approach[C].IEEE International Symposium on Biomedical Imaging.Chicago: IEEE, 2011.1809-1814.http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5872758 |
| [7] | 孙伟峰.基于非局部信息的信号与图像处理算法及其应用研究[D].济南: 山东大学, 2010. Sun W F. Signal and image processing algorithm based on nonlocal information and application[D]. Jinan: Shandong University, 2010.http://cdmd.cnki.com.cn/Article/CDMD-10422-2010102604.htm |
| [8] | 陈创泉, 房少梅. 基于增强的同质相似性和旋转不变性的MRI去噪[J]. 佛山科学技术学院学报(自然科学版), 2015, 33(4): 14–21. Chen C Q, Fang S M. MRI denoising based on enhanced homogeneity and rotation invariance[J]. Journal of Foshan University of Science and Technology (Natural Science Edition), 2015, 33(4): 14–21.DOI:10.3969/j.issn.1008-0171.2015.04.004 |
| [9] | 黄学优, 张长江. 双树复小波域的MRI图像去噪[J]. 中国图象图形学报, 2016, 21(1): 104–113. Huang X Y, Zhang C J. MR image denoising in double-tree complex wavelet domain[J]. Chinese Journal of Image and Graphics, 2016, 21(1): 104–113. |
| [10] | Luisier F, Blu T, Wolfe P J. A CURE for noisy magnetic resonance imgaes:chi-square unbiased risk estimation[J]. IEEE Transactions on Image Processing, 2012, 21(8): 3454–3465.DOI:10.1109/TIP.2012.2191565 |
| [11] | Yu G. Variance stabilizing transformations of Poisson, binomial and negative binomial distributions[J]. Statistics & Probability Letters, 2009(79): 1621–1629. |
| [12] | 王小平. 医药统计中的方差齐次性变换[J]. 数理医药学杂志, 2007, 20(5): 615–617. Wang X P. Homogeneous transformation of variance in medical statistics[J]. Journal of mathematical medicine, 2007, 20(5): 615–617.DOI:10.3969/j.issn.1004-4337.2007.05.010 |
| [13] | Xu J, Zhang L, Zuo W, Zhang D, Feng X. Patch group based nonlocal self-similarity prior learning for image denoising[C]. IEEE International Conference on Computer Vision, 2015. 244-252.http://ieeexplore.ieee.org/xpl/articleDetails.jsp?arnumber=7410393 |
| [14] | Wang S, Liu Z W, Dong W S, Jiao L C, Tang Q X. Total variation based image deblurring with nonlocal self-similarity constraint[J]. Electronics Letters, 2011, 47(16): 916–918.DOI:10.1049/el.2011.1409 |
| [15] | 程巧翠, 高协平. 平移不变的小波域近邻系数阈值MR图像去噪[J]. 中国图象图形学报, 2009, 14(7): 1284–1290. Cheng Q C, Gao X P. Translation-invariant wavelet domain nearest neighbor coefficient threshold MR image denoising[J]. Chinese Journal of Image and Graphics, 2009, 14(7): 1284–1290. |
| [16] | 周亚同, 陈子一, 马尽文. 从高斯过程到高斯过程混合模型:研究与展望[J]. 信号处理, 2016, 32(8): 960–972. Zhou Y T, Chen Z Y, Ma J C. Mixed model from Gaussian process to Gaussian process:research and prospect[J]. Signal processing, 2016, 32(8): 960–972. |
| [17] | 樊勇.基于高斯噪声的图像去噪算法研究[D].重庆: 西南石油大学, 2014. Fan Y. Research on image denoising algorithm based on Gaussian noise[D]. Chongqing: Southwest Petroleum University, 2014.http://cdmd.cnki.com.cn/Article/CDMD-10615-1014415832.htm |
| [18] | 王芳.基于双树复小波变换的微弱生物医学信号处理及其应用研究[D].重庆: 重庆大学, 2014. Wang F. Weak biomedical signal processing based on double-tree complex wavelet transform and its application[D]. Chongqing: Chongqing University, 2014.http://cdmd.cnki.com.cn/Article/CDMD-10611-1014044322.htm |
