
 , 王谭1
, 王谭11. 北京理工大学 深圳研究院, 广东 深圳 518057;
2. 北京空间机电研究所, 北京 100083
2017-07-13 收稿, 2017-09-20 录用
深圳市科技创新计划资助项目(JCYJ20170412112640428,JCYJ20170224172022809)
*通讯作者: 程灏波, E-mail: chb@bit.edu.cn
摘要: 为了消除数字全息再现像产生的散斑噪声,一种基于边缘检测各向异性扩散方程的去噪算法被提出。在各向异性扩散方程(PM)基础上,通过将边缘检测算子结合梯度算子引导扩散过程,边缘检测算子对噪声具有低敏感度,可以更好地区分边缘信息,达到数字全息再现像去噪目的。通过去噪效果图对比和与中值滤波、均值滤波、小波变换滤波算法峰值信噪比(PNSR)的比较,表明本文提出的算法具有更好的去噪效果,在去除噪声的同时有效保护了图像的细节信息。
关键词: 数字全息散斑去噪各项异性扩散边缘检测
Study on Denoising Technology to Reproduction Image Detail
WU Yumin1, DUAN Haiyan2, WEN Yongfu1, CHENG Haobo1

 , WANG Tan1
, WANG Tan11. Shenzhen Research Institute, Beijing Institute of Technology, Shenzhen 518057, Guangdong, P. R. China;
2. Beijing Institute of Space Mechanics and Electricity, Beijing 100083, P. R. China
*Corresponding author: CHENG Haobo, E-mail: chb@bit.edu.cn
Abstract: In order to eliminate speckle noise in digital holographic reconstructed image, a denoising method based on edge detection anisotropic diffusion equation (PM) is proposed. The diffusion process is guided by the edge detection operator instead of the gradient operator. The edge detection operator is less sensitive to noise, and can better recognize the edge information of reconstructed image. Compared to median filtering, mean filtering, wavelet transform filtering algorithm of peak signal-to-noise ratio (PNSR), the experiments show that the proposed algorithm has better denoising effect, and can effectively protect the details of the image in the process of denoising.
Key words: digital holographyspeckle denoisinganisotropic diffusionedge detection
1 引言近年来,光电成像器件和计算机技术迅猛发展,数字全息显微技术也逐步发展成熟起来,并以其非接触、实时、无损、三维成像等特点广泛应用于医学影像领域[1, 2]。数字全息[3]是光学全息术和数字技术相结合的产物,数字全息术用CCD或CMOS来记录干涉后的全息图,通过计算机模拟衍射过程实现物体的全息再现。
由于激光的高相干性,光源照射到粗糙物体表面后发生散射后形成散斑[4],并且在数字再现时,相干噪声也被重建出来,影响到再现像的质量,降低了图像的分辨率,限制了对微结构测量和识别微小物体识别等方面的应用,因此在数字全息过程中,对再现像的相干噪声的抑制非常必要。
目前, 通用的抑制数字全息散斑噪声的方法有两种:第一种是从硬件上考虑,采用部分相干光或者低相干光源,但是该方法对光路的结构、光源的亮度和光源的稳定性有严格要求。以不同方式记录多幅全息图,通过平均叠加处理实现相干噪声的抑制,这要求极高的光路稳定性和重复性。第二种方法是利用数字图像处理技术,对全息图或者再现像进行处理,抑制或者消除散斑噪声,如采用中值滤波和均值滤波抑制激光散斑[5],采用小波变换抑制散斑噪声[6],采用带孔径函数的维纳滤波法滤除散斑噪声[7]。但是这类方法最大的问题是在滤除噪声的同时损失了部分细节信息,降低了再现像的分辨率。
针对这一问题,本文提出了一种结合边缘检测的各向异性扩散方程的去噪算法。通过将边缘检测算子引入到扩散方程中实现对噪声和边缘更好的区分,达到控制扩散过程的目的,优化了各向异性扩散方程抑制散斑噪声的能力。实验表明,该算法在去除噪声的同时能较好地保留再现像的细节信息。
2 结合边缘检测的各向异性扩散去噪算法2.1 各向异性扩散模型(P-M)P-M模型实质上是改进的热扩散非线性的偏微分方程[8],能够在保持一定程度特征的同时去除噪声,其中图像的梯度算子决定了扩散的速度。作为一种成熟的数字图像, 去噪技术广泛应用于边缘检测、图像增强、图像分割以及目标识别等领域。
P-M模型各向异性扩散方程为:
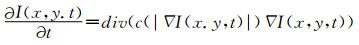 | (1) |
(1) 无法去除大的孤立噪声点。图像在大的噪声点处梯度也会很大,也可能被误认作边缘,此时函数扩散系数减小,无法达到扩散去噪的效果。
(2) 从数学的角度看,P-M模型是病态的,不保证解的唯一性。
(3) 梯度算子对噪声的敏感程度高,抗噪性能不强,对于噪声引起的伪边缘无法区分开来。
为了实现数字全息再现像的去噪,我们需要对P-M模型进行进一步的改进。
2.2 各向异性扩散模型的改进针对梯度算子识别噪声能力不强的问题,我们引入了边缘检测算子。边缘检测算子的本质通过图像与边缘检测算子相卷积,然后以图像一阶导数中的最值点或者二阶导数的零点来检测边界,在这里我们选用的是Canny边缘检测算子[9]。
Canny边缘检测算子核心是通过在图像中找到局部梯度极大值点,然后用双阈值算法检测和连接边缘,具体的步骤如下:(1)用高斯滤波器对输入的图像进行平滑;(2)用一阶偏导有限差分计算平滑后图像的梯度幅值和方向;(3)对梯度幅值采用非极大值抑制,找出图像梯度中的局部极大值点,把非极大值点置零而得到细化的边缘;(4)用双阈值算法检测和连接边缘。Canny边缘检测算子相比其它算子,对噪声的敏感度更低,可以更好地检测出伪边缘,因此,Canny算子可以很好地替代梯度算子作为P-M扩散方程的扩散阈值。改进后的P-M模型扩散方程为:
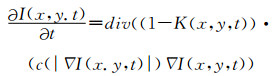 | (2) |
2.3 数字全息散斑噪声去噪数字全息显微中,最初记录的全息图引入的主要噪声是散斑噪声,可以看成一种均匀分布的乘积性噪声,如式(3)所示:
 | (3) |
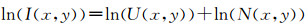 | (4) |
图 1
Fig. 1
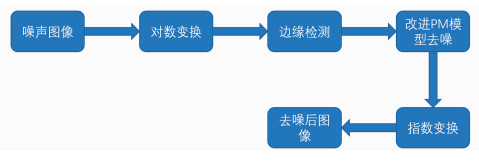 | 图 1 数字全息再现像去噪流程图Fig.1 Noise removal flow chart of digital holography reconstructed image |
3 实验验证利用数字全息显微系统对一个晶圆表面结构进行观测, 晶圆的长宽尺寸为4.76 mm×3.57 mm,高度为1 μm左右,晶圆的整体结构是一个凸起的圆柱体,三维图效果如图 2所示。
图 2
Fig. 2
 | 图 2 晶圆结构三维图Fig.2 Three-dimensional structure of nuclei of crystal |
通过全息显微镜配套软件得到再现像后,将再现像导入MATLAB进行本文算法提出的去噪步骤。为了区分不同去噪算法的效果,我们对不同去噪算法的再现像进行相同区域的截取,作放大观察,截取的区域如图 3(a)中红色矩形框所示,截取部分再现像如图 4所示。
图 3
Fig. 3
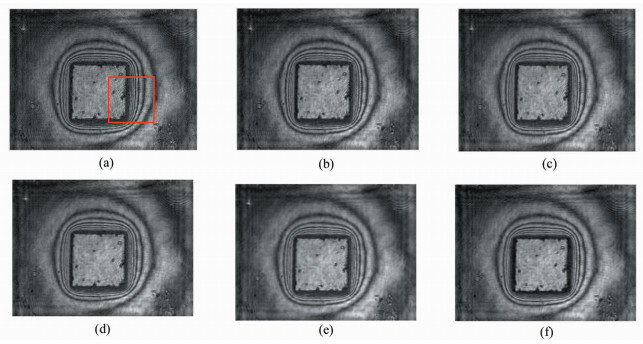 | 图 3 (a) 原全息再现像图;(b)均值滤波再现像图;(c)中值滤波再现像图;(d)小波去噪再现像图;(e) P-M滤波再现像图;(f)本文算法再现像图Fig.3 (a) Hologram reconstruction image; (b) Reconstructed image of mean filter; (c) Reconstruction image of median filter; (d) Reconstruction image of wavelet; (e) Reconstruction image of PM; (f) Reconstruction image of paper algorithm |
图 4
Fig. 4
 | 图 4 (a) 原全息部分再现像图;(b)均值滤波部分再现像图;(c)中值滤波部分再现像图;(d)小波去噪部分再现像图;(e) P-M滤波部分再现像图;(f)本文算法部分再现像图Fig.4 (a) Holographic partial reconstruction image; (b) Mean filter partial reconstruction image; (c) Median filter partial reconstruction image; (d) Wavelet filterpartial reconstruction image; (e) P-M filterpartial reconstruction image; (f) The proposed algorithm partially reconstruction image |
通过对比,可以看出图 4(f)图像边缘附近的二次干涉条纹和周围的散斑噪声得到了明显去除,结合图像的PSNR,证明本文的去噪方法在保护图像边缘的同时,实现了噪声的有效去除,同其它去噪方式相比有着更高的峰值信噪比,保留了图像的细节信息,具有更为清晰的轮廓。
表1
Table 1
| 表 1 滤波结果对比 Table 1 Table of different filtering effects |
参考文献
| [1] | Rappaz B, Marquet P, Cuche E, Emery Y, Depeursinge C, Magistretti P. Measurement of the integral refractive index and dynamic cell morphometry of living cells with digital holographic microscopy[J]. Optics Express, 2005, 13(23): 9361–9373.DOI:10.1364/OPEX.13.009361 |
| [2] | Kemper B, Bally G V. Digital holographic microscopy for live cell applications and technical inspection[J]. Applied Optics, 2008, 47(4): 42. |
| [3] | Goodman J W, Awrence R W. Digital image fortnulation form electronically detected holograms[J]. Applied Physics Letters, 1967, 11(3): 77–79.DOI:10.1063/1.1755043 |
| [4] | Collier R J, Burckhardt C B, Lin L H, Sanford R J. Optical holography[J]. Physics Today, 1972, 25(9): 51–52.DOI:10.1063/1.3070999 |
| [5] | Jorge Garcia-Sucerquia, Jorge Alexis Herrera Ramírez, Daniel Velásquez Prieto. Reduction of speckle noise in digitalholography by using digital image processing[J]. Optik-International Journal for Light and Electron Optics, 2005, 116(1): 44–48.DOI:10.1016/j.ijleo.2004.12.004 |
| [6] | Sharma A, Sheoran G, Jaffery Z A. Improvement of signal-to-noise ratio in digital holography usingwavelettransform[J]. Optics and Lasers in Engineering, 2008, 46(1): 42–47.DOI:10.1016/j.optlaseng.2007.07.004 |
| [7] | Cai X O. Reduction of speckle noise in the reconstructed image of digital holography[J]. Optik-International Journal for Light and Electron Optics, 2010, 121(4): 394–399.DOI:10.1016/j.ijleo.2008.07.026 |
| [8] | Perona P, Malik J. Scale-space and edge detection using anisotropic diffusion[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2002, 12(7): 629–639. |
| [9] | Canny J. A Computational Approach to Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(6): 679. |
