基于主成分分析与支持向量机的渠道闸前冰输移与堆积判别模型1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

梁乃生, 脱友才^,²⁾, 邓云, 贾云霄四川大学水力学与山区河流开发保护国家重点实验室,成都 610065

CLASSIFICATION MODEL OF ICE TRANSPORT AND ACCUMULATION IN FRONT OF CHANNEL FLAT SLUICE BASED ON PCA-SVM¹⁾

Liang Naisheng, Tuo Youcai^,²⁾, Deng Yun, Jia YunxiaoState Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University,Chengdu 610065,China

通讯作者: 2) 脱友才,副研究员,主要研究方向: 寒区水力学. E-mail:tuoyoucai@scu.edu.cn

收稿日期:2020-11-20网络出版日期:2021-03-18

基金资助:

1) 四川大学水力学与山区河流开发保护国家重点实验室开放课题基金.SKHL1604

Received:2020-11-20Online:2021-03-18
作者简介 About authors

摘要
冬季渠道输水过程中浮冰容易在闸前形成堆积体,导致过水断面束窄,严重时影响渠道的输水效率和安全运行. 为判断渠道闸前浮冰的输移状态,开展了明渠水槽平板闸孔自由出流条件下的室内物理模型试验,提出了一种基于主成分分析与支持向量机(principal component analysis and support vectormachine,PCA-SVM)的闸前冰堆积与输移判别模型.通过相关性分析法确定输入特征间存在信息重叠,进而采用主成分分析法对特征向量进行降维,提取贡献率为86%的第一主成分和贡献率为7%的第二主成分作为输入特征,利用网格搜索方法确定多项式、高斯径向基和Sigmoid核函数的最优参数,通过混淆矩阵确定最优核函数为高斯径向基,最优核函数参数C为137,$\gamma$为0.37,建立PCA-SVM模型对试验数据进行监督学习.结果显示,模型在验证集上预测精确率为0.94,准确率为0.97,F1-Score为0.97,上游水流弗汝徳数($Fr_{1}$)和闸前水流弗汝徳数($Fr_{2}$)是渠道闸前冰输移与堆积的主要影响因素,闸孔相对开度($H/e$)和闸门相对淹没水深($H_{1}/H$)是次要影响因素.进一步将已建立的模型应用在倒虹吸口浮冰状态判别试验中,验证开发模型的分类性能.研究成果可为冬季输水渠道的调度管理和安全运行提供重要参考.
关键词： 浮冰;闸孔;弗汝德数;支持向量机;渠道;物理模型试验

Abstract
Floating ice is easy to formed an ice jam in front of flat sluice of channel water delivery during the ice-affected seasons, which will affect the efficiency and safe operation of the channel in severe cases. Here, an experimental for free outflow of flat sluice in the open channel were studied based on indoor physical model test. In order to judge the condition of ice float in front of gates of the water conveyance channel. A discriminant model of ice accumulation and entrainment in front of gate based on Principal Components Analysis-Support Vector Machine(PCA-SVM) algorithm is proposed. The correlation analysis method is used to determine the information correlation between input features, and then the PCA method is used to reduce the dimension of the feature vectors. The aim is to improve the computational performance of the model. The first principal component with a contribution rate of 86% and the second principal component with a contribution rate of 7% were extracted as input features. The optimal parameters of Polynomial kernel function (POL), Gaussian Radial basis kernel function (RBF) and Sigmoid kernel function (SIG) were determined by grid search method. The optimal kernel function was determined as RBF by confusion matrix, and the optimal kernel function parameters C were 137 and $\gamma $ were 0.37. The PCA-SVM model was used for supervised learning of the experimental data. It is found that the $Fr_{1}$ and $Fr_{2}$ are the main influencing factors of ice entrainment or jam in front of gates, and the $H/e$ and $H_{1}/H$ are the secondary influencing factors. Furthermore, the established model was applied to the identify the floating ice state in front of the inverted siphon. The aim is to verify the classification performance of the developed model. The results are of the great value for the dispatching management and safe operation of water delivery channels during ice period.
Keywords：floating ice;flat sluice;Froude number;support vector machine;channel;physical model test

PDF (6575KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
梁乃生, 脱友才, 邓云, 贾云霄. 基于主成分分析与支持向量机的渠道闸前冰输移与堆积判别模型¹⁾. 力学学报[J], 2021, 53(3): 703-713 DOI:10.6052/0459-1879-20-391
Liang Naisheng, Tuo Youcai, Deng Yun, Jia Yunxiao. CLASSIFICATION MODEL OF ICE TRANSPORT AND ACCUMULATION IN FRONT OF CHANNEL FLAT SLUICE BASED ON PCA-SVM¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(3): 703-713 DOI:10.6052/0459-1879-20-391

引言

输水渠道是解决水资源时间和空间分布不均衡而修建的水利设施,闸门是渠道中调控水量的水工建筑物,而在冬季冰凌随水流运动到闸门前段范围时,由于闸前水流条件的变化,浮冰可能会在闸前形成堆积体,导致过水断面束窄,上游水位雍高,影响输水效率?^{[1- 3]}.因此,有效预测冰凌在闸前的输移与堆积状态,对于渠道输水效率和安全运行具有重要意义.

闸前水流受到闸孔出流收缩断面的影响,流线发生弯曲形成湍流漩涡,漩涡强度与闸前水深和出口流速有关?^[4-6].闸前浮冰在这种浮力-水力作用下的堆积和输移状态的判别较为复杂,目前主要通过物理模型实验来开展研究?^[7-8].Ashton等研究了闸门中孔淹没出流条件下浮冰在闸前的输移与堆积情况,采用回归分析方法拟合判别函数对浮冰在闸前的状态进行判别?^[9].Fu等研究了浮冰在倒虹吸口前的输移与堆积状态,采用回归分析方法拟合临界数据点得到判别函数?^[10].Mu和吴艳等采用回归分析的方法分析了浮冰通过桥墩墩柱断面所需的临界水力判别条件?^[11-12],但是由于边界条件的不同,物理模型实验数据回归拟合得到的结果差异较大,且存在一定的主观因素.

由于闸前浮冰输移与堆积是一个非线性发展过程,基于数据驱动算法的机器学习模型在处理非线性边界值问题上具有优势?^[13-14].Sun采用机器学习方法对加拿大的开河时间以及开河时的流量峰值进行预测研究,预测结果显示基于数据驱动的统计模型具有良好的性能?^[15-16].Seidou等?^[17]将人工神经网络模型与热力学湖泊冰模型分别应用在加拿大湖泊和水库冰层厚度研究中,发现在数据质量和数量不充分的情况下,人工神经网络模型具有较高的预测精度.王涛等?^[18]采用改进BP神经网络方法对黄河宁蒙河段的冰情问题进行预测,通过融合影响冰情发展的多个因子来提高预测的精度.支持向量机(support vector machine,SVM)是一种基于小样本统计学习理论的算法,可以解决实际问题中出现的非线性和高维数等问题?^[19-21].刘彦涛?^[22]基于神经网络和支持向量机模型对冰塞水位进行预测,得到支持向量机模型在小样本条件下预测精度高于BP神经网络模型.Kalke等?^[23]采用支持向量机算法对无人机拍摄的河冰图像进行分类研究,从图像中提取并计算了表面冰浓度,将其用于后续模型计算中. 主成分分析(principal componentsanalysis,PCA)方法是从特征元素中提取相互独立的有效信息从而降低输入维度一种统计分析方法?^[24],Ren等?^[25]采用主成分分析的方法剔除了冗余信息,有效分析了影响黄河上游水温的主要因素,Noori等?^[26]采用PCA-SVM方法对伊朗Sofichay河流量进行预测,发现PCA-SVM模型预测准确率高于普通SVM模型.闸前冰输移与堆积状态的判别,具有非线性过程且高维特性,符合采用机器学习模型研究的特征,但目前未见该类方法在闸前冰状态方面的研究.

本文首先通过室内物理模型试验开展了平板闸孔自由出流条件下闸前冰堆积与输移的试验,采用PCA方法对输入特征进行降维处理,提取第一主成分和第二主成分作为模型的输入特征,建立基于主成分分析与支持向量机(principalcomponent analysis and support vectormachine,PCA-SVM)的闸前堆冰判别模型,识别闸前冰输移与堆积的主要影响因素,模型输出结果可直接用于平板闸孔前冰堆积与输移的预测.本文建立的PCA-SVM闸前堆冰判别模型对冬季输水渠道调度管理和安全运行具有重要的参考价值.

1 试验设计与数据来源

1.1 试验装置

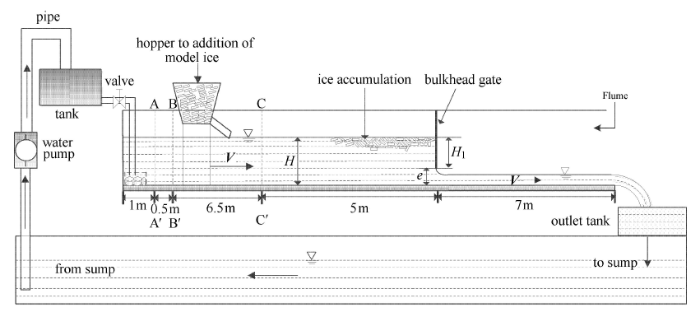
本文的明渠闸前输冰物理模型试验在长20m,宽0.4m,高1m的循环式玻璃水槽内开展. 水槽底部用金属框架固定,在距离进水口约1m(A-A')和1.5m(B-B')两个位置布置两道消能栅,进水口底部采用卵石铺垫,进行水流消能,以保证进水水流的平稳.平板闸门安装在距离进水口约13m位置处,闸门与水槽边壁接触位置采用防水胶处理,保证其密闭性,闸孔出流方式为自由出流,在靠近B-B'位置布设冰块投放箱,以保证冰块自由运动到闸前,下游距离闸门约7m处有冰块收集箱,试验装置示意图如图1所示.试验中模拟冰块(简称冰块)为聚乙烯材质,其比重为0.91.冰力学模型试验要求浮冰运动相似,模型中的浮冰密度弗汝德数和真冰相等,即模型冰的密度和真冰相等,因此模拟冰选择了密度为910,kg/m$^{3}$的聚乙烯材质塑料块. 根据华北地区多年天然河道冰情概况,确定原型冰厚度在0.10$\sim$0.55m?^[27],冰盘的大小约为2m,按照比尺1$:$50,模型冰厚度在0.002$\sim$0.011m,经过前期的预试验,为了更好的模拟浮冰在闸前的堆积与输移过程,试验选择长和宽为0.04m的浮冰,厚度为0.006m冰块,浮冰数量共约2000块.流速测量在C-C'位置,测量设备为南京水利科学研究院生产的旋桨流速仪,流速测量范围为0.01$\sim$3m/s.

图1

新窗口打开|下载原图ZIP|生成PPT
图1实验装置示意图

Fig. 1Schematic diagram of experimental device

1.2 工况与方法

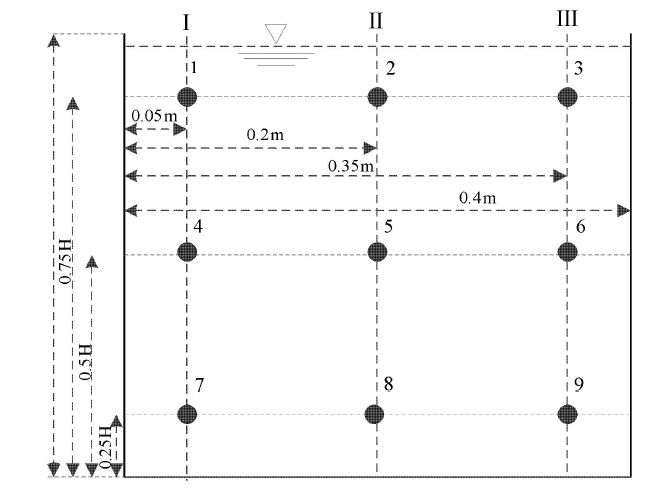
经过预实验发现,来流条件和闸孔开度是影响闸前冰输移与堆积的因素. 因此,实验设置4个闸孔开度下不同的水位变幅条件,试验共设置7组107个工况.每组工况下固定闸孔开度,调整进水阀门,使闸前水位按照工况设计表变化,详细工况设置如表1所示.试验步骤为：(1) 调整闸孔开度至预设值;(2) 调整进水流量阀门按工况水位范围变化,水位变化幅度0.05m/次;(3)待水流平稳以后,将冰块从投放箱推入水槽中,观测记录冰块在闸前的运动状态,测量上游断面平均流速$V$、闸前水位$H$和闸前冰堆积体厚度$t_{i}$.在冰块堆积上游C-C'位置处横断面布置9个测点测量流速.其中I和III测线距离边壁约0.05m,II测线距离边壁约0.2m,表面流速测点(1,2,3)距离水面约为总水深的0.25倍,中心测点(4,5,6)距离水面约为总水深的0.5倍,底部测点(7,8,9)距离水面约为水深的0.75倍,详细测点布置如图2所示,平均流速$V$为这9个测点流速的平均值.

Table 1
表1
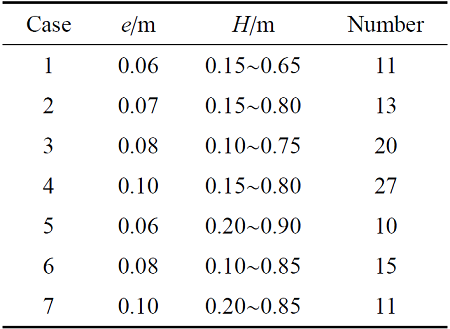
表1工况设计
Table 1Operating condition design

新窗口打开|下载CSV

图2

新窗口打开|下载原图ZIP|生成PPT
图2C-C'位置测点布置图

Fig. 2The measuring point arrangement of section C-C'

2 现象与结果分析

2.1 试验现象

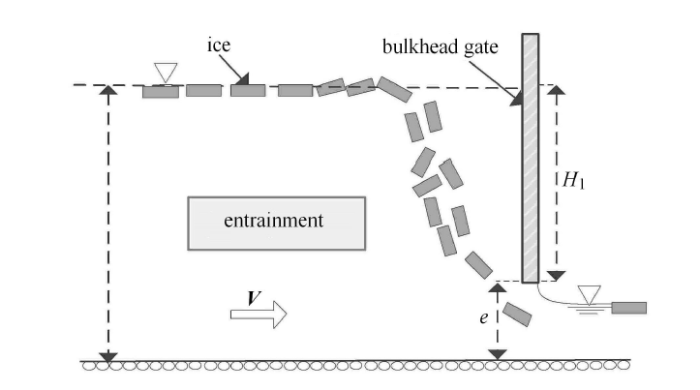
冰块在闸前的运动状态,可总结为通过闸门、在闸前形成平衡稳定堆积体和形成平铺上溯堆积体3种情况. 研究将后两种情况视为浮冰在闸前堆积.当浮冰输移通过闸门时,有两种情况：一是当水深和闸孔开度相当时浮冰运动到闸前直接通过闸门;二是水深较深,浮冰运动到闸前时,受到闸前卷吸漩涡的影响,翻转下潜通过闸门,其示意图如图3所示.当浮冰在闸前形成平衡稳定堆积体时,继续来冰时,冰块下潜输移通过闸门,形成堆积体大小与淹没水深和闸孔开度有关,堆积体的主视图如图4所示.本实验过程中受到冰块数量和水槽高度的限制,该工况下上游来冰多数在闸前堆积,少量冰块通过闸门,我们在研究中定义该状态为浮冰堆积.当浮冰在闸前形成平铺上溯堆积时,发现随着冰流量增加和水流量的增加,浮冰沿渠道向上游堆积发展,没有冰块通过闸门,堆积体示意图如图5所示.

图3

新窗口打开|下载原图ZIP|生成PPT
图3浮冰下潜通过闸门示意图

Fig. 3Ice entrainment through the submerged gate

图4

新窗口打开|下载原图ZIP|生成PPT
图4平衡稳定堆积体示意图

Fig. 4Schematic of balanced and stable accumulation

图5

新窗口打开|下载原图ZIP|生成PPT
图5平铺上溯堆积体示意图

Fig. 5Juxtapositioning of ice at the submerged gate

2.2 结果分析

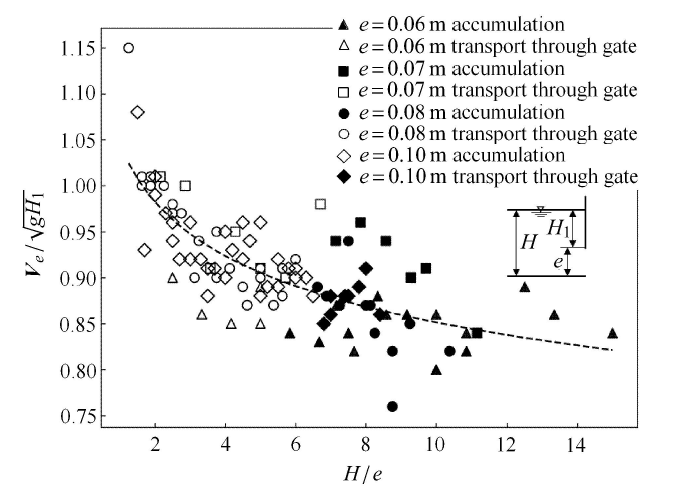
根据试验数据,绘制闸门上游水流弗汝德数($Fr_{1}$)与闸门相对开度($H/e$)的散点图,如图6所示.采用最小二乘法对数据进行拟合,拟合公式如式(1),均方误差(mean square error,MSE)为1.9$\times$10$^{ - 4}$.图6数据显示随着上游水流弗汝德数的减小浮冰逐渐由下潜通过闸门演变为在闸前堆积,图6中圈出的部分为临界区,若采用回归分析的方法寻找该区域的分界点比较困难.于是,采用质量守恒方程求闸门出口水流弗汝德数($Fr_{2}$)并绘制其与闸门相对开度($H/e$)之间的散点图,绘制结果如图7所示,采用最小二乘法拟合数据点得到式(2),MSE为1.5$\times$10$^{ -3}$,图7中圈出了数据的临界区域.由图6和图7中的临界区域可以看出,在平板闸孔自由出流条件下,采用回归分析方法拟合临界数据点存在以下问题：临界工况数量有限,拟合的分类函数适用范围有限.

(1)$Fr_1 =dfrac{V}{\sqrt {gH} } = 0.59\left( {\frac{H}{e}} \right)^{ - 0.81}$

(2)$Fr_2 = \frac{VH}{e\sqrt {gH_1 } } = 1.04\left( {\frac{H}{e}} \right)^{ - 0.089}$

图6

新窗口打开|下载原图ZIP|生成PPT
图6上游水流弗汝德数与闸孔相对开度关系

Fig. 6The relationship between the $Fr_{1}$ versus $H/e$

图7

新窗口打开|下载原图ZIP|生成PPT
图7闸孔出口弗汝德数与闸孔相对开度关系

Fig. 7The relationship between the $Fr_{2}$ versus $H/e$

浮冰运动到闸前时出现下潜行为与闸前水流弗汝德数和卷吸漩涡密切相关?^[28-29],当浮冰在闸前发生堆积时,采用$Fr_{1}$与冰块相对厚度($t_{i}/H$)关系绘制散点图如图8所示.当$Fr_{1}$大于0.13时,即位于图8中的$A$区域时,冰块随水流通过闸门,闸前没有堆积体.当$Fr_{1}$的范围在0.07$\sim$0.13,即位于图8中的$B$和$C$区域时,浮冰在闸前形成堆积体.堆积体形状分为两种：一是$Fr_{1}$的范围在0.096$\sim$0.13时,即图8中的B区域,浮冰在闸前形成平衡稳定堆积体,堆积体形状如图4所示.二是当$Fr_{1}$的范围在0.07$\sim$0.096,即图8中的C区域时,浮冰在闸前形成平铺上溯堆积体,堆积体形状如图5所示.当水流弗汝德数较小时浮冰容易在闸前形成平铺上溯堆积体,随着水流弗汝德数的增大浮冰容易在闸前形成平衡稳定堆积体.

图8

新窗口打开|下载原图ZIP|生成PPT
图8$Fr_{1}$与$t_{i}/H$的变化关系

Fig. 8The relationship between $Fr_{1}$ versus $t_{i}/H$

3 判别模型

由水槽试验结果可知,冰块在闸前呈现输移与堆积的特征,其堆积体形状因水流条件和闸孔开度不同而存在差异.为此,将影响闸前浮冰状态的$Fr_{1}$,$Fr_{2}$,$H/e$,$H_{1}/H$和浮冰在闸前的输移状态作为输入特征,建立基于PCA-SVM的闸前冰输移与堆积判别模型,对冰块在闸前的状态进行分类.

3.1 数据预处理

首先对各特征数据进行相关性分析,设样本特征$x^{(0)}_{ij}$表示原始样本中第$i$个样本的第$j$个特征,$i =1, 2,\cdots, n$, $n$为样本个数;$j =1, 2,\cdots , m$,$m$为特征个数.将收集到的试验数据集定义为矩阵(3)

(3)$\boldsymbol {X}^{(0)}=\left[\boldsymbol{x}_{i j}^{(0)}\right]=\left[\begin{array}{cccc}x_{11}^{(0)}, & x_{12}^{(0)}, & \cdots & x_{1 m}^{(0)} \\x_{21}^{(0)}, & x_{22}^{(0)}, & \cdots & x_{2 m}^{(0)} \\ \vdots & \vdots & \cdots & \vdots \\x_{n 1}^{(0)}, & x_{n 2}^{(0)}, & \cdots & x_{n m}^{(0)}\end{array}\right]$

对各变量进行相关系分析,求变量间的皮尔逊相关系数,计算公式为式(4)

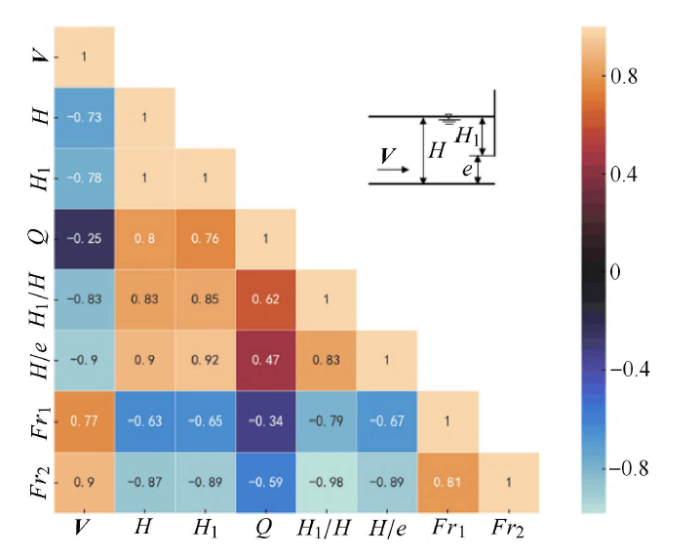
(4)$\rho = \frac{\sum_{i = 1}^n {\left( x^{(0)}_{ij} - \frac{1}{n}\sum_{i = 1}^n x^{(0)}_{ij}\right)\left( {x^{(0)}_{ij + \tau } - \frac{1}{n}\sum_{i = 1}^n {x^{(0)}_{ij + \tau } } } \right)} }{\sqrt{\sum_{i = 1}^n {\left( {x^{(0)}_{ij} - \frac{1}{n}\sum_{i = 1}^n {x^{(0)}_{ij} } } \right)^2} } \sqrt{\sum_{i = 1}^n {\left( {x^{(0)}_{ij + \tau } - \frac{1}{n}\sum_{i = 1}^n {x^{(0)}_{ij + \tau } } }\right)^2} } }$

式中,$x^{(0)}_{ij + \tau }$表示原始样本中第$i$个样本的第$j + \tau $个特征,$\tau <m$. $\rho $的取值范围为$ -1 \sim1 $,其中$\rho =1$表示两个特征完全线性正相关, $\rho=-1$表示两个特征完全线性负相关, $\rho =0$表示两个特征线性无关,但是可能存在其它非线性相关性.采用热力图的形式绘制相关性的计算结果,如图9所示. 由分析结果可知,${\pmb V}$与$H/e$,$H_{1}/H$呈强负相关,与$Fr_{1}$和$Fr_{2}$呈强正相关,来流流量$Q$与上游流速和上游水流$Fr_{1}$呈弱负相关.

图9

新窗口打开|下载原图ZIP|生成PPT
图9各影响因素皮尔逊相关性系数

Fig. 9The coefficient of Pearson correlation of variable

由相关性分析结果可知,输入特征之间存在较强的信息重叠,本研究采用PCA方法对标准化后的样本数据进行处理,提取输入变量的主要信息,以综合考虑各影响因素的基础上提高分类的准确率?^[24].主成分分析的核心思想是将高维相关联的特征降为少数不关联特征,同时尽可能多的反映原来的信息?^[30].为保证数据在输入尺度上具有同样的重要性,先采用标准化的方法对数据进行预处理,使结果映射在$0 \sim1$之间,标准化公式如式(5)所示

(5)$x_{ij} ^{(1)} = \frac{nx^{(0)}_{ij} -\sum_{i = 1}^n {x^{ ( 0 )}_{ij} } }{\sqrt{\frac{1}{n - 1}\sum_{i = 1}^n {\left( {nx^{ ( 0 )}_{ij} - \sum_{i = 1}^n{x^{ ( 0 )}_{ij} } } \right)^2} } }$

式中,$x^{(0)}_{ij}$是原始数据,$x^{(1)}_{ij}$是标准化后的样本数据,$i$是输入数据的样本数,$j$是输入数据的特征维数,$n$是样本数据的个数. 经过归一化处理后的特征矩阵${\pmb X}^{(1)}$如式(6),协方差矩阵${\pmb S}$的计算如式(7)

(6)$\boldsymbol{X}^{(1)}=\left[x_{i j}^{(1)}\right]=\left[\begin{array}{cccc}x_{11}^{(1)}, & x_{12}^{(1)}, & \cdots & x_{1 m}^{(1)} \\x_{21}^{(1)}, & x_{22}^{(1)}, & \cdots & x_{2 m}^{(1)} \\\vdots & \vdots & \cdots & \vdots \\x_{n 1}^{(1)}, & x_{n 2}^{(1)}, & \cdots & x_{n m}^{(1)}\end{array}\right]$

(7)$S=\frac{1}{n-1} X^{(1)} X^{(1) \mathrm{T}}$

式中,${\pmb X}^{(1)T}$表示${\pmb X}^{(1)}$ 的转置,通过求解特征方程得到协方差矩阵${\pmb S}$的$m$个非负特征$\lambda _{k}$ ($k =1, 2, \cdots$, $m$),并使其按照从大到小的顺序排列为$\lambda _{1}>\lambda _{2}>\cdots >\lambda _{m} \geqslant0$,求解其对应的正交单位特征向量$\mu_{k}$,则其主成分计算公式为式(8)

(8)${\pmb Z}_k = \left( {\pmb u}_k \right)^{T}{\pmb X}^{(1)}$

式中,${\pmb Z}_{k}$表示第$k$个主成分($k \leqslant m$),第$k$个主成分${\pmb Z}_{k}$的贡献率$v_{k}$的计算公式为式(9)

(9)$v_k = \frac{\lambda _k }{\sum_{k = 1}^m {\lambda _k } }$

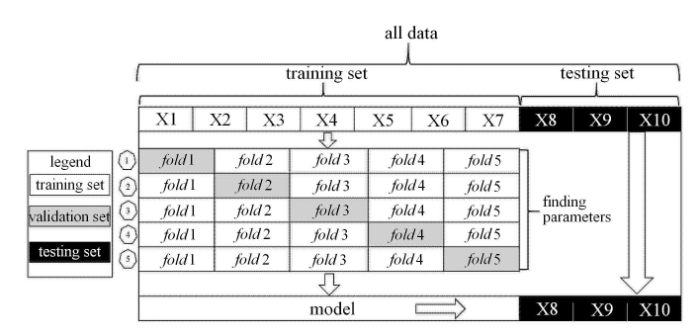
合适的输入特征是模型计算精度的关键?^[31],根据相关性分析结果,选择闸门淹没水深($H_{1}/H$)、闸孔相对开度比($H/e$)、上游水流弗汝德数($Fr_{1}$)和闸孔出口水流弗汝德数($Fr_{2}$)四个特征进行PCA分析,提取第一主成分和第二主成分作为SVM的输入.研究受到水槽尺寸和流量限制,试验得到的冰堆积样本数较少,为了减小因样本划分不同而引入的差异,采用5折交叉验证的方法对模型进行训练. 输入数据划分时,将标准化后样本的70%划分为训练集并记为X1$\sim$X7,剩余30%划分为验证集并记为X8$\sim$X10. 对于训练集部分X1$\sim$X7,将其等分成5份(即fold1$\sim$fold5),依次选择其中一份作为测试集,其余作为训练集,完成5折交叉验证?^[31].模型交叉验证的方案示意图如图10所示.

图10

新窗口打开|下载原图ZIP|生成PPT
图10交叉验证程序的方案

Fig. 10The scheme of the cross-validation procedure

3.2 判别算法

SVM算法是基于结构风险最小化原则,适合于小样本数据集知识挖掘的方法?^[19,32]. 对于样本分类问题,设样本数据集为${\pmb Z}_{i}=[{\pmb Z}_{i1}, {\pmb Z}_{i2}]$,$y_{i}$为${\pmb Z}_{i}$对应的标签,浮冰在闸前堆积标记为“$+1$”,浮冰输移通过闸门标记为“$-1$”. 则样本分类超平面式为式(10),分类决策函数为式(11)

(10)$\omega^{T} \cdot \varphi(Z)+b=0$

(11)$f(\boldsymbol{Z})=\operatorname{sign}\left(\omega^{\mathrm{T}} \varphi(\boldsymbol{Z})+b\right)$

式中,${\pmb \omega} =( \omega _{1},\omega _{2},\cdots ,\omega_{m})$为${\pmb Z}$对应的权值向量,$b$为位移项,决定了超平面与原点之间的距离,${sign}( \ )$表示符号函数,该问题求解的拉格朗日函数可描述为式(12)

(12)$\min L\left( {\omega ,b,\varphi ,\alpha } \right) = \frac{1}{2}\left| {\left|\omega \right|} \right|^2 - \sum_{i = 1}^n {\alpha _i \left( {y_i \left( {\omega ^{T}\varphi \left( Z\right) + b} \right) - 1} \right)}$

其中,$\alpha =( \alpha _{1}, \alpha _{2}, \cdots , \alpha_{p} )$为拉格朗日算子,$\alpha _{i} \geqslant0$. 求解函数式(12)得到$\omega $和$b$,并代入式(11)得式(13)

(13)$\left.\begin{array}{l}f(Z)=\sum_{i=1}^{p} \alpha_{i} y_{i} \varphi\left(\boldsymbol{Z}_{i}\right)^{\mathrm{T}} \varphi(Z)+b \\\text { s.t. }\left\{\begin{array}{l}\alpha_{i} \geqslant 0 ; \quad i=1,2, \cdots, p \\\sum_{i=1}^{p} \alpha_{i} y_{i}=0\end{array}\right.\end{array}\right\}$

为了解决标准化后样本数据在原始空间不可分的问题,将标准化后的样本数据在原始空间作映射变换,则变换后的空间内积函数的值可变成核函数的直接计算值,计算公式如式(14)

(14)$k\left( { {\pmb Z}_{i} , {\pmb Z}_h } \right) = {\pmb \varphi} \left( {{\pmb Z}_i }\right)^{T}{\pmb \varphi} \left( {{\pmb Z}_{h} } \right)$

式中,${\pmb \varphi} ({\pmb Z}_{i}),{\pmb \varphi} ({\pmb Z}_{h} )$为原始空间的映射变换函数,函数${\pmb k} ({\pmb Z}_{i},{\pmb Z}_{h})$为核函数.本研究用到的核函数类型有多项式核(polynomialkernel function,POL)、高斯径向基核(radial basis kernel function,RBF)和Sigmoid核(sigmoidkernel function, SIG),计算公式如式(15),$\sim$式(17)所示

POL:

(15)$k\left( {{\pmb Z}_{i} , {\pmb Z}_h } \right) = (\gamma {\pmb Z}_i^{T}{\pmb Z}_h + 1)^3$

RBF：

(16)$k\left( {{\pmb Z}_{i} , {\pmb Z}_h } \right) = \exp ( - \gamma \cdot\left\| {{\pmb Z}_i - {\pmb Z}_h } \right\|^2)$

SIG：

(17)$k\left( {{\pmb Z}_{i} , {\pmb Z}_h } \right) = \tanh \left( {\gamma {\pmb Z}_i^{T}{\pmb Z}_h + 1} \right)$

其中,${\pmb Z}_{i}$和${\pmb Z}_{h}$表示不同的输入特征,$\gamma$为高斯核带宽参数,tanh是双曲正切函数. 引入松弛变量$\xi _i$和hinge损失函数,可将式(12)写成式(18)

(18)$\begin{array}{l}\min L\left(\omega, b, \varphi, \alpha, \xi_{i}, u\right)=\frac{1}{2}\|\omega\|^{2}+C \sum_{i=1}^{p} \xi_{i}- \\\quad \sum_{i=1, j=1}^{p} \alpha_{i}\left\{y_{i}\left[\omega^{\mathrm{T}} \exp \left(-\gamma \cdot\left\|x_{i}-x_{j}\right\|^{2}\right)+b\right]-1-\xi_{i}\right\}- \\\sum_{i=1}^{p} u_{i} \xi_{i}\end{array}$

其中,$u_i \geqslant 0$为拉格朗日算子.

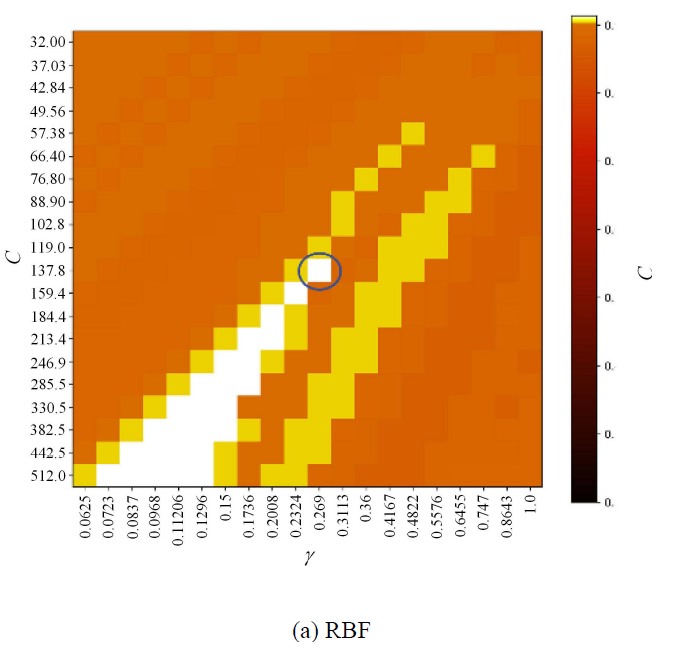
核函数中的参数取值是决定计算准确的关键. 采用网格搜索方法(GridSearchCV,GS)确定最优核参数?^[33-34]. GS算法将搜索数据组成网格空间,采用穷举的方法对每一个网格点中的数据取值. 本研究最优值的搜索结果如图11所示. 其中,RBF参数C搜索范围为32.0$\sim$512.0,$\gamma $搜索范围为0.0625$\sim$1.0,最优参数$C=137.8$,$\gamma =0.27$;SIG的参数C搜索范围为0.01$\sim$10$^{10}$, $\gamma $搜索范围为10$^{ - 9}\sim$10$^{3}$,最佳参数$C=10^{4}$,$\gamma =0.1$;POL的参数$C$搜索范围为1.0$\sim$8190,$\gamma$搜索范围为0.031,25$\sim$32.0,最佳参数$C =1.0$,$\gamma =19.5$.

图11

新窗口打开|下载原图ZIP|生成PPT
图11GS搜索的结果

Fig. 11The parameter of kernel function with GS such

图11

新窗口打开|下载原图ZIP|生成PPT
图11GS搜索的结果(续)

Fig. 11The parameter of kernel function with GS such (continued)

模型分类结果通过混淆矩阵进行评价?^[34]. 闸前冰输移与堆积的混淆矩阵如表2所示,当冰在闸前堆积时,PCA-SVM模型预测正确记为TP,预测错误记为FN. 当冰下潜通过闸门时,模型预测正确记为TN,预测错误记为FP. 引入准确率(Accuracy,Acc)、精确率(Precision,Pre)、召回率(Recall,Rec)和$F$1-Score计算各核函数的得分情况,计算公式如式(19)$\sim$式(22)所示,其中$F$1-Score是精确率和召回率的综合评价指标. 各核函数的得分情况如表3所示. RBF的精确率在测试集上为0.87,在验证集上为0.94,高于SIG和POL核函数;其次,对于准确率和$F$1-Score值的得分情况,RBF核函数也显示出优势. 因此,选择RBF作为SVM模型的核函数来开展试验数据的分类研究

(19)$Acc = \frac{TP + TN}{TP + TN + FP + FN}$

(20)$Pre = \frac{TP}{TP + FP}$

(21)$Rec = \frac{TP}{TP + FN}$

(22)$F1 - score = \frac{2\times Rec\times Pre}{Pre + Rec}$

Table 2
表2
表2闸前冰输移与堆积混淆矩阵
Table 2Confusion matrix of ice transportation and accumulation in front of the gate

新窗口打开|下载CSV

Table 3
表3
表3分类报告
Table 3Classification report

新窗口打开|下载CSV

3.3 模型输出

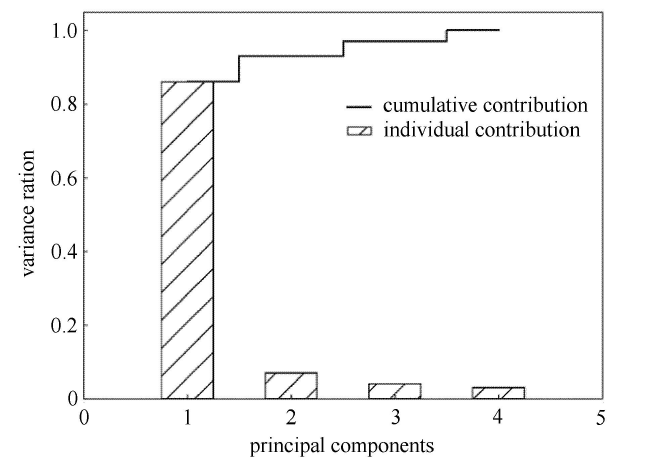
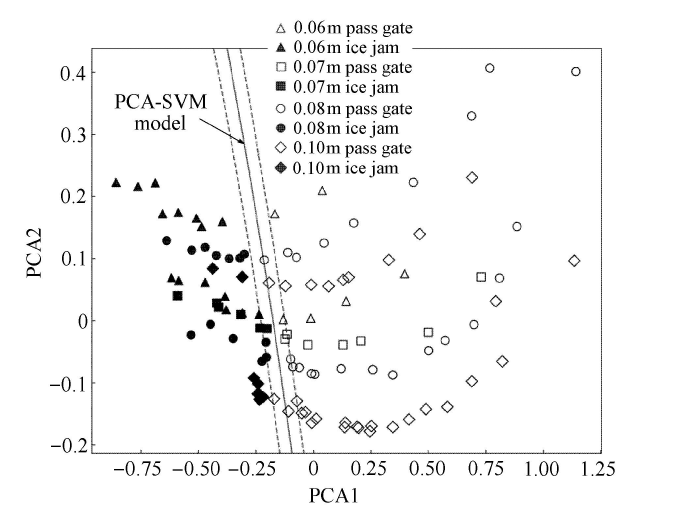
模型输出的各主成分贡献率如图12柱状图所示,其中各主成分的占比为86%,7%,4%和3%,图中阶梯折线图为各主成分的累计贡献率. 提取前两个主成分信息,以解释93%的原数据信息. 用PCA1作为第一轴和PCA2作为第二轴绘制分类结果如图13. 由图13可知当闸孔开度不变时,不同来流条件的数据点沿PCA1轴方向变化,而第一主成分贡献率为86%,因此认为在输入特征中主要影响因素是$Fr_{1}$和$Fr_{2}$. 在相同来流条件下,关于闸孔开度变化的变量沿PCA2轴方向变化,结合第二主成分贡献率为7%,认为$H_{1}/H$和$H/e$是次要影响因素.

图12

新窗口打开|下载原图ZIP|生成PPT
图12主成分分析法提取浮冰闸前状态信息

Fig. 12PCA was used to extract the information of float ice before the gate

图13

新窗口打开|下载原图ZIP|生成PPT
图13PCA-SVM模型在平板闸孔出流试验中的应用

Fig. 13Application of PCA-SVM model in classification of floating ice in front of flat sluice

4 模型应用

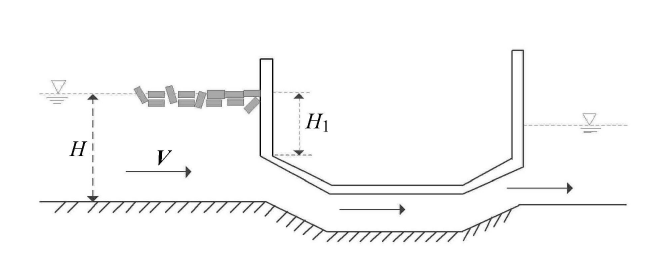
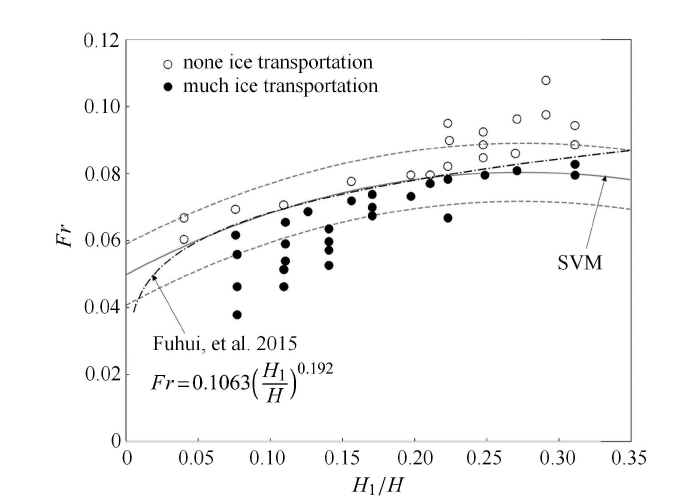
采用Fu等文献[10]中的试验开展模型应用分析,其试验装置如图14所示,出流方式为淹没出流,Fu等采用回归分析的方法拟合了函数曲线,拟合结果如图15中标注所示.应用本文建立的支持向量机模型对Fu等试验数据进行分类,模型输入为闸门相对淹没水深、上游水流弗汝德数和闸前冰状态.核函数选择RBF,核参数$C=100$,$\gamma =0.8$. 将模型输出结果和Fu等的结果进行对比,对比结果如图15所示,分类结果基本与原作者方法一致. SVM分类结果的ACC为97%,REC为93%,F1-Score为97%. 从分类结果看出支持向量机模型在倒虹吸淹没出流试验数据中,能很好的学习到数据规律,并完成堆积与输移状态的分类.

图14

新窗口打开|下载原图ZIP|生成PPT
图14倒虹吸试验装置示意图

Fig. 14Schematic diagram of inverted siphon test device

图15

新窗口打开|下载原图ZIP|生成PPT
图15SVM模型在倒虹吸试验中的应用

Fig. 15Application of SVM in the inverted siphon test

支持向量机模型作为一种机器学习方法从数据本身规律出发,挖掘数据潜在的知识信息,完成数据的分类预测. 本研究开发了基于Python3语言的PCA-SVM分类模型,在应用时通过替换输入数据和核参数取值,可以完成对闸前浮冰堆积与输移状态的分类.

5 结论

针对明渠输水闸前冰的输移与堆积的问题,开展了水槽试验研究,提出了一种闸前冰输移与堆积状态判别的PCA-SVM模型. 模型输入数据包括影响冰堆积的上游水流弗汝德数、闸孔出口弗汝德数、闸门相对开度和闸门相对淹没水深4个因素,采用PCA的方法对输入数据进行降维,提取前两个主成分作为模型输入. 在此基础上,模型对比分析了RBF、SIG和POL核函数在闸前冰输移与堆积问题上分类的性能,通过混淆矩阵的评分得到RBF核函数具有较优的分类性能. 分类结果显示,上游水流弗汝徳数和闸孔出口水流弗汝徳数是影响闸前冰输移与堆积的主要因素,闸门相对淹没水深和相对开度是次要因素. 本研究拓宽了明渠水流中闸前浮冰状态分类预测的研究思路,未来可根据实际渠道中闸门布置形式及更复杂的水力条件对模型进行进一步优化,使其得到更广泛的应用.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

付辉, 杨开林, 郭永鑫, 等. 南水北调典型倒虹吸防冰塞安全运行试验
水科学进展, 2013,24(5):736-740

URL [本文引用: 1]

研究倒虹吸等局部水工建筑物的防冰塞安全运行条件对于南水北调输水工程的冰期安全运行有着重要的意义。通过真冰条件下的倒虹吸冰水动力学试验,模拟了不同水力条件时冰块在倒虹吸进口前的堆积和演变过程,得到了倒虹吸防冰塞安全运行时各相关水力参数间的关系。根据实验结论对南水北调中线工程京石段倒虹吸的冰期输水能力和调控进行了分析,为该输水工程倒虹吸冰期的安全运行提供参考。

( Fu

Hui

, Yang

Kailin

, Guo

Yongxin

, et al. An experimental study on ice jam prevention of typical inverted siphon for South-to-North Water Diversion Project
Advances in Water Science, 2013,24(5):736-740 (in Chinese))

[本文引用: 1]

[2]

Lindenschmidt

K-E

, Das

, Rokaya

, et al. Ice-jam flood risk assessment and mapping
Hydrological Processes, 2016,30(21):3754-3769

DOI URL

[3]

梁娜娜. 输水工程的水力过渡过程及运行控制研究
[硕士论文]. 大连:大连理工大学, 2019

( Liang

Nana

. Research of hydraulic transition process and hydraulic control for water diversion project
[Thesis]. Dalian: Dalian University of Technology, 2019(in Chinese))

[4]

邓淯宸. 水电站叠梁门分层取水进水口漩涡特性及临界淹没水深研究
[硕士论文]. 西安: 西安理工大学, 2019

[本文引用: 1]

( Deng

Yuchen

. Study on the characteristics and the critical submergence of vortex in multi-level stop-log gates intake of hydropower stations. [Thesis]
Xian: Xian University of Technology, 2019 (in Chinese))

[本文引用: 1]

[5]

陈云良. 进水口前立轴旋涡水力特性的研究
[博士论文]. 成都: 四川大学, 2006

( Chen

Yunliang

. Research for hydraulic characteristics of vertical vortex at hydraulic intakes
[PhD Thesis]. Chengdu: Sichuan University, 2006 (in Chinese))

[6]

孙洪亮, 刘亚坤, 刘洁洁, 等. 弧形闸门前旋涡临界淹没水深研究
水动力学研究与进展A辑, 2017,32(3):374-379

[本文引用: 1]

( Sun

HongLiang

, Liu

Yakun

, Liu

Jiejie

, et al. Study on the critical submergence of vortex before radial gate
Chinese Journal of Hydrodynamics, 2017,32(3):374-379(in Chinese))

[本文引用: 1]

[7]

郑永朋, 牟献友, 冀鸿兰, 等. 闸孔出流条件下闸前冰块堆积形态研究
人民黄河, 2020,42(6):27-31, 36

[本文引用: 1]

( Zheng

Yongpeng

, Mou

Xianyou

, Ji

Honglan

, et al. Research on Accumulation Morphology of Ice in Front of Sluice Under the Condition of Outflow from Sluice Opening
Yellow River, 2020,42(6):27-31, 36 (in Chinese))

[本文引用: 1]

[8]

裴少锋, 刘亚坤, 倪汉根. 闸前漩涡水力特性及形成条件的试验研究
水利与建筑工程学报, 2012,10(5):55-60

[本文引用: 1]

( Pei

Shaofeng

, Liu

Yakun

, Ni

Hangen

. Experimental study on hydraulic characteristics and formation conditions of upstream vortex
Journal of Water Resources and Architectural Engineering, 2012,10(5):55-60 (in Chinese))

[本文引用: 1]

[9]

Ashton

. Ice entrainment through sumberged gate
//Martin Jasek. Proceedings the 19th IAHR International Symposium on Ice, Using new technology to understand water-ice interaction, Vancouver, 2008-7-6-11. Vancouver: St.Joseph Communications Press, 2008, 179-188

[本文引用: 1]

[10]

, Yang

, Guo

, et al. Safe operation of inverted siphon during ice period
Journal of Hydrodynamics, 2015,27(2):204-209

[本文引用: 2]

[11]

, Bao

, Chen

. Floating ice transport conditions at the cross-sections between pier columns in open ice-water two-phase flow canals
Water, 2020,12(6):1-19

[本文引用: 1]

[12]

吴艳, 朱明远, 穆祥鹏, 等. 渠道墩柱断面过冰能力研究
水利水电技术, 2017,48(9):126-131

[本文引用: 1]

( Wu

Yan

, Zhu

Mingyuan

, Mu

Xiangpeng

, et al. Study on ice-passing capacity of pier-column section in channel
Water Resources and Hydropower Engineering, 2017,48(9):126-131 (in Chinese))

[本文引用: 1]

[13]

汪运鹏, 杨瑞鑫, 聂少军, 等. 基于深度学习技术的激波风洞智能测力系统研究
力学学报, 2020,52(5):1304-1313

[本文引用: 1]

( Wang

Yunpeng

, Yang

Ruixin

, Nie

Shaojun

, et al. Deep-learning-based intelligent force measurement system using in a shock tunnel
Chinese Journal of Theoretical and Applied Mechanics, 2020,52(5):1304-1313 (in Chinese))

[本文引用: 1]

[14]

谢晨月, 袁泽龙, 王建春, 等. 基于人工神经网络的湍流大涡模拟方法
力学学报, 2021,53(1):1-16

[本文引用: 1]

( Xie

Chenyue

, Yuan

Zelong

, Wang

Jianchun

, et al. Artificial neural network-based subgrid-scale models for large-eddy simulation of turbulence
Chinese Journal of Theoretical and Applied Mechanics, 2021,53(1):1-16 (in Chinese))

[本文引用: 1]

[15]

Sun

. River ice breakup timing prediction through stacking multi-type model trees
Science of the Total Environment, 2018,644:1190-1200

[本文引用: 1]

[16]

Sun

, Trevor

. Combining k-nearest-neighbor models for annual peak breakup flow forecasting
Cold Regions Science and Technology, 2017,143:59-69

[本文引用: 1]

[17]

Seidou

, Ouarda

TBMJ

, Bilodeau

, et al. Modeling ice growth on Canadian lakes using artificial neural networks
Water Resources Research, 2006,42(11):1-15

[本文引用: 1]

[18]

王涛, 杨开林, 郭永鑫. 神经网络理论在黄河宁蒙河段冰情预报中的应用
水利学报, 2005,36(10):1204-1208

[本文引用: 1]

( Wang

Tao

, Yang

Kailin

, Guo

Yongxin

. Application of artificial neural networks to forecasting of river ice condition
Journal of Hydraulic Engineering, 2005,36(10):1204-1208 (in Chinese))

[本文引用: 1]

[19]

Cortes

, Vapnik

. Support-vector networks
Machine Learning, 1995,20(3):273-297

[本文引用: 2]

[20]

周志华. 机器学习
北京: 清华大学出版社, 2017: 121-139

( Zhou

Zhihua

. Machine learning
Beijing: Tsinghua University Press, 2017: 121-139(in Chinese))

[21]

邓乃扬, 田英杰. 支持向量机-理论、算法与拓展
北京:科学出版社, 2009: 81-111

[本文引用: 1]

( Deng

Naiyang

, Tian

Yingjie

. Support Vector Machine-Theory, Algorithm and Extension
Beijing: Science Press, 2009: 81-111(in Chinese))

[本文引用: 1]

[22]

刘彦涛. 基于支持向量机的冰塞水位预测
合肥工业大学学报(自然科学版), 2010,33(10):1550-1552

[本文引用: 1]

( Liu

Yantao

. Forecasting of ice jam stage based on support vector machine
Journal of Hefei University of Technology(Natural Science), 2010,33(10):1550-1552 (in Chinese))

[本文引用: 1]

[23]

Kalke

, Loewen

. Support vector machine learning applied to digital images of river ice conditions
Cold Regions Science and Technology, 2018,155:225-236

[本文引用: 1]

[24]

高惠璇. 应用多元统计分析
北京:北京大学出版社, 2017: 265-280

[本文引用: 2]

( Gao

Huixuan

. Applied multivariate statistical analysis
Beijing: Peking University Press, 2017: 265-280(in Chinese))

[本文引用: 2]

[25]

Ren

, Song

, Wu

, et al. Reservoir effects on the variations of the water temperature in the upper Yellow River, China, using principal component analysis
Journal of Environmental Management, 2020,262(15):110339.1-110339.10

[本文引用: 1]

[26]

Noori

, Karbassi

, Moghaddamnia

, et al. Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction
Journal of Hydrology, 2011,401(3-4):177-189

[本文引用: 1]

[27]

徐国宾, 李大冉, 黄焱, 等. 南水北调中线输水工程若干冰力学问题试验研究
水科学进展, 2010,21(6):808-815

[本文引用: 1]

( Xu

Guobin

, Li

Daran

, Huang

Yan

, et al. Laboratory study of problems in ice mechanics encountered in the middle route of south-to-north water transfer project
Advances in Water Science, 2010,21(6):808-815 (in Chinese))

[本文引用: 1]

[28]

Ashton

. Froude criterion for ice-block stability
Journal or Glaciology, 1974,13(68):307-313

[本文引用: 1]

[29]

王军. 冰盖前缘处冰块稳定性研究
人民黄河, 1997: 9-12, 28

[本文引用: 1]

( Wang

Jun

. Studies on the stability of ice at the front edge of the ice cover
Yellow River, 1997: 9-12, 28 (in Chinese))

[本文引用: 1]

[30]

Galelli

, Humphrey

, Maier

, et al. An evaluation framework for input variable selection algorithms for environmental data-driven models
Environmental Modelling & Software, 2014,62:33-51

[本文引用: 1]

[31]

, Liu H

. Classification method based on the deep structure and least squares support vector machine
Electronics Letters, 2020,56(11):538-541

[本文引用: 2]

[32]

何明辉, 毛嘉成, 范如玉, 等. 基于SVM回归的圆柱壳体抗脉冲强度预估模型
力学学报, 2009,41(3):383-388

[本文引用: 1]

( He

Minghui

, Mao

Jiacheng

, Fan

Ruyu

, et al. The regression prediction model for the strength of cylinder shell against pulse loading based on support vector machine
Chinese Journal of Theoretical and Applied Mechanics, 2009,41(3):383-388 (in Chinese))

[本文引用: 1]

[33]

吴峰, 陈后金, 姚畅, 等. 基于网格搜索的PCA-SVM道路交通标志识别
铁道学报, 2014,36(11):60-64

[本文引用: 1]

( Wu

Feng

, Chen

Houjin

, Yao

Chang

, et al. Traffic sign recognition based on PCA-SVM with grid search
Journal of the China Railway Society, 2014,36(11):60-64 (in Chinese))

[本文引用: 1]

[34]

Wang

, Shu

, Cao

, et al. A ROC curve method for performance evaluation of support vector machine with optimization strategy
// International Forum on Computer Science-Technology and Applications, Chongqing, 2009-12-25-27, Chongqing, IEEE, 2009: 117-1

[本文引用: 2]