,*,??,2), 赵海斌,*,**,3)STUDY ON EVOLUTIONARY ALGORITHMS FOR INITIAL ORBIT DETERMINATION OF NEAR-EARTH ASTEROIDS WITH TOO-SHORT-ARC1)
Li Xinran,*,??,2), Zhao Haibin,*,**,3)通讯作者: 2) 李鑫冉, 助理研究员, 主要研究方向: 小行星轨道. E-mail:lixr@pmo.ac.cn;赵海斌, 研究员, 主要研究方向: 太阳系小天体观测和研究, E-mail:meteorzh@pmo.ac.cn
收稿日期:2020-03-12网络出版日期:2021-03-18
| 基金资助: |
Received:2020-03-12Online:2021-03-18
作者简介 About authors
摘要
近地小行星的巡天项目不断涌现, 得到了海量的观测数据.而巡天观测方式使获得的数据弧段过短, 传统方法在定轨和识别上存在极大困难,加之短弧定轨问题本身的病态性,如何有效利用这些短弧数据对于发现、监测和评估小行星的威胁具有重要意义.在进化算法下构建极短弧定轨的计算框架, 选用三变量的$(a,e,M)$优选法,保持维数较低的同时, 使优化结果不再依赖观测量.采用参数较少、操作简便的差分进化算法,利用不同偏心率小行星的轨道模拟数据进行试验,对获得的最优解及其分布聚集区域进行分析, 大偏心率轨道由于其本身的复杂性,会对算法搜索的灵敏度产生影响, 需缩小搜索空间以提高搜索能力.结果表明算法在小偏心率问题中表现较好,可以得到有效结果为后续工作提供参考信息, 大偏心率问题在传统方法失效的情况下,虽然最优解在整体分布中并不明显, 但分布仍包含真实解,可结合分布密度和适值大小进行分析. 未来需要对大偏心率问题作进一步研究,考虑其观测位置和观测时刻对算法产生的影响, 分类计算.
关键词：
Abstract
Surveying projects of near-earth asteroids continue to emerge, and obtain massive observation data. However, this pattern makes the obtained arc too short, and the traditional methods have great difficulty in orbit determination and identification with ill-posed problem in itself when the arc is short. Then how to effectively use these short arc is of great significance for discovering, monitoring and evaluating the threat of asteroids. Under the evolutionary algorithms, a calculation framework for too-short-arc is constructed with three-variable $(a,e,M)$ optimization, which keeps the dimensionality low while makes the optimization results no longer rely on observational measurements. The differential evolution algorithm with fewer parameters and simple operation is used to conduct experiments using orbital simulation data of asteroids with different eccentricity, then the optimal solutions and their aggregation regions are analyzed. The large eccentricity orbits will have an impact on the sensitivity of the algorithm search due to its complexity, it is need to reduce the search space to improve the search ability. The results show that the algorithm performs well in small eccentricity problem, and can obtain valid results to provide information for subsequent work. And for large eccentricity problem, while the traditional method fails, the distribution of the algorithm still contains the real solution. For the phenomenon that the optimal solution is not obvious in the global distribution, it can be analyzed by combining the distribution density and fitness value. Further research on the issue of large eccentricity is needed in the future, the influence of different observation positions and observation time on the algorithm should be considered, and calculate by classification.
Keywords：
PDF (672KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
李鑫冉, 赵海斌. 近地小行星极短弧定轨的进化算法研究1). 力学学报[J], 2021, 53(3): 902-911 DOI:10.6052/0459-1879-20-084
Li Xinran, Zhao Haibin.
引言
近地小行星是太阳系内一类特殊的天体, 部分近地小行星轨道可能与地球相交, 对地球安全和人类生存环境构成潜在威胁,如6500万年的全球物种大灭绝[1]、2013年俄罗斯的车里雅宾斯克陨石坠落事件[2-3]、发现于2004年6月著名的危险小行星(99942) Apophis[4]. 因此, 发现、监测近地小行星并计算其与地球的碰撞概率、开展危险程度的评估等相关研究是十分重要的,而其中能利用较少数据尽早确定近地小行星的轨道参数尤为关键,小行星参数的精确度对碰撞模型和危害评估的结果有很大影响[5],准确的轨道参数可以为后续的预警工作提供可靠的输入,而这就涉及到小行星的定轨问题.NASA 在 2005 年提出对至少90%的直径超过 140 m 的近地天体进行编目和特性获取[6],Pan-STARRS[7]、Catalina[8]、NEOWISE[9]及LSST[10]、NEOCam[11]等大量的近地小行星大视场巡天项目的开展使得巡天能力不断增强, 得到了大量的观测数据. 但同时, 新的观测方式也使得无法对巡天中探测到的每一个目标进行后续的跟踪观测,因此获得的弧长都很短, 通常只有一个晚上的拍摄[12]. 为了提高巡天效率,未来采集的数据将会更为稀疏, 并且轨道参数分布范围很广, 包含众多大偏心率轨道,这些短而稀疏的数据给轨道确定以及识别带来了很大困难. 对于这些过短的观测弧段尤其是大偏心率极短弧段, 利用传统的 Laplace 和 Gauss方法无法进行定轨, 加之短弧定轨本身具有的病态性[12-16],使得定轨难度大幅度增加. 由此, 如何有效利用这些数据对小行星进行极短弧定轨,对巡天项目的充分利用及小行星的探测研究都有着重要意义. 近年来针对这类问题,极短弧定轨的概念被明确提出并成为研究热点.极短弧的具体弧长目前尚无严格的定义,通常无法用经典方法得到合理定轨结果的观测弧段即称为极短弧,以区别于传统意义上的短弧定轨[12-13,17-18].
除经典计算方法外, 优选法也可被利用来解决定轨问题,优选法克服了经典方法中迭代不收敛的现象, 但更适合于解决一维的优选问题.对于多维情况, 计算过程过于复杂. 此外, 方法对于初值的要求较高,而初值选取本身就是一个初轨计算问题, 对于极短弧轨道计算问题也不适用.
Ansalone 和Curti[18]针对极短弧定轨问题下天基的模拟资料,应用遗传算法(genetic algorithm, GA), 将观测首末时刻的斜距作为优选变量,使定轨问题转换为一个优化问题, 但采用的参数与通常选法相差较多.王志胜等[19]传算法运用到短弧定轨的问题上来, 研究基于测角资料的卫星短弧定轨. 刘磊等[20]将遗传算法应用于天基的短弧定轨问题, 采用双$\rho$迭代模型,对稀疏数据进行定轨. 李鑫冉和王歆[21-22]对参数调整后将遗传算法应用到了极短弧定轨问题中,在地基的空间目标定轨问题中得到了较好的应用.进化算法在优选问题中可以将生物进化中优胜劣汰的现象应用到对最优解的搜寻中,在探索过程中通过积累经验, 启发式地寻找最终解. 算法已有较为成熟的理论基础,在多个领域都有研究和应用[23-24]. 算法对先验信息的依赖性较小,受数据中的噪声影响也较小, 采用进化算法研究定轨问题已成为新的趋势.除遗传算法外, 进化算法中还包含多种不同进化机制的算法, 算法各有特点和优势,粒子群算法(particle swarm optimization, PSO)、差分进化算法(differentialevolution, DE), 及基于统计学思想的分布估计法(estimation of distributionalgorithm, EDA)等已被应用于解决空间目标的短弧定轨问题,并在近圆轨道下有较好表现.
本文将进化算法引入小行星的极短弧定轨问题, 构建计算框架,以差分进化算法为代表采用模拟资料进行计算验证,并比较算法在不同偏心率下短弧定轨问题中的表现, 探讨大偏心率下算法的特征.
1 进化算法
20 世纪 60 年代进化算法基于模拟自然进化的方法首次被提出, 70 年代出现了相关的理论研究, 直至 21 世纪基本成熟[25].这其中最具代表性的就是GA算法, 算法通过模拟自然进化中优胜劣汰的过程搜索最优解,基于适应度来选择父代进行杂交, GA 算法产生的子代有概率发生变异,从而在进化的同时寻找新的可能性. 从 20 世纪 70 年代 被 Holland 和 De Jong提出以来被广泛应用, 收敛性和全局搜索能力已得到证明[25].
PSO算法于 1995 年被 Kennedy 和 Eberhart[26] 提出,源于对鸟类捕食行为的研究, 即鸟类找到食物最简单有效的方法就是搜寻当前距离食物最近的鸟的附近区域.与GA算法不同, 它基于群体智能而不是遗传操作, 利用群体中个体对信息的分享,使整个群体的运动在问题求解空间中产生从无序到有序的演化, 最终获得最优解.
DE方法在 1996 年由 Storn 和 Price[27]提出,是目前最有效的随机参数优选算法之一, 它模拟生物进化,将初始种群中两个个体的向量差作为变异方向, 叠加到第三个个体上,以此产生新个体, 反复迭代使得适应环境的个体被保留下来.不同于遗传算法原本采用二进制编码适用于离散问题的求解,它适用于求解连续变量的优化问题. 算法构造思想借鉴了GA算法和PSO算法,算法保留了GA算法的进化过程,同时以类似于PSO算法中的更新方法替代GA算法中的遗传操作, 因此参数和算子较少,计算复杂性降低.
进化算法的进化机制多种多样, 但通常的流程是相同的.一般将需要被优选的变量称为个体,通过优选方法随机生成一定数量的个体组成初始种群. 种群内个体数目称为种群数,种群数越大搜索能力也越强, 但计算效率随之降低. 适值函数用于评估个体优劣,即优选法中的目标函数, 对于最小化问题, 个体适值越小则越优秀.通过进化在满足预定条件时终止即得到最优解. 具体流程如图1.
图1
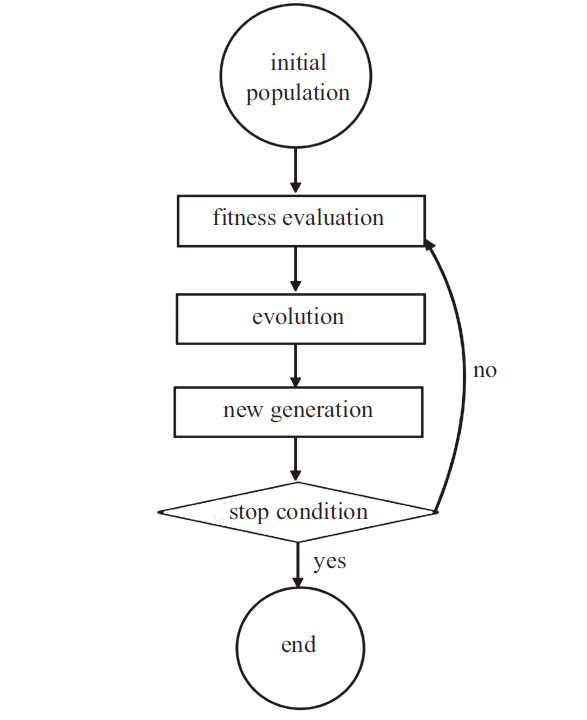新窗口打开|下载原图ZIP|生成PPT图1进化算法流程图
Fig. 1The flowchart of Evolutionary Algorithm
2 初轨计算的差分进化算法
DE 算法的主要步骤与GA算法类似, 主要包括变异(mutation)、交叉(crossover)、选择(selection)三种操作,但次序不同. 算法随机生成初始种群${X}=\left\{ {x_{1} ,x_{2} ,...,x_{NP} } \right\}$, 其中$NP$为种群数, $x_{i} =\left\{ {x_{i1} ,x_{i2} ,...,x_{iD} } \right\}$为$D$维向量, $D$为优选变量的维数. DE 算法先进行变异操作, 对每个个体$x_{i} $变异得到个体$V_{i} $,变异方式较GA算法大为简化, 常见的变异方式有以下三种(1) DE/rand/1
$\begin{eqnarray*} V_{i} =x_{r0} +S(x_{r1} -x_{r2} ) \end{eqnarray*}$
(2) DE/best/1
$\begin{eqnarray*} V_{i} =x_{best} +S(x_{r1} -x_{r2} ) \end{eqnarray*}$
(3) DE/target-to-best/1
$\begin{eqnarray*} V_{i} =x_{i} +S(x_{best} -x_{i} )+S(x_{r1} -x_{r2} ) \end{eqnarray*}$
其中$r$为互不相同的均匀分布的随机整数, $r_{i} \in [1,NP]$且$r_{i} \ne i$;$S$为缩放因子, 一般在区间[0, 1]中取值, 但多数文献建议取较大的值,综合文献[27,28,29,30], 范围在$[0.4,1]$比较合适, $ S $取值决定了算法的全局搜索能力,越大的取值全局搜索能力越强; $x_{best} $为由适值函数所确定的当代最优的个体,DE/*/*是 DE 算法变异的表达方式, 两个*依次表示变异基和差分数量.经变异所得的种群$V=\left\{ {V_{1} ,V_{2} ,...,V_{NP} } \right\}$和原种群$X$交叉操作, 得到新种群$U$. 具体如下
$\begin{eqnarray*} U_{ij} =\left\{ {\begin{array}{ll} V_{ij} , & \mbox{, } r<CR\ {or}\ j=rand \\ x_{ij} , & \mbox{, } {others} \\ \end{array}} \right. \end{eqnarray*}$
其中$r$为[0, 1]区间均匀分布的随机数, $rand$ 为$[1,D]$上均匀分布的随机整数,$CR$为交叉概率. 此操作使得$U_{i} $以一定概率接受变异个体的分量,但确保至少有一个分量来自变异个体, $CR$决定了种群的多样性,文献中建议$CR$取0.1或0.9[27-30]作为初始尝试值. 最后进行选择操作,DE算法采用了贪婪操作, 如果新个体优于初始个体, 则取而代之,否则初始个体保留下来, 进入下一次的进化
$\begin{eqnarray*} x_{i} (k+1)=\left\{ {\begin{array}{ll} U_{i}, &\mbox{, } F\left( {U_{i} } \right)<F\left( {x_{i} } \right) \\ x_{i} (k), & \mbox{, } {others} \\ \end{array}} \right. \end{eqnarray*}$
这里 $k $表示进化代数, 表示$x_{i} (k)$进化到第 $k$ 代的个体, 函数$F\left( \cdot \right)$表示求解个体的适值. 从选择方式可看出最优个体一定会进入下一代,每一代种群不会劣于前一代.
通过上述三个操作完成了一次种群的进化, 并通过不断迭代求解出最优解.算法常用操作中的选择和交叉操作都只有一种方式, 而变异操作选择也比较少,且基本形式是相同的.
3 $(a,e,M)$优选法
3.1 变量选择
对于优化问题, 优化变量过高会带来求解困难的问题,即使如今计算能力已有了大幅度的提升. 因此本文采用了3个Kepler根数,即历元时刻$t_{0} $的$(a,e,M_{0} )$作为优化变量, 与Ansalone 和Curti[18]采用首尾观测时刻的斜距作为优化变量的方法不同, 在只增加一维的情况下, 使得优化结果不再需要依赖观测量就可以得到完整的解, 便于资料处理.3.2 初始种群生成生成和终止条件
根据先验信息定义优选变量的值域, 由于进化算法对初值要求较低,无确切信息时可将范围取的大一些: $a\in [a_{l} ,a_{u} ]$, $e\in [e_{l} ,e_{u}]$, $M_{0} \in [M_{l} ,M_{u} ]$.初始种群中每个个体的每个变量都在取值范围内随机选取,重复$NP$次即得到整个种群$\left\{ {x_{NP} } \right\}$.终止条件选取较为普通的迭代次数达最大进化代数$G$终止或连续$C$代没有进化.3.3 适值函数
令已知一组观测量$\left\{ {t_{i} ,\alpha_{i} ,\delta _{i} ,i=1,2,..., n}\right\}$, $(\alpha_{i} ,\delta _{i} )$代表$t_{i} $时刻的赤经和赤纬,则由历元时刻$t_{0} $的$(a,e,M_{0} )$可得$t_{i} $时刻黄道坐标下的近点角$M_{i}$, $f_{i} $和$E_{i} $, 进一步可得$\left.\begin{array}{l}r_{i}=a\left(1-e \cos E_{i}\right) \\\rho_{i}=\pm \sqrt{r_{i}^{2}-R_{i}^{2}+\left(L_{i} \cdot \boldsymbol{R}_{i}\right)^{2}}-\boldsymbol{L}_{i} \cdot \boldsymbol{R}_{i} \\\boldsymbol{r}_{i}=\rho_{i} \boldsymbol{L}_{i}+\boldsymbol{R}_{i} \\\boldsymbol{R}_{i}=\boldsymbol{R}_{\mathrm{S}}+\boldsymbol{R}_{\mathrm{e}}\end{array}\right\}$
其中 $L_{i} =\left( {\cos \delta _{i} \cos \alpha_{i} ,\cos \delta _{i}\sin \alpha_{i} ,\sin \delta _{i} } \right)^{T}$, $r_{i} $为$t_{i}$时刻目标的日心位置矢量, $r_{i} =\left| {r_{i} } \right|$, $\rho _{i}$为目标斜距, $R_{i} $为测站的日心位置矢量可由测站地心位置矢量$R_{e}$和地日位置矢量$R_{S} $得到.由于地球与小行星的为相对位置分地内和地外两种情况,因此依据$R$和$L$的夹角对观测几何进行分类讨论.
当$R\cdot L<0$时, 即图2所示, 此时观测目标的所在位置有A, B, C三种情况:
图2
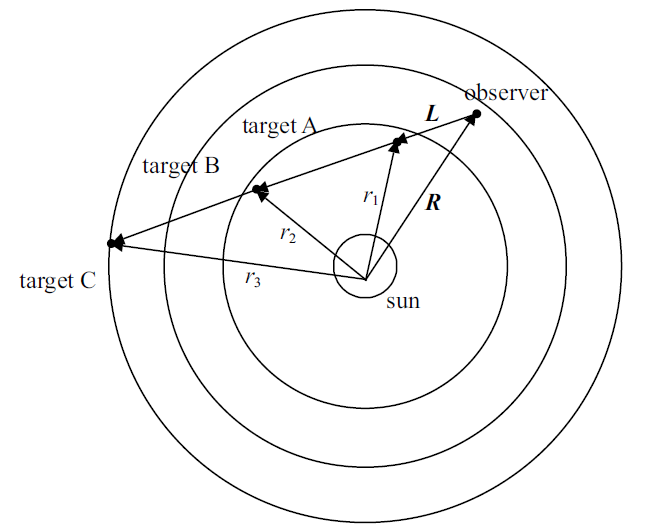新窗口打开|下载原图ZIP|生成PPT图2$R\cdot L<0$时地球与小行星的位置
Fig. 2The locations of Earth and asteroid when $R\cdot L<0$
(1) 当$\left| r \right|<\sqrt {R^{2}-(L\cdot R)^{2}} $时,即观测目标距日心的最大距离小于观测路径距离日心的垂直距离, 这显然是不可能的,因此直接剔除此类情况;
(2) 当$\left| r \right|>\left| R \right|$时, 即小行星的轨道高于地球, 处于位置C;
(3) 其他, 此时目标位置有两种可能A或B, 无法根据已有条件确定其具体位置, 需分别计算. 但这一计算非常容易, 不会造成过多负担.
当$R\cdot L>0$时, 即图3所示, 有2种情况.
图3
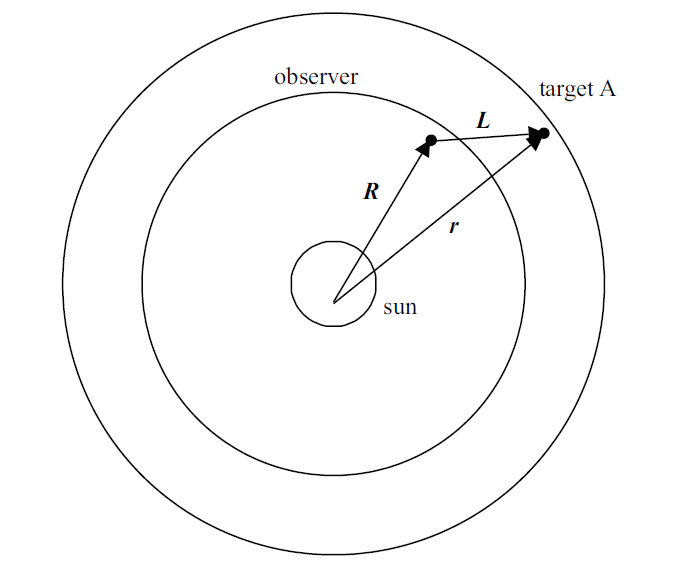新窗口打开|下载原图ZIP|生成PPT图3$R\cdot L>0$时地球与小行星的位置
Fig. 3Locations of Earth and asteroid when $R\cdot L>0$
(1) $\left| r \right|<\left| R \right|$时, 目标轨道低于地球, 但考虑到$R$和$L$的夹角, 此情况不可能发生;
(2) 其他, 此时目标只可能位于A, 即轨道在地球之上.
基于上述分析, 则可得式(1). 当目标位于图2位置B、C, 及图3位置A时, 式中取“$+$”, 其他情况取“-”,则任意一对观测时刻$(t_{k} ,t_{j} )$且$t_{k} >t_{j} $, 可得对应的$(r_{k},r_{j} )$、$(f_{k} ,f_{j} )$, 此时有适值函数
$\begin{eqnarray*} \varDelta_{jk} =f_{k} -f_{j} -\cos^{-1}\left( {\frac{r_{k} \cdot r_{j} }{r_{k} r_{j} }} \right), \\F\left( {x_{i} } \right)=F\left( {(a,e,M)_{i} } \right)=\left( {\frac{2}{N(N-1)}\sum\limits_{j=1}^{N-1} {\sum\limits_{k=j+1}^N {\left( {\Delta _{jk} } \right)^{2}} } } \right)^{\frac{1}{2}} \end{eqnarray*}$
可以看出, 适值越小表示个体越优.
3.4$(i,\varOmega ,\omega )$的求解
通过以上计算已可得$t_{0} $的$(a,e,M_{0} )$, 从而得到每个观测时刻的位置矢量$r_{i} $, 从而可得$(i,\varOmega ,\omega )$, 考虑到计算精度, 可由每对$(r_{i} ,r_{j} )$得到的$(i,\varOmega ,\omega )$取多组结果的中值作为最后结果.4 数值试验
基于DE算法采用MATLAB编写程序, 算法参数选择$NP=300$, $S=1.0$, $CR=0.9$,变异方法选择DE/rand/1,最大迭代次数$G=200$,连续迭代次数$C=30$最优适值的相对变化小于10$^{-12}$则提前结束计算.考虑到近地小行星, 令值域选择范围为$a\in [0.8,4.0],M\in [0,2\pi ]$.选取三组偏心率不同的轨道, 分别计算其轨道根数, 并与传统的Laplace方法进行比较.表1给出了实测数据与模拟数据的定轨结果,模拟数据基于其观测数据的初始时刻、观测时刻和测站数据生成,同时保留了观测的几何构型, 其中POD代表已获得的轨道根数, 作为参考标准.
Table 1
表1
表1小行星实测数据与模拟数据定轨结果
Table 1
 |
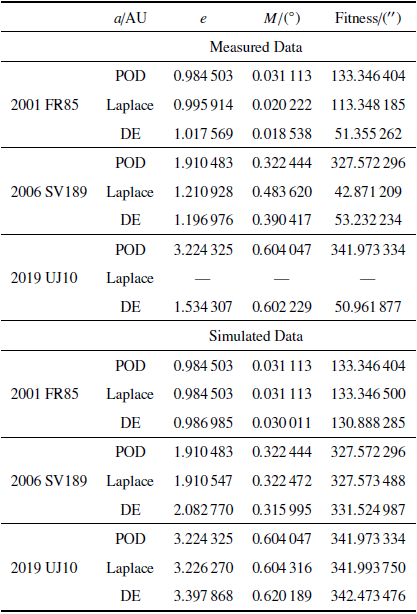新窗口打开|下载CSV
可以看出, 模拟数据下两种方法都可得到初轨结果, Laplace方法更接近准确值.采用实测数据时, 当偏心率较小, DE算法的结果偏差稍大, 当偏心率逐渐增大时,Laplace方法的结果偏离程度增大, 至$e>0.6$时, 已得不到有效结果,而DE算法虽然出现偏差, 依然可以得到有效解为后续工作提供轨道范围的参考信息.另一方面, Laplace方法只能由单一解判断轨道信息, 当计算出现困难时,得到的结果完全无效, 无法指导后续工作. 而进化算法的结果并不仅仅是单一的解,有效范围内的解都是有效的, 可根据多组解的分布判断结果的有效性,并提示其存在范围. 对于大偏心率极短弧轨道, DE算法的适用性更广.
极短弧定轨问题本身存在困难, 当偏心率增大时变得更为复杂,稀疏数据中的误差也可能对计算带来很大影响, 因此, 为了重点关注算法的计算规律,采用模拟数据对问题进行简化, 主要探讨DE算法在极短弧下解的特征.增加不同偏心率的小行星进行比较, 选取MPC中小行星共9组, 已经确定的轨道如表2,偏心率覆盖[0, 0.7]的范围, 每组数据的时间跨度为1-3天, 数据点不足10个.
Table 2
表2
表2小行星轨道根数
Table 2
 |
新窗口打开|下载CSV
图4给出了小行星2001 FR85在一次完整计算过程中轨道半长径$a$和适值的变化.
图4
新窗口打开|下载原图ZIP|生成PPT图4半长径$a$和适值$F$的收敛过程其中$e\in [0.0,0.3]$, $NP=300$. 可以看出DE算法的效率很高, 收敛速度很快.
Fig. 4The convergence process of the semi-major and fitness value
考虑到大偏心率定轨相较近圆轨道更为复杂, 不易求解,试验时偏心率$e$的取值范围不直接扩大到[0, 1], 而是对9组数据进行进行分类计算: 当$e\in [0.0,0.3]$时,值域选择范围为$e\in [0.0,0.3]$; 当$e\in [0.3,0.6]$时, 值域选择范围为$e\in[0.3,0.6]$; 当$e\in [0.6,1)$时, 值域选择范围为$e\in [0.6,0.9]$.为避免随机数对结果的影响, 采用不同随机数对每组数据重复计算300次. 计算发现,与在空间碎片的计算结果不同, 优化结果的适值差异明显,并不像近圆轨道的解那样彼此接近, 因此适值的差异性同样需要关注. 表3 列出了2001FR85, 2006 SV189, 2019 UJ10各自适值最小的前5组优选结果.算法虽然不同于空间碎片近圆轨道下可以迅速准确找到轨道信息的表现,但从适值大小分析, 真实解在适值上仍具有较为明显的优势,且小偏心率的适值优势比大偏心率更加突出. 仅依靠1-3天的观测数据,得到的最优解与MPC中给的轨道根数基本一致.
Table 3
表3
表3各组小行星轨道根数
Table 3
 |
新窗口打开|下载CSV
图5给出了9条轨道的$(a,e)$概率密度分布图, 图中颜色越浅表示聚集度越高.可以看到, 当偏心率较小($e<0.1)$时, 最优解主要集中分布在真实轨道附近,且与适值最小的结果相吻合, DE算法可以得到有效的结果.而当偏心率逐渐增大($e>0.3)$时, 求得解的分布区域发生偏离, 或出现多个分布区域,且分布最集中的区域也并不是真实解的所在区域, 分布不再明显集中于真实轨道附近.2018 XB5和2011 HT有多个分布聚集的区域,真实解包含在其中的某个区域但不是聚集度最有优势的区域. 虽然DE算法搜索到了真解, 但它在获得的多个解中并没有明显优势, 个体分布较少.小偏心率的轨道更为稳定从而更易被搜索得到解, 而当偏心率增大时,进化过程对观测数据的敏感性可能产生变化.
图5
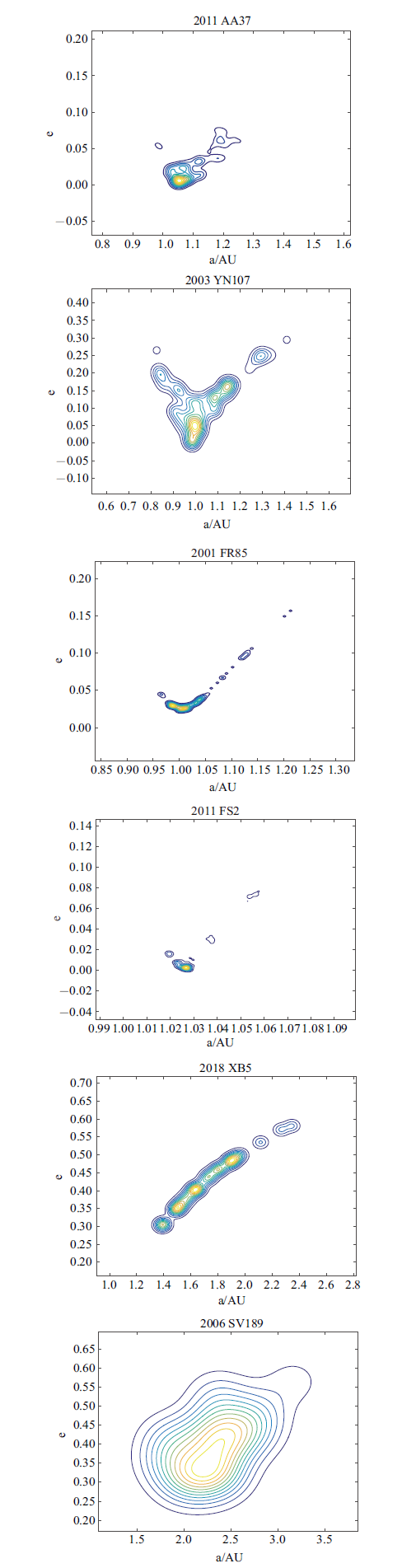新窗口打开|下载原图ZIP|生成PPT图5概率密度分布图
Fig. 5Probability Density
图5
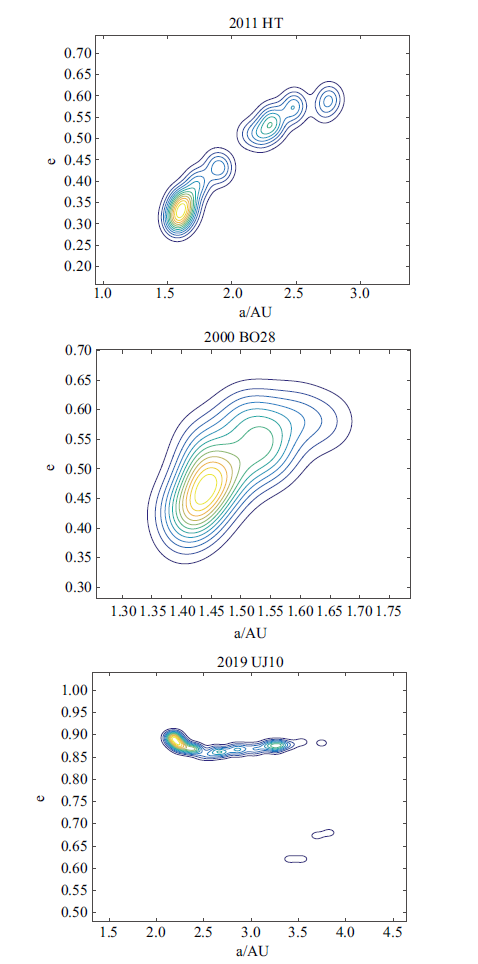新窗口打开|下载原图ZIP|生成PPT图5概率密度分布图(续)
Fig. 5Probability Density (continued)
因此, 对于小偏心率轨道, 算法易于直接寻找到最优解, 而对于大偏心率轨道,需结合分布密度和解的适值进行选择, 偏心率的增大使轨道更为复杂,也导致算法在搜寻最优解的灵敏度上有所下降,在搜寻过程中容易发生最优解搜寻方向的偏离, 虽然可以找到适值最优的解,但数量较少, 适值不具有优势的解会被大量搜索到, 真实解的小范围内的聚集现象,在整体分布上没有明显优势.
2011 FS2仅包含半天的观测数据, 而2019 UJ10偏心率较大,其在概率密度分布图上的聚集更加难以显现. 因此将搜索的解空间进行缩小,提高算法的灵敏度, 再次进行试验. 表4中列出了2011 FS2分别在$e\in[0.0,0.3]$和$e\in [0.1,0.2]$内搜寻的结果, 均为适值最小的5个解.可以看到随着搜索区间的缩小, 搜索效率得到提高, 最优解的存在被凸显出来. 将2019UJ10的搜索空间缩小至$e\in [0.6,0.7]$得到了图6的概率密度分布图. 可知,虽然仍有另一个干扰解的存在, 但算法明显搜索到真实解的存在区域,并且在此范围内呈现聚集状. 因此算法在计算大偏心率及过短弧段的轨道时,搜索空间中真实解是存在的, 只是在大范围搜索中不易搜到, 聚集分布不明显.计算时可以通过将区间进行约束划分, 分段计算最优解,来提高算法的灵敏度及搜索能力, 提升聚集程度, 同时, 结果需结合解的分布聚集区域和适值最优的个体考虑.
Table 4
表4
表4小行星2011 FS2轨道根数
Table 4
 |
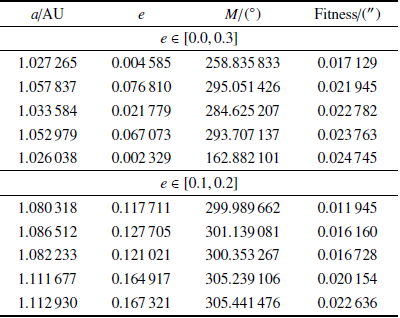新窗口打开|下载CSV
图6
新窗口打开|下载原图ZIP|生成PPT图6$e\in [0.6,0.7]$概率密度分布图
Fig. 6Probability density of $e\in [0.6,0.7]$
不同类型轨道受误差的影响不同,对多组模拟数据加入随机观测误差在DE算法下进行比较. 表5给出了分别加入$0.{1}”$, $0.{2}”$误差的2001FR85, 2006SV189和2019UJ10的定轨结果. 可以看到在$0.{1}”$的误差下,仍可得到有效的定轨结果. 当误差扩大到$0.{2}”$时, 解的分布仍涵盖真实解,可提示轨道信息的参考范围, 但随着偏心率增大, 受误差影响也增大了,大偏心率的轨道定轨结果会受到明显影响.图7给出了约束解空间后加入$0.{2}”$误差的2011 FS2的概率密度分布图,星号表示真实解所在位置, 在加入误差后解的分布仍覆盖真实解.
Table 5
表5
表5加入误差的定轨结果
Table 5
 |
新窗口打开|下载CSV
图7
新窗口打开|下载原图ZIP|生成PPT图7加入$0.{2}”$误差2011 FS2的概率密度分布图
Fig. 7Probability Density of 2011 FS2 with $0.{2}”$ error
5 结论
极短弧定轨问题采用经典方法存在很大困难, 甚至无法得到有效解,包括DE算法在内的进化算法将这一反问题正向处理, 避免了经典方法固有的病态性,并且DE算法参数较少, 操作简便, 易于实现. 进化算法计算框架基本一致,只是进化机制和侧重不同, 对于不同需求的问题改用不同进化算法时操作更为便捷,如EDA方法更注重整体搜索, DE算法更注重局部搜索,换用不同进化算法时计算框架可保持不变.根据进化算法的特点, 将其应用于近地小行星的极短弧定轨进行探索.对于小偏心率轨道,DE算法利用少于3天的少量数据得到的轨道信息与利用多天多站定轨下的信息一致,可为后续工作提供可参考的信息. 对于复杂的大偏心率轨道和弧段更短的轨道,进化算法的表现不如小偏心率轨道下良好, 搜索灵敏度降低, 不易搜索到最优解,仅在局部有向最优解聚集的现象. 因此, 需要缩小搜索空间提高算法灵敏度,并结合分布区域和适值最优进行讨论. 加入误差后, 较小的误差对定轨结果影响较小,随着误差增大, 尽管适值最优解受到干扰, 尤其大偏心率轨道的定轨受影响较大,解的分布仍涵盖真实解所在区域.
小行星轨道较为多样, 大偏心率轨道数量较多,并且实际观测中观测位置不同、与地球的相对位置不同, 也会对算法产生影响,尤其对于极短弧定轨问题, 数据量较少, 观测数据差异和误差的影响更不可忽视.在模拟数据的研究基础上, 未来需对观测位置和时刻做进一步研究,在不同情况下分类计算, 提高算法在大偏心率下的搜索效率,完善进化算法在小行星极短弧定轨方面的应用.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
DOIURLPMID [本文引用: 1]
The Cretaceous-Paleogene boundary approximately 65.5 million years ago marks one of the three largest mass extinctions in the past 500 million years. The extinction event coincided with a large asteroid impact at Chicxulub, Mexico, and occurred within the time of Deccan flood basalt volcanism in India. Here, we synthesize records of the global stratigraphy across this boundary to assess the proposed causes of the mass extinction. Notably, a single ejecta-rich deposit compositionally linked to the Chicxulub impact is globally distributed at the Cretaceous-Paleogene boundary. The temporal match between the ejecta layer and the onset of the extinctions and the agreement of ecological patterns in the fossil record with modeled environmental perturbations (for example, darkness and cooling) lead us to conclude that the Chicxulub impact triggered the mass extinction.
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 3]
[本文引用: 1]
[本文引用: 1]
DOIURL [本文引用: 1]
稀疏测向数据下的天基初轨确定具有重要的应用价值。针对地基Laplace和Gauss方法在天基 稀疏测向初定轨中存在的不收敛和平凡解问题，提出了一种新的模型——双ρ迭代模型 ，研究了优化算法中的变尺度方法和遗传算法作为解算算法，最后进行了仿真。结果表明， 双ρ迭代模型可以较好地解决地基方法在天基测向初定轨应用中的上述问题，利用变尺 度法的双ρ迭代模型具有90％以上的解算成功率，且具有良好的解算速度和收敛性， 而采用改进的遗传算法可以解算其余算例，二者结合使用可以达到较好的初定轨效果。
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
//
[本文引用: 1]
[本文引用: 3]
[本文引用: 1]
[本文引用: 1]
[本文引用: 2]
