带滩槽地形的连续弯道中纵向流速横向分布解析1)

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2022-01-01

刘玉娇, 余明辉^,²⁾, 田浩永武汉大学水资源与水电工程科学国家重点实验室, 武汉 430072

THE LATERAL DISTRIBUTION OF DEPTH-AVERAGED VELOCITY IN CONSECUTIVE BENDS WITH POOL-POINT BAR¹⁾

Liu Yujiao, Yu Minghui^,²⁾, Tian HaoyongState Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China

通讯作者: 2) 余明辉, 教授, 主要研究方向: 水力学及河流动力学. E-mail:mhyu@whu.edu.cn

收稿日期:2020-06-16接受日期:2020-09-29网络出版日期:2021-02-07

基金资助:

1) 国家自然科学基金.11972265
国家重点研发计划资助项目.2016YFC0402604

Received:2020-06-16Accepted:2020-09-29Online:2021-02-07
作者简介 About authors

摘要
本文基于沿水深积分的动量方程,假定二次流项和弯道附加应力项沿横断面呈线性分布,提出了预测弯道垂线平均纵向流速的解析计算方法,进一步提出了河槽区和河滩区垂线平均纵向流速沿断面分布的求解模式,并将其应用于带滩槽地形的反向连续弯道水槽中. 根据实测数据率定计算参数,该模式可计算不同出口水深条件下断面垂线平均纵向流速分布,计算结果与实测数据吻合良好.分析了线性分布假设中参数随水深变化的取值规律和沿横断面分布特点,并对参数进行了敏感性分析,分析表明线性假设中一次项系数分区位置对流速峰值的大小和位置影响较大,常数项根据地形横比降变化进行分区取值,流速计算值对常数项在水平段和斜坡段分区位置较为敏感,并根据参数的敏感度提出了参数沿水槽的均值作为参考值.讨论了动量方程中二次流项和弯道附加应力项沿弯道的横向分布规律,进一步认识线性假设的适用范围,结果表明线性假设在本文试验水槽中适用于弯道沿程.研究成果有助于认识带滩槽地形的连续弯道纵向流速分布特征及其形成机制.
关键词： 连续弯道;纵向流速;滩槽;明渠水流;解析解

Abstract
This paper proposes an analytical approach to modeling the lateral distribution of depth-averaged streamwise velocity for flow in consecutive bends with pool-point bar based on the depth-integrated Navier-Stokes equations. The additional secondary flow and yet fully developed flow are assumed to be a linear function of the lateral distance. Then, the model for calculating the average vertical velocity distribution along the cross section of the pool region and the point bar regions is presented, and it is applied to consecutive bends with pool-point bar. By calibrating the calculated parameters from the measured data, the model can calculate the average longitudinal velocity distribution of vertical cross-section under different outlet water depth. The modeled results agree well with experimental data. The value rules of the parameters have analyzed for different water depth and along the cross-sections. Sensitivity analysis is performed on the parameters which showed that the region division of the coefficient of the first degree term in the linear hypothesis has great influence on the size and position of the peak flow velocity. The region division of the constant term value is according to the traverse gradient. The region edge between the flat bed and the sloping bed of the constant term has a significant influence on the results. According to the sensitivity of parameters, the mean value of parameters along the flume is presented as a reference value. The transverse distribution of the secondary flow term and the additional stress term in the depth-integrated Navier--Stokes equations along the experimental channel is discussed to further understand the applicability of the linear hypothesis. The results show that the linear hypothesis is suitable for the curve path in the flume. The research results are helpful to understand the longitudinal velocity distribution characteristics and the formation mechanism of the consecutive bends with pool-point bar.
Keywords：consecutive bends;streamwise velocity;pool-point bar;open channel flow;analytic solutions

PDF (2146KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
刘玉娇, 余明辉, 田浩永. 带滩槽地形的连续弯道中纵向流速横向分布解析¹⁾. 力学学报[J], 2021, 53(2): 580-588 DOI:10.6052/0459-1879-20-208
Liu Yujiao, Yu Minghui, Tian Haoyong. THE LATERAL DISTRIBUTION OF DEPTH-AVERAGED VELOCITY IN CONSECUTIVE BENDS WITH POOL-POINT BAR¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2021, 53(2): 580-588 DOI:10.6052/0459-1879-20-208

引言

天然河道的演变是水流携带泥沙并与河道边界相互交换相互影响的辩证统一体. 其中, 纵向流速分布规律与河道过流能力^[1]和泥沙输移^[2]的密切相关, 也与崩岸、切滩等突发现象相关. 对于河流流速的分布规律, 研究主要从模型试验^[3-5]、数值模拟^[6-9]和解析解计算^[10-13]进行. 解析解由于效率高, 方法简单, 在实际应用方面被广泛采用^[14]. 在顺直复式河道中, Shiono和Knight^[15]提出了SKM方法, 认为二次流导致的切应力沿横断面为线性分布, 对动量方程沿水深积分, 推导出垂线平均纵向流速(以下简称为$U_{\rm d}$, 下标d表示为垂线平均量)的解析解; Devi等^[16]进一步根据实测数据量化二次流中的参数, 发现参数与定水深和变化的水深之间有不同的关系; 复式河槽漫滩区域常为顺直的, 但主河槽则倾向于弯曲的, 存在弯道环流的影响, Ervine等^[17]考虑了复式河道弯曲主槽中水流的强三维性, 认为二次流项与$U_{\rm d}$的二次方成正比关系, 对SKM方法进行了改进; Knight等^[18]分析了环流结构与二次流项取值正负之间的关系, 认为环流中心左侧和右侧二次流项符号相反; Liu等^[19]和Huai等^[20]则进一步在动量方程中增加了滩地植被影响, 在解析解公式中考虑了植被对流速的影响; Zhong等^[21]考虑了在两岸及水面结冰条件下, 解析解的形式, 并分析了床面阻力、冰盖阻力和二次流等因素的影响; 杨中华和高伟^[22]比较了三种不同的积分假定, 将计算值与实测值比较, 得出最为吻合的计算公式; 许唯临^[11]将二次流项归并入雷诺切应力项, 对复式顺直河道和复式游荡型河道中漫滩流速进行了研究, 复式游荡型河道流速计算其采用了分层计算的方法. 哈岸英等^[23]利用SKM方法研究了冲积河流漫滩水流水力因子随水深的变化特性, 提出了定量划分复式断面滩与槽的判别指标. Rezaei和Knight^[24]探究了SKM方法在非对称复合水槽中的应用. Sharifi和Sterling^[2]利用SKM方法计算床面切应力的横向分布, 并将其与泥沙输移公式进行的对比, 以获得对泥沙输移的预测.

弯曲型河道是常见的天然河道形态, 水流经过弯道时受到离心力的作用, 产生横向压力梯度, 形成弯道横向环流, 横向环流与纵向流速结合形成弯道螺旋流^[25]. 纵向水流在弯道进口处, 主流靠近凸岸侧, 沿着弯道, 主流逐渐向弯道凹岸侧移动, 在出口处, 主流贴近凹岸. Tang和Knight^[26]将 SKM 方法应用于弯道中, 基于弯道水流充分发展的条件下, 认为二次流横向变化率与横向位置为线性关系, 推导出弯道$U_{\rm d}$的解析式. 天然弯曲河流常为多个弯道相连, 床面形态存在着深槽和边滩分布^[27], 本文尝试以SKM方法为基础, 推导出弯道中$U_{\rm d}$横向分布计算公式, 运用实测资料率定计算参数, 将其应用于带滩槽地形的反向连续弯道中$U_{\rm d}$横向分布解析计算研究, 为下一步的弯道纵向流速快速预测奠定基础.

1 带滩槽地形弯道垂线平均纵向流速解析解推导

1.1 理论基础

结合水流连续方程, 曲线坐标系下, 单位体积上的水流纵向动量方程可简化为

(1)$\begin{eqnarray} &&\dfrac{\partial \rho U^{2}}{\partial s}+\dfrac{\partial \rho UV}{\partial r}+\dfrac{\partial \rho UW}{\partial z}+\dfrac{2\rho UV}{r}+\dfrac{\partial \rho \overline {u'v'} }{\partial r}+ \\&&\qquad \dfrac{\partial \rho \overline {u'w'} }{\partial z}+\dfrac{2\rho \overline {u'v'} }{r}=-\dfrac{\partial \overline p }{\partial s}+\rho f_{s} \end{eqnarray}$

式中, $s$, $r$, $z$分别表示水流的切向、径向和垂向三个方向, $U$, $V$, $W$和$u'$, $v'$, $w'$分别为$s$, $r$, $z$方向的时间平均流速分量和脉动流速分量, 上划线表示时间平均值, $p$为压强, $f_s$为$s$方向的单位体积力, $\rho $为水流密度, $g$为重力加速度

(2)$\begin{eqnarray} \label{eq2} &&f_{s} =gS_{0}\end{eqnarray}$

(3)$\begin{eqnarray} -\dfrac{\partial \bar{p}}{\partial s}=-\dfrac{\partial \rho g H}{\partial s}=-\rho g \dfrac{\partial H}{\partial s} \end{eqnarray}$

(4)$\begin{eqnarray} \tau_{rs}=-\rho \overline{u' v'},\ \ \tau_{zs}=-\rho \overline{u'w'} \end{eqnarray}$

式中, $S_{0}$为床面纵比降, $S_{0} =-\partial z_{\rm b} /\partial s$, $z_{\rm b}$为床面高程, $H$为水深, $\tau_{rs}$和$\tau_{zs} $分别表示垂直于$r$和$z$平面上的切向雷诺应力.

将式(2)$\sim\!$式(4)代入式(1)中, 动量方程可表达为

(5)$\begin{eqnarray} \dfrac{\partial \tau_{rs} }{\partial r}+\dfrac{\partial \tau_{zs} }{\partial z}-\rho g\dfrac{\partial }{\partial s}\lt(z_{\rm b} +H+\dfrac{U^{2}}{g})=\dfrac{\partial \rho UV}{\partial r}+ \\ \qquad \dfrac{\partial \rho UW}{\partial z}+\dfrac{2\rho \overline {u'v'} }{r}+2\rho \lt(\dfrac{UV}{r}) \end{eqnarray}$

对式(5)沿垂线进行积分可得

(6)$\begin{eqnarray} \label{eq6} && \dfrac{\partial H\left( {\tau_{rs} } \right)_{\rm d}}{\partial r}-\tau_{\rm b} \sqrt {1+\left( {1/S_{r} } \right)^{2}} +\rho gHS_{\rm e} = \\&&\qquad \rho \dfrac{\partial H\left( {UV} \right)_{\rm d} }{\partial r}+2\rho \int_0^H {\left( {\dfrac{\overline {u'v'} }{r}+\dfrac{UV}{r}} \right)} {\rm d}z \end{eqnarray}$

其中

(7)$\begin{eqnarray} \label{eq7} &&\left( {UV} \right)_{\rm d} =\dfrac{1}{H}\int_0^H {UV} {\rm d}z \end{eqnarray}$

(8)\begin{eqnarray} \label{eq8} \left( {\tau_{rs} } \right)_{\rm d} =\dfrac{1}{H}\int_0^H {\tau_{rs} } {\rm d}z \end{eqnarray}$

(9)$\begin{eqnarray} \label{eq9}S_{\rm e} =\dfrac{nU_{\rm a} }{R^{2/3} }\end{eqnarray}

(10)$\begin{eqnarray} \label{eq10} \int_{0}^{H} {\dfrac{\partial \tau_{zs} }{\partial z}} {\rm d}z= {\tau_{zs} }|_{z=H} -{\tau_{zs} }|_{z=0} =-\tau_{\rm b} \sqrt {1+\left( {1/S_{r} } \right)^{2}}\qquad \end{eqnarray}$

式中, $\tau_{\rm b}$为床面切应力; 1/$S_{r}$为床面横比降; 脚标d表示垂线平均值; $S_{\rm e}$为总水头能量的比降, 用于表示$-\partial (z_{\rm b} +H+U^{2}/g)/\partial s$^[24]; $U_{\rm a}$为断面平均流速; $n$为糙率, 若实验水槽为水泥面, 查表得糙率值为0.014^[28]; $R$为水力半径.

1.2 解析解推导

Tang和Knight^[26]根据van Balen等^[29]180$^\circ$弯道试验数据, 分析了二次流项和二次流附加项的横断面分布规律, 发现其沿横断面为线性分布, 本文对式(6)右边二次流项和弯道附加应力项也采用线性分布假设, 即

(11)$\begin{eqnarray} \label{eq11} \rho \dfrac{\partial H\left( {UV} \right)_{\rm d} }{\partial r}+2\rho \int_0^H {\left( {\dfrac{\overline {u'v'} }{r}+\dfrac{UV}{r}} \right)} {\rm d}z=m+kr \end{eqnarray}$

式中, $m$和$k$分别为线性分布规律常数项和一次项系数, 根据等式左边可知,

$m$的单位为kg/(m$\cdot$s$^{2})$, $k$的单位为kg/(m$^{2}$$\cdot$s$^{2})$,

随弯道平面形态及研究断面所处位置的不同而变化, 可采用实测资料率定获得.

式(6)可写为

(12)$\begin{eqnarray} \label{eq12} &&\rho gHS_{_{\rm e} } +\dfrac{\partial H\left( {\tau_{rs} } \right)_{\rm d} }{\partial r}-\tau_{\rm b} \sqrt {1+\left( {1/S_{r} } \right)^{2}} =m+kr \end{eqnarray}$

(13)$\begin{eqnarray} \label{eq13}&&\tau_{\rm b} =\dfrac{f}{8}\rho U_{\rm d}^{2} \end{eqnarray}$

(14)$\begin{eqnarray} \label{eq14}\left( {\tau_{rs} } \right)_{\rm d} =\rho \lambda \left( {\dfrac{f}{8}} \right)^{1/2}HU_{\rm d} \dfrac{\partial U_{\rm d} }{\partial r} \end{eqnarray}$

(15)$\begin{eqnarray} \label{eq15}f=\dfrac{8g}{n^{2}R^{1/3}} \end{eqnarray}$

式中, $\lambda $为无量纲涡黏性系数, 其取值在河道内变化不大, 取值为0.07^[10,19]; $f$为阻力系数.

将式(13)和式(14)代入式(12)中, 可得

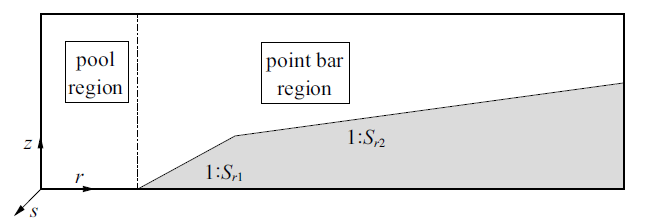
(16)$\begin{eqnarray} \label{eq16} &&\rho gHS_{\rm e} +\dfrac{\partial }{\partial r}\left[{\rho \lambda H^{2}\left( {\dfrac{f}{8}} \right)^{1/2}U_{\rm d} \dfrac{\partial U_{\rm d} }{\partial r}} \right]-\\&&\qquad \dfrac{f}{8}\rho U_{\rm d}^{2}\sqrt {1+\left( {1/S_{r} } \right)^{2}} =m+kr \end{eqnarray}$

本文将带滩槽地形的横断面形态概化成如图1所示(图中灰色区域为滩地), 河槽区床面高程不变, 河滩区床面线性抬高. 对不同的床面形态, 由式(16)可求得$U_{\rm d}$横向分布的解析解, 解析解的表达式如下.

(a)对河槽区, 即水深恒定的区域, $U_{\rm d}$的解析解为

(17)$\begin{eqnarray} \label{eq17} U_{\rm d} =\left( {A_{1} {\rm e}^{\gamma r}+A_{2}{\rm e}^{-\gamma r}+\omega_{1} }\right)^{1/2} \end{eqnarray}$

其中

(18)$\begin{eqnarray} \label{eq18} &&\omega_{1} =\dfrac{8gS_{\rm e} H}{f}-\dfrac{8}{\rho f}\left( {m+kr} \right) \end{eqnarray}$

(19)$\begin{eqnarray} \gamma=\sqrt{\dfrac{2}{\lambda}}\left(\dfrac{f}{8}\right)^{1/4} \dfrac{1}{H} \end{eqnarray}$

图1

新窗口打开|下载原图ZIP|生成PPT
图1带滩槽地形断面形态概化图

Fig.1A sketch of a cross-section with a pool-point bar

(b)对河滩区, 即床面线性变化的区域(床面横比降为$1/S_{r} )$, $U_{\rm d}$的解析解为

(20)$\begin{eqnarray} \label{eq20} U_{\rm d} =\left( {A_{3} \xi^{\alpha }+A_{4} \xi^{-\left( {\alpha +1}\right)}+\omega_{2} \xi +\eta } \right)^{1/2} \end{eqnarray}$

其中

(21)$\begin{eqnarray} \label{eq21} &&\alpha =-\dfrac{1}{2}+\dfrac{1}{2}\sqrt {1+\dfrac{\sqrt {1+\left( {1/S_{r} }\right)^{2}} }{\lambda }\sqrt {8f} } \end{eqnarray}$

(22)$\omega_{2} =\dfrac{gS_{\rm e} +kS_{r} /\rho }{\sqrt {1+\left( {1/S_{r} } \right)^{2}} \left( {\dfrac{f}{8}} \right)-\dfrac{\lambda }{S_{r}^{2}}\left( {\dfrac{f}{8}} \right)^{1/2}}$

(23)$\begin{eqnarray} \label{eq23} \eta =\dfrac{-m-HkS_{r}}{\rho \dfrac{f}{8}\sqrt {1+\left( {1/S_{r} } \right)^{2}} } \end{eqnarray}$

式中, $A_{1}$$\sim$$A_{4}$为未知的系数, $\xi $表示床面上的水深, $\xi=H-r/S_{r} $.

1.3 边界条件

对于$U_{\rm d} $的解析式, 存在两种边界条件, 一是无滑移边界, 二是交界面处要满足连续性, 即:

(1)两岸(左岸和右岸)边界处流速为0;

(2)滩槽交界处, 主槽和滩地流速相等$U_{{\rm d},i} =U_{{\rm d},i+1}(i$和$i+1$表示参数取值不同的两个相邻区域);

(3)滩槽交界处, 主槽和滩地流速梯度相等, 即$\partial U_{{\rm d},i} /\partial r=\partial U_{{\rm d},i+1} /\partial r$.

根据上述边界条件, 解析式中系数$A_{1}$, $A_{2}$, $A_{3}$, $A_{4}$均可求解.

2 解析解模型的应用

2.1 带滩槽地形的连续弯道纵向流速断面横向分布试验介绍

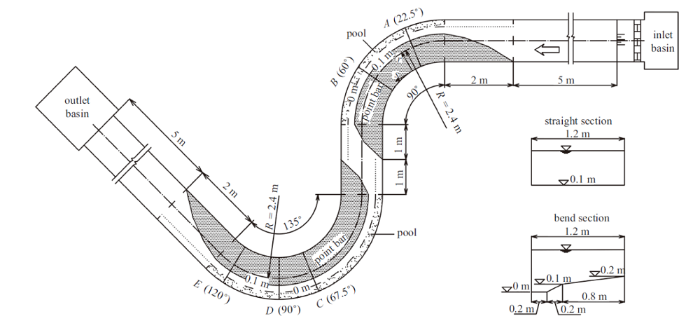
试验在武汉大学泥沙重点实验室的反向连续弯道水槽中进行, 水槽进出口均有一段长7 m的顺直段, 上下游两弯道曲率保持恒定, 上游弯道的中心角为90$^\circ$, 下游弯道的中心角为135$^\circ$, 水槽宽度为1.2 m, 弯道中心线曲率半径为2.4 m, 两弯道间的顺直连接段长2 m, 水槽横断面形状如图2(b)所示, 过渡段中间断面和进出口5 m内顺直段均为矩形断面, 底部高程为0.1 m, 弯道横断面形状为凸岸高凹岸低, 由凸岸到凹岸, 床面高程以1:8的横比降由0.2 m减小为0.1 m (水深减小0.1 m), 接着以1:2的横比降床面高程减小到0 m (水深减小0.1 m), 之后床面高程和水深保持不变, 顺直段内矩形断面与弯道内滩槽地形断面通过渐变的方式进行连接.

图2

新窗口打开|下载原图ZIP|生成PPT
图2连续弯道试验布置

Fig.2Layout of the consecutive bends experiment

试验采用三维超声多普勒流速仪(ADV)进行三维流速测量, 仪器采样频率为200 Hz, 断面的测点布置横向间距为5 cm, 垂向间距为2 cm, 靠近床面区域加密测量, 测点垂向间距减小为1 cm, 由于测量探头的大小及仪器采样体积为探头下方5 cm, 因此在边壁和水面5 cm以内无法进行测量, 纵向流速的垂线平均值根据各测线的流速数据取垂线平均获得.

三组工况的水力学条件如表1所示, 典型天然弯曲河流的$Fr$范围为0.07$\sim$0.26^[30], 三种试验工况的$Fr$取值在此范围内, 并保持流量不变, 研究水深变化的影响, 采用试验测量的五个断面(断面$A$$\sim$$E$)进行验证.

Tab.1
表1
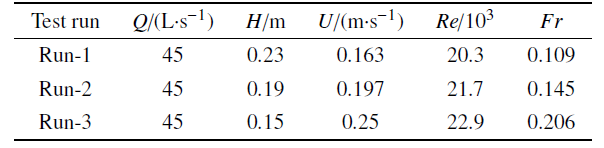
表1试验条件
Tab.1Experimental conditions

新窗口打开|下载CSV

表中, $Q$为进口流量, $H$为出口断面水深, $U$为进口断面平均流速, $Fr$为佛汝德数, $Re$为雷诺数.

2.2 结果与分析

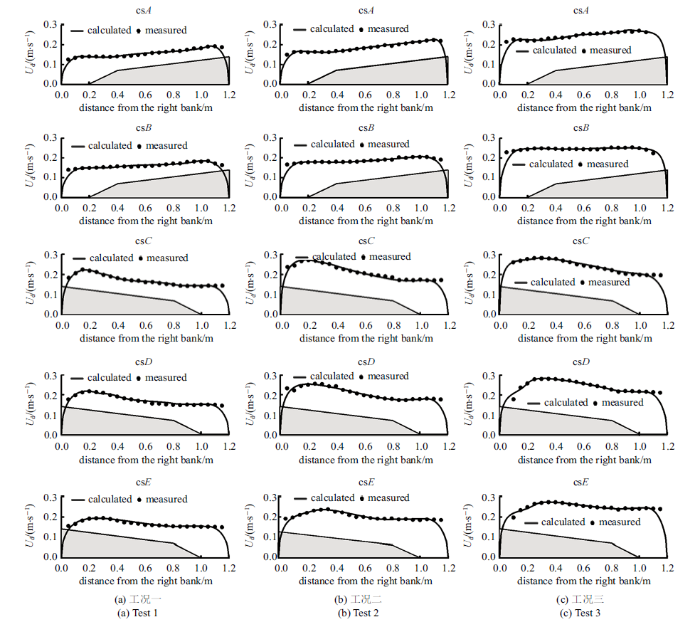
图3为解析解的拟合曲线与试验结果的比较(图中灰色区域为滩地), 图中圆点为根据实测的三维流速数据计算出的$U_{\rm d}$, 由图可知实测的$U_{\rm d}$沿横断面的分布规律为深槽流速较小, 流速沿横向变化率较小, 滩地上流速较大, 流速沿横向变化率增大, $U_{\rm d}$的最大值在靠近凸岸侧, 下游弯道中$U_{\rm d}$横向分布较上游弯道更不均匀, 由工况一到工况三, 出口水深逐渐减小即水流流速增大, 在下游弯道中$U_{\rm d}$的最大值逐渐向凹岸偏移.

图3

新窗口打开|下载原图ZIP|生成PPT
图3流速计算值与实测值对比

Fig.3Comparison of modelled depth-averaged velocity distribution with experimental data

图3中曲线为计算出的拟合曲线, 水深恒定不变的河槽区(距凹岸0$\sim$0.2 m范围内)采用式(17)进行拟合, 床面线性变化的边坡区(距凹岸0.2$\sim$1.2 m范围内)由式(20)拟合, 参数$m$的取值根据地形分为三个区域, 分别为水平段$m_{1}$、横比降为1/2的斜坡段$m_{2}$和横比降为1/8的斜坡段$m_{3}$, 参数$k$的取值分为两个区域(靠近凹岸侧为$k_{1}$, 靠近凸岸侧为$k_{2})$, 分区位置在主流附近, 解析解表达式中的系数$A_{1}$$\sim$$A_{4}$可根据边界条件求解. 由图可知拟合曲线与实测数据吻合良好, 在床面地形变化处, $U_{\rm d}$沿程变化率较大时以及$U_{\rm d}$峰值的大小与位置, 计算值对实测值均能较好拟合, 随着出口水深减小, $U_{\rm d}$最大值的位置变化, 计算结果也能较好地反映这一规律, 仅在靠近边壁处拟合曲线与实测数据稍有偏差, 凹岸侧偏差可能是凹岸次生反向小环流影响导致, 凸岸边壁附近偏差则可能是由于水深较浅, 水流结构较为复杂导致, 各断面的均方根误差均小于0.015 m/s, 平均相对误差均在5%以内, 实测值与计算值之间误差较小. 综上所述, 在带有滩槽的反向连续弯道中, 此解析式能较好拟合不同水流条件下沿程各断面垂线平均纵向流速的横向分布规律.

3 计算参数敏感性分析及取值

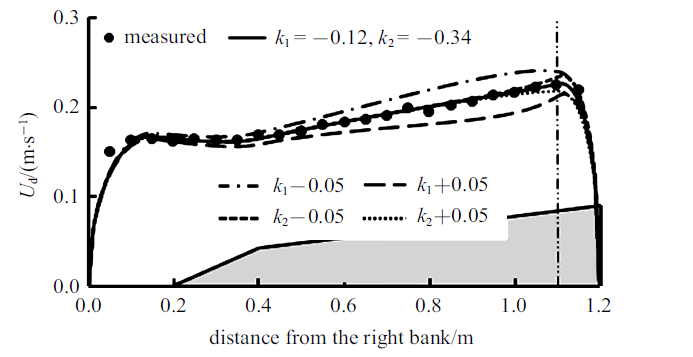
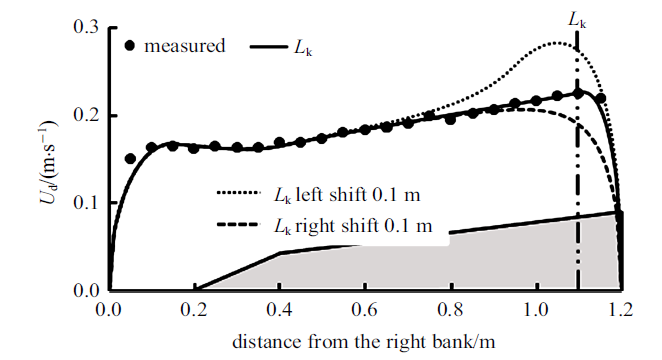
对参数$m$和$k$的取值进行敏感性分析, 此处以工况二的断面$A$拟合结果为基础进行分析. 图4对$k$的数值大小进行了敏感性分析, 在0$\sim$1.1 m和1.1$\sim$1.2 m取值不同(分别表示为$k_{1}$和$k_{2})$, 将$k_{1}$和$k_{2}$的取值分别在原基础上增大和减小0.05 (每次仅变化一个参数的取值), 由图可知$k_{1}$数值变化对凹岸深槽区域流速计算值基本无影响, 主要变化发生在靠近凸岸的边滩附近, 且计算值变化较小, $k_{2}$的变化仅影响1$\sim$1.2 m内的局部区域, 流速计算值变化较小, 流速最大值的大小和位置未发生明显变化; 图5对$k_{1}$和$k_{2}$分区位置的敏感性进行了分析, 虚线$L_{k}$表示分界位置, 将初始分界位置分别向左和向右移动0.1 m, 由图可以发现, 分界位置的变化对流速的峰值影响较大, 流速最大值变化明显, 且位置也发生变化, 由此可将主流线的位置作为$k$分区的初步依据.

图4

新窗口打开|下载原图ZIP|生成PPT
图4$k$变化时垂线平均流速计算值

Fig.4Modelled depth-averaged velocity for various $k$ values

图5

新窗口打开|下载原图ZIP|生成PPT
图5$k$分区调整时垂线平均流速计算值

Fig.5Modelled depth-averaged velocity for various $k$ values in different panels

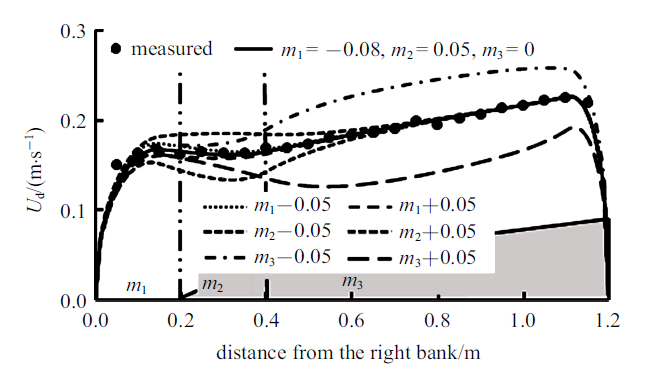
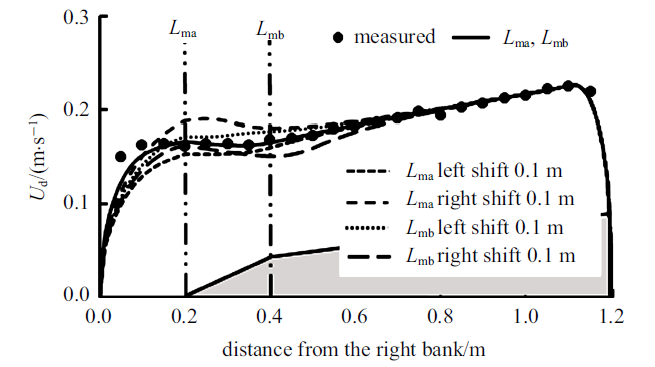
参数$m$分为三个区域进行取值, 为$m_{1}$ (0$\sim$0.2 m), $m_{2}$ (0.2$\sim$0.4 m)和$m_{3}$ (0.4$\sim$1.2 m), 图6为对参数$m$取值的敏感性分析结果, 分别对$m_{1}$, $m_{2}$和$m_{3}$的初始值增大和减小0.05 (每次仅变化一个参数的取值), 由图可知, $m_{1}$的取值增大或减小对流速计算值基本无影响, $m_{2}$的取值变化仅在0.2$\sim$0.4 m附近的流速计算值产生影响, 流速计算值变化较小, $m_{3}$取值变化对整个断面的流速计算值基本均有影响, 在0.4$\sim$1.2 m区域内, 流速计算值发生明显变化; 图7为$m$分区位置变化的敏感性分析结果, 图中虚线$L_{\rm ma}$

图6

新窗口打开|下载原图ZIP|生成PPT
图6$m$变化时垂线平均流速计算值

Fig.6Modelled depth-averaged velocity for various $m$ values in different panels

图7

新窗口打开|下载原图ZIP|生成PPT
图7$m$分区位置变化时垂线平均流速计算值

Fig.7Modelled depth-averaged velocity for various panels of $m$

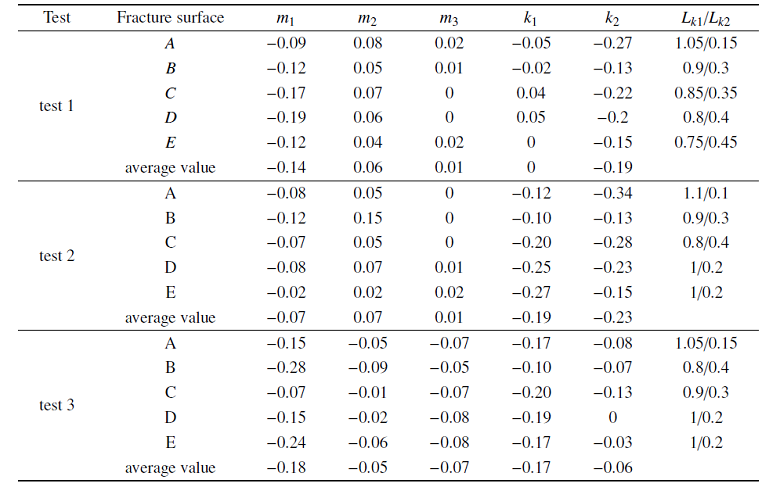
参数$m$和$k$的取值如表2所示, $L_{k1}$和$L_{k2}$分别为$k_{1}$和$k_{2}$取值区域的长度, 由表中数据可知, $m$和$k$的值与Tang和Knight^[26]文中的取值是相近的. 沿断面水平段$m_{1}$的取值小于斜坡段$m_{2}$和$m_{3}$的取值, 可能与凹岸主槽侧流速较小有关, 参数$m$的取值整体上随水深的减小逐渐减小, 水深减小到一定程度, 河滩区$m_{2}$和$m_{3}$的取值由正变为负; $k_{1}$和$k_{2}$取值分区的界限与主流位置较为接近, 分区的位置变化较小, 可能与主流位置变化较小相关, $k_{1}$和$k_{2}$取值的相对大小整体上由工况一的$k_{1}$大于$k_{2}$变为工况三的$k_{1}$小于$k_{2}$. 根据参数的取值敏感性分析可知$m_{1}$, $m_{2}$和$k_{1}$, $k_{2}$的取值变化对计算结果的影响较小, 计算结果对$m_{3}$的值较为敏感, 但$m_{3}$的取值沿程变化较小, 因此给出各参数沿水槽的均值作为初步取值参考.

Tab.2
表2
表2参数取值
Tab.2The values of parameters

新窗口打开|下载CSV

4 讨论

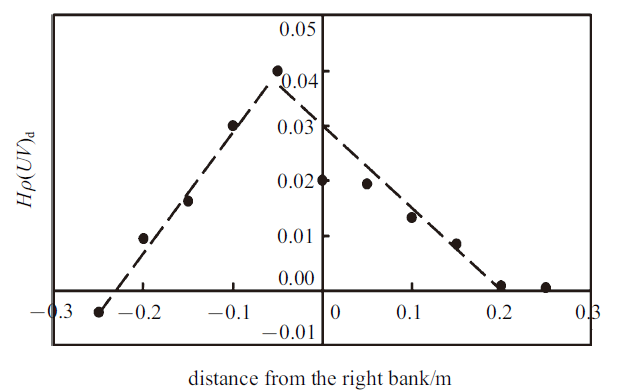
本文对二次流项和二次流附加项采用与Tang和Knight^[26]相同的线性假设, 其仅分析弯道出口附近135$^\circ$ 断面的数据, 本文将解析解用于弯道中的多个断面, 此处增加绘制van Balen等^[29]的180$^\circ$ 弯道进口附近29$^\circ$ 断面的二次流项$\rho H(UV)_{\rm d}$和二次流附加项$2 \rho \int_{0}^{H}\left(\dfrac{\overline{u'v'}}{r}+\dfrac{U V}{r}\right){\rm d} z$的断面分布(如图8和图9所示), 由图可知其在弯道进口断面也符合线性假设. 进一步分析二次流项和二次流附加项在本文试验水槽中的断面分布规律, 选取工况二cs$C$断面实测数据进行讨论, 由图10和图11可知二次流项和二次流附加项的断面分布符合线性分布规律, 由此可知线性假设在本试验中也是符合的. 由此可知, 对二次流项和二次流附加项沿横断面的线性分布假设在弯道沿程多个断面均适用, 并在本文连续弯道中也是符合的, 表明本文采取的线性假设在本文的研究问题中是合理的.

图8

新窗口打开|下载原图ZIP|生成PPT
图8二次流项$\rho H(UV)_{\rm d}$ 29$^\circ$ 横断面分布^[29]

Fig.8Lateral distribution of secondary flow term, $\rho H(UV)_{\rm d}$ at cross-section of 29$^\circ$^[29]

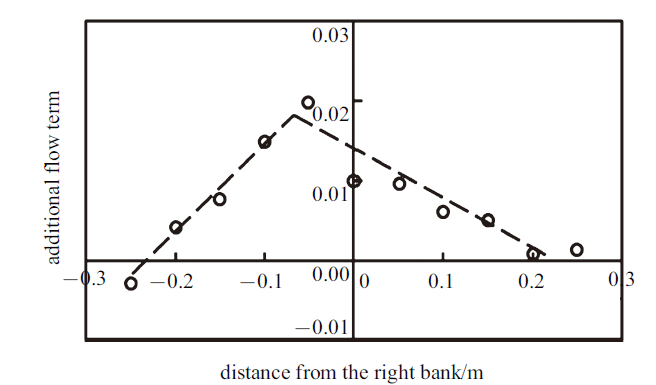
图9

新窗口打开|下载原图ZIP|生成PPT
图9二次流附加项$2 \rho \int_{0}^{H}\left(\dfrac{\overline{u'v'}}{r}+\dfrac{U V}{r}\right){\rm d} z$ 29$^\circ$ 横断分布^[29]

Fig.9Lateral distribution of additional secondary flow term, $2 \rho \int_{0}^{H}\left(\dfrac{\overline{u'v'}}{r}+\dfrac{U V}{r}\right){\rm d} z$ at cross-section of 29$^\circ$^[29]

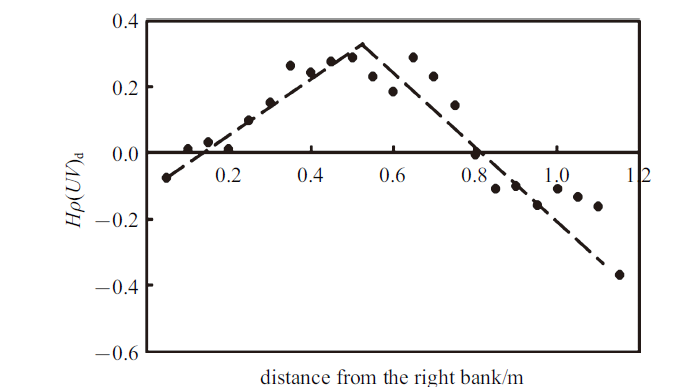
图10

新窗口打开|下载原图ZIP|生成PPT
图10二次流项$\rho H(UV)_{\rm d}$横断面分布(cs$C$)

Fig.10Lateral distribution of secondary flow term, $\rho H(UV)_{\rm d}$ (cs$C$)

图11

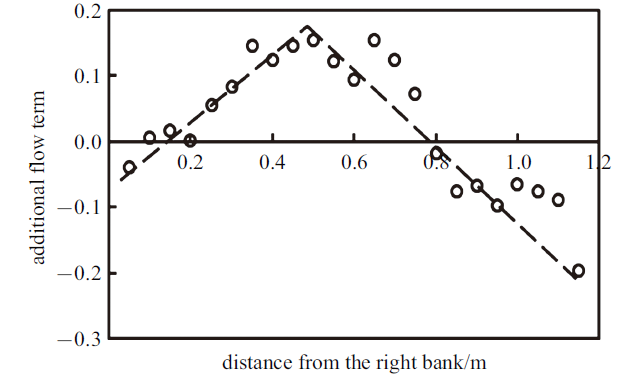
新窗口打开|下载原图ZIP|生成PPT
图11二次流附加项$2 \rho \int_{0}^{H}\left(\dfrac{\overline{u'v'}}{r}+\dfrac{U V}{r}\right){\rm d} z$横断分布(cs$C$)

Fig.11Lateral distribution of additional secondary flow term, $2 \rho \int_{0}^{H}\left(\dfrac{\overline{u'v'}}{r}+\dfrac{U V}{r}\right){\rm d} z$ (cs$C$)

本文推导出弯道中的$U_{\rm d}$沿横断面解析解表达式, 与带滩槽地形的反向连续弯道实测数据符合良好, 根据实测数据率定的参数$m$和$k$的取值与Tang和Knight^[26]的取值是相近的, 表明参数的取值对与不同的弯道存在相近的范围, 并分析了参数取值随水位变化的规律, 但具体的参数取值与水流条件和弯道形态之间的关系仍需更加深入的研究, 以更好地推广应用解析解公式.

5结论

本文基于SKM方法, 对动量方程进行垂线积分, 推导出了弯道中$U_{\rm d}$的横向分布解析解公式, 将其应用于带滩槽地形的反向连续弯道中.

(1)将解析解公式应用于有滩槽的反向连续弯道, 调整线性假设中参数的值, 可以使计算值与实测值在不同的出口水流条件下, 对沿程各断面流速值横向分布规律都能吻合良好, 表明本文的线性假设具有一定的合理性.

(2)参数取值, 一次项系数$k$的大小对流速横向分布趋势有较大影响, $k$的分区对主流有较大的影响, 调整分区可使计算值更好拟合滩地区流速的峰值大小和位置. 常数项$m$整体上随水深的减小而减小, 可对$m$按照斜率变化分区对局部流速计算值进行调整, 河槽区$m$的取值小于河滩区, 流速计算值对$m$在河槽区与河滩区间分界线的变化较为敏感, 河滩区内$m$的分区则对流速计算值影响较小.

(3)本文推导的解析解公式应用范围较广, 可用于地形变化的反向连续弯道中, 但对于该模式的应用需要进行更加详细的研究: ①增加试验工况, 进一步分析参数$m$和$k$取值与进出口水流条件(流量、水位和断面平均流速等)和弯道形态(曲率、比降和过渡段长度等)之间的规律, 总结参数分区依据和合理的取值范围; ②分析$m$和$k$的物理意义, 利用更加详细精确的数据计算其表示的各项具体分布规律, 以更深入理解$m$和$k$取值变化规律的具体原因.

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Abril

, Knight

. Stage-discharge prediction for rivers in flood applying a depth-averaged model
Journal of Hydraulic Research, 2004,42(6):616-629

[本文引用: 1]

[2]

Sharifi

, Sterling

. Using the Shiono and Knight model to predict sediment transport//European IAHR Congress
HeriotWatt University, Edinburgh: Scotland, 2010

[本文引用: 2]

[3]

王虹, 王连接, 邵学军等. 连续弯道水流紊动特性试验研究
力学学报, 2013,45(4):525-533

[本文引用: 1]

( Wang

Hong

, Wang

Lianjie

, Shao

Xuejun

, et al. Turbulence characteristics in consecutive bends
Chinese Journal of Theoretical and Applied Mechanics, 2013,45(4):525-533 (in Chinese))

[本文引用: 1]

[4]

Farhadi

, Sindelar

, Tritthart

, et al. An investigation on the outer bank cell of secondary flow in channel bends. Journal of Hydro-Environment Research, 2018,18:1-11

[5]

王千, 刘桦, 房詠柳等. 孤立波与淹没平板相互作用的三维波面和水动力实验研究
力学学报, 2019,51(6):1605-1613

[本文引用: 1]

( Wang

Qian

, Liu

Hua

, Fang

Yongliu

, et al. An experimental study of 3-d wave surface and hydrodynamic loads for interaction between solitary wave and submerged horizontal plate
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(6):1605-1613 (in Chinese))

[本文引用: 1]

[6]

杨燕华, 白玉川. 连续弯道水流运动的三维数值模拟
泥沙研究, 2011 ( 6):46-49

[本文引用: 1]

( Yang

Yanhua

, Bai

Yuchuan

. Three-dimensional numerical simulation of flow in successive bends
Journal of Sediment Research, 2011,6:46-49 (in Chinese))

[本文引用: 1]

[7]

Gholami

, Bonakdari

, Zaji

, et al. Simulation of open channel bend characteristics using computational fluid dynamics and artificial neural networks
Engineering Applications of Computational Fluid Mechanics, 2015,9(1):355-369

[8]

吴霆, 时北极, 王士召等. 大涡模拟的壁模型及其应用
力学学报, 2018,50(3):453-466

( Wu

Ting

, Shi

Beiji

, Wang

Shizhao

, et al. Wall-model for large-eddy simulation and its applications
Chinese Journal of Theoretical and Applied Mechanics, 2018,50(3):453-466 (in Chinese))

[9]

张嫚嫚, 孙姣, 陈文义. 一种基于几何重构的Youngs-VOF耦合水平集追踪方法
力学学报, 2019,51(3):775-786

[本文引用: 1]

( Zhang

Manman

, Sun

Jiao

, Chen

Wenyi

. An interface tracking method of coupled youngs-vof and level set based on geometric reconstruction
Chinese Journal of Theoretical and Applied Mechanics, 2019,51(3):775-786 (in Chinese))

[本文引用: 1]

[10]

王韦, 蔡金德. 弯曲河道内水深和流速平面分布的计算
泥沙研究, 1989(2):46-54

[本文引用: 2]

( Wang

Wei

, Cai

Jinde

. Computation for distribution of d and velocity in curved open channels
Journal of Sediment Research, 1989(2):46-54 (in Chinese))

[本文引用: 2]

[11]

许唯临. 复式河道漫滩水流计算方法研究
水利学报, 2002,33(6):0021-0027

[本文引用: 1]

( Xu

Weilin

. Study on computational method of overbank flow in channels with compound cross section
Journal of Hydraulic Engineering, 2001,6:21-26 (in Chinese))

[本文引用: 1]

[12]

Tang

, Knight

. A general model of lateral depth-averaged velocity distributions for open channel flows
Advances in Water Resources, 2008,31(5):846-857

[13]

Yang

, Nie

, Liu

, et al. Modeling depth-averaged velocity and boundary shear stress in rectangular compound channels with secondary flows
Journal of Hydraulic Engineering, 2013,139(1):76-83

[本文引用: 1]

[14]

孙东坡, 朱岐武, 张耀先等. 弯道环流流速与泥沙横向输移研究
水科学进展, 2006,17(1):61-66

[本文引用: 1]

( Sun

Dongpo

, Zhu

Qiwu

, Zhang

Yaoxian

, et al. Study of circulating velocity profile and lateral sediment transport in curved channels
Advances in Water Science, 2006,17(1):61-66 (in Chinese))

[本文引用: 1]

[15]

Shiono

, Knight

. Turbulent open-channel flows with variable depth across the channel
Journal of Fluid Mechanics, 1991,222:617-646

[本文引用: 1]

[16]

Devi

, Khatua

, Das

. A numerical solution for depth-averaged velocity distribution in an open channel flow
ISH Journal of Hydraulic Engineering, 2016,22(3):262-271

[本文引用: 1]

[17]

Ervine

, Babaeyan-Koopaei

, Sellin

RHJ

. Two-dimensional solution for straight and meandering overbank flows
Journal of Hydraulic Engineering, 2000,126(9):653-669

[本文引用: 1]

[18]

Knight

, Omran

, Tang

. et al. Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows
Journal of Hydraulic Engineering, 2007,133(1):39-47

[本文引用: 1]

[19]

Liu

, Luo

, Liu

. et al. Modeling depth-averaged velocity and bed shear stress in compound channels with emergent and submerged vegetation
Advances in Water Resources, 2013,60:148-159

[本文引用: 2]

[20]

Huai

, Gao

, Zeng

. et al. Two-dimensional analytical solution for compound channel flows with vegetated floodplains
Applied Mathematics & Mechanics, 2009,30(9):1121-1130

[本文引用: 1]

[21]

Zhong

, Huai

, Chen

. Analytical model for lateral depth-averaged velocity distributions in rectangular ice-covered channels
Journal of Hydraulic Engineering, 2019,145(1):04018080

[本文引用: 1]

[22]

杨中华, 高伟. 考虑滩槽相互作用的漫滩水流二维解析解
四川大学学报 (工程科学版), 2009,41(5):42-46

[本文引用: 1]

( Yang

Zhonghua

, Gao

Wei

. Two dimensional analytical solution for overbank flows with interaction between the main channel and floodplain
Journal of Sichuan University (Engineering Science Edition), 2009,41(5):42-46 (in Chinese))

[本文引用: 1]

[23]

哈岸英, 吴腾, 陈刚. 冲积河流滩槽定量划分方法及应用
水利学报, 2012,43(1):10-14

[本文引用: 1]

( Ha

Anying

, Wu

Teng

, Chen

Gang

. Quantitative division method for floodplain and main channel of alluvial river and its application
Journal of Hydraulic Engineering, 2012,43(1):10-14 (in Chinese))

[本文引用: 1]

[24]

Rezaei

, Knight

. Application of the Shiono and Knight method in compound channels with non-prismatic floodplains
Journal of Hydraulic Research, 2009,47(6):716-726

[本文引用: 2]

[25]

Rozovskii

. Flow of Water in Bends of Open Channels
London: Acad. of Sci. of the Ukrainian SSR, Kiev, 1957

[本文引用: 1]

[26]

Tang

, Knight

. The lateral distribution of depth-averaged velocity in a channel flow bend
Journal of Hydro-environment Research, 2015,9(4):532-541

[本文引用: 5]

[27]

Tubino

, Repetto

, Zolezzi

. Free bars in rivers
Journal of Hydraulic Research, 1999,37(6):759-775

[本文引用: 1]

[28]

Chow

. . Open-Channel Hydraulics
London: McGraw-Hill, 1959

[本文引用: 1]

[29]

Van Balen

, Uijttewaal

WSJ

, Blanckaert

. Large-eddy simulation of a mildly curved open-channel flow
Journal of Fluid Mechanics, 2009,630:413-442

[本文引用: 6]

[30]

, Yu

, Wei

. et al. The mechanisms of energy transformation in sharp open-channel bends: Analysis based on experiments in a laboratory flume
Journal of Hydrology, 2019,571:723-739

[本文引用: 1]