A GFEM WITH C$^1$ CONTINUITY1)
TianRong中图分类号:TB115,O346.1
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (19046KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
1 无额外自由度单位分解广义有限元方法
单位分解广义有限元方法的研究一般认为源于Melenk和Babu${\check{ s}}$ka的单位分解方法(PUM)[1]和单位分解有限元方法(PUFEM)[2](类似的思想又可追溯到该作者早期的工作[3]). 几乎同时,Duarte和Oden[4-5]提出类似的方法,称为hp-cloud方法. 该方法在思想上非常相近但发表时间更早的工作,可见于由我国旅美****石根华提出的数值流形方法(NMM)[6-7]. 单位分解函数概念本身非常简单,既可使用无网格插值方法构造[8],也可直接使用有限元的形函数,如扩展有限元法[9-10]. 作为有限元方法的自然延伸,基于有限元形函数的单位分解方法获得了极大的关注和成功的应用,如Strouboulis等[11-18] 和Duarte 等[19-23]深入发展的广义有限元. 为了清晰指代,下面的叙述中"广义有限元法(GFEM)"主要指代基于有限元形函数的单位分解方法[24-28].广义有限元的核心是单位分解(partition of unity)逼近
$$u^h\left( x \right) = \sum\limits_{i \in I} {N_i u_i } + \sum\limits_{i \in I} {N_i \sum\limits_k {\varphi _k^{(i)} a_{i(k)} } }(1)$$
其中,$\sum\limits_i {N_i \left( x \right)} \equiv 1$构成了全域上的一个单位分解,$\varphi _k^{(i)} $为节点$i$支撑域上的用户自定义局部近似函数,$a_{i(1)} ,\mbox{ }a_{i(2)} ,...$为局部近似函数引入的节点$i$的广义自由度或额外自由度. 在现有的广义有限元方法中,节点上自由度个数会随着局部近似函数的阶次变化而变化. 本文提出一种"无广义自由度的广义有限元方法"(下称"新方法").
如图1,令${P}_i^r $为$\varOmega ^e$中以节点$i$为中心的"节点集(nodal patch)",$r$代表该单元片尺寸. 根据网格类型,节点集可通过"基于网格"和"无网格插值"两种方式确定：对于规则网格(图1(a)),为环绕该节点$i$的$m \ge 1$层单元;对于非规则网格(图1(b)),则直接取为以节点$i$为圆心(球心)的影响圆(球). 节点$i$为节点集${P}_i^r $的"片星节点(patch star)". 若无特别说明,下标$i$特指该"片星节点". 指标$j$表示"非片星节点". $I_i = \left\{ {k \in I:x_k \in {P}_i^r } \right\}$表示单元片${P}_i^r $上所有节点的集合. $J_i = \left\{ {k \in I:x_i \in {P}_k^r } \right\}$为包含节点$i$的单元片"片星节点"集合. $I_i $和$J_i $两个集合的内容相同,但含义不同.
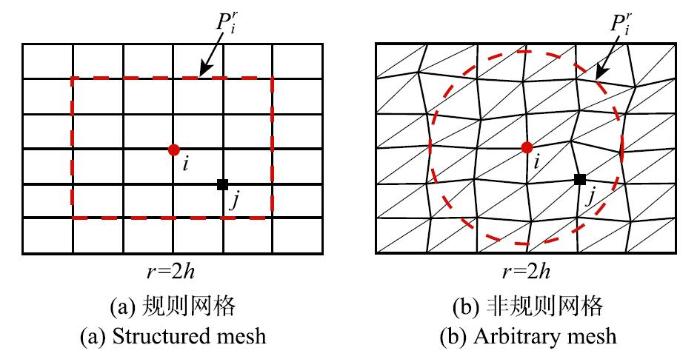显示原图|下载原图ZIP|生成PPT图 1单元片的定义...
-->Fig. 1Definition of nodal patch...
-->
首先,基于节点集$I_i $在单元片${P}_i^r $上构造场函数的一个局部近似
$$u_i^{{ loc}} \left( {{ x}} \right) = \sum\limits_{k \in I_i } {\phi _k^{(i)} \left( {{ x}} \right)u_k } ,\mbox{ }{{ x}},{{ x}}_k \in {P}_i^r(2) $$
其中,上标"($i)$"表示节点$k$所在节点集. 要求$\phi _k^{(i)} \left( {{ x}} \right)$"当且仅当"在片星节点处满足插值性质
$$u_i^{{ loc}} \left( {{{ x}}_i } \right) = u_i ,\mbox{ }\phi _i^{(i)} \left( {{{ x}}_i } \right) \equiv 1(3) $$
其中,$\phi _k^{(i)} \left( {{ x}} \right)$为局部函数,$u_k $为定义在${P}_i^r $节点处的未知数.
将局部近似$u_i^{{ loc}} \left( {{ x}} \right)$作为标准有限元节点位移$u_i $在单元片上的一个局部近似,则构造出一种新的有限元逼近
$$u^h\left( {{ x}} \right) = \sum\limits_i {N_i u_i^{{ loc}} \left( {{ x}} \right)} = \sum\limits_i {\left( {N_i \sum\limits_{k \in I_i } {\phi _k^{(i)} \left( {{ x}} \right)u_k } } \right)}(4) $$
新的逼近格式(4)与标准有限元$u^h\left( {{ x}} \right) = \sum\limits_i {N_i u_i} $一样,基于同一网格同时不引入新的节点和自由度. 将式(4)中的项展开、然后按相同节点归类、合并后得到[29-35]
$$ u^h\left( {{ x}} \right) = \sum\limits_i {\left( {N_i \phi _i^{(i)} \left( {{ x}} \right) + \sum\limits_{k \in J_i ,k \ne i} {N_k \phi _i^{(k)} \left( {{ x}} \right)} } \right)u_i }=\\ \sum\limits_i {\left( {\sum\limits_{k \in J_i } {N_k \phi _i^{(k)} \left( {{ x}} \right)} } \right)u_i } (5) $$
其中,$\phi _i^{(k)} \left( {{ x}} \right)$为单元片$k$上构造出的关于节点$i$的局部插值函数. 注意,$\phi _i^{(k)} \left( {{ x}} \right)$与$\phi _k^{(i)} \left( {{ x}} \right)$不等价.
比较式(5)和式(1),可以清楚地看出,式(5)实质上也是一种单位分解插值. 然而,新单位分解插值具有两个独一无二的特点：(1)不包含任何广义自由度; (2)只要局部逼近函数在各自的"片星"处插值,则无论其在"非片星"处插值 与否,最终构造出的逼近函数一定是全局插值的(证明略).
新方法的特性如下：
(1) 具有现有GFEM的高阶性质. 通过增大单元片尺寸,可以得到"高阶"的局部函数,从而实现高阶插值.
(2) 不包含广义自由度. 新方法不包含广义自由度并且待求的总自由度不会随着局部函数的阶次改变而改变. 这是现有GFEM不具有的特点. 这一特点直接导致线性无关性(linear independence)和与标准有限元一样的稳定性两大特性(前期工作已经证明这一点). 这两点特性是与现有GFEM最大的、最本质的区别.
(3)具有插值性质. 局部函数可以采用某种插值方法,如拉格朗日插值或径向基函数等,或者采用具有"单点插值"特性的某种逼近方法来构造. 对于后者,可以使用最小二乘法(LS)来构造局部函数,只需强制该最小二乘拟合函数在"片星处"插值即可--该"单点插值"约束很容易满足. 在这些情况下,所构造出的全局逼近函数自然具有全局插值性质.
2 C$^{1}$连续性--一种直角坐标网格上的
2.1 连续性证明
用$\tilde {N}_i $记新的形函数$$\tilde {N}_i = \sum\limits_{k \in J_i } {N_k \phi _i^{(k)} }(6)$$
该形函数是由若干函数组合而成. 新的形函数导数形式如下
$$ \partial _x \tilde {N}_i \left( {{ x}} \right) = \sum\limits_{k \in J_i } {\partial _x N_k \left( {{ x}} \right)\phi _i^{(k)} \left( {{ x}} \right)} + \sum\limits_{k \in J_i } {N_k \left( {{ x}} \right)\partial _x \phi _i^{(k)} \left( {{ x}} \right)}(7) $$
下面考察该形函数导数在节点${{ x}}_i $处的连续性. 考虑到$N_i \left( {{{ x}}_i } \right) \equiv 1$,$N_{k \ne i} \left( {{ { x}}_i } \right) \equiv 0$,有
$$\partial _x \tilde {N}_i \left( {{{ x}}_i } \right) = \sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)\phi _i^{(k)} \left( {{{ x}}_i } \right)} + \partial _x \phi _i^{(i)} \left( {{{ x}}_i } \right)(8) $$
如果局部函数在节点集上所有节点处满足插值性质,即$\phi _i^{(k)}\left( {{{ x}}_i } \right) \equiv 1$,则有
$$\partial _x \tilde {N}_i \left( {{{ x}}_i } \right) = \sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} + \partial _x \phi _i^{(i)} \left( {{{ x}}_i } \right)(9) $$
可以证明,在直角坐标网格上,$\sum\limits_{k \in J_i } {\partial_x N_k \left( {{{ x}}_i } \right)} \equiv 0$.
证明如下. 图2给出一个网格尺寸为$h_x \times h_y $的直角坐标网格上一个典型节点片上的有限元形函数导数在片心节点处的取值. 圆圈加亮显示的是片心节点${{ x}}_i $,$k$遍历该节点片上的9个节点. 括号中的两个数分别对$x$和$y$方向的导数. 其中,片心节点${{ x}}_i $的导数$\partial _x N_i \left( {{{ x}}_i } \right)$,$\partial _y N_i \left( {{{ x}}_i } \right)$在${{ x}}_i $的取值依赖于所在单元,固有4组取值,分别标记于所在单元. 在节点处计算新的形函数导数时,由于有限元形函数导数定义依赖于单元,所以需要按单元为单位计算$\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $. 计算结果如图2(b)所示.
从图2可以看出,在直角坐标网格上,新的形函数在节点处的导数单值且唯一,与单元无关,具有连续性. 同理,可以证明,$\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} = 0$与节点在求解域上的位置无关. 证毕.
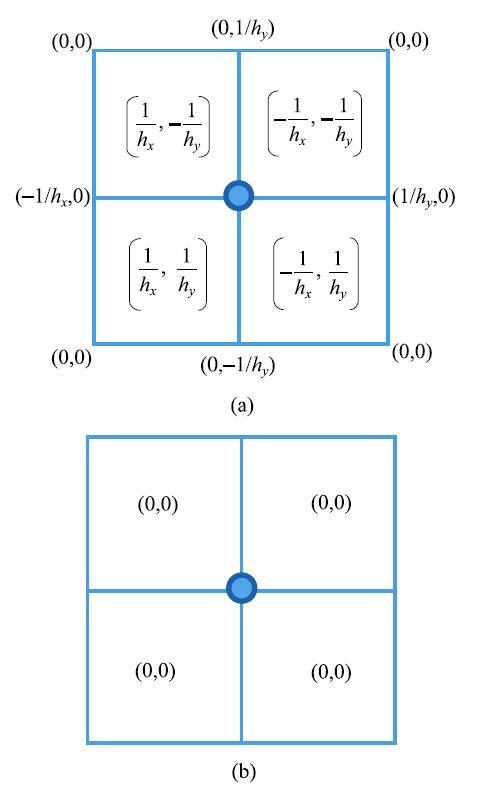显示原图|下载原图ZIP|生成PPT图 2有限元形函数导数及其$\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $. (a) $\partial _x N_k \left( {{{ x}}_i } \right)$取值;(b) $\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $按单元累加的结果...
-->Fig. 2FE shape function derivatives and their $\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $...
-->
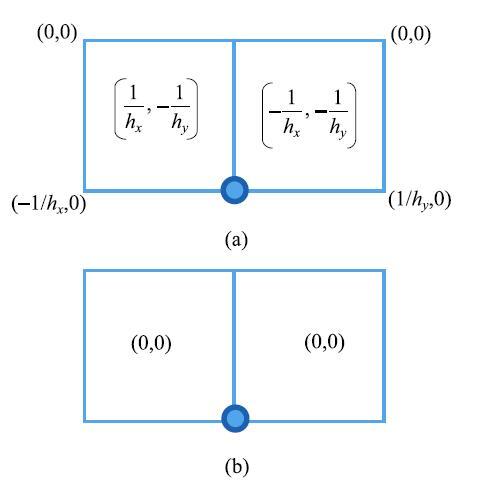显示原图|下载原图ZIP|生成PPT图 3求解域边界处有限元形函数导数及其$\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $. (a) $\partial _x N_k \left( {{{ x}}_i } \right)$取值;(b) $\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $按单元累加的结果\\...
-->Fig. 3FE shape function derivatives and their $\sum\limits_{k \in J_i } {\partial _x N_k \left( {{{ x}}_i } \right)} $ on the boundary of domain...
-->
最后有$\partial _x \tilde {N}_i \left( {{{ x}}_i } \right) = \partial _x \phi _i^{(i)} \left( {{{ x}}_i } \right)$,即在直角坐标网格上,新的形函数具有与局部函数$\phi $相同的连续性.
至此,我们得到满足C$^{1}$连续性的两个前提条件：(1) 直角坐标网格. (2) 局部函数"在节点集上的所有节点处,处处满足插值性质,即$\phi _i^{(k)} \left( {{{ x}}_i } \right) \equiv 1$". 显然,在直角坐标网格上,拉格朗日多项式插值是最佳选择(其它选项包括径向基函数插值). 从计算代价考虑,本文考虑拉格朗日多项式插值作为局部函数构造方法.
由于可以很容易构造出高阶连续可导的拉格朗日多项式局部函数,因此$\tilde {N}$可以具有至少C$^{1}$连续性. 这里"至少"的含义是,如果强制节点集具有片心几何对称特性(可能需要在求解域外布置节点),则可导出新的插值函数具有与局部函数$\phi $完全相同的光滑性,即C$^{n}$连续性.
2.2 形函数及其导数的图像
为了显示形函数的光滑特性,我们在图4的网格上绘制相应的形函数及其高阶导函数. 为了不失一般性,假设该直角坐标网格尺寸在两个坐标方向分别为$h_x $和$h_y $,网格不一定需要均匀. 对于求解域内、远离边界的节点--"节点集"具有"关于片心节点的几何对称性",新的形函数及其一阶和二阶导数见图5. 从图中可以观测到,对于域内节点,形函数具有片心节点的对称或反对称性,且高阶 可导.为了进一步了解形函数在边界处的图像,选取求解域边界处最具代表性的$A, B, C$三点(图6),绘制其形函数及其一阶和二阶导数的图像. 见图7. 从图中同样可以观测到,由于在边界处用于构造局部函数的"节点集"不再满足"关于片心节点的几何对称性",形函数仅一阶可导.
显示原图|下载原图ZIP|生成PPT图 4绘制形函数及其导数所用的直角坐标网格\\...
-->Fig. 4Cartesian grid used to plot shape functions and derivatives...
-->
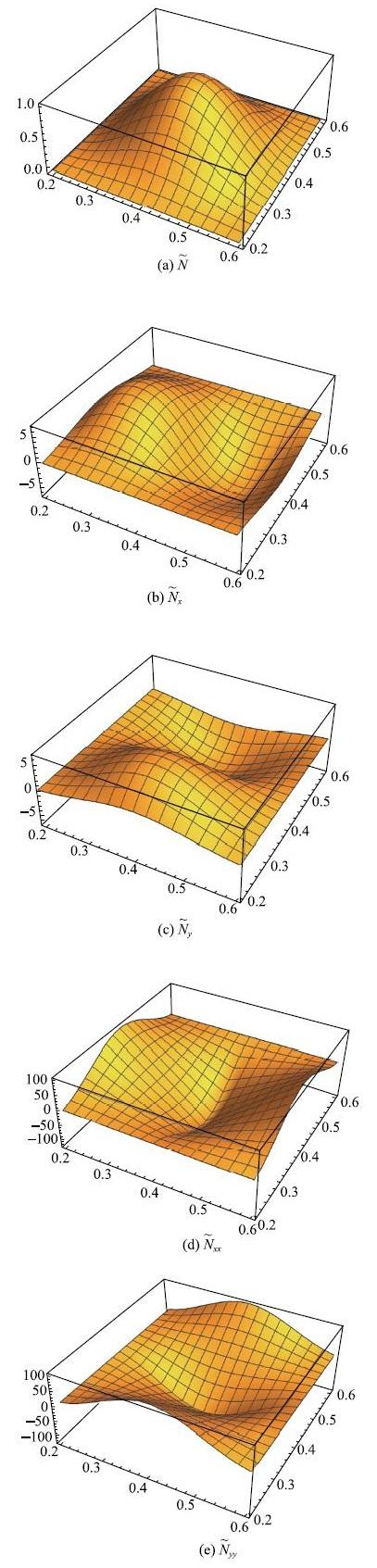显示原图|下载原图ZIP|生成PPT图5C$^{1}$型无额外自由度GFEM形函数及其一阶和二阶导数\\...
-->Fig. 5Shape functions of C$^{1}$ extra-dof free GFEM...
-->
显示原图|下载原图ZIP|生成PPT图6边界节点位置示意\\...
-->Fig. 6Sketch of boundary nodes location...
-->
接下来,运用新的插值格式,对图8显示的非多项式波函数"理论解"进行插值研究. 取该理论解是为了验证高阶插值的优势. 求解域为[0,0]$\times $[1,1]的正方形区域,网格为6$\times $11个节点的直角坐标网格,该网格$h_{x}$! = $h_{y}$,用以验证插值格式对非均匀网格的适应性. 取求解域底边界和对角线两条典型剖面,绘制"数值解"与理论解,研究插值函数及其导数的连续性. 如图9和图10.
通过插值研究,发现：(1)插值函数无论在域内还是边界处均具有C$^{1}$连续性; (2)在网格与自由度不改变前提下,仅通过改变节点集大小,可以改变插值阶次; (3)随着插值阶次的提高,二阶导函数的光滑性也得到改善. 此外,我们不加论证直接给出该格式的另外两个重要特点：(1)具有Kronecker delta性质;(2)精确满足线性本征边界条 件.
显示原图|下载原图ZIP|生成PPT图 7边界节点处形函数及导数(从上到下依次为：$\tilde {N}$, $\tilde {N}_x $, $\tilde {N}_y $, $\tilde {N}_{xx} $, $\tilde {N}_{yy} )$ \\...
-->Fig. 7Shape functions and derivatives at boundary nodes (from top to bottom: $\tilde {N}$, $\tilde {N}_x $, $\tilde {N}_y $, $\tilde {N}_{xx} $, $\tilde {N}_{yy} )$...
-->
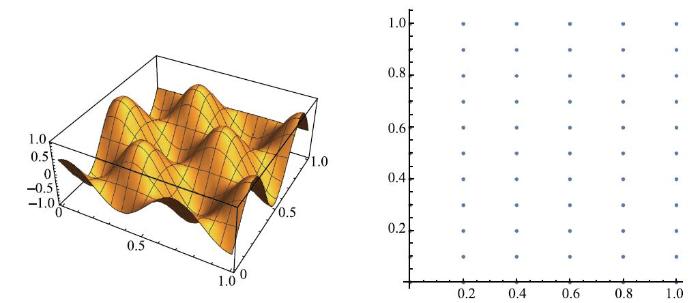显示原图|下载原图ZIP|生成PPT图 8理论解与所用的计算网格...
-->Fig. 8Exact solution and mesh used for shape function tests...
-->
显示原图|下载原图ZIP|生成PPT图 9沿对角线剖面上$u,\mbox{ }u_{,x} + u_{,y} ,\mbox{ }u_{,xx} + u_{,yy} $的插值结果与精确解比较...
-->Fig. 9Interpolated $u,\mbox{ }u_{,x} + u_{,y} ,\mbox{ }u_{,xx} + u_{,yy} $ along the diagonal of the square domain...
-->
显示原图|下载原图ZIP|生成PPT图 10底边界剖面上$u,\mbox{ }u_{,x} + u_{,y} ,\mbox{ }u_{,xx} + u_{,yy} $的插值结果与精确解比较...
-->Fig. 10Interpolated $u,\mbox{ }u_{,x} + u_{,y} ,\mbox{ }u_{,xx} + u_{,yy} $ along the lower horizontal boundary of the square domain...
-->
3 数值算例
采用上述C$^{1}$型插值,求解二维Poisson方程$$\left.\begin{array}{ll} \nabla ^2u = f~~\mbox{ in }\Omega u = \bar {u}~~\mbox{ on }\partial \Omega \end{array}\right\}(10) $$
其中,$\nabla ^2 = \dfrac{\partial ^2}{\partial x^2} + \dfrac{\partial ^2}{\partial y^2}$为二维拉普拉斯算子. 以收敛性测试为目的,人为定义如下的精确解
$$\left.\begin{array}{ll} u(x,y) = xy(1-x)(1-y)\sin x\sin y \bar {u} = 0 \end{array}\right\}(11) $$
满足上述精确解的右端项 $f $可由PDE直接求的.
收敛性测试的误差用下列的场变量的L$_{2}$模与"能量"模计算
$$\left\| u \right\| = \left[ {\int_{\Omega } {\left( {u^h - u^{{ exact}}} \right)^{ T}\left( {u^h-u^{{ exact}}} \right)} { { d}\varOmega }} \right]^{\frac{1}{2}}(12) $$
$$\left\| e \right\| = \left[ {\int_{\Omega } {\left( {\nabla u^h-\nabla u^{{ exact}}} \right)^{ T}\left( {\nabla u^h - \nabla u^{{ exact}}} \right)} { { d}\varOmega }} \right]^{\frac{1}{2}}(13) $$
由于本文提出的广义有限元插值格式的高阶光滑特性,对上述PDE的求解,既可以采用弱形式离散,也可以对PDE强形式进行直接离散.
3.1 基于PDE弱形式求解
基于加权余量法,导出Poisson方程的弱形式为$$\int_\varOmega {\left( {\nabla \cdot \nabla u + f} \right)w\mbox{d}\varOmega } = 0(14) $$
应用高斯散度定理
$$ -\int_\varOmega {\left( {\nabla \cdot \nabla u} \right)w\mbox{d}\varOmega } = \int_\varOmega {\nabla u \cdot \nabla w\mbox{d}\varOmega } - \int_{\partial \varOmega } {\nabla u \cdot nw\mbox{d}S}(15) $$
得到弱形式如下
$$\int_\varOmega {\nabla u \cdot \nabla w\mbox{d}\varOmega }-\int_{\partial \varOmega } {\nabla u \cdot nw\mbox{d}S}-\int_\varOmega {wf\mbox{d}\varOmega } = 0(16) $$
应用本文C$^{1}$型插值的Galerkin离散,并顾及权函数的任意性(假设其在边界处取值为0),得到离散方程
$$\left.\begin{array}{lll} {{ {Ku}}} = {{ F}} {{ K}} = \int_\varOmega {\nabla {{\tilde { N}}}^{ T}\nabla {{\tilde { N}}}} \mbox{d}\varOmega ,\quad {{{ F} = }}\int_\Omega {{{\tilde { N}}}^{ T}f} \mbox{d}\varOmega \end{array}\right\}(17) $$
计算采用5$\times $5直角坐标网格,求解域为[0,0]$\times $ [1,1]的正方形区域. 整个网格上共6$\times $6个节点,每一个节点一个自由度.
图11给出沿(0,0)-(1,1)对角剖面上的$u$,$u_{,x}$,$u_{,xx}$的数值解,以及与精确解的对比. 图11(a)对应广义有限元方法直接退化为标准有限元方法的情形(节点集仅包含一个点). 从图可以看出,由于标准有限元形函数的C$^{0}$特点,所得到的场函数的导数$u_{,x}$不连续,场函数的二阶导为0. 改变节点集半径至1$h$,($h$为网格尺寸),即每个节点集包含9个节点,计算结果显示于图11(b). 可以看出,场函数导数$u_{,x}$变得连续,二阶导$u_{,xx}$不连续,表现出C$^{1}$连续性. 进一步,将节点集扩大到2$h$,每个节点集包含25个节点,计算结果显示于图11(c). 从图中可以看出,沿该剖面上场函数、一阶导、二阶导均连续. 但需要说明的是,由于节点集对称性问题,二阶导在边界处不具有二阶导连续性. 因此,对于$2h$基,仍然不是全求解域上C$^{2}$连续(但通过配置节点集分布,可以实现C$^{2}$ 连续).
图11所示的3种计算工况,网格和自由度总数均保持不变、仅通过调节节点集的大小,实现标准有限元和两种不同阶次的C$^{1}$型广义有限元之间的转换. 随着节点集尺寸的增大,插值精度也得到 提高.
图12给出3种节点集尺寸的收敛性测试曲线. 可以看出,方法精度和收敛速率随节点集的扩大而提高,方法无需改变网格和自由度总数,获得高阶收敛.
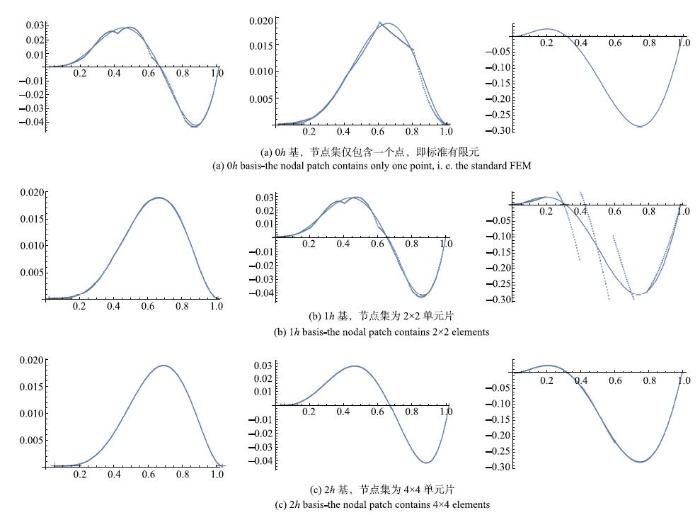显示原图|下载原图ZIP|生成PPT图 11弱形式计算结果. 从左到右依次为$u$,$u_{,x}$,$u_{,xx}$...
-->Fig. 11Results from weak form calculation. From left to right: $u$, $u_{,x}$, $u_{,xx}$...
-->
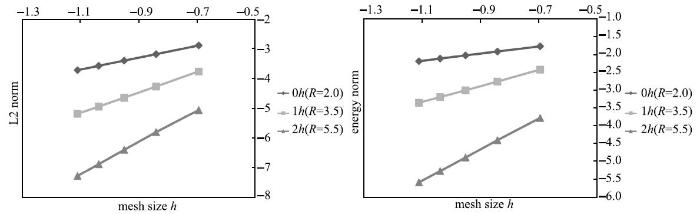显示原图|下载原图ZIP|生成PPT图 12弱形式收敛性测试结果. $R$为收敛率,0$h$, 1$h$, 2$h$分别对应三种不同节点集尺寸. 0$h$时,GFEM退化为标准有限元...
-->Fig. 12Convergence test results. $R$ is convergence rate. 0$h$, 1$h$, 2$h$ stand for three nodal patch sizes. $0h$ means that GFEM degenerates into the standard FEM
-->
3.2 基于PDE强形式直接离散
由于该插值格式的高阶光滑性,可以对PDE强形式直接离散.对Poisson方程的直接离散得$$ -\sum\nolimits_i {\left( {\tilde {N}_{i,xx} + \tilde {N}_{i,yy} } \right)u_i } = f_i(18) $$
式中$u_i$, $f_i$ 为定义在节点处的场量和体载荷密度. $n$个节点联立$n$个方程. 在每一个节点处建立与自由度数相同的联系方程组,组装成总体方程系统为
$$\left[ \!\!\begin{array}{cccc} {-{{\tilde N}_{1,xx}}\left( {{x_1}} \right)-{{\tilde N}_{1,yy}}({x_1})}& \ldots &{-{{\tilde N}_{n,xx}}\left( {{x_1}} \right)-{{\tilde N}_{n,yy}}({x_1})}\ \vdots & \ldots & \vdots \\ {-{{\tilde N}_{1,xx}}\left( {{x_n}} \right)-{{\tilde N}_{1,yy}}({x_n})}& \ldots &{-{{\tilde N}_{1,xx}}\left( {{x_n}} \right)-{{\tilde N}_{1,yy}}({x_n})} \end{array}\!\!\right]_{n \times n}$$$$\left( {\begin{array}{*{20}{c}} {{u_1}}\ \vdots \\ {{u_n}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{f_1}}\ \vdots \\ {{f_n}} \end{array}} \right) = 0$$
总体矩阵为
$${ K} \!=\! {\left[ \!\!{\begin{array}{*{20}{c}} {-{{\tilde N}_{1,xx}}\left( {{x_1}} \right)-{{\tilde N}_{1,yy}}({x_1})}\!\!& \ldots &\!\!{-{{\tilde N}_{n,xx}}\left( {{x_1}} \right)-{{\tilde N}_{n,yy}}({x_1})}\ \vdots \!\!& \ldots &\!\! \vdots \\ {-{{\tilde N}_{1,xx}}\left( {{x_n}} \right)-{{\tilde N}_{1,yy}}({x_n})}\!\!& \ldots &\!\!{-{{\tilde N}_{1,xx}}\left( {{x_n}} \right)-{{\tilde N}_{1,yy}}({x_n})} \end{array}}\!\! \right]_{n \times n}}$$
由于标准有限元的局部紧致性,总体矩阵仍然具有稀疏带状特点. 这一离散格式似乎与差分方法类似. 但它实际上更接近于有限元方法：该插值格式可以给出任意点处的导数插值,而差分所有的导数均只能定义在节点处. 所以与"差分"不同,它具有有限元的"插值"的特点.
这里需要注意的是,当将该C$^{1}$光滑插值用于强形式PDE的直接离散时,$\mbox{C}^0$有限元形函数在节点处导数不唯一的特点会导致新插值方法在节点处的导数计算需特殊处理.
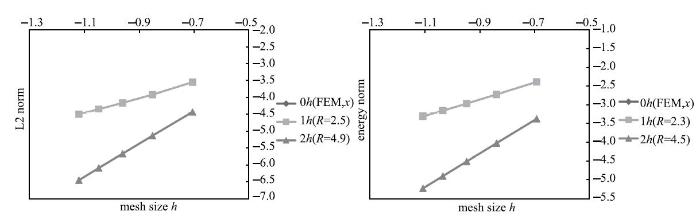
图13和图14分别给出基于$h$和2$h$两种节点集所构造出的C$^{1}$型GFEM的计算结果和收敛性测试结果. 该计算结果验证了新的插值格式的光滑性以及对PDE强形式直接离散求解的正确性.
3.3 两类计算结果比较
我们将基于强、弱两种形式的计算结果在图15和图16进行比较. 可以看出,新的插值方法无论是基于那种PDE的形式,均可以给出满意的解答;仅从图中曲线已难以分辨出二者的差异.
显示原图|下载原图ZIP|生成PPT图 13强形式的计算结果. 从左到右依次为$u$,$u_{,x}$,$u_{,xx}$. 标准有限元无法直接求解PDE强形式,所以没有对应结果...
-->Fig. 13Results from strong form calculation. From left to right: $u$, $u_{,x}$, $u_{,xx}$. Since the standard FEM is not able to solve a strong-form PDE, no corresponding results are available
-->
显示原图|下载原图ZIP|生成PPT图 14强形式收敛性测试结果. $R$为收敛率. C$^{0}$标准有限元无法用于PDE强形式求解,图中未给出对应结果...
-->Fig. 14Convergence test results. $R$ is convergence rate. Since the standard C$^{0}$ FEM is not able to solve a strong-form PDE,\\ no corresponding results are available
-->
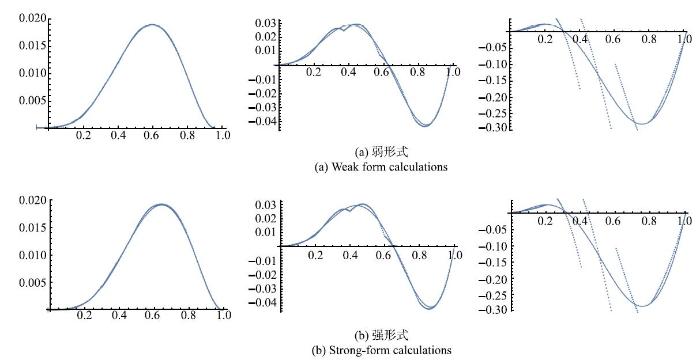
显示原图|下载原图ZIP|生成PPT图 15强、弱形式的计算结果比较. 基于1$h$基计算的$u$, $u_{,x}$, $u_{,xx}$...
-->Fig. 15Comparison between results from calculations: $u$, $u_{,x}$, $u_{,xx}$ based on 1$h$ basis
-->
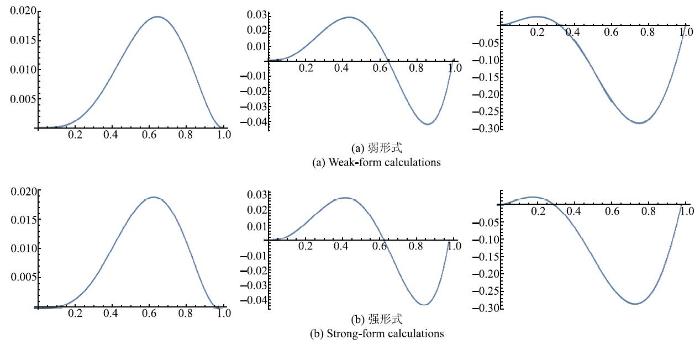
显示原图|下载原图ZIP|生成PPT图 16强、弱形式的计算结果比较. 基于2$h$基计算的$u, u,x, u,xx$...
-->Fig. 16Comparison between results from calculations: $u, u,x, u,xx$ based on 2$h$ basis
-->
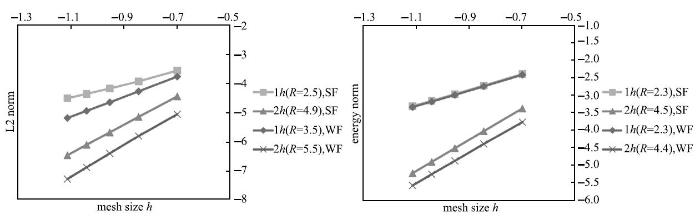
进一步,我们将收敛性曲线绘制在同一副图中进行比对. 从图17可以看出,新的插值格式对于弱形式和强形式求解所能达到的收敛阶,特别是"能量"误差模的收敛阶是相同的;在精度上,无论是场函数还是其导数,基于弱形式的计算精度更好一些. 但同时,基于强形式计算,无需进行数值积分,总体矩阵的集成上计算代价要小. 对于高阶方法而言更是如此.
显示原图|下载原图ZIP|生成PPT图 17弱形式与强形式计算结果比较. SF：强形式,WF：弱形式...
-->Fig. 17Convergence comparisons between the results obtained For strong and weak forms. SF: strong form, WF: weak form
-->
4 结论
无额外自由度单位分解广义有限元方法是为解决现有单位分解插值的线性相关性/总体矩阵病态的问题而提出的. 本文在无额外自由度单位分解插值的基础上,进一步基于C$^{0}$标准有限元单位分解函数,构造出具有C$^{1}$连续性的无额外自由度广义有限元格式. 当节点集严格关于片心节点对称(此时,需要在求解域外布置虚点),该插值格式具有与局部函数相同的光滑性,即C$^{n}$连续.由于其高阶光滑特性,该插值格式可同时用于PDE强形式与弱形式的求解. 针对Poisson方程的数值测试表明,无论用于哪一种PDE形式的求解,方法均可在不改变网格和自由度数的情况下,仅通过改变节点集大小的方式,实现高阶插值.
当用于PDE强形式的直接离散时,方法相对于有限差分的特点是：可以方便地在域内任意点处进行场量及其导数的插值计算.
使用该插值格式的条件是：网格须是直角坐标网格(不要求均匀). 因此,该插值格式目前主要适用于欧拉网格.
该插值格式可以用于流体力学问题和使用欧拉背景网格求解动量方程的固体力学方法,如材料物质点法(material point method)[36]. 对于强形式的欧拉网格求解,该插值格式与"差分"不同之处在于,它具有有限元的"插值"的特点. 对于弱形式的积分求解,由于该插值具有导数连续性,特别是采用2$h$及以上高阶基的情形,插值函数的导数也足够光滑,因此可以允许积分网格独立于插值网格. 这一特点将使得弱形式的积分计算的实施更加灵活方便.
该插值格式无需改变标准有限元形函数,即可获得高阶光滑性. 因此具有计算实施方便的特点. 计算代价方面,如本文采用的拉格朗日多项式插值,计算代价增加并不明显;考虑到其高阶精度和收敛性,构造拉格朗日多项式局部函数的代价完全可以接受.
未来的工作包括将该插值格式用于改善"材料物质点法"的精度等. 如基于强形式求解动量方程以彻底避免数值积分误差、利用其高阶光滑性减少弱形式计算时的跨网格噪声等.
附录：形函数在相邻单元公共边上的连续性
逼近函数(4)的一阶和二阶导数分别为
$$\frac{\partial u^h\left( {{x}} \right)}{\partial x} = \sum\limits_i {\left( {\partial _x N_i\sum\nolimits_k {\phi _k^{(i)} u_k } } \right)}+\ \sum\limits_i {\left( {N_i \sum\nolimits_k {\partial _x \phi_k^{(i)} u_k } } \right)}~~~(\mbox{A1})$$
$$\frac{\partial ^2u^h\left( {{ x}} \right)}{\partial x^2} =2\sum\limits_i {\left( {\partial _x N_i \sum\nolimits_k {\partial_x \phi _k^{(i)} u_k } } \right)} +\ \sum\limits_i {\left( {N_i \sum\nolimits_k {\partial _{xx} \phi_k^{(i)} u_k } } \right)}~~~(\mbox{A2})$$
显然,如果局部函数$\phi$具有C$^{n}$连续性,上述一、二阶导数中的第二项亦C$^{n}$连续.第一项看上去非连续的. 但是,可以证明,在直角坐标网格(不要求均匀)上,该项中非连续部分自动相互抵消,从而使得形函数具有高阶连续性
证明如下.
首先,我们给出一个典型节点集$P_{i}$上的局部函数$\phi _k^{(i)}\left( {{ x}} \right)$的表达式.由于是直角坐标网格,局部函数可以通过拉格朗日插值多项式构造如下
$$\phi _{k(m,l)}^{(i)} \left( {{ x}} \right) = L_x L_y =\frac{\prod\limits_{m \ne k} {\left( {\xi-k} \right)}}{\prod\limits_{m \ne k} {\left( {m-k} \right)}}\frac{\prod\limits_{l \ne k} {\left( {\eta-k} \right)}}{\prod\limits_{l \ne k} {\left( {l-k} \right)}}(\mbox{A3})$$
其中,$L_{x}$, $L_{y}$分别代表两个坐标方向上的插值函数,($m$,$l)$为节点集$P_{i}$上的第$j$个节点的坐标,({\it $\xi $}, {\it$\eta$})为插值点坐标,这些坐标均是以节点$i$为原点的局部坐标,$k$遍历节点集上所有局部坐标的可能取值.根据拉格朗日插值多项式的特点,该局部函数具有以下性质：
性质 当插值点({\it $\xi $}, {\it $\eta$})位于$P_{i}$的某条网格线上时,则与该插值点不共网格线的所有节点的局部函数自动为0,仅与该插值点共边或共点的节点的局部函数才非零.
比如,在一个半径为一个网格宽度的节点集上,当插值点正好落在网格线上时,则该网格线上的三个节点的局部函数非零,其余6个节点的局部函数全部为0.当插值点正好与节点重合,则仅该节点的局部函数非零(为1),其他为0.
接下来,我们讨论给定"左""右"两个相邻单元($I$-1, $I$, $J$,$J$-1)和($I$+1, $I$, $J$, $J$+1)的公共边$\overline {IJ}$上形函数导数形式. 为简化表述,使用图示的节点编号.当插值点位于$\overline {IJ} $上时,$N_{I\pm 1} \equiv 0$,$N_{J\pm1} \equiv 0$.
$$\dfrac{\partial u^h\left( {{ x}}\right)}{\partial x} = \partial _x N_I \sum\nolimits_k {\phi_k^{(I)} u_k } + \partial _x N_{I-1} \sum\nolimits_k {\phi_k^{(I-1)} u_k } +$$ $$ ~~~~~\partial _x N_J \sum\nolimits_k{\phi _k^{(J)} u_k } + \partial _x N_{J-1} \sum\nolimits_k {\phi_k^{(J-1)} u_k } +\ N_I \sum\nolimits_k {\partial _x \phi_k^{(I)} u_k } + N_J \sum\nolimits_k {\partial _x \phi _k^{(J)}u_k } (\mbox{A4})$$
以附图1中的编号为例,以边$\overline {7,12}$上的某点处的插值为例,根据拉格朗日插值特点,我们知道在节点集$P_{6}$和$P_{7}$上,局部函数$\varphi_2^{(6)} $,$\varphi _7^{(6)} $,$\varphi _{12}^{(6)} $和$\varphi_2^{(7)} $,$\varphi _7^{(7)} $,$\varphi _{12}^{(7)}$非零,其余均为0. 同理,节点集$P_{11}$和$P_{12}$上仅有$\varphi_7^{(11)} $,$\varphi _{12}^{(11)} $,$\varphi _{17}^{(11)} $和$\varphi _7^{(12)} $,$\varphi _{12}^{(12)} $,$\varphi_{17}^{(12)} $非零.
附图1 均匀直角坐标网格示意...
-->Fig. A1 Sketch of the cartesian grid
-->
对于节点集$P_{6}$,插值点$x$方向局部坐标$\xi=1$,节点2,7,12的$x$方向局部坐标$m$ =1,两者相同,因此,节点2,7,12处的$x$方向拉格朗日插值多项式均为1,即
$$L_x (1) = \frac{\prod\limits_{k \ne 1} {\left( {1-k}\right)} }{\prod\limits_{k \ne 1} {\left( {1-k} \right)} }\equiv 1(\mbox{A5})$$
对于节点集$P_{6}$,节点2,7,12处$y$方向局部坐标$l$ =$-1, 0, 1$,$y$方向拉格朗日插值多项式为
$$\left.\begin{array}{l} L_y (\eta ) = \dfrac{\prod\limits_{k \ne-1} {\left( {\eta-k} \right)}}{\prod\limits_{k \ne-1} {\left( {-1-k} \right)} }\\ L_y (\eta ) = \dfrac{\prod\limits_{k \ne 0} {\left( {\eta-k} \right)}}{\prod\limits_{k \ne 0} {\left( {0-k} \right)} } \\ L_y (\eta ) = \dfrac{\prod\limits_{k \ne 1} {\left( {\eta-k} \right)}}{\prod\limits_{k \ne 1} {\left( {1-k} \right)} } \end{array}\right\}(\mbox{A6})$$
其中,{\it $\eta $}为相对节点6定义的插值点局部$y$坐标.可以看出,这些局部函数仅与2, 7, 12的纵坐标与插值点坐标相关.因此,容易得到
$$ \phi _2^{(6)} + \phi _7^{(6)} + \phi_{12}^{(6)} = \frac{\prod\limits_{k \ne-1} {\left( {\eta-k}\right)} }{\prod\limits_{k \ne-1} {\left( {-1-k} \right)}} +\ \frac{\prod\limits_{k \ne 0} {\left( {\eta-k} \right)}}{\prod\limits_{k \ne 0} {\left( {0-k} \right)} } +\frac{\prod\limits_{k \ne 1} {\left( {\eta-k} \right)}}{\prod\limits_{k \ne 1} {\left( {1-k} \right)} }(\mbox{A7})$$
同理,对于节点集$P_{7}$,可以得到
$$ \phi _2^{(7)} + \phi _7^{(7)} + \phi _{12}^{(7)} =\frac{\prod\limits_{k \ne-1} {\left( {{\eta }'-k} \right)}}{\prod\limits_{k \ne-1} {\left( {-1-k} \right)} } +\\ \frac{\prod\limits_{k \ne 0} {\left( {{\eta }'-k} \right)}}{\prod\limits_{k \ne 0} {\left( {0-k} \right)} } +\frac{\prod\limits_{k \ne 1} {\left( {{\eta }'-k} \right)}}{\prod\limits_{k \ne 1} {\left( {1-k} \right)} }(\mbox{A8})$$
其中,${\eta}'$为相对节点6定义的插值点局部$y$坐标. 显然,$\eta = {\eta}'$,因此,我们得到
$$\phi _2^{(6)} + \phi _7^{(6)} +\phi _{12}^{(6)} = \phi _2^{(7)} + \phi _7^{(7)} + \phi_{12}^{(7)}(\mbox{A9})$$
返回形函数的一般写法,可得
$$\sum\nolimits_k {\phi_k^{(I)} u_k } = \sum\nolimits_k {\phi _k^{(I-1)} u_k}(\mbox{A10})$$
同理
$$\sum\nolimits_k {\phi _k^{(J)} u_k } =\sum\nolimits_k {\phi _k^{(J-1)} u_k}(\mbox{A11})$$
同时,对于直角坐标网格,有限元形函数具有如下性质(不失一般性,假设$\overline{IJ} $与$y$坐标轴平行)
$$\partial _x N_I =-\partial _x N_{I-1} ,\mbox{ }\partial _y N_I =\partial _y N_{I-1} ,\mbox{ }(x,y) \in IJ(\mbox{A12})$$
最终,形函数沿$x$,$y$方向偏导数成为
$$\frac{\partialu^h\left( {{ x}} \right)}{\partial x} = N_I \sum\nolimits_k{\partial _x \phi _k^{(I)} u_k } + N_J \sum\nolimits_k {\partial_x \phi _k^{(J)} u_k }(\mbox{A13})$$
$$ \frac{\partial u^h\left( {{ x}} \right)}{\partial y} = 2\partial _yN_I \sum\nolimits_k {\phi _k^{(I)} u_k } + 2\partial _y N_J\sum\nolimits_k {\phi _k^{(J)} u_k } +$$ $$ N_I \sum\nolimits_k{\partial _y \phi _k^{(I)} u_k } + N_J \sum\nolimits_k {\partial_y \phi _k^{(J)} u_k } (\mbox{A14})$$
当$\overline {IJ} $与$y$坐标轴平行,$\partial _y N_I $连续.形函数导数仅与插值点所在网格线$\overline {IJ}$上的节点的有限元形函数和局部函数相关,与左右两侧单元无关;形函数导数在该网格线上具有连续性.对于$\overline {IJ}$与$x$坐标轴平行的情形,上述导数的表达形式只需将$x$和$y$对调即可.形函数导数的连续性结论不变.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | . |
| [3] | . |
| [4] | . |
| [5] | . |
| [6] | . |
| [7] | . |
| [8] | . . |
| [9] | . . |
| [10] | . . |
| [11] | . |
| [12] | . |
| [13] | . |
| [14] | . |
| [15] | . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . |
| [21] | . |
| [22] | . |
| [23] | . |
| [24] | |
| [25] | . . |
| [26] | . . |
| [27] | |
| [28] | . . |
| [29] | . |
| [30] | . |
| [31] | . |
| [32] | . . |
| [33] | . . |
| [34] | . . |
| [35] | . |
| [36] |
