, 李云, 杜成斌河海大学工程力学系,南京 210098
IMPROVED EXTENDED SCALED BOUNDARY FINITE ELEMENT METHODS1)
JiangShouyan, LiYun, DuChengbin中图分类号:TB115
文献标识码:A
版权声明:2019力学学报期刊社力学学报期刊社 所有
基金资助:
作者简介:
-->
展开
摘要
关键词：
Abstract
Keywords：
-->0
PDF (1084KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNoteRisBibtex收藏本文-->
经过近二十年的发展,基于单位分解理论提出的扩展有限元法(XFEM)[1] 为含裂纹体结构的数值仿真模拟提供了新的有效途径[2- 4],XFEM通过在常规有限元法的位移模式中引入扩充函数项描述特殊的求解特性(如：不连续性、 应力奇异性),因此网格划分时无需遵从材料界面,但由此也带来了一系列问题,特别是不连续单 元刚度矩阵的求解需要特别的技术,如：分区域积分法[5-6],即将不连续单元划分成若干子四边形或子三角形单元,数值积分先在子单元内完成再累加形成不连续单元的刚度矩阵;Bordas等[7]发展了光滑的扩展有限元法,通过散度定理将面积分转化成线积分,简化了不连续单元的数值积分;Ventura[8]提出了一种无需进行单元子划分的不连续单元的数值积分方法,先将非多项式函数等效成多项式函数,再进行积分求解刚度矩阵,但该方法仅对三角形或四面体单元有较好的精度;Natarajan等[9]在文献[10]的基础上基于Schwarz--Christoffel保角映射定理发展了简化的数值积分方法进行不连续单元刚度矩阵的求解,也无需对不连续单元进行子划分. 此外,构造XFEM法位移模式时,需要预先知道裂尖渐进解析场的形式,并由此引入额外自由度[11-12],文献[13]在构造求解双材料界面裂纹问题的XFEM位移模式时,根据双材料界面裂纹尖端位移场的解析解,对于裂尖单元选取了十二项改进函数,裂尖单元结点的附加自由度数为24;文献[14,15]运用XFEM求解动力问题时,同样需要预先知道动载下裂尖位移场的解析解以便构造XFEM位移模式;但是,对于一些更复杂的工况,无法知道裂尖渐进解析场的形式时,XFEM的位移模式构造便产生了困难.
比例边界有限元法(scaled boundary finite element method,SBFEM)是由Wolf和Song在20世纪90 年代末率先提出和发展起来的一种半解析的数值计算方法[16 - 17],该方法在计算过程中仅需离散结构的边界,降低了一维数值模拟的维度, 而且可以半解析地表征裂纹尖端的奇异性[18],目前,已广泛应用于断裂问题领域[19 - 22]. Natarajan等[23]和大连理工大学李建波等[24 - 27]基于 XFEM和SBFEM的思想提出了扩展比例边界有限元法(X-SBFEM)的概念, 该方法的核心是采用XFEM模拟裂纹贯穿单元、SBFEM模拟裂尖单元, 从而避免了构造裂尖单元复杂扩充函数以及采用特殊的数值积分技术进行裂尖单元刚度矩阵的求解.
文中在文献[23,24,25,26,27]的基础上,借助XFEM和SBFEM的主要思想,将不连续单元作为SBFEM的子域处理, 采用SBFEM求解单元刚度矩阵,从而避免了XFEM中求解不连续单元刚度矩阵需要进一步进行单元子划分的缺陷; 同时,借助XFEM的主要思想,将裂纹与单元边界交点的真实位移作为单元结点的附加自由度考虑, 赋予了单元结点附加自由度明确的物理意义,可以直接根据位移求解结果得出裂纹与单元边界交点的位移, 而在常规XFEM中,需要进一步根据XFEM位移模式通过后处理求解裂纹与单元边界交点的位移, 文中将该方法称为改进型扩展比例边界有限元法(improved extended scaled boundary finite element methods,$i$XSBFEM),以期结合XFEM和SBFEM的主要优点,为裂纹的断裂扩展模拟提供一条新的途径.
1 扩展有限元法
1.1 XFEM位移模式
对于裂纹类强不连续问题,XFEM的位移模式可表示为$${\boldsymbol{u}}^{h}({\boldsymbol{x}}) = \sum\limits_{i \in I} {N_i ({\boldsymbol{x}})} {\boldsymbol{u}}_i +\\ \qquad \sum\limits_{i \in I_{{abs}}^{\ast } } {N_i^\ast } ({\boldsymbol{x}})[H({\boldsymbol{x}})-H({\boldsymbol{x}}_i )]{\boldsymbol{a}}_i+ \\ \qquad \sum\limits_{i \in I_{{br}}^{\ast } } {N_i^\ast } ({\boldsymbol{x}})\sum\limits_{j = 1}^n {[F_j } ({\boldsymbol{x}}) - F_j ({\boldsymbol{x}}_i )]{\boldsymbol{b}}_i^j \tag{1}$$
式中,$I$为求解域中所有结点的集合;$N_i ({\boldsymbol{x}})$为结点$i$处的常规有限元插值形函数;${\boldsymbol{u}}_i $为常规有限元部分在结点$i$处的未知量;$N_i^\ast ({\boldsymbol{x}})$为单位分解函数,其形式可以和$N_i ({\boldsymbol{x}})$相同,也可以不同,文中取二者相同;$H({\boldsymbol{x}})$ 为Heaviside改进函数;$I_{{ abs}}^{\ast } $为Heaviside改进结点集合;${\boldsymbol{a}}_i $为与Heaviside改进相关的结点未知量;$I_{{br}}^{\ast } $为裂尖改进结点集合;${\boldsymbol{b}}_i^j $为与裂尖改进相关的结点未知量.
如图1所示,对于被裂纹完全贯穿单元的结点采用Heaviside函数进行改进;对于被裂纹部分切割的单元,即包含裂尖的单元,采用裂尖改进函数进行改进;对于既含有改进结点又含有常规结点的单元,称为混合单元(blending element).
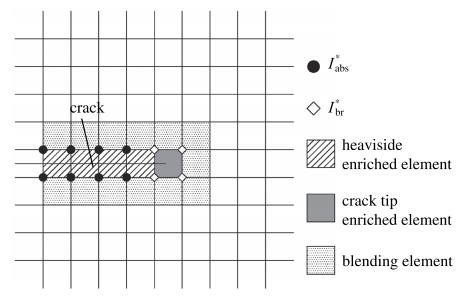显示原图|下载原图ZIP|生成PPT图1XFEM中改进单元和改进结点的选取...
-->Fig. 1A strategy for enriched elements and nodes in XFEM...
-->
Heaviside函数可表达为
\begin{equation} \label{eq2} H({\boldsymbol{x}}) = \left\{ {{\begin{array}{lll} + 1,& {({\boldsymbol{x}}-{\boldsymbol{x}}^\ast ) \cdot {\boldsymbol{n}} > 0} \\ -1, & {({\boldsymbol{x}}-{\boldsymbol{x}}^\ast ) \cdot {\boldsymbol{n}} < 0} \end{array} }} \right.\tag{2}\end{equation}
其中,${\boldsymbol{x}}$为考察点,${\boldsymbol{x}}^\ast $为考察点在裂纹面上的投影点,${\boldsymbol{n}}$为${\boldsymbol{x}}^\ast $处裂纹面的单位外法向.
对于裂尖单元结点的改进函数形式通常取为以下4项
式中,$r$和$\theta $}为裂纹尖端局部坐标系.
1.2 XFEM离散方程
采用Galerkin方法建立基本方程的离散形式,试探函数${\boldsymbol{u}}$ 的近似函数${\boldsymbol{u}}^h$和权函数${\boldsymbol{v}}$的近似函数${\boldsymbol{v}}^h$相同, 由于${\boldsymbol{v}}^h$的任意性,可得离散系统的控制方程为\begin{equation} \label{eq4} \left[ {{\begin{array}{*{20}c} {{\boldsymbol{K}}_{uu} } & {{\boldsymbol{K}}_{ua} } & {{\boldsymbol{K}}_{ub} } \\ {{\boldsymbol{K}}_{au} } & {{\boldsymbol{K}}_{aa} } & {{\boldsymbol{K}}_{ab} } \\ {{\boldsymbol{K}}_{bu} } & {{\boldsymbol{K}}_{ba} } & {{\boldsymbol{K}}_{bb} } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {\boldsymbol{u}} \\ {\boldsymbol{a}} \\ {\boldsymbol{b}} \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {{\boldsymbol{F}}_u } \\ {{\boldsymbol{F}}_a } \\ {{\boldsymbol{F}}_b } \\ \end{array} }} \right\}\tag{4} \end{equation}
式中,${\boldsymbol{K}}_{ij} \left( {i,j = u,a,b} \right)$为整体刚度矩阵,${\boldsymbol{F}}_i \left( {i = u,a,b} \right)$为整体载荷列阵.
1.3 XFEM面临的数值困难
与常规有限元法相比,式(1)给出的XFEM位移模式由于引入了改进函数项,给XFEM的数值求解带来了一系列困难,也因此影响XFEM的数值求解精度和收敛性,具体表现在以下几个方面.(1) {求解刚度矩阵的被积函数含有不连续函数或奇异函数. }常规的处理方法是将不连续单元进行子划分,根据裂纹的位置进一步将单元划分成若干三角形或四边形子单元,在子单元内需要布置足够数量的高斯积分点进行数值积分,图2为笔者前期XFEM研究中采用的单元子划分方式 [29-30].
(2)混合单元处不满足单位分解条件.XFEM中,只有部分结点被改进的单元称为混合单元,如图1所示. 对于裂纹问题,采用式(1)给出的位移模式时,含有裂尖改进结点的混合单元均不满足单位分解条件,降低了数值求解的精度. Fries[30]建议的校正扩展有限元法通过拓展改进结点域有效解决了这一问题,但是增加了附加自由度数.
(3) 引入了附加自由度. 由于XFEM位移模式增加了不连续改进函数项,引入了附加自由度,附加自由度数与改进函数有关. 式(1)给出的位移模式中,裂纹贯穿单元的结点$i(i \in I_{{ abs}}^{\ast } )$引入了2个附加自由度,含裂尖单元单元的结点$i(i \in I_{{br}}^{\ast } )$引入了8个附加自由度.
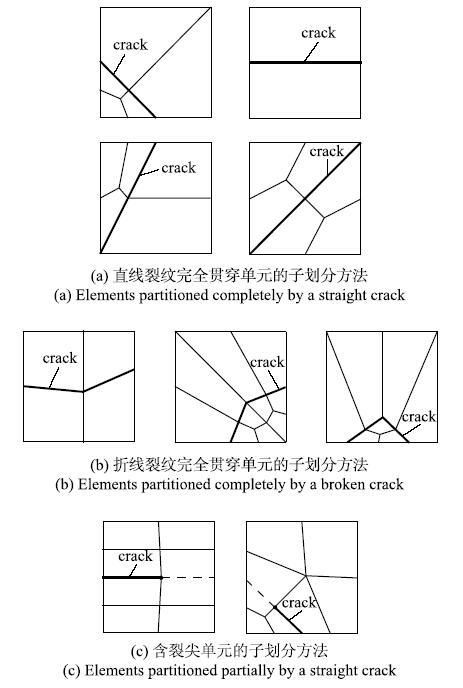显示原图|下载原图ZIP|生成PPT图2不连续单元的子划分方法...
-->Fig.2Element partitioning method for these elements containing a discontinuous interface...
-->
(4) 病态的总体刚度矩阵. XFEM基于单位分解理论在局部进行插值强化,由于单位分解插值的线性相关性,XFEM的总体刚度矩阵条件数随$h^{ - 6}$变化(常规有限元为$h^{-2})^{[11].
2 不连续单元刚度矩阵的求解
与XFEM类似,无需按照材料的内部界面进行网格剖分,仍然采用两个正交的水平集函数表征材料内部裂纹面, 并基于水平集函数判断单元切割类型[31]. 如图3所示,对于被裂纹切割单元作为SBFE的子域处理,采用SBFEM求解单元刚度矩阵. 考虑到SBFEM本身的特性,即在选取比例中心时需要满足对单元所有边界具有较好的可见度, 因此,对于含有裂尖的单元,选取围绕裂尖单元一圈的共计若干层单元作为超级单元, 并将此超级单元作为SBFE的一个子域求解刚度矩阵,超级单元内部的结点位移可通过SBFE的位移模式求解得到.借助XFEM的思想,对于被裂纹完全切割的单元,单元结点包含附加自由度,在结点每个方向增加1个自由度, 附加自由度的物理意义为裂纹与单元边界交点的结点真实位移. 如图4所示,对于裂 纹贯穿单元的4个结点均包含附加自由度,对于包含裂尖的超级单元,仅被裂纹切割的单元边界中的2个结点包含附加自由度. 相比于XFEM,附加自由度的数目有所减少.
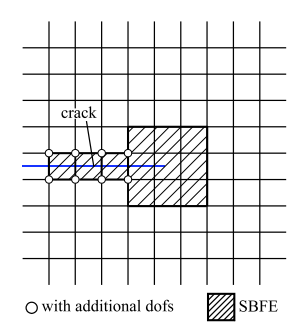显示原图|下载原图ZIP|生成PPT图3$i$XSBFEM中单元类型和改进结点的选取...
-->Fig.3A strategy for elements types and enriched nodes in the improved XSBFEM...
-->
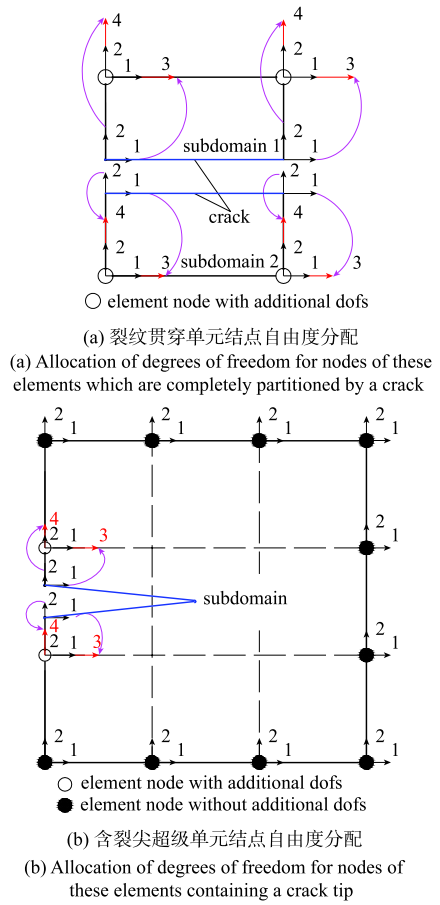显示原图|下载原图ZIP|生成PPT图4SBFE子域的结点自由度分配...===
-->Fig.4Allocation of degrees of freedom for nodes for SBF...E
-->
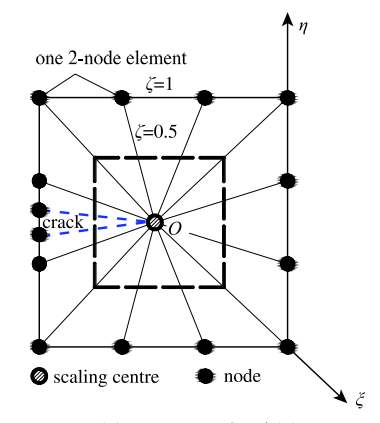显示原图|下载原图ZIP|生成PPT图5SBFM子域示意图...
-->Fig.5Schematic of SBFE subdomain...
-->
构成SBFE子域的2结点线单元上的任意点坐标为
\begin{equation} \label{eq5} {\boldsymbol{x}}_{b} \left( \eta \right) = {\boldsymbol{N}}\left( \eta \right){\boldsymbol{x}}_{b}\tag{5} \end{equation}
式中,${\boldsymbol{x}}_{b} $为边界上的结点坐标;${\boldsymbol{N}}\left( \eta \right)$为2
结点线单元形函数.
对于SBFE子域内任意一点,该点在笛卡尔坐标下的坐标${\boldsymbol{x}}$可用比例边界坐标$\xi $和$\eta $表示为$${\boldsymbol{x}} = {\boldsymbol{x}}_0 + \xi {\boldsymbol{x}}_b \left( \eta \right)\tag6$$ 式中,${\boldsymbol{x}}_0 $为比例中心坐标;$\xi $为归一化的由比例中心指向边界的径向坐标,在比例中心处$\xi = 0$,在边界处$\xi = 1$.
SBFE子域的位移模式可以表示为
\begin{equation} \label{eq6} {\boldsymbol{u}}\left( {\xi ,\eta } \right) = {\boldsymbol{N}}\left( \eta \right){\boldsymbol{u}}\left( \xi \right)\tag{7} \end{equation}
式中,${\boldsymbol{u}}\left( \xi \right)$为沿径向的位移,由一组$N$个解析函数式构成. 将位移模式(7)代入应力--应变关系式得到应变为
\begin{equation} \label{eq7} {\boldsymbol{\varepsilon }}\left( {\xi ,\eta } \right) = {\boldsymbol{Lu}}\left( {\xi ,\eta } \right)\tag{8} \end{equation}
式中,${\boldsymbol{L}}$为比例边界坐标系中的线性算子矩阵,可表达为
\begin{equation} \label{eq8} {\boldsymbol{L}} = {\boldsymbol{b}}_1 \left( \eta \right)\frac{\partial }{\partial \xi } + \frac{1}{\xi }{\boldsymbol{b}}_2 \left( \eta \right)\frac{\partial }{\partial \eta }\tag{9} \end{equation}
且
$$ \label{eq9} {\boldsymbol{b}}_1 \left( \eta \right) = \frac{1}{\left| {\boldsymbol{J}} \right|}\left[ {{\begin{array}{*{20}c} {y_{b} \left( \eta \right)_{,\eta } } 0 \\ 0 {-x_{b} \left( \eta \right)_{,\eta } } \\ {-x_{b} \left( \eta \right)_{,\eta } } {y_{b} \left( \eta \right)_{,\eta } } \\ \end{array} }} \right]\tag{10}$$
$$ \label{eq10} {\boldsymbol{b}}_2 \left( \eta \right) = \frac{1}{\left| {\boldsymbol{J}} \right|}\left[ {{\begin{array}{*{20}c} {-y_{b} \left( \eta \right)} 0 \\ 0 {x_{b} \left( \eta \right)} \\ {x_{b} \left( \eta \right)} {-y_{b} \left( \eta \right)} \\ \end{array} }} \right]\tag{11}$$
雅可比矩阵的行列式为
\begin{equation} \label{eq11} \left| {\boldsymbol{J}} \right| = x_{b} \left( \eta \right)y_{b} \left( \eta \right)_{,\eta }-x_{b} \left( \eta \right)_{,\eta } y_{b} \left( \eta \right)\tag{12} \end{equation}
应力${\boldsymbol{\sigma }}\left( {\xi ,\eta } \right)$为
$$ {\boldsymbol{\sigma }}\left( {\xi ,\eta } \right) = {\boldsymbol{DB}}_1 \left( \eta \right){\boldsymbol{u}}\left( \xi \right)_{,\xi } + \frac{1}{\xi }{\boldsymbol{DB}}_2 \left( \eta \right){\boldsymbol{u}}\left( \xi \right)\tag{13} $$
\begin{equation} \label{eq12} \begin{array}{l} {\boldsymbol{B}}_1 \left( \eta \right) = {\boldsymbol{b}}_1 \left( \eta \right){\boldsymbol{N}}\left( \eta \right) \\ {\boldsymbol{B}}_2 \left( \eta \right) = {\boldsymbol{b}}_2 \left( \eta \right){\boldsymbol{N}}\left( \eta \right)_{,\eta } \\ \end{array}\tag{14} \end{equation}
根据虚功原理[17],可得到以下两个方程
$$\label{eq13} {\boldsymbol{E}}_0 \xi ^2{\boldsymbol{u}}\left( \xi \right)_{,\xi \xi } + \left( {{\boldsymbol{E}}_0 + {\boldsymbol{E}}_1 ^{T}-{\boldsymbol{E}}_1 } \right)\xi {\boldsymbol{u}}\left( \xi \right)_{,\xi }-{\boldsymbol{E}}_2 {\boldsymbol{u}}\left( \xi \right) = 0\\ \tag{15}$$
$$\label{eq14} {\boldsymbol{F}} = \left. {\left( {{\boldsymbol{E}}_0 \xi {\boldsymbol{u}}\left( \xi \right)_{,\xi } + {\boldsymbol{E}}_1^{T} {\boldsymbol{u}}\left( \xi \right)} \right)} \right|_{\xi = 1}\tag{16}$$
式中,${\boldsymbol{F}}$为载荷列阵;且
\begin{equation} \label{eq15} {\boldsymbol{E}}_0 = \int_\eta {{\boldsymbol{B}}_1 \left( \eta \right)^{T}{\boldsymbol{DB}}_1 \left( \eta \right)\left| {\boldsymbol{J}} \right|{d}\eta }\tag{17} \end{equation}
\begin{equation} \label{eq16} {\boldsymbol{E}}_1 = \int_\eta {{\boldsymbol{B}}_2 \left( \eta \right)^{T}{\boldsymbol{DB}}_1 \left( \eta \right)\left| {\boldsymbol{J}} \right|{d}\eta }\tag{18} \end{equation}
\begin{equation} \label{eq17} {\boldsymbol{E}}_2 = \int_\eta {{\boldsymbol{B}}_2 \left( \eta \right)^{T}{\boldsymbol{DB}}_2 \left( \eta \right)\left| {\boldsymbol{J}} \right|{d}\eta }\tag{19} \end{equation}
式(15)的通解可以表示为
\begin{equation} \label{eq18} {\boldsymbol{u}}\left( \boldsymbol\xi \right) =\boldsymbol \phi \xi ^{-\lambda }{\boldsymbol{c}} = \sum {c_i \xi ^{-\lambda _i }\boldsymbol\phi _i }\tag{20} \end{equation}
式中,$\boldsymbol\phi _i $可看作模态位移,$ \lambda _i $为$ \xi$方向的比例因子,$c_i $为积分常数. 单个模态位移可表示为
\begin{equation} \label{eq19} {\boldsymbol{u}}\left( \xi \right) = \xi ^{ - \lambda }\boldsymbol\phi\tag{21} \end{equation}
式(21)满足方程(15)和(16),经过处理可得到以下特征值问题
\begin{equation} \label{eq20} \left[ {{\begin{array}{*{20}c} {{\boldsymbol{E}}_0^{-1} {\boldsymbol{E}}_1^{T} } & {-{\boldsymbol{E}}_0^{-1} } \\ {{\boldsymbol{E}}_1 {\boldsymbol{E}}_0^{-1} {\boldsymbol{E}}_1^{T}-{\boldsymbol{E}}_2 } & {-{\boldsymbol{E}}_1 {\boldsymbol{E}}_0^{-1} } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} \boldsymbol \phi \\ {\boldsymbol{q}} \\ \end{array} }} \right] = \lambda \left[ {{\begin{array}{*{20}c} \boldsymbol \phi \\ {\boldsymbol{q}} \\ \end{array} }} \right]\tag{22} \end{equation}
式(22)的求解可得到2$n$个模态,求解得到的特征向量包含模态位移向量$\boldsymbol\phi $和等效模态结点力向量${\boldsymbol{q}}$. 对于有限域问题,根据比例中心处($ \xi = 0)$应当含有有限位移的条件,仅与非负特征值$\boldsymbol\lambda $对应的$n$阶特征向量为有效解. $n$阶模态位移向量记为${\boldsymbol{\varPhi }}_{n\times n} $,$n$阶等效模态结点力向量记为${\boldsymbol{Q}}_{n\times n} $
根据求出的边界上($ \xi = 1)$结点位移,可得积分常数为
\begin{equation} \label{eq21} {\boldsymbol{c}} = {\boldsymbol{\varPhi }}^{ - 1}{\boldsymbol{u}}\tag{23} \end{equation}
等效结点力列阵可表示为
\begin{equation} \label{eq22} {\boldsymbol{F}} = {\boldsymbol{Qc}} = {\boldsymbol{Q\varPhi }}^{ - 1}{\boldsymbol{u}} \tag{24} \end{equation}
因此,可得子域刚度矩阵为
\begin{equation} \label{eq23} {\boldsymbol{K}} = {\boldsymbol{Q\varPhi }}^{-1}\tag{25} \end{equation}
因此,在XFEM中,对于被裂纹切割单元的刚度矩阵,可根据SBFEM的基本理论应用式(25)求解得出.
3 应力强度因子的计算
由J积分法推导得到的相互作用积分法(M积分法)在XFEM中应用较为广泛,能够较易分离出I型和II型应力强度因子,但是计算时需要提供辅助的应力场和位移场,给计算求解带来很多不便. 而在SBFEM中,可直接基于奇异位移和奇异应力结果求解应力强度因子.3.1 位移法
如图6所示,在裂尖局部坐标系中,对于各向同性材料,相应裂尖奇异应力项的裂尖位移场与应力强度因子的关系为$$ u_x^{s} \left( {r,\theta } \right) = \frac{K_{I} }{G}\sqrt {\frac{r}{2\pi }} \cos \frac{\theta }{2}\left[ {\frac{1}{2}\left( {\kappa-1} \right) + \sin ^2\frac{\theta }{2}} \right] +\\ \qquad \frac{K_{{II}} }{G}\sqrt {\frac{r}{2\pi }} \sin \frac{\theta }{2}\left[ {\frac{1}{2}\left( {\kappa + 1} \right) + \cos ^2\frac{\theta }{2}} \right] \tag{26a} $$
$$u_y^{s} \left( {r,\theta } \right) = \frac{K_{I} }{G}\sqrt {\frac{r}{2\pi }} \sin \frac{\theta }{2}\left[ {\frac{1}{2}\left( {\kappa + 1} \right)-\cos ^2\frac{\theta }{2}} \right] -\\ \qquad \frac{K_{{II}} }{G}\sqrt {\frac{r}{2\pi }} \cos \frac{\theta }{2}\left[ {\frac{1}{2}\left( {\kappa-1} \right) - \sin ^2\frac{\theta }{2}} \right] \tag{26b}$$
式中,$K_{I}$和$K_{ II}$为I型和II型应力强度因子,$G$为剪切模量,对于平面应变问题,$\kappa = 3-4\nu $,对于平面应力问题,$\kappa = {\left( {3-\nu } \right)} \mathord{\left/ {\vphantom {{\left( {3-\nu } \right)} {\left( {1 + \nu } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 + \nu } \right)}$,$\nu $为泊松比.
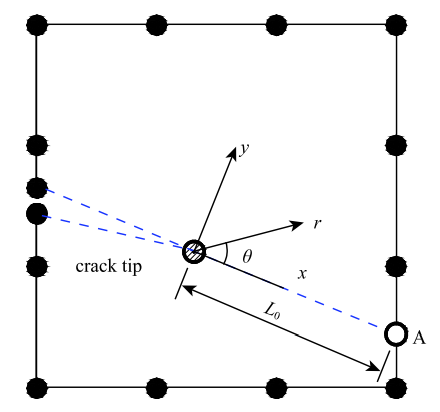显示原图|下载原图ZIP|生成PPT图6含裂尖的SBFE子域及局部坐标系的定义...
-->Fig.6A cracked domain modeled by SBFEM and the definition of local coordinate system
-->
根据裂纹开口处($r = r_0 $,$\theta = \pm \pi)$的张开位移,可得I型和II型应力强度因子为
$$\label{eq24} \left\{ {{\begin{array}{*{20}c} {K_{I} } \\ {K_{{II}} } \\ \end{array} }} \right\} = \frac{G}{\kappa + 1}\sqrt {\frac{2\pi }{r_0 }} \left\{ {{\begin{array}{*{20}c} {u_y^{s} \left( {r_0 ,\pi } \right)-u_y^{s} \left( {r_0 ,-\pi } \right)} \\ {u_x^{s} \left( {r_0 ,\pi } \right)-u_x^{s} \left( {r_0 ,-\pi } \right)} \\ \end{array} }} \right\}\tag{27} $$
3.2 应力法
此外,应力强度因子$K_{I}$和$K_{ II}$也可直接基于裂尖处($\theta = 0)$的奇异应力$\sigma _{yy}^{ s} $和$\sigma _{xy}^{s} $获得,即$$ \label{eq25} \left\{ {{\begin{array}{*{20}c} {K_{I} } \\ {K_{{II}} } \\ \end{array} }} \right\} = \sqrt {2\pi r} \left\{ {{\begin{array}{*{20}c} {\sigma _{yy}^{s} \left( {\theta = 0} \right)} \\ {\sigma _{xy}^{s} \left( {\theta = 0} \right)} \\ \end{array} }} \right\}\tag{28} $$
对于含裂纹的均匀SBFEM子域,奇异项的特征值近似等于$-$0.5,奇异项的位移可表达为
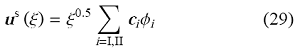
相应的边界上($\xi = 1)$结点位移为
\begin{equation} \label{eq27} {\boldsymbol{u}}_{b}^{s} = \sum\limits_{i = {I,{II}} {{\boldsymbol{c}}_i \phi _i }}\tag{30} \end{equation}通过式(13)和式(30)可得到奇异应力模态,并线性插值得到裂尖前缘($\theta = 0)$的应力模态${\boldsymbol{\psi }}_i \left( {\boldsymbol\theta = 0} \right)$. 在裂尖前缘$\xi = r \mathord{\left/ {\vphantom {r {L_0 }}} \right. \kern-\nulldelimiterspace} {L_0 }$,奇异应力为
\begin{equation} \label{eq28} \sigma \left( {r,\theta = 0} \right) = \sqrt {\frac{L_0 }{r}} \sum \limits_{i = {I,{II}}} {c_i \psi _i \left( {\theta = 0} \right)}\tag{31} \end{equation}
将式(31)代入式(28),得到求解应力强度因子的表达式为
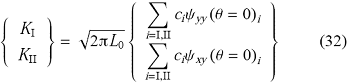
4 数值算例
4.1 纯I型裂纹问题
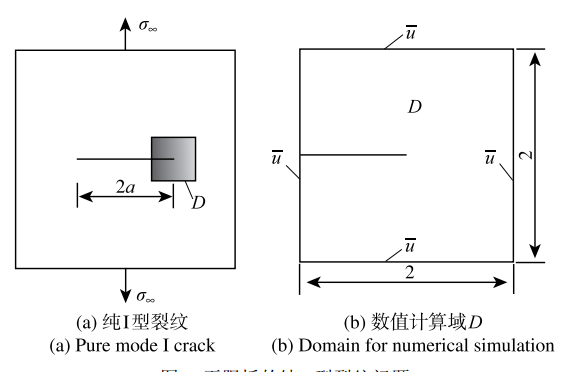
本算例为无限大板的纯I型裂纹问题,如图7(a)所示. 数值计算时,选取包含尖端的有限域$D$,如图7(b),按平面应变问题考虑,弹性模量取为100,泊松比取为0.3,有限域$D$的边长为2,被离散成$N\times N$个均匀网格,在$D$的边界上施加已知的位移边界条件.纯I型裂纹问题的解析位移场为[32]
\begin{equation} \label{eq30} \left. {{\begin{array}{l} {u_x = \frac{1}{G}\sqrt {\frac{r}{2\pi }} \cos \frac{\theta }{2}\left(1 - 2\nu + \sin ^2\frac{\theta }{2}\right)} \\[5mm] {u_y = \frac{1}{G}\sqrt {\frac{r}{2\pi }} \sin \frac{\theta }{2}\left(2 - 2\nu-\cos ^2\frac{\theta }{2}\right)} \\ \end{array} }} \right\}\tag{33} \end{equation}
式中,$G$为剪切模量,$\nu $为泊松比.
通过下式考察数值结果的收敛性
\begin{equation} \label{eq31} e_2 = \frac{\left\| {{\boldsymbol{u}} - {\boldsymbol{u}}^{h}} \right\|_{L^2} }{\left\| {\boldsymbol{u}} \right\|_{L^2} } = \left( {\frac{ \sum\limits_{i = 1}^{NP} {(u({\boldsymbol{x}}_i ) - u^{h}({\boldsymbol{x}}_i ))^2} }{ \sum\limits_{i = 1}^{NP} {u^2({\boldsymbol{x}}_i )} }} \right)^{1 / 2}\tag{34} \end{equation}
式中,$u^{h}({\boldsymbol{x}}_i )$为离散域的结点总数;$u^{ h}({\boldsymbol{x}}_i )$为考察结点的精确解;$u^{ h}({\boldsymbol{x}}_i )$为该结点处的数值解.
显示原图|下载原图ZIP|生成PPT图7无限板的纯I型裂纹问题...
-->Fig.7Pure mode I crack model in infinite plate
-->
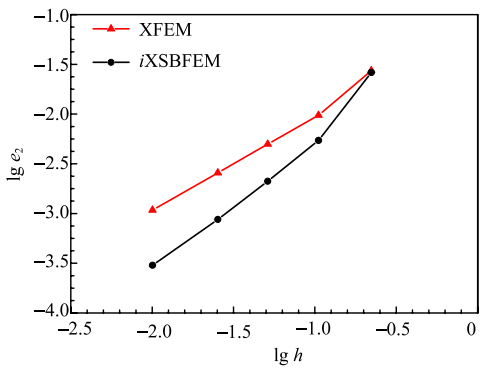
表1给出了分别采用常规XFEM和$i$XSBFEM求解控制方程所需的总自由度数,从表中可以看出,在相同网格条件下,采用$i$XSBFEM求解控制方程时总的自由度数总是较小,因此,在相同网格条件下采用$i$XSBFEM的求解效率更高. 图8给出了分别采用常规XFEM和$i$XSBFEM得到的基于位移范数的相对误差收敛性分析结果,可以看出,对于纯I型裂纹问题,$i$XSBFEM的收敛性相对较好,这是由于SBFEM模拟裂纹问题时,可以解析地求解出裂纹尖端的高阶应力奇异性. 相比于文献[23,24,25,26,27]提出的XSBFEM,文中提出的$i$XSBFEM对于被裂纹完全切割的单元也采用SBFEM法进行改进,求解被裂纹完全切割单元的刚度矩阵时也无需进一步对该单元进行子划分.
Table 1
表1
表1裂纹问题控制方程求解总的自由度数
Table 1Total degrees of freedom for the meshes used for crack problem
| Mesh | Total degrees of freedom | |
|---|---|---|
| iXSBFEM | XFEM | |
| 9x9 | 180 | 328 |
| 19x19 | 800 | 948 |
| 39x39 | 3240 | 3388 |
| 79x79 | 12 920 | 13 068 |
| 199x199 | 80 360 | 80 508 |
新窗口打开
显示原图|下载原图ZIP|生成PPT图8纯I型裂纹问题：基于位移范数的相对误差收敛性分析结果...
-->Fig.8Pure mode I crack: Convergence results for the relative error in the displacement norm
-->
4.2 纯II型裂纹问题
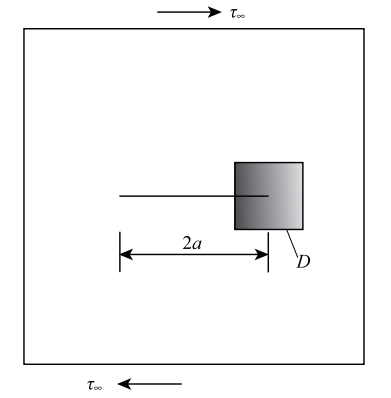
本算例为无限大板的纯II型裂纹问题,如图9所示,数值计算的计算参数同算例1.纯II型裂纹问题的解析位移场为[32]
\begin{equation} \label{eq32} \left. {{\begin{array}{ll} {u_x = \frac{1}{G}\sqrt {\frac{r}{2\pi }} \sin \frac{\theta }{2}\left(2 - 2\nu + \cos ^2\frac{\theta }{2}\right)} \\[5mm] {u_y =-\frac{1}{G}\sqrt {\frac{r}{2\pi }} \cos \frac{\theta }{2}\left(1 - 2\nu-\sin ^2\frac{\theta }{2}\right)} \\ \end{array} }} \right\}\tag{35} \end{equation}
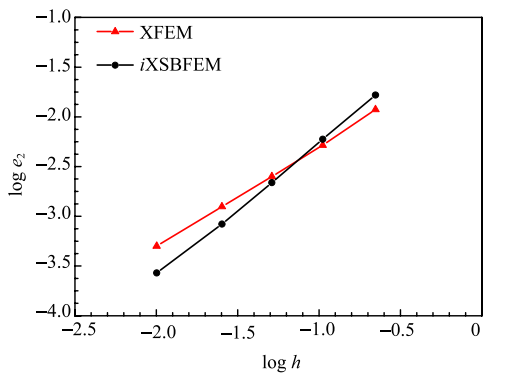
===图10给出了分别采用常规XFEM和$i$XSBFEM得到的基于位移范数的相对误差收敛性分析结果,同样地可以看出,对于纯II型裂纹问题,$i$XSBFEM的收敛性仍相对较好.
显示原图|下载原图ZIP|生成PPT图9无限板的纯II型裂纹问题...
-->Fig.9Pure mode II crack model in infinite plate
-->
显示原图|下载原图ZIP|生成PPT图10纯II型裂纹问题：基于位移范数的相对误差收敛性分析结果...
-->Fig.10Pure mode II crack: Convergence results for the relative error in the displacement norm
-->
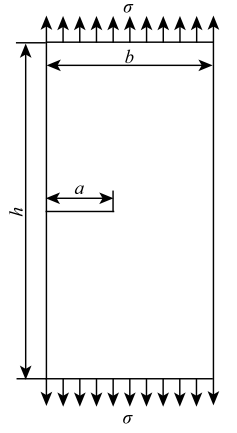
4.3 有限尺寸拉伸板的边缘裂纹问题
本算例主要考察应用改进XSBFEM求解有限尺寸拉伸板的边缘裂纹应力强度因子的有效性,如图11所示. 拉伸板宽$b$=1 m,高$h$=2 m,受轴向拉伸荷载$\sigma $=1.0 kPa的作用. 数值计算时,按平面应变问题考虑,为消除刚体位移,板的下边缘竖向约束,同时板的左下角水平向约束,板被离散成59$\times $119个单元,单元总数为7201,结点总数为7200,弹性模量$E$取为1.0 MPa,泊松比$\nu $取为0.2. 裂纹宽度分别取为0.1 m, 0.2 m, 0.3 m, 0.4 m, 0.5 m和0.6 m.对于边缘裂纹问题,应力强度因子的解析解为[33]
$$\align \label{eq33} &K_{I} = 1.12-0.23\left( {\frac{a}{b}} \right) + 10.56\left( {\frac{a}{b}} \right)^2 -\\ &\qquad 21.74\left( {\frac{a}{b}} \right)^3 + 30.42\left( {\frac{a}{b}} \right)^4 \sigma \sqrt {\pi a}\tag{34} \endalign$$
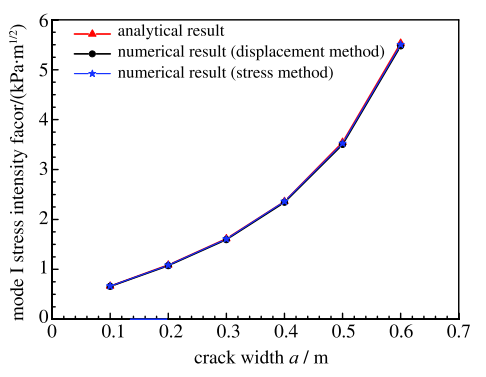
===图12给出了采用$i$XSBFEM计算得到的不同边缘裂纹宽度下拉伸板的应力强度因子值,并给出该问题的解析解作为比较,从图中可看出,数值解与解析解吻合较好,从而验证了数值方法的有效性.
显示原图|下载原图ZIP|生成PPT图11有限尺寸拉伸板边缘裂纹问题...
-->Fig.11Edge crack problem of a finite tension plate
-->
显示原图|下载原图ZIP|生成PPT图12有限尺寸拉伸板边缘裂纹问题：数值解与解析解得到的应力强度因子比较...
-->Fig.12Edge crack problem of a finite tension plate：Comparisons of numerical and analytical results for stress intensity factor
-->
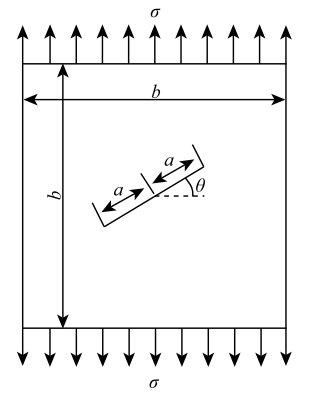
4.4 倾斜裂纹问题
算例1、算例2和算例3给出的是简单拉伸、剪切荷载情况下的断裂问题. 本算例为I、II型复合裂纹问题,如图13所示,拉伸板中心包含一倾斜中心裂纹,裂纹倾角为$\theta $,裂纹长度为$2a$,该板在无限远处受单轴拉伸荷载$\sigma $作用.该问题应力强度因子的解析解为[34-35]
\begin{equation} \label{eq34} \left. {{\begin{array}{ll} {K_{I} = \sigma \sqrt {\pi a} \cos ^2\theta } \\[3mm] {K_{{II}} = \sigma \sqrt {\pi a} \cos \theta \sin \theta } \\ \end{array} }} \right\}\tag{35} \end{equation}
数值计算时,取拉伸板边长$b$=16 m,裂纹半长度$a$=0.5 m,拉伸荷载$\sigma $=1.0 kPa,按平面应变问题考虑,为消除刚体位移,板的下边缘竖向约束,板的左下角水平向约束, 离散网格单元总数为7245,结点总数为7256,弹性模量取为1.0 MPa,泊松比取为0.2.
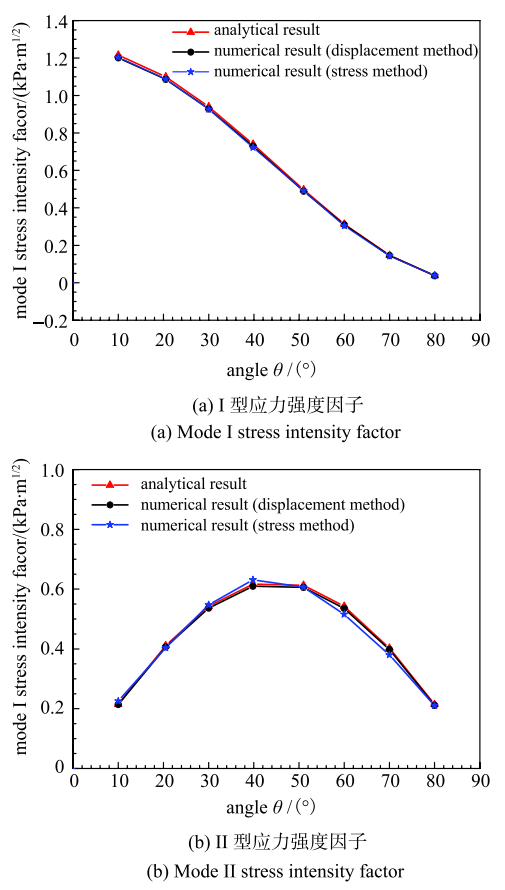
图14给出了采用$i$XSBFEM计算得到的裂纹不同倾斜角度下拉伸板的I型和II型应力强度因子值,并给出该问题的解析解作为比较,从图中可看出,数值解与解析解吻合较好,从而验证了数值方法的有效性.
显示原图|下载原图ZIP|生成PPT图13拉伸板的倾斜中心裂纹问题...
-->Fig.13An inclined centre crack under tensile loads
-->
显示原图|下载原图ZIP|生成PPT图14裂纹不同倾角下拉伸板的应力强度因子...
-->Fig.14Stress intensity factors of the tensile plate with different crack inclination angles
-->
5 结论
借助XFEM和SBFEM的主要思想,采用两个正交的水平集函数表征材料内部裂纹面,并基于水平集函数判断单元切割类型;将XFEM中的不连续单元作为SBFEM的子域处理,采用SBFEM求解单元刚度矩阵,从而避免了XFEM中求解不连续单元刚度矩阵需要进一步进行单元子划分的缺陷;同时,借助XFEM的主要思想,将裂纹与单元边界交点的真实位移作为单元结点的附加自由度考虑,赋予了单元结点附加自由度明确的物理意义,可以直接根据位移求解结果得出裂纹与单元边界交点的位移,而在常规XFEM中,需要进一步根据XFEM位移模式通过后处理求解裂纹与单元边界交点的位移;类似于SBFEM,应力强度因子基于裂尖处的奇异位移(应力)直接获得,无需借助其他的数值方法.建议的数值方法称为$i$XSBFEM,该方法结合了XFEM和SBFEM的主要优点,为裂纹的断裂扩展模拟提供一条新的途径. 最后,通过若干数值算例验证了建议方法的有效性,相比于常规XFEM,$i$XSBFEM的基于位 移范数的相对误差收敛性较好;采用$i$XSBFEM计算得到的裂尖应力强度因子与解析解也吻合较好.
文中建议的$i$XSBFEM在模拟裂纹扩展时无需进行网格重剖分,且可较易拓展运用于动力裂纹扩展问题以 及弹塑性问题的模拟,在动力问题中,动力刚度矩阵可基于连分式法求解比例边界有限元方程得到; 而在弹塑性问题中,弹塑性本构矩阵$D_{ ep}$不再是常数,可在比例边界坐标系下将$D_{ ep}$展开成多项式函数得到. 这些将在后续研究工作中进行思考和实现.
The authors have declared that no competing interests exist.
参考文献 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子
| [1] | . |
| [2] | |
| [3] | . |
| [4] | . . |
| [5] | . |
| [6] | . . |
| [7] | . |
| [8] | . |
| [9] | . |
| [10] | . |
| [11] | . . |
| [12] | . . |
| [13] | . . |
| [14] | . . |
| [15] | . . |
| [16] | . |
| [17] | . |
| [18] | . |
| [19] | . |
| [20] | . . |
| [21] | . . |
| [22] | . . |
| [23] | . |
| [24] | . . |
| [25] | . . |
| [26] | . . |
| [27] | . . |
| [28] | . |
| [29] | . |
| [30] | . |
| [31] | . . |
| [32] | . |
| [33] | |
| [34] | . |
| [35] | . |
