Wen-Di Chen ^1,
, Hai-Rui Guo ^2,,
, Wei-Li Sun ^2,
, Tao Ye ^2,
, Yang-Jun Ying ^2,
, Yin-Lu Han ^3,
, Qing-Biao Shen ^3,
,

Corresponding author: Hai-Rui Guo, guo_hairui@iapcm.ac.cn

1.Graduate School of China Academy of Engineering Physics, Beijing 100088, China
2.Institute of Applied Physics and Computational Mathematics, Beijing 100094, China
3.Key Laboratory of Nuclear Data, China Institute of Atomic Energy, Beijing 102413, China
Received Date:2020-01-03
Available Online:2020-05-01
Abstract:A microscopic approach is employed to study the optical potential for the ⁷Li-nucleus interaction system without any free parameters. It is obtained by folding the microscopic optical potentials of the constituent nucleons of ⁷Li over their density distributions. We employ an isospin-dependent nucleon microscopic optical potential, which is based on the Skyrme nucleon-nucleon effective interaction and derived using the Green's function method, as the nucleon optical potential. The harmonic oscillator shell model is used to describe the internal wave function of ⁷Li and obtain the nucleon density distribution. The ⁷Li microscopic optical potential is used to predict the reaction cross-sections and elastic scattering angular distributions for the target range from ²⁷Al to ²⁰⁸Pb and energy range below 450 MeV. Generally, the results can reproduce the measured data reasonably well. In addition, the microscopic optical potential is comparable to a global phenomenological optical potential by fitting the presently existing measured data.

HTML

--> --> -->

The optical potential is an usual and basic tool used in the dynamic analyses of nuclear reactions. At present, most optical potentials are phenomenological. They have several parameters, and they are determined by fitting experimental data. When the experimental data are not sufficient, it is difficult to obtain a reliable phenomenological optical potential. In contrast, the microscopic optical potential (MOP) is theoretically derived from the nucleon-nucleon interaction, it has no free parameters, and does not rely on the experimental data. Therefore, to obtain optical potentials through a microscopic approach represents a goal of nuclear physics. It is of great significance for the analyses of nuclear reactions lacking experimental data.
The studies of nuclear reactions involving a light-particle projectile or ejectile are an important part of nuclear physics and highly useful for practical applications. Thus, we have already obtained the MOPs for the nucleon [1], deuteron [2], triton [3], and ^3,4,6He [4-6]. In recent years, the weakly bound ⁷Li induced reactions has been a topic of great interest. Breakup, complete and incomplete fusion, and some other reaction mechanisms were addressed by experimental and theoretical nuclear physicists [7, 8]. The ⁷Li optical potential is required in the theoretical analyses.
To date, there are several ⁷Li optical potentials employed to analyze the experimental data. A semi-microscopic optical potential, whose real part is generated by the double folding model and nucleon-nucleon effective interaction and whose imaginary part is in the Woods-Saxon form, is given by Woods et al. [9] and used to analyze elastic scattering data for the ¹⁵N and ²⁵Mg target. Deshmukh et al. [10] provided a Wood-Saxon form optical potential, while it can only be used for ¹¹⁶Sn. An optical potential provided by Camacho et al. [11] meets the dispersion relation of real and imaginary parts; however, it is only suitable for the ²⁸Si target. Recently, Xu et al. [12] provided a new global phenomenological optical potential (GOP) based on the present experimental data, which is applicable to a more extensive incident energy and target region.
Since the measured ⁷Li scattering data are not sufficient to date, a ⁷Li MOP is obtained in the present work by folding the MOPs of its internal nucleons over their density distributions. The isospin-dependent nonrealistic nucleon MOP derived using the Green's function method in our previous work [1, 13-15] is adopted to be the MOP for the constituent nucleons. The shell model is applied to construct the internal wave function and generate nucleon density distributions. The ⁷Li elastic-scattering angular distributions and reaction cross-sections are calculated by the MOP and compared with the experimental data, and the results are calculated by the GOP [12].
This paper is organized as follows: the theoretical model and formulas of the MOP are presented in Sec. 2; the calculated results and analysis are provided in Sec. 3; the summary and conclusion are given in Sec. 4.

The MOP for ⁷Li is generated by the folding model [16] and expressed as

$ U(\vec R) = \int {{U_n}(\vec R + \vec r){\rho _n}(\vec r) + {U_p}(\vec R + \vec r){\rho _p}(\vec r){\rm d}\vec r},$

(1)

where

$ \int {{\rho _n}{\rm d}\vec r} = N;\;\;\int {{\rho _p}{\rm d}\vec r} = Z. $

(2)

$ U_n $ and $ U_p $ represent the MOPs for neutrons and protons, respectively. $ \rho _n $ and $ \rho _p $ are the density distributions of neutrons and protons in the ground state of ⁷Li, respectively. $ \vec R $ is the relative coordinate between the centers of mass of the target and ⁷Li, and $ \vec r $ is the internal coordinate of ⁷Li.
The isospin-dependent nonrealistic nucleon MOP [1, 13-15] is adopted to be $ U_n $ and $ U_p $ for neutrons and protons, respectively. A brief introduction for it is given as follows: From the perspective of many-body theory, the nucleon optical potential is equivalent to the mass operator of the single-particle Green's function [17]. Based on the Skyrme nucleon-nucleon effective interaction SKC16 [14], which simultaneously describes nuclear matter properties, ground state properties, and neutron-nucleus scattering, the first- and second-order mass operators of the single-particle Green's function were derived through the nuclear matter and local density approximations. The real part of the nucleon MOP was denoted by the first-order mass operator, and the imaginary part of the nucleon MOP was denoted by the imaginary part of the second-order mass operator. The incident energy of the nucleon is regarded as one seventh of the incident energy of ⁷Li.
The shell model is adopted to give an appropriate nucleon density in ⁷Li. Because a 1p-shell model space can efficiently describe its structure [18], and as we are here only concerned with the ground-state properties of ⁷Li, the harmonic oscillator potential is adopted to describe the mean interaction for the nucleons in ⁷Li, and the internal Hamiltonian of ⁷Li is expressed as

$ {H_{{}^7{\rm Li}}} = \sum\limits_{i = 1}^7 {{T_i}} + \sum\limits_{i = 1}^7 {\frac{1}{2}m{\omega ^2}r_i^2} , $

(3)

where $ m $ is the nucleon mass, and $ r_i $ is coordinate of the $ i $th nucleon in ⁷Li relative to the center of mass of ⁷Li. $ T_i $ represents the kinetic energy of the $ i $th nucleon.
As the harmonic oscillator potential is used in the shell model, the ground-state wave function of ⁷Li is expressed as

$ {\Phi _{\rm g.s.}} = N {\cal{A}} \left\{ {({{\vec r}_6}\cdot{{\vec r}_7}){r_5}Y_1^{\mu}({\hat r}_5)\exp \left\{ - \frac{\beta }{2}\sum\limits_{i = 1}^7 {r_i^2} \right\} \zeta } \right\}, $

(4)

where $ {\cal{A}} $ is the antisymmetrization operator of the nucleons, and $ N $ is the normalization factor. $ \zeta $ represents the spin and isospin part. $ {\Phi _{\rm g.s.}} $ is determined by the parameter $ \beta = m \omega / \hbar $, under the conditions of meeting antisymmetrization, spin, and parity ($ I^{\pi} = 3/2^{-} $). On basis of the constraint condition,

$ \sum\limits_{i = 1}^7 {{{\vec r}_i}} = 0, $

(5)

a set of Jacobi coordinates is used to replace $ r_i $ and expressed as

$ \begin{split} {{\vec r}_1} =& \frac{1}{2}{{\vec \xi }_1} + \frac{1}{3}{{\vec \xi }_2} + \frac{1}{4}{{\vec \xi }_3} + \frac{1}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}, \\ {{\vec r}_2} =& - \frac{1}{2}{{\vec \xi }_1} + \frac{1}{3}{{\vec \xi }_2} + \frac{1}{4}{{\vec \xi }_3} + \frac{1}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}, \\ {{\vec r}_3} = &- \frac{2}{3}{{\vec \xi }_2} + \frac{1}{4}{{\vec \xi }_3} + \frac{1}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}, \\ {{\vec r}_4} =& - \frac{3}{4}{{\vec \xi }_3} + \frac{1}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}, \\ {{\vec r}_5} =& - \frac{6}{7}{{\vec \xi }_6}, \quad {{\vec r}_6} = \frac{1}{2}{{\vec \xi }_4} - \frac{2}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}, \\ {{\vec r}_7} = &- \frac{1}{2}{{\vec \xi }_4} - \frac{2}{3}{{\vec \xi }_5} + \frac{1}{7}{{\vec \xi }_6}. \end{split} $

(6)

The value of $ \beta $ is determined by

$ \left\langle {r_{\rm rms}^2} \right\rangle = \left\langle {{\Phi _{\rm g.s.}}} \right|{\frac{1}{7}\sum\limits_{i = 1}^7 {r_i^2}}{\left| {{\Phi _{\rm g.s.}}} \right\rangle } , $

(7)

where $ \sqrt {\left\langle {r_{\rm rms}^2} \right\rangle } $ is the nuclear matter root-mean-square radius of ⁷Li and set as 2.50 fm, which was obtained by fitting the reaction cross-section in Ref. [19]. It is convenient to rewrite Eq. (4) as follows:

$ {\Phi _{\rm g.s.}} = N{\cal{A}}\left\{ {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)\zeta } \right\}, $

(8)

where

$ \begin{split} &{\phi _1}(1234) = \exp \left\{ - \frac{\beta }{2}\sum\limits_{i = 1}^4 {r_i^2} \right\}, \\ &{\phi _2}(5) = {r_5}Y_1^m({{\hat r}_5})\exp \left\{ - \frac{\beta }{2}r_5^2\right\}, \\ & {\phi _3}(67) = ({{\vec r}_6}\cdot{{\vec r}_7})\exp \left\{ - \frac{\beta }{2}(r_6^2 + r_7^2)\right\}. \end{split} $

(9)

Then, we can obtain a detailed expression for $ \left\langle {r_{\rm rms}^2} \right\rangle $,

$ \left\langle {r_{\rm rms}^2} \right\rangle = \frac{{{A_0} - 2{A_1} - {A_2} + 2{A_3} + {A_4} - {A_5}}}{{{N_0} - 2{N_1} - {N_2} + 2{N_3} + {N_4} - {N_5}}}, $

(10)

where

$ \begin{split} {A_0} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right\rangle _\xi }, \\ {A_1} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(1264){\phi _2}(5){\phi _3}(37)} \right\rangle _\xi }, \\ {A_2} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(5234){\phi _2}(1){\phi _3}(67)} \right\rangle _\xi }, \\ {A_3} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(5264){\phi _2}(1){\phi _3}(37)} \right\rangle _\xi }, \\ {A_4} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(1267){\phi _2}(5){\phi _3}(34)} \right\rangle _\xi }, \\ {A_5} =& \left\langle {{\phi _1}(1234){\phi _2}(5){\phi _3}(67)} \right|{{\hat O}_A}{\left| {{\phi _1}(5267){\phi _2}(1){\phi _3}(34)} \right\rangle _\xi }, \\ {{\hat O}_A} = &\frac{1}{7}\sum\limits_{i = 1}^7 {r_i^2}.\\[-20pt] \end{split} $

(11)

$ {\left\langle {...} \right\rangle _\xi } $ means that the coordinates $ \{ \vec r_i, i = 1-7 \} $ are replaced by the Jacobi coordinates $ \{ \vec \xi _i, i = 1-6 \} $. The formulas for $ N_i $ are the same as $ A_i $, while $ {{\hat O}_A} $ is replaced by $ {{\hat O}_N} = 1 $. Thus we can obtain

$ \left\langle {r_{\rm rms}^2} \right\rangle = \frac{{12}}{{7\beta }} $

(12)

and therefore $ \beta $ = 0.2743 fm^-2.
$ \rho _n $ and $ \rho _p $ are defined as

$ {\rho _{n(p)}}(\vec r) = \left\langle {{\Phi _{\rm g.s.}}} \right| {\sum\limits_{i = 1}^7 {\delta (\vec r - {{\vec r}_i}){\delta _{{\tau _{n(p)}},{\tau _i}}}} } {\left| {{\Phi _{\rm g.s.}}} \right\rangle }, $

(13)

where $ \tau _i $ is the isospin of $ i $th nucleon. $ \tau _n $ and $ \tau _p $ are the isospins of the neutron and proton, respectively. It would be convenient to calculate $ \rho _i $ first, whose formula is the same as Eq. (10), while only $ {{\hat O}_A} $ is replaced by $ {{\hat O}_{\rho ,i}} = {\delta (\vec r - {{\vec r}_i})} $. $ \rho _p = \rho _1 + \rho _2 + \rho _5 $, $ \rho _n = \rho _3 + \rho _4 + \rho _6 + \rho _7 $, and they have analytical expressions as

$ {\rho _{n(p)}}(\vec r) = \left( {{a_{n(p)}} + {b_{n(p)}}{r^2}} \right)\exp \left( - \frac{7}{{6}}\beta {r^2}\right), $

(14)

where $ a_n $ = 0.0921 fm^-3, $ a_p $ = 0.0621 fm^-3, $ b_n $ = 0.0081 fm^-5 and $ b_p $ = 0.0076 fm^-5. The density distributions are plotted in Fig. 1.
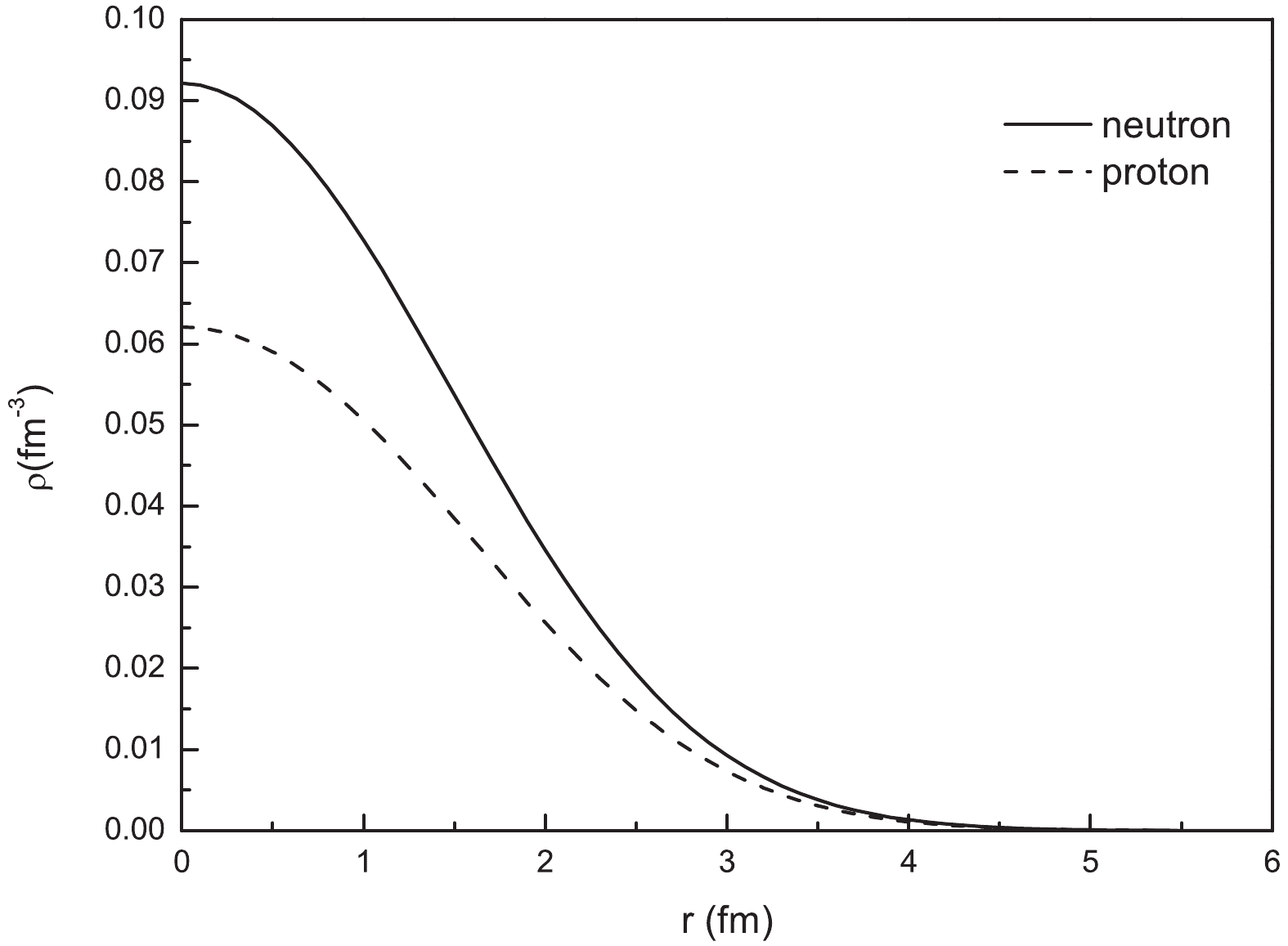Figure1. Neutron ($\rho _n$) and proton ($\rho _p$) density distributions.

The MOP for the ⁷Li+⁵⁸Ni collision system at incident ⁷Li energies of 10, 100, and 300 MeV is shown in Fig. 2 as an example. The depth of the real part ($ V $) decreases with the increase of the radius and energy. However, the depth of the imaginary part ($ W $) increases a little first and decreases as the radius increases at EL = 10, 100 MeV, while it decreases monotonously with the increase of the radius at a higher incident energy, 300 MeV. This means the contribution of $ W $ changes from the dominant surface absorption to the volume absorption as the incident energy increases. The real part of the spin-orbit potential $ V_{\rm so}{\vec s} \cdot {\vec l} $ is likewise obtained by the folding model, and $ V_{\rm so} $ is shown in Fig. 2, while the imaginary part of the spin-orbit potential is omitted as it is usually very small.
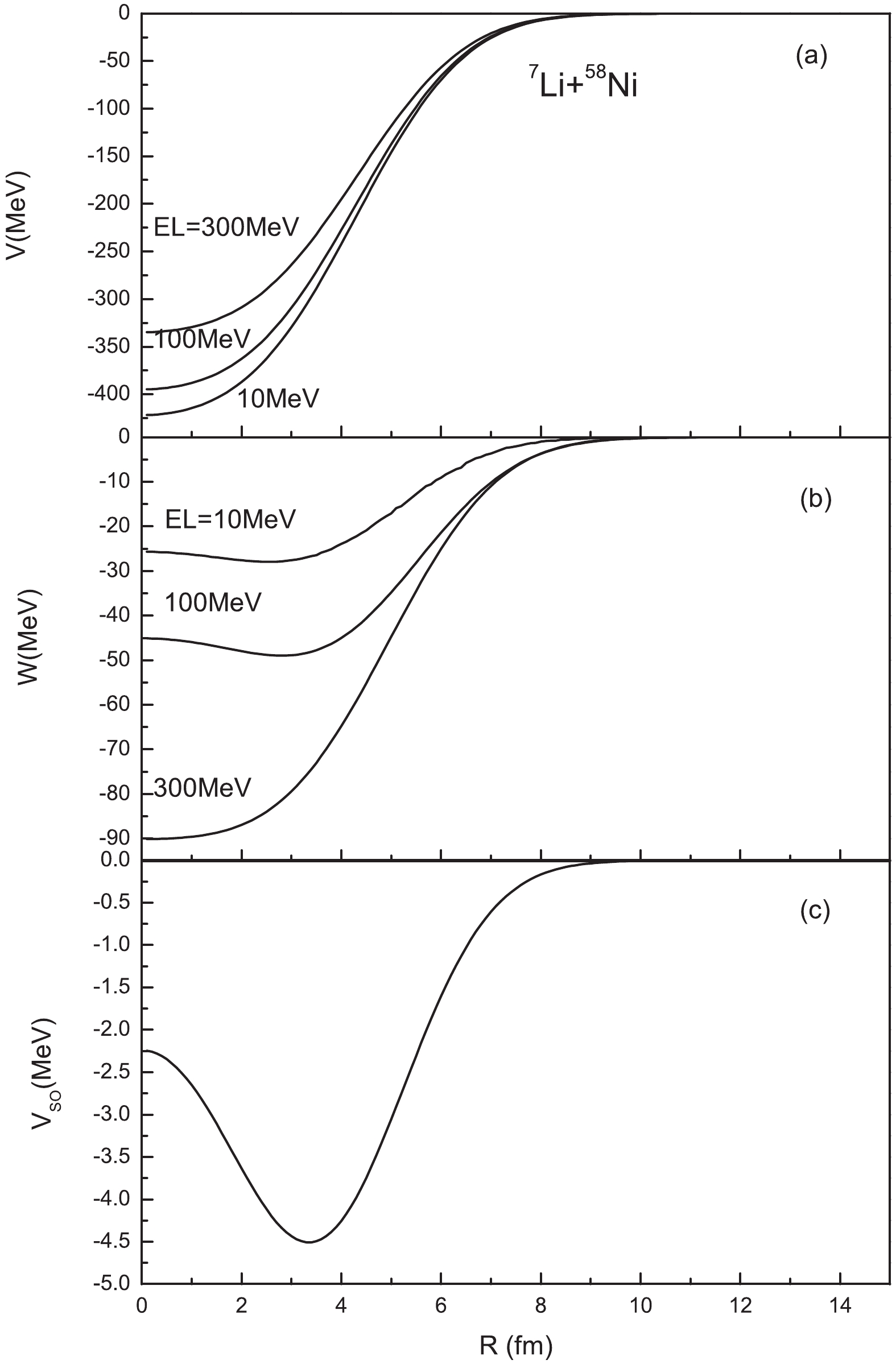Figure2. MOP for ⁷Li+⁵⁸Ni system (a) real part ($V$), (b) imaginary part ($W$) and (c) real part of spin-orbit potential ($V_{\rm so}$).

The ⁷Li elastic-scattering angular distributions and reaction cross-sections are predicted using the MOP. Comparisons are made with experimental data and the results calculated by the GOP [12].
Figure 3 shows the elastic-scattering angular distribution for ²⁷Al target at incident energies from 6.0 to 24.0 MeV. The result calculated by the MOP is in good agreement with experimental data [20, 21] except for the underestimation at EL = 11.0 MeV for large angles. In addition, the MOP result fits the experimental data slightly better than the result calculated by the GOP [12] below 14 MeV at larger angles.
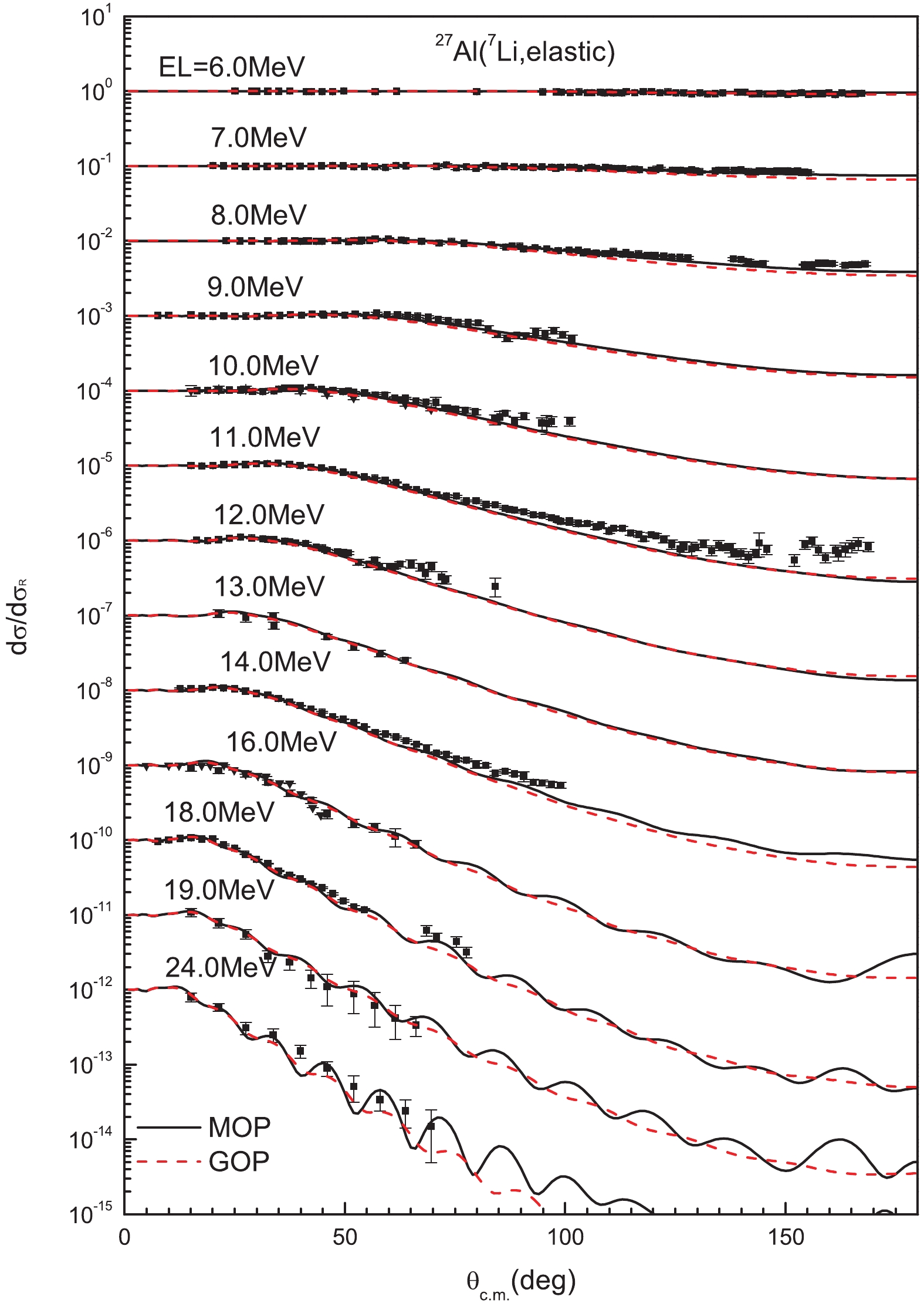Figure3. (color online) Calculated elastic-scattering angular distributions in Rutherford ratio for ²⁷Al compared with experimental data [20, 21]. Solid and dashed lines denote results calculated by MOP and the GOP [12], respectively. Graph results from top to bottom are multiplied 10⁰, 10^?1, 10^?2, respectively.

The calculated elastic-scattering angular distribution for ⁵⁸Ni target at incident energies from 14.22 MeV to 42.0 MeV is plotted in Fig. 4. The MOP efficiently reproduces the experimental data [22-24], except the slight underestimation above 70° at 16.25 MeV and 18.28 MeV, where the GOP performs slightly better.
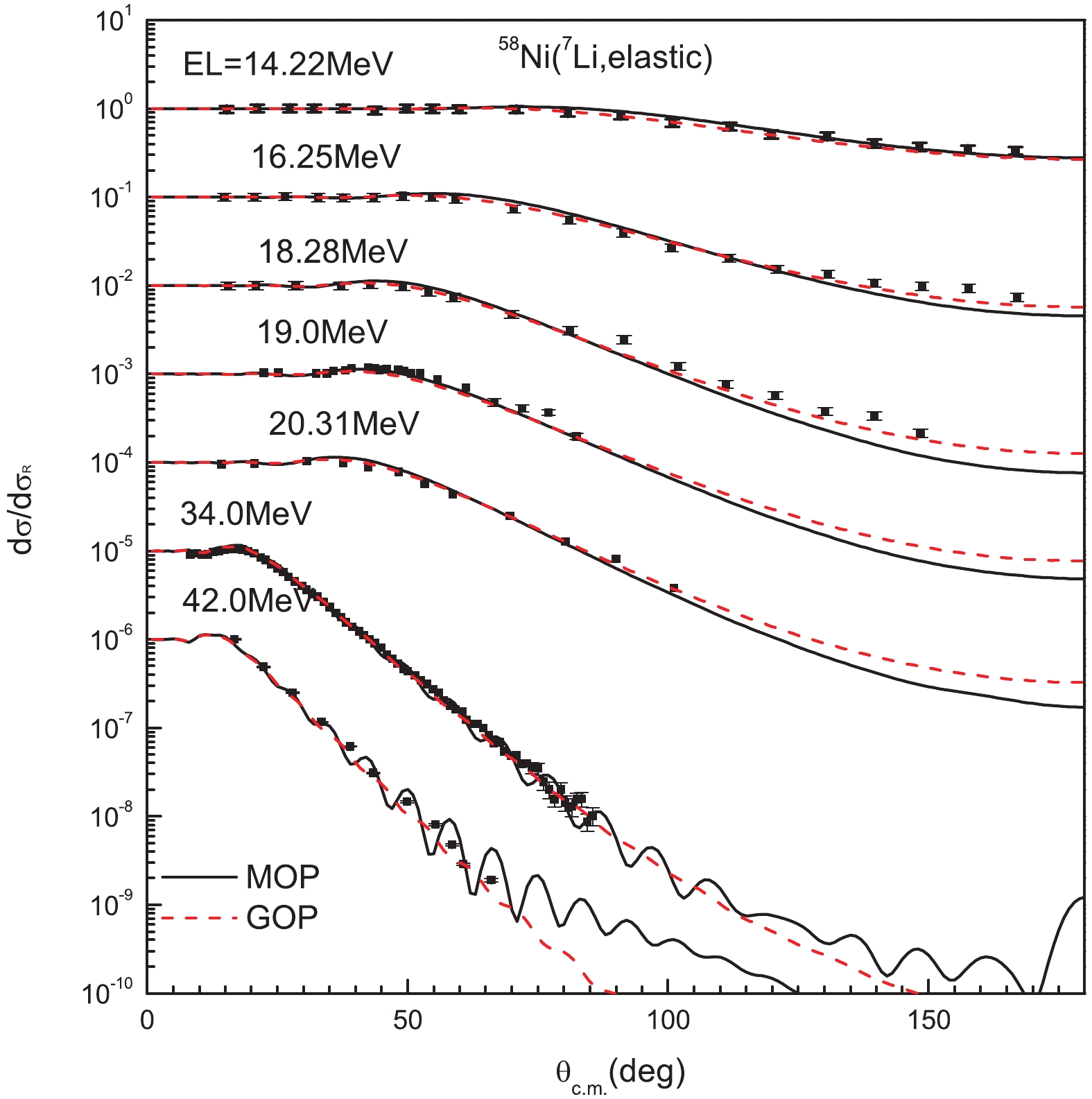Figure4. (color online) Same as Fig. 3 for ⁵⁸Ni. Experimental data are taken from Refs. [22-24]. Results from top to bottom are multiplied by 10⁰, 10^?1, 10^?2, respectively.

The elastic-scattering angular distributions for ⁶⁵Cu at incident energy 25.0 MeV and ⁸⁹Y at incident energy 60.0 MeV are shown in Fig. 5. For ⁶⁵Cu, the theoretical result from the MOP is lower than the measured values [25] above 70°. Reasonable agreement with the experimental data [26] is obtained for ⁸⁹Y.
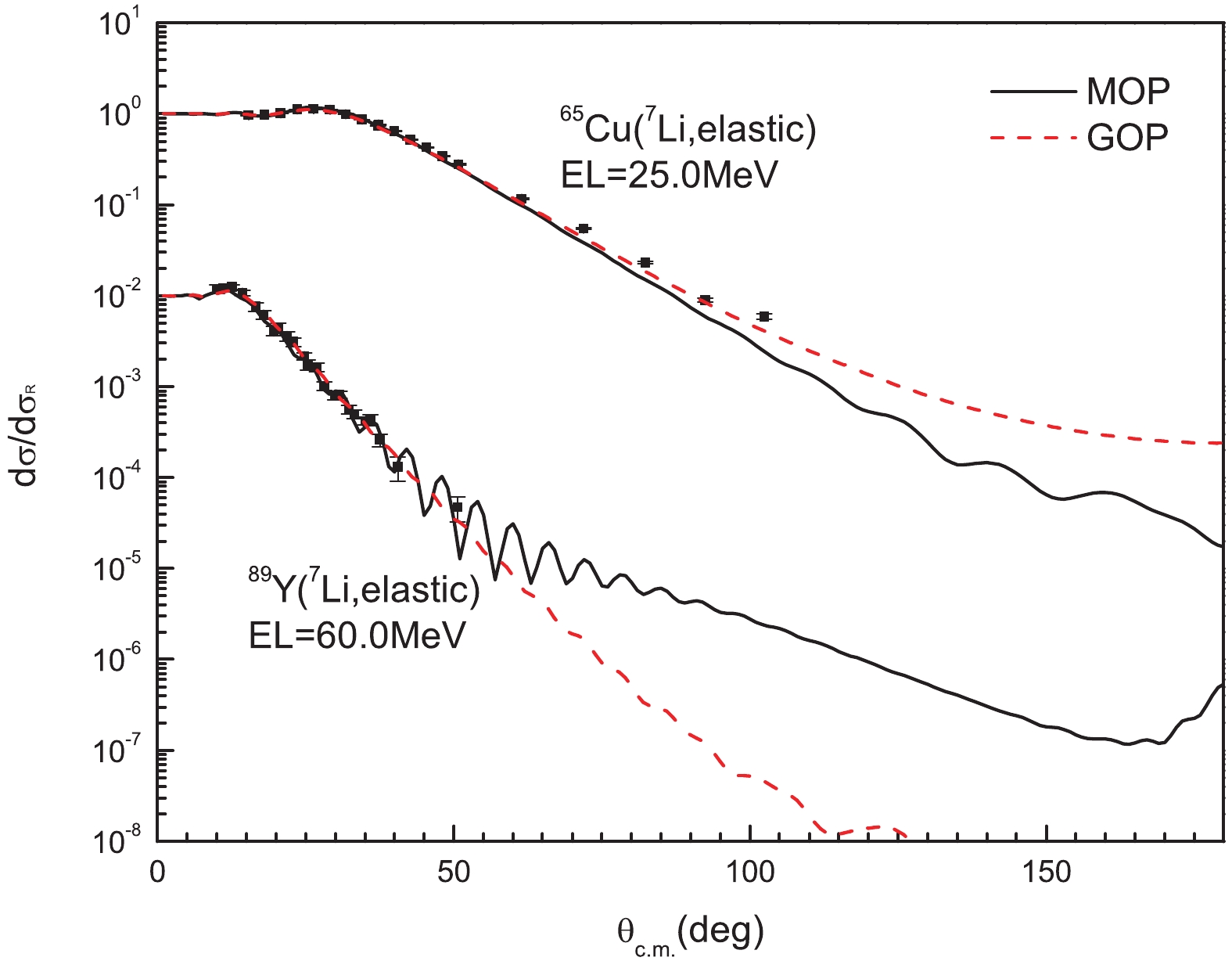Figure5. (color online) Same as Fig. 3 for ⁶⁵Cu and ⁸⁹Y. Experimental data are taken from Refs. [25, 26]. The data for ⁸⁹Y are multiplied by 10^?2.

Figure 6 shows the elastic-scattering angular distribution for the ¹¹⁶Sn target at incident energies from 18.0 MeV to 35.0 MeV. The calculated result from the MOP is in good agreement with experimental data [10] except at incident energies 22.0, 24.0, and 26.0 MeV at large angles. The MOP reproduces the measurements slightly better than the GOP at relatively lower energies.
Figure6. (color online) Same as Fig. 3 for ¹¹⁶Sn. Experimental data are taken from Ref. [10]. Results from top to bottom are multiplied by 10⁰, 10^?1, 10^?2, respectively.

The calculated elastic-scattering angular distribution for ¹³⁸Ba targets is compared with experimental data [27, 28] in Fig. 7. When the scattering angles are less than 80°, good agreement with experimental data is obtained for the MOP. The GOP works better at larger angles.
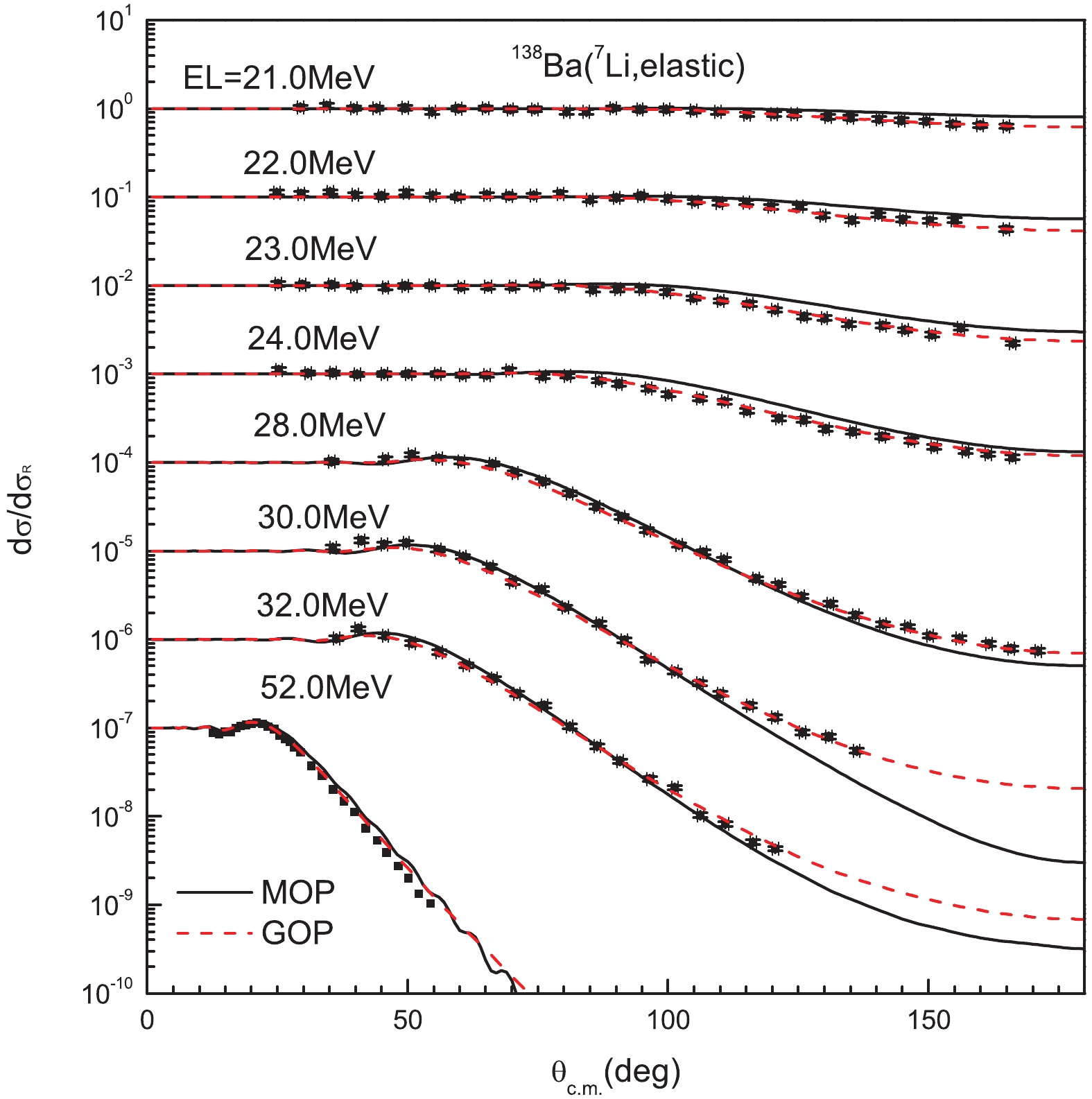Figure7. (color online) Same as Fig. 3 for ¹³⁸Ba. The experimental data are taken from Refs. [27, 28]. The results from top to bottom are multiplied respectively by 10⁰, 10^?1, 10^?2.

In Fig. 8, the calculated elastic-scattering angular distribution for ²⁰⁸Pb is shown from 27.0 MeV to 52.0 MeV. The MOP result is in satisfying agreement with experimental data [29-32] and comparable to the GOP result in fitting the measured data, except for the case at 39 MeV above 70°.
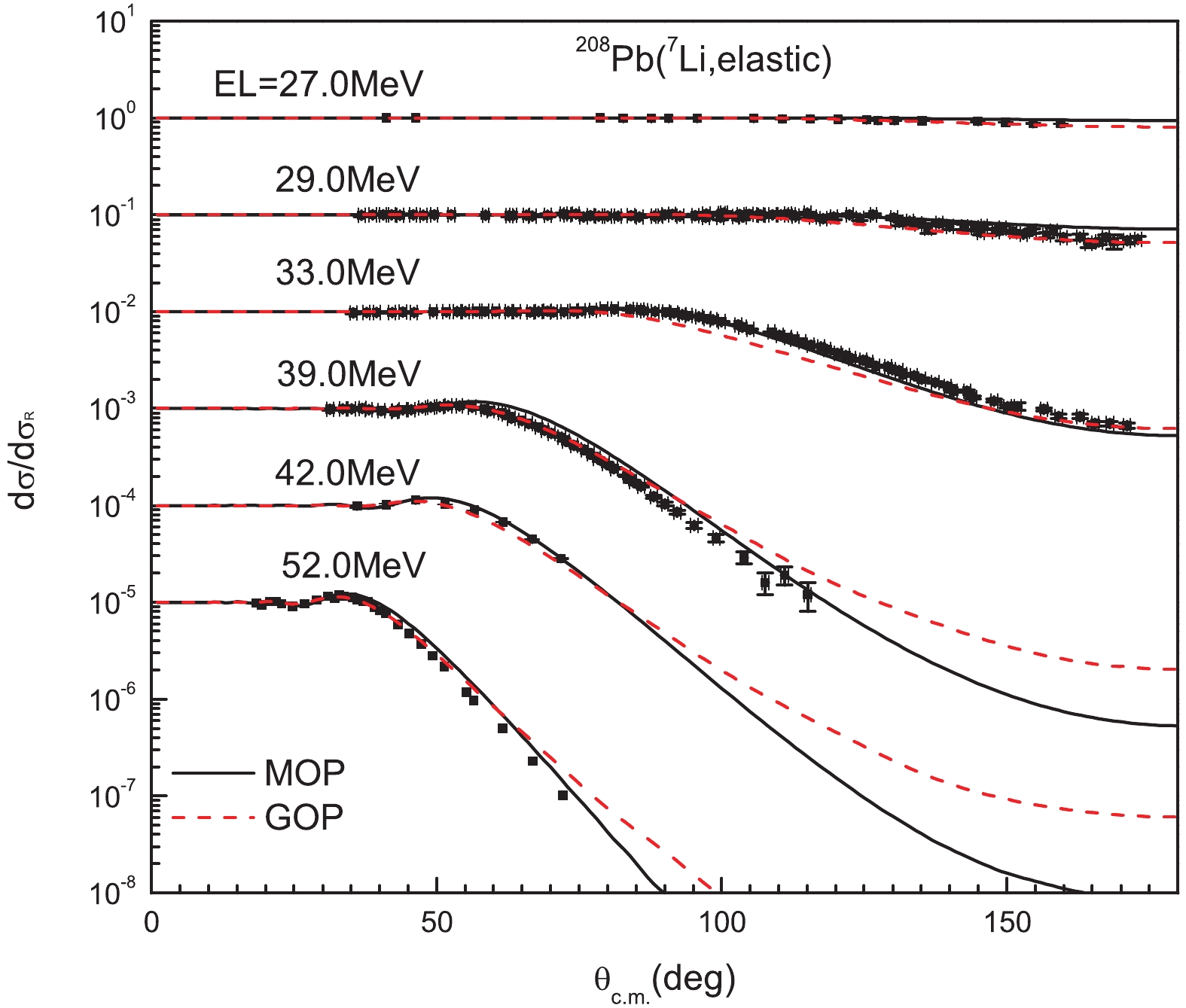Figure8. (color online) Same as Fig. 3 for ²⁰⁸Pb. Experimental data are taken from Refs. [29-32]. Results from top to bottom are multiplied by 10⁰, 10^?1, 10^?2, respectively

Figure 9 shows the elastic-scattering angular distribution at some specific scattering angles for ²⁷Al target. The calculated result by the MOP is slightly larger than that by the GOP at incident energies below 15 MeV and has a little better agreement with the measured values [33-36] when EL$\leqslant $9 MeV. However, all calculated results from the MOP and the GOP underestimate the experimental data [37] at incident energies from 9 MeV to 11 MeV for large angles.
Figure9. (color online) Calculated elastic-scattering angular distributions in Rutherford ratio for ²⁷Al at some scattering angles compared with experimental data [33-37]. Solid and dashed lines denote results calculated by MOP and GOP [12], respectively. The results from top to bottom are multiplied by 10⁰, 10^?1, 10^?2, respectively.

The reaction cross-sections of ⁷Li-induced reactions on ¹³C, ²⁷Al, ²⁸Si, ⁶⁴Zn, ^natCu, ¹¹⁶Sn, ¹³⁸Ba, and ²⁰⁸Pb are also calculated and shown in Fig. 10 and Fig. 11. Figure 10 presents the results for ¹³C, ²⁸Si, ^natCu and ²⁰⁸Pb. The theoretical result for ¹³C is within the measurement error range [38]. The MOP result for ²⁸Si is in good agreement with experimental data [39-43] below 30 MeV; however, it becomes a little larger from 90 MeV to 200 MeV. The reaction cross-section for ^natCu is obtained by averaging the reaction cross-sections for ⁶³Cu and ⁶⁵Cu over the natural abundance. The MOP result is in good agreement with the experimental data [44] except for the energy point of 160 MeV. The MOP result for ²⁰⁸Pb reproduces the experimental data [30, 45] reasonably well below 70 MeV; however, it yields an underestimation at 300 MeV. Figure 11 shows that the MOP reproduces experimental data for ²⁷Al [21, 46], ⁶⁴Zn [47], ¹¹⁶Sn [10], and ¹³⁸Ba [28] well. The MOP results are comparable to the GOP results in fitting the measured reaction cross-sections except for ²⁰⁸Pb.
Figure10. (color online) Reaction cross-sections calculated by MOP compared with experimental data for ¹³C [38], ²⁸Si [39-43], ^natCu [44] and ²⁰⁸Pb [30, 45] and results calculated by GOP [12]. Data are shifted upwards by adding 0, 2, 4 and 6 b, respectively. Solid and dashed lines denote results calculated by MOP and GOP, respectively.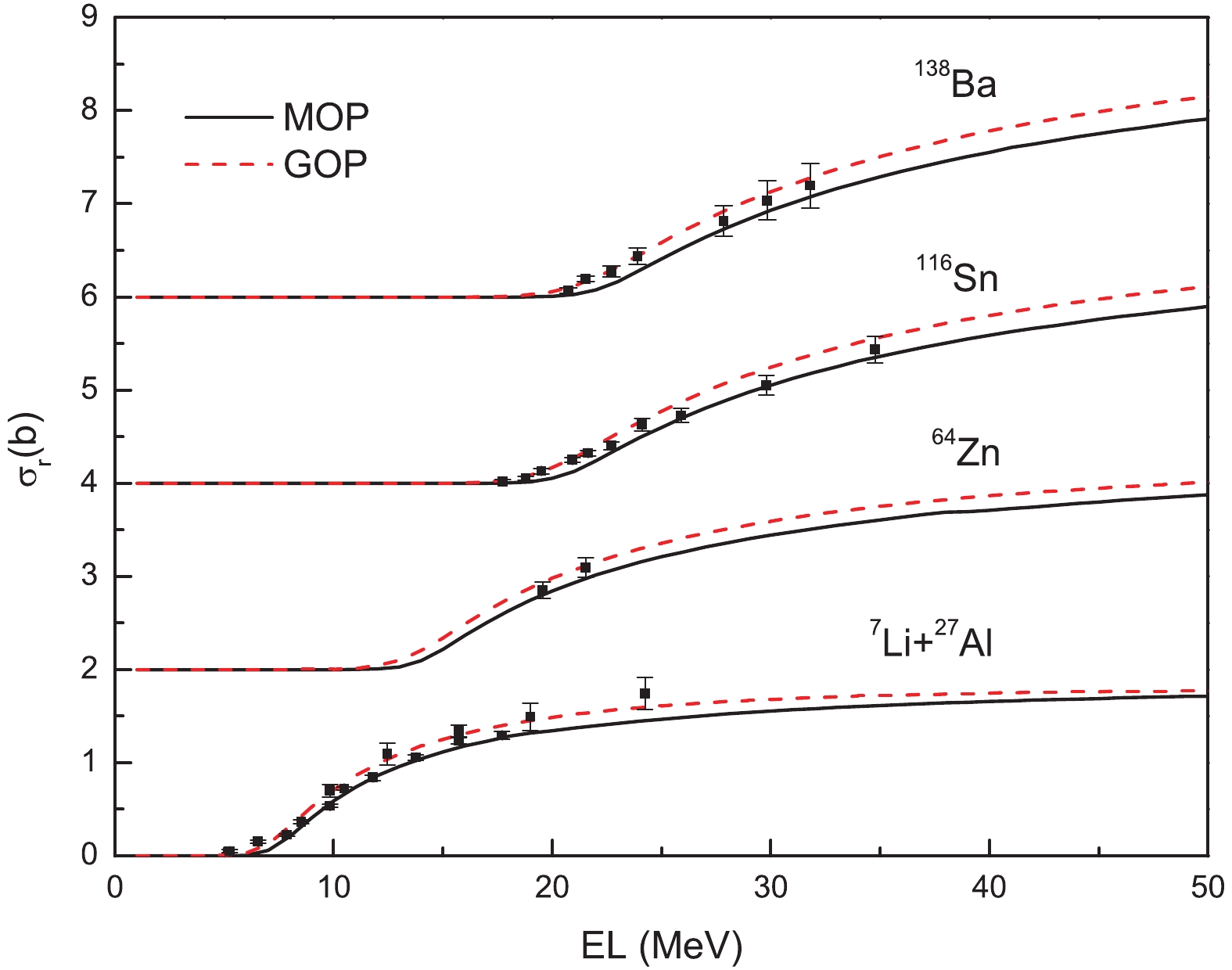

Figure11. (color online) Same as Fig. 10 for ²⁷Al, ⁶⁴Zn, ¹¹⁶Sn, and ¹³⁸Ba. Experimental data are taken from Refs. [10, 21, 28, 46, 47].

The application of the MOP to the prediction of ⁷Li elastic scattering from light target nuclei was attempted. The elastic-scattering angular distribution for ¹⁶O is calculated and compared with experimental data [48-51], as shown in Fig. 12. The theoretical result from the MOP is only consistent with the magnitude of measured data in forward angles and gives an overestimation in relatively larger angles. Therefore, the MOP is not suitable for light nuclei. On the one hand, it may be interpreted that the Negele's nuclear density [52] adopted to calculate the nucleon MOP [1, 13-15] is not suitable for light nuclei. On the other hand, a light nucleus, such as ¹⁶O, has unique structure characteristics and reaction mechanisms [53, 54], which may also lead to discrepancy between the MOP results and measured values.
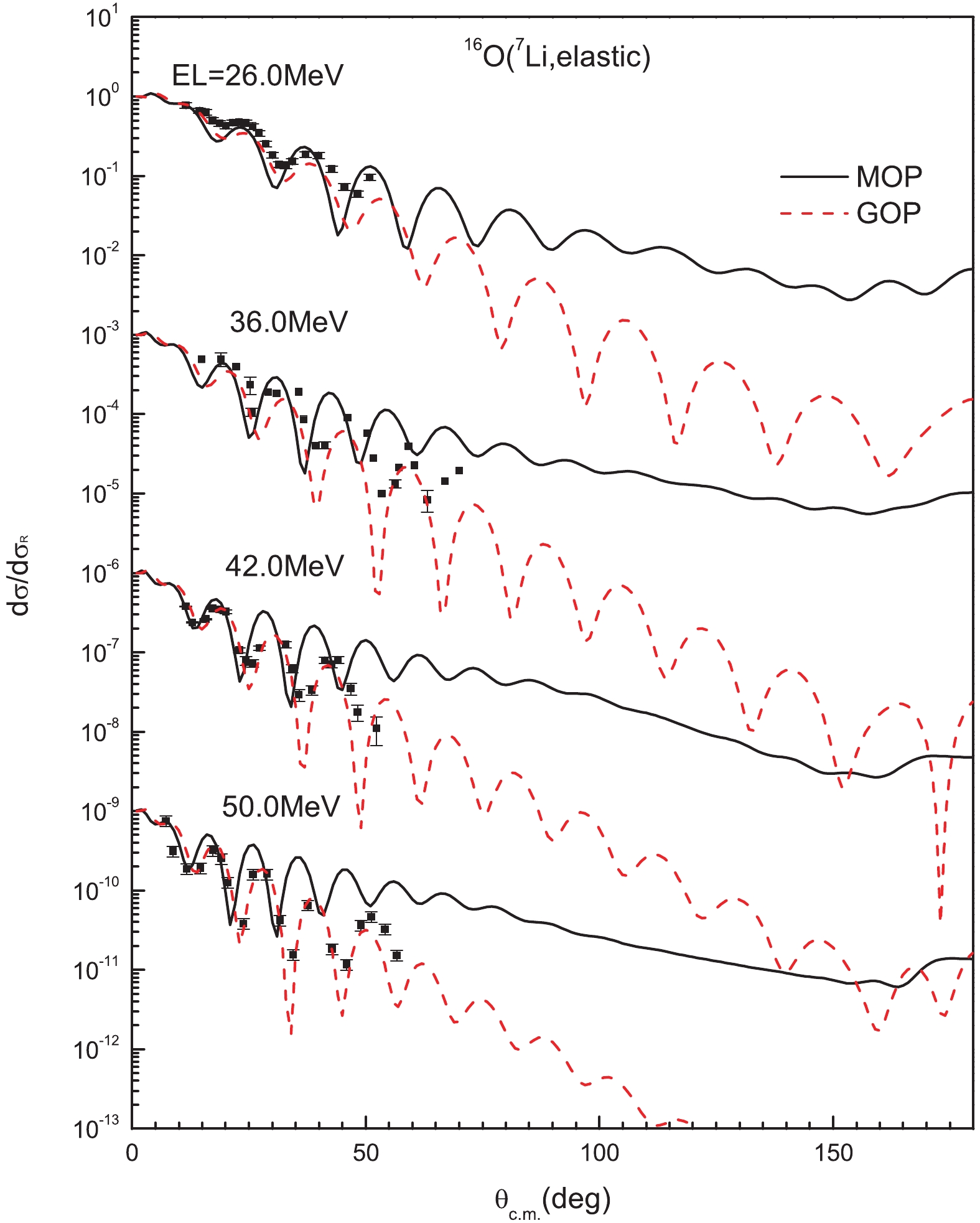Figure12. (color online) Same as Fig. 3, for ¹⁶O. Experimental data are taken from Refs. [48-51]. Results from top to bottom are multiplied by 10⁰, 10^-3, 10^-6, and 10^-9, respectively.

Furthermore, some discrepancies between the calculated and measured elastic-scattering angular distributions appear at relatively larger angles, such as the case for ¹³⁸Ba target at 28.0 MeV. To investigate how to improve the MOP to provide a better global agreement with experimental data, the notch perturbation method [55, 56] is employed to analyze the sensitivity of the calculated elastic scattering angular distributions to the optical potential. The perturbation is performed by setting $ V $, $ W $, or $ V_{\rm so} $ to zero in a region of width 0.5 fm centered at radius R. The scattering sensitivity is assessed by $ {\chi ^2}/\chi _0^2 $, where the $ {\chi ^2} $ and $ \chi _0^2 $ are the chi-squares corresponding to the perturbed and original potentials, respectively. $ \chi _0^2 $ is calculated by

$ \chi _0^2 = \frac{1}{N _{\theta}}\sum\limits_{i = 1}^N {{{\left[ {\frac{{{\sigma ^{T} _0}({\theta _i}) - {\sigma ^{E}}({\theta _i})}}{{\Delta {\sigma ^{E}}({\theta _i})}}} \right]}^2}}, $

(15)

where $ {N _{\theta }} $ is the angle numbers of the experimental elastic-scattering angular distributions for ⁷Li+¹³⁸Ba at EL = 28.0 MeV. $ \sigma ^{T} _0 (\theta _i) $, $ \sigma ^{E} (\theta _i) $ and $ \Delta \sigma ^{E} (\theta _i) $ represent the theoretical value without perturbation, experimental value, and experimental error for the $ i $th measured scattering angle, respectively. The theoretical value with perturbation, $ \sigma ^{T} (\theta _i) $, is used to calculate $ {\chi ^2} $ in the same method.
Figure 13 shows the MOP for the ⁷Li+¹³⁸Ba system at EL = 28.0 MeV and $ {\chi ^2}/\chi _0^2 $. $ {\chi ^2}/\chi _0^2 $ for $ V_{\rm so} $ of the MOP approximately remains at unity, hence it is acceptable to ignore the impact from changing $ V_{\rm so} $ and focus on only $ V $ and $ W $. The peaks of $ {\chi ^2}/\chi _0^2 $ are located mainly in the surface interaction region 6 < R < 12 fm.
Figure13. (color online) Notch perturbation analysis of MOP for ⁷Li+¹³⁸Ba reaction at EL = 28.0 MeV, (a) $V$ of MOP; (b) $W$ of MOP; (c) radial sensitivity of elastic scattering to MOP. Solid, dashed, and dotted curves in (c) represent results of perturbing $V$, $W$, and $V_{\rm so}$, respectively.

We adjust the $ V $ and $ W $ of the MOP in the sensitive region 6 < R < 12 fm by multiplying $ N_{R} $ and $ N_{I} $, respectively, and calculate the corresponding $ {\chi ^2}/\chi _0^2 $. It can be seen in Figure 14 shows that a better agreement with experimental data at large angles is obtained when $ N_{R} $ = 0.89 and $ N_{I} $ = 1.00. This implies that a weaker real part in the surface region of the MOP may be more suitable for reproducing the measured data. In contrast, a smaller $ {\chi ^2} $ is obtained when $ N_{R} $ = 1.00 and $ N_{I} $ = 1.89, which means that a stronger imaginary part in the surface region may perform better. A correction of the MOP results is expected from the breakup effect, which is not considered in the folding model, as it onlny provides a repulsive contribution to the real part and an absorptive contribution to the imaginary part in the surface region.
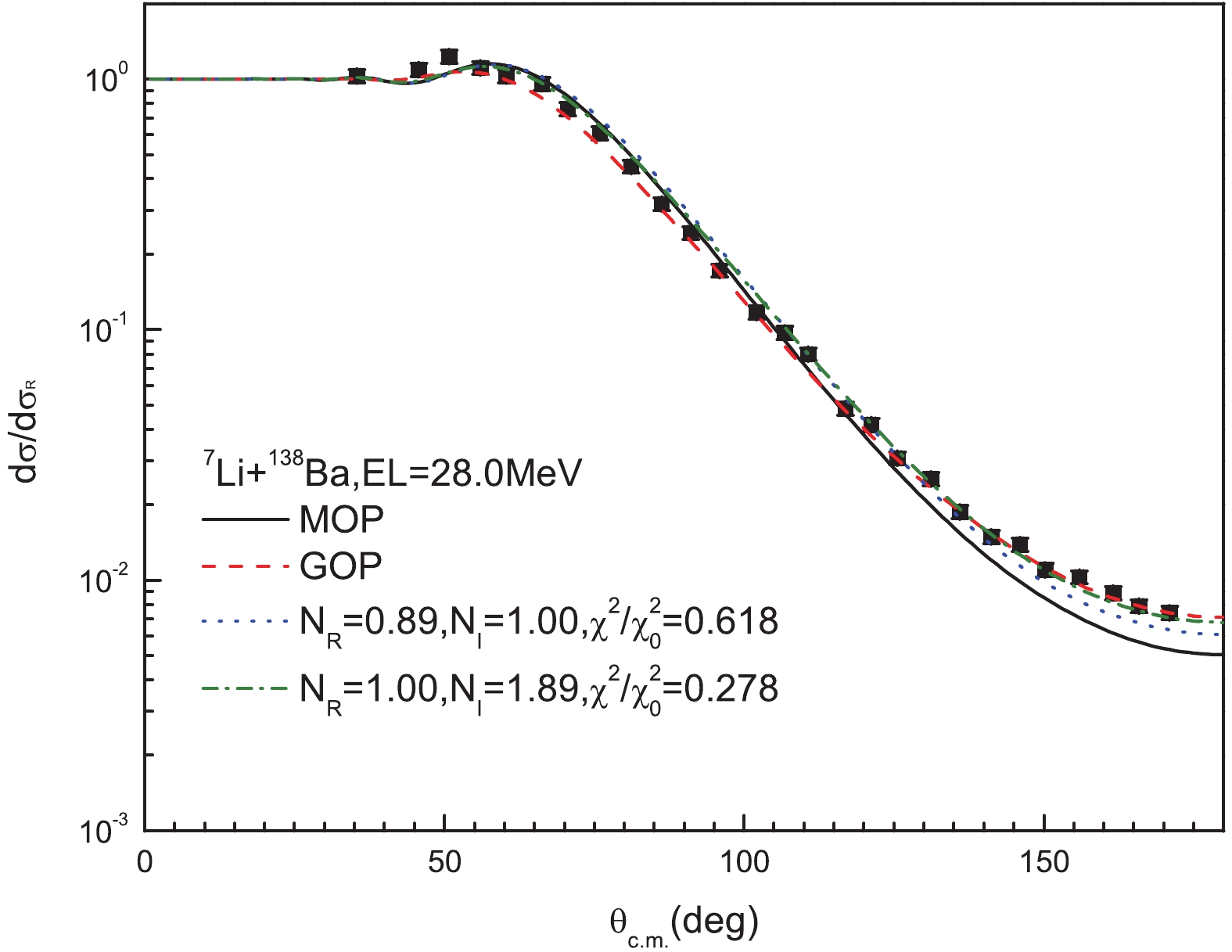Figure14. (color online) Calculated elastic-scattering angular distributions in Rutherford ratio for ¹³⁸Ba at EL = 28.0 MeV. Solid, dashed, dotted, and dash-dotted lines denote results calculated by MOP, GOP [12], MOP with adjusted $V$ and MOP with adjusted $W$, respectively. Adjustments of $V$ and $W$ are made only within sensitive region 6 < R < 12 fm.

The ⁷Li microscopic optical potential without any free parameters is obtained by the folding model. The internal wave function of ⁷Li is obtained by the shell model, and a nucleon MOP base on the Skyrme nucleon-nucleon effective interaction is adopted. The reaction cross-sections and elastic-scattering angular distributions for target from ²⁷Al to ²⁰⁸Pb at incident energies below 450 MeV are calculated by the ⁷Li microscopic optical potential. Generally, reasonable agreement with the experimental data is obtained, and the MOP is comparable to the GOP in reproducing the measurements in numerous cases. However, some discrepancies between the calculated and measured elastic-scattering angular distributions occur at relatively larger angles. The reason is analyzed, and it is found that the MOP can be improved by adding a repulsive contribution to the real part and an absorptive contribution to the imaginary part in the surface region, which may be achieved by considering the breakup effect. This will be the subject of our future study.