Yi-Feng Lv ^1,
, Jing-Bin Lu ^1,
, Gao-Long Zhang ^2,3,
, Yi-Heng Wu ^4,
, Cen-Xi Yuan ^5,
, Guan-Jian Fu ^6,
, Guang-Xin Zhang ^2,
, Zhen Huang ^2,
, Ming-Li Wang ^2,
, Shi-Peng Hu ^7,
, Hui-Bin Sun ^7,
, Huan-Qiao Zhang ^8,
, Cheng-Qian Li ^1,
, Ke-Yan Ma ^1,
, Ying-Jun Ma ^1,
, Yun-Zuo Liu ^1,
, D. Testov ^9,
, P. R. John ^9,
, J. J. Valiente-Dobon ^10,
, A. Goasduff ^9,
, M. Siciliano ^10,11,
, F. Galtarossa ^10,
, F. Recchia ^9,
, D. Mengoni ^9,
, D. Bazzacco ^9,
, 1.College of physics, Jilin University, ChangChun 130012, China
2.School of Physics and Nuclear Energy Engineering, Beihang University, Beijing 100191, China
3.Beijing Advanced Innovation Center for Big Data-Based Precision Medicine, Beihang University, Beijing 100083, China
4.School of Physics and Electronic Engineering, An Qing Normal University, An qing, 246133, China
5.Sino-French Institute of Nuclear Engineering and Technology, Sun Yat-Sen University, Zhuhai 519082, China
6.School of Physics Science and Engineering, Tongji University, Shanghai 200092, China
7.College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen 518060, China
8.China Institute of Atomic Energy, Beijing 102413, China
9.Dipartimento di Fisica and INFN, Sezione di Padova, Padova, Italy
10.INFN, Laboratori Nazionali di Legnaro, Legnaro (Padova), Italy
11.Irfu/CEA, Universite de Paris-Saclay, Gif-sur-Yvette, France
Received Date:2019-05-26
Available Online:2019-10-01
Abstract:Excited states of odd-odd nucleus ⁹²Nb and odd-A nucleus ⁹³Nb were populated in the ⁶Li+ ⁸⁹Y reaction with an incident energy of 34 MeV. The processes that produce ^92,93Nb and can be measured by a combination of light charged particle and gamma ray measurements are discussed. Twenty new transitions are observed and eight new levels are constructed in ⁹²Nb, and in addition two new transitions are added to the level scheme of ⁹³Nb. Using shell model calculations, the low-lying structure of ⁹²Nb is investigated and compared with the experimental results.

HTML

--> --> -->

Over the past few years, much effort in both theory and experiment has been directed to the study of reactions induced by weakly-bound nuclei, especially the elastic scattering, breakup and fusion [1-5]. The occurrence of breakup of weakly-bound nuclei may lead to further reactions, which makes the whole reaction process more complicated [4]. ^92,93Nb are the residues of the ⁶Li+⁸⁹Y experiment performed at LNL-INFN in Italy, with the goal of studying the reaction mechanisms of a weakly-bound nuclear system [6, 7]. In the following, the processes that produce ^92,93Nb nuclei and that involve fusion-evaporation and can be identified with γ-particle coincidence measurements are discussed. Since gamma-gamma coincidence measurements were performed in the present experiment, it was an opportunity to further explore the level schemes of ^92,93Nb.
It is well known that the level structure of nuclei N=50,51 is dominated by single-particle excitations, even for states with high spin. On the other hand, nuclei with N≥55 exhibit collective behavior [8, 9].
As it si a nearly spherical nucleus with N=51 in the A~90 mass region, the studies of the excited states of ⁹²Nb are of importance for establishing and testing the residual interactions in shell model calculations. Previously, the level structure of ⁹²Nb was mainly investigated by proton and ³He induced reactions [10-13], and the energies of excited states were extended up to 3797 keV by the ⁸⁸Sr (⁷Li, 3n)⁹²Nb experiment [14]. Recently, high-spin states of ⁹²Nb were studied in the heavy ion fusion-evaporation reaction ⁸²Se (¹⁴N,4n)⁹²Nb [15]. For the middle-low excited states of ⁹²Nb, the information is relatively scarce, and thus it is important to further explore this nucleus experimentally. From the theoretical point of view, ⁹²Nb was studied within the framework of the shell model, and its low-lying levels below E_level=2287 keV [12] were described by taking the even-even nucleus ⁸⁸Sr as the inert core, while the valance nucleons occupy the πp_1/2, g_9/2 and νd_5/2 orbitals. Nevertheless, from the theoretical point of view, further study of ⁹²Nb is still necessary.
As a “transitional” nucleus with N=52, the excitation of ⁹³Nb is relative intricate [8]. In an earlier work, ⁹³Nb was studied in the (n, nγ) and (p,2nγ) reactions [16]. The I^π=3/2^- at 1840 keV and I^π=5/2^- at 2013 keV were identified as mixed-symmetry states, which can be viewed as low-energy collective modes where protons and neutrons move uncoupled. High-spin states were studied in the ⁸²Se(¹⁶O, p4n)⁹³Nb reaction, with the level schemes up to excitation energy of 11 MeV [17]. An M1 rotational band was reported and showed the characteristics of oblate collective rotational band. The investigation of the level structure of ⁹³Nb can provide additional information for a systematic study of nuclei with N=52.
In this work, the low-lying structure of ⁹²Nb was further studied, and its proposed level scheme was calculated using the shell model code NushellX with SNE valence space, and compared with the experimental results. In addition, two new transitions were observed in ⁹³Nb, as discussed in the following section.

The study of the ⁶Li+⁸⁹Y reaction was performed at LNL-INFN in Italy. A 550 μg/cm^{2 89}Y target, which was supported by a 340 μg/cm^{2 12}C foil, was bombarded by the E_lab=34 MeV ⁶Li³⁺ beam with an average intensity of 1.0 enA, provided by the Tandem-XTU accelerator. The γ-rays were detected by the GALILEO array, which is composed of 25 Compton-suppressed high-purity germanium (BGO-HPGe) detectors arranged in 4 rings: 10 at 90° and 15 at 119°, 129°, 152° with respect to the beam direction [18]. The EUCLIDES 4π Si-telescope array, which consists of 5 segmented and 35 single plates of ΔE/E Si telescopes (the thicknesses of the ΔE and E detectors are 130 μm and 1000 μm, respectively) was used to collect the emitted light charged particles [19]. The distance between the center of the Si telescopes and the center of the target was around 6.2 cm. An Al cylinder was inserted inside EUCLIDES, so that backward angles larger than 150° were unshielded. The thickness of the Al cylinder was 200 μm, so as to stop the intense scattered beam particles from destroying the Si detectors. The energy and efficiency calibrations of each Ge detector in the real geometrical conditions were performed with the following standard sources: ⁶⁰Co, ²⁴¹Am, ¹³³Ba, ¹⁵²Eu, ⁸⁸Y, covering the energy region from 39.522 keV (¹⁵²Eu) to 2734 keV (⁸⁸Y). After further delicate energy calibrations and gain matching with characteristic γ-rays of the residual nuclei, the recorded γ-γ coincidence events were sorted into a two-dimensional E_γ-E_γ symmetric matrix, and two asymmetric ADO matrices. In this experiment, about 14×10⁶ γ-γ coincidence events (without any particle selection) were collected.
The fusion reaction induced by a weakly-bound projectile at near-barrier energies is complicated due to low breakup threshold [6, 20]. When the projectile completely fuses with the target nucleus without breakup (BU), the process is a direct complete fusion (DCF). When the projectiles breakup, then: 1) if all the fragments fuse with the target nucleus, the process is a sequential complete fusion (SCF); or 2) if only part of the fragments fuse with the target nucleus, the process is an incomplete fusion (ICF) [6]. In addition, when a medium-mass target nucleus is involved, the fusion process can evaporate not only neutrons but also light charged particles including protons and alpha particles. In the present experiment, ⁹²Nb can be produced in a complete fusion of ⁶Li with the ⁸⁹Y target nuclei, followed by the 1p2n evaporation channel. As a result, the characteristic γ-rays from ⁹²Nb are in coincidence with protons emitted from the compound nucleus, as shown in Fig. 1(a). In addition, the ⁹²Mo residue from the reaction can only be produced by the CF process. The yield ratio of ⁹²Nb to ⁹²Mo (⁹²Nb/⁹²Mo) in the present experiment is around 0.38, which is larger than given by the statistical evaporation model (around 0.26). Such an increment of the ⁹²Nb/⁹²Mo ratio indicates that the ICF process may contribute to the production of ⁹²Nb. Fig. 1(b) shows the γ-ray spectrum measured in coincidence with deuterons, in which the characteristic gamma rays of ⁹²Nb are clearly visible. It is concluded that ⁹²Nb can also be populated in the ICF process of ⁶Li, where alpha particles from the breakup of ⁶Li fuse with the ⁸⁹Y target nucleus, and simultaneously, the other fragment (deuteron) escapes and is detected. In summary, the ⁹²Nb residue observed in this experiment was populated in the ⁸⁹Y(⁶Li, p2n)⁹²Nb and ⁸⁹Y(α,n)⁹²Nb reactions.
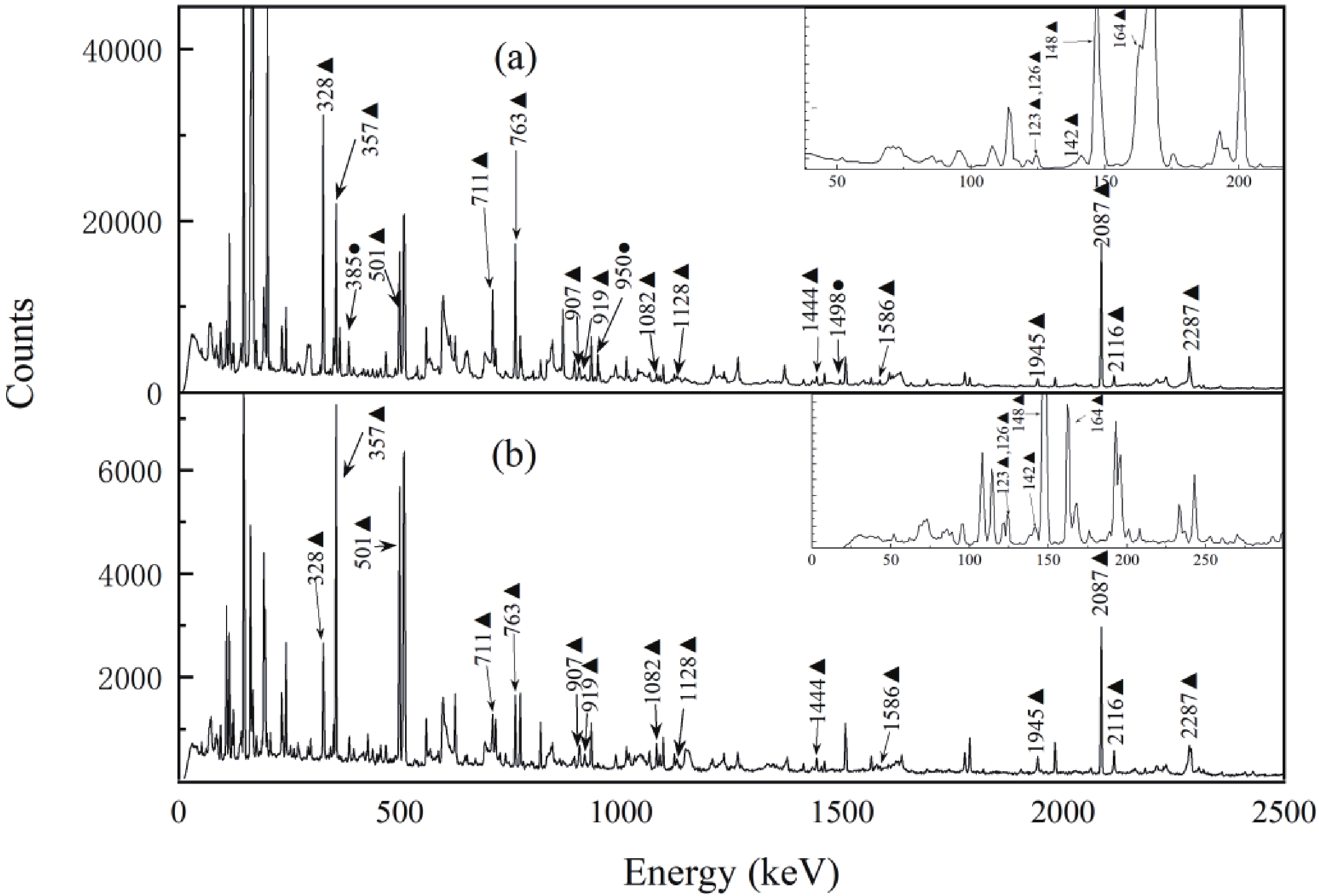Figure1. γ-energy spectra in coincidence with protons (a) and deuterons (b). Representative γ-rays from ⁹²Nb and ⁹³Nb are marked with black triangles and black circles, respectively.

The ⁹³Nb residue in the present experiment can be produced by the complete fusion of ⁶Li with ⁸⁹Y , followed by the 1p1n evaporation channel, as can be seen in the proton gated spectrum shown in Fig. 1(a). The cross-section for alpha particle stripping from ⁶Li on a ⁸⁹Y target producing ⁹³Nb is small, and this process can be neglected.

The level structure of ⁹²Nb was studied by several researchers [10-14]. The high-spin states of ⁹²Nb were recently studied in the ⁸²Se(¹⁴N,4n)⁹²Nb reaction by Wu et al [15]. The projectile used in the present experiment brings lower excitation energy to the compound nucleus, so that the relatively lower excited states of ⁹²Nb can be populated and the middle-low level structure of ⁹²Nb studied. The proposed level scheme of ⁹²Nb is shown in Fig. 2, which is extended up to ~5.4 MeV excitation energy, and 20 new transitions and 8 new levels are added to ⁹²Nb. Sample coincidence spectra, gated on 2287, 387, 328 and 115 keV, are shown in Fig. 3(a)-(d). The relative intensities (I_γ) and the initial and final states ($ E_{\rm i}^\pi $ and $ E_{\rm f}^\pi $) of the observed transitions in ⁹²Nb are summarized in Table 1.
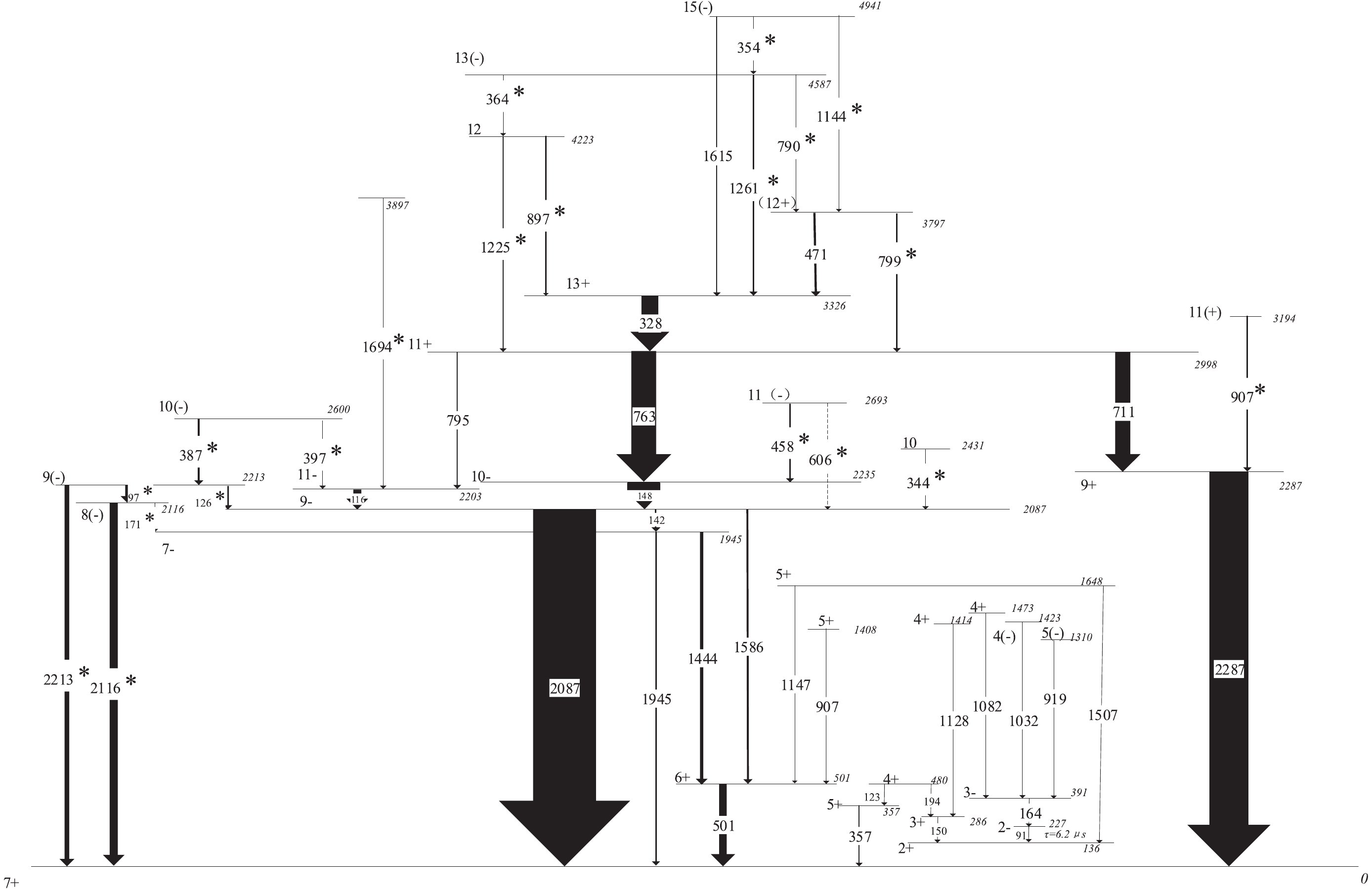Figure2. Level scheme of ⁹²Nb proposed by the present work. New transitions are denoted with asterisks. The width of arrows indicates relative intensity of γ-rays.

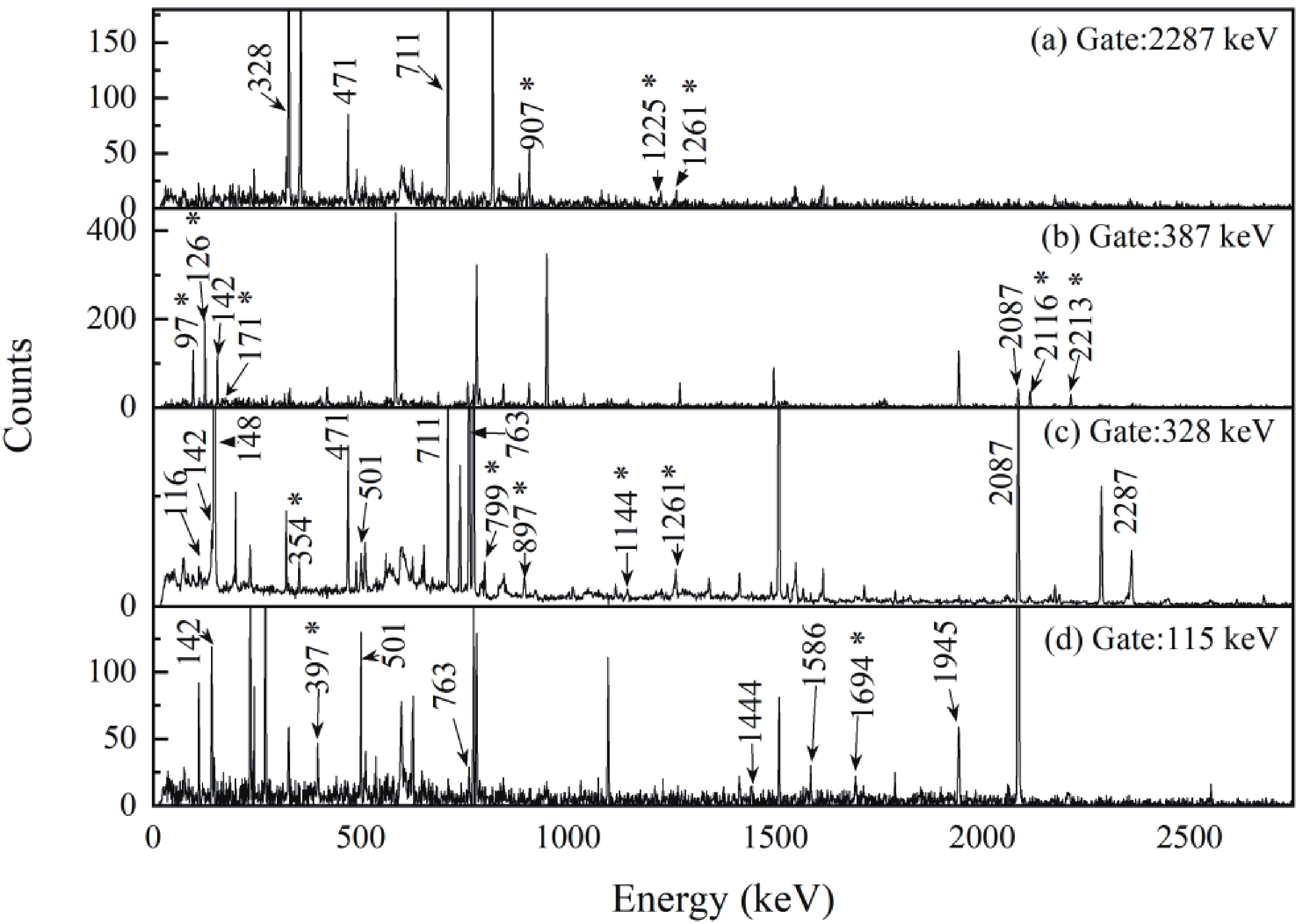Figure3. Typical prompt γ-γ coincidence spectra for ⁹²Nb, gated on 2287, 387, 325, and 115 keV, respectively.

Eγ /keV	Iγa	Eiπ→Efπ	RADOc	Jiπ→Jfπ
97*	8.79(159)	2213→2116	0.71(13)	9(?)→8(?)
116	15.08(80)	2203→2087	1.40(10)	11?→9?
126*	2.68(23)	2213→2087	1.58(25)	9(?)→9?
142	3.07(27)	2087→1945	1.63(33)	9?→7?
148	53.81(280)	2235→2087	0.94(5)	10?→9?
171*	0.49(18)	2116→1945	—	8(?)→7?
328	27.18(151)	3326→2998	1.52(9)	13+→11+
344*	0.82(12)	2431→2087	0.96(23)	10→9?
354 *	0.66(8)	4941→4587	1.46(37)	15(?)→(13?)
364*	0.43(7)	4587→4223	0.96(30)	(13?)→12(?)
387*	3.03(41)	2600→2213	0.96(13)	10(?)→9(?)
397*	0.92(25)	2600→2203	0.94(36)	10(?)→11?
458*	1.92(18)	2693→2235	0.71(15)	11(?)→10?
471	3.53(25)	3797→3326	0.88(8)	(12+)→13+
501	12.77(180)	501→0	0.80(11)	6+→7+
606*	Wb	2693→2087	—	11(?)→9(?)
711	23.85(126)	2998→2287	1.80(11)	11+→9+
763	39.35(168)	2998→2235	0.95(6)	11+→10?
790*	0.66(11)	4587→3797	1.00(25)	(13?)→(12+)
795	1.78(26)	2998→2235	—	11+→11?
799*	2.07(26)	3797→2998	—	(12+)→13+
897*	1.67(76)	4223→3326	0.91(16)	12?→11+
907*	2.29(34)	3194→2287	1.78(49)	11(+)→9+
1144*	0.19(6)	4941→3797	—	15?→(12+)
1225*	1.67(18)	4223→2998	0.95(46)	12(?)→11+
1261*	4.09(52)	4587→3326	1.51(20)	(13?)→13+
1444	5.05(62)	1945→501	0.94(12)	7?→6+
1586	3.09(45)	2087→501	—	9?→6+
1694*	Wb	3897→2203	—	→11?
1945	2.74(56)	1945→0	1.37(27)	7?→7+
2087	100	2087→0	1.40(8)	9?→7+
2116*	12.83(358)	2116→0	0.83(19)	8(?)→7+
2213*	7.67(170)	2213→0	1.66(67)	9(?)→7+
2287	61.98(367)	2287→0	1.66(14)	9+→7+
a The errors of the relative intensity include the fitting and efficiency corrections. Wb The intensities of transitions are too weak. c The errors of the ADO ratios include the fitting and efficiency corrections.

Table1.Transition energies (E_γ) of ⁹²Nb, relative intensities of γ-rays (I_γ), initial and final states for γ-rays, ADO ratios, initial and final spins of the transitions.

In order to obtain the multipolarity of the newly observed γ-rays, the angular distributions of each γ-ray from the oriented residues (ADO) were analyzed. Assuming that γ₁ and γ₂ are the cascading transitions in the same nucleus, the ADO ratio of γ₁ is deduced by I_γ1(152°)/I_γ1(90°), where I_γ1(152° or 90°) represents the intensity of γ₁-rays collected by the detectors at 152° or 90° , and in coincidence with γ₂-rays measured by all detectors. By calculating the ADO ratio of γ-rays with known multipolarity in ⁹²Mo, ⁹¹Mo, ⁹²Nb, ⁹³Nb, ⁹⁰Zr, ⁸⁹Zr produced in the present experiment, typical ADO ratios I_γ(152°)/I_γ(90°) for quadrupole and dipole transitions are around 1.6 and 0.8, respectively, as shown in Fig. 4(a). The spins of the states of ⁹²Nb are assigned tentatively. For the two lower transitions, 97 and 126 keV, the intensity balance rule is used, which supports to some extent the spin assignment of the levels .
Figure4. (color online) (a) Representative ADO ratios in ⁹²Mo, ⁹²Nb, ⁹¹Mo, ⁹³Nb, ⁸⁹Zr, ⁹⁰Zr. Typical R_ADO is given as around 1.6 indicating stretched quadrupole (or ΔI=0) transition, and around 0.8 indicating stretched dipole transition; (b) R_ADO of transitions plotted against energies of γ-rays in ⁹²Nb.

Two new transitions, 504 and 572 keV, are added to the level scheme of ⁹³Nb feeding into the 2180 keV state, as shown in Fig. 5. From the summed spectrum of 689 and 541 keV, shown in Fig. 6, the peaks of the new transitions 504 and 572 keV can be clearly seen. The ADO ratios for the two transitions are 1.45 and 0.94, indicating quadrupole and dipole properties, respectively. Therefore, the spins of the 2752 keV and 2684 keV states are assigned as 21/2, and 19/2, respectively. The relative intensities of partial γ-rays from ⁹³Nb are given in Table 2.
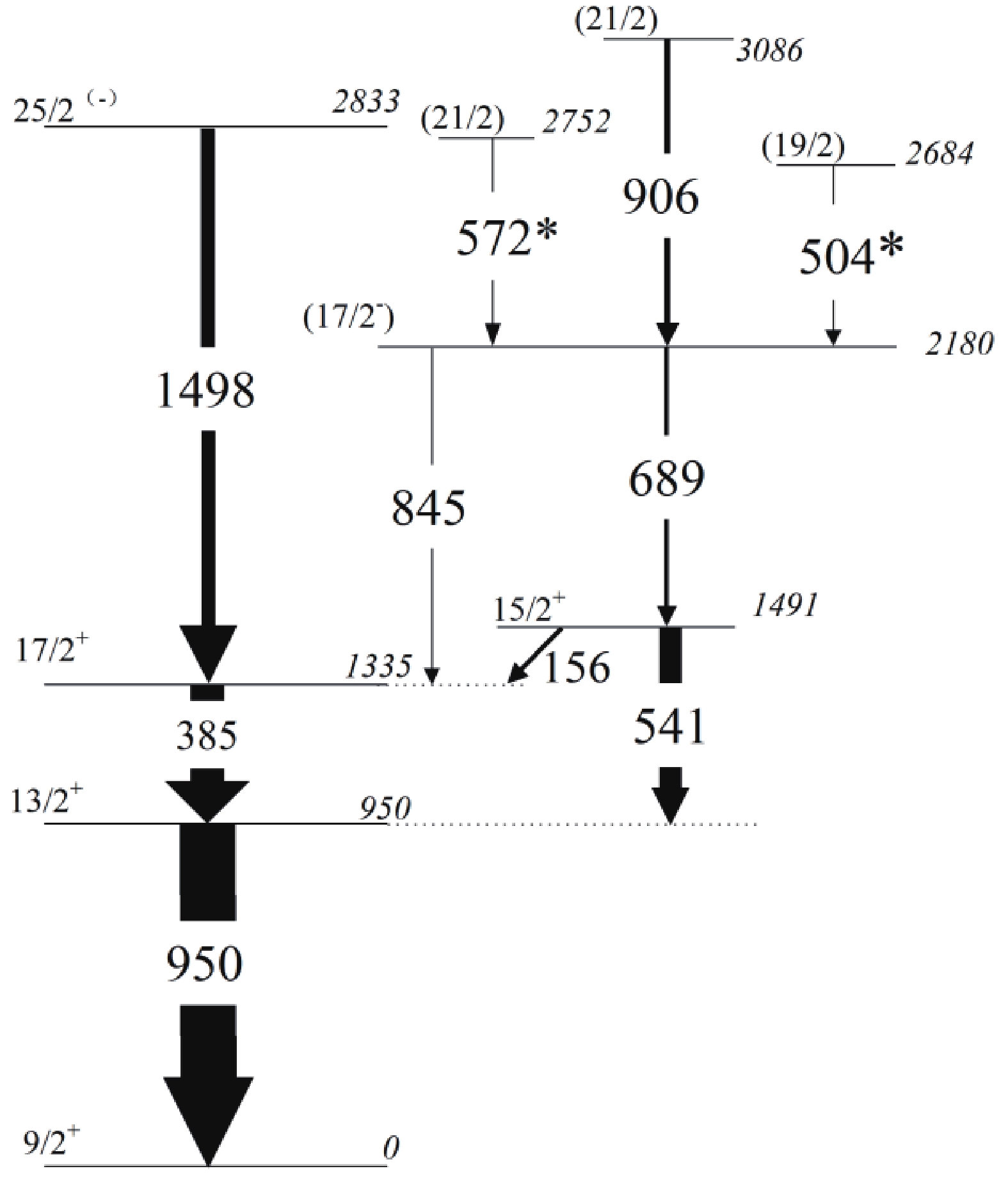Figure5. Level scheme of ⁹³Nb proposed in the present work. New transitions are marked with asterisks. The width of the arrows indicates the relative intensity of γ-rays.

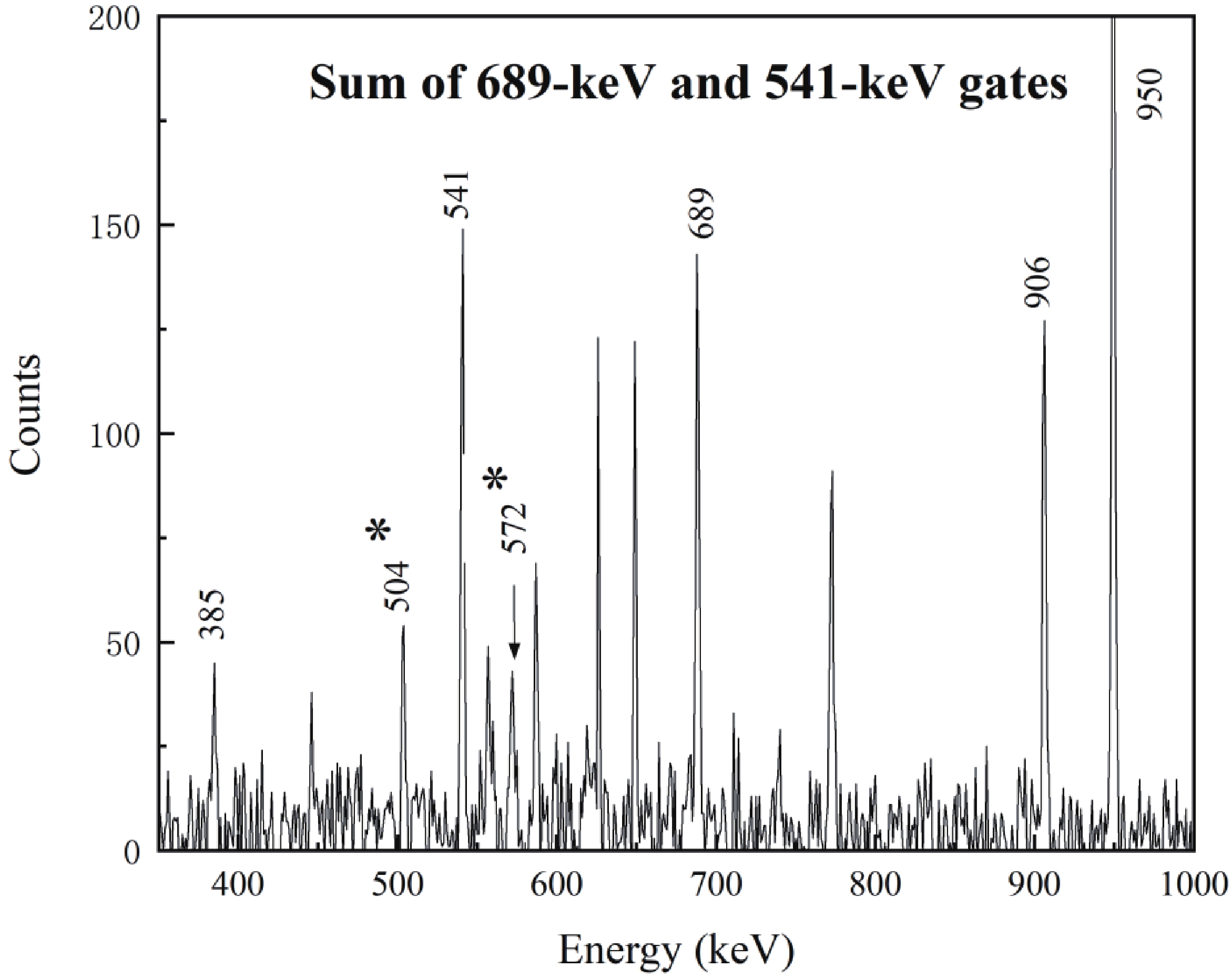Figure6. Typical prompt γ-γ coincidence spectrum for ⁹³Nb with two new transitions marked with asterisks.

Eγ/keV	Iγa	E iπ→Efπ	Jiπ→Jfπ
156	8.1(19)	1491→1335	15/2+→17/2+
385	58.8(69)	1335→950	17/2+→13/2+
504 *	2.8(6)	2684→2180	(19/2)→(17/2?)
541	39.9(69)	1491→950	15/2+→13/2+
572*	1.5(5)	2752→2180	(21/2)→(17/2?)
689	7.1(21)	2180→1491	(17/2?)→15/2+
845	2.2(3)	2180→1335	(17/2?)→17/2+
906	10.8(24)	3086→2180	(21/2)→(17/2?)
950	100	950→0	13/2+→9/2+
1498	25.7(36)	2833→1335	25/2(?)→17/2+
a The errors on the relative intensity include the fitting and efficiency corrections.

Table2.Transition energies (E_γ) of ⁹³Nb, relative intensities of γ-rays (I_γ), initial and final spins of the transitions.

The excitation of a nearly spherical nucleus is usually considered to be of two types: single particle excitations inside a major shell, and excitations that cross the shell gap(s) [21]. The core excitation has been previously reported in A~90 neighboring nuclei, e.g., ⁸⁹Y [22], ^91-94Mo [8, 23-25], and ^94-96Ru [26], which exhibit the characteristics of several parallel transitions with energy around 2 MeV feeding into the same level. The low-lying states may be dominated by single particle excitations inside one major shell. As it is a nearly spherical nucleus, the states of ⁹²Nb should be amenable to shell model calculations.
In order to study the levels in ⁹²Nb, we performed shell model calculations with the code NushellX. The SNE model space and SNET interaction were adopted, which were previously used for level structures of nearly spherical nuclei ⁸⁵Br [27], ⁹⁶Ru [26], ⁹⁴Mo [8]. The model space includes 8 proton orbitals (1f_5/2, 2p_3/2, 2p_1/2, 1g_9/2, 1g_7/2, 2d_5/2, 2d_3/2, 3s_1/2) and 9 neutron orbitals (1f_5/2, 2p_3/2, 2p_1/2, 1g_9/2, 1g_7/2, 2d_5/2, 2d_3/2, 3s_1/2, 1h_11/2) relative to the inert ⁵⁶Ni (Z = 28, N = 28) core.
The low-excited states of ⁹²Nb behave like single particle excitation, and thus we describe the low-excited states of ⁹²Nb as pure configurations, which means that each state corresponds to one proton orbital and one neutron orbital. The pure configuration calculations were also carried out for the low-excited states of ⁹¹Zr, ⁹³Mo, ⁹⁵Ru [28]. Since the Fermi levels of ⁹²Nb lie at the πg_9/2 and νd_5/2 orbitals, the quasi-magic nucleus ⁹⁰Zr is taken as the inert core to describe the low-lying states of ⁹²Nb, so that the 1f_5/2, 2p_3/2, 2p_1/2 proton orbitals and the 1f_5/2, 2p_3/2, 2p_1/2, 1g_9/2 neutron orbitals are fully occupied. The first six positive parity states of ⁹²Nb (I^π=2⁺~7⁺) have been previously interpreted as the π(1g_9/2)$\otimes $ν(2d_5/2) configuration, and the first two negative parity states of 2^- and 3^- are dominated by the π(2p_1/2)$\otimes $ν(2d_5/2) configuration [11, 13]. As ⁹²Nb has one neutron more than ⁹¹Nb, it should have similar level structure for low-excited states, as shown in Fig. 7. Hence, the low-lying levels of ⁹²Nb are described as ⁹¹Nb$\otimes $νd_5/2 as shown in Table 3, where the negative parity states I^π=7^-, 8^-, 9^-₍₁₎, 9^-₍₂₎, 10^-₍₁₎, 10^-₍₂₎ are described as a proton excited from the p_1/2 orbital to the g_9/2 orbital, and the positive parity states 9⁺, 11⁺, 12⁺, 13⁺ are described as a pair of protons excited from the p_1/2 orbital to the g_9/2 orbital. The calculation results for the one proton-neutron coupled configuration, πg_9/2$ \otimes$νd_5/2, and for the two proton-hole neutron-particle coupled configuration, πp_1/2^-1(g_9/2)²$\otimes $νd_5/2 and π(p_1/2)^-2 (g_9/2)³$\otimes $νd_5/2 , are listed in Table 3. As can be seen from this table, the shell model predictions for the low-excited states agree well with the experimental data, which confirms the assignments of Ref. [13] , where the first six positive parity states I^π=2⁺~7⁺ and the first two negative parity states 2^- and 3^- are πg_9/2$\otimes$νd_5/2 and πp_1/2^-1(g_9/2)²$\otimes $νd_5/2, respectively.
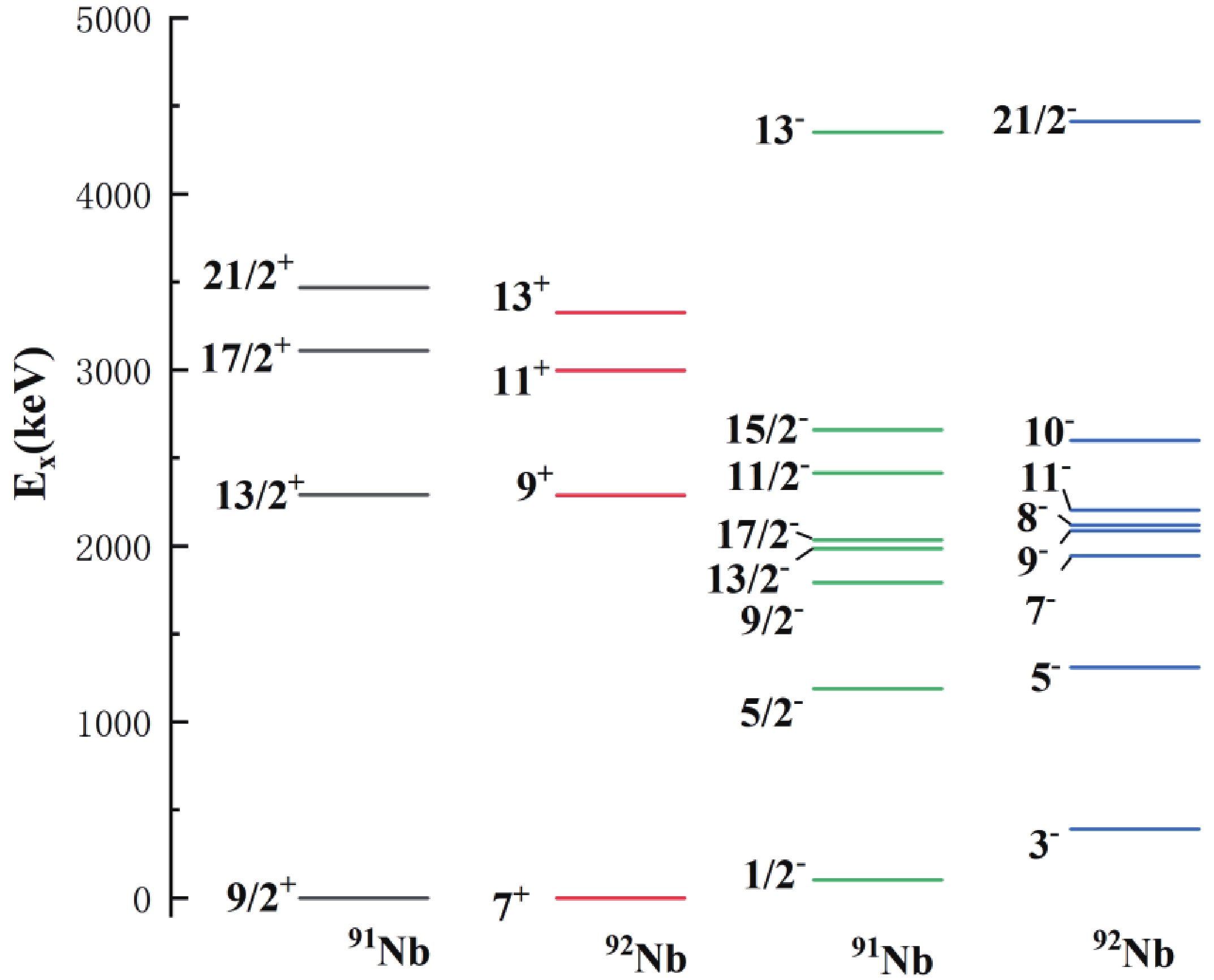Figure7. (color online) Comparison of the low-lying states of ⁹¹Nb and ⁹²Nb.

I π	configuration	Eexp/MeV	Ecal1/MeV
2+	πg9/2$ \otimes$νd5/2	0.136	0.326
3+		0.286	0.402
4+		0.480	0.495
5+		0.357	0.372
6+		0.501	0.515
7+		0	0
2?	π(p1/2)-1(g9/2)2$ \otimes$νd5/2	0.227	0.275
3?		0.391	0.314
7?		1.945	1.83
8?		2.116	2.028
9?(1)		2.088	1.900
9?(2)		2.213	2.54
10?(1)		2.235	2.203
10?(2)		2.6	2.643
9+	π(p1/2)-2(g9/2)3$ \otimes$νd5/2	2.287	2.552
11+		2.998	3.295
12+		3.797	3.859
13+		3.326	3.528
1 the result of shell model calculation with pure configurations.

Table3.Dominant configurations of the low-lying excited states of ⁹²Nb proposed by the shell model calculations with a pure configuration and SNET interaction, calculated results and experimental level energies.

For the higher excited states of ⁹²Nb, ⁹⁰Zr is not an ideal core anymore, which makes the configuration of the high-excited states more complicated, as the pure configurations cannot describe the high-excited states properly. In order to study the high-excited states of ⁹²Nb, a large-basis shell model calculation is necessary.
To obtain a more appropriate description of the observed high-excited states of ⁹²Nb, large-basis shell model calculations are used. ⁹²Nb has 13 valence protons and 23 valence neutrons outside the ⁵⁶Ni core. Due to the large number of active orbitals, truncation of the model space is necessary. In the calculations of ⁹²Nb, the valance space is restricted to π(1f_5/2^4-6, 2p_3/2^2-4, 2p_1/2^0-2, 1g_9/2^1-6, 1g_7/2^0-0, 2d_5/2^0-0, 2d_3/2^0-0, 3s_1/2^0-0)$ \otimes$(1f_5/2^6-6, 2p_3/2^4-4, 2p_1/2^2-2, 1g_9/2^9-10, 1g_7/2^0-1, 2d_5/2^0-2, 2d_3/2^0-0, 3s_1/2^0-0, 1h_11/2^0-1). A comparison between the experimentally determined excitations and the large-basis shell model results is shown in Table 4.

I π	Eexp /MeV	Ecal2/MeV	configuration	partition(%)
9+	2.287	2.111	6 4 0 3$ \otimes$6 4 2 10 0 1 0 0 0	50.24
			4 4 2 3$ \otimes$6 4 2 10 0 1 0 0 0	13.84
11+	2.998	3.146	6 4 0 3$ \otimes$6 4 2 10 0 1 0 0 0	58.88
12+	3.797	3.746	6 4 0 3$ \otimes$6 4 2 10 0 1 0 0 0	64.89
13+	3.326	3.325	6 4 0 3$ \otimes$6 4 2 10 0 1 0 0 0	61.88
8?	2.116	2.320	6 4 0 3$ \otimes$6 4 2 10 0 0 0 0 1	38.79
			6 4 2 1$ \otimes$6 4 2 10 0 0 0 0 1	21.59
9?	2.088	2.232	6 4 0 3$ \otimes$6 4 2 10 0 0 0 0 1	30.85
			6 4 2 1$ \otimes$6 4 2 10 0 0 0 0 1	12.36
9?(2)	2.213	2.777	6 4 1 2$ \otimes$6 4 2 10 0 1 0 0 0	52.03
10?	2.235	1.863	6 4 0 3$ \otimes$6 4 2 10 0 0 0 0 1	41.57
10?(2)	2.6	2.841	6 4 1 2$ \otimes$6 4 2 10 0 1 0 0 0	49.4
13?	4.587	4.797	6 4 0 3$ \otimes$6 4 2 10 0 0 0 0 1	31.97
15?	4.941	5.207	6 4 0 3$ \otimes$6 4 2 10 0 0 0 0 1	65.92
2 the result of shell model calculation with mixed configurations.

Table4.Main partition of the wave function for high-spin states of ⁹²Nb. Each angular momentum is composed of several different partitions. Each partition is of the form p=π[p(1), p(2), p(3), p(4)] $ \otimes$ν[n(1), n(2), n(3), n(4), n(5), n(6), n(7), n(8), n(9), n(10)], where p(i) represents the number of valence protons in the 1 f_5/2, 2p_3/2, 2p_1/2 and 1g_9/2 orbitals, and n(j) represents the number of valence neutrons in the 1 f_5/2, 2p_3/2, 2p_1/2, 1g_9/2, 1g_7/2, 2d_5/2 2d_3/2 3s_1/2 1h_11/2 orbitals, respectively. One neutron is excited to the g_7/2 and h_11/2 orbitals in these calculations.

Excited states of ^92,93Nb were studied in the reactions induced by the weakly-bound nucleus ⁶Li. The states of ⁹²Nb were populated in the ⁸⁹Y(⁶Li, p2n)⁹²Nb and ⁸⁹Y(α, n)⁹²Nb reactions, and of ⁹³Nb in the ⁸⁹Y(⁶Li, pn)⁹³Nb reaction. A total of 20 new transitions, 8 new states of ⁹²Nb and two transitions in ⁹³Nb were observed and added to the level schemes of the two nuclei. The multipolarity of the states of ^92,93Nb was analyzed following the ADO ratio. Shell model calculations were performed with the code NushellX to reconstruct the level structure of ⁹²Nb, where SNE valence space and SNET interaction were used. For the low-excited states, a pure configuration with ⁹⁰Zr as an inert core was employed. Large-basis shell model calculations were performed to study the higher excited states of ⁹²Nb. The results agree well with the experimental data.
　We are grateful to the INFN-LNL staff for providing stable ⁶Li beam throughout the experiment. This research was also supported by the HIRFL User Project, CAS.