Xiao-Bao Wang ^1,
, Yu-Hang Meng ^1,2,
, Ya Tu ^2,
, Guo-Xiang Dong ^1,,
,

Corresponding author: Guo-Xiang Dong, gxdong@zjhu.edu.cn

1.School of Science, Huzhou University, Huzhou 313000, China
2.School of Physics Science and Technology, Shenyang Normal University, Shenyang 110034, China
Received Date:2019-06-17
Accepted Date:2019-09-21
Available Online:2019-12-01
Abstract:We study the structure of neutron-rich calcium isotopes in the shell model with realistic interactions. The CD-Bonn and Kuo-Brown (KB) interactions are used. As these interactions do not include the three-body force, their direct use leads to poor results. We tested whether the adjustment of the single particle energies (SPEs) would be sufficient to include the three-body correlations empirically. It turns out that the CD-Bonn interaction, after the adjustment of SPEs, gives good agreement with the experimental data for the energies and spectroscopy. For the KB interaction, both the SPEs and monopole terms require adjustments. Thus, the monopole problem is less serious for modern realistic interactions which include perturbations up to the third order. We also tested the effect of the non-central force on the shell structure. It is found that the effect of the tensor force in the CD-Bonn interaction is weaker than in the KB interaction.

HTML

--> --> -->

The exotic features of neutron-rich calcium isotopes have drawn quite a lot of attention and have brought challenges for nuclear physicists. Based on the recent experimental discoveries, ^{52, 54}Ca have high excited $ 2^+_1 $ states, and thus have a double closed shell [1]. The charge radii of ⁴⁰Ca and ⁴⁸Ca are nearly the same. However, the charge radius of the “doubly-magic” ⁵²Ca is larger than expected [2]. The mass and the neutron skin thickness are quite important for testing the current nuclear models [3,4]. Thus, the description of the nuclear structure of neutron-rich calcium isotopes is an important test for nuclear models, and many theoretical works have been performed recently, see for example Refs. [5-10].
We rely on the realistic effective interactions, obtained starting from the nuclear forces, to get a microscopic understanding of the nuclear structure. In this paper, we perform a theoretical study of the structure of neutron-rich calcium isotopes in the shell model with several realistic interactions. The Kuo-Brown interaction is a pioneering realistic interaction, proposed by Gerry Brown and Tom Kuo in 1966, derived from the reaction-matrix G method using the Hamada-Johnston nucleon-nucleon potential [11, 12]. Other nuclear potentials have been obtained later, such as the Argonne V18 potential [13], CD-Bonn potential [14], chiral effective field theory potential at next-to-next-to-next-to-leading-order (N3LO) [15], etc. Methods of renormalizing the nuclear potentials in the valence space have also been developed, such as the Lee-Suzuki method [16], unitary transformation method [17], etc. The model-independent low momentum nucleon-nucleon interaction $ V_{{\rm low}\text{-}k} $ [18] is in particular very popular nowdays.
Previously, we have studied [19-22] the systematics of the shell model effective interactions, and the effects of monopole components on the shell evolution. We have found that the three-body (3bd) force is essential for a good description of the neutron-rich oxygen isotopes, and that it involves a central force and an increased spin-orbit splitting [23]. In the present study, we focus on neutron-rich calcium isotopes and use realistic interactions. It has been demonstrated that it is difficult to get a reasonable description of calcium isotopes without the inclusion of the 3bd force [5,7]. We also test whether a phenomenological way of including the three-body force can give reasonable results for the nuclear structure of calcium isotopes. The present paper is organized as follows. We introduce the basic concepts in Section 2. In Section 3, we provide the analysis of the effective interactions and perform shell model calculations. Conclusions are drawn in Section 4.

The full A-body Schr?dinger equation is extremely difficult to solve. Thus, an effective valence-space Hamiltonian $ H_{\rm eff} $ is introduced with the help of the projection operator, as

$ PH_{\rm eff}P |\Psi_{\alpha}> = E_{\alpha} P |\Psi_{\alpha}>, $

(1)

where P is the projection operator which projects onto the valence space, $ E_{\alpha} $ is a subset of the eigenvalues of the full A-body Hamiltonian, and the effective Hamiltonian $ H_{\rm eff} $ is

$ H_{\rm eff} = \sum^d_{i = 1} \varepsilon_i a^{\dagger}a + V_{\rm eff}, $

(2)

where $ \varepsilon_i $ denotes the single particle energies (SPEs) of the d orbitals in valence space, and $ V_{\rm eff} $ is the effective interaction between the valence particles.
Many-body perturbation theory (MBPT) provides a diagrammatic way to calculate $ \varepsilon_i $ and $ V_{\rm eff} $ starting from the nuclear forces [24]. The one-body diagram and three-body correlations (one valence and two core nucleons) can contribute to $ \varepsilon_i $. As the exact treatment of the three-body force is complicated, adjusting SPEs may be seen as an economic way of including the 3bd correlations. The single particle states, which have a spectroscopic factor of unity, are important to fix the single particle energies.
The shell model effective interaction $ V_{\rm eff} $ can be derived by including the perturbation diagrams up to the third order in $ V_{{\rm low}\text{-}k} $ by way of the Q-box plus the folded-diagram method. Two-body and three-body diagrams (two valence and one core nucleon) contribute to the two-body matrix elements (TBMEs) of $ V_{\rm eff} $.
The angular momentum averaged TBMEs can be expressed as

$ V(jj';T) = \frac{\sum_{J}(2J+1)V(jj'jj';JT)}{\sum_{J}(2J+1)}, $

(3)

which is often called the monopole part of the effective interaction [25]. The summations are performed over all Pauli-allowed values of the angular momentum J. The effective single particle energy (ESPE) $ \tilde{ \varepsilon} $ can be defined as [26,27]

$ \tilde{ \varepsilon}_{j} = \varepsilon_{j}+\sum_{j'}V_{jj'}\langle\psi|\widehat{N}_{j'}|\psi\rangle, $

(4)

where $ \langle\psi|\widehat{N}_{j'}|\psi\rangle $ is the occupancy number in the $ j' $ shell and $ V_{jj'} $ is the monopole matrix element [25]. Thus, the monopole interaction can have a dominating effect on the shell evolution.
The exact treatment of the three-body diagram is involved, and is often missing when calculating TBMEs. Thus, the use of realistic interactions usually leads to incorrect spectroscopy. A simple 3bd term, which introduces corrections to the monopole elements, was shown to be powerful, as seen in Ref. [28].
We also use the spin-tensor decomposition method [29-32] to decompose the effective interaction into the central force, tensor force and spin-orbit interaction.

In the present paper, we focus on the study of the nuclear structure of neutron-rich calcium isotopes. A realistic effective interaction starting from the CD-Bonn potential and renormalized with $ V_{{\rm low}\text{-}k} $ [8] is used, in which the $ \hat{Q} $-box plus the folded-diagrams are used to collect the irreducible valence-linked Goldstone diagrams up to the third order in $ V_{{\rm low}\text{-}k} $. As a comparison, the realistic Kuo-Brown interaction [11,12] is also employed. We also use in this work the GXPF1B5 [33,34] and KB3G [35] interactions. All effective interactions are for the $ fp $-shells. We use the shell model code KSHELL [36]. As was shown in Ref. [9], starting from the neutron number $ N = 36 $ (⁵⁶Ca), the neutron $ g_{9/2} $ orbit starts to be occupied and has to be included into the model space. Thus, the current model space is suitable for neutron numbers less than 36. In Refs. [5, 7, 37], it was shown that the 3bd force can have a large impact on neutron-rich nuclei. As the exact treatment of the 3bd force is involved, we test whether a phenomenological way of including the 3bd force can give reasonable results. As discussed in the previous section, the adjustments of SPEs and monopole terms can be seen as a way to include the many-body correlations.
To fit SPEs for the $ fp $ shells, it seems that ⁴¹Ca is a good choice. However, the $ sd $-$ fp $ cross-shell excitation is strong around ⁴⁰Ca, and becomes weaker when adding more neutrons. As pointed out in Ref. [8], the $ (\frac{3}{2}^-)_1 $ state in ⁴⁷Ca, and the $ (\frac{1}{2}^-)_1 $and $ (\frac{5}{2}^-)_2 $ states in ⁴⁹Ca can be good choices for fixing SPEs, since their experimental spectroscopic factors are very close to unity. In the current study, we test both choices for fixing SPEs using the CD-Bonn and KB interactions. All obtained SPEs are shifted so as to reproduce the binding energy of ⁴⁹Ca, as shown in Table 1.

	CD-Bonn	CD-Bonn'	KB	KB'	KB''	KB3G	GXPF1B5
1f7/2	?8.224	?7.787	?8.602	?8.033	?8.536	?8.6	?8.624
2p3/2	?5.415	?5.844	?4.552	?6.090	?5.832	?6.6	?5.679
2p1/2	?2.623	?4.173	?2.327	?4.419	?4.162	?4.6	?3.837
1f5/2	0.285	?5.211	0.168	?5.457	?1.689	?2.1	?1.883

Table1.SPEs used for the effective interactions. SPEs for the CD-Bonn, KB and KB'' interactions are fitted to ^{47, 49}Ca, and SPEs for the CD-Bonn' and KB' interactions are fitted to ⁴¹Ca. All SPEs are shifted so as to reproduce the binding energy of ⁴⁹Ca. The shifts are the absolute values of SPEs of the 1$f_{7/2}$ orbital. SPEs for the GXPF1B5 [33,34] and KB3G [35] interactions are also listed for comparison.

The monopole matrix elements are shown in Fig. 1 central, spin-orbit, and tensor forces are also shown. As we focus on neutron-rich calcium isotopes, the neutron-neutron parts are shown only. KB3G is the KB interaction after monopole correction [35]. As a test, we also perform a monopole correction by replacing the KB' monopole elements with the GXPF1B5 elements, labeled KB''. SPEs for the KB'' interaction are fixed to ^{47, 49}Ca, as in Table 1.
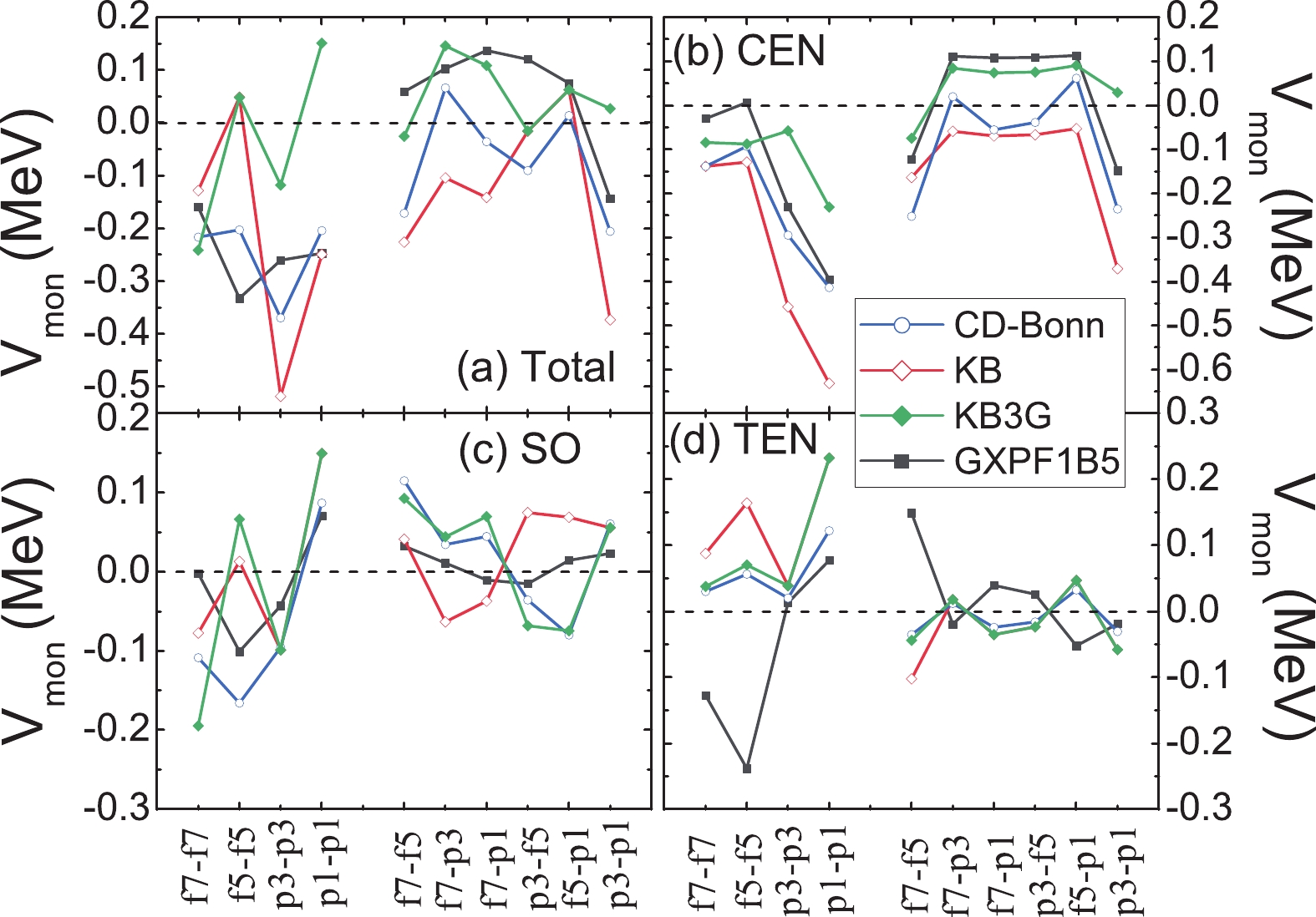Figure1. (color online) Monopole terms of the effective interactions. Panel (a) shows the total interaction. Panels (b-d) show the central, spin-orbit and tensor forces, respectively.

In general, for neutron-neutron interactions, the monopole parts of the realistic interactions are more attractive than for the effective interactions adjusted to the experimental data. The discrepancies are mainly due to the central force, as seen in Fig. 1 (b). The interaction derived from the CD-Bonn potential contains more correlations than from the KB interaction, which includes core-polarization due to the expansion up to the second order of the perturbation [11,12]. Thus, the effective interactions from the CD-Bonn potential are closer to the empirical interactions. For the spin-orbit interactions in Fig. 1 (c), it is seen that the CD-Bonn interaction is close to KB3G. Tensor forces in realistic interactions are quite similar.
ESPEs of calcium isotopes are shown in Fig. 2. The empirical interactions are fitted to the experimental data, which may be seen as a phenomenological way of incorporating effectively the three-body forces and other many-body correlations. Thus, by comparing the results for the CD-Bonn or KB interactions with those for GXPF1B5 or KB3G, it may be seen whether the effects of the three-body force can be included as a simple adjustment of SPEs. It can be seen in Fig. 2 (c-d) that after fitting SPEs to ⁴¹Ca, the resulting shell gap at $ N = $28 is much smaller than for the empirical interactions. The gaps between other orbitals are also smaller, and the orbitals cross when adding neutrons.
Figure2. (color online) Neutron ESPEs of calcium isotopes. The dashed line in panels (c) and (d) are for the effective interactions with single particle energies fitted to ⁴¹Ca, and the solid lines are for the same interactions but with single particle energies fitted to ^{47, 49}Ca.

The adjustments of SPEs simply shift the EPSE curves, as seen in Eq. (4). After fitting of SPEs to ^{47, 49}Ca, the shell structure around ⁴⁸Ca becomes quite close to that for the empirical interactions. As listed in Table 1 , SPEs for the realistic interactions obtained by fitting to ^{47, 49}Ca are close to the empirical SPEs. One can also note that the gap at $ N = $32 and 34 appears for CD-Bonn and KB after the adjustment of SPEs.
As can be seen from Eq. (4), the interplay between SPEs and the monopole interactions determines the shell structure. In Fig. 1, it is seen that although the derived CD-Bonn interaction from MBPT contains more correlations than the KB interaction, there are still systematic discrepancies from the empirical interactions, especially for the central force. Thus, ESPEs for the CD-Bonn and KB interactions differ in detail from the empirical ones. For example, with an increasing number of neutrons, the $ f_{7/2} $ orbital is more bound for CD-Bonn and KB than for GXPF1B5 and KB3G. This occurs because the monopole terms between neutrons are more attractive for the CD-Bonn and KB interactions. Thus, discrepancies may appear for neutron-rich calcium isotopes. We plan to investigate them in further shell-model calculations in the future.
The binding energies of calcium isotopes are shown in Fig. 3. As shown in Refs. [5,7] the binding energies of neutron-rich calcium isotopes, for realistic interactions without the 3bd force, increase almost linearly with the neutron number. This is also the case if SPEs are fitted to ⁴¹Ca, as shown for the CD-Bonn' and KB' interactions in Fig. 3. When SPEs are adjusted to the single particle states in ^{47, 49}Ca, the binding energies for the CD-Bonn and KB interactions are close to the experimental data. Thus, 3bd correlations can be included as an adjustment of SPEs. All other interactions show a similar trend as the experimental data.
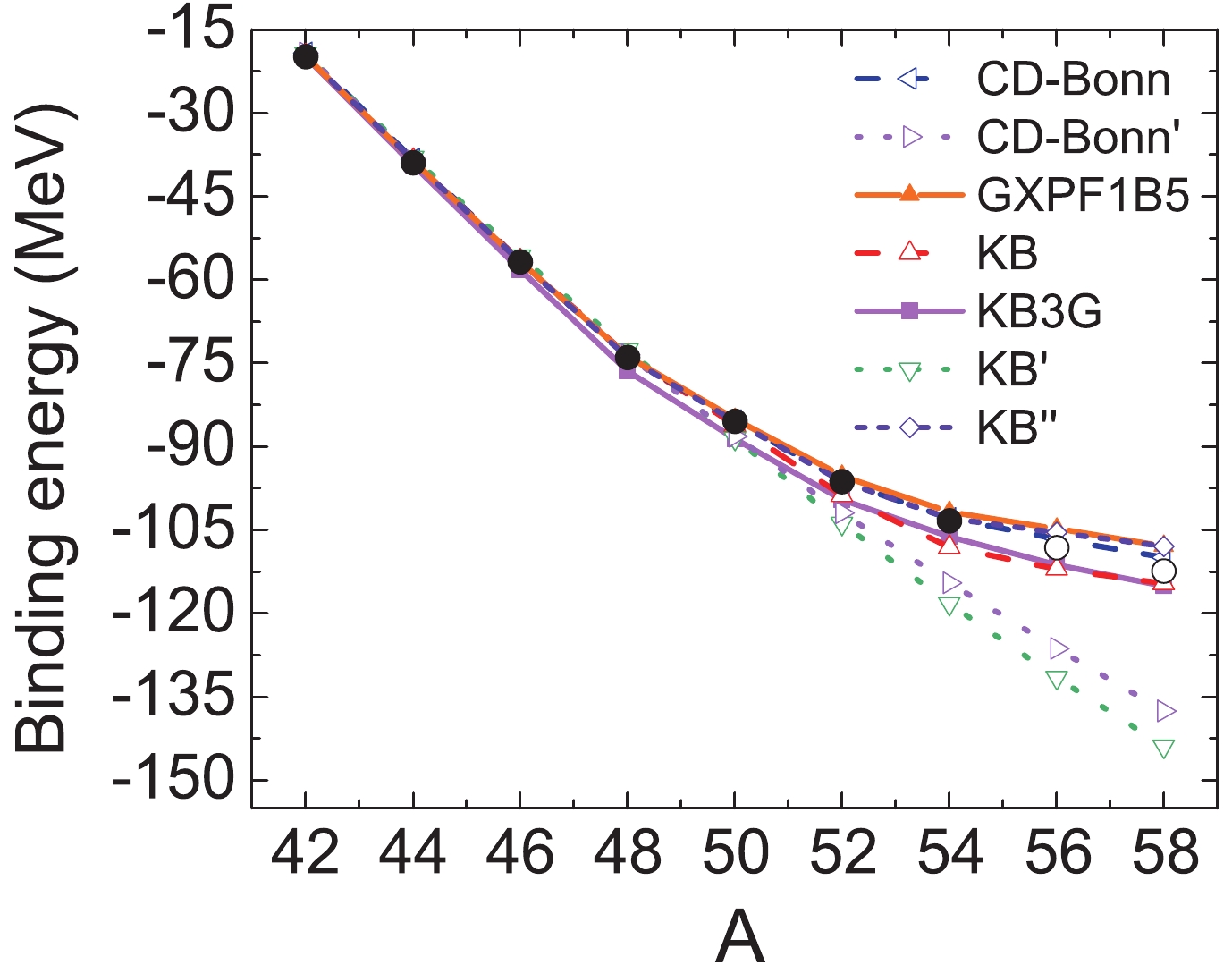Figure3. (color online) Ground state energy of calcium isotopes relative to ⁴⁰Ca for different interactions. The experimental values are given by solid points, and the extrapolated values are shown as open circles, taken from Ref. [38].

The two-neutron separation energy S$ _{2n} $ for calcium isotopes is shown in Fig. 4. The sudden drop of S$ _{2n} $ indicates shell closure, as can be seen in Fig. 4. S$ _{2n} $ calculated for the CD-Bonn' and KB' interactions is nearly linear with increasing neutron number, and quite different from the experimental data. Although it may seem that the KB interaction gives similar binding energy as the experimental data, significant discrepancies can be seen for A larger than 50, which may reflect the defect of the monopole terms. The general trend for KB3G is close to the data, but slight discrepancies are seen for $ A = 46 $ and 48. In the KB'' interaction, we have used the monopole terms of GXPF1B5. S$ _{2n} $ for the KB'' interaction is very close to the data. The results for the CD-Bonn interaction and GXPF1B5 are quite satisfactory.
Figure4. (color online) Same as Fig. 2, but for the two-neutron separation energy.

The excitation energy of the 2$ ^+_{1} $ states in calcium isotopes are shown in Fig. 5. The systematic behavior of the 2$ ^+_{1} $ state gives information about the shell structure. In Fig. 5 (a), the results for the CD-Bonn and CD-Bonn' interactions are given. The results for KB, KB', KB'' and KB3G are shown in Fig. 5 (b). It can be seen that the CD-Bonn interaction reproduces the experimental data well, while the GXPF1B5, KB, KB'' and KB3G interactions give reasonable results, except for ⁵⁴Ca. The 2$ ^+_{1} $ state of ⁵⁴Ca for KB3G has a low energy, while for KB and KB'' the energy is higher. In general, since SPEs for these realistic interactions have been adjusted, they agree much better with the experimental data than for the CD-Bonn' and KB' interactions.
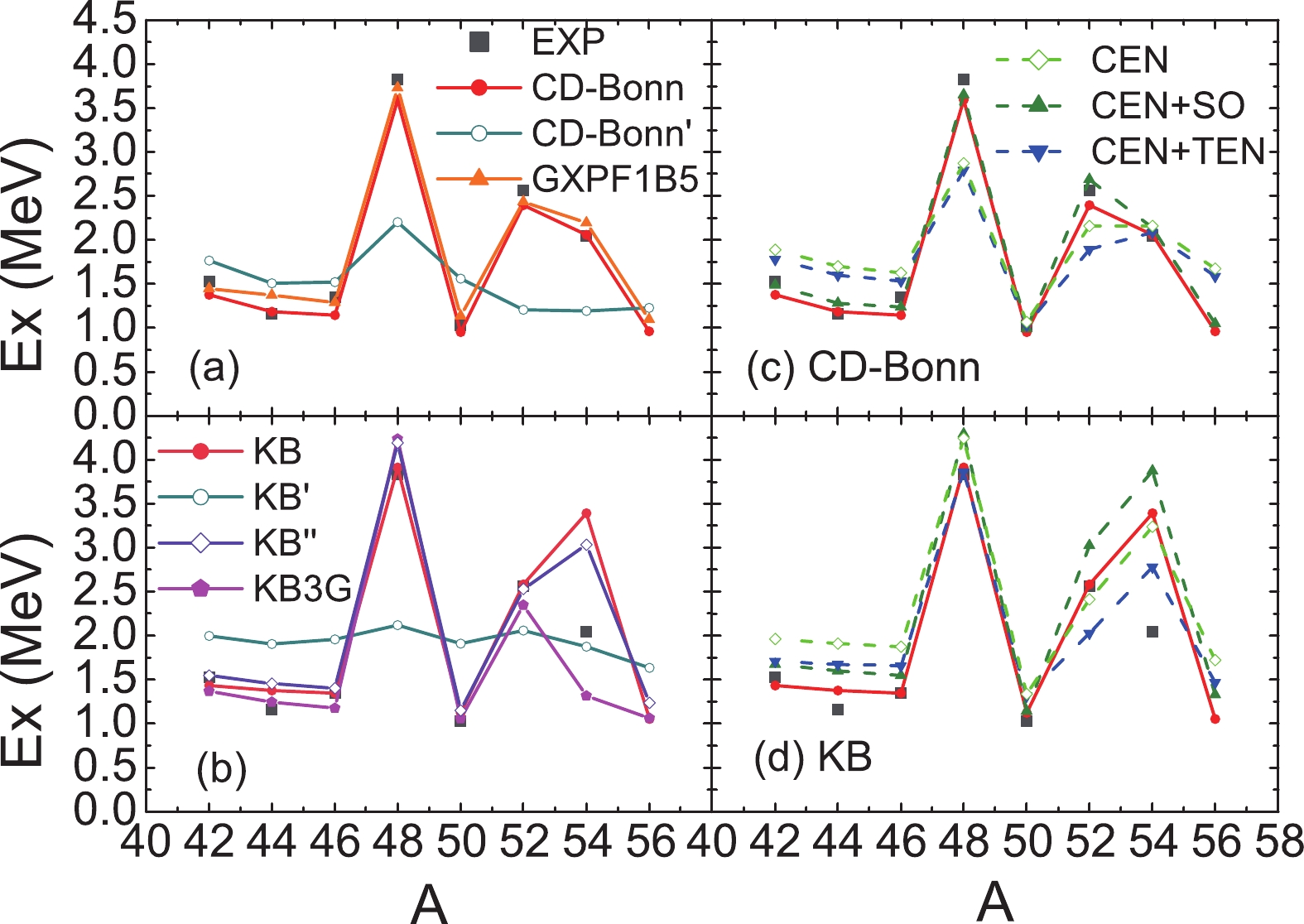Figure5. (color online) The first 2⁺ excitation energy of calcium isotopes. The results for different effective interactions are shown in panels (a) and (b). The results for the central force (“CEN”), central plus spin-orbit force (“CEN+SO”), and central plus tensor force (“CEN+TEN”) for the CD-Bonn and KB interactions are shown in panels (c) and (d), respectively.

SPEs for the CD-Bonn' and KB' interactions are simply fitted to ⁴¹Ca, and it seems that many-body correlations can not be included in these SPEs. The results for the binding energy are poor, which is commonly the case for realistic interactions without the 3bd force. Furthermore, from the results for the 2$ ^+_{1} $ state, the change of the shell structure is not properly described.
In Fig. 5 (c) and (d), we show the effect of the central, spin-orbit and tensor forces on the systematics of the 2$ ^+_{1} $ state. In this calculation, SPEs are taken for the CD-Bonn and KB interactions. It can be seen that the general trend is given by the central force. Thus, the most important correlations are included in SPEs for the central forces. The spin-orbit force lowers the 2$ ^+_{1} $ states in ^{42, 44, 46, 56}Ca, and pushes up the 2$ ^+_{1} $ states in ^{48, 52, 54}Ca, which reflects its attractive and repulsive features in different shells. In general, the tensor force lowers the 2$ ^+_{1} $ states for neutron-rich calcium isotopes. The tensor force in the CD-Bonn interaction is weaker than in the KB interaction, as seen in Fig. 1. The interplay of the spin-orbit and tensor forces gives a better description of the shell evolution, as indicated by the 2$ ^+_{1} $ states in Fig. 5 (c-d).
The excitation energies of bound states in ⁴⁸Ca and ⁴⁹Ca are shown in Figs. 6 and 7, respectively. In these figures, SPEs have been adjusted to the single particle states in ^{47, 49}Ca. Thus, as seen in Fig. 7, the excitation energies of the $ (\frac{1}{2}^-)_1 $, $ (\frac{5}{2}^-)_2 $ states in ⁴⁹Ca are nearly in perfect agreement. The empirical interaction GXPF1B5, which originated from GX1A, was tuned mostly to calcium isotopes, as explained in Refs. [33,34], and gives results which are closest to the experimental data. The results for the CD-Bonn interaction are very similar to GXPF1B5. The spectroscopy for the KB interaction is not good, due to the monopole defects. The KB3G interaction is a monopole-corrected version of KB, and it gives improved results. We also replaced the monopole terms of KB with GXPF1B5, labeled KB'', and it can be seen in the figures that it gives a better spectroscopy than KB, but worse than GXPF1B5, indicating that the multipole terms in the interactions are quite important for the spectroscopic description.
Figure6. Excitation energies of ⁴⁸Ca compared to the experimental data [39].

Figure7. Excitation energies of ⁴⁹Ca compared to the experimental data [39].

The energy of the yrast states of ^51-57Ca is shown in Fig. 8. Since most experimental data for the yrast states of ^51-57Ca are missing, we take the results for the empirical interactions as a guideline, especially for the GXPF1B5 interaction which has been fitted to the most recent experimental data. It is seen that the results for ⁵¹Ca are quite close. However, clear discrepancies can be seen for ^53-57Ca. In particular, the energy of the yrast states for the KB interaction is systematically higher than for the GXPF1B5 and KB3G interactions. Thus, the adjustment of SPEs is not sufficient to cure the KB interaction. The energy for the CD-Bonn interaction is only slightly higher and fairly close to the empirical interactions.
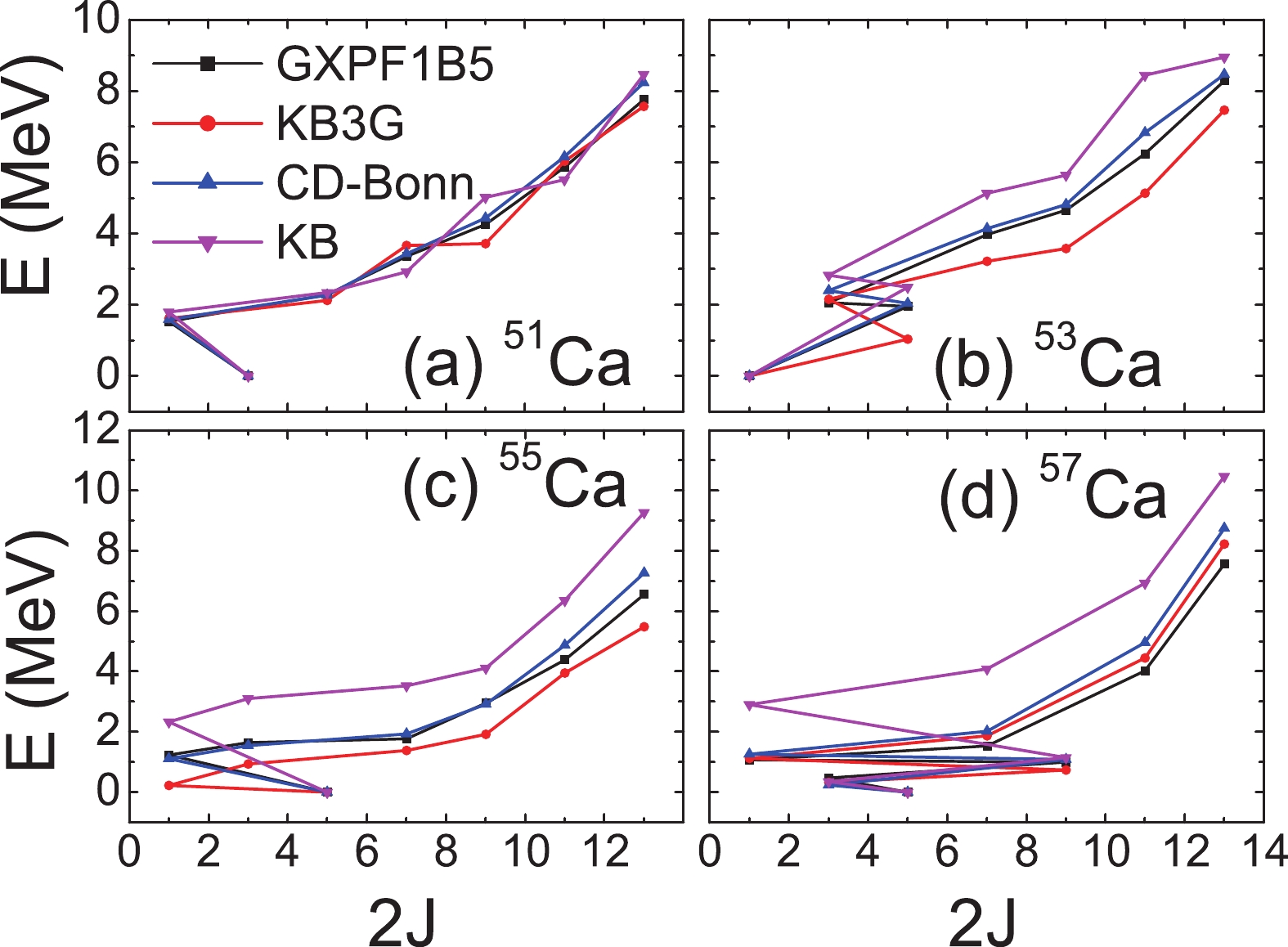Figure8. (color online) Calculated yrast states of ^51-57Ca.

We also calculated the one-neutron pickup spectroscopic factors (SFs), listed for ⁴⁹C in Table 2. A spectroscopic factor of unity indicates a single particle nature. From the table, one can see that all interactions give SFs very close to unity for the $ {3/2}_1^- $ and $ {1/2}_1^- $ states, in agreement with the experiments. Thus, the single particle nature of these states is very robust. For the $ {5/2}^- $ state, the second excited state is a single particle state, but the first one is not. For the KB and CD-Bonn interactions, if their SPEs are not treated properly, SFs of the $ {5/2}_1^- $ and $ {5/2}_2^- $ states are incorrect, as shown for the KB' and CD-Bonn' interactions in the table. Some of the empirical interactions give "inverted" SFs for the $ {5/2}^- $ states, such as the KB3G and FPD6 interactions. GXPF1B5 gives nearly the same SFs for the first and second $ {5/2}^- $ states, deviating from the experiments. A good result for SFs indicates that the many-body wavefunctions obtained from diagonalization are reasonable. If SPEs for the realistic interactions are adjusted properly, a satisfactory description can be obtained.

	$3/2^-_1 $	$1/2^-_1 $	$5/2^-_1 $	$5/2^-_2 $
Exp.	0.84	0.91	0.11	0.84
CD-Bonn	0.86	0.92	0.00	0.86
CD-Bonn'	0.60	0.68	0.68	0.05
KB	0.94	0.96	0.00	0.94
KB'	0.69	0.77	0.67	0.00
KB"	0.95	0.96	0.00	0.94
KB3G	0.95	0.97	0.95	0.00
FPD6 [40]	0.92	0.94	0.93	0.01
GX1A [41]	0.95	0.97	0.02	0.94
GX1B [34]	0.95	0.96	0.02	0.94
GXPF1B5 [33, 34]	0.95	0.96	0.56	0.41

Table2.The one-neutron pickup spectroscopic factors for ⁴⁹Ca. The experimental values are from Ref. [42].

In the present paper, we used the realistic interactions, the CD-Bonn and KB interactions, to calculate the nuclear structure properties of calcium isotopes. It was pointed out in Refs. [5, 7, 37] that the calculations for realistic interactions without the inclusion of the 3bd force lead to poor results. Thus, in the present work, we studied whether an empirical way of incorporating 3bd correlations is sufficient. In our studies, the empirical interactions GXPF1B5 and KB3G, fitted to the experimental data, were used as an effective way of including many-body correlations.
We adjusted their SPEs to the single particle states, identified by a spectroscopic factor of unity, as suggested in Ref. [8]. From the studies of ESPEs, it was found that the evolution of the shell structure for the CD-Bonn and KB interactions is similar to the empirical interactions, especially around ⁴⁸Ca. After fixing SPEs, the calculated binding energy, two-neutron separation energy and excitation energies in neutron-rich isotopes for the CD-Bonn interaction were found to be very close to the experimental data.
The KB interaction, which was the first realistic interaction derived around half a century ago, contains less correlations than the CD-Bonn interaction. The adjustment of SPEs for the KB interaction improves the results considerably, but there are still significant discrepancies with respect to the experimental data. As suggested in Refs. [28, 35], the correction of the monopole can also be seen as an inclusion of 3bd correlations. Thus, we used KB3G, the monopole-corrected version of the KB interaction, and another version of KB (labeled KB''), where the monopole term is replaced by the term from GXPF1B5. The KB3G interaction is one of the most popular $ fp $ shell empirical interactions, which gives a good description of calcium isotopes. It was found that the KB'' interaction also gives a good description. For the spectroscopic properties of ^{48, 49}Ca, the KB family gives worse agreement than the GXPF1B5 and CD-Bonn interactions.
The effective interaction from the CD-Bonn potential contains more correlations than the traditional KB interaction. We found that the monopole matrix elements for the CD-Bonn interaction are fairly similar to the empirical interactions. This is the reason why ESPEs for the CD-Bonn interaction are close to those for the GXPF1B5 and KB3G interactions. Of course, the common monopole problems still exist. For example, the central channel of the monopole elements is still systematically more attractive for the CD-Bonn interaction. Thus, when adding neutrons to calcium isotopes, the orbital becomes more bound. Discrepancies were also found for the energy of the yrast states of ^51-57Ca, since those for the CD-Bonn interaction are slightly higher than for the empirical interactions for ^53-57Ca.
Thus, the real 3bd forces have to be used as a reliable way to consistently include many-body correlations. In cases where it is difficult to include the 3bd force microscopically, or if there is insufficient experimental data to systematically correct the effective interactions or their monopole terms, the prescription proposed here is an economical way of including correlations from the 3bd force, at least for the energies and spectroscopy. The problem of transitions, such as the M1 strength in ⁴⁸Ca, where both the 3bd force and the g-orbit contributions were found to be important [7], is left to future investigations.
We also tested the systematics of the 2$ ^+_{1} $ states in calcium isotopes and found that after fixing of SPEs, the general pattern is given by the central force of the effective interactions. The interplay of the spin-orbit and tensor forces leads to final results which are in close agreement with the experimental data. In the CD-Bonn interaction, the tensor force gives a smaller effect than the spin-orbit interaction, while in the KB interaction, the effects of the tensor and spin-orbit interactions are similar.