空间玻尔兹曼熵的研究进展与应用

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-29

高培超^,¹^,²^,³, 程昌秀^,³^,⁴, 叶思菁³, 沈石³, 张红⁵^,⁶

1.北京师范大学地表过程与资源生态国家重点实验室,北京 100875

2.香港理工大学土地测量与地理资讯学系,香港 999077

3.北京师范大学地理科学学部地理数据与应用分析中心,北京 100875

4.国家青藏高原科学数据中心, 北京 100101

5.华东师范大学城市与区域科学学院,上海 210046

6.西南交通大学地球科学与环境工程学院,成都 611756

The review and applications of spatial Boltzmann entropy

GAO Peichao^,¹^,²^,³, CHENG Changxiu^,³^,⁴, YE Sijing³, SHEN Shi³, ZHANG Hong⁵^,⁶

1. State Key Laboratory of Earth Surface Processes and Resource Ecology, Beijing Normal University, Beijing 100875, China

2. Department of Land Surveying and Geo-Informatics, The Hong Kong Polytechnic University, Hong Kong 999077, China

3. Center for Geodata and Analysis, Faculty of Geographical Science, Beijing Normal University, Beijing 100875, China

4. National Tibetan Plateau Data Center, Beijing 100101, China

5. School of Urban & Regional Science, East China Normal University, Shanghai 210046, China

6. Faculty of Geosciences & Environmental Engineering, Southwest Jiaotong University, Chengdu 611756, China

通讯作者: 程昌秀(1973-), 女, 新疆人, 教授, 主要从事地理时空数据分析等研究。E-mail: chengcx@bnu.edu.cn

收稿日期:2020-03-31修回日期:2021-03-25网络出版日期:2021-07-25

基金资助:

第二次青藏高原综合考察研究.2019QZKK0608
香港研究资助局基金.152219/18E
国家自然科学基金项目.41901316
成都市重点研发支撑计划.2019-YF05-02119-SN
地表过程与资源生态国家重点实验室开放基金.2020-KF-03
中央高校基本科研业务费专项资金.2019NTST02

Received:2020-03-31Revised:2021-03-25Online:2021-07-25

Fund supported:

Second Tibetan Plateau Scientific Expedition and Research Program.2019QZKK0608
Research Grants Council of Hong Kong.152219/18E
National Natural Science Foundation of China.41901316
Key Research and Development Program of Chengdu.2019-YF05-02119-SN
State Key Laboratory of Earth Surface Processes and Resource Ecology.2020-KF-03
Fundamental Research Funds for the Central Universities.2019NTST02

作者简介 About authors
高培超(1991-), 男, 河南人, 讲师, 中国地理学会会员(S110014357M), 主要从事信息地理学研究。E-mail: gaopc@bnu.edu.cn

摘要
区域性、综合性、复杂性是新时代地理学的三大特征,其中复杂性研究是地理学飞跃的新路径。熵作为系统复杂性的核心指标,其研究、推广和应用对新时代的地理学有着重要意义。近年来地理学中熵的研究热点为玻尔兹曼熵（玻熵）。玻熵的概念最早提出于1872年,是著名的热力学第二定律的核心,但玻熵在地学的应用长期停滞在探讨层面。其瓶颈在于缺乏针对空间数据计算玻熵的模型和方法,但该瓶颈在近5年得以突破。本文从玻熵的热力学概念与地理学推广难题、空间数据的玻熵计算模型、计算方法、实际应用4个方面进行及时且系统地综述。主要结论有：① 目前的研究热点集中在空间栅格数据的玻熵,已研发出针对定性和定量型栅格数据的计算模型;② 算法百家齐放,已呈现出基于边缘总长度、基于Wasserstein距离、基于多尺度层次的三大类算法;③ 已形成景观生态学和遥感图像处理两类应用;④ 未来研究需重视针对更多类型的空间数据的算法、使用玻熵替代香农熵验证先前研究中的结论、拓展玻熵应用等。
关键词： 空间数据;玻尔兹曼熵;香农熵;空间信息论;景观生态学;区域可持续性

Abstract

The field of geography has three unique characteristics, namely, regionality, integration, and complexity. Among them, complexity has become increasingly crucial to geography in the current era. Entropy is a key concept and an indicator of the complexity of a system; thus, the research and application of entropy play a fundamental role in the development of geography. During recent years, Boltzmann entropy (i.e., thermodynamic entropy) has emerged as a research hotspot in the entropy for geography. Proposed as early as the year 1872, it is the core of the well-known Second Law of Thermodynamics. However, its application in geography had remained at a conceptual level for lack of computational methods with spatial data. Fortunately, much progress has been made globally towards computing and applying spatial Boltzmann entropy (i.e., the Boltzmann entropy of spatial data). This paper aims to perform a comprehensive review of such progress, in terms of the thermodynamic origination of Boltzmann entropy, the difficulties in applying it to geography, computational models and algorithms of spatial Boltzmann entropy, and all the applications up to now. Four major conclusions can be drawn as follows: (1) The current focus of research is placed on the Boltzmann entropy of spatial raster data. Models have been developed for computing Boltzmann entropy with both qualitative and quantitative raster data. (2) Many algorithms have been developed and can be classified into three categories, namely total edge-based, Wasserstein distance-based, and multiscale hierarchy-based. (3) It has witnessed two groups of applications of spatial Boltzmann entropy to geography, namely landscape ecology and remote sensing image processing. (4) Future research is recommended to develop algorithms for more types of spatial data, validating previous conclusions drawn using Shannon entropy, and extending the applications of spatial Boltzmann entropy.

Keywords：spatial data;Boltzmann entropy;Shannon entropy;spatial information theory;landscape ecology;reginal sustainability

PDF (2329KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex 收藏本文
本文引用格式
高培超, 程昌秀, 叶思菁, 沈石, 张红. 空间玻尔兹曼熵的研究进展与应用. 地理学报[J], 2021, 76(7): 1579-1590 doi:10.11821/dlxb202107001
GAO Peichao, CHENG Changxiu, YE Sijing, SHEN Shi, ZHANG Hong. The review and applications of spatial Boltzmann entropy. Acta Geographica Sinice[J], 2021, 76(7): 1579-1590 doi:10.11821/dlxb202107001

1 引言

地理学通常被称为是研究世界的学科（The World Discipline/Subject）^[1,2],旨在通过综合普适的或多个专门的定律、模型、指标等途径来刻画和理解地球关键带^[3]（陆地表层、河流湖泊、海岸带及近海海域等）的地理要素（包括自然与人文）及其综合体（即区域系统）的时空格局、演变过程、动力机制^[4,5,6,7]。这些途径有著名的地理学三大定律、地理加权回归、地理探测器^[8]等。熵作为热力学中解译世界变化的工具,也长期在地理学中扮演着重要角色。熵是复杂系统的核心指标,而地理学的新时代特征是复杂性^[9,10],因此熵的研究愈发得到重视,对新时代地理学意义重大。

当前,熵在地理学中主要有两大用途。首先,熵被用于关联地理学研究对象的时空变化表征与深层次的热力学机理。热力学中认为,封闭系统的熵自发地、不可逆转地渐增至最大值。这正是著名的热力学第二定律（又称熵定律）。同时,熵与热力学无序和系统不确定性有着紧密的内在联系。因此,熵作为联系热力学机理的“桥梁”,被长期、广泛地应用于地理系统（包括自然、人文系统、及其耦合系统）的研究中。例如,针对景观格局的应用可追溯至20世纪50年代,并形成了三大方向：刻画景观格局的空间异质性、尺度依赖性、不可预测性^[11]。又如,学术界试图从热力学本质上理解系统可持续性和区域可持续发展,因此熵也用于构建可持续/高质量发展指数^[12]、用于评估和指导城市建设^[13]。其次,熵作为信息量的测度指标,被广泛地应用于地图制图学、地理信息科学与系统、遥感图像处理等领域。例如,熵被用于测度地图的信息量^[14],进而对制图综合进行指导^[15]。以熵为核心,地图制图学发展出地图信息论^[16]的分支学科。在遥感图像处理领域,熵作为衡量图像信息量的标准指标^[17],被用于降维^[18]、融合^[19]、配准^[20]、分割^[21]等。

尽管熵是源自热力学的概念,但在上述应用中的计算方法却几乎完全来自通信领域的信息论。具体而言,“熵”的概念是1851年由德国科学家Clausius首次引入^[22],并于1872年由奥地利物理学家Boltzmann首次使用公式明确地表达（即玻尔兹曼熵、简称玻熵或称热力学熵）^[23]。20世纪40年代始创的信息论中再次使用了“熵”的概念,并于1948年由美国数学家Shannon提出计算公式（即香农熵、信息熵）^[24]。香农熵的公式简洁、变量含义明确且容易测定。相比之下,玻熵的计算困难重重。不过,多数****认为2种熵本质相同、数值可互换^[25]。因此,在上述两大应用中,理论探讨时或采用玻熵或采用香农熵,但实际计算时均采用了香农熵算法。

然而,香农熵的使用带来了难以解决的困境。首先,通过香农熵而获得的热力学解译在近年来被严重质疑。例如,Vranken等****^[11]发现：基于香农熵测定的空间异质性与热力学毫无关联、香农熵尺度依赖性的热力学解释与复杂理论相悖、基于香农熵的不可预测性只在特定条件下与热力学有关。美国地理学家Cushman将这些发现评论为“令人震惊”的,并呼吁重返玻熵^[26]。其次,香农熵无法完整地刻画空间数据的信息量（或无序）。香农熵的设计初衷为刻画通讯信号（例如电报）的信息量,仅考虑了信号中不同成分的占比（或称为信源产生该成分的概率）,因此也被广泛地称为统计信息量。在仅考虑统计信息时,香农熵和玻熵存在数值转换的可能性。而空间数据的信息量不仅在于成分的占比,更在于组分和配置。尽管学术界对香农熵算法做出了多种改进^[27],但依然效果欠佳。因此,越来越多的****认为2种熵具有本质的不同。景观生态学界认为,2种熵仅是形式相似^{[11, 28]},生物学界^[29]和物理学界^[30]均有类似观点。实际上,Shannon本人也曾明确其熵并非推导自玻熵^[31],2种熵仅在特定条件下才可互转^[32]。

因为上述困境和新的认识,最近5年学术界重新聚焦于古老的玻熵,见证了其长足的进步,实现了自1872年玻熵的概念提出后针对空间数据的首次计算,并形成实际应用。本文将从概念、模型、计算、应用4个方面对这些进展进行系统的综述。

2 玻熵的概念模型与计算难题

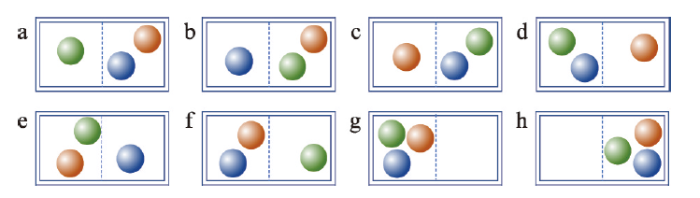
玻熵涉及两大概念：系统的宏观态（Macrostate）和微观态（Microstate）。前者指系统状态的宏观描述,通常使用若干可量测的宏观特性（称为状态函数、宏观参数,如压强、体积、温度）来实现^[33]。后者指从微观的角度刻画系统的内部细节（如组分位置）。如在图1所示的封闭系统中,宏观态均为“容器中有3个气体分子”,微观态却不尽相同。

图1

新窗口打开|下载原图ZIP|生成PPT
图1宏观态为内含3个不同类型气体分子的密闭容器及其8种微观态

Fig. 1A closed container and its 8 microstates (macrostate: it contains three gas molecules)

在宏、微观态概念的基础上,玻尔兹曼提出了玻熵的概念模型（玻尔兹曼公式）：

（1）

S = k_{B} \log W

式中：S即系统的玻熵;W是宏观态所对应微观态的个数;k_B是玻尔兹曼常数取值为1.3807×10^-23J/K。图1中所示的密闭容器具有8种微观态,因此玻熵为k_B log8。

玻尔兹曼公式简洁,但其在地理学中的应用长期停留在探讨层面^{[11, 26]}。应用瓶颈在于计算困难,具体原因有：① 缺少通用、普适的宏观态定义方法,如美国社会学家Bailey所言“玻熵尽管重要,但物理学领域外的****缺少宏观态的定义方法,例如,如何定义一块景观格局的宏观态?”^[34]② 即便宏观态有了良好的定义,微观态数的实验测定亦难实现,理论推导缺少方法^[35]。

3 空间玻熵的计算模型

2016年起,学术界在空间数据的玻熵研究方面取得了系列进展。首要进展为计算模型实现了空间玻熵计算模型从无到有的突破（共计2类3种）。

2类计算模型分别适用于定性型和定量型栅格数据。定性型是指以栅格形式存储的类别型空间数据,可细分为名义型和次序型。名义型中不同类别无顺序之分,例如土地利用/覆盖类型图、景观镶嵌体;次序型中不同类别有顺序之分,例如疫情风险等级地图。定量型是以栅格形式存储的连续型空间数据,包括间隔型和比率型2类。前者如地表摄氏温度梯度,后者如数字高程模型。与前者相比,后者支持乘除运算,但是实际应用中往往不严格区分二者,在地理学（尤其景观生态学）中通常将二者合并统称为景观梯度^[36]。

3.1 针对定性型栅格数据的计算模型

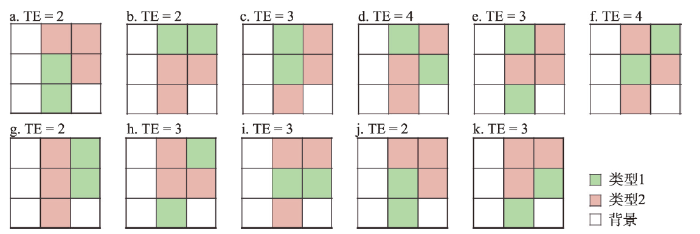
空间玻熵的计算思想最早是针对定性型栅格数据提出的。2016年Cushman通过类比热力学中的算例,首次提出了针对景观镶嵌体的玻熵计算思想——基于边缘总长度（景观格局指数Total Edge, TE）的计算模型^[37]。该模型使用了5项（组）宏观参数,分别是几何范围、细胞（景观镶嵌体的基本单元）的类型数、各类型的占比、分辨率（或细胞总数）、TE。微观态定义为细胞的空间配置,个数通过穷举法获得。

以图2a中的景观镶嵌体为例,其几何范围为绿色和粉红色区域,共有2类、5个细胞。其中类型1的细胞有2个、类型2有3个,边缘总长度为2。微观态的穷举过程如下：首先,在保持除TE外的所有宏观参数不变的条件下,穷举细胞的空间配置方式,如图2b~2k所示。然后,统计与原景观镶嵌体具有相同TE的穷举结果个数,此处为3。此个数即微观态数,可代入玻尔兹曼公式求解玻熵,得到

k_{B} \log 3

。

图2

新窗口打开|下载原图ZIP|生成PPT
图2景观镶嵌体(a)、可能的空间配置方式(b~k)及其边缘总长度(TE)

Fig. 2A landscape mosaic (a), possible configurations (b-k), and the corresponding total edges (TE)

该计算模型的优点是宏观态的定义对所有定性型栅格数据具有普适性,宏观参数均可快捷地计算。其缺点是,微观态数的计算方法缺乏可操性。在栅格数据的尺寸较大时,穷举结果数可能是天文数字。例如,设栅格数据的大小仅为100行100列,且仅包括2类、每类个数相同的细胞,则穷举结果的理论个数高达

C_{10000}^{5000}

,实际实现难度大。

第二种计算思想为基于斑块的计算模型,由中国****于2019年提出^[38]。首先,宏观参数被试验性地设置为栅格数据的细胞总数N以及各类型细胞的具体个数N_i。在此情况下,微观态数的计算可通过数学上的排列组合公式完成：

（2）

W = C_{N}^{N_{1}} \times C_{N - N_{1}}^{N_{2}} \times C_{N - N_{1} - N_{2}}^{N_{3}} \times ? \times C_{N - N_{1} - ? - N_{m - 1}}^{N_{m}}

式中：m为类型数。将该微观态数带入玻熵公式并化简,得到：

（3）

S = k_{B} \log (N!) - k_{B} \overset{m}{\sum_{i = 1}} \log (N_{i}!)

然而,这种方式定义下的玻熵,只能刻画栅格数据的组分、无法刻画配置。因此,Zhao等^[38]增加了对拓扑关系的考虑,将计算模型修正为：

（4）

\frac{S}{k_{B}} = \log (N!) - \overset{m}{\sum_{i = 1}} \log (N_{i}!) - \overset{m}{\sum_{i = 1}} \overset{n_{i}}{\sum_{j = 1}} \log (k_{ij}!)

式中：n_i为类型i的细胞相互之间所形成的斑块数（细胞在上下左右的任一方向相连形成斑块）;k_ij为类型i的细胞所形成的第j个斑块中所包含的细胞数。

该修正版在本文中被命名为基于斑块的计算模型,其优点是具有解析形式,缺点有：① 修正之后的计算模型所对应的宏观态定义不明确;② 在实际计算中容易因数值较大的阶乘运算产生数值溢出的问题,如假设栅格数据的大小仅为10行10列,公式（4）中首项中包括的阶乘数值高达9.3326×10¹⁵⁷。

3.2 针对定量型栅格数据的计算模型

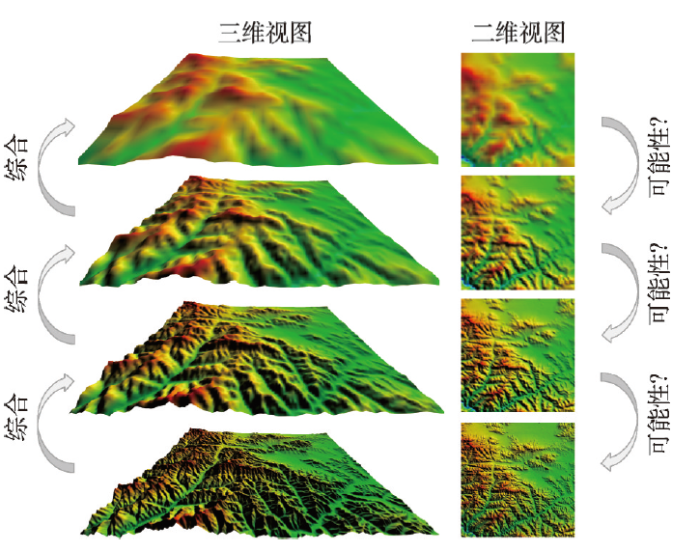
针对定量型栅格数据的计算模型于2017年提出^[39],其核心思想是通过尺度变换建立宏观态与微观态之间的联系。该模型认为所有的定量型栅格数据均有普适的宏观态定义,即栅格数据的多尺度表达（图3）。同时认为,在热力学中微观态难以测定的本质原因是观测尺度可以无限细分,从而导致无穷尽。但对于栅格数据而言,其原分辨率即为最天然的观测尺度,因此限定了微观态的数量,使其测定成为可能。

图3

新窗口打开|下载原图ZIP|生成PPT
图3定量型空间栅格数据的多尺度层次表达结构

Fig. 3The multiscale hierarchy of a quantitative spatial raster data

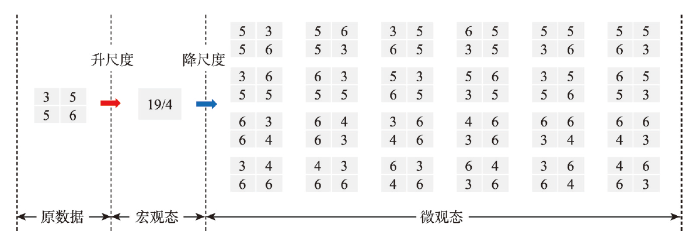
具体而言,定量型栅格数据的宏观态定义为其多尺度层次表达结构中与原表达最相似的层次。多尺度层次表达结构通过制图综合中的升尺度（Up-scaling）操作获得。为了使层次尽可能得丰富,升尺度操作中采用大小为

2 \times 2

的窗口对栅格数据进行滑动均值化。宏观参数定义为窗口中所有细胞（针对定量型数据也称像素）的最大值、最小值、平均值（或和值）。微观态的求取方法是对综合的过程求逆,即在宏观参数限定的情况下将宏观态降尺度（Down-scaling）至原分辨率（图4）,结果的个数即为微观态数。可见,该模型实际上是通过刻画尺度变换中的不确定性反映无序程度,统一了熵、无序、不确定性等概念。

图4

新窗口打开|下载原图ZIP|生成PPT
图4针对定量型空间栅格数据计算玻熵的核心思想

Fig. 4The core idea in computing the Boltzmann entropy of a quantitative spatial raster data

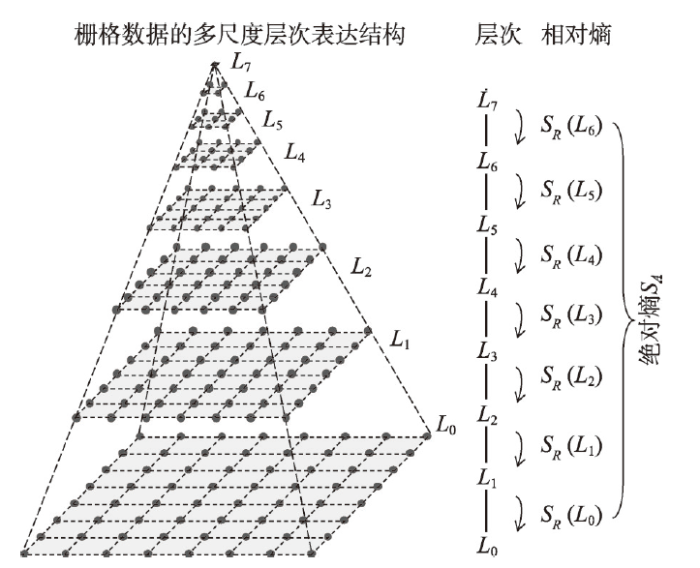
此外,该模型引入了相对和绝对玻熵的概念。将上述微观态数直接代入公式（1）得到的结果称为相对玻熵,因其刻画的是栅格数据相对于其宏观态的不确定性。在多尺度层次表达结构中,相对熵可在任意相邻的两层间计算（图5）,所有层的相对熵之和称为绝对玻熵。其含义为,从栅格数据的最抽象状态逐层降尺度到原栅格数据的可能性大小;换言之,栅格数据相对于最抽象的状态（不确定性为零）的不确定性。

图5

新窗口打开|下载原图ZIP|生成PPT
图5相对玻熵(S_R)与绝对玻熵(S_A)

Fig. 5Relative (S_R) and absolute (S_A) Boltzmann entropies

4 空间玻熵的算法

以上述3种模型为蓝本,学术界分别发展了3类具体的计算途径：基于TE的算法^{[37, 40]}、基于Wasserstein距离的算法^{[38, 41]}、基于多尺度层次的算法^{[39, 41-45]}。在实现过程中,由于技术考虑,有些算法甚至已经脱离了原模型的核心思想。

4.1 基于TE的算法

实现TE计算模型困难的关键在于穷举数据趋近于无穷大,难以获得穷举结果的集合（即统计学中的整体）。因此,Cushman^[40]提出使用样本集代替整体：不再测定整体中具有给定TE的个体数（W）,而是通过测定样本集中具有给定TE的个体占比来估算

W

。在此基础上,提出2种算法及基于随机排序的样本集生成方法^[40]。

假设栅格数据的行列数分别为

N_{r}

和

N_{c}

,方法原理可表述为：① 设立一定的映射关系,将栅格数据转换为长度为

N_{r} \times N_{c}

的单维序列;② 随机地重排该序列中的元素;③ 将此序列按照原映射关系还原为栅格形式,形成新的栅格数据;④ 将前述过程重复足够多的次数（

N_{\max}

）,形成

N_{\max}

个新的栅格数据作为样本集。

在获得上述样本集后,需统计与原栅格数据拥有相同TE的样本个数,并最终将个数转换为占比（

P_{TE}^{'}

）。基本算法如下式所示：

（5）

S^{'} = k_{B} \log P_{TE}^{'}

注意

S^{'}

是负数,因此

S^{'}

并非严格意义上的

S

估算。由于

P_{TE}^{'}

的数值取决于样本集的大小（

N_{\max}

）,因此Cushman也将

S^{'}

命名为相对熵。

基本算法中采用样本集代替了整体,降低了穷举的难度,但在栅格数据尺寸较大时穷举依然困难。Cushman在处理尺寸为

16 \times 16

的栅格数据时,采用的

N_{\max}

数值高达10万,并建议在栅格数据尺寸增大时持续地增加

N_{\max}

的数值。然而,栅格数据尺寸的增长所带来的穷举结果将呈现指数型增加。因此,Cushman提出了改进算法：

（6）

{\hat{S}}^{'} = k_{B} \log (\frac{1}{\sqrt[]{2 π} σ} e^{- \frac{{(te - μ)}^{2}}{2 σ^{2}}})

式中：

te

表示原栅格数据的TE;

μ

和

σ

分别表示所有样本的TE之均值和标准差;e表示自然数。从式（6）可见,改进算法的原理是假设所有样本的TE服从正态分布,然后基于正态分布预测样本集中TE与原栅格数据相同的个体占比。需要说明是,虽然改进算法能避免无限制地增加

N_{\max}

,但依然需要数量相当的样本用于估计均值和标准差。

4.2 基于Wasserstein距离的算法

基于斑块的计算模型存在阶乘运算数值溢出的问题（3.1节）,难以技术实现。为解决该问题,Zhao等提出了基于Wasserstein距离的算法^[38]。具体算法如下：首先,舍弃公式（4）中的首项,仅使用第2项、第2项作为熵值的估算。其次,引入对数函数展开式,降低第2项、第2项中阶乘运算的数值大小。对数函数展开式如下：

（7）

\log (x!) = \log 1 + \log 2 + ? + \log (x - 1) + \log x

根据公式（7）,公式（4）中的第2项、第2项将分别转换为以下形式：

（8）

f (x, a_{1}, a_{2}, ?, a_{x}) = a_{1} \log 1 + a_{2} \log 2 + ? + a_{x} \log x

由于

a_{1}, a_{2}, ?, a_{x}

均为整数,故可视为对数项

\log 1, \log 2, ?, \log x

的频率分布。

对于任何栅格数据,公式（4）中的第2项、第2项均能转换为如公式（8）所示的频率分布（分别记为分布

C

和分布

S

）。但频率分布并非指标,无法进行方便的对比。于是,Zhao等引入了Wasserstein距离（又称为Wasserstein metric、Earth-Mover距离）。该距离是最优传输理论中的核心概念^[46],用于表征将原概率分布转换为新概率分布所需的最小传输质量,通俗地理解为2个分布间的距离。为了利用Wasserstein距离,Zhao等首先将分布

C

和

S

均转换为概率分布（记为

φ_{c}

和

φ_{s}

）,具体方法为将

a_{1}, a_{2}, ?, a_{x}

均除以它们之和。然后,分别计算

φ_{c}

和类狄拉克分布（

δ

）的Wasserstein距离

d (φ_{c}, δ)

、

φ_{s}

和

δ

的Wasserstein距离

d (φ_{s}, δ)

。最后,玻熵计算如下：

（9）

W_{dis} = (1 - d (φ_{c}, δ)) \times (1 - d (φ_{s}, δ))

需要说明的是,首先,W_dis与玻尔兹曼公式已无关。此外,在Zhao等的原文中,斑块仅基于四邻域系统（von Neumann邻域）定义。实际上,斑块也可基于八邻域系统（Moore邻域）定义^[47,48],并在后续研究中被证明效果更好^[41]。

4.3 基于多尺度层次的算法

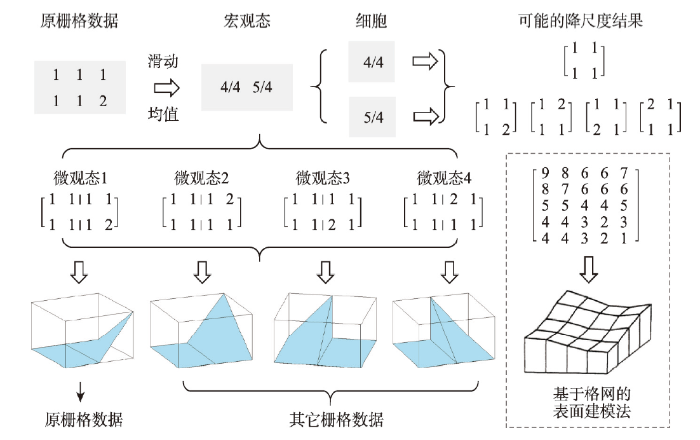
针对定量型栅格数据,学术界开发了2种基于多尺度层次的算法：重采样（Resampling-based）^[39]和聚合（Aggregation-based）^[44],分别是原计算模型（3.2节）的直接实现和改进实现。2种算法的核心原理相同,均基于大小为

2 \times 2

的滑动窗口完成多尺度层次结构的创建,区别在于滑动窗口的步长。在重采样算法中,步长为单个细胞的边长（图6）;而在聚合算法中,步长为滑动窗口的宽度。2种算法各有优劣,总结如下：

图6

新窗口打开|下载原图ZIP|生成PPT
图6基于重采样技术的玻尔兹曼熵算法

Fig. 6Resampling-based algorithm for computing Boltzmann entropy

（1）重采样算法适用于计算任意大小栅格数据的相对熵和绝对熵。但在计算相对熵时,计算量较大（由重采样法生成的多尺度表达层次较多）,且计算结果不具有完全的热力学一致性（Thermodynamic Consistency）^[44]。

（2）使用聚合算法计算的熵均具有完全的热力学一致性,且绝对熵涉及的计算量较小（多尺度表达层次较少）。但在计算相对熵时,仅适用于长和宽均为偶数的栅格数据;在计算绝对熵时,栅格数据的长和宽均须为2的指数。

为解决上述2种算法存在的问题,学术界做出了诸多努力。例如,为提高算法效率,后续研究中推导了微观态数的解析解,并提供了并行算法^[42]。也有****基于头尾分割法（Head/tail Breaks）发展了一种快速估算绝对玻熵的算法^[49,50,51]。此外,Nowosad提出了滑动窗口中包括空值时的微观态数求解法^[45],使得上述2种算法可适用于不规则的栅格数据、点格局（Point Patterns),例如空气质量监控站点的分布等。

5 空间玻熵的应用

随着计算难题的突破,空间玻熵已在遥感图像处理和地理学中得到应用,计算工具也相继被开发。目前开源的计算工具有3种,分别为针对定量型栅格数据的C#语言版软件^[42]、R语言版软件^[45];针对定性型数据的基于Matlab的软件^[41]。典型应用如下。

5.1 在图像处理中的应用

从理论上而言,玻熵在刻画空间信息时比香农熵具有绝对优势。该优势在图像处理中已得到证明。例如,2019年的研究基于玻熵刻画灰度图像的相似性,进而将玻熵应用于高光谱遥感图像的高效降维（波段选择）^[52]。该研究获得以下结论：① 基于玻熵的指标能够完整地刻画图像相似性（同时刻画组分和配置）,且效果优于目前所有基于香农熵的指标;② 基于玻熵的波段选择算法优于所有基于香农熵的算法。使用基于玻熵选择的波段进行图像分类实验时,分类精度比基于香农熵的算法最高可优化27%。

即便与基于更先进、更复杂的波段选择算法相比,基于玻熵的算法也表现更优或具有很强的竞争力^[53]。此外,玻熵被用于衡量遥感图像的信息量^[54]。

5.2 在景观生态学的应用

空间玻熵的计算突破后,地理****迅速讨论了玻熵的景观生态学应用^{[40, 55-57]}。中日两国****认为玻熵可用于日本里山（Satoyama）景观的生物多样性与生态系统服务评价^[57]。

2020年,Xu等^[58]将玻熵用于中国黄土丘陵沟壑区的景观可持续性评价。其方法为：首先基于专家经验,并以土地利用类型、高程、坡度为自变量创建土地适宜性函数;而后利用该函数评价研究区的土地适宜性;进而分区（子流域）计算土地适宜性栅格数据的玻熵,熵值越大说明土地适宜性的空间分布越无序或数值波动越大,进而说明可持续性越低;最后,利用自然断点法将熵值分为5级,分级评价可持续性。评价结果说明,与2000年相比,2015年米脂县的景观可持续性有较大的改善。

6 讨论

通过前面的回顾,我们发现空间玻熵已形成初步的应用。实际上,正如引言中提及,玻熵对于地理学而言具有重要意义,其潜在的应用更加广泛。例如,由于玻熵刻画了尺度变换中的空间不确定性,而香农熵所刻画的不确定性正是信息论的基石^[59],因此玻熵可作为香农熵的替代、并为空间或地图信息论等提供理论基础。值得一提的是,空间信息论正是地理信息科学领域的欠缺。例如,地理学第一定律提出者Tobler指出：信息论中的很多基本假设（如数据是空间无关的）在地理学中常不适用^[60]。国内****同样质疑了信息论在测度空间信息时的适用性^[61],并指出空间信息的测度研究“远没有达到以米计长度、以千克论质量、以安培量电流的定量程度,这与空间信息的重要地位极不相称”^[17]。

玻熵作为通往热力学的桥梁,应广泛地用于区域景观变化动力学的机理探究和土地利用可持续性的评价。例如,在中国2017年启动的第二次青藏高原综合科学考察研究中,重点目标包括研究青藏高原环境演变背后的机理、探究人类活动对青藏高原的影响等。通过长时间序列地理数据的玻熵变化趋势计算,可为这些目标的实现提供不同的视角和新颖的观点。读者或许会疑惑：热力学的经典适用范围是与外界无能量交换的、独立封闭的系统,但青藏高原是非封闭系统、与外界存在着明显的能量交换,如何使用玻熵建立对青藏高原的热力学认知?实际上,诺贝尔奖获得者Prigogine^[62]的耗散理论（Dissipative Theory）已将热力学的适应范围扩展至与外界存在频繁能量交换开放系统。从开放系统和熵的角度来看,实现可持续发展的青藏高原是指系统内部玻熵较低、能且持续保持的热力学系统,而实现高质量发展的青藏高原是指有能力接纳外部输入玻熵的热力学系统。

通过本文综述,我们发现尽管空间玻熵的计算已实现突破,并初步形成了概念、模型、计算、应用的4层研究体系,但依然处于萌芽阶段。回想与熵紧密相关的分形,其发展历程可能存在借鉴意义。在Mandelbrot发表《英国海岸线有多长?》,并正式提出分形维数的计算前,进行了数十载的修正、验算,此后分形又经过几十年的推广、应用与验证^[63]。因此,空间玻熵的研究任重且道远,我们期待未来能有更多突破。

7 结语

最近5年地理学界在空间玻熵研究方面取得了系列进展,实现了自1872年玻熵的概念提出后、针对空间数据的首次计算,并形成实际应用。本文对这些进展进行了及时且系统综述。主要结论：① 目前的研究热点集中在空间栅格数据的玻熵,已研发出针对定性和定量型栅格数据的计算模型;② 算法百家齐放,已呈现出基于TE、Wasserstein距离、多尺度层次的3大类算法;③ 已形成景观生态学和遥感图像处理2类应用。

未来研究中建议丰富空间玻熵的算法。空间数据可分为栅格数据和矢量数据,但目前缺少针对矢量数据的算法。其难点在于宏观态的定义和微观态数的测算,建议尝试本文中多尺度层次算法的思想。此外,空间玻熵的计算应适用于单要素数据（如景观生态学的廊道）和多要素数据（如土地利用类型图）,只有这样才能更好地服务于地理要素耦合研究、促进对陆地表层各要素演化规律的探究^[64]。在应用层面,建议将玻熵作为香农熵的重要补充、甚至在部分应用（热力学解译、空间信息测度等）中作为替代。

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1]

Bonnett

. Geography as the world discipline: Connecting popular and academic geographical imaginations
Area, 2003,35(1):55-63.

DOI:10.1111/area.2003.35.issue-1 URL [本文引用: 1]

[2]

Uhlenwinkel

. Factual knowledge and conceptual understanding
Geography, 2014,99(1):28-35.

DOI:10.1080/00167487.2014.12094388 URL [本文引用: 1]

[3]

Zhu

Yongguan

, Li

Gang

, Zhang

Ganlin

, et al. Soil security: From earth's critical zone to ecosystem services
Acta Geographica Sinica, 2015,70(12):1859-1869.

DOI:10.11821/dlxb201512001 [本文引用: 1]

Soil is an important natural resource that humans rely on and civilization is based upon. As the critical component of the Earth's critical zone, pedosphere is most active in Earth's surface system. Moreover, soil processes are considered as the control point for the flows and transformations of material, energy and information. In wake of the increasing attention to soil's multi-functions, traditional soil concept on its functions and roles is being challenged. Therefore, the concept of soil security is proposed, which is a strategic framework with the aim of soil sustainable development, and it can provide guidelines for the sustainable utilization and conservation of soil resources. In this review, the connotations of Earth's critical zone and soil security, and the difference and close relationship between each other are discussed. The ecosystem services in the framework of soil security are summarized. Finally, perspectives on future soil security research needs in the context of ecosystem services are proposed.

[ 朱永官, 李刚, 张甘霖, 等. 土壤安全:从地球关键带到生态系统服务
地理学报, 2015,70(12):1859-1869.]

[本文引用: 1]

[4]

Song

Changqing

, Zhang

Guoyou

, Cheng

Changxiu

, et al. Nature and basic issues of geography
Scientia Geographica Sinica, 2020,40(1):6-11.

DOI:10.13249/j.cnki.sgs.2020.01.002 [本文引用: 1]

A discipline has typically the following four key features, namely independent research objects, independent research questions, unique characteristics, and unique social services. This paper first discusses the nature of Geography from three aspects, to reveal the characteristics of modern Geography. First, the research object of Geography is changing from simple to complex evolution. In performing geographic research, we should well recognize the complexity of geographic systems. Second, the framework of geographic research questions is structured by the fusion among geographic features, space, and time. This paper explains the essential distinction between different geographic research questions, which promotes the development of the methods and technologies for answering these questions. Third, the philosophy of combining reductionism and holism is growing continuously. A new pattern of research has been formed based on new disciplines and technologies, which is the parallel development of the research on geographic features and that on systems. This paper then identifies the essential characteristics of geographic research, summarizes the key research questions in Geography, and discusses the multiple effects of driving mechanisms on the laws of Geography. An understanding of the fundamental characteristics and the modern value of Geography illustrated in this paper will be contribute to the societal development of Geography.

[ 宋长青, 张国友, 程昌秀, 等. 论地理学的特性与基本问题
地理科学, 2020,40(1):6-11.]

[本文引用: 1]

[5]

Bojie

, Leng

Shuying

, Song

Changqing

. The characteristics and tasks of geography in the new era
Scientia Geographica Sinica, 2015,35(8):939-945.

DOI:10.13249/j.cnki.sgs.2015.08.939 [本文引用: 1]

Geography is a subject of "exploring the laws of nature, declaring the human essence", with characteristics of comprehensiveness and interactiveness. Since the 1980s, Geography plays an important role in global environmental change research programs. Theories, methods and techniques of Geography have become the basis for solving the problems of the sustainable development of human society is facing. Originated in the global environment change research, and combined with the social science research, The " Future Earth" research plan represents the direction of the development of Geography in the new period. In contemporary, Geography research methods have shift from survey, observation, and records, drawings and other traditional research methods to the modern scientific methods such as spatial statistics, earth observation, GIS, indoor and outdoor simulation and modeling, decision-making system, etc., and are gradually tend to comprehensive and quantitative. As the problems that Geography is facing are more complex and more comprehensive, the Geography research issues become more comprehensive and diverse, and attract more extensive subjects to participate in. In more and more field, the angle of Geography are considered. The discipline boundary that concepts and tools belonging to is blurring. In the new era, the geography, is heading for geographical science. China is an ideal geography test sites of studying the problem of the sustainable development of human society. The future development of Chinese Geography needs to deepen the comprehensive and integrated understanding of the complex man-land system, and strengthen the research of global problems. To achieve the goal of geographical science and social service value, the internationalization level of Chinese geographical science needs to be promoted, and the ability of using advanced technology to parse geographical phenomenon needs to be improved.

[ 傅伯杰, 冷疏影, 宋长青. 新时期地理学的特征与任务
地理科学, 2015,35(8):939-945.]

[本文引用: 1]

[6]

Song

Changqing

. On paradigms of geographical research
Progress in Geography, 2016,35(1):1-3.

DOI:10.18306/dlkxjz.2016.01.001 [本文引用: 1]

Spatial differentiation of natural and human factors in the land surface system of the Earth is the main concern of Geography. Given the complexity of the land surface system, different research methods should be applied to different issues concerning the system. Based on past geographical research, four paradigms were generalized, including geographical empirical paradigm, geographical positivist paradigm, geographical system science paradigm, and geographical big data paradigm. Appropriate paradigms should be employed for different scientific questions, and multiple paradigms should be applied to some complicated questions.

[ 宋长青. 地理学研究范式的思考
地理科学进展, 2016,35(1):1-3.]

[本文引用: 1]

[7]

Bojie

. Geography: From knowledge, science to decision making support
Acta Geographica Sinica, 2017,72(11):1923-1932.

DOI:10.11821/dlxb201711001 [本文引用: 1]

Geography is a subject to explore spatial distribution, time evolution and regional characteristics of geographical elements or geographical complexes. Geography is unique in bridging social sciences and natural sciences, and has characteristics of comprehensiveness, interdisciplinary research and regionalism. With the development of geographical science technology and research methods, geography is in the gorgeous historical process towards geographical science. Research themes of geography are focusing on the comprehensive research on the earth surface. The research paradigms of geography are shifting from geography knowledge description, coupling pattern and process, to the simulation and prediction of complex human and earth system. The development of Chinese geography needs to be rooted in the major needs of national strategy, and plays important roles in the studies of urbanization development, coupling ecological processes and services, water resources management and geopolitics. Under the country's major needs, China's geography tends to achieve the geography theory innovation, new method and technology application and developed disciplinary system with Chinese characteristics, and make more contribution to national and global sustainable development.

[ 傅伯杰. 地理学: 从知识, 科学到决策
地理学报, 2017,72(11):1923-1932.]

[本文引用: 1]

[8]

Wang

Jinfeng

, Xu

Chengdong

. Geodetector: Principle and prospective
Acta Geographica Sinica, 2017,72(1):116-134.

DOI:10.11821/dlxb201701010 [本文引用: 1]

Spatial stratified heterogeneity is the spatial expression of natural and socio-economic process, which is an important approach for human to recognize nature since Aristotle. Geodetector is a new statistical method to detect spatial stratified heterogeneity and reveal the driving factors behind it. This method with no linear hypothesis has elegant form and definite physical meaning. Here is the basic idea behind Geodetector: assuming that the study area is divided into several subareas. The study area is characterized by spatial stratified heterogeneity if the sum of the variance of subareas is less than the regional total variance; and if the spatial distribution of the two variables tends to be consistent, there is statistical correlation between them. Q-statistic in Geodetector has already been applied in many fields of natural and social sciences which can be used to measure spatial stratified heterogeneity, detect explanatory factors and analyze the interactive relationship between variables. In this paper, the authors will illustrate the principle of Geodetector and summarize the characteristics and applications in order to facilitate the using of Geodetector and help readers to recognize, mine and utilize spatial stratified heterogeneity.

[ 王劲峰, 徐成东. 地理探测器: 原理与展望
地理学报, 2017,72(1):116-134.]

[本文引用: 1]

[9]

Song

Changqing

, Cheng

Changxiu

, Shi

Peijun

. Geography complexity: New connotations of geography in the new era
Acta Geographica Sinica, 2018,73(7):1204-1213.

DOI:10.11821/dlxb201807002 [本文引用: 1]

Since the 20th century, geography came into being with distinctive disciplinary characteristics by sustained effort of geographers. This paper puts forward predicament from cognitive and thought in the new era, and depicts new geographic characteristics from five aspects: new technology, new orders, new data, new approaches and new driving factors. According to new content of geo-regionality and new approaches of geo-comprehensiveness, the paper proposes that complexity research would be a successful new path in geography, and the complexity would be the third characteristic of geography. Then, the paper details some complex spatial patterns, complex time processes and complex spatio-temporal mechanisms in geography research. Based on the concept of a geographic complex system, this paper presents core issues and corresponding complex research tools. Finally, the paper puts forward new challenges and new requirements for geography in the new era.

[ 宋长青, 程昌秀, 史培军. 新时代地理复杂性的内涵
地理学报, 2018,73(7):1204-1213.]

[本文引用: 1]

[10]

Cheng

Changxiu

, Shi

Peijun

, Song

Changqing

, et al. Geographic big-data: A new opportunity for geography complexity study
Acta Geographica Sinica, 2018,73(8):1397-1406.

DOI:10.11821/dlxb201808001 [本文引用: 1]

Since 2010, big data has played a significant role in various fields of science, engineering and society. The paper introduces the concepts of geographic big-data, the fourth paradigm and nonlinear complex geographic system, and discusses interactive relationships of these concepts. It is proposed that geographic big-data and the fourth paradigm would become a new opportunity to research on geography complexity. Then the paper discusses how to use the methods of geographic big-data and complexity science to examine geography complexity. For example, based on big-data, a series of indicators of statistical physics fields could be constructed to describe the complex nonlinear characteristics of the real geographic world. Deep learning, complex network and multi-agent methods can be used to model and simulate the complex nonlinear geographic systems. These methods are important for a better understanding of the complexity of geographic phenomena and processes, as well as the analysis, simulation, inversion and prediction of complex geographic systems. Finally, the paper highlights that the combination of geographic big-data and complexity science would be the mainstream scientific method of geography in the 21st century.

[ 程昌秀, 史培军, 宋长青, 等. 地理大数据为地理复杂性研究提供新机遇
地理学报, 2018,73(8):1397-1406.]

[本文引用: 1]

[11]

Vranken

, Baudry

, Aubinet

, et al. A review on the use of entropy in landscape ecology: Heterogeneity, unpredictability, scale dependence and their links with thermodynamics
Landscape Ecology, 2015,30(1):51-65.

DOI:10.1007/s10980-014-0105-0 URL [本文引用: 4]

[12]

Fang

Chuanglin

, Wang

Zhenbo

, Liu

Haimeng

. Exploration on the theoretical basis and evaluation plan of Beautiful China construction
Acta Geographica Sinica, 2019,74(4):619-632.

DOI:10.11821/dlxb201904001 [本文引用: 1]

Beautiful China construction (BCC) is of fundamental importance for the sustainable development of the Chinese nation and a Chinese practice of the 2030 UN sustainable development agenda. The Chinese government has made strategic arrangements for the BCC with a five-pronged approach. President Xi Jinping proposed the schedule and roadmap for the BCC at the National Ecological Environmental Protection Conference. But at present, the theoretical basis, evaluation index system, evaluation criteria and construction effect of the BCC are not clear. This paper puts forward the basic connotation of the BCC from a broad and narrow perspective, regards the theory of man-earth harmony and Five-dimensional integration as the core theoretical basis of the BCC, and further constructs the evaluation index system of the BCC, which includes five dimensions: ecological environment, green development, social harmony, institutional improvement and cultural heritage, and uses the United Nations human development index (HDI) evaluation method to scientifically evaluate the construction effect of 341 prefecture-level cities (states) in China in 2016. The results show that the average value of the BCC Index (Zhongke Beauty Index) is 0.28, which is generally at a low level. The average of the sub-indexes of the ecological environment beauty index, the green development beauty index, the social harmony beauty index, the system perfect beauty index and the cultural heritage beauty index are respectively 0.6, 0.22, 0.29, 0.22, and 0.07. The sub-index values are all low, and the regional development is quite different, which indicates that the construction process of Beautiful China is generally slow and unbalanced. In order to implement the schedule and roadmap for the BCC with high quality and high standards, it is recommended that we construct and publish a general evaluation system for the BCC process, carry out dynamic monitoring and phased comprehensive evaluation of the BCC process, compile and publish the evaluation standards for BCC technology, do a good job in the comprehensive zoning of Beautiful China, carry out pilot projects for the construction of Beautiful China's model areas according to local conditions, and incorporate the achievements of Beautiful China into the assessment indicators of all levels of government.

[ 方创琳, 王振波, 刘海猛. 美丽中国建设的理论基础与评估方案探索
地理学报, 2019,74(4):619-632.]

[本文引用: 1]

[13]

Pelorosso

, Gobattoni

, Leone

. The low-entropy city: A thermodynamic approach to reconnect urban systems with nature
Landscape and Urban Planning, 2017,168:22-30.

DOI:10.1016/j.landurbplan.2017.10.002 URL [本文引用: 1]

[14]

Li Z

, Huang P

. Quantitative measures for spatial information of maps
International Journal of Geographical Information Science, 2002,16(7):699-709.

DOI:10.1080/13658810210149416 URL [本文引用: 1]

[15]

Cheng

Xiaoqiang

, Yang

Min

, Gui

Zhipeng

, et al. An algorithm creating thumbnail for web map services based on information entropy and trans-scale similarity
Acta Geodaetica et Cartographica Sinica, 2017,46(11):1891-1898.

[本文引用: 1]

[ 成晓强, 杨敏, 桂志鹏, 等. 信息量与相似度约束下的网络地图服务缩略图自动生成算法
测绘学报, 2017,46(11):1891-1898.]

[本文引用: 1]

[16]

Zhilin

, Liu

Qiliang

, Gao

Peichao

. Entropy-based cartographic communication models: Evolution from special to general cartographic information theory
Acta Geodaetica et Cartographica Sinica, 2016,45(7):757-767.

[本文引用: 1]

[ 李志林, 刘启亮, 高培超. 地图信息论: 从狭义到广义的发展回顾
测绘学报, 2016,45(7):757-767.]

[本文引用: 1]

[17]

Zhang

Ying

, Zhang

Jingxiong

. Measure of information content of remotely sensed images accounting for spatial correlation
Acta Geodaetica et Cartographica Sinica, 2015,44(10):1117-1124.

[本文引用: 2]

[ 张盈, 张景雄. 顾及空间相关性的遥感影像信息量的度量方法
测绘学报, 2015,44(10):1117-1124.]

[本文引用: 2]

[18]

Gao P

, Zhang

, Jia

, et al. Efficient approach for computing the discrimination ratio-based variant of information entropy for image processing
IEEE Access, 2020,8(1):92552-92564.

[本文引用: 1]

[19]

Sahu D

, Parsai

. Different image fusion techniques: A critical review
International Journal of Modern Engineering Research, 2012,2(5):4298-4301.

[本文引用: 1]

[20]

Razlighi Q

, Kehtarnavaz

. Spatial mutual information as similarity measure for 3-D brain image registration
IEEE Journal of Translational Engineering in Health and Medicine, 2014,2:27-34.

DOI:10.1109/JTEHM.2014.2299280 URL [本文引用: 1]

[21]

Feixas

, Bardera

, Rigau

, et al. Information Theory Tools for Image Processing
San Rafael, CA: Morgan & Claypool Publishers, 2014.

[本文引用: 1]

[22]

Swati B

, Venkanna

B V

. Basic Thermodynamics
Delhi, India: PHI Learning, 2010.

[本文引用: 1]

[23]

Boltzmann

. Further studies on the thermal equilibrium of gas molecules
Sitzungsberichte Akademie der Wissenschaften, 1872,66:275-370.

[本文引用: 1]

[24]

Shannon C

. A mathematical theory of communication
The Bell System Technical Journal, 1948,27(3):379-423.

DOI:10.1002/bltj.1948.27.issue-3 URL [本文引用: 1]

[25]

Bekenstein J

. Information in the holographic universe
Scientific American, 2003,289(2):58-65.

PMID:12884539 [本文引用: 1]

[26]

Cushman S

. Thermodynamics in landscape ecology: The importance of integrating measurement and modeling of landscape entropy
Landscape Ecology, 2015,30(1):7-10.

DOI:10.1007/s10980-014-0108-x URL [本文引用: 2]

[27]

Gao P

, Li Z

, Zhang

. Thermodynamics-based evaluation of various improved Shannon entropies for configurational information of gray-level images
Entropy, 2018,20(1):19. DOI: 10.3390/e20010019.

DOI:10.3390/e20010019 URL [本文引用: 1]

[28]

Naveh

, Lieberman A

. Landscape Ecology: Theory and Application
New York: Springer, 1990.

[本文引用: 1]

[29]

Longo

, Miquel P

, Sonnenschein

, et al. Is information a proper observable for biological organization?
Progress in Biophysics and Molecular Biology, 2012,109(3):108-114.

DOI:10.1016/j.pbiomolbio.2012.06.004PMID:22796169 [本文引用: 1]

In the last century, jointly with the advent of computers, mathematical theories of information were developed. Shortly thereafter, during the ascent of molecular biology, the concept of information was rapidly transferred into biology at large. Several philosophers and biologists have argued against adopting this concept based on epistemological and ontological arguments, and also, because it encouraged genetic determinism. While the theories of elaboration and transmission of information are valid mathematical theories, their own logic and implicit causal structure make them inimical to biology, and because of it, their applications have and are hindering the development of a sound theory of organisms. Our analysis concentrates on the development of information theories in mathematics and on the differences between these theories regarding the relationship among complexity, information and entropy.Copyright © 2012 Elsevier Ltd. All rights reserved.

[30]

Atkins

P W

. The Second Law
New York: Scientific American Library, 1994.

[本文引用: 1]

[31]

Batty

. Space, scale, and scaling in entropy maximizing
Geographical Analysis, 2010,42(4):395-421.

DOI:10.1111/j.1538-4632.2010.00800.x URL [本文引用: 1]

[32]

Spinnangr S

. Energy, entropy and sustainable development with focus on nuclear fusion
[D]. The University of Bergen, 2017.

[本文引用: 1]

[33]

Hobbie R

, Roth B

. Intermediate physics for medicine and biology
Cham: Springer Science & Business Media, 2015.

[本文引用: 1]

[34]

Bailey K

. Entropy systems theory. Systems Science and Cybernetics
Oxford: Eolss Publishers, 2009: 149-166.

[本文引用: 1]

[35]

Dalarsson

, Dalarsson

, Golubovic

. Introductory Statistical Thermodynamics. Amsterdam: Academic Press, 2011.

[本文引用: 1]

[36]

Gao P

, Cushman S

, Liu

, et al. FracL: A tool for characterizing the fractality of landscape gradients from a new perspective
ISPRS International Journal of Geo-Information, 2019,8(10):466. DOI: 10.3390/ijgi8100466.

DOI:10.3390/ijgi8100466 URL [本文引用: 1]

[37]

Cushman S

. Calculating the configurational entropy of a landscape mosaic
Landscape Ecology, 2016,31(3):481-489.

DOI:10.1007/s10980-015-0305-2 URL [本文引用: 2]

[38]

Zhao

, Zhang X

. Calculating spatial configurational entropy of a landscape mosaic based on the Wasserstein metric
Landscape Ecology, 2019,34(8):1849-1858.

DOI:10.1007/s10980-019-00876-x URL [本文引用: 4]

[39]

Gao P

, Zhang

, Li Z

. A hierarchy-based solution to calculate the configurational entropy of landscape gradients
Landscape Ecology, 2017,32(6):1133-1146.

[本文引用: 3]

[40]

Cushman S

. Calculation of configurational entropy in complex landscapes
Entropy, 2018,20(4):298.

DOI:10.3390/e20040298 URL [本文引用: 4]

[41]

Zhang

, Wu Z

, Lan

, et al. Calculating the Wasserstein metric-based Boltzmann entropy of a landscape mosaic
Entropy, 2020,22(4):381. DOI: 10.3390/e22040381.

DOI:10.3390/e22040381 URL [本文引用: 4]

[42]

Gao P

, Zhang

, Li Z

. An efficient analytical method for computing the Boltzmann entropy of a landscape gradient
Transactions in GIS, 2018,22(5):1046-1063.

DOI:10.1111/tgis.v22.5 URL [本文引用: 2]

[43]

Gao P

, Li Z

. Computation of the Boltzmann entropy of a landscape: A review and a generalization
Landscape Ecology, 2019,34(9):2183-2196.

DOI:10.1007/s10980-019-00814-x URL

[44]

Gao P

, Li Z

. Aggregation-based method for computing absolute Boltzmann entropy of landscape gradient with full thermodynamic consistency
Landscape Ecology, 2019,34(8):1837-1847.

DOI:10.1007/s10980-019-00854-3 URL [本文引用: 2]

[45]

Nowosad

. Boltzmann entropy of a landscape gradient. R package version 0.2.3. 2018. https://cran.r-project.org/web/packages/belg/index.html .

URL [本文引用: 3]

[46]

Vaserstein L

. Markov processes over denumerable products of spaces, describing large systems of automata
Problemy Peredachi Informatsii, 1969,5(3):64-72.

[本文引用: 1]

[47]

Chunyang

, Chen

Jin

, Shi

Peijun

, et al. City expansion model of metropolitan area in china: A case study of Beijing
Acta Geographica Sinica, 2003,58(2):294-304.

[本文引用: 1]

[ 何春阳, 陈晋, 史培军, 等. 大都市区城市扩展模型
地理学报, 2003,58(2):294-304.]

[本文引用: 1]

[48]

Long

Ying

, Shen

Zhenjiang

, Mao

Qizhi

, et al. Form scenario analysis using constrained cellular automata
Acta Geographica Sinica, 2010,65(6):643-655.

[本文引用: 1]

[ 龙瀛, 沈振江, 毛其智, 等. 基于约束性 CA 方法的北京城市形态情景分析
地理学报, 2010,65(6):643-655.]

[本文引用: 1]

[49]

Zhang

, Wu Z

. A head/tail breaks-based method for efficiently estimating the absolute Boltzmann entropy of numerical raster data
ISPRS International Journal of Geo-Information, 2020,9(2):103. DOI: 10.3390/ijgi9020103.

DOI:10.3390/ijgi9020103 URL [本文引用: 1]

[50]

Jiang

Bin

. Head/tail breaks: A new classification scheme for data with a heavy-tailed distribution
The Professional Geographer, 2013,65(3):482-494.

DOI:10.1080/00330124.2012.700499 URL [本文引用: 1]

[51]

Gao P

, Liu

, et al. Unified metrics for characterizing the fractal nature of geographic features
Annals of the American Association of Geographers, 2017,107(6):1315-1331.

DOI:10.1080/24694452.2017.1310022 URL [本文引用: 1]

[52]

Gao P

, Wang J

, Zhang

, et al. Boltzmann entropy-based unsupervised band selection for hyperspectral image classification
IEEE Geoscience and Remote Sensing Letters, 2019,16(3):462-466.

DOI:10.1109/LGRS.2018.2872358 URL [本文引用: 1]

[53]

Sawant S

, Manoharan

. Unsupervised band selection based on weighted information entropy and 3D discrete cosine transform for hyperspectral image classification
International Journal of Remote Sensing, 2020,41(10):3948-3969.

DOI:10.1080/01431161.2019.1711242 URL [本文引用: 1]

[54]

Liu B

, Deng

, Liu H

, et al. A multilevel visual feature-based approach for measuring the spatial information in remote sensing images
IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2019,12(10):4110-4122.

DOI:10.1109/JSTARS.4609443 URL [本文引用: 1]

[55]

Liang X

, Jia

, Chen

, et al. Landscape sustainability in the loess hilly gully region of the Loess Plateau: A case study of Mizhi County in Shanxi Province, China
Sustainability, 2018,10(9):3300. DOI: 10.3390/su10093300.

DOI:10.3390/su10093300 URL [本文引用: 1]

[56]

Liu

, Yang Z

, Wang C

, et al. Temporal-spatial variations and influencing factor of land use change in Xinjiang, Central Asia, from 1995 to 2015
Sustainability, 2019,11(3):696. DOI: 10.3390/su11030696.

DOI:10.3390/su11030696 URL

[57]

Jiao Y

, Ding Y

, Zha Z

, et al. Crises of biodiversity and ecosystem services in Satoyama landscape of Japan: A review on the role of management
Sustainability, 2019,11(2):454. DOI: 10.3390/su11020454.

DOI:10.3390/su11020454 URL [本文引用: 2]

[58]

Xu J

, Liang X

, Chen

. Landscape sustainability evaluation of ecologically fragile areas based on Boltzmann entropy
ISPRS International Journal of Geo-Information, 2020,9(2):77. DOI: 10.3390/ijgi9020077.

DOI:10.3390/ijgi9020077 URL [本文引用: 1]

[59]

Bauman

. Culture as Praxis
London: SAGE Publications, 1999.

[本文引用: 1]

[60]

Tobler W

. Introductory comments on information theory and cartography
Cartographic Perspectives, 1997,27:4-7.

[本文引用: 1]

[61]

Liu

Honglin

. The study of the method of measuring map information
Journal of the PLA Institute of Surveying and Mapping, 1992(3):49-55.

[本文引用: 1]

[ 刘宏林. 地图信息度量方法的研究
解放军测绘学院学报, 1992(3):49-55.]

[本文引用: 1]

[62]

Prigogine

, Nicolis

, Babloyantz

. Thermodynamics of evolution
Physics Today, 1972,25(11):23-28.

[本文引用: 1]

[63]

Mandelbrot B

. How long is the coast of Britain? Statistical self-similarity and fractional dimension
Science, 1967,156(3775):636-638.

PMID:17837158 [本文引用: 1]

Geographical curves are so involved in their detail that their lengths are often infinite or, rather, undefinable. However, many are statistically "selfsimilar," meaning that each portion can be considered a reduced-scale image of the whole. In that case, the degree of complication can be described by a quantity D that has many properties of a "dimension," though it is fractional; that is, it exceeds the value unity associated with the ordinary, rectifiable, curves.

[64]

Song

Changqing

, Cheng

Changxiu

, Yang

Xiaofan

, et al. Understanding geographic coupling and achieving geographic integration
Acta Geographica Sinica, 2020,75(1):3-13.

DOI:10.11821/dlxb202001001 [本文引用: 1]

Coupling, as a classic physical concept, provides a suite of ideas and methods for describing interactions of multi-agents across disciplines. In contrast, the concept of integration is not from a certain discipline, but it is widely used in many natural and socioeconomic sciences fields due to its great generalization capacity. Both concepts are frequently mentioned in Earth science. Geography, as a multi-disciplinary research area between natural and socioeconomic sciences, owns regional, comprehensive, and complex characteristics. The understanding of coupling varies across geographic sciences. This paper presents an advanced understanding from six geographic perspectives based on different disciplines and scenarios, which is helpful to accurately explore patterns, processes, and mechanisms of land surface system. Firstly, this paper clarifies six perspectives on geographic coupling, and presents corresponding research cases, which include geographic spatial coupling, geographic features coupling, geographic interfaces coupling, geospatial scale coupling, geographic relationship coupling and geographic coupling interpretation. Secondly, the paper interprets the concept of integration from a geographic perspective, and introduces a pathway to achieving an integration in Heihe River Basin's research practice. Finally, the paper proposes intrinsic connections between geographic coupling and geographic integration.

[ 宋长青, 程昌秀, 杨晓帆, 等. 理解地理“耦合”实现地理“集成”
地理学报, 2020,75(1):3-13.]

[本文引用: 1]