丁亮¹, 钮心毅^,2, 宋小冬²1. 浙江工业大学建筑工程学院,杭州 310014
2. 同济大学建筑与城市规划学院,上海 200092

Validating gravity model in multi-centre city: A study based on individual mobile trajectory

DING Liang¹, NIU Xinyi^,2, SONG Xiaodong²1. College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China
2. College of Architecture and Urban Planning, Tongji University, Shanghai 200092, China

通讯作者: 钮心毅(1971-), 男, 浙江湖州人, 博士, 教授, 研究方向为城乡规划方法与技术。E-mail: niuxinyi@tongji.edu.cn

收稿日期:2018-06-11修回日期:2019-12-21网络出版日期:2020-02-25

基金资助:

国家自然科学基金项目.51778432 国家自然科学基金项目.51808495 中国博士后科学基金项目.2018M632499 高密度人居环境生态与节能教育部重点实验室(同济大学)开放课题.201830216

Received:2018-06-11Revised:2019-12-21Online:2020-02-25

Fund supported:

National Natural Science Foundation of China.51778432 National Natural Science Foundation of China.51808495 China Postdoctoral Science Foundation.2018M632499 Open Projects Fund of Key Laboratory of Ecology and Energy-saving Study of Dense Habitat (Tongji University), Ministry of Education.201830216

作者简介 About authors
丁亮(1986-),男,浙江绍兴人,博士后,助理研究员,研究方向为城乡规划方法与技术E-mail:DL861103@126.com。





摘要
长期以来由于规模变量、距离衰减系数取值缺乏依据,引力模型在城市研究中的应用容易受到质疑,加之中国城市的多中心化使得模型应用的外部条件发生改变,模型验证工作的必要性再次显现。本文使用2015年移动通信用户的个体移动轨迹数据,使用Huff当年的验证方法,通过变量检验、参数校正两个步骤,验证Huff的引力模型。研究发现：① 城市内部商业中心和就业中心的吸引力与中心的规模呈正比,与距中心的距离呈反比,符合引力模型规律。② 在上海中心城区空间尺度、200 m网格空间单元下,商业中心吸引力的距离衰减系数平均值为2.5,就业中心吸引力的距离衰减系数平均值为3.0,表明居民就业通勤对距离更加敏感,距离衰减比购物出行更加显著。③ 经变量检验、参数校正后的引力模型可用于对商业中心、就业中心优化调整后的势力范围进行预测,预测准确率可分别达到78.5%和71.9%。就业中心势力范围预测准确性略低,这是由于就业中心吸引力衰减除受距离影响外,还受家庭、房价等因素影响,会对预测结果产生扰动。最后,研究还证实了距离衰减系数存在空间分层异质性：距离衰减系数不是唯一值,受道路可达性、至就业（商业）中心距离、至地铁站距离、人口密度影响,不同地区的距离衰减系数存在较显著差异。
关键词： 引力模型;多中心;模型验证;距离衰减;空间分层异质性;个体移动轨迹

Abstract
Due to the lack of empirical studies of scale variables and distance exponents, the effective application of the gravity model in urban study is challenging. With the development of multi-centralized Chinese cities, the gravity model must be validated because several relevant external conditions have changed. The purpose of this study is to validate Huff's Gravity Model using an individual mobile trajectory of mobile communication user in 2015. We follow Huff's two-step validation method: variable validation and parameter correction. Our main conclusions are as follows. First, attractions of commercial and employment centres conform to the law of the gravity model in which the attraction is proportional to the scale of a centre and inversely proportional to the distance from a centre. Second, in the spatial scale of Shanghai central city with spatial units in a 200-m grid, the mean distance exponent for commercial centres is 2.5 and that for employment centres is 3.0. The distance decay for commuting is greater than that for shopping trips, which means commuting is more sensitive to distance. Third, the gravity model can be used to predict the influence areas of adjusted commercial and employment centres based on validated variables and corrected parameters. Our results indicate that the prediction accuracies can reach 78.5% and 71.9% for the commercial and employment centres, respectively. The prediction accuracy for employment centres is slightly lower. This is because the attraction of employment centres is influenced not only by distance but also by factors such as family and housing prices, which will affect the prediction results. Lastly, in this study, we verify the spatial stratified heterogeneity of distance decay and determine that the distance exponent is not a unique constant because it has different values in different areas. Factors such as accessibility, distance to each centre, distance to a subway station and population density will affect distance decay.
Keywords：gravity model;multi-centre;model validation;distance decay;spatial stratified heterogeneity;individual mobile trajectory


PDF (7642KB)元数据多维度评价相关文章导出EndNote|Ris|Bibtex收藏本文
本文引用格式
丁亮, 钮心毅, 宋小冬. 基于个体移动轨迹的多中心城市引力模型验证. 地理学报[J], 2020, 75(2): 268-285 doi:10.11821/dlxb202002005
DING Liang. Validating gravity model in multi-centre city: A study based on individual mobile trajectory. Acta Geographica Sinice[J], 2020, 75(2): 268-285 doi:10.11821/dlxb202002005

1 引言

反映空间相互作用的引力模型（又称重力模型、场强模型）是城市地理、城市规划的经典模型之一,在实践中有广泛应用^{[1,2,3,4,5,6,7,8,9]}。但是由于缺乏实证,模型中的规模变量、距离衰减系数取值往往缺乏依据。从引力模型研究的经典文献来看并非如此,变量、系数取值有较严谨的实证。引力模型最早由Reilly提出,通过对Texas州大城市主要商场、家庭购物清单的“调查”发现两座城市之间的市场界限“大致”与人口规模呈正比、与距离的平方呈反比,据此“归纳”出了零售引力（Retail Gravitation）模型^[10]。此后,Converse等对引力模型进行了演绎,分别提出了断裂点公式^[11]和概率公式^[12],并用居民购物出行的调查数据做“实证”,经变量检验、参数校正后再将模型投入应用。说明在引力模型研究的早期阶段,研究者极为重视用实证数据验证模型。但此后可能是应用需求的增加,逐渐忽视了变量检验和参数校正;城市系统日趋复杂也加大了模型验证工作的难度。特别是模型中的距离衰减系数,当前在0.5~3.0之间取值已成为约定俗成的做法^[13],一般依据万有引力公式直接取2也不会受到质疑。而且现实中最初只针对居民前往商场购物出行的引力模型应用已经扩展到了就业通勤、信息联系、企业联系等^{[14,15,16,17]}。

随着城市的多中心化,小汽车普及、地铁线路成网使居民出行方式发生了显著改变。有****提出这些变化是否“挑战了传统基于单中心假设的城市模型,空间是否依然存在逻辑?传统的地理空间的距离衰减性是否存在?”^[18]。如果空间相互作用的规律已发生改变,那么需要重新审视引力模型应用的理论基础。随着数据存储、分析技术进步,为验证引力模型创造了条件。已有****使用手机通话数据、浮动车GPS数据、企业工商注册数据等开展相关研究,证明了引力模型中的距离衰减规律依然存在^{[14,15,16,17,18]},其方法是以某一间隔距离汇总吸引量,再用幂函数拟合吸引量——距离曲线,如果拟合的幂函数曲线与实测结果有较高相关系数则表明吸引力衰减符合引力模型规律。还有****更进一步,提出拟合幂函数的指数的绝对值就是距离衰减系数^{[15, 17, 19]},但是这一方法并未得到公认,而且指数是唯一值,掩盖了不同地区距离衰减的差异。与Huff当年的验证工作相比,验证的深度有待加强,验证的方法有待商榷。

本文借助近年来出现的个体移动轨迹数据,用Huff当年的方法,对现在广泛应用的引力模型——Huff的引力模型进行验证。首先与Huff的验证内容一致,探讨在当前多中心城市中商业中心对居民购物出行的吸引力是否依然符合引力模型规律,特别是吸引力的距离衰减有何特征。随后针对模型应用扩展的现实需求,探讨就业中心对居民就业通勤的吸引力是否也同样符合引力模型规律,其距离衰减与购物出行的距离衰减特征有何差异。希望本文所做的验证工作能为日后引力模型得到更加严谨地应用提供帮助。

2 引力模型验证方法和数据

2.1 Huff的引力模型和验证方法

Huff的引力模型是对Converse的断裂点公式的演绎,将非此即彼的市场区划分方法演进为居民受商业中心吸引的概率。并通过调查证明了居民选择购物目的地的比例符合引力模型规律;通过实测值——模拟值的拟合计算得到距离衰减系数,发现各商业中心到各社区的距离衰减系数从2.115~3.779不等,用拟合的距离衰减系数代入公式划分城市内部零售业商圈^[12]。Huff的引力模型公式如下：

（1）Pij=SjTij-?∑j=1nSjTij-?
（2）∑j=1nPij=1
式中：P_ij为i社区属于商业中心j市场区的概率;S_j为商业中心j的规模;T_ij为i社区与商业中心j之间的距离; ?为距离衰减系数;n为商业中心的数量。

模型中有两个变量（规模和距离）,一个参数（距离衰减系数）。Huff选取商业中心的面积作为规模变量;距离变量实测得到,以时间表示;距离衰减系数需要通过计算进行校正,具体方法为：① 调查社区居民前往商业中心购物的人数,每个社区分别汇总,计算前往各商业中心的人数比例,这是实测值,有且只有一个结果;② 将规模和距离变量代入模型,设定距离衰减系数的取值区间和精度将其逐一代入模型,计算得到每个社区属于各商业中心市场区的概率,这是模拟值（Huff并未说明距离衰减系数取值区间和精度,若从0.50取值到5.00,精度为0.01,则每个社区需要计算450个模拟值）;③ 逐一计算每个社区的实测值和模拟值的相关系数,相关系数最高的那个距离衰减系数就是该社区校正后的值;④ 计算每个社区的平均值得到校正后的距离衰减系数。本研究就使用该方法验证引力模型。

2.2 研究范围、数据和空间单元

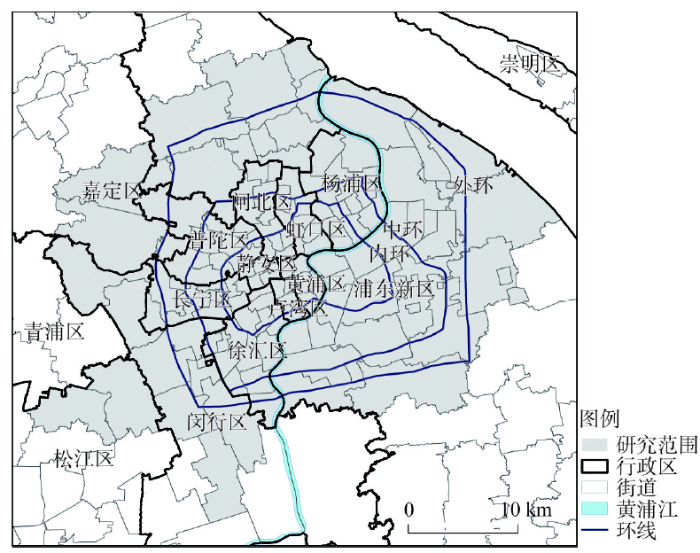
2.2.1 研究范围 Huff对引力模型验证的空间尺度是城市,非区域。与其一致,本文选取上海中心城区（图1）为研究范围,总共涉及128个街道,面积1180 km²,是上海城镇体系的核心,是一个相对独立的城市范围,具有当前多中心城市的典型特征。

图1

新窗口打开|下载原图ZIP|生成PPT
图1研究范围

注：卢湾区已于2011年并入黄浦区,闸北区已于2015年并入静安区。
Fig. 1Study area



2.2.2 研究数据 验证引力模型需要3种数据源：① 商业中心规模;② 商业中心和居住地之间的距离;③ 居民选择购物出行目的地的比例,其中③的数据最关键。受数据调查难度限制,Huff只对3个社区开展了问卷调查,发放了2650份问卷回收了766份,回收率只有28.9%,其实很难具有全局代表性。近年来出现的手机信令数据记录了个体较为连续的移动轨迹,能从中识别用户的居住地、工作地、游憩活动目的地信息,可以替代问卷调查,得到覆盖面更广、样本量更大的数据,支持全市层面的分析。当前,手机信令数据的识别处理技术已经取得了较大进展^{[20,21,22,23,24]},基本能保证识别结果具有全局代表性。使用手机信令数据已经在个体行为、城市空间等相关研究中取得了诸多成果^{[21, 23-30]}。

本文使用的手机信令数据由上海联通^①(①上海联通手机用户约占上海手机总用户的30%,样本应能覆盖各类人群。从后续识别结果来看,居住地、工作地识别结果作为一种抽样数据基本与官方统计数据吻合,可认为样本具有代表性。)提供,采集时间为2015年11月连续10个工作日和6个休息日。首先通过判断工作日夜间居住时间和日间工作时间经常连接的基站,识别居住地和工作地^[23];随后通过判断休息日在非本人居住地、非本人工作地、非交通枢纽的某一小范围内连续停留,识别游憩地^②[24]( ② 这里识别得到的游憩地是指居住地、工作地、交通枢纽之外的场所,包括商场、影剧院、公园等长时间停留场所,不包括地铁站、公交站、便利店等短时停留的场所。)。从524.5万活跃用户（10个工作日至少出现过6次的用户）中识别出了323万人的居住地,其中80.5万人同时有居住地和工作地^③ (③以上海市域230个街道为空间单元汇总居住地识别结果,和第六次人口普查各街道有工作的常住人口数相关系数0.87,工作地识别结果和第三次经济普查各街道就业岗位数相关系数0.78。表明识别结果基本能代表全市就业者的居住、就业活动分布。);识别出了6个休息日总计229.7万人、588.1万人次的本地居民居住地和游憩地（居住地、工作地、游憩地均以基站坐标表示）。

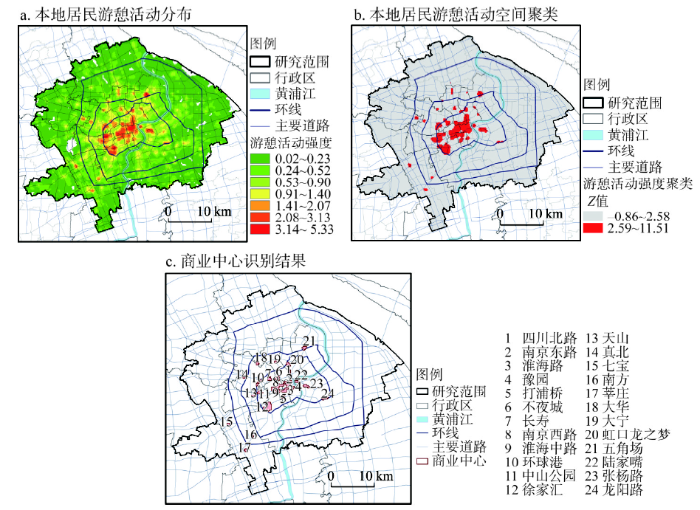
商业中心规模在引力模型中的真实含义其实是商业中心吸引顾客的“效用”,Huff认为商品种类越多对顾客吸引力越大,可以用商业设施面积表征。但在量化规模之前,需要先确定商业中心的位置和范围。在Huff所处的20世纪60年代,城市系统并不复杂,凭经验就可确定商业中心。Huff就是凭经验在3个社区20英里（约32 km）半径范围内选取14个商业中心,再调查商业设施面积,得到商业中心规模变量。但在当前高强度开发、商业商务功能混合的城市中重复Huff当年的工作有两个难点。首先,商业中心很难凭经验确定,易受主观判断影响,也很难客观划分商业中心边界^[24]。使用个体移动轨迹数据,当前一般使用空间聚类方法,即依据个体在活动目的地的集聚程度识别城市就业中心、商业中心^{[18, 23-24, 31]}。借助这一方法可使商业中心位置、范围的识别工作变得简单、客观。其次,商业设施面积很难通过调查获取（很难将商业综合体中的商店面积分离出来,沿街商业的面积也很难调查）。考虑到上海中心城区开发强度普遍较高,一般土地面积越大、商业设施面积也越大,可用商业中心空间范围的面积代替商业设施面积,表征商业中心规模。采用上述商业中心位置、范围确定方法、规模量化方法,本研究依据识别到的本地居民游憩目的地,生成游憩活动分布图（图2a）,使用局部空间自相关的聚类方法识别游憩活动强度高值聚类区（图2b）,结合商业用地筛选出商业中心（图2c）,以商业中心空间范围的面积（表1）表征商业中心规模。

图2

新窗口打开|下载原图ZIP|生成PPT
图22015年上海中心城区商业中心识别

注：识别过程为：① 每个用户每天的游憩活动量为1,按在游憩地的停留时间分配权重后再按游憩地汇总游憩活动量,在ArcGIS中对游憩地的游憩活动量做核密度分析（800 m搜索半径、200 m网格单元）得到本地居民游憩活动强度;② 对①的结果做局部空间自相关分析（以反距离法表达空间关系,取800 m距离阈值）,在1%显著性水平下（Z Score> 2.58）选出高值聚类区（图b中红色部分）;③ 由于商场的日均人流量远大于其他游憩场所,高值聚类区一般包括商业中心,再从中筛选商业用地,就能识别得到商业中心及其具体空间范围（图c）。得到24个商业中心,这些商业中心通过同一个参数聚类得到,同属于城市级商业中心。
Fig. 2Identification of commercial centres in Shanghai central city in 2015



Tab. 1
表1
表12015年上海商业中心面积
Tab. 1Area of commercial centres in Shanghai central city in 2015

商业中心	面积(hm2)	商业中心	面积(hm2)	商业中心	面积(hm2)	商业中心	面积(hm2)
徐家汇	236	五角场	56	打浦桥	40	天山	24
南京西路	188	环球港	56	龙阳路	36	真北	24
南京东路	116	中山公园	52	四川北路	32	陆家嘴	24
淮海路	72	虹口龙之梦	52	豫园	32	七宝	24
张杨路	68	淮海中路	48	莘庄	28	南方	20
不夜城	60	长寿	44	大华	28	大宁	20

注：商业中心面积即图2c中识别得到的商业中心具体空间范围的面积。

新窗口打开|下载CSV

商业中心和居住地之间的距离在引力模型中是指时间距离,Huff通过实测商业中心几何中心到社区几何中心的最短时间获取。考虑到当前城市中交通方式多样化、交通拥堵较严重,两点之间的出行时间波动较大,居民出行仍然使用路程概念,本文使用实测的最短路程表征距离：在ArcGIS中建立道路的网络数据集,使用交通起止点（origin-destination, OD）成本矩阵分析工具计算空间单元（30168个200 m网格）质心相互之间的最短空间距离（长度）,事先准备好数据表,后续分析根据居住地、游憩地所属的空间单元编号,从表中提取距离值。

2.2.3 研究的空间单元 Huff验证引力模型使用的空间单元是社区,使用手机信令数据,虽然也可按社区汇总人数,但由于每个基站覆盖约800 m半径的区域,定位在基站上的人并非处在基站之下,而是位于基站覆盖的区域内,直接按社区汇总会产生较大误差。需要对基站连接的人数做800 m半径的核密度分析才能更接近真实的空间分布^[27]。考虑到基站密度（平均每9 hm²就有1个基站）、覆盖半径等因素,选取200 m网格作为核密度分析的空间单元。考虑到商业中心和居住地之间的距离需要以两者几何中心的最短路程表征,空间单元越大,误差越大,本文直接使用200 m网格作为空间单元,不再归并到社区。研究范围内共有30168个空间单元,每个单元的人数即密度和面积的乘积。

3 商业中心引力模型验证

3.1 变量检验

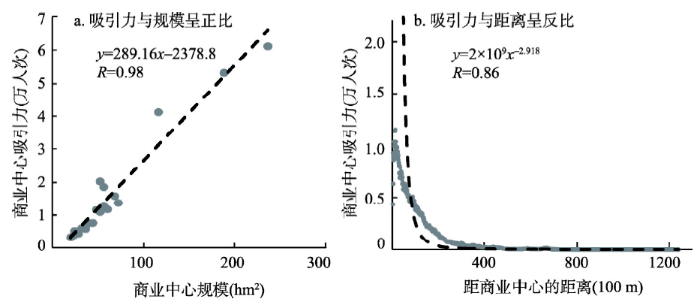
变量检验即检验商业中心的吸引力是否：① 与商业中心规模呈正比,② 与距商业中心的距离呈反比。分别汇总各商业中心吸引到的游憩活动人次,代表商业中心吸引力。由图3a可见,吸引力与规模呈较显著的直线正相关（通过1%显著性检验,下文相关分析若能通过1%显著性检验不再赘述）,相关系数R为0.98,属于极强相关。表明商业中心规模越大,吸引的游憩活动人次越多,符合引力模型规律。

图3

新窗口打开|下载原图ZIP|生成PPT
图3上海中心城区商业中心吸引力的变量检验

注：不同间隔距离拟合的幂函数不同,50 m间隔距离拟合的幂函数相关系数为0.85,200 m间隔距离为0.87,500 m间隔距离为0.87, 1000 m间隔距离为0.88。说明吸引力随距离衰减的规律不会因显示的间隔距离不同而发生质的变化。
Fig. 3Variable validation for commercial centres in Shanghai central city



筛选在商业中心有游憩记录的人的居住地,分别计算居住地和游憩地之间的最短路程,为便于显示,按100 m间隔汇总每一距离区间内的人次。由图3b可见,吸引力与距离呈较显著的幂函数负相关,相关系数R为0.86,属于极强相关。表明商业中心吸引力随距离下降,符合引力模型规律。说明引力模型在当前多中心城市中依然成立。

3.2 距离衰减系数校正

首先计算商业中心吸引力的实测值,得到每个空间单元中的居民前往各商业中心的购物出行比例：分别对每个商业中心按居住地汇总居民在该商业中心的游憩记录,1次记录计1人次,多次记录计多人次,对居住地做核密度分析（Population值选人次）,得到24个商业中心吸引到的居民的来源地分布。每个网格中的密度值与面积的乘积就代表居住在该网格中的居民受某一商业中心吸引的人次,每个网格有24组人次数据,其比例就代表每个商业中心对该网格的吸引力大小。以56432号网格为例,其中的居民受各商业中心吸引的比例如表2所示。

Tab. 2
表2
表2第56432号网格中的居民受各商业中心吸引的实测值—模拟值比较
Tab. 2Comparison of measured and simulated values of inhabitants attracted by commercial centres in No.56432 grid

商业中心	实测值	模拟值	商业中心	实测值	模拟值	商业中心	实测值	模拟值	商业中心	实测值	模拟值
大宁	0.32	0.34	环球港	0.04	0.04	四川北路	0.02	0.02	七宝	0.00	0.00
不夜城	0.17	0.04	中山公园	0.03	0.03	徐家汇	0.02	0.04	张杨路	0.00	0.01
南京西路	0.12	0.11	淮海中路	0.03	0.02	中环	0.01	0.01	打浦桥	0.00	0.01
虹口龙之梦	0.05	0.08	长寿	0.03	0.03	陆家嘴	0.01	0.01	南方	0.00	0.00
五角场	0.05	0.04	大华	0.03	0.03	淮海路	0.01	0.02	莘庄	0.00	0.00
南京东路外滩	0.04	0.10	龙阳路	0.02	0.01	天山	0.01	0.00	豫园	0.00	0.01

新窗口打开|下载CSV

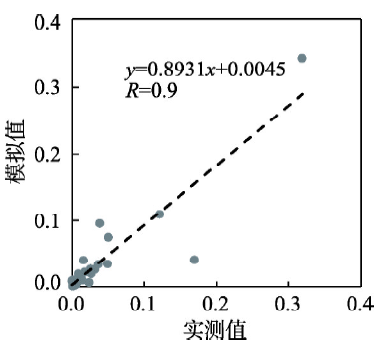
使用Huff的引力模型公式,规模变量取商业中心面积,距离变量取居住地（200 m网格）与商业中心的最短路程,设定距离衰减系数的取值区间为0.1~9.9（超出这一区间视为异常值,不再计算）,精度为0.1,逐一代入公式计算。每个网格与1个商业中心会产生99个模拟值,24个商业中心会产生2376个模拟值。仍然以56432号网格为例,当距离衰减系数取1.7时,依据模型计算得到的居民受各商业中心吸引的比例（表2）与实测比例的直线相关系数最高,达到0.9（图4）。1.7就是该网格的距离衰减系数。

图4

新窗口打开|下载原图ZIP|生成PPT
图4第56432号网格中的居民受各商业中心吸引的实测值—模拟值拟合

Fig. 4Data fitting of measured and simulated values of inhabitants attracted by commercial centres in No.56432 grid



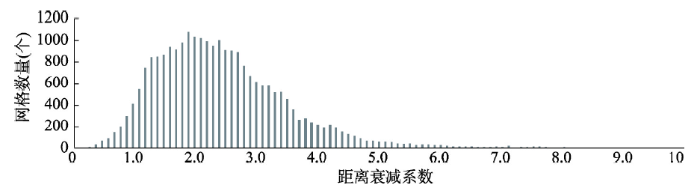
使用相同方法计算其余网格的距离衰减系数。由图5可见,各网格的距离衰减系数均不同,距离衰减系数整体接近正态分布。说明：① 不同地区距离衰减系数不同,与Huff当年的发现一致;② 绝大多数居民购物出行的空间阻力相似,受距离之外的因素扰动较小。多数网格的距离衰减系数位于0.5~5.0之间,求平均值后得到商业中心的距离衰减系数为2.5。

图5

新窗口打开|下载原图ZIP|生成PPT
图5上海中心城区商业中心吸引力距离衰减系数

Fig. 5Distance exponent of the attraction of commercial centres in Shanghai central city

3.3 模型应用——势力范围划分的实测和模拟结果比较

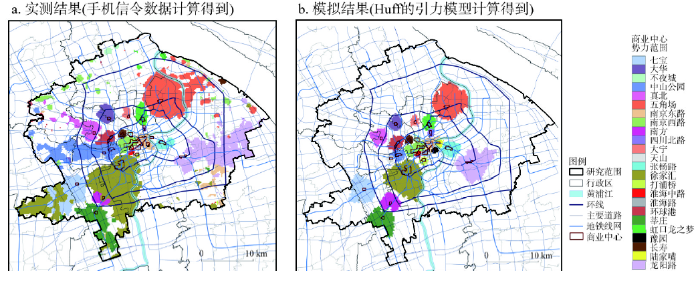
Huff的引力模型的实际应用就是势力范围划分：依据引力“取大”原则,将空间划分为若干个中心的势力范围（又称影响范围、势力圈、腹地）^{[1-3, 6, 8, 23-24]}。上文已经使用手机信令数据计算得到了每个网格中的居民前往所有商业中心的比例,依据“取大”原则,比例最高的中心就是该网格所属的势力范围。再引入绝对势力范围的概念,即比例最高的中心只有其比例高于一定值（0.27）,才能表示居住在该网格中的居民购物出行主要前往这一中心,是这个中心的绝对势力范围^[24]。据此划分24个商业中心的绝对势力范围（图6a）,是实测结果。

图6

新窗口打开|下载原图ZIP|生成PPT
图6上海中心城区商业中心势力范围划分的实测结果和模拟结果比较

Fig. 6Comparison of measured and simulated results for the influence areas of each commercial centre in Shanghai central city



使用Huff的引力模型公式,规模变量取商业中心面积,距离变量取网格与商业中心的最短路程,距离衰减系数取2.5。依据引力“取大”原则,划分24个商业中心的绝对势力范围（图6b）,得到模拟结果。

由图6可见,实测结果和模拟结果高度相似,以模拟结果为标准,两者有78.5%的网格所属势力范围相同。不同的是龙阳路、莘庄、中山公园、徐家汇、四川北路的绝对势力范围分别沿地铁2号线东段、1号线南段、2号线西段、9号线西段、3号线北段向外围地区延伸,徐家汇、五角场、曹安的绝对势力范围分别沿虹梅高架、五洲大道、曹安公路向外围地区延伸,而南方、豫园、天山的绝对势力范围分别被徐家汇、南京东路、中山公园“吞并”。说明：① 虽然居民出行仍使用距离概念,但地铁和快速路、公路等车速较高的交通线路会通过缩短出行时间对居民选择购物出行目的地产生影响;② 即使同属于城市级商业中心,但传统人气较高、规模较大的商业中心对居民的吸引力更强,一定程度上“屏蔽”了新兴的小规模商业中心的引力。同时也证明了Huff提出的商业中心对居民的吸引力实际取决于其能提供的效用^[12]。

上述分析表明,势力范围划分的实测结果和模拟结果具有较高的相似性,虽然存在差异,但差异的原因可解释。若规划新的商业中心或调整现有商业中心规模,使用Huff的引力模型公式,规模变量取商业中心面积,距离变量取网格与商业中心的最短路程,距离衰减系数取2.5,可对优化后的商业中心绝对势力范围进行预测,准确率可约达78.5%。

4 就业中心引力模型验证

4.1 就业中心引力模型验证

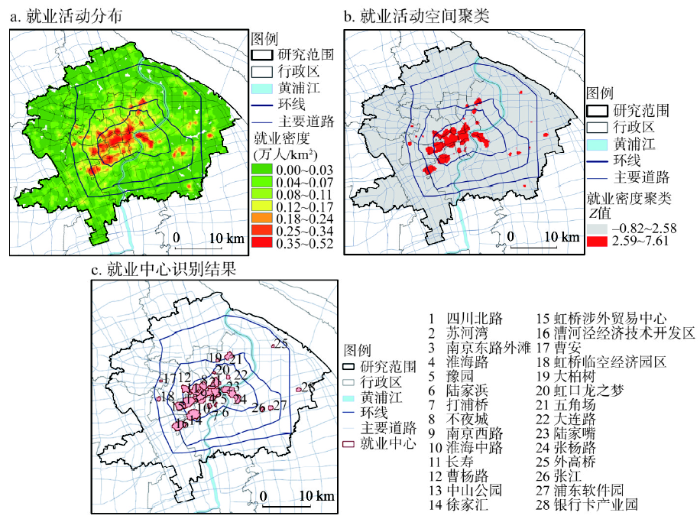
虽然Huff的引力模型最初只是针对零售业（商业）中心提出来的,但现实中模型应用已经扩展到了就业通勤^[14],且未经过严谨验证,其中Reilly、Converse、Huff的验证工作都只是针对零售业,此后虽也有****做过验证工作^{[14-15, 17-19]},但都不如Huff严谨。与购物出行相似,居民前往就业中心的通勤活动也是日常生产、生活的重要组成部分,了解其受就业中心吸引的规律有助于更好地认识城市中居民的日常活动规律。就业中心引力模型验证也是非常有意义的一项工作,下文就用居住地、工作地信息,采用与上文相同的方法验证就业中心的引力模型。

① 与识别商业中心的方法基本相同,依据本地居民工作地生成就业活动分布（图7a）,使用局部空间自相关识别就业活动高值聚类区（图7b）,将高值聚类区划分为28个就业中心（图7c）,以就业中心面积代表规模（表3）。

图7

新窗口打开|下载原图ZIP|生成PPT
图72015年上海中心城区就业中心识别

Fig. 7Identification of employment centres in Shanghai central city in 2015



Tab. 3
表3
表32015年上海中心城区就业中心面积
Tab. 3Area of employment centres in Shanghai central city in 2015

就业中心	面积(hm2)	就业中心	面积(hm2)	就业中心	面积(hm2)	就业中心	面积(hm2)
南京西路	480	南京东路外滩	224	淮海中路	116	大柏树	48
徐家汇	460	曹杨路	220	淮海路	92	张江	48
张杨路	408	四川北路	196	打浦桥	80	豫园	36
长寿	400	陆家嘴	188	浦东软件园	76	外高桥	32
漕河泾经济技术开发区	380	五角场	184	唐镇	68	虹口龙之梦	28
中山公园	372	不夜城	172	虹桥临空经济园区	60	陆家浜	28
虹桥涉外贸易中心	264	苏河湾	148	江浦	52	曹安	24

新窗口打开|下载CSV

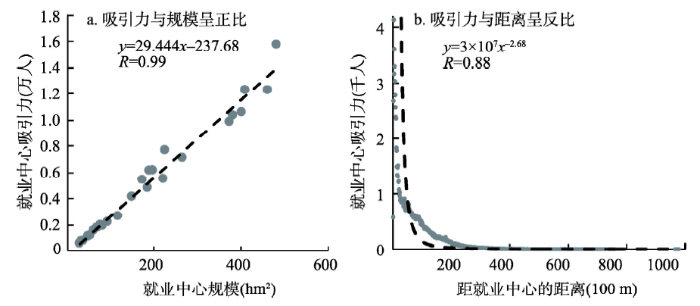
② 检验变量。分别汇总各就业中心吸引到的就业人数,代表就业中心吸引力。筛选工作地在就业中心的人的居住地,计算其就业通勤距离,按100 m间隔汇总每一距离区间内的人数。由图8可见,吸引力与规模呈较显著的直线正相关,与距离呈较显著的幂函数负相关,相关系数分别达到0.99和0.88,都属于极强相关。表明就业中心的吸引力与规模呈正比、与距离呈反比,符合引力模型规律。

图8

新窗口打开|下载原图ZIP|生成PPT
图8上海中心城区就业中心吸引力的变量检验

Fig. 8Variable validation for employment centres in Shanghai central city



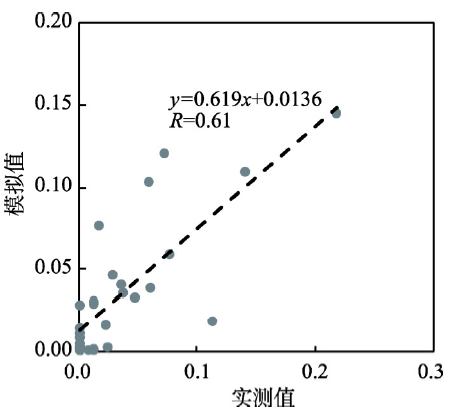
③ 校正距离衰减系数。仍然以56432号网格为例,其中的居民受各就业中心吸引的实测比例如表4所示。在2772（28个就业中心,每个产生99个模拟值）个模拟之中,当距离衰减系数取2.1时,依据模型计算得到的居民受各就业中心吸引的比例（表4）与实测值的直线相关系数最高（图9）,2.1就是该网格的距离衰减系数。

Tab. 4
表4
表4第56432号网格中的居民受各就业中心吸引的实测值—模拟值比较
Tab. 4Comparison of measured and simulated values of inhabitants attracted by employment centres in No.56432 grid

就业中心	实测值	模拟值	就业中心	实测值	模拟值	就业中心	实测值	模拟值	就业中心	实测值	模拟值
南京西路	0.22	0.15	大柏树	0.05	0.03	虹口龙之梦	0.01	0.03	打浦桥	0.00	0.01
不夜城	0.14	0.11	五角场	0.04	0.04	浦东软件园	0.01	0.00	淮海路	0.00	0.01
苏河湾	0.08	0.06	张杨路	0.04	0.04	徐家汇	0.01	0.03	江浦	0.00	0.01
长寿	0.07	0.12	曹杨路	0.03	0.05	张江	0.01	0.00	陆家浜	0.00	0.00
中山公园	0.06	0.04	淮海中路	0.02	0.02	外高桥	0.01	0.00	陆家嘴	0.00	0.03
四川北路	0.06	0.10	南京东路外滩	0.02	0.08	曹安	0.00	0.00	唐镇	0.00	0.00
虹桥涉外贸易中心	0.11	0.02	虹桥临空经济园区	0.02	0.00	漕河泾经济技术开发区	0.00	0.01	豫园	0.00	0.01

新窗口打开|下载CSV

图9

新窗口打开|下载原图ZIP|生成PPT
图9第56432号网格中的居民受各就业中心吸引的实测值—模拟值拟合

Fig. 9Data fitting of measured and simulated values of inhabitants attracted by employment centres in No.56432 grid



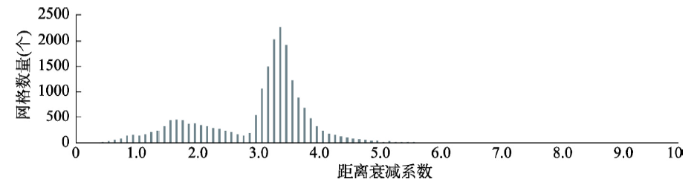
④ 以相同方法计算其余网格的距离衰减系数。由图10可见,各网格的距离衰减系数也不同,但并未呈正态分布。各网格距离衰减系数平均值3.0。

图10

新窗口打开|下载原图ZIP|生成PPT
图10上海中心城区就业中心吸引力距离衰减系数

Fig. 10Distance exponent for the attraction of employment centres in Shanghai central city



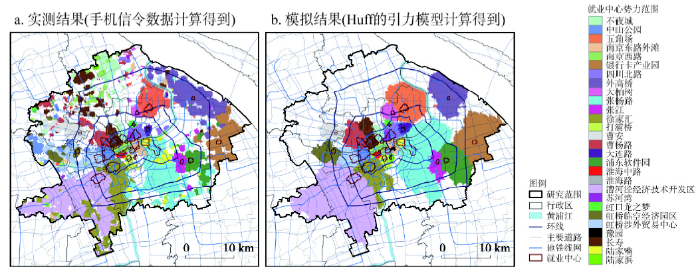
⑤ 比较势力范围划分的实测结果和模拟结果。由图11可见,两者也高度相似,以模拟结果为标准,有71.9%的网格所属势力范围相同。地铁、快速路、公路等快速交通线路会对势力范围分布的实测结果产生影响。使用Huff的引力模型公式,可对优化后的就业中心绝对势力范围进行预测,准确率可达到71.9%左右。

图11

新窗口打开|下载原图ZIP|生成PPT
图11上海中心城区就业中心势力范围划分的实测结果和模拟结果比较

Fig. 11Comparison of measured and simulated results of the influence areas of each employment centre in Shanghai central city

4.2 就业中心和商业中心吸引力的距离衰减规律比较

从上文分析结果中可发现,虽然引力模型最早是针对零售业（商业）中心提出来的,但就业中心的吸引力也符合引力模型规律,只是距离衰减系数与商业中心存在较显著差异。

就业通勤中各网格的距离衰减系数不符合正态分布,而在1.7和3.4处出现两个峰值,在两者之间的2.8处出现一个低值（图10）。说明居民的就业通勤除受距离影响外,还受其他因素影响。随着现代城市商业中心提供的产品、服务差异缩小,居民往往依据就近原则选择购物目的地,购物出行中往往会将距离作为选择出行目的地的主要考虑因素之一。与之不同,工作地的可选择范围较小（居民需要根据自己的专业、特长选择适合的工作,并非完全由居民自己决定,还受劳动报酬、可承受的通勤距离等因素影响）,考虑到换工作的成本,工作一旦选定,工作地往往具有唯一性、固定性。虽然大多数居民会倾向于在工作地附近选择居住地^[32],但家庭、房价等因素会限制居住地的选择,对就业通勤的距离衰减产生扰动：如双职工家庭就很难实现两人都能就近工作,有学龄儿童的家庭还会受到选择就读学校的影响使居住地选择更加复杂^[33,34];高房价、高租金会迫使居民住到离工作地较远的地区;即使就近居住若遇公司搬迁也有可能不得不远距离通勤。

从距离衰减系数的平均值来看,就业中心吸引力的距离衰减系数3.0高于商业中心（2.5）。说明购物出行和就业通勤对距离的敏感性存在较显著差异：购物出行属于非规律性活动,居民可承受的出行距离较长;而就业通勤属于规律性活动,通常每周至少有5个工作日都需要在工作地和居住地之间通勤,居民可承受的出行距离相对较短,距离衰减更大。

就业中心吸引力随距离衰减的这种特征也使得就业中心势力范围的实测结果和模拟结果的差异大于商业中心。如浦东金桥地区不属于任何就业中心的绝对势力范围,不仅是由于中环线及地铁6号线为居民较远距离通勤提供可能,还因为这一地区房价相对较低,居民之所以选择居住在此并不完全受与工作地之间距离的影响。不夜城、长寿、曹杨路等就业中心有地铁1号线、7号线、11号线经过,与外围房价相对较低的地区联系较便捷,使得这3个就业中心在10 km之外仍然有绝对势力范围。

5 距离衰减系数的空间分层异质性探讨

5.1 研究假设和分析方法

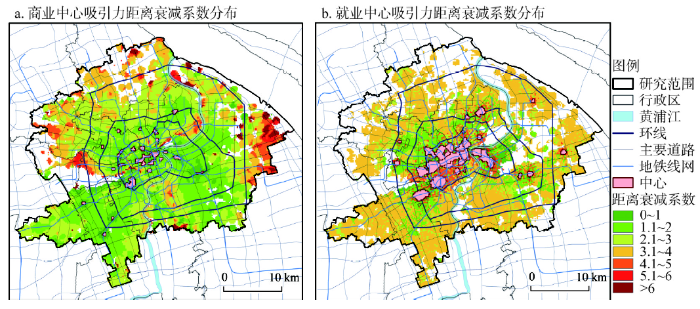
距离衰减系数是引力模型中最具有探讨意义的参数。除商业中心和就业中心吸引力距离衰减系数差异外,上文还证实了不同地区距离衰减系数不同,可将距离衰减系数值显示在空间上（图12）,进一步分析其分布特征。

图12

新窗口打开|下载原图ZIP|生成PPT
图12上海中心城区距离衰减系数分布

Fig. 12Distribution of the distance exponent in Shanghai central city



由图12可见,无色彩显示的地区为距离衰减系数未通过1%显著性检验或距离衰减系数为异常值（0或大于9.9）,主要位于外围非城市建成区（虹桥枢纽、村庄、农田等）,居住人口稀少,距离衰减具有不确定性,符合常理。距离衰减系数通过1%显著性检验的地区呈现出较显著的空间分层异质性（Spatial Stratified Heterogeneity,简称空间分异性或区异性）：① 距离衰减系数由中心向外围递增,这与中心地区区位较好、道路可达性较高（至其他任意地区的便捷程度较高）、出行空间阻力较小,外围地区可达性相对较差、出行空间阻力较大的直观感受一致;② 越接近商业中心、就业中心距离衰减系数越小,这可能与临近这些中心的地区至中心的出行选择性更多（可选择步行、非机动车）、出行更加方便有关^[18]。为检验上述观测结果的可靠性,使用地理探测器检验距离衰减系数的空间分层异质性及其影响因素。

地理探测器（Geodetector）是由王劲峰等^[35,36]提出并不断完善（http://geodetector.org）,主要用于探测空间分层异质性及其背后的驱动力,基本思想是“假设研究区分为若干层（子区域）,如果子区域的方差之和小于区域总方差,则存在空间分异性;如果两变量的空间分布趋于一致,则两者存在统计关联性”。地理探测器是一种分层统计方法,无线性假设、对多自变量共线性免疫,还能探测两变量的交互作用,是分析空间数据空间分层异质性的有力工具^[35,36]。当前已被广泛应用于公共健康、土地利用、区域经济等^{[37,38,39,40,41,42,43,44,45]}领域。地理探测器的具体公式如下：

（3）q=1-∑h=1LNhσh2Nσ2
式中：q为空间分异影响因素探测力指标;h = 1, 2, 3,……, L为因变量或自变量的分层;N_h和N分别为h和全区的单元数; σh2和 σ2分别是层h和全区的因变量的方差。q的值域为[0, 1],越趋近于1,说明因变量的空间分层异质性越明显。如果分层是由自变量生成的,则q值表示自变量解释了100×q%的因变量,q值越大,自变量对因变量的解释力越强。

5.2 结果分析

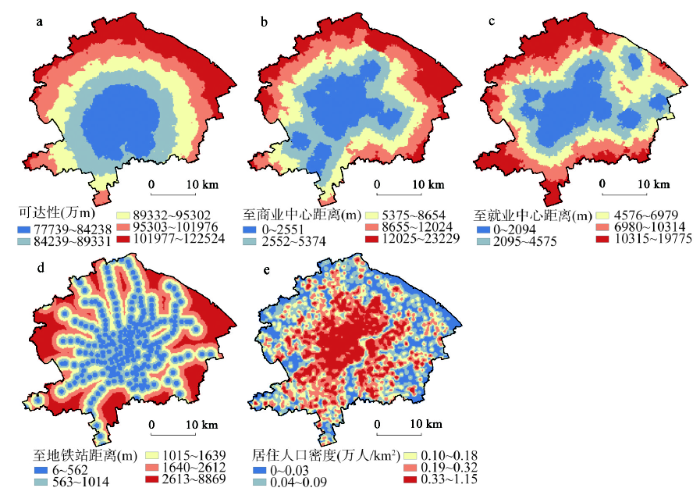
首先,以图12中的分类对距离衰减系数的空间分层异质性做检验。商业中心吸引力距离衰减系数的q值为0.934,就业中心吸引力距离衰减系数的q值为0.922,P值均小于0.05（通过5%显著性水平检验）。表明商业中心和就业中心吸引力的距离衰减系数都存在较显著的空间分层异质性,前者空间分异更加显著。

其次,依据对图12的观测结果,选取道路可达性^④ (④可达性评价方法有多种,考虑到本文可达性评价的目的是得到可达性分布图,属于全局评价、仅考虑路程（路网上的便捷程度）,适合使用距离法评价^[46,47,48]。评价方法为以道路交叉口为评价节点,权重均为1,计算研究范围内每一个道路交叉口至其他所有道路交叉口的网络距离（以路程表征）。距离和越小,表明该交叉口至其他所有交叉口越便捷,可达性越高。对道路交叉口可达性值做克里金插值分析,输出像元大小与研究空间单元一致,均为200 m网格,得到可达性分布图。)、至商业（就业）中心距离作为影响因素,检验其对距离衰减系数空间分布的影响。此外,至地铁站距离、居住人口密度可能也是影响距离衰减系数的因素（一般情况下越临近地铁站出行越便捷,出行的空间阻力越小;人口密度越高的地区开发建设越成熟,出行越便捷、空间阻力越小）,也将其加入检验模型。使用分位数分类法,将上述影响因素各自分为5类（图13）。

图13

新窗口打开|下载原图ZIP|生成PPT
图13上海中心城区距离衰减系数空间分层异质性的影响因素

注：① 可达性的距离值越小表示可达性越高;② 地铁站影响通常以直线距离测度,因此至地铁站距离以直线距离表征;③ 居住人口密度值仅表示手机信令数据识别到的居住人口密度,不代表真实值。
Fig. 13Spatial stratified heterogeneity factors of distance decay in Shanghai central city



由表5、表6可知,上述4个因素对距离衰减系数空间分布的影响均通过5%显著性检验,表明这4个因素能解释距离衰减系数的空间分层异质性。其中至商业中心距离的解释力（q值）最大,达到了32.5%,可达性略低也达到了30.3%,至地铁站距离、居住人口密度的解释力较低,分别仅为8.6%和8.2%。而对就业中心距离衰减系数而言,这4个因素的解释力均在5%以下。在上述4个因素两两交互作用下,距离衰减系数空间分布受到的影响均大于任何一种因素的独自作用（表7、表8）。

Tab. 5
表5
表5商业中心吸引力距离衰减系数空间分层异质性影响因素探测
Tab. 5Detection of spatial stratified heterogeneity factors of commercial centres

	可达性	至商业中心距离	至地铁站距离	居住人口密度
q值	0.303	0.325	0.086	0.082
p值	0.000	0.000	0.000	0.000

新窗口打开|下载CSV

Tab. 6
表6
表6就业中心吸引力距离衰减系数空间分层异质性影响因素探测
Tab. 6Detection of spatial stratified heterogeneity factors of employment centres

	可达性	至就业中心距离	至地铁站距离	居住人口密度
q值	0.036	0.037	0.015	0.032
p值	0.000	0.000	0.000	0.000

新窗口打开|下载CSV

Tab. 7
表7
表7商业中心吸引力距离衰减系数空间分层异质性影响因素交互作用
Tab. 7Interaction between pairs of factors in distance decay of commercial centres

	可达性	至商业中心距离	至地铁站距离	居住人口密度
可达性	0.303
至商业中心距离	0.372	0.325
至地铁站距离	0.327	0.331	0.086
居住人口密度	0.314	0.331	0.121	0.082

新窗口打开|下载CSV

Tab. 8
表8
表8就业中心吸引力距离衰减系数空间分层异质性影响因素交互作用
Tab. 8Interaction between pairs of factors in distance decay of employment centres

	可达性	至就业中心距离	至地铁站距离	居住人口密度
可达性	0.036
至就业中心距离	0.089	0.037
至地铁站距离	0.059	0.048	0.015
居住人口密度	0.061	0.062	0.042	0.032

新窗口打开|下载CSV

检验结果表明商业中心、就业中心吸引力距离衰减系数空间分布的内在机制存在较显著差异,前者的分布更有规律性：至商业中心距离、可达性是产生商业中心吸引力距离衰减系数空间分层异质性的主要原因。就业中心吸引力距离衰减系数空间分布虽然也显著受到这4个因素影响,且因素共同作用下对距离衰减系数的影响更大,但可解释性都较低。这可能与就业通勤被影响因素较多,各因素均不具有绝对影响力有一定关系。

6 结论和讨论

6.1 结论

在当前多中心城市中,商业中心的吸引力仍然符合引力模型规律：吸引力与规模呈正比、与距离呈反比。以200 m网格为空间单元,上海中心城区商业中心吸引力的距离衰减系数平均值为2.5。用拟合后的变量、参数计算得到的商业中心的势力范围与实测结果高度吻合。

在完成基本验证工作之外,本文还发现：① 地铁、快速路、公路等快速交通线网会改变时空结构,与以路程表征的出行目的地选择产生差异;传统人气较高、规模较大的商业中心会对其周边新兴的小规模商业中心形成“屏蔽”。上述两个原因都会导致商业中心吸引力实测值与模型预测值产生偏差。② 就业中心的吸引力也符合引力模型规律。以200 m网格为空间单元,上海中心城区就业中心吸引力的距离衰减系数平均值3.0高于购物出行,表明居民对规律性的通勤活动的距离敏感性相对较高。③ 就业中心吸引力在随距离衰减的规律之下,还受家庭、房价等因素影响,局部地区与引力模型有较大差异。

最后,本文还对距离衰减系数的空间分层异质性做了检验和归因：距离衰减系数具有较显著的空间分层异质性。距离衰减系数不是唯一值,城市中不同地区道路可达性不同、至商业（就业）中心距离远近、至地铁站距离远近、人口密度差异,都会影响居民对出行距离的敏感性。距离衰减系数在空间上呈由中心道路可达性高的地区向外围递增、由临近商业（就业）中心的地区向外围递增、由地铁站附近向外围递增、由人口密度高的地区向外围递增的分布特征。其中至商业中心距离、可达性对商业中心吸引力距离衰减系数空间分层异质性的解释力分别高达32.5%和30.3%。

6.2 讨论

6.2.1 关于研究数据 本文使用手机信令数据,从中识别用户的居住地、工作地和游憩地代替问卷调查。使用手机信令数据最大的问题在于样本是否具有代表性、识别结果是否会造成二次误差、能否反映真实情况。本文的重点不是数据处理方法,因此使用已有方法处理数据,识别结果与人口普查、经济普查的相关系数较高,说明识别结果作为大样本抽样应该具有代表性。此外,手机信令数据通过基站定位,存在百米级左右误差。本文通过核密度分析尽量使居住地、工作地、游憩地的分布更加接近真实。考虑到在上海中心城及其影响区1180 km²范围内开展研究,这一误差对结果影响应该不大。

引力模型的规模变量应是商业中心提供的“效用”,Huff用商业设施面积代表效用表征规模变量。由于在现代高强度开发、商业商务功能混合的城市中商业设施面积很难获取,本文使用商业中心面积表征规模变量。在上海中心城区普遍高强度开发的环境下,一般土地面积越大、商业设施面积越大,由此产生的误差应该影响不大。

6.2.2 关于距离衰减系数 本文使用最原始的方法校正距离衰减系数。以200 m网格为空间单元,每个网格逐一拟合吸引比例的实测值和模拟值,24个商业中心、30168个空间单元需要进行71679168次计算。这一方法是Huff提出来的,受当时问卷调查样本量和数据处理技术限制,只对3个社区的距离衰减系数做了校正。在手机信令数据和计算机技术的帮助下,当前已可实现用全市层面的大样本数据校正距离衰减系数。虽然计算量较大,但可以从个体出行目的地选择中揭示引力模型最本源的规律,反应不同地区距离衰减的不同特征。

经研究校正后的购物出行距离衰减系数2.5,就业通勤距离衰减系数3.0,仅代表以200 m网格为空间单元的距离衰减系数。这是由于不同尺度的空间单元距离计算误差、平均的交通条件不同,距离衰减系数也不同。若模型应用的空间单元尺度改变,距离衰减系数需要重新校正。但可以明确的是就业通勤对距离更加敏感。此外,不同时期、不同城市的交通条件不同,影响出行目的地选择、可承受出行距离的因素不同,距离衰减系数需要分别校正后才能将模型投入应用。

研究得到的距离衰减系数值只是针对上海中心城区而言,未必适合其他城市。但研究发现在多中心城市中,引力模型依然适用,距离衰减系数视出行目的、交通条件而异的结论具有普适性。研究使用的方法和技术同样适用于其他城市的研究。

6.2.3 关于模型应用 构建模型的意义在于总结规律,并在不断验证中修正对规律的认识,模型的作用在于对无法调查的情景做模拟,例如预测未来,而非取代现状调查。用实际调查的数据分析吸引力更加切合实际,模型只能起到补充作用^[49]。随着数据获取条件改善,现状分析应倡导使用观测数据,并用观测数据检验变量、校正参数,最后将检验后的变量、校正后的参数代入模型对未来进行预测。

参考文献 View Option 原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

[1] Huff D L . The delineation of a national system of planning regions on the basis of urban spheres of influence
Regional Studies, 1973,7(3):323-329.
[本文引用: 2]

[2] Huff D L, Lutz J M . Ireland's urban system
Economic Geography, 1979,55(3):196-212.
[本文引用: 1]

[1] Wang De, Zhao Jinhua . HAP: A computer assisted hinterland division system, its development and application
City Planning Review, 2000,24(12):37-41.
[本文引用: 2]

[ 王德, 赵锦华 . 城镇势力圈划分计算机系统的开发研究与应用
城市规划, 2000,24(12):37-41.]
[本文引用: 2]

[4] Liu Jisheng, Chen Yanguang . The gravitational models of franctal cities: Theoretical basis and applied methods
Scientia Geographica Sinica, 2000,20(6):528-533.
[本文引用: 1]

[ 刘继生, 陈彦光 . 分形城市引力模型的一般形式和应用方法: 关于城市体系空间作用的引力理论探讨
地理科学, 2000,20(6):528-533.]
[本文引用: 1]

[5] Wang De, Guo Jie . Hinterland and its dynamic changes in Hu-Ning-Hang Region
Urban Planning Forum, 2003(6):6-11, 95.
[本文引用: 1]

[ 王德, 郭洁 . 沪宁杭地区城市影响腹地的划分及其动态变化研究
城市规划汇刊, 2003(6):6-11, 95.]
[本文引用: 1]

[6] Pan Jinghu, Shi Peiji, Dong Xiaofeng . Measurements for urban hinterland area of cities at prefecture level or above in China
Acta Geographica Sinica, 2008,63(6):635-645.
[本文引用: 2]

[ 潘竟虎, 石培基, 董晓峰 . 中国地级以上城市腹地的测度分析
地理学报, 2008,63(6):635-645.]
[本文引用: 2]

[7] Gu Chaolin, Pang Haifeng , Study on spatial relation of Chinese urban system: Gravity model approach
Geographical Research, 2008,27(1):1-12.
[本文引用: 1]

[ 顾朝林, 庞海峰 . 基于重力模型的中国城市体系空间联系与层域划分
地理研究, 2008,27(1):1-12.]
[本文引用: 1]

[8] Qiu Yue, Wei Suqiong, Chen Jindong . Spatial pattern of urban hinterlands of cities at prefecture level or above in the economic zone on the western coast of the Taiwan Straits based on field-strength model
Geographical Research, 2011,30(5):795-803.
[本文引用: 2]

[ 邱岳, 韦素琼, 陈进栋 . 基于场强模型的海西区地级及以上城市影响腹地的空间格局
地理研究, 2011,30(5):795-803.]
[本文引用: 2]

[9] Zhong Yexi, Lu Yuqi . Measuring method of urban hinterland based on spatial linkage: A case of Jiangsu province
Scientia Geographica Sinica, 2012,32(5):536-543.
[本文引用: 1]

[ 钟业喜, 陆玉麒 . 基于空间联系的城市腹地范围划分: 以江苏省为例
地理科学, 2012,32(5):536-543.]
[本文引用: 1]

[10] Reilly W J . Methods for the Study of Retail Relationship
University of Texas Bulletin, 1929.
[本文引用: 1]

[11] Converse P D . New laws of retail gravitation
Journal of Marketing, 1949,14(3):379-384.
[本文引用: 1]

[12] Huff D L . Determination of intra-urban retail trade areas
Los Angeles, Real Estate Research Program, Graduate Schools of Business Administration,University of California, 1962.
[本文引用: 3]

[13] Xu Xueqiang, Zhou Yixing, Ning Yuemin . Urban Geography. Beijing: Higher Education Press, 1999.
[本文引用: 1]

[ 许学强, 周一星, 宁越敏 . 城市地理学. 北京: 高等教育出版社, 1999.]
[本文引用: 1]

[14] Calabrese F, Di L G, Liu L , et al. Estimating origin-destination flows using mobile phone location data
IEEE Pervasive Computing, 2011,10(4):36-44.
[本文引用: 4]

[15] Krings G, Calabrese F, Ratti C , et al. Urban Gravity: A model for intercity telecommunication flows
Journal of Statistical Mechanics Theory & Experiment, 2009,L07003:1-8.
[本文引用: 4]

[16] Kang C G, Zhang Y, Ma X J , et al. Inferring properties and revealing geographical impacts of intercity mobile communication network of China using a subnet data set
International Journal of Geographical Information Science, 2013,27(3):431-448.
[本文引用: 2]

[17] Gao S, Liu Y, Wang Y L , et al. Discovering spatial interaction communities from mobile phone data
Transactions in GIS, 2013,17(3):463-481.
[本文引用: 4]

[18] Zhou Suhong, Hao Xinhua, Liu Lin . Validation of spatial decay law caused by urban commercial center's mutual attraction in polycentric city: Spatio-temporal data mining of floating cars' GPS data in Shenzhen
Acta Geographica Sinica, 2014,69(12):1810-1820.
[本文引用: 4]

[ 周素红, 郝新华, 柳林 . 多中心化下的城市商业中心空间吸引衰减率验证: 深圳市浮动车GPS时空数据挖掘
地理学报, 2014,69(12):1810-1820.]
[本文引用: 4]

[19] Wei Ye, Xiu Chunliang, Wang Qi . An empirical study on polycentric urban spatial structure of Shenyang in the perspective of spatial association
Human Geography, 2014,29(3):83-88.
[本文引用: 2]

[ 魏冶, 修春亮, 王绮 . 空间联系视角的沈阳市多中心城市结构研究
人文地理, 2014,29(3):83-88.]
[本文引用: 2]

[20] Ahas R, Silm S, J?rv O , et al. Using mobile positioning data to model locations meaningful to users of mobile phones
Journal of Urban Technology, 2010,17(1):3-27.
[本文引用: 1]

[21] Becker R A, Caceres R, Hanson K , et al. A tale of one city: Using cellular network data for urban planning
IEEE Pervasive Computing, 2011,10(4):18-26.
[本文引用: 2]

[22] Xu Y, Shaw S L, Zhao Z , et al. Understanding aggregate human mobility patterns using passive mobile phone location data: A home-based approach
Transportation, 2015,42(4):625-646.
[本文引用: 1]

[23] Ding Liang, Niu Xinyi, Song Xiaodong . Measuring the employment center system in Shanghai Central City: A study using mobile phone signaling data
Acta Geographica Sinica, 2016,71(3):484-499.
[本文引用: 5]

[ 丁亮, 钮心毅, 宋小冬 . 上海中心城就业中心体系测度: 基于手机信令数据的研究
地理学报, 2016,71(3):484-499.]
[本文引用: 5]

[24] Ding Liang, Niu Xinyi, Song Xiaodong . A study on spatial characteristics of commercial centers in Shanghai Central City
Urban Planning Forum, 2017(2):63-70.
[本文引用: 6]

[ 丁亮, 钮心毅, 宋小冬 . 上海中心城区商业中心空间特征研究
城市规划学刊, 2017(2):63-70.]
[本文引用: 6]

[25] Ratti C, Frenchman D, Pulselli R M , et al. Mobile landscapes: Using location data from cell phones for urban analysis
Environment and Planning B-Planning & Design, 2006,33(5):727-748.


[26] Manfredini F, Pucci P, Tagliolato P . Toward a systemic use of manifold cell phone network data for urban analysis and planning
Journal of Urban Technology, 2014,21(2):39-59.


[27] Niu Xinyi, Ding Liang, Song Xiaodong . Understanding urban spatial structure of Shanghai Central City based on mobile phone data
Urban Planning Forum, 2014(6):61-67.
[本文引用: 1]

[ 钮心毅, 丁亮, 宋小冬 . 基于手机数据识别上海中心城的城市空间结构
城市规划学刊, 2014(6):61-67.]
[本文引用: 1]

[28] Wang De, Wang Can, Xie Dongcan , et al. Comparison of retail trade areas of retail centers with different hierarchical levels: A case study of East Nanjing road, Wujiaochang, Anshan road in Shanghai
Urban Planning Forum, 2015(3):50-60.


[ 王德, 王灿, 谢栋灿 , 等. 基于手机信令数据的上海市不同等级商业中心商圈的比较: 以南京东路、五角场、鞍山路为例
城市规划学刊, 2015(3):50-60.]


[29] Yan Longxu, Zhang Shangwu, Wang De , et al. Identification and evaluation of living centers system in Shanghai
Urban Planning Forum, 2016(6):65-71.


[ 晏龙旭, 张尚武, 王德 , 等. 上海城市生活中心体系的识别与评估
城市规划学刊, 2016(6):65-71.]


[30] Zhong Weijing, Wang De, Xie Dongcan , et al. Dynamic characteristics of Shanghai's population distribution using cell phone signaling data
Geographical Research, 2017,36(5):972-984.
[本文引用: 1]

[ 钟炜菁, 王德, 谢栋灿 , 等. 上海市人口分布与空间活动的动态特征研究: 基于手机信令数据的探索
地理研究, 2017,36(5):972-984.]
[本文引用: 1]

[31] Vasanen A . Functional polycentricity: Examining metropolitan spatial structure through the connectivity of urban sub-centers
Urban Studies, 2012,49(16):3627-3644.
[本文引用: 1]

[32] Mcmillen D P, Mcdonald J F . Population density in suburban Chicago: A bid-rent approach
Urban Studies, 1998,55(7):1119-1130.
[本文引用: 1]

[33] Meng Xiaochen, Wu Jing, Shen Fanpu . The study review of urban jobs-housing balance
Urban Development Studies, 2009,16(6):23-28, 35.
[本文引用: 1]

[ 孟晓晨, 吴静, 沈凡卜 . 职住平衡的研究回顾及观点综述
城市发展研究, 2009,16(6):23-28, 35.]
[本文引用: 1]

[34] Chai Yanwei, Zhang Yan, Liu Zhilin . Spatial differences of home-work separation and the impacts of housing policy and urban sprawl: Evidence from household survey data in Beijing
Acta Geographica Sinica, 2011,66(2):157-166.
[本文引用: 1]

[ 柴彦威, 张艳, 刘志林 . 职住分离的空间差异性及其影响因素研究
地理学报, 2011,66(2):157-166.]
[本文引用: 1]

[35] Wang J F, Zhang T L, Fu B J . A measure of spatial stratified heterogeneity
Ecological Indicators, 2016,67:250-256.
[本文引用: 2]

[36] Wang Jinfeng, Xu Chengdong . Geodetector: Principle and prospective
Acta Geographica Sinica, 2017,72(1):116-134.
[本文引用: 2]

[ 王劲峰, 徐成东 . 地理探测器: 原理与展望
地理学报, 2017,72(1):116-134.]
[本文引用: 2]

[37] Wang J F, Li X H, Christakos G , et al. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China
International Journal of Geographical Information Science, 2010,24(1):107-127.
[本文引用: 1]

[38] Wang J F, Hu Y . Environmental health risk detection with GeogDetector
Environmental Modelling & Software, 2012,33:114-115.
[本文引用: 1]

[39] Ding Yue, Cai Jianming, Ren Zhoupeng , et al. Spatial disparities of economic growth rate of China's national-level ETDZs and their determinants based on geographical detector analysis
Progress in Geography, 2014,33(5):657-666.
[本文引用: 1]

[ 丁悦, 蔡建明, 任周鹏 , 等. 基于地理探测器的国家级经济技术开发区经济增长率空间分异及影响因素
地理科学进展, 2014,33(5):657-666.]
[本文引用: 1]

[40] Huang J X, Wang J F, Bo Y C , et al. Identification of health risks of hand, foot and mouth disease in China using the geographical detector technique
International Journal of Environmental Research and Public Health, 2014,11:3407-3423.
[本文引用: 1]

[41] Zhan Donsheng, Zhang Wenzhong, Yu Jianhui , et al. Analysis of influencing mechanism of residents' livability satisfaction in Beijing using geographical detector
Progress in Geography, 2015,34(8):966-975.
[本文引用: 1]

[ 湛东升, 张文忠, 余建辉 , 等. 基于地理探测器的北京市居民宜居满意度影响机理
地理科学进展, 2015,34(8):966-975.]
[本文引用: 1]

[42] Ju H R, Zhang Z X, Zuo L J , et al. Driving forces and their interactions of built-up land expansion based on the geographical detector: A case study of Beijing, China
International Journal of Geographical Information Science, 2016,30(11):2188-2207.
[本文引用: 1]

[43] Li Jiaming, Lu Dadao, Xu Chengdong , et al. Spatial heterogeneity and its changes of population on the two sides of Hu Line
Acta Geographica Sinica, 2017,72(1):148-160.
[本文引用: 1]

[ 李佳洺, 陆大道, 徐成东 , 等. 胡焕庸线两侧人口的空间分层异质性及其变化
地理学报, 2017,72(1):148-160.]
[本文引用: 1]

[44] Liu Yansui, Li Jintao . Geographic detection and optimizing decision of the differentiation mechanism of rural poverty in China
Acta Geographica Sinica, 2017,72(1):163-173.
[本文引用: 1]

[ 刘彦随, 李进涛 . 中国县域农村贫困化分异机制的地理探测与优化决策
地理学报, 2017,72(1):163-173.]
[本文引用: 1]

[45] Yang Siqi, Xing Xiaoyue, Dong Weihua , et al. The spatio-temporal response of influenza A (H1N1) to meteorological factors in Beijing
Acta Geographica Sinica, 2018,73(3):460-473.
[本文引用: 1]

[ 杨斯棋, 邢潇月, 董卫华 , 等. 北京市甲型H1N1流感对气象因子的时空响应
地理学报, 2018,73(3):460-473.]
[本文引用: 1]

[46] Li Pinghua, Lu Yuqi . Review and prospectation of accessibility research
Progress in Geography, 2005,24(3):69-78.
[本文引用: 1]

[ 李平华, 陆玉麒 . 可达性研究的回顾与展望
地理科学进展, 2005,24(3):69-78.]
[本文引用: 1]

[47] Chen Jie, Lu Feng, Cheng Changxiu . Advance in accessibility evaluation approaches and applications
Progress in Geography, 2007,26(5):100-110.
[本文引用: 1]

[ 陈洁, 陆锋, 程昌秀 . 可达性度量方法及应用研究进展评述
地理科学进展, 2007,26(5):100-110.]
[本文引用: 1]

[48] Song Xiaodong, Niu Xinyi . The computer-aided evaluation on accessibility
Urban Planning Forum, 2000(3): 18-22,75-79.
[本文引用: 1]

[ 宋小冬, 钮心毅 . 再论居民出行可达性的计算机辅助评价
城市规划汇刊, 2000(3): 18-22,75-79.]
[本文引用: 1]

[49] Long Guoqiang . Further discussion of the method to determine the influence area of city
Urban Problems, 1988(1):12-16.
[本文引用: 1]

[ 隆国强 . 确定城市吸引范围方法的进一步探讨
城市问题, 1988(1):12-16.]
[本文引用: 1]