删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

旅游季节性测度指标的敏感度研究

本站小编 Free考研考试/2021-12-29

刘泽华¹^,, 章锦河²^,, 彭红松², 张瑜², 汤国荣²

1. 南京财经大学工商管理学院,南京 210023

2. 南京大学地理与海洋科学学院,南京 210023

Sensitivity analysis of the measures of tourism seasonality

LIUZehua¹^,, ZHANGJinhe²^,, PENGHongsong², ZHANGYu², TANGGuorong²

1. School of Business Administration, Nanjing University of Finance and Economics, Nanjing 210023, China

2. School of Geographic and Oceanographic Sciences, Nanjing University, Nanjing 210023, China

通讯作者:章锦河(1970-), 男, 安徽望江人, 教授, 博导, 研究方向为旅游地理学。E-mail: Zhangjinhe@nju.edu.cn
收稿日期:2017-01-25
修回日期:2017-09-14
网络出版日期:2018-02-10
版权声明:2018《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
基金资助:

国家自然科学基金项目(41671145);国家旅游局规划项目(15TAAG011);国家旅游局旅游业青年专家培养计划(TYETP201312)

作者简介:
-->作者简介：刘泽华(1979-), 男, 山东兰陵人, 博士, 讲师, 研究方向为旅游地理学。E-mail: liuzehua_tourism@163.com

展开

摘要
常用的旅游季节性测度指标有季节性强度指数（R_sd）、基尼系数（G）、泰尔系数（T）、季节性比率（R_sr）、不均匀系数（R_hl）等,国内外****对其相互关系、客流变动对各项指标的影响程度仍存在争议。构建旅游季节性测度指标的敏感度指标客流量变动效应（s_i）和客流量相对变动效应（p_i）,通过蒙特卡洛方法计算不同旅游季节性强弱尺度（Int）下的各项旅游季节性测度指标的相关系数、以及不同旅游季节性强弱尺度（Int）和不同客流量变动大小尺度（Δ）的组合条件下各项旅游季节性测度指标对各个月份的μ_si、μ^*_si和μ^*_pi,发现：① R_sd、G、T这3项指标相关系数极高,R_sr与R_sd、G、T 3项指标的相关系数随着Int的增大而增大,R_hl与R_sd、G、T、R_sr4项指标间的相关系数随着Int的增大而减小;② R_sr和R_hl对各月份的s_i以及R_sd、G、T、R_sr对不同月份的μ_si、μ^*_si及μ^*_pi均受Int和Δ的影响,其大小及排序相应产生变动,即在不同的旅游地,其季节性的强弱和客流量变动的大小都会导致各项旅游季节性测度指标对不同月份客流量变动的敏感度及排序存在差异,因此不能简单的认为某项指标对淡旺季客流或平季客流量变动更敏感。

关键词：旅游季节性;测度指标;敏感度分析;蒙特卡洛
Abstract
Standard Deviation (R_sd), Gini coefficient (G), Theil index (T), seasonality ratio (R_sr), and ratio of highest to lowest-season demand (R_hl) are popular measures of tourism seasonality; however the relationship between these measures and their influence on changes in tourism flow varies in literatures. Two sensitivity indices were developed to reflect the effect of the changes of tourism flow on the tourism seasonality measures (s_i) and the relative effect of the changes of tourism flow on the tourism seasonality measures (p_i). The correlation coefficient of measures of tourism seasonality in various scales (Int), the

μ si

μ si *

, and

μ pi *

and changes of tourism flow (Δ) are calculated by the Monte Carlo method. The results show that: (1) All the correlation coefficients between R_sd, G and T are over 0.970. Therefore, the tourism seasonality of some destinations with the three measures is significantly consistent. The correlation coefficients of R_sr and R_sd (or G, T) are between 0.446 to 0.845, and increase with increasing Int. The differences of using R_sr and R_sd (or G, T) are increased with Int. The correlation coefficients of R_hl and R_sd (or G, T, R_sr) are in the range of 0.003-0.772, and smaller with increasing Int. The differences of using R_hl and R_sd (or G, T, R_sr) are decreased with increasing Int. (2) Besides s₁₂ of R_hl, the only coefficient affected by m₁, s_i of R_sr and R_hl to the other months are influenced by R_sr and R_hl, Δ,

m ?

and m_i. In addition to s₁₂>0, the value, even the sign, of s_i has no correlation to R_sr and R_hl, and cannot consider to be more sensitive to a specific month. (3) The

μ si

μ si *

, and

μ pi *

of R_sd, G, T and R_sr for each month are varied by Int and Δ. Values and rank order change respectively to Int and Δ. Among them, s₁₂ is always positive, increasing tourism flow increases the value of the measures of tourism seasonality; and to the other months, changing tourism flow may increase, decrease, or no change measures of tourism seasonality. Range of seasonal variation and changes of tourism flow could affect the sensitivity of different measures of tourism seasonality and the rank order in different months. Therefore, no such particular measure is discovered in this research that it is more sensitive than other measures related to the tourism flows, and neither are any measures more sensitive to the changes in the peak season, off-season, or shoulder season.

Keywords：tourism seasonality;measure;sensitivity analysis;Monte Carlo

-->0
PDF (5969KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
刘泽华, 章锦河, 彭红松, 张瑜, 汤国荣. 旅游季节性测度指标的敏感度研究[J]. 地理学报, 2018, 73(2): 295-317 https://doi.org/10.11821/dlxb201802007
LIU Zehua, ZHANG Jinhe, PENG Hongsong, ZHANG Yu, TANG Guorong. Sensitivity analysis of the measures of tourism seasonality[J]. Acta Geographica Sinica, 2018, 73(2): 295-317 https://doi.org/10.11821/dlxb201802007

1 引言

旅游季节性即旅游现象各要素（包括客流量、游客花费、旅游交通等）在时间分布上的不均衡性,长期以来被认为是旅游业的基本特征之一,也是旅游业面临的主要问题之一^[1],而从数量上度量旅游需求随时间的变化很有必要^[2],对旅游规划和经营决策都很有帮助^[3]。合适的旅游季节性测度指标是判断及分析旅游季节性的工具,因此国内外****构建了多项指标并对不同案例地的旅游季节性特征进行分析,取得了丰富的成果。但各项指标的相互关系如何、旅游客流的变化会引起指标怎样的变动、指标值的变动反映了旅游季节性怎样的变化等问题,是正确理解和应用各项相关指标的前提,仍有待深入研究。

2 旅游季节性测度指标研究述评

2.1 旅游季节性特征测度指标构建及应用进展

国内外****研究旅游季节性特征常用的测度指标主要有季节性强度指数、基尼系数、泰尔系数、季节性比率、不均匀系数等。
季节性强度指数和季节差异系数均基于标准差方法设计。以各月客流的平均值作为1（或100）,各月客流的相对值则为各月度季节指数（seasonal index）^[7],计算该年各月度季节指数的标准差即得到季节差异系数（Coefficient of seasonal variation, CSV）^{[4,5,6,7,8,9]},也有****直接称为标准差（Standard Deviation）^[10]。而以各月客流的平均值作为1时,季节差异系数则等同于变异系数（Coefficient of Variation, CV）^[2],有****称之为离差系数^[11]。另外,国内****多使用各月客流比例（或百分比的分子）的标准差。20世纪90年代初期,保继刚等、陆林等****即使用该指数分析旅游客流季节性^[12,13],该指数在国内应用最为广泛,被****们称作季节性（时间）强度指数^{[3, 12, 14-20]}、季节集中指数^{[13, 21-26]}、月集中指数^[27],或直接称为均方差^[28]、标准差^[29]、季节性指数^[11]等。季节差异系数与季节性强度指数是简单的线性关系,有****认为季节性强度指数是客流量变异系数的具体结果^[30]。用R_sd表示季节性强度指数,计算方法为公式（1）。
基尼系数（Gini coefficient）是意大利经济学家Gini根据洛伦茨曲线于1912年提出的定量测定收入分配差异程度的指标^[31],国外****将其引入到旅游研究,用以描述旅游客流时间分布特征^{[2, 6, 8-10, 32-36]},近年来也有部分国内旅游****使用该指标^{[18, 37-39]},用G表示基尼系数,计算方法为公式（2）,另一常见的计算方法为公式（3）。泰尔系数（Theil index）又名泰尔熵标准（Theil's entropy measure）,由Theil 1967年利用信息理论中的熵概念来计算收入不平等而得名^[40],国外****把其引入到旅游季节性的测度^{[2, 6]},但目前尚未见到国内****使用该指标,用T表示泰尔系数,计算方法为公式（4）。
季节性比率（Seasonality Ratio）是各月客流量最大值与平均值之比^{[4-6, 8]},其倒数则被称作季节性指标（Seasonality Indicator）,也有****使用客流量最大3个月的值之和占全年客流总量的比例作为指标^[41],以上3种指标设计思路基本一致。用R_sr、R_si分别表示季节性比率和季节性指标,计算方法分别为公式（5）、（6）。不均匀系数是客流量最大值和最小值之比（Ratio of highest to lowest-season demand）^{[22, 41]},其倒数则被称为淡旺比^{[23, 25]}。用R_hl、R_lh分别表示不均匀系数和淡旺比,计算方法分别为公式（7）、（8）。
根据各指标的计算方法可知季节性强度指数、基尼系数、泰尔系数、季节性比率和不均匀系数5项指标值均随着旅游客流时间分布不均衡程度增加而增加,但取值范围各不相同（表1）,当旅游客流时间分布完全均匀时,季节性强度指数、基尼系数、泰尔系数均为0,而季节性比率、季节性指标、不均匀系数均为1;当全部客流完全集中在1个时段时,各项指标均不相等。
Tab. 1
表1
表1旅游季节性测度指标特征
Tab. 1Measures of seasonality

指标	计算公式		范围	指标含义
R_sd	$\begin{matrix} R_{sd} = \frac{\sqrt{\frac{\overset{n}{\sum_{i = 1}} (v_{i} {- \overset{?}{v})}^{2}}{n}}}{\overset{n}{\sum_{i = 1}} v_{i}} = \sqrt{\frac{\overset{n}{\sum_{i = 1}} (f_{i} {- \frac{1}{n})}^{2}}{n}} \end{matrix}$	（1）	[0, $\begin{matrix} \frac{\sqrt{n - 1}}{n} \end{matrix}$ ]	R_sd越小,则旅游客流时间分布越均衡,反之则越不均衡。
G	$\begin{matrix} G = \frac{2}{n} (\overset{n}{\sum_{i = 1}} i x_{i} - \frac{n + 1}{2}) \end{matrix}$	（2）	[0, $\begin{matrix} \frac{n - 1}{n} \end{matrix}$ ]	G越小,则旅游客流时间分布越均衡,反之则越不均衡。
	$\begin{matrix} G = \frac{\overset{n}{\sum_{i = 1}} \overset{n}{\sum_{j = 1}} \| f_{i} - f_{j} \|}{2 n^{2}} \end{matrix}$	（3）
T	$\begin{matrix} T = \overset{n}{\sum_{i = 1}} (f_{i} \times logn f_{i}) \end{matrix}$	（4）	[0, logn)	T越小,则旅游客流时间分布越均衡,反之则越不均衡。
R_sr	$\begin{matrix} R_{sr} = \frac{v_{\max}}{\overset{?}{v}} = n f_{\max} \end{matrix}$	（5）	[1, n]	R_sr越小,则旅游客流时间分布越均衡,反之则越不均衡。
R_si	$\begin{matrix} R_{si} = \frac{\overset{?}{v}}{v_{\max}} = \frac{1}{n f_{\max}} \end{matrix}$	（6）	[ $\begin{matrix} \frac{1}{n} \end{matrix}$ , 1]	R_si越小,则旅游客流时间分布越不均衡,反之则越均衡。
R_hl	$\begin{matrix} R_{hl} = \frac{v_{\max}}{v_{\min}} \end{matrix}$	（7）	[1,+∞)	R_sl越小,则旅游客流时间分布越均衡,反之则越不均衡。
R_lh	$\begin{matrix} R_{lh} = \frac{v_{\min}}{v_{\max}} \end{matrix}$	（8）	(0,1]	R_lh越小,则旅游客流时间分布越不均衡,反之则越均衡。

注：n为时段的数量;v_i为第i个时段客流量;

v ?

为客流量平均值;v_max为客流量最大值;V_min为客流量最小值;f_i为第i个时段客流量占全部客流量的比例;f_max为客流量最大值占全部客流量的比例;x_i为对各时段客流量从小到大排序后第i个时段客流量占全部客流量的比例。

新窗口打开

2.2 旅游季节性测度指标的比较研究述评

国外****对旅游季节性测度指标的比较研究起步较早,Yacoumis 1980年认为季节差异系数优于季节性比率^[4];Wanhill 1980年认为季节差异系数和季节性比率均没有考虑偏度,且易受旅游客流极值影响,故基尼系数相对更好^[5];Lundtorp 2001年对多项指标进行比较后认为季节差异系数是从统计学中借用的简单指标,季节性指标受最大值影响较大,更适合研究旅游目的地容量,基尼系数受到峰值的影响相对较小,并且对旺季之外的客流变化更敏感,适用于研究旅游季节性^[7];Duro 2016年认为基尼系数对中间值敏感,泰尔系数对淡季客流的变化更敏感,而变异系数是中性的^[2]。其中Wanhill和Lundtorp关于基尼系数更适合测度旅游季节性的观点得到了较多****的认同^[33,34,35],然而众多案例地的实证研究结果与之并不一致,如Wanhill对斯里兰卡1967-1979年旅游季节性进行分析,发现基尼系数和季节差异系数的排序结果较为接近,和季节性比率的排序结果差别较大,而这3项指标对1979年斯里兰卡前13个客源国的入境旅游季节性的排序结果十分接近^[5],但该研究并没有对此给出解释。Sutcliffe等使用季节差异系数、基尼系数和泰尔系数3项指标对西班牙1951-1976年入境旅游季节性进行排序,发现结果一致,而且3项指标间的相关系数均高于0.989^[6]。Koenig等使用季节差异系数、基尼系数和季节性比率对英国1994-2000年各地区各细分市场的国内旅游季节性进行分析,发现3个指标的排序非常相似,仅在少数案例中有所不同,同时认为这些指标不能完全描述季节性的信息^[8]。Koenig-Lewis等2005年在比较多位****的研究成果后认为仍需对各项季节性测度指标进行深入研究^[42]。Cuccia等认为基尼系数和季节性比率等指标都易于计算和扩展,但是容易被动荡影响,同时提出这些指标的稳健性（robustness）仍未确定^[43]。Cantis等以及Fernández-Morales等****则认为由于基尼系数、泰尔系数、季节差异系数等指标没有考虑月份的自然顺序,不同的季节性模式可能导致相同的指数值,因此还需分析季节性模式^{[9, 44]}。Lundtorp 2001年在比较季节性指标和基尼系数的敏感度时,分别计算了两者的导数及弹性^[7],但其关于两者敏感度的结论仅在客流变化很小时近似有效。
国内也有部分****对各项旅游季节性测度指标进行了探讨,有****认为季节性强度指数表示的不是集中性,而是不均匀程度,所以叫季节性集中指数并不恰当,应当称为不均匀指数^[28]。也有****认为基尼系数与季节性强度指数之间具可替代性^[18],但基尼系数相对更好^{[18, 38]}。有****则认为基尼系数为旅游流季节分布不均匀性的绝对值,季节性强度指数则为旅游流季节分布不均匀性的相对值^[18],并且得到一些****的认同^{[19, 45]}。但从季节性强度指数和基尼系数的构建思路来看,两者都是无量纲的相对值,上述观点并不完全正确。而由于季节性强度指数计算的“标准差”,使用的不是客流绝对数据,而是客流的相对比例,因此,有关****“季节性强度指数取值无上限”的描述^[18]属于误解。
综观已有研究成果,****们对各项旅游季节性测度指标的相互关系、客流变动对各项指标的影响程度等方面仍存在争议,缺乏深入的分析,而在部分案例地实证研究中,****们对使用这些指标对旅游季节性进行测度时表现出的不同特征缺乏合理的解释。本文拟通过计算指标间的线性相关系数分析不同条件下各项指标间的相关关系,并使用敏感度分析方法,探索不同条件下客流数据的变动对各项指标的影响,包括同一指标对不同月份客流变化的敏感度以及不同指标对同一客流变化的敏感度,以期更好地理解各项指标的性质,为判断及分析旅游季节性提供依据及借鉴。

3 研究方法

3.1 敏感度分析方法

为探索客流数据的变动对各项旅游季节性测度指标的影响,需要进行敏感度分析（Sensitivity analysis）。敏感度分析也称作灵敏度分析^[46,47]或敏感性分析^[48,49],目的是分析不同参数对模型结果的影响及相对重要性,获得参数影响的相对排名^[50],从而更好的解释模型的结构、机制、情景对结果的影响^[51,52],并也用于各类指标的构建及优化^[52]。敏感度分析已经应用到多个科学领域^{[51, 53-54]},可分为局部敏感度分析（local sensitivity analysis）和全局敏感度分析（global sensitivity analysis）^{[46, 53, 55]},或者分为定量和定性方法^[52],也有****根据所使用的计算和展示方法分为数学方法、统计方法和图形方法^[56]。
局部敏感度分析也称为一次变化法（one factor at a time, OAT）,即每次改变一个参数,计算模型结果的变化,同时保持所有其他参数为固定值（中心值^[46]或标准值^{[51-52, 55]}）,用偏导数方法即可得到最简单的局部敏感度系数S_i^{[46, 52, 57-58]},而对无法直接求偏导数的模型,则可通过有限差分方法,对参数变化很小的Δx_i,计算局部敏感度系数的近似值S_i^{' [58]},其中Δx通常为参数取值范围的某一部分（1%~10%）^[58]或一个标准差^[46]。局部敏感度系数计算简单,应用广泛,但该方法仅探讨了参数的一部分范围,而参数不同区域的敏感度不同^[59],同时该方法不能解释参数间的交互作用^[60],仅当模型是线性的或参数变化范围很小时有效^[55]。常见的全局敏感度分析方法有Morris方法^[61]、傅里叶幅度灵敏度检验法（Fourier Amplitude Sensitivity Testing, FAST）^[62,63,64]及扩展^[59]、Sobol方法^[65,66]等。其中Morris方法属于定性敏感度方法,计算第i个参数的基本效应d_i(x)（Elementary Effects, EE）,并计算其均值μ_i和标准差σ_i。Campolongo等2007年在此基础上进一步提出了指标μ^*_i,即基础效应d_i绝对值均值^[67],同时比较μ_i、μ^*_i和σ_i,可更好了解参数的敏感度^[67,68]。Morris方法计算量小、模型无关、可识别无影响的因子^{[52, 60]},被认为是较好的方法^[53],得到广泛应用^[69],但并不一定能识别出所有有影响的参数^[70]。

3.2 旅游季节性测度指标的敏感度分析方法

对旅游季节性测度指标进行敏感度分析,不仅要考虑理论上的科学性,而且要有实践指导意义。R_sr和R_hl的构建方法相对较为简单,可以参考局部敏感度方法以及Lundtorp的方法^[7],推导出敏感度表达式,而R_sd、G、T等指标则无法直接推导出其敏感度表达式,因此根据敏感度分析的基本步骤^[50],借鉴Morris方法^[61]及改进指标^[67,68],结合旅游业的实践需要,构建并计算各项旅游季节性测度指标的敏感度,步骤如下：
（1）确定分析对象。从各项旅游季节性测度指标的计算方法可知（公式（1）~（8））,仅基尼系数的计算需要对各月客流量进行排序,其他指标以及基尼系数的其他算法不受到月度数据大小排序的影响,各项季节性指标对各个自然月份的敏感度是等同的。为探讨不同淡旺季客流量变动对各项旅游季节性测度指标的影响,分析对象为排序后的各月份客流量。设v_i为第i个自然月份客流量,M_i为对各月份客流量从小到大排序后的第i个月份,m_i为M_i月份的客流量,则m₁≤ m₂≤…m_i_-1≤m_i≤…m₁₂,y = y（m₁, m₂,…,m₁₂）为某一旅游季节性测度指标。
（2）确定月度客流量的取值范围（Int）。由于R_sd、G、T、R_sr等指标均为无量纲的相对指标,客流量的绝对规模不影响指标值,因此为研究旅游季节性的强弱对各指标敏感度的影响,需选择不同的月度客流量相对变化范围,即把月度最小和最大客流量的比例控制在一定范围内。用Int表示原始月度客流量的取值范围,选择1~1.0001、1~1.001、1~1.01、1~1.1、1~2、1~1×10、1~1×10²、1~1×10³、1~1×10⁴、1~1×10⁵、1~1×10⁶、1~1×10⁷共12个尺度,并参考Morris方法,将其取值范围上限映射到1,则v_i的取值范围相应分别为0.9999~1、0.9991~1、0.9901~1、0.9091~1、0.5~1、1×10^-1~1、1×10^-2~1、1×10^-3~1、1×10^-4~1、1×10^-5~1、1×10^-6~1、1×10^-7~1。
（3）确定客流量的变动比例（Δ）。现实中旅游地的各月客流量有可能发生很大的突变,因此不仅需分析客流量较小的变动对旅游季节性测度指标的影响,还需探讨较大的客流量变动的影响。用Δ表示月度客流量增加的比例,选择1×10^-5、1×10^-4、1×10^-3、1×10^-2、1×10^-1、1、1×10、1×10²、1×10³、1×10⁴共10个尺度进行分析。
（4）确定抽样方法和次数。简单蒙特卡洛方法可用于各类敏感度分析,而为了保证足够的精度,对每种Int和Δ的组合使用简单蒙特卡洛方法抽取r = 5×10⁴次。由于Int和Δ分别有12和10个尺度,故对每一项旅游季节性测度指标,总抽样次数为R = r×12×10 = 6×10⁶次。
（5）计算旅游季节性测度指标值（y）。每次简单蒙特卡洛抽样生成某一Int尺度下的12个随机数,用以模拟各月客流量

\begin{matrix} v_{1} 、 v_{2} 、 \dots 、 v_{12} \end{matrix}

,对其从小到大排序得到

\begin{matrix} m_{1} 、 m_{2} 、 \dots 、 m_{12} \end{matrix}

,并计算各项y值,然后依次计算

\begin{matrix} m_{1} 、 m_{2} 、 \dots 、 m_{12} \end{matrix}

分别增加不同Δ后的各项y值。
（6）设计并计算敏感度指标。借鉴Morris方法的基本效应d_i,建立旅游季节性测度指标（y）对从小到大排序后第i个时段客流量变动效应s_i（公式（9））,即y值变化量与客流变化量的比值,并计算其均值μ_si和绝对值的均值

\begin{matrix} μ_{si}^{*} \end{matrix}

（公式（10）~（11））。μ_si的正负表明客流量变化对y的影响方向,

\begin{matrix} μ_{si}^{*} \end{matrix}

的大小则表明影响程度,两者结合则可比较该y值对不同月份的敏感度。如果某月份的

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

都较高,说明y值对该月份客流量的变化更为敏感,并且客流量的增加引起y值增加（当μ_si为负时,则为引起y值降低）;如果

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

都较低,则说明y对该月份客流量的变化较不敏感;如果

\begin{matrix} | μ_{si} | \end{matrix}

较低而

\begin{matrix} μ_{si}^{*} \end{matrix}

较高,则说明该月份客流量的变化对y值有不同方向（正负）的影响,该月份客流量的增加既有可能使y值增加,也有可能使y值降低。
由于各项旅游季节性测度指标（y）的上下限不同,s_i、μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

不能直接比较不同旅游季节性测度指标对同一月份客流量变化的敏感度,因此引入客流量相对变动效应p_i（公式（12））,即y值的变动比例,并计算其绝对值的均值

\begin{matrix} μ_{pi}^{*} \end{matrix}

（公式（13））,用以比较不同旅游季节性测度指标对同一月份客流量变化的敏感度。由于μ_si已经能够表明客流量变化对y值的影响方向,所以无需计算相对变动效应的μ_pi。如果某项旅游季节性测度指标的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值相对较高,则说明其对该月份的客流量变化更为敏感。

\begin{matrix} s_{i} = \frac{y (m_{1}, m_{2}, \dots, m_{i - 1}, m_{i} (1 + Δ), \dots, m_{12}) - y (m_{1}, m_{2}, \dots, m_{i}, \dots, m_{12})}{m_{i} Δ} \end{matrix}

（9）

\begin{matrix} μ_{si} = \frac{1}{r} \overset{r}{\sum_{j = 1}} s_{i} (j) \end{matrix}

（10）

\begin{matrix} μ_{si}^{*} = \frac{1}{r} \overset{r}{\sum_{j = 1}} | s_{i} (j) | \end{matrix}

（11）

\begin{matrix} p_{i} = \frac{y (m_{1}, m_{2}, \dots, m_{i - 1}, m_{i} (1 + Δ), \dots, m_{12}) - y (m_{1}, m_{2}, \dots, m_{i}, \dots, m_{12})}{y (m_{1}, m_{2}, \dots, m_{i}, \dots, m_{12})} \end{matrix}

（12）

\begin{matrix} μ_{pi}^{*} = \frac{1}{r} \overset{r}{\sum_{j = 1}} | p_{i} (j) | \end{matrix}

（13）
式中：m_i为对各时段客流量从小到大排序后第i个时段客流量;

\begin{matrix} y = y (m_{1}, m_{2}, \dots, m_{12}) \end{matrix}

为需分析的旅游季节性测度指标;Δ为客流量变动比例;r为抽样次数;

\begin{matrix} s_{i} (j) \end{matrix}

为第j组样本第i个时段客流量的变动效应;

\begin{matrix} p_{i} (j) \end{matrix}

为第j组样本第i个时段客流量的相对变动效应。

4 研究结果

4.1 旅游季节性测度指标相关分析结果

本文使用简单蒙特卡洛抽样生成的随机模拟数据,计算12个Int尺度下的旅游季节性测度指标间的相关系数,结果表明旅游季节性测度指标间的相关关系可分为3种类型（图1）：① R_sd、G、T这3项指标在不同Int尺度下相关性均非常高,两两间相关系数均在0.970以上,其中又以R_sd和G的相关性最高,相关系数均在0.991以上;② R_sr与R_sd、G、T 3项指标的相关系数随着Int的增大而增大,其中当Int < 1~10时,相关系数相对较低,在0.446和0.617之间,当Int ≥ 1~10时,相关系数在0.713和0.845之间;③ R_hl与其他4项指标间的相关系数均随着Int的增大而减小,其中和R_sd、G、T这3项指标的相关系数在Int < 1~100时为0.738和0.772之间,当Int ≥ 1~100时,相关系数则迅速减小,尤其是当Int ≥ 1~10⁵时则小于0.1;而R_hl和R_sr的相关系数更低,当Int < 1~10时,相关系数在0.512和0.597之间,当Int ≥ 1~10时,相关系数则同样迅速减小,当Int ≥ 1~10⁴时则小于0.1,当Int =1~10^-7时仅为0.003。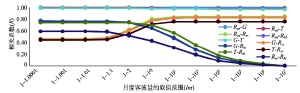

显示原图|下载原图ZIP|生成PPT
图1不同Int尺度下旅游季节性测度指标间的相关系数
-->Fig. 1The correlation coefficients of the measures in different intervals
-->

以上结果表明R_sd、G、T这3项指标相互间有极强的替代性,在不同的情况下使用这3项指标对旅游季节性的强弱进行分析,其结果将有很高的一致性,这与已有的实证研究相符^{[5-6, 8]};而R_sr与其他3项指标的结果是否一致,与案例地的季节性强弱有关,如果案例地旅游季节性较强,则分析结果趋于一致,如果案例地旅游季节性较弱,则分析结果则有较大差异,这或能解释已有研究中使用这4项指标对不同案例地旅游季节性排序产生不同差异^{[5, 8]}的原因。使用R_hl分析旅游季节性和使用R_sd、G、T、R_sr等指标分析,其结果的差异随着旅游地季节性的增强而增大。从指标设计的思路上看,R_sd、G、T这3项指标考虑的是测度所有客流数据的不均衡性,R_sr则强调在平均客流基础上,突出最大客流的重要性,R_hl则强调旅游客流量变动的最大幅度,因此需根据不同的管理需求,选择相应适合的旅游季节性测度指标。

4.2 季节性比率和不均匀系数的敏感度变动效应表达式

（1）季节性比率（R_sr）的敏感度
R_sr使用客流量最大值和客流量平均值计算,当最大月（M₁₂）客流量增加为

\begin{matrix} m_{12} (1 + Δ) \end{matrix}

后,仍为12个月中的最大值,故R_sr对M₁₂的敏感度s₁₂计算公式较为简单（公式（14））,且s₁₂>0,说明客流量的增加引起R_sr的提高。s₁₂受原有客流量均值

\begin{matrix} \overset{?}{m} \end{matrix}

、客流量变动比例Δ和原R_sr值3个因素的影响,随着

\begin{matrix} \overset{?}{m} \end{matrix}

和Δ的增大而减小,但原R_sr值增加有可能引起s₁₂的减少、不变或增加。其他11个月份（M₀₁~M₁₁）客流量增加后,存在小于、等于或大于原有客流量最大值3种可能（公式（15））,如果客流量增加后仍小于或等于原有客流量最大值（

\begin{matrix} m_{i} (1 + Δ) \leq m_{12} \end{matrix}

）,则s_i<0,说明客流量的增加反而引起R_sr的降低,此时s_i受到

\begin{matrix} \overset{?}{m} \end{matrix}

、Δ、原R_sr值和m_i4个因素的影响,其绝对值随着

\begin{matrix} \overset{?}{m} \end{matrix}

、Δ和m_i的增大而减小,但随着原R_sr值的增大而增大;如果客流量增加后大于原有客流量最大值（

\begin{matrix} m_{i} (1 + Δ) ＞ m_{12} \end{matrix}

）,则s_i有可能为负值、0或者正值,说明客流量的增加有可能引起R_sr的降低、不变或提高,此时s_i仍受到

\begin{matrix} \overset{?}{m} \end{matrix}

、Δ、原R_sr值和m_i4个因素的影响,随着

\begin{matrix} \overset{?}{m} \end{matrix}

和原R_sr值的增大而减小,但Δ和m_i的增加,有可能引起s_i的减少、不变或增加。

\begin{matrix} s_{12} = \frac{1}{\overset{?}{m}} (\frac{12 - R_{sr}}{12 + R_{sr} Δ}) \end{matrix}

（14）

\begin{matrix} s_{i} = \{\begin{matrix} - \frac{R_{sr}}{\overset{?}{m} + \frac{m_{i} Δ}{12}}, m_{i} (1 + Δ) \leq m_{12} \\ \frac{1 + Δ}{(\overset{?}{m} + \frac{m_{i} Δ}{12}) Δ} - \frac{R_{sr}}{m_{i} Δ}, m_{i} (1 + Δ) ＞ m_{12} \end{matrix} i = 1,2, 3, \dots, 10,11 \end{matrix}

（15）
（2）不均匀系数（R_hl）的敏感度
R_hl仅使用客流量最大值和最小值进行计算,当客流量最小月份（M₀₁）客流量增加后,存在3种可能（公式（16））：当客流最小值时（

\begin{matrix} m_{1} (1 + Δ) ＜ m_{2} \end{matrix}

）以及在客流量最大、最小值之间（

\begin{matrix} m_{2} \leq m_{1} (1 + Δ) \leq m_{12} \end{matrix}

）时,s₁为负值,此时客流量的增加反而引起R_hl的降低,两种情形下,

\begin{matrix} s_{1} \end{matrix}

分别受Δ、原R_hl值、m₁3个因素以及Δ、原R_h_l值、m₁、m₂4个因素的影响,其绝对值均随着Δ和

\begin{matrix} m_{1} \end{matrix}

的增大而减小,并分别随着原R_hl值以及原R_hl值、

\begin{matrix} m_{2} \end{matrix}

的增大而增大;当超过客流量最大值（

\begin{matrix} m_{12} ＜ m_{1} (1 + Δ) \end{matrix}

）时,s₁有可能为负值、0或正值,客流量的增加有可能引起R_hl的降低、不变或提高,此时s₁受Δ、原R_hl值、m₁和m₂4个因素的影响,随着原R_hl和m₂的增大而减小,随着m₁的增大而增大,但Δ的增加,有可能引起s₁的减少、不变或增加。客流量中间的10个月份（M₀₂~M₁₁）客流量增加后,存在两种可能（公式（17））：当低于或等于原有的客流量最大值时（

\begin{matrix} m_{i} (1 + Δ) \leq m_{12} \end{matrix}

）,s_i为0,R_hl不发生改变;大于原有的客流量最大值时（

\begin{matrix} m_{12} ＜ m_{i} (1 + Δ) \end{matrix}

）,s_i值有可能为负值、0或者正值,说明客流量的增加有可能引起R_hl的降低、不变或提高,此时s_i受Δ、原R_hl值、m₁、m_i4个因素的影响,随着原R_hl值和m_i的增大而减小,随着m₁的增大而增大,Δ的增加则有可能引起s_i的减少、不变或增加。R_hl对客流量最大月份（M₁₂）的敏感度s₁₂较为简单（公式（18））,s₁₂>0,客流量的增加引起R_hl的提高,此时s₁₂仅受客流量最小值m₁的影响,随着m₁的增大而减小。

\begin{matrix} s_{1} = \{- \begin{matrix} - \frac{R_{hl}}{m_{1} (1 + Δ)}, m_{1} (1 + Δ) ＜ m_{2} \\ \frac{R_{hl}}{Δ} (\frac{1}{m_{1}} - \frac{1}{m_{2}}), m_{2} \leq m_{1} (1 + Δ) \leq m_{12} \\ \frac{1 + Δ}{m_{2} Δ} - \frac{R_{hl}}{m_{1} Δ}, m_{12} ＜ m_{1} (1 + Δ) \end{matrix} \end{matrix}

（16）

\begin{matrix} s_{i} = \{\begin{matrix} 0, m_{i} (1 + Δ) \leq m_{12} \\ \frac{1 + Δ}{m_{1} Δ} - \frac{R_{hl}}{m_{i} Δ}, m_{12} ＜ m_{i} (1 + Δ) \end{matrix} i = 2,3, \dots, 10,11 \end{matrix}

（17）

\begin{matrix} s_{12} = \frac{1}{m_{1}} \end{matrix}

（18）
（3）R_sr和R_hl的敏感度影响因素
比较R_sr和R_hl的客流量变动效应s_i表达式,发现除R_hl对客流量最大月份（M₁₂）的敏感度s₁₂仅受m₁的影响外,两项指标对各月份的敏感度均受到多个因素的影响,包括旅游地季节性的强弱（即R_sr值或R_hl值）、客流量变动比例Δ、原有客流量m_i等,同时R_sr的s_i还受到原有客流量均值

\begin{matrix} \overset{?}{m} \end{matrix}

的影响,在这些因素的综合影响下,除s₁₂>0外,其他s_i的大小和符号并不确定,这表明当某月份客流量增加时,其R_sr值和R_hl值既有可能增加,也有可能不变或者减少,同时也不能简单的认为R_sr和R_hl对某一个月份客流量变动更为敏感。

4.3 旅游季节性测度指标的客流量变动效应分析结果

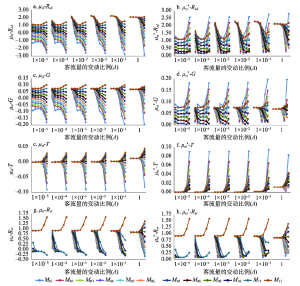
由于****们对R_sd、G、T、R_sr的敏感度存在较大争议,而R_hl的客流量变动效应s_i相对较为简单,因此重点对R_sd、G、T、R_sr进行分析,发现它们对不同月份的μ_si以及

\begin{matrix} μ_{si}^{*} \end{matrix}

均受月度客流量的变化范围（Int）和客流量的变动比例（Δ）的影响,在不同的Int和Δ的组合下,各月份μ_si以及

\begin{matrix} μ_{si}^{*} \end{matrix}

的值及排序有所差异。
（1）Δ ≤ 1且Int ≤ 1~10时,R_sd、G、T、R_sr的各月份μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

受到Int和Δ的影响发生变动（图2）,但排序均为

\begin{matrix} μ_{s 01} < μ_{s 02} \dots < μ_{si} < \dots μ_{s 11} < μ_{s 12} \end{matrix}

。R_sd、G、T客流较小的8个月份（M₀₁~M₀₈）的μ_si值在不同的Int和Δ的组合下出现正值、负值或零;而当Int和Δ尺度相等或接近时（如Int = 1~1.0001、Δ = 1×10^-4时）,

\begin{matrix} μ_{s 01}^{*} 、 μ_{s 02}^{*} 、 μ_{s 03}^{*} \end{matrix}

接近于0,并且此时

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

有较大差异,说明这种情况下客流量增加有可能导致R_sd、G、T等3项指标值增大,也有可能导致指标值减小。R_sd、G、T客流量较大的4个月份（M₀₉~M₁₂）的多数μ_si为正值,其

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

较为一致,说明客流量增加有可能导致R_sd、G、T的指标值增大。多数情况下,客流量较小的6个月（M₀₁~M₀₆）多为

\begin{matrix} μ_{s 01}^{*} > μ_{s 02}^{*} > μ_{s 03}^{*} > μ_{s 04}^{*} > μ_{s 05}^{*} > μ_{s 06}^{*} \end{matrix}

,客流量较大的6个月（M₀₇~M₁₂）则多为

\begin{matrix} μ_{s 12}^{*} > μ_{s 11}^{*} > μ_{s 10}^{*} > μ_{s 09}^{*} > μ_{s 08}^{*} > μ_{s 07}^{*} \end{matrix}

,并且

\begin{matrix} μ_{s 01}^{*} \end{matrix}

最大,

\begin{matrix} μ_{s 12}^{*} \end{matrix}

次之,而

\begin{matrix} μ_{s 02}^{*} \end{matrix}

和

\begin{matrix} μ_{s 11}^{*} \end{matrix}

、

\begin{matrix} μ_{s 03}^{*} \end{matrix}

和

\begin{matrix} μ_{s 10}^{*} \end{matrix}

、

\begin{matrix} μ_{s 04}^{*} \end{matrix}

和

\begin{matrix} μ_{s 09}^{*} \end{matrix}

、

\begin{matrix} μ_{s 05}^{*} \end{matrix}

和

\begin{matrix} μ_{s 08}^{*} \end{matrix}

、

\begin{matrix} μ_{s 06}^{*} \end{matrix}

和

\begin{matrix} μ_{s 07}^{*} \end{matrix}

等较为接近。

显示原图|下载原图ZIP|生成PPT
图2Δ ≤ 1且Int ≤ 1~10时各项指标 $μ si$ 和 $μ si *$
注：每个Δ内,Int依次为（1~1.0001,1~1.001,1~1.01,1~1.1,1~2,1~10）。
-->Fig. 2Value of $μ si$ and $μ si *$ of the measures when Δ ≤ 1 and Int ≤ 1~10
-->

R_sr的μ_s₁₂总为正值,并且

\begin{matrix} μ_{s 12}^{*} \end{matrix}

最大,其他11个月份（M₀₁~M₁₁）的μ_si在不同的Int和Δ组合下出现正值、负值或零,说明最旺季客流量增加导致R_sr值增大,而其他各月份客流量增加有可能导致R_sr值增大,也有可能导致其减小。M₀₁~M₁₁的μ_si均在Int和Δ尺度相等或接近时（如Int = 1~1.0001、Δ = 1×10^-4）相差较大,而当Int较大、Δ较小时（如Int = 1~10、Δ = 1×10^-4）则极为接近,同时

\begin{matrix} μ_{si}^{*} \end{matrix}

值也存在相应的规律。M₀₁~M₀₉的

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

差别较小,M₁₀~M₁₁的

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

则在特定的Int和Δ组合下有较为明显的差别,如Int = 1~1.001、Δ = 1×10^-4时的

\begin{matrix} | μ_{s 10} | \end{matrix}

和

\begin{matrix} μ_{s 10}^{*} \end{matrix}

。
以上结果表明R_sd、G、T的各月份

\begin{matrix} μ_{si}^{*} \end{matrix}

值及排序均受到Int和Δ的影响而变动,出现不同的总体排序结果,未出现在不同情形下均最敏感的月份,但对旺季及淡季客流量变动相对更敏感,而对平季客流相对不敏感。R_sr对最旺季（M₁₂）客流量变动最敏感,对其他各月份客流量变动的敏感度较为一致。
（2）Δ ≤ 1且Int ≥ 1~100时,R_sd、G、T、R_sr的各月份μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

值及排序受Int和Δ的影响较小（图3）,仅Δ = 1时有较为明显的变动。各项指标的

\begin{matrix} μ_{si} \end{matrix}

排序仍为

\begin{matrix} μ_{s 01} < μ_{s 02} \dots < μ_{si} < \dots μ_{s 11} < μ_{s 12} \end{matrix}

,其中当Δ<0.01时,R_sr其他各月（M₀₁~M₁₁）的μ_si极为接近。R_sd、T、R_sr3项指标的最大月（M₁₂）以及G的最大2个月份（M₁₁、M₁₂）的多数

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

相等,而其他各月份的

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

不相等,说明这些月份的客流量增加有可能导致这4项旅游季节性测度指标值增大,也有可能导致其减小。比较R_sd、G、T各月份

\begin{matrix} μ_{si}^{*} \end{matrix}

则发现,当Δ<1时,为

\begin{matrix} μ_{s 01}^{*} > μ_{s 02}^{*} > μ_{s 03}^{*} > μ_{s 04}^{*} > μ_{s 12}^{*} > μ_{s 05}^{*} > μ_{s 11}^{*} > μ_{s 06}^{*} > μ_{s 10}^{*} > μ_{s 07}^{*} > μ_{s 09}^{*} > μ_{s 08}^{*} \end{matrix}

,并且

\begin{matrix} μ_{s 08}^{*} \end{matrix}

和

\begin{matrix} μ_{s 09}^{*} 、 μ_{s 07}^{*} \end{matrix}

和

\begin{matrix} μ_{s 10}^{*} 、 μ_{s 06}^{*} \end{matrix}

和

\begin{matrix} μ_{s 11}^{*} 、 μ_{s 05}^{*} \end{matrix}

和

\begin{matrix} μ_{s 12}^{*} \end{matrix}

等较为接近;当Δ = 1时,

\begin{matrix} μ_{s 01}^{*} \end{matrix}

以及

\begin{matrix} μ_{s 07}^{*} 、 μ_{s 08}^{*} 、 μ_{s 09}^{*} 、 μ_{s 10}^{*} 、 μ_{s 11}^{*} \end{matrix}

有较明显的增大,

\begin{matrix} μ_{s 02}^{*} 、 μ_{s 03}^{*} 、 μ_{s 04}^{*} 、 μ_{s 05}^{*} 、 μ_{s 06}^{*} \end{matrix}

以及

\begin{matrix} μ_{s 12}^{*} \end{matrix}

有较明显的减小,同时各月份

\begin{matrix} μ_{si}^{*} \end{matrix}

值排序有所改变,为

\begin{matrix} μ_{s 01}^{*} > μ_{s 02}^{*} > μ_{s 03}^{*} > μ_{s 12}^{*} > μ_{s 04}^{*} > μ_{s 11}^{*} > \end{matrix} \begin{matrix} > μ_{s 10}^{*} > μ_{s 09}^{*} > μ_{s 08}^{*} > μ_{s 05}^{*} > μ_{s 07}^{*} > μ_{s 06}^{*} \end{matrix}

。R_sr各月份

\begin{matrix} μ_{si}^{*} \end{matrix}

值中,

\begin{matrix} μ_{s 12}^{*} \end{matrix}

最大,当Δ ≤ 0.1时,其他11个月份的

\begin{matrix} μ_{si}^{*} \end{matrix}

值极为接近,而随着Δ的增大,其他11个月份的

\begin{matrix} μ_{si}^{*} \end{matrix}

的差异逐渐明显。以上结果表明R_sd、G、T对最淡季（M₀₁）客流量变动最敏感,对其他淡季客流量变动也较敏感,对旺季以及平季客流量变动的敏感度相对较小;而R_sr对最旺季（M₁₂）客流量变动最敏感,对其他各月份客流量变动的敏感度的差别较小。

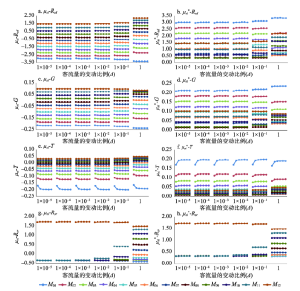显示原图|下载原图ZIP|生成PPT
图3Δ ≤ 1且Int ≥ 1~100时各项指标 $μ si$ 和 $μ si *$
注：每个Δ内,Int依次为（1~10²,1~10³,1~10⁴,1~10⁵,1~10⁶,1~10⁷）。
-->Fig. 3Value of $μ si$ and $μ si *$ of the measures when Δ ≤ 1 and Int ≥ 1~100
-->

（3）Δ ≥ 10且Int ≤ 1~10时,R_sd、G、T、R_sr的各月份μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

总体上随着Int的增大而增大,但随着Δ的增大而减小,并且Δ的影响明显更大（图4）,各月份μ_si多为正值,排序多为

\begin{matrix} μ_{s 01} > μ_{s 02} \dots \end{matrix} \begin{matrix} > μ_{si} > \dots μ_{s 11} > μ_{s 12} \end{matrix}

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

值较为一致,

\begin{matrix} μ_{si}^{*} \end{matrix}

值的排序也相应为

\begin{matrix} μ_{s 01}^{*} > μ_{s 02}^{*} > \dots \end{matrix} \begin{matrix} μ_{si}^{*} > \dots μ_{s 11}^{*} > μ_{s 12}^{*} \end{matrix}

,说明此时客流增加引起R_sd、G、T、R_sr值增加,另外当Δ =10、Int = 1~2以及Int = 1~10时,较小月份（M₀₁、M₀₂）的

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

值不相等,说明这种情形下客流增加量有可能导致旅游季节性测度指标值增大或减小。以上结果表明R_sd、G、T、R_sr对各月份客流量的敏感度均随着月度客流量排序的增加而变小,即对最淡季（M₀₁）客流量变动最敏感,对最旺季（M₁₂）客流量不敏感。

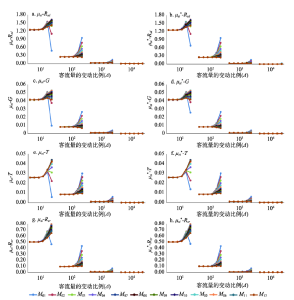显示原图|下载原图ZIP|生成PPT
图4Δ ≥ 10且Int ≤ 1~10各指标 $μ si$ 和 $μ si *$
注：每个Δ内,Int依次为（1~1.0001,1~1.001,1~1.01,1~1.1,1~2,1~10）。
-->Fig. 4Value of $μ si$ and $μ si *$ of the measures when Δ ≥ 10 and Int ≤ 1~10
-->

（4）Δ ≥ 10且Int ≥ 1~100时,R_sd、G、T、R_sr的各月份μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

受Int的影响相对较小,受Δ的影响则较为明显（图5）,总体上均随着Δ的增大而减小,并且

\begin{matrix} | μ_{si} | \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

两者相等的月份也随之增多。当Δ = 10时,R_sd、G、T的μ_si排序为

\begin{matrix} μ_{s 01} < μ_{s 02} < μ_{s 03} < μ_{s 12} < μ_{s 11} < μ_{s 04} < μ_{s 10} < \end{matrix} \begin{matrix} μ_{s 09} < μ_{s 08} < μ_{s 05} < μ_{s 07} < μ_{s 06} \end{matrix}

\begin{matrix} μ_{si}^{*} \end{matrix}

排序多为

\begin{matrix} μ_{s 01}^{*} \end{matrix}

最大,中间月份（M₀₅~M₁₀）的

\begin{matrix} μ_{si}^{*} \end{matrix}

次之,然后是旺季月份（M₁₁、M₁₂）,其他淡季（M₀₂、M₀₃、M₀₄）的

\begin{matrix} μ_{si}^{*} \end{matrix}

最小;而R_sr的μ_si排序

\begin{matrix} 为 μ_{s 01} < μ_{s 02} < μ_{s 03} < μ_{s 12} < μ_{s 11} < μ_{s 10} < μ_{s 09} < μ_{s 04} < μ_{s 08} < μ_{s 07} < μ_{s 05} < μ_{s 06} \end{matrix}

\begin{matrix} μ_{si}^{*} \end{matrix}

排序为

\begin{matrix} μ_{s 01}^{*} < μ_{s 02}^{*} < \end{matrix} \begin{matrix} μ_{s 03}^{*} < μ_{s 12}^{*} < μ_{s 11}^{*} < μ_{s 10}^{*} < μ_{s 09}^{*} < μ_{s 04}^{*} < μ_{s 05}^{*} < μ_{s 08}^{*} < μ_{s 06}^{*} < μ_{s 07}^{*} \end{matrix}

。而当Δ ≥ 100时,各月份μ_si多为

\begin{matrix} μ_{s 01} > μ_{s 02} > \dots μ_{si} \dots > μ_{s 11} > μ_{s 12} \end{matrix}

,且

\begin{matrix} μ_{si}^{*} \end{matrix}

排序为

\begin{matrix} μ_{s 01}^{*} > μ_{s 02}^{*} > \dots > μ_{si}^{*} > \dots > μ_{s 11}^{*} > μ_{s 12}^{*} \end{matrix}

,仅当Δ = 100时,μ_s₀₁的顺序位置有所不同。以上结果表明当Δ = 10时,R_sd、G、T对最淡季（M₀₁）客流量变动最敏感,对平季客流量的变动较为敏感,而对旺季以及其他淡季客流量的变动不敏感;R_sr对平季客流量的变动更敏感,对旺季客流量变动较为敏感,对最淡季（M₀₁）客流量变动最不敏感;当Δ ≥ 100时,各项指标的敏感度均随着月度客流量排序的增加而变小,即对最淡季（M₀₁）客流量变动最敏感,对最旺季（M₁₂）客流量变动最不敏感。

显示原图|下载原图ZIP|生成PPT
图5Δ ≥ 10且Int ≥ 1~100时各指标的 $μ si$ 和 $μ si *$
注：每个Δ内,Int依次为（1~10²,1~10³,1~10⁴,1~10⁵,1~10⁶,1~10⁷）。
-->Fig. 5Value of $μ si$ and $μ si *$ of the measures when Δ ≥ 10 and Int ≥ 1~100
-->

（5）旅游季节性测度指标的敏感度变动效应总体特征
综合以上分析可以看出,对不同大小排序的月份而言,R_sd、G、T、R_sr的μ_si及

\begin{matrix} μ_{si}^{*} \end{matrix}

受到Int和Δ的影响,其值及排序均相应产生变动,其中仅当Δ较小而Int较大时（Δ ≤ 1且Int ≥ 1~100）,各项季节性指标的μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

的值和排序均较为稳定;而当Int和Δ都较小时（Δ ≤ 1且Int ≤ 1~10）,μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

的值受Int和Δ的影响均较为明显,不同Int和Δ组合下

\begin{matrix} μ_{si}^{*} \end{matrix}

的排序不一致;当Δ较大时（Δ ≥ 10）,

\begin{matrix} μ_{si} \end{matrix}

和

\begin{matrix} μ_{si}^{*} \end{matrix}

的值随Δ的增大而减小,而Int的影响较小。其中,R_sd、G、T、R_sr的s₁₂总为正值,客流量的增加引起该旅游季节性测度指标值增大,而对其他月份而言,Int和Δ对各项旅游季节性测度指标各月份的μ_si以及

\begin{matrix} μ_{si}^{*} \end{matrix}

的影响并不是单向的,即在不同Int和Δ的组合下,客流量的变化既有可能引起某项旅游季节性测度指标增大,也有可能不变或减小。
在多数Int和Δ的组合下（表2）,R_sd、G、T在Δ较小时（Δ ≤ 1）,多为对旺季和淡季的客流量变动更为敏感,对平季的客流量变动相对更不敏感,在Δ较大时（Δ ≥ 10）,则多为对淡季的客流量变动更为敏感,而对旺季的客流量变动更不敏感,仅当Δ = 10且Int ≥ 1~100时对最淡季客流量变动最敏感,对平季的客流量变动较为敏感,而对旺季以及其他淡季的客流量变动不敏感;R_sr在Δ较小时（Δ ≤ 1）,对最旺季的客流量变动更为敏感,对其他各月份客流量变动的敏感度较为一致,在Δ较大时（Δ ≥ 10）,多为各月份客流量的敏感度随着月度客流量排序的增加而变小,即对最淡季的客流量变动最敏感,对最旺季的客流量变动不敏感,仅当Δ = 10且Int ≥ 1~100时对平季的客流量变动更敏感,对旺季的客流量变动较为敏感,对最淡季的客流量变动最不敏感。
Tab. 2
表2
表2旅游季节性测度指标的敏感度变动效应比较
Tab. 2The comparison of the effect of tourism flow changing on the tourism seasonality measures

	R_sd、G、T	R_sr
Δ ≤1且Int ≤ 1~10	对旺季及淡季客流量变动相对更敏感,但不存在各情形下均最敏感的月份。	对最旺季的客流量变动更为敏感,对其它各月份客流量变动的敏感度较为一致。
Δ ≤1且Int ≥ 1~100	对最淡季客流量变动最敏感,对其它淡季客流量变动较敏感,对旺季以及平季的客流量变动的敏感度相对较小。	对最旺季的客流量变动更为敏感,对其它各月份客流量变动的敏感度较为一致。
Δ=10且Int ≥ 1~100	对最淡季客流量变动最敏感,对平季客流的的变动较为敏感,而对旺季以及其它淡季客流量的变动不敏感。	对平季客流量的变动更敏感,对旺季客流量变动较为敏感,对最淡季客流量变动最不敏感。
Δ ≥10且Int ≤ 1~10 以及Δ ≥100且Int ≥1~100	随着月度客流量排序的增加而变小,即对最淡季客流量变动最敏感,对最旺季客流量变动最不敏感。	随着月度客流量排序的增加而变小,即对最淡季客流量变动最敏感,对最旺季客流量变动最不敏感。

新窗口打开

4.4 旅游季节性测度指标敏感度相对变动效应分析结果

R_sd、G、T、R_sr的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值及相互排序受Int和Δ的影响产生变动（图6）,在多数Int和Δ组合下以及大多数月份,T对客流量的变动最敏感,其他组合下则为R_sr最敏感,而在不同的Int和Δ组合下,R_sd、G、R_sr都有可能是最不敏感的。具体表现为：

显示原图|下载原图ZIP|生成PPT
图6各月份的旅游季节性测度指标 $μ pi *$
注：每个Δ内,Int依次为（1~1.0001,1~1.001,1~1.01,1~1.1,1~2,1~10,1~10²,1~10³,1~10⁴,1~10⁵,1~10⁶,1~10⁷）。
-->Fig. 6Value of $μ pi *$ of the measures of tourism seasonality
-->

（1）Δ ≤ 1时,R_sd、G、T 3项旅游季节性测度指标中,T各月份

\begin{matrix} μ_{pi}^{*} \end{matrix}

值均为最大,说明T对客流量的变动比G和R_sd更敏感,而G和R_sd的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值虽较为接近,但其中M₀₁~M₀₅、M₁₀~M₁₂等月份G的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值多大于R_sd,M₀₆~M₀₉等月份的G的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值多小于R_sd,说明G和R_sd两项指标中,G对客流量较小和较大月份（淡、旺季）的客流量变动相对更为敏感,R_sd则对客流量中间月份客流量的变动更为敏感。R_sr的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值在4项旅游季节性测度指标中的相对排序变化较大,当Δ ≤ 1且Int ≤ 1~10时,其各月份

\begin{matrix} μ_{pi}^{*} \end{matrix}

值为4项指标中最小,说明当旅游地季节性较弱时R_sr最不敏感。而当Δ ≤ 1且Int ≥ 1~100时,R_sr的M₀₁~M₀₆以及M₁₁等月份

\begin{matrix} μ_{pi}^{*} \end{matrix}

值多为4项指标中最小,而M₀₇、M₀₈、M₁₂等月份则为4项指标中最大值,M₀₉、M₁₀等月份则仅小于T,说明R_sr有可能最敏感,也有可能最不敏感。
（2）Δ ≥ 10时,R_sd、G、T、R_sr这4项旅游季节性测度指标中,T的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值最大,G的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值小于R_sd,说明T对客流量的变动最敏感,而R_sd比G更敏感。R_sr在4项旅游季节性测度指标中的相对排序仍变化较大,其中当Δ ≥ 10且Int ≤ 1~10时,R_sr的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值最小,此时R_sr最不敏感;而当Δ ≥ 10且Int ≥ 1~100时,

\begin{matrix} μ_{pi}^{*} \end{matrix}

值的排序为T > R_sr > R_sd > G,并且R_sd和R_sr的

\begin{matrix} μ_{pi}^{*} \end{matrix}

值较为接近,此时G最不敏感。

5 讨论

5.1 研究对象及敏感度指标的设计

明确分析对象以及相应的输出函数是敏感度分析的首要问题^[50],即明确“什么是敏感的”和“对什么敏感”^[49],因此对旅游季节性测度指标进行敏感度分析,首先要明确欲分析探讨的是旅游季节性测度指标对何种旅游客流量变动的敏感度,以及如何测量该敏感度。从R_sd、G、T的设计思路（公式（1）~（4））来看,在不对各月客流量（即v_i）进行排序的情况下,这3项指标对各自然月客流量变动的敏感度是等同的,而****们更关注极端客流以及淡旺季客流变动对旅游季节性测度指标的影响,因此选择对排序后的各月客流量（即m_i）研究,构建客流量变动效应s_i,并通过计算μ_si和

\begin{matrix} μ_{si}^{*} \end{matrix}

分析旅游季节性测度指标对不同月份客流量变动的敏感度。另外已有的敏感度指标多用于单一模型中不同参数的比较,这些指标无法比较同一参数（即旅游客流量）的变动所引起不同模型结果（即旅游季节性测度指标）的变化,因此设计了相对变动效应指标p_i以及

\begin{matrix} μ_{pi}^{*} \end{matrix}

进行比较分析。同Morris方法一样,μ_si、

\begin{matrix} μ_{si}^{*} \end{matrix}

及

\begin{matrix} μ_{pi}^{*} \end{matrix}

值仅用于敏感度的相对排序,仍属于定性方法。
本文针对单一月份客流量变化所引起的旅游季节性指标的变化进行了探讨,而2个以及多个月份客流量同时变化在旅游地中更为常见,其对旅游季节性测度指标的影响需要进行深入研究。同时还可参考及应用其他常见的敏感度分析方法,对旅游季节性测度指标的敏感度进行全面分析。

5.2 n、Int和Δ的选择

各项旅游季节性测度指标值均受所分析时段的数量n影响,理论上n可以是任意大于1的自然数,而现实中具体到不同时间间隔,如天、星期、月份或者季度,“n”值相应为365（366）、52、12和4。由于“月”的尺度是国内外****在分析季节性时最常用的,而“天、星期以及季度”等尺度由于分辨率过细或者过粗,其对实践的指导意义相对较弱,国内外研究相对较少,故仅选择“月”的尺度,即n = 12进行研究。因不同时段数量（n）的旅游季节性测度指标值无法直接进行比较,故暂未考虑某一时段客流量为0的情形。
Δx的大小影响敏感度分析的结果^{[46, 58, 60]},并且本文研究结果表明Int的大小也影响敏感度分析的结果,因此需根据具体的研究内容选择合理的Int和Δ。本文选择的Int和Δ能基本涵盖旅游地客流量可能的变动,但理论上Int和Δ的范围是连续且无穷的,实践中旅游客流量的变动也可能遇到更极端的情形,同时各项旅游季节性测度指标均为非线性模型,因此本文尚未涉及的Int和Δ,其各项旅游季节性测度指标敏感度的规律仍有待探讨。另外本文仅探讨了客流量增加（Δ > 0）对旅游季节性测度指标的影响,而当客流量减少时（Δ < 0）,旅游季节性测度指标的敏感度如何、以及其与客流量增加时的规律有何异同等仍有待分析。

5.3 抽样次数和抽样方法

在不同的敏感度分析中,****们使用简单蒙特卡洛方法进行抽样的次数有所差异,有1×10³次^[71,72]、5×10³次^[52]、2¹⁴即16384次^[60]等,有****认为当抽样次数大于5×10³时,简单蒙特卡洛抽样的结果足够精确^[71]。本文为保证精度增加了抽样次数,对每种Int和Δ的组合均抽样5×10⁴次,分析4项旅游季节性指标（R_sd、G、T、R_sr）对12个月份的敏感度s_i和p_i则共得到12×10×4×12×2 = 11520组结果,将每组5×10⁴个s_i或p_i值等分为10个5×10³的小组并进行单因子方差分析,结果显示11109组（96.43%）显著性概率高于0.05,说明其10个小组的s_i或p_i值不存在显著差异,即5×10³次抽样得到的结果已经较为稳定,而411组（3.57%）显著性概率小于0.05,其中有59组（0.51%）显著性概率值小于0.01,说明不同小组的s_i或p_i值存在显著差异,其μ_si、

\begin{matrix} μ_{si}^{*} \end{matrix}

以及

\begin{matrix} μ_{pi}^{*} \end{matrix}

值显著不同,因此,少数情形下5×10³次抽样并不能保证有足够的精度,需要进一步探讨不同情形下所需的合理抽样次数。
简单蒙特卡洛方法较为简单,但计算成本较高,****们为了更有效率的计算敏感度指标,选择并改进了多种抽样方法及研究指标,如Morris筛选方法^[61]及改进^{[59, 67, 73]}、拉丁超立方抽样（Latin hypercube sampling, LHS）^[74,75,76],径向抽样（radial sample）^{[53, 77]}、旋梯（winding stairs）^[77,78]、拟蒙特卡罗方法（quasi-Monte Carlo, QMC）^[60]等,如何在结合旅游客流变动实际规律的基础上借鉴这些成果,设计出更有效率的抽样方法,有待进一步研究。

5.4 本研究结果与已有研究结果的比较分析

综合R_sr和R_hl的对各月份的s_i以及R_sd、G、T、R_sr对不同月份的μ_si、

\begin{matrix} μ_{si}^{*} \end{matrix}

及

\begin{matrix} μ_{pi}^{*} \end{matrix}

,发现它们均受Int和Δ的影响,其大小及排序相应产生变动,因此在不同的旅游地,其季节性的强弱和客流量变动的大小都会导致各项旅游季节性测度指标对不同月份客流量变动的敏感度及排序存在差异。这一结果表明****们的各种观点都仅在一定Int和Δ的条件下成立,如基尼系数对中间值敏感、泰尔系数对淡季客流的变化更敏感、变异系数则是中性的^[2],季节差异系数优于季节性比率^[4],基尼系数相对更好^[5],以及季节性指标受最大值影响较大、基尼系数受到峰值的影响相对较小并且对旺季之外的客流变化更敏感^{[6, 33-35]}等。

6 结论

旅游季节性是旅游业的基本特征之一,也是旅游业面临的主要问题,适当的测度指标是判断及分析旅游季节性的工具。国内外****构建了多项指标并对不同案例地的旅游季节性特征进行了分析,取得了丰富的成果,但对常用旅游季节性测度指标的相互关系、客流变动对各项指标的影响程度等方面仍存在争议,而这是正确理解和应用各项指标的前提。对国内外****常用的季节性强度指数（R_sd）、基尼系数（G）、泰尔系数（T）、季节性比率（R_sr）、不均匀系数（R_hl）,构建旅游季节性测度指标的敏感度指标客流量变动效应（s_i）和客流量相对变动效应（p_i）,通过蒙特卡洛方法计算不同旅游季节性强弱尺度（Int）下的各项旅游季节性测度指标的相关系数、不同旅游季节性强弱尺度（Int）和不同客流量变动大小尺度（Δ）的条件下各项旅游季节性测度指标对各个月份的μ_si、

\begin{matrix} μ_{si}^{*} \end{matrix}

和

\begin{matrix} μ_{pi}^{*} \end{matrix}

,结果表明：
（1）R_sd、G、T 3项指标之间的相关系数均非常高,均在0.970以上,有较高的相互替代性,使用R_sd、G、T这3项指标进行旅游季节性分析的结果极为一致;R_sr与R_sd、G、T 3项指标的相关系数相对较低,在0.446和0.845之间,并随着Int的增大而增大,使用R_sr分析旅游季节性的结果和R_sd、G、T 3项指标得到的结果,其间差异随着旅游地季节性的增强而减小;R_hl与R_sd、G、T、R_sr4项指标间的相关系数更低,在0.003和0.772之间,并随着的Int增大而减小,使用R_hl分析旅游季节性的结果和R_sd、G、T、R_sr4项指标得到的结果,其间差异随着旅游地季节性的增强而增大。
（2）除R_hl对客流量最大月份（M₁₂）的敏感度

\begin{matrix} s_{12} \end{matrix}

仅受

\begin{matrix} m_{1} \end{matrix}

的影响外,R_sr和R_hl两项指标对其他各月份的敏感度均受旅游地季节性的强弱（即R_sr值或R_hl值）、客流量变化量比例Δ、原有客流量均值

\begin{matrix} \overset{?}{m} \end{matrix}

、原有客流量m_i等因素的综合影响,除s₁₂> 0外,其他s_i的大小和符号并不确定,因此不能简单的认为R_sr和R_hl对某一个月份客流量变动更为敏感。
（3）R_sd、G、T、R_sr对不同月份的μ_si、

\begin{matrix} μ_{si}^{*} \end{matrix}

及

\begin{matrix} μ_{pi}^{*} \end{matrix}

均受Int和Δ的影响,其大小及排序相应产生变动。其中,s₁₂总为正值,客流量的增加引起旅游季节性测度指标值增大,而对其他月份而言,客流量的变化既有可能引起某项旅游季节性测度指标值增大,也有可能是不变或减小;在不同的旅游地,其季节性的强弱和客流量变动的大小都会导致各项测度指标对不同月份客流量变动的敏感度及排序存在差异,因此不能简单的认为某项测度指标对淡旺季客流或平季客流量变动更敏感。
综上所述,本文对国内外****常用的旅游季节性测度指标的敏感度进行了初步分析,但仍需参考及应用其他敏感度分析方法,对其进一步深入探讨。同时由于旅游客流数据由所处时间段的先后顺序及相应的旅游客流量规模两个数值构成,而各项旅游季节性指标仅针对客流量规模的不均衡性进行设计,没有考虑客流量所在时段的时间先后顺序,已有****注意到不同的季节性模式可能导致相同的指标值^{[9, 44]},因此这些测度指标存在共同的局限,即客流量所在时段的先后顺序对指标值无影响,无法反映出旅游客流相对集中在研究期的哪一部分时段,是集中在前半期、后半期还是中期,而该特征对旅游季节性的测度也非常重要,有待设计相应的指标进行分析。
The authors have declared that no competing interests exist.

旅游季节性测度指标的敏感度研究

本站小编 Free考研考试/2021-12-29

Sensitivity analysis of the measures of tourism seasonality

1 引言

2 旅游季节性测度指标研究述评

2.1 旅游季节性特征测度指标构建及应用进展

2.2 旅游季节性测度指标的比较研究述评

3 研究方法

3.1 敏感度分析方法

3.2 旅游季节性测度指标的敏感度分析方法

4 研究结果

4.1 旅游季节性测度指标相关分析结果

4.2 季节性比率和不均匀系数的敏感度变动效应表达式

4.3 旅游季节性测度指标的客流量变动效应分析结果

4.4 旅游季节性测度指标敏感度相对变动效应分析结果

5 讨论

5.1 研究对象及敏感度指标的设计

5.2 n、Int和Δ的选择

5.3 抽样次数和抽样方法

5.4 本研究结果与已有研究结果的比较分析

6 结论

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

相关话题/指标 旅游 计算 客流量 比例

领限时大额优惠券,享本站正版考研考试资料!

广州鳄鱼公园野生动物旅游中的生命权力运作

基于机器学习的南京市旅游地个性及其文化景观表征

中国外商旅游饭店业投资的空间动态差异与驱动要素解析

基于能量的鄱阳湖—长江相互作用表征指标研究

《高铁网络时代区域旅游空间格局》评介

智慧旅游城市旅游竞争力评价

阳朔“西街现象”的形成机理分析——旅游地发展中的游客理性消费与政府“无为而治”

发达地区农村家庭旅游目的地选择行为特征与影响机制——以苏南地区为例

基于从业者的旅游历史街区商业空间发展特征及机理——扬州“双东”案例

高铁网络化下中国城市旅游场强空间格局及演化

旅游季节性测度指标的敏感度研究

本站小编 Free考研考试/2021-12-29

Sensitivity analysis of the measures of tourism seasonality

1 引言

2 旅游季节性测度指标研究述评

2.1 旅游季节性特征测度指标构建及应用进展

2.2 旅游季节性测度指标的比较研究述评

3 研究方法

3.1 敏感度分析方法

3.2 旅游季节性测度指标的敏感度分析方法

4 研究结果

4.1 旅游季节性测度指标相关分析结果

4.2 季节性比率和不均匀系数的敏感度变动效应表达式

4.3 旅游季节性测度指标的客流量变动效应分析结果

4.4 旅游季节性测度指标敏感度相对变动效应分析结果

5 讨论

5.1 研究对象及敏感度指标的设计

5.2 n、Int和Δ的选择

5.3 抽样次数和抽样方法

5.4 本研究结果与已有研究结果的比较分析

6 结论

参考文献文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

相关话题/指标 旅游 计算 客流量 比例

参考文献原文顺序
文献年度倒序
文中引用次数倒序
被引期刊影响因子

相关话题/指标旅游计算客流量比例