删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

学校分区问题混合元启发算法研究

本站小编 Free考研考试/2021-12-29

1. 河南大学黄河中下游数字地理技术教育部重点实验室, 开封 475000

2. 河南大学计算机与信息工程学院,开封 475000

A hybrid metaheuristic algorithm for the school districting problem

KONGYunfeng¹^,, ZHUYanfang¹, WANGYujing¹^,²

1. Key Laboratory of Geospatial Technology for the Middle and Lower Yellow River Regions, Ministry of Education, Henan University, Kaifeng 475000, Henan, China

2. College of Computer and InformationEngineering, Henan University, Kaifeng 475000, Henan, China

收稿日期:2016-07-4
修回日期:2016-10-22
网络出版日期:2017-02-15
版权声明:2017《地理学报》编辑部本文是开放获取期刊文献，在以下情况下可以自由使用：学术研究、学术交流、科研教学等，但不允许用于商业目的.
作者简介:
-->作者简介：孔云峰(1967-), 男, 博士, 博士生导师, 主要从事空间分析、空间优化等研究。E-mail: yfkong@henu.edu.cn

展开

摘要
中国城市义务教育学校采用单校划片或多校划片的方式确定招生范围,落实就近入学的法律要求。针对多校划片这一新的学校分区问题,提出“先学校分组,再学生分派”的策略进行划片,并设计了学校分组线性规划模型和学校分区混合元启发算法。分区算法包括初始解构造、邻域搜索算子、破坏重建扰动、集合划分问题（SPP）建模与求解等基本模块,在多启动迭代局部搜索（ILS）算法框架中进行问题求解。通过多启动、随机搜索、破坏重建扰动等机制提升算法的多样性,并引入SPP模型提升算法的全局寻优能力。选择一个县级市和一个市辖区分别进行学校划片实验,结果表明：混合元启发算法优化性能优异且收敛性好,适用于求解单校划片和多校划片问题;SPP模型在单校划片问题中具有明显的优势。

关键词：学校分区问题;空间连续约束;邻域搜索;混合元启发算法
Abstract
School districting has been widely introduced for compulsory education in urban areas of China in recent years according to the national policy of nearby school enrollment. A new enrollment policy for compulsory schools was issued by the Ministry of Education of China in 2016. According to the policy, a new school districting scheme for a district consisting of multiple schools is recommended to cities with uneven provision of compulsory schools, which aims to stabilize the apartment price in some existing school districts, and also to appease the public criticism on the phenomenon of school choice. This paper proposes a hybrid metaheuristic algorithm for solving both the classical single-school and the new multi-school districting problems. A two-stage strategy of "school grouping first and student assigning second" was used for multi-school districting. The school grouping problem was solved by mixed linear programming. An algorithm of multi-start iterated local search (ILS) with set-partitioning modeling (M-ILS-SPP) was introduced to solve the student assigning problem, which is a difficult problem due to the constraints of district contiguity and school capacity. Each run of ILS starts with an initial solution generated by the region growth method, and then executes neighborhood search and ruin-and-recreate perturbation iteratively. The proposed algorithm adopted four neighborhood search operators, three ruin methods and two solution acceptance rules. In addition, a model of set-partitioning problem (SPP) was used to choose a better solution from the historical districts identified by ILS. Two cases were used to test the performance of the proposed algorithm. The results from multiple scenarios of school districting show that the M-ILS-SPP algorithm for single-school or multi-school districting problems is effective in terms of solution quality and algorithm convergence. It is also found that the newly-designed neighborhood operators which move more spatial units simultaneously and the use of three perturbation methods randomly are critical for finding high quality district solutions. In addition, the set-partitioning modeling overcomes the short-sight limitation of local search operators and is capable of finding globally best solutions, especially for the single-school districting problem.

Keywords：school districting problem;spatial contiguity;neighborhood search;hybrid metaheuristic

-->0
PDF (756KB)元数据多维度评价相关文章收藏文章
本文引用格式导出EndNote Ris Bibtex 收藏本文-->
孔云峰, 朱艳芳, 王玉璟. 学校分区问题混合元启发算法研究[J]. , 2017, 72(2): 256-268 https://doi.org/10.11821/dlxb201702006
KONG Yunfeng, ZHU Yanfang, WANG Yujing. A hybrid metaheuristic algorithm for the school districting problem[J]. 地理学报, 2017, 72(2): 256-268 https://doi.org/10.11821/dlxb201702006

1 引言

中国城市义务教育学校采用单校划片或多校划片方式确定招生范围。根据2016年国家教育部的通知,在教育资源相对均衡的地方,要通过单校划片方式,落实学生就近入学;在教育资源配置不均衡、择校现象突出的地方,推行多校划片方式,将热点学校分散至每个片区,确保各片区之间大致均衡。学校划片是根据学校分布、学校规模、适龄学生人数、所在社区、交通状况等要素,按照公平和就近入学原则,确定义务教育学校招生范围,确保适龄学生就近或相对就近入学。
学校分区问题研究已有50余年的历史,但因各国或各地区义务教育政策的差异及政策不断调整,现有学校分区方法在解决实际问题中仍面临诸多挑战。首先,现有学校分区文献多针对单校划片问题,尚无针对多校划片问题的文献。其次,多数文献使用数学模型求解学校分区问题^[1-7]。相关模型能够优化学生入学距离,但不能保证学区空间连续。个别文献^[8-9]考虑到了学区空间连续性要求,但提出的模型或算法缺乏通用性。第三,求解学校分区问题可借鉴空间连续约束区划问题算法,但常见区划问题与学校分区问题在分区原则、分区约束和目标定义上有显著的差异,导致相关算法要么不适用,要么需要作较大修订。如MIDAS^[10]、SKATER^[11]和REDCAP^[12]等区划算法建立在空间单元相似的基础上,难以用于学校分区问题;经典的区划算法AZP^[13]适用性强但性能有限;大量元启发算法较好地应用于求解各类区划问题^[14-26],但尚未用于学区划分。
鉴于求解空间连续约束学校分区问题的算法仍不成熟,特别是尚无关于多校划片问题的文献报道,本文提出了一个“先学校分组,再学生分派”策略：使用数学模型求解学校分组问题,再使用基于邻域搜索的混合元启发（M-ILS-SPP）算法将学生分派到学校,获得空间连续的学区。算法在扩展区划问题邻域搜索算子的基础上,使用多启动迭代局部搜索(iterated local search, ILS)进行邻域搜索,并引入集合划分模型（set-partitioning problem, SPP）克服局部搜索类算法“短视”的局限。案例实验表明本文算法优化性能优异,适用于求解单校划片或多校划片问题。

2 文献回顾

学校分区问题是将一个行政区域内较小的地理空间单元分组,将单元内学生指派到学校,在满足一定约束条件的前提下,使学生入学距离最短。约束条件包括分区内入学学生人数不大于学校招生名额、分区空间连续等。
线性规划模型是求解学校分区问题的常用方法。模型通常以学校招生规模、学生种族比例等为约束条件,以学生入学距离为目标,将学生分派到学校^[1-7]。这些模型属于指派问题（assignment problem, AP）、交通问题（transportation problem, TP）或空间配置问题（spatial allocation problem, SAP）范畴,虽然模型相对容易求解,但所获得的解决方案通常不能满足分区连续的要求。
空间连续约束是求解学校分区问题的难点。有****将学生与学校距离平方和作为优化目标,力图使分区更加紧凑^[1-2]。然而,因学生和学校地理分布具有不均衡性,该方法仍不能保证分区具有连续性,也不能保证学生入学距离最短。Caro等^[8]建立了一个整型线性规划模型,顾及分区连续、学校学额、最远入学距离、种族平衡等约束,目标是学生总体入学距离最短。借助GIS软件功能,作者开发了一个交互式学校分区软件系统,包含数据准备、数据预处理、学校分区和后处理等模块。使用两个案例进行了4个场景的学校分区实验,获得了较为满意的学校分区方案。然而,该模型建立的空间连续约束缺乏通用性,不能满足所有案例情形。模型的计算复杂度也较高,如其中一个案例场景需长达10 h的计算时间。
Ferland等^[9]将学校分区问题表达为一个道路网络图,设置学校处于网络结点,分配学生在路段上,基于学校各年级班级数量、最高班额和路段上的学生数量等数据进行学区划分。该方法首先设置一个距离阈值,根据路段与学校的距离,将路段划分为3类：仅有一个学校在阈值内的路段、有多所学校在阈值内的路段和超过阈值的路段。再依次序将3类路段分配到学校,并在最后一步顾及路段的连续性。若路段划分方案违背约束,通过人工交互进行修改。该方法在应用中具有可行性,但不能保证学校分区的质量。
学校分区问题也是一个典型的区划问题^[27],可借鉴较为成熟的区划问题算法。常见区划问题算法包括精确算法、区域种子生长算法、基于聚类的算法、启发改进类算法等^[28]。空间连续约束区划问题模型属于NP-Hard问题,计算复杂度很高^[29],难以高效求解常见区划问题^[32]。区域生长算法思路简单且应用广泛,然而该方法仅顾及局部相邻单元,求解质量不高,当分区约束条件过多或约束过紧时,也难以找到可行解。
基于最小生成树的区划算法MIDAS^[10]和SKATER^[11]是将空间单元表达为网络图,根据相邻空间单元的相似性构建最小生成树,通过树分割算法获得空间连续分区,能有效地划分出区内同质、区间异质的区域。凝聚层次聚类分析也是根据相邻空间单元的相似性建立聚类树,相关算法及改进在区划问题中表现出良好的性能^[12]。然而,这些成熟算法采用的“相邻单元相似”原则难以应用于学校分区问题。
经典的区划算法AZP将n个空间单元随机划分为k个区域,在顾及分区空间连续约束的前提下,尝试将某个单元重新分配到另一个区域,持续改进区划方案^[13]。该算法设计思路简单,易于扩展,但属于爬山算法,搜索过程容易陷入局部最优而过早停滞。针对AZP算法的不足,****尝试从多个角度改进,如在邻域搜索过程中引入更复杂的邻域算子、分区合并和分割、分区中心调整等方法^[14-16],并通过模拟退火、禁忌搜索等元启发机制改进分区质量^[17-22]。近年来,遗传、进化、分散搜索等群智能算法也逐步进入到区划问题中^[23-26],设计了多种多样的解表达方法、交叉与变异算子和适宜度评价函数。该类算法设计灵活,但参数设置较多,也较难发现满足空间连续的解,因而计算效率往往偏低。
Ko等^[22]研究了一个与学校分区问题接近服务区划分问题,将区划问题和区位问题整合,通过区内服务转移的方式降低服务设施的负荷和服务的不均衡型。在构造问题初始解的基础上,作者设计了一个邻域搜索算子,在模拟退火算法框架中迭代改进服务分区。案例实验验证了该算法的有效性。该算法思路可用于求解学校分区问题,但仅使用一个邻域搜索算子容易使搜索过程陷入局部最优。
综上,求解空间连续约束学校分区问题的算法仍不够成熟。教育部提出的多校划片是一个新的学校分区问题类型,尚无相关问题的研究报道。区划领域发展了一系列元启发算法,但这些算法无法直接应用于学校分区问题。本文借鉴求解区划问题的邻域搜索算法,进行算子扩展和算法机制改进,将其应用于学校分区问题。

3 问题定义

遵循就近入学原则,本文学校分区问题描述如下：给定学校位置及招生规模、空间单元、单元内入学学生数量和道路网络,划分学校招生片区,分区目标是学生平均入学距离最短。多校划片是将整个区域划分为若干片区,每个片区包含若干所学校,要求片区规模适中,片区内入学人数小于学校招学生人数,且每个片区均有优质学校,使每个学生有选择优质学校的机会。单校划片是多校划片的一个特例,即片区数量等于学校数量。
令集合U ={1, 2…n}表示n个空间单元,每一个空间单元i具有属性q_i和p_i,分别表示空间单元i内学校招生人数和上学学生人数,q_i= 0表明空间单元i内无学校。变量d_ij表示空间单元i与单元j之间的距离;c_ij代表空间单元i和j是否邻接。学校分区问题定义为：将空间单元集合U划分为k个子集(即学区),记为集合R ={r₁, r₂…, r_k},在满足特定的约束条件的前提下使学生平均入学距离最短。约束条件包括：

\begin{matrix} U = r_{1} ? r_{2} ? \dots ? r_{k} \end{matrix}

（1）

\begin{matrix} r_{i} ? r_{j} = ?, ? r_{i}, r_{j} \in R, r_{i} \neq r_{j} \end{matrix}

（2）

\begin{matrix} r_{i} \neq ?, ? r_{i} \in R \end{matrix}

（3）

\begin{matrix} \sum_{i∈rj} p_{i} \leq \sum_{i∈rj} q_{i}, ? r_{j} \in R \end{matrix}

（4）

\begin{matrix} A \leq \sum_{i∈rj} p_{i} \leq B, ? r_{j} \in R \end{matrix}

（5）

\begin{matrix} 学区 r_{i} 空间连续, ? r_{i} \in R \end{matrix}

（6）
约束（1）保证每一个空间单元必须划分到某个学区;约束（2）要求学区之间没有重叠;约束（3）要求学区至少包括一个空间单元;约束（4）要求学区内入学总人数不能超过区内学校总学额;约束（5）是对学区规模的限制,即每个学区的学额处于[A, B]区间内;约束（6）要求学区必须是连续的。基于已知变量c_ij可建立满足约束（6）的线性不等式^[30-32]。仅考虑条件（1）~（5）,学校分区问题可建立带容量约束的区位问题模型^[33],但不能保证分区的空间连续性。考虑条件（1）~（6）使学校分区问题成为一个特殊的区划问题。
学校分区问题以学生入学距离为目标。单校划片时,使用d_ij计算学生入学总距离;多校划片时,允许择校使学生入学距离计算较为复杂。单元i学生到片区r入学距离

\begin{matrix} d_{ir} \end{matrix}

可采用以下方法估算：根据学生被分派到热门学校的机会概率,将学生到片区内最近学校距离与热门学校的距离进行加权平均。学生与学校距离可采用直线距离、曼哈顿距离或交通网络距离。在空间单元面积较大时,应选择合适的点位（如小区门口或居住地中心点）作为距离计算依据。
学校分区问题与基本空间单元选择相关。首先,学生居住地可以表达为点状或面状。点状数据可制作泰森多边形,依据多边形邻接关系获取邻接变量c_ij。其次,区位问题对于单元尺度选择较为敏感^[34],学校划片应选择合适的空间单元尺度。单元过大,难以准确计算学生和学校之间距离,入学距离目标偏离实际。单元过小,往往会增加求解的复杂度。因此,实际应用中应充分考虑道路、住宅小区、通行障碍等地理因素准备基本空间单元。

4 算法设计

4.1 算法思路

空间连续约束及多校划片需求使学校分区问题具有挑战性。相对于单校划片,多校划片存在额外的约束条件增加了问题求解难度,如片区内招生规模约束、片区规模不宜差异过大、每个片区应包含一定比例的优质学校等。鉴于区划领域没有合适的算法求解多校划片这一难题,本文采用“先学校分组,再学生分派”的策略进行学校划片,即将多校划片分解为两个子问题进行求解。前者采用数学模型将学校分组,为多校划片奠定基础;后者采用混合元启发算法进行分区。基本步骤是：
（1）学校分组：建立K-Medoids模型将学校分组,要求分组具有空间聚集性,各组学校招生规模与平均规模差异不超过限值,且组内有一定比例的优质学校。
（2）构造初始解：将学校所在空间单元作为种子区域,使用种子区域生长算法获得初始解;当难以获得可行解时,首先满足分区空间连续约束,放松招生人数约束,获得一个非可行解。
（3）混合元启发改进：设计若干邻域搜索算子进行分区调整及非可行解修复,采用多启动ILS算法进行局部搜索改进,并引入SPP模型进一步优化分区方案。与常见区划问题邻域搜索算法相比,因约束条件较紧,初始解和当前解中学校分区存在不满足分区约束的情况,本文邻域算子允许基于非可行解进行搜索,设计两个邻域解接受准则,通过迭代搜索获得可行解。针对ILS算法仍难于发现可行解的情况,SPP模型进一步从全局的角度选择最优分区组合,有可能发现可行解。
单校划片是多校划片问题的一个特例,无需进行学校分组,直接构造初始解,再进行分区方案改进。
与求解区划问题的邻域搜索算法类似,本文使用邻域搜索改进分区质量,并通过算法改进克服相关算法求解学校分区问题的局限。① 常见区划问题采用单个单元移动和两个单元交换算子进行邻域搜索改进,本文扩充两个邻域算子,扩大邻域搜索范围;② 针对学校分区中学额约束较紧而难于发现可行解的情况,设计了两个邻域解接受准则;③ 为提升邻域搜索的多样性,常见区划算法通常采用分区合并和分割、区域中心调整策略进行搜索扰动,根据学校分区特点,本文提出了3个新的扰动方法;④ 为克服邻域搜索容易陷入局部最优,本文引入SPP模型从全局的角度寻优,克服邻域搜索“短视”的局限。
为处理空间连续约束,本文将地理空间表达为网络图G ={V, E},即将空间单元U作为结点V,根据单元邻接关系（c_ij）建立网络边E。使用图论中的基本算法设计与空间连续相关的常用函数,如边界单元判断、分区空间连续判断和邻域空间构造等。

4.2 学校分组

根据学校分组约束条件和空间聚集目标,可采用空间聚类算法将学校分组。考虑到学校数量有限,本文使用K-Medoids模型求解学校分组问题。令集合

\begin{matrix} S = {s_{1}, s_{2} \dots, s_{m}} \end{matrix}

为U的一个子集,是包含m个学校的空间单元,h_i表示学校S_i是否为热校,构造如下的学校分组问题数学模型：

\begin{matrix} Minimize : \sum_{i∈S} \sum_{j∈S} d_{ij} x_{ij} \end{matrix}

（7）

\begin{matrix} Subject to : \sum_{j∈S} x_{ij} = 1, ? i \in S \end{matrix}

（8）

\begin{matrix} \sum_{j∈S} x_{ji} - m y_{i} \leq 0, ? i \in S \end{matrix}

（9）

\begin{matrix} \sum_{j∈S} y_{j} = K \end{matrix}

（10）

\begin{matrix} A y_{j} \leq \sum_{i∈S} q_{i} x_{ij} \leq B y_{j}, ? j∈S \end{matrix}

（11）

\begin{matrix} y_{j} \leq \sum_{i∈S} h_{i} x_{ij}, ? j∈S \end{matrix}

（12）

\begin{matrix} x_{ij}, y_{j} = \{0,1\}, ? i, j \in S \end{matrix}

（13）
模型中：二进制决策变量x_ij表示学校i是否属于分组j;二进制决策变量y_j表示学校j是否为分组中心点。目标（7）使学校分组尽可能空间聚集。约束条件（8）要求一所学校只能属于一个分组;条件（9）确保学校不能分配到非中心点;条件（10）是分组数量约束;条件（11）保证组内学校招生数量处于[A, B]区间,即组内学校招生规模不能过小或过大;条件（12）保证组内至少有一个优质学校。

4.3 构造初始解

采用区域生长算法构造学区划分初始解。算法步骤如下：
（1）根据学校分组结果,将学校所在单元的分区编号设置为学校分组编号,作为种子区域;
（2）根据当前分区的边界单元,构造相邻的未分区单元及目标分区列表;
（3）评估列表中每一个单元加入目标分区是否违背分区约束条件（分区内招生人数大于或等于入学人数）,以及到目标分区的距离;
（4）从列表中随机选择最优或次优的一个单元,将其加入目标分区;
（5）重复执行步骤（2）~（4）直到所有空间单元分配到特定的分区中。
该算法能够获得一个初始分区方案,分区具有空间连续性,但部分分区可能违背招生数量约束条件。后续算法将尝试找到可行解或者尽可能降低学区超额招生数量。步骤（4）采取了随机选择方式,可使本算法重复执行时获得不同的初始解,为多启动算法提供不同的初始解。

4.4 邻域搜索算子

学校初始分区通过邻域搜索算子进行改进。本文设计了4个邻域搜索算子（图1）：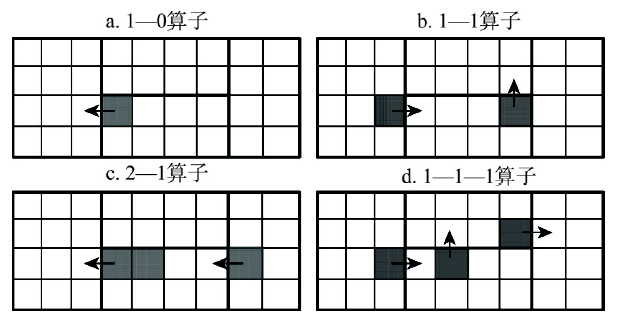

显示原图|下载原图ZIP|生成PPT
图1邻域搜索算子示意图
-->Fig. 1Examples of the neighborhood operators
-->

（1）1—0移动：将某个边界单元移动到相邻的分区中,涉及2个分区发生变化。
（2）1—1移动：某个分区移入一个相邻单元,同时移出一个边界单元,涉及2个或3个分区发生变化。
（3）2—1移动：某个分区中移入一个相邻单元,同时移出两个单元,涉及2个或3个分区发生变化。
（4）1—1—1移动：同时移动3个单元,最多涉及4个分区。
以1—0移动为例,说明邻域搜索算子的执行步骤：① 根据当前分区方案,构造边界单元列表L（不包括包含学校的单元）;② 若列表L为空,结束算子搜索;否则,从列表中随机选取一个单元u;③ 判断所选择单元u是否边界点,若不是边界点,从列表L删除单元u,转步骤（2）;④ 单元u从所在分区移出后,评估分区目标值是否得到改善。若无改善,从列表L删除单元u,转步骤（2）;⑤ 单元u从所在分区移出后,判断该分区是否保持空间连续。若分区不连续,从列表L删除单元u,转步骤（2）;⑥ 将单元u移动到目标分区,并从列表L删除单元u;⑦ 更新当前解、最优解及分区池,转步骤（2）。
算子执行中,步骤（3）~（5）依次调用边界单元判断函数、单元移动评估函数、分区空间连续判断函数和单元移动操作函数。单元移动后分区目标值是否得到改善是更新分区方案的依据。针对当前解S和算子邻域解S',计算学生入学距离D_S和D'_S、超额招生人数O_S和O'_S。使用算子寻找可行解时,若单元移动后所涉及分区的超额招生人数有降低（O'_S<O_S）或者超额招生人数保持不变但入学距离减少（O'_S=O_S且D'_S<D_S）,接受邻域解。使用算子改进分区方案时,采用入学距离改变值和超额招生人数变化值加权累加计算的方式,判断是否接受单元移动。引入目标值评估函数F(S, S')=D_S-D'_S+α(O_S-O'_S),其中,系数α与学生平均入学距离相关（如5倍的入学距离）。若F(S, S')>0,接受邻域解。该评估函数既能够缩短学生入学距离,也能够以较小的距离增加为代价减少学校招生超额数量。
邻域搜索过程中,如成功进行了单元移动,所形成的新分区将更新到分区池,该分区池将用于建立SPP模型进行方案改进;如发现更好的分区方案,算子将更新当前最优解,并将最优解加入解池,该解池用于破坏重建扰动。
其他邻域搜索算子与1—0算子类似,主要区别在于邻域空间构造方法不同、需要判断多个分区是否空间连续,以及目标评估涉及更多的分区。

4.5 破坏重建扰动

为避免迭代邻域搜索陷入局部最优,本文采用破坏重建扰动扩大搜索空间,提升邻域搜索的多样性。本文设计3种破坏方法：边界区域破坏、分区破坏和不稳定单元破坏。第一种方法是随机选择a个边界点,破坏边界点及其b阶邻域单元;第二种方法是随机选择c个分区,破坏分区内的单元;第三种方法是选择邻域算子改进过程中所属分区最不稳定的2d个单元,随机选取d个单元进行破坏。参数a、b、c、d表示破坏强度。重建方法采用与初始解构造相同的算法。
破坏重建扰动是迭代局部搜索算法提升搜索质量的有效手段。然而,破坏强度太小,难以跳出局部最优解;破坏强度过大,又容易获得低质量的非可行解,影响算法收敛性。一般地,选择破坏强度参数使被破坏的单元数量为总单元数量的5%~15%。
破坏重建所获得的分区可能出现空间不连续的状况。针对这一状况,重建算法以增加学校招生人数为代价尝试进行修复;若不能修复,仍使用当前解分区方案进行邻域搜索。

4.6 混合元启发算法

本文提出一个混合元启发算法（M-ILS-SPP）求解学校分区问题。① 基于初始解构造方法、邻域搜索算子及破坏重建扰动机制,采用ILS算法进行学校分区方案改进;② 为避免迭代搜索过程过于依赖初始解,采用多启动方法,在多次启动中,分别构造不同的初始解,增加ILS搜索的多样性;③ 鉴于邻域搜索算子有“短视”局限（仅局部改进）,算法引入SPP模型进行方案改进。其原理是：在初始解、单元移动操作和扰动操作完成后,记录所发现的分区;在搜索完成后构建SPP模型并求解,尝试从全局的角度进一步改进分区方案。算法流程如下：
算法1：混合元启发算法（M-ILS-SPP）
参数：多启动次数M、迭代循环次数N和破坏重建强度参数a, b, c, d
（1）InputData( ) //输入案例数据：空间单元、邻接关系、距离、学校分组
（2）rPool=[ ] //初始化分区池
（3）sPool=[ ] //初始化分区方案池
（4）S*=null //保存最优解
（5）For (i=0; i<M; i++)
（6） S*=S=CreateAnInitialSolution( ) //构造初始分区方案S
（7） UpdateRegionPool(S, rPool)
（8） UpdateSolutionPool(S, sPool)
（9） For ( j=0; j<N; j++)
（10） If (overload(S)>0) //缩减超额招生人数,寻找可行解
（11) S=MinimizeOverload(S, S*, rPool, sPool)
（12） S=MinimizeTotalDistance(S, S*, rPool, sPool) //缩减入学距离
（13） S=RuinRecreate(S, sPool, a,b,c,d) //破坏重建扰动
（14）model=BuildSPPModel(rPool)
（15）S*=SolvingSPPModel(model)
（16）Output(S*)
算法参数包括多启动次数M、迭代次数N和破坏重建扰动的破坏强度参数（a, b, c, d）。步骤（1）读入案例数据,如空间单元集合U、空间单元邻接关系c_ij、空间单元间距离d_ij,学校分组,并计算空间单元i与学校分组之间r的距离d_ir。定义结构数组rPool和sPool分别记录后续操作所发现的分区和当前最优解。步骤（5）~（13）完成M次ILS搜索,首先构造一个初始解,然后迭代进行邻域搜索改进和破坏重建扰动。缩减超额招生函数MinimizeOverload( )和缩减入学距离函数MinimizeTotalDistance( )均调用邻域搜索算子进行邻域搜索。函数overload( )计算分区方案的超额招生人数。
为提升分区优化性能,算法采用多种随机搜索机制：初始解构造算法中随机选择最优或次优单元进行区域生长;邻域搜索中随机选择算子执行顺序及随机构造算子邻域空间;随机选择3种破坏扰动方法,破坏的分区或单元也是随机选择的。多启动、破坏重建扰动及以上随机机制使算法的多样性得到增强,从而有效避免局部搜索陷入局部最优状态。
ILS搜索完成后,步骤（14）建立SPP模型,并求解该模型获得更优的分区组合。将分区池rPool表示为分区集合

\begin{matrix} Ω = {r_{1}, r_{2}, r_{3} \dots} \end{matrix}

,即ILS搜索所发现的所有分区。分区r_i包括区内空间单元集合U_i、区内学生入学总距离D_i和区内学校超额招生人数（W_i（

\begin{matrix} i \in Ω \end{matrix}

）。SPP模型如下：

\begin{matrix} Minimize : \sum_{i∈Ω} (bigM \times W_{i} + D_{i}) x_{i} \end{matrix}

（14）

\begin{matrix} Subject to : \sum_{i∈Ω,j∈Ui} x_{i} = 1, ? j \in U \end{matrix}

（15）

\begin{matrix} \sum_{i∈Ω} x_{i} = K \end{matrix}

（16）

\begin{matrix} x_{i} = \{0, 1\}, ? i \in Ω \end{matrix}

（17）
模型中,二进制决策变量x_i表示分区r_i是否被选中。目标函数（14）中,参数

\begin{matrix} bigM \end{matrix}

是一个与D_i相比足够大的整数,用于选择超额招生人数最少的分区方案。约束（15）保证每一个空间单元均被分配某一个分区;约束（16）为分区数量限制。

5 算法实验及性能分析

5.1 案例数据

本文选择一个县级市（GY）和一个市辖区（ZY）分别进行初级中学和小学学区划分。案例区GY包括297个行政村或社区空间单元,39个单元内设置有初级中学（图2a）,入学总人数为36824人,学校总学额为37902名,并设定10所学校为热门学校,共招生19233名学生。案例区ZY包括324个居住社区空间单元,15个单元内设置有小学（图2b）,入学总人数为3873人,学校总学额为4095名,并设定5所学校为热门学校,共招生2600名学生。是否热门学校根据学校资源、规模、班额等特征判断^[35]。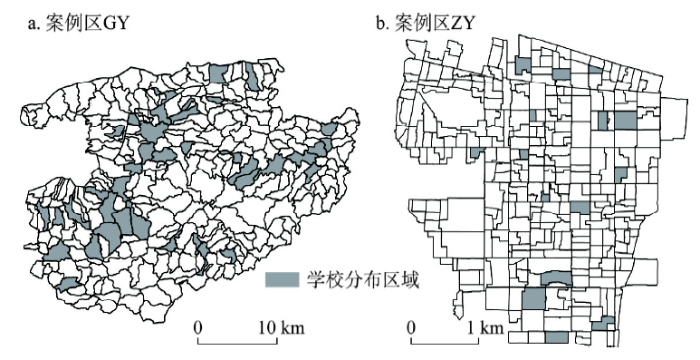

显示原图|下载原图ZIP|生成PPT
图2案例区GY和ZY示意图
-->Fig. 2The study areas: GY and ZY
-->

5.2 实验结果及分析

实验计算环境为：HP桌面计算机,配置AMD Athlon II X4 645 CPU和4 GB内存,Windows XP操作系统,安装Python 2.7、ArcGIS 10.0和IBM CPLEX 12.6优化器。在ArcGIS中准备案例数据,包括空间单元及其属性p_i和q_i、单元邻接关系c_ij和单元与学校距离d_ij。按单元内主要居民区中心点与学校点坐标计算直线距离。本文算法使用Python语言编程实现,K-Medoids模型和SPP模型使用Python语言建模,调用CPLEX优化器求解。
针对两个案例区GY和ZY,分别完成单校划片和多校划片实验。案例区GY多校划片分别模拟4~8个分区,案例区ZY分别模拟3~5个分区。学校分组规模要求：给个组内招生人数大于平均规模的60%且小于平均规模的140%,且至少有一个热门学校。算法参数选择为：多启动次数为10,ILS迭代次数为10（多校划片）或20（单校划片）,目标函数系数α为5;破坏扰动强度参数a、b、c和d设置使被破坏的单元数约为全部单元总数的10%,即2、3、1和10（多校划片）或2、3、3和10（单校划片）。以案例区GY划分5个学区为例,学校分组、初始解和最终分区如图3所示。

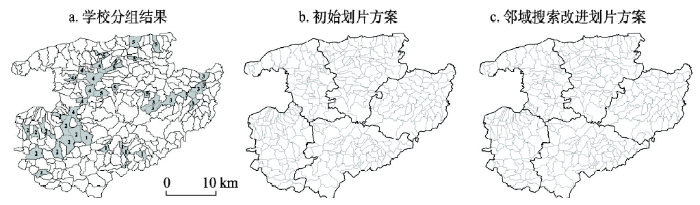显示原图|下载原图ZIP|生成PPT
图3学校划片过程示意图
-->Fig. 3Examples of school groups, initial districts and final districts
-->

本文还通过数学模型计算了分区目标值下界,用于验证本文算法的性能。即在学校分组的基础上,依据约束条件（1）~（5）并以最短入学距离为目标,构建整型规划模型,再使用CPLEX求解。若精确求解获得的最优分区方案能够满足分区连续性要求,则该方案的目标值即为学区划分的最优目标值。
针对每个案例的分区方案,混合元启发算法运行10次,结果统计如表1所示。表中,“数学模型”栏是整型规划模型的求解结果,入学距离均是无空间连续约束的最优目标值。当划片数量为4和5时,模型能够获得空间连续的分区方案。“M-ILS算法”栏中分别列出了算法10次运行获得10个分区方案的学生入学距离平均值、最好入学距离以及入学距离的标准差百分比。“M-ILS-SPP算法”栏是SPP模型改进结果。可以看出：① 算法收敛性良好,M-ILS算法求解多校划片目标值标准差为0.00%~0.23%,求解单校划片目标值标准差为0.86%和1.10%;而增加SPP模型后,算法收敛性有所提高,特别是针对单校划片问题。② 对于最优解已知的两个分区方案,多启动ILS算法及SPP模型均获得了最优解;对于多校划片方案,SPP模型能略微改进分区方案,目标改进0~0.17%。③ 针对单校划片,多启动ILS虽然能够发现入学距离较短的分区方案,但不能保证入学人数不高于招生人数这一约束条件,而SPP模型能够发现满足约束条件的分区方案。④ 案例区ZY中,空间连续约束的入学距离目标值非常接近无空间连续约束的最优目标值。综上,本文提出的多启动ILS与SPP模型组合算法具有良好的寻优能力和收敛性。
Tab. 1
表1
表1学校划片结果统计
Tab. 1Solution results on school districting instances

案例区	划片数量	数学模型		多启动ILS(M-ILS)算法			多启动ILS-SPP(M-ILS-SPP)算法
案例区	划片数量	入学距离(km)	分区连续	入学距离均值(km)	最好入学距离(km)	标准差(%)	入学距离均值(km)	最好入学距离(km)	标准差(%)	SPP改进(%)
GY	4	107648.06	是	107648.06	107648.06	0.00	107648.06	107648.06	0.00	0.00
GY	5	99098.15	是	99098.15	99098.15	0.00	99098.15	99098.15	0.00	0.00
GY	6	97819.38	否	99670.59	99570.09	0.12	99546.57	99536.49	0.02	0.12
GY	7	97359.92	否	99212.62	99069.17	0.23	99034.18	99025.61	0.02	0.18
GY	8	91286.51	否	94368.16	94260.15	0.10	94210.98	94192.28	0.03	0.17
GY	39	81321.49	否	84626.82*	83713.52*	1.10	84872.52	84500.09	0.57	-
ZY	3	2861.76	否	2863.86	2862.01	0.05	2863.86	2862.01	0.05	0.00
ZY	4	2654.27	否	2661.99	2659.30	0.07	2661.94	2659.30	0.07	0.00
ZY	5	2604.72	否	2609.60	2606.35	0.06	2609.47	2606.35	0.06	0.00
ZY	15	2610.82	否	2676.91	2650.10	0.86	2666.96	2644.65	0.67	0.37

注：*M-ILS算法获得分区方案均不满足约束条件,平均超额招生124.4人。

新窗口打开
实验也发现：① 邻域搜索算子1—1—1计算复杂度较高,但对于单校划片或多校划片数量较多时,能有效降低学校超额招生数量;② 破坏重建扰动能有效避免邻域搜索陷入局部最优的情况,且随机选择破坏方法优于仅采用一种破坏方法;③ 随机调用邻域搜索算子优于固定顺序。
算法计算复杂度与空间单元数量、分区数量和算法参数设置相关。算法及主要模块计算时间统计如表2所示。可以看出：① 算法所需计算时间主要用于邻域搜索,其次是破坏重建扰动和初始解构造;② SPP过程约占总时间的2.8%~9.7%,主要用于模型求解。本文算法采用Python语言设计,若改写为C/C++或其他语言,计算效率有望较大幅度地提高。考虑到学校划片是若干年进行一次的规划,本文算法计算时间可以接受。
Tab. 2
表2
表2算法及主要模块计算时间(s)统计
Tab. 2Computation times (s) of the algorithm and major algorithm components

案例区	分区数量	总时间	构造初始解	邻域搜索	破坏重建扰动	空间连续检测	分区池更新	SPP模型求解
GY	4	13.13	3.70	5.88	3.15	2.58	0.17	0.22
GY	5	13.77	4.03	6.55	2.79	2.79	0.17	0.30
GY	6	22.13	4.27	13.30	3.94	5.21	0.31	0.52
GY	7	25.97	4.42	17.47	3.49	4.37	0.24	0.48
GY	8	30.89	4.52	20.21	4.93	5.63	0.41	1.11
GY	39	278.80	6.47	227.46	37.58	5.90	1.89	6.94
ZY	3	35.44	2.28	22.16	9.20	15.77	0.58	1.67
ZY	4	36.00	2.31	24.69	6.70	13.89	0.71	2.19
ZY	5	37.38	2.37	26.39	5.58	10.49	0.75	2.88
ZY	15	195.51	3.06	148.32	33.01	29.28	1.34	10.53

注：表中初始解构造、邻域搜索和破坏重建扰动时间包含所需空间连续检测和分区池更新时间。

新窗口打开

6 结论与讨论

6.1 结论

针对义务教育学校多校划片这一难题,本文提出了“先学校分组,再学生分派”的划片策略,并构造了一个K-Medoids模型用于学校分组,设计了一个混合元启发算法确定学校分区。算法包括初始解构造、邻域搜索算子、破坏重建扰动、SPP建模与求解等基本模块,在多启动迭代局部搜索算法框架中进行问题求解。通过多启动、随机邻域搜索、破坏重建扰动等机制实现提升算法的多样性,并引入SPP模型提升算法的全局寻优能力和收敛性。模拟案例实验表明本文算法适用于求解单校划片和多校划片问题,优化性能优异且收敛性良好。
与现有区划问题算法相比,本文算法具有多个优势：① 设计的2—1、1—1—1邻域搜索算子扩大了邻域搜索空间;② 引入的SPP模型能充分利用历史搜索信息,从全局的角度改进分区质量,弥补局部搜索算法存在“短视”的局限;③ 算法允许初始解和当前解是非可行解,邻域搜索算子既能用于降低分区目标值,也可以较少的目标值增加为代价降低违背约束条件的程度,从而使算法适用于求解分区约束较紧案例。
区划问题类型繁多,从分区目标的角度,有3类区划问题：① 同质性区划,即分区内差异最小化和分区间差异最大化,如自然地理和农业区划;② 功能性区划,即分区内交互作用最大化,而区间交互作用最小化,如经济功能区和城市功能区划分;③ 均衡性区划,如分区人口数量或其他属性均等化的选区、警察巡逻区和销售区划分,供应与需求均衡的学区和医疗服务区划分。本文设计的邻域搜索算子、ILS算法及SPP建模方法在空间连续约束区划问题中具有应用潜力;学校分区问题属于第3类均衡性区划,本文算法作简单修改可用于求解此类问题。

6.2 讨论

案例研究也发现,因学生与学校在空间分布上存在不平衡性,导致一些学校招生片区形状不够紧凑,有一定数量的学生未分派到最近的学校。学校区位问题是义务教育管理中的战略性问题,而学校分区问题受限于学校空间布局。良好的学校布局和资源配置,能够保证学生就近入学,也有利于义务教育公平。因此,在义务教育管理实践中,有必要首先通过区位模型对学校布局进行战略规划,以此为基础进行学区划分。
本文算法在应用中,应注意一些实际问题：① 采用居住社区或自然村落作为基本空间单元,单元不宜过大或过小;② 依据空间单元人口统计、出生率和其他社会经济属性预测适龄学生数量,或者通过调查获得入学学生人数;③ 建立道路网络,并选择合适的点位计算学生居住地与学校之间的距离;④ 针对民办学校较多的区域,应掌握民办学校生源的分布规律,调整空间单元的学生数量。
进一步的研究工作包括：改进邻域构造方法,降低邻域搜索算子的计算复杂度,进而降低算法计算时间;加入在线学习机制实现算法参数自适应选择;扩充本文算法求解类似空间连续约束区划问题,如医疗服务区、选区、销售区、警察巡逻区等分区问题。
The authors have declared that no competing interests exist.