HTML
--> --> -->While SC and frontogenesis theories are commonly applied in diagnosing the structure of synoptic- and sub-synoptic-scale fronts, it is essentially within the scope of equilibrium dynamics. At the poleward edge of the summer monsoon system, the interactions between monsoon circulation and westerly disturbances lead to the formation and maintenance of a quasi-stationary front, called the “monsoon front”. Different from typical synoptic-scale fronts, the monsoon front stays in a certain latitudinal zone for a relatively long time. For example, from late May to mid-August, the monsoon front and the associated rain belt periodically stay in the 15°?20°N, 30°N and 40°N zones of eastern China for about 20?30 days (Wang and LinHo, 2002; Ding and Chan, 2005; Ding et al., 2007; Xue et al., 2015). At the same time, the corresponding high-level jet, marine subtropical high, and other members of the monsoon system will synchronously move northwards and stay there (Chen, 2002). A related question is whether SC will appear near this periodical quasi-stationary monsoon front, just as it does near the synoptic-scale frontal zone. Evidence of the existence of monsoon-front SC has been found in some previous studies. Through a series of numerical experiments, He et al. (1995) found an SC at the entrance of the western Pacific subtropical high-level jet above the mei-yu frontal zone. Liu et al. (2003), based on observational analysis, identified one clockwise and one counterclockwise SC co-existing in the north and south of the mei-yu front, respectively. Ding et al. (2007) confirmed the climatic existence of these two SCs. The strong updraft associated with the mei-yu rain belt diverges into two branches aloft. Of these branches, one goes to the south and descends near the equator, which constitutes an indirect circulation, e.g., the anti-Hadley Cell, while the other flows in the opposite direction and descends in the north of the mei-yu front, which constitutes a direct cell. However, there is little in the literature on the following two issues: Firstly, what is the thermodynamic mechanism responsible for the formation and maintenance of SCs in the mei-yu front region? Secondly, what is the effect of the SC on the structural evolution of the upper-level jet?front system at the northern edge of the East Asian summer monsoon (EASM) and associated precipitation processes? Yuan et al. (2000) conducted a set of numerical experiments on the maintenance of two local meridional SCs in the EASM and Indian monsoon respectively, by solving a linear elliptic diagnostic equation with the gradient wind balance assumption. The results of that study indicated a local anti-Hadley cell and a local Hadley cell in meridional panels that were highly consistent with the observational analysis and provided a systematic assessment of the relative contribution of each of the forcing terms in the linear diagnostic equation. Building upon previous studies, in the present paper, the SCs near the mei-yu front are studied by solving a primitive S?E equation with the thermal-wind balance assumption. Each of the forcing terms and corresponding sub-forced circulations is quantitatively estimated, and the relationship between SCs and the frontogenesis process near the mei-yu front is analyzed in detail.
The paper is organized as follows: Section 2 describes the data and the S?E equation. Descriptions of the domain, period and statistical characteristics of the SC are given in section 3. In section 4, the S?E diagnostic equation is solved to obtain its numerical solution, and the relative contribution of every forcing term in forming the SC is analyzed. In addition, the enhancement effect of the SC on the frontogenesis of the monsoon front is investigated through the diagnostic analysis of a typical development case of the SC and the mei-yu front. Finally, a discussion and conclusions follow in section 5.
2.1. Data
This study uses the 6-h-resolution National Centers for Environmental Prediction (NCEP) reanalysis dataset (Kalnay et al., 1996) to diagnose and analyze the flow and circulation. The horizontal resolution of the NCEP reanalysis dataset is 1° × 1°, with 26 layers in the vertical direction.This study also uses the rain belt as the indicator of the monsoon front. The rainfall data are from the Tropical Rainfall Measuring Mission (TRMM) multi-satellite precipitation analysis product-3B42 dataset (Huffman et al., 2007), which has a temporal resolution of 3 h and a spatial resolution of 0.25° × 0.25°, covering a continuous 50°S?50°N area. The TRMM-3B42 dataset merges TRMM precipitation radar observations with microwave rainfall estimations from polar-orbiting satellites and infrared rainfall estimations from geostationary satellites. The data from June to August during the years 2001?13 were selected. In order to further examine the overall convection distribution near and in the warm region of the mei-yu front, the hourly infrared image observations from multiple geostationary meteorological satellites with a grid spacing of 0.05° were used. The data were obtained from the Weather Satellite Image Archive of Kochi University, Japan (
2
2.2. S?E equation
32.2.1. Geostrophic momentum approximation form
In the study of frontogenesis, by adopting geostrophic momentum approximation, Sawyer (1956) and Eliassen (1962) linked the horizontal momentum equation to the thermodynamic equation through the thermo-wind balance (Lagouvardos et al., 1992) to establish the classical two-dimensional SC diagnostic equation—the S?E equation. The adiabatic inviscid form for the S?E equation is:Equation (1) is an equation of SC stream function (
where vag is the ageostrophic component of the normal-to-front wind speed and ω is vertical velocity. The prerequisite for the establishment of Eq. (2) is that the variation of the ageostrophic component (uag) of the along-front wind speed is negligible
3
2.2.2. Primitive version of the S?E equation
Taking ageostrophic deformation, diabatic heating and friction forcing into consideration, Keyser et al. (1985a, b) extended Eq. (1) to the form of a primitive equation. The primitive version of the S?E equation is applicable even when the ageostrophic motion component (uag) in the x direction is relatively large (Keyser et al., 1985b). It appears as follows:where
The
In Eq. (3), the uag is introduced when calculating baroclinicity and inertial stability. However, the postulated condition of
Forcing terms of ageostrophic motion are introduced into the primitive version of the S?E equation:
On the rhs of Eq. (5), based on the non-divergence assumption of uag in the x direction, the first term is omitted. Since the time interval used in this study is 6 h, the time span for averaging is 13 years and the horizontal air motion along the front assumes the maintenance of quasi-geostrophic balance, the time derivative of
According to Xu (1989a), if the geostrophic potential vorticity (or moist potential vorticity) is positive, i.e.,
the basic quasi-two-dimensional geostrophic flow is stable to symmetric perturbations, meaning Eq. (3) would be an elliptic equation and can be numerically resolved.
3.1. Domain and period
The rectangular region of 117°?124°E and 30°?55°N was selected as the domain of interest (DoI). In the DoI (Zone A in Fig. 1a), the axis of the jet stream of the high-level (200 hPa) zonal geostrophic component of wind is located at about 38°N. Below, there are a pair of vertical downward and upward air motions. The upward motion center is found in the Yangtze?Huaihe River basin of China and extends eastwards to southwestern Japan, corresponding to the main rainfall areas of the mei-yu in China and baiu in Japan (Ninomiya, 2004).
Figure1. (a) The domain of interest denoted by “A”, overlaid vertical velocity at 400 hPa (Pa s?1, solid lines denote downdraft, dotted lines denote updraft at 0.02 intervals), wind vectors at 200 hPa (blue arrows), and geopotential height at 500 hPa (red solid lines at 40 gpm intervals) over the period of 28 June to 12 July during 2001 to 2013. (b) Time?latitude cross section of TRMM-estimated average maximum daily precipitation (mm d?1) over the longitudes 117°?124°E during June?July?August from 2001 to 2013.The DoI is located to the west of the western North Pacific subtropical high, which has a close relationship with the EASM. The period from 28 June to 12 July (Period A in Fig. 1b) is consistent with the mei-yu season of the Yangtze?Huaihe River basin, which is the second phase of the EASM rain belt that moves stepwise northwards during summertime. This period shows relatively stationary precipitation and circulation characteristics in a climatological sense (Wang and LinHo, 2002; Ding and Chan, 2005), and is thus the focus in this study.
It is also shown that the value of averaged q in the DoI during Period of A in Fig. 1a is between 0.0068 and 4.8316 (Fig. 2a); in other words, the elliptic condition of the S?E equation in the midlatitude troposphere is satisfied on average. In fact, however, the ellipticity cannot always be ensured in every grid point in each meridional plane, even if the basic geostrophic flow in most areas of the plane is stable. Figure 2b shows the statistical distribution of q in the DoI between 975 hPa and 250 hPa for the cases in which the S?E equation were well resolved numerically. Physically, it means in these cases the quasi-two-dimensional geostrophic flow is stable to inviscid symmetric perturbations (Xu and Clark, 1985; Xu, 1989a). The minimum value of q in each latitude is below zero, which means that at some specific times in some grid points, the elliptic condition [Eq. (6)] is not satisfied. There are 29 076 of 2 918 552 samples of q no more than zero, accounting for about 1% of the total grid number in the resolution-convergence cases. Following Stoelinga (2013), in a single sample plane, if the criterion of Eq. (6) at a grid point is violated, we then adjust the values of the baroclinic parameter N*2, S*2 at this point to make q > 0 and no more than 10?4 hPa?1 s?1 to ensure the ellipticity. Compared to Fig. 2b, Fig. 2c presents more negative values of q for the cases in which the S?E equation are not well resolved. These negative values are likely to appear in the lower latitudes near the mei-yu front. The statistics show there are 46 553 of 1 624 168 samples of q that are less than or equal to zero, accounting for about 2.9% of the total grid number in the resolution-divergence cases—more than that in Fig. 2b, by 2.9 times in proportion. Therefore, it can be deduced that, in the stable large-scale geostrophic flow in the meridional planes, the S?E equation is easier to apply.
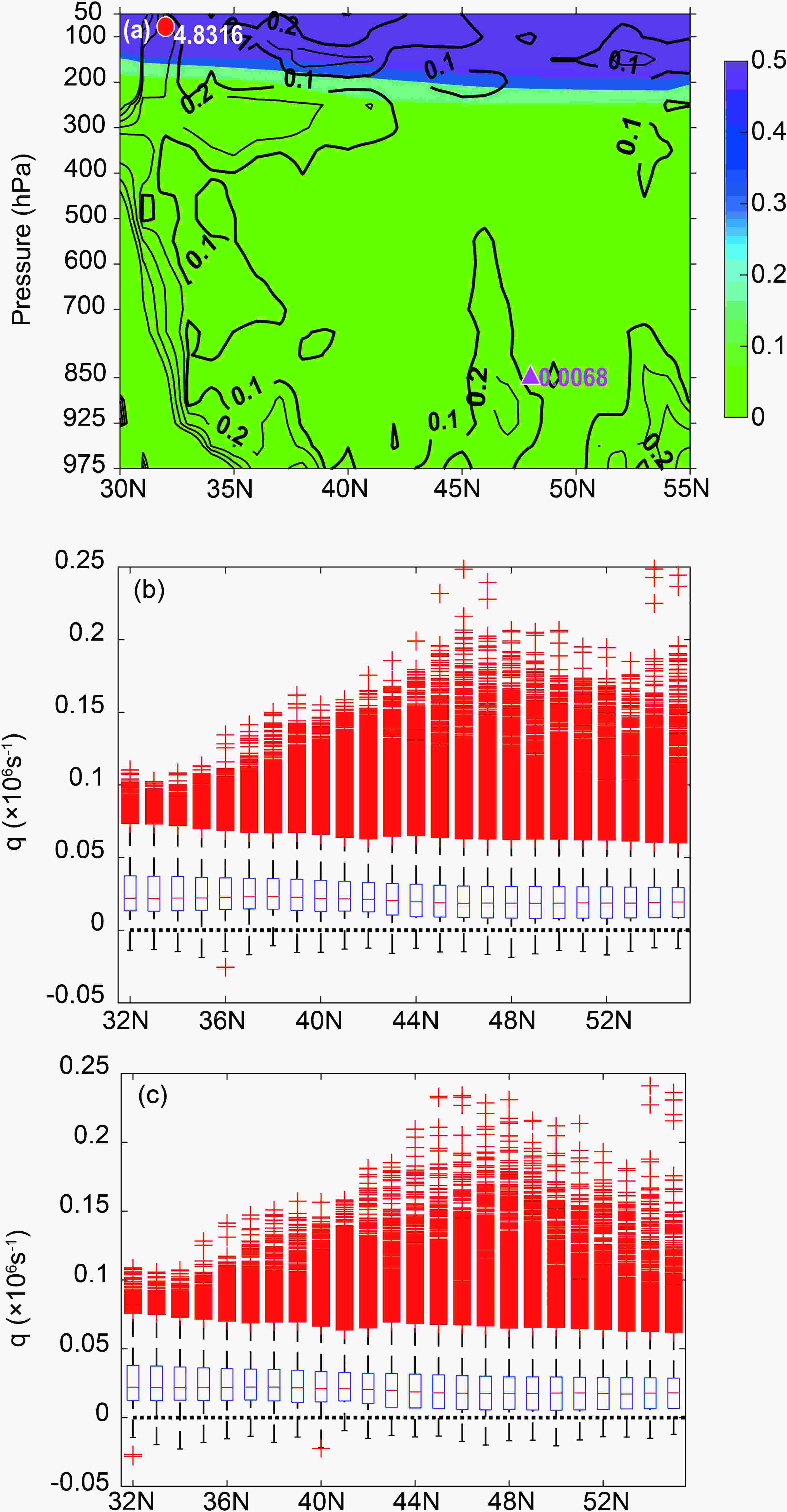Figure2. (a) Values of averaged geostrophic potential vorticity 
2
3.2. Vertical structure of SC
Figure 3 shows the vertical cross section of the SCs in the DoI plotted directly from NCEP reanalysis data. The southerly ageostrophic airflow meets with the midlatitude northerly ageostrophic airflow at around 38°N. An obvious zonal geostrophic airstream center is at an altitude of 200 hPa, with a maximum along-front geostrophic wind speed of more than 28 m s?1. The location of the zonal geostrophic airstream center is consistent with the westerly high-level jet axis (not shown). On the south side of it is the upward branch of ageostrophic airflow with a maximum rising speed of more than ?0.11 Pa s?1, located near 400 hPa. Below and to the north of the high-level westerly airstream center is the downward branch with an intensity of 0.04 Pa s?1, the center of which is located near 700 hPa. Asymmetrical to each other, the downward and upward branches jointly constitute one vertical SC. There is also a downward branch near 30°N, located below 700 hPa with an intensity of around 0.03 Pa s?1. This downward branch, together with the upward branch to the north of it, may constitute a counterclockwise vertical circulation cell, i.e., a thermally indirect circulation cell in the lower troposphere near the monsoon front.
Figure3. Cross section of averaged zonal geostrophic wind velocity (cyan lines at intervals of 4 m s?1), upward motion velocity (red lines at intervals of 0.02 Pa s?1), and downward motion velocity (shading) over the period from 28 June to 12 July during 2001 to 2013. The direction of secondary circulation, i.e., scaled (vag, ω), is shown with blue arrows. The maximum rising (AMax) and sinking speed (DMax) are denoted in the top of the figure.4.1. S?E equation–based diagnosis of mei-yu SC
In this section, along every longitude with a 1° interval over 117°?124°E, at each time in the selected period mentioned above, the atmospheric temperature, geopotential height, and winds were taken to set up a y?p plane for diagnosis. The latitudinal range of 30°?55°N was selected so that both the airflow in the monsoon front area and the balanced airflow of midlatitude westerlies could be considered simultaneously. Vertically, a total of 24 layers were taken between 975 hPa and 20 hPa. Since the values of vertical velocity of the layers at and above 70 hPa are 0, these layers were ignored when calculating the vertical velocity. The vag and ω components in Fig. 3 were used to check the non-divergence assumption in the y?p plane. From the mass continuity equation
Substituting the vag, ω and V into the lhs of Eq. (7), and then considering time-averaging, the values of the lhs of Eq. (7) in the free atmosphere of the midlatitudes are mostly below 10?6 s?1 (Fig. 2a)—significantly less than the values near the monsoon front and in the planetary boundary layer (PBL). Therefore, the assumption [Eq. (7)] in this study is reasonable. This assumption is also found in the algorithm provided by the post-processing software of the WRF model (Stoelinga, 2013). Next, we take the Ekman pumping effect as the lower boundary condition and substitute it into the following equation:
where ZPBL is the thickness of the PBL, assumed to be 1000 m,
In this study, the diagnoses were conducted in each meridional panel along the latitudes with a 1° interval over a limited area, which is indicated by rectangle “A” in Fig. 1a, during the period 28 June to 12 July in 2001?13. Hence, a total of 6240 sample planes were obtained and, based on Fig. 2, the q in every grid point in each sample should be further checked. Once the q in each grid point of a sample plane is positive, Eq. (3) is resolved numerically to obtain the corresponding ψ, ω and vag in the plane. In this study, the numerical solution method was “successive over-relaxation”, with an acceleration factor of 1.63 and an iteration error threshold of 1.0. It is worth noting that not every diagnostic equation can be resolved correctly—about 36% of the iteration processes in resolving Eq. (3) are divergent and fail to obtain the resolutions. The numbers of convergence times when taking each term as an only forcing term on the rhs of Eq. (3) in this study are listed in Table 1. These numbers range from 458 to 529, which is about 64% of the total 6240 samples. Table 1 also indicates that, regardless of any kind of forcing, the proportion of convergence samples increases from west to east, which implies that the air flows in the east part of the DoI are more stable. After these manipulations, the composite fields of resolved ψ, ω and vag can be used to describe the overall characteristics of the resolved SCs and demonstrate the relative contribution to the formation and maintenance of SCs by the forcing terms listed in Eq. (3). The results are presented in following sections.
| Longitude | Forcing | ||||||
| $ {Q}_{\rm{con}} $ | $ {Q}_{\rm{she}} $ | $ {Q}_{\rm{g}} $ | $ {Q}_{\rm{ag}} $ | $ {Q}_{\rm{d}} $ | $ {Q}_{\rm{tot}} $ | Average | |
| 117°E | 458 | 477 | 482 | 480 | 477 | 481 | 61% |
| 118°E | 473 | 483 | 491 | 483 | 494 | 496 | 62% |
| 119°E | 474 | 488 | 495 | 487 | 497 | 491 | 63% |
| 120°E | 482 | 492 | 503 | 499 | 510 | 489 | 64% |
| 121°E | 504 | 506 | 496 | 520 | 503 | 497 | 65% |
| 122°E | 503 | 516 | 528 | 529 | 518 | 521 | 67% |
| 123°E | 518 | 527 | 506 | 512 | 524 | 501 | 66% |
| 124°E | 510 | 526 | 508 | 517 | 503 | 507 | 66% |
| Average | 63% | 64% | 64% | 65% | 65% | 64% | 64% |
| Note: $ {Q}_{\rm{con}} $ denotes geostrophic confluence forcing, $ {Q}_{\rm{she}} $ denotes geostrophic shear forcing, and $ {Q}_{\rm{tot}}={Q}_{\rm{g}}+{Q}_{\rm{ag}}+{Q}_{\rm{d}} $. | |||||||
Table1. Numbers and average percentages of convergence cases in the iterations of numerically resolving Eq. (3) along each longitude over (117°?124°E, 30°?55°N) for the period 28 June to 12 July during 2001 to 2013.
3
4.1.1. Large-scale geostrophic deformation forcing
The horizontal confluence and shear of the large-scale geostrophic wind field were the earliest-found forcing terms of the S?E equation (Sawyer, 1956; Eliassen, 1962). As shown in Fig. 4a, the composite horizontal confluence forcing term,
Figure4. (a, d, g) Large-scale dynamical forcing terms (lines at 4 × 10?7 m s?2 hPa?1 intervals) including (a) averaged geostrophic confluence forcing, (d) averaged geostrophic shear forcing, as well as (g) the sum of (a) and (d). (b, e, h) The averaged ageostrophic flow vectors of (vag, ω) (black arrows) plotted directly from the convergence data samples, and (b), (e) and (h) correspond to (a), (d) and (g), respectively. The maximum rising (AM) and sinking speeds (DM) are also denoted in the top of each sub-figure. (c, f, i) The averaged stream function 
Though the forcing effect of the large-scale geostrophic deformation determines the basic structure and position of SC, its observed rising velocity cannot be fully represented yet. When the S?E equation is used in observational diagnosis, such a phenomenon usually occurs: As early as in the 1950s, Sawyer (1956) found in his study of frontogenesis that the intensity of the upward branch of the SC diagnosed was smaller than the observed value; and the maximum sinking speed diagnosed in the jet?front system by Shapiro (1981) using the S?E equation was only about 50% of the observation. Bui et al. (2009) and Lagouvardos et al. (1992) drew similar conclusions. This may imply that, during the formation of the SC, there are other forcing terms at work. These forcing terms may include not only ageostrophic dynamical forcing, latent heat forcing and boundary layer friction forcing, which explicitly appear on the RHS of Eq. (3), but also other thermodynamic effects hidden in the environment.
3
4.1.2. Ageostrophic dynamical forcing
It is the inherent requirement of the primitive-equation form of the S?E equation, i.e., Eq. (3), to introduce the ageostrophic dynamical forcing term Qag, which enables the forcing terms on the rhs of the S?E equation to contain ageostrophic forcing. Thus, some effects of the response circulation are present on the lhs of the equation (Keyser et al., 1985a).Based on Eq. (3), we can obtain the streamfunction response and the vertical velocity component corresponding to ageostrophic forcing. As seen in Fig. 5, at the higher level of the troposphere on the north side of 45°N, the ageostrophic dynamical forcing term forces out a very weak direct circulation whose intensity is obviously less than the original flow in Fig. 5b; near 30°N there is a dominant upward motion that is also determined by the lateral boundary condition.
Figure5. As in Fig. 4 except for the ageostrophic forcing at intervals of 4 × 10?7 m s?2 hPa?1 in (a) and response stream function at intervals of 50 m hPa s?1 in (c).3
4.1.3. Diabatic heating forcing
Though early diagnostic studies on frontal zone SC were carried out based on an adiabatic assumption (Namias and Clapp, 1949; Sawyer, 1956; Eliassen, 1962; Hoskins and Bretherton, 1972; Shapiro, 1981; Keyser et al., 1985a, b), water phase change associated with the SC near the frontal zone will alter the thermal structure of the atmosphere and lead to adjustment in mass, which in turn causes changes in horizontal and vertical air motion. Prior studies (Thorpe and Nash, 1984; Huang and Emanuel, 1991) indicated that condensation may intensify upward motion in the frontal zone, and evaporation enhances downward motion. However, since only a small part of condensed water vapor can evaporate in the downdraft, it is possible that including the evaporation effects on the latent heating processes might lead to an overestimation of the magnitude of downdrafts. Xu (1989a) linked the latent heating only to the upward motion in his formulations (2.4)?(2.5), and following these expressions, in this study we assumewhere the expression of
Substituting the vertical velocity
Figure6. As in Fig. 5 except for the diabatic heating forcing at intervals of 0.4 × 10?7 m s?2 hPa?1 in (a) and response stream function at intervals of 50 m hPa s?1 in (c).According to the above analyses, between the mei-yu front zone and midlatitude high-level jet, on average, there exists an SC that rises in the warm area and sinks in the cold area, and its position is dictated by the large-scale geostrophic deformation. In addition, the SC intensity and structure are adjusted by both the diabatic heating effects of the mei-yu front zone precipitation and the Ekman pumping effect of the boundary layer.
2
4.2. The mei-yu SC’s influence on frontogenesis
SC is a response circulation forced out by the basic dynamical and thermal fields near the frontal zone, but it also reacts on these basic fields. According to Keyser and Pecnick (1985a), in the derivation procedure of the S?E equation, the momentum equation and heat flux conservation equation are transformed together into the frontogenesis diagnostic equation. Using the streamfunction components as in Figs. 4c, f and i to calculate the frontogenetical function, we can obtain the results shown in Fig. 7. Along the high-level jet axis that tilts northwards with altitude appears an obvious frontogenesis area, which increases in intensity and tilts northwards with altitude. Most of the frontogenesis area is within the substantial updraft area, thus being conducive to the occurrence of monsoon convection and precipitation. South of 32°N and north of 38°N are frontolysis areas; the area between 36°N and 38°N is a downdraft area. Judging from the structure of the dynamic frontogenesis region, the main area that is conducive to convective precipitation is restricted to a narrow zone between 32°N and 36°N.
Figure7. Geostrophic dynamical forcing frontogenesis function (lines at intervals of 5 × 10?6 m?1 hPa?1 s?2) and areas with Richardson number < 0.25 (shading) over 117°?124°E averaged during the period from 28 June to 12 July. The cyan dotted line denotes the axis of the jet and the green dotted line indicates the northern edge of upward motion of the mei-yu area.To further verify the effect of the forced SC on the evolution of jet?front systems and the occurrence of monsoon convection, the frontogenesis characteristics of 34 typical deep convection events that occurred over the DoI from 28 June to 12 July during 2004 to 2013 were analyzed. Based on the 0.05° × 0.05° gridded multi-satellite datasets from Kochi University, Japan, the threshold of deep convection was set to be the maximum gridded brightness temperature of less than ?52 °C . The results indicated that every single deep convection case experienced a horizontal potential temperature contraction process (i.e., frontogenesis) with a tilting of the high-level front region, and most of them (24 of 34 cases) had substantial cold advection in the cyclonic shear region for time spans of about 12?30 h. All of these frontal characteristic parameters are listed in Table 2.
| No. | Date and time (yyyymmddhh) | Deepconvection frequency | Max. $\dfrac{ {{\partial} } {{\theta } } }{ {{\partial} } {{x} } }$ (10?12 K m?1) | Ave. $\dfrac{ {{\partial} } {{\theta } } }{ {{\partial} } {{x} } }$ (10?12 K m?1) | Max. $\dfrac{ {{\partial} } {{\theta } } }{ {{\partial} } {{y} } }$ (10?12 K m?1) |
| 1 | 2004070606 | 0.28 | 7.7 | 0.9 | ?28.8 |
| 2 | 2004070712 | 0.34 | 8.3 | 0.6 | ?18.7 |
| 3 | 2004071012 | 0.29 | 11.2 | ?0.3 | ?30.3 |
| 4 | 2005062906 | 0.29 | 24.1 | 2 | ?33.4 |
| 5 | 2005063012 | 0.33 | 16.1 | 0.6 | ?33.8 |
| 6 | 2005070212 | 0.31 | 7.7 | 0.4 | ?41.2 |
| 7 | 2005070618 | 0.57 | 3.9 | ?1.5 | ?35.7 |
| 8 | 2005070800 | 0.36 | 5.5 | 0 | ?37.5 |
| 9 | 2006063018 | 0.42 | 5.3 | 0 | ?32.7 |
| 10 | 2006070312 | 0.52 | 7 | 0.2 | ?27 |
| 11 | 2006070506 | 0.33 | 13.5 | ?0.1 | ?28.2 |
| 12 | 2006071106 | 0.28 | 10.1 | 0.7 | ?47.7 |
| 13 | 2007070512 | 0.27 | 3.1 | ?0.3 | ?48.6 |
| 14 | 2007070706 | 0.59 | 6 | ?0.2 | ?40.9 |
| 15 | 2007070818 | 0.4 | 4.5 | ?0.3 | ?48.7 |
| 16 | 2008070406 | 0.39 | 15.3 | 0.2 | ?18.5 |
| 17 | 2008071106 | 0.39 | 13.2 | 0 | ?24.9 |
| 18 | 2009062812 | 0.31 | 16.7 | 1.1 | ?43.7 |
| 19 | 2009070700 | 0.27 | 9.8 | 0.4 | ?30.1 |
| 20 | 2009071206 | 0.3 | 8.8 | 0.3 | ?38.3 |
| 21 | 2010070212 | 0.45 | 2.3 | 0.1 | ?25.6 |
| 22 | 2011070518 | 0.32 | 14.6 | 0.4 | ?41.3 |
| 23 | 2011071218 | 0.31 | 4.7 | ?0.1 | ?34.4 |
| 24 | 2012062912 | 0.33 | 18.4 | 0.9 | ?50.4 |
| 25 | 2012070212 | 0.47 | 10.3 | ?0.5 | ?39 |
| 26 | 2012070412 | 0.39 | 8.6 | ?0.1 | ?41.4 |
| 27 | 2012070706 | 0.36 | 7.1 | 0.1 | ?23 |
| 28 | 2012070918 | 0.59 | 9.7 | 0.5 | ?51.7 |
| 29 | 2012071012 | 0.46 | 13.5 | 0.5 | ?51.7 |
| 30 | 2012071218 | 0.38 | 8.6 | 0.1 | ?33.5 |
| 31 | 2013062812 | 0.49 | 12.9 | ?0.1 | ?39.2 |
| 32 | 2013070118 | 0.64 | 11.3 | 0.9 | ?40.5 |
| 33 | 2013070412 | 0.28 | 8.8 | 0 | ?56.8 |
| 34 | 2013070912 | 0.39 | 10.8 | 0.5 | ?35.3 |
| Average | 0.38 | 10.0 | 0.2 | ?36.8 |
Table2. Horizontal gradients of potential temperature in the upper-level frontal region and the corresponding deep convection frequencies in the warm region of the front for the period of 28 June to 12 July during 2004 to 2013.
The above results may also indicate that the process of the mei-yu zone precipitation is probably triggered in the upper or lower layer, and that the precipitation system, by coupling, is capable of developing into a deep precipitation system throughout the entire troposphere.
Keyser and Pecnick (1985a, b) pointed out that the cyclonic shear with the along-jet cold advection could laterally displace the subsidence branch of the direct transverse SC into the warm region of the high-level front, thus causing the tilting of the front, and then resulting in frontogenesis and further enhancement of the direct SC, all of which forms a positive feedback mechanism. Ding (2005) argued that the enhancement of the SC’s updraft is one of the triggers of deep convection in the warm regions of monsoon fronts. Figure 8 illustrates the concurrence of the frontogenesis of the monsoon high-level front and deep convection activities in a case that occurred from 0600 UTC 6 to 0000 UTC 7 July 2007. When the shear forcing is relatively weak (Fig. 8e), the convection is not vigorous (Fig. 8a). With the enhancement of the shear forcing of the cold advection (Fig. 8f), deep convection begins to occur in the region near the common updraft axis of the direct and indirect circulations (Fig. 8b). After another 6?12 h, the frontogenesis area becomes obviously tilted and extends downwards to the mid-troposphere. The subsidence branch of the direct cell moves under the jet axis and into the warm region of the front (Figs. 8c and d), and the intensity of the convection reaches its peak. By that time, the shear forcing has weakened (Figs. 8g and h).
Figure8. (a?d) Cross sections of potential temperature (contoured with intervals of 10 K, solid) and its meridional gradient (shaded, intervals of 1 × 10?12 K m?1) and downward vertical velocity (contoured with intervals of 0.5 Pa s?1, dotted): (a) 18 hours; (b) 12 hours; (c) 6 hours prior to, and (d) at 0000 UTC 7 July 2007. (c?h) Cross sections of potential temperature and its zonal gradient (red contours with intervals of 0.5 × 10?12 K m?1) and zonal wind velocity component (shaded, intervals of 12 m s?1) and vector arrows of air flow in the transverse plane (v, ω) over the same time period as in (a?d). In the lowest portion in every panel, the zonally averaged frequency of deep convection events (mean value > 0.25) over 117°?124°E is illustrated using gray lines and scales at the location of 35°N.The S?E equation gives a direct and simplified way to clarify the relationship between horizontal geostrophic deformation and the transverse SC, which is in general linked to the frontogenesis process.
Following the investigation of Keyser and Pecnick (1985b), in order to further clarify the frontogenesis mechanism due to horizontal shear forcing in monsoon front zones, the S?E equation with only geostrophic shear forcing terms is utilized and the diagnosis results are shown in Fig. 9. It is clear that, with the enhancement of cyclonic shear on the cyclonic side of the upper-level jet (Figs. 8a?d), the circulation response to the shear terms in the mei-yu front region shifts from an indirect cell (Figs. 9a and b) to a direct cell (Figs. 9c and d). An obviously tilted-with-altitude subsidence branch has been laterally “placed” into the warm region of the front zone (Fig. 9d), strengthened and has extended downwards to the low levels over 34°?35°N, similar to the synergistic interaction between an upper-level front and a surface front diagnosed and simulated by Mak et al. (2017), in which the downward motion of upper- and lower-level ageostrophic circulation cells were merged together along a tilted-with-altitude surface. At the same time, a strengthened downward velocity maximum appears in the mid-to-upper-level frontogenesis region associated with vigorous convections (Fig. 9d vs. Fig. 8h), implying a link between the changing SC, frontogenesis, and intensifying convection. As Shapiro (1981) and Keyser and Pecnick (1985b) indicated, with the cold advection along the high-level jet axis, the shear forcing on the cyclonic shearing side of the jet can intensify the transverse SC; then, the enhanced subsidence in the SC promotes the high-level frontogenesis through the “tilt” effect, and the frontogenesis in turn promotes the SC’s vertical motion. This positive feedback process can persist until the high-level cold advection exists and can provide a favorable condition for deep convection in the warm regions of the frontal zone (Ding, 2005; Mak et al., 2017).
Figure9. As in Fig. 4f except for 0600 UTC 6 July 2007 to 0000 UTC 7 July 2007 at 6-h intervals.Frontogenesis of the forced-out SC was calculated using geostrophic frontogenesis equation. The results showed that, along the jet axis in the troposphere, the SC forced out by large-scale geostrophic dynamical forcing generates an intensified frontogenesis region that tilts northwards with altitude, and the direct cell’s subsidence branch originally in the cold region is strengthened and moves southwards to the warm region of the front zone. At the same time, the frontogenesis enhances the SC, and all of these processes constitute a positive feedback mechanism that maintains until the cold advection becomes weakened. Most of the frontogenesis region is within the upward motion area, which is conducive to the development of deep convective precipitation systems. Based on the above discussion, a conceptual model can be created for forced SC and frontogenesis in the mei-yu region (Fig. 10).
Figure10. Schematic illustration of the forced transverse secondary circulation of the mei-yu front with the pattern of frontogenesis and instability.In addition, as a classic tool for diagnosis, the S?E equation is effective in analyzing frontogenesis and the SC circulation mechanism. Although the research results presented in this paper show that the structure of frontal SC is determined basically by the dynamic field, the intensity of the dynamically forced-out circulation rising branch diagnosed using the S?E equation is less than that of the original intensity, and most of the other forcing terms enter into the diagnosis process in the form of parameterization schemes, which leads to relatively large errors. In fact, how to increase the magnitude of dynamically forced circulation determines the accuracy of S?E diagnosis. The ultimate solution to this problem lies in basic theory. For example, is there a more accurate description of the S?E equation’s initial equilibrium assumption, the thermo-wind balance? Is it necessary to find other equilibrium assumptions for different atmospheric environments in order to better describe the constraints on atmospheric motion? These aspects need theoretical improvement and further observational evidence. Although the modern three-dimensional primitive equation numerical model can represent the characteristics of the original circulation better, it remains a problem as to how to break it up into circulation responses corresponding to different forcing terms.
Acknowledgements. This research work was jointly supported by the National Key R&D Programs of China (Grant No. 2018YFC1507300) and the National Natural Science Foundation of China (Grant No. 41505086). The authors express special thanks to Dr. Hailong LIU for providing the technical methods for processing the TRMM data. We are sincerely grateful to the reviewers for their efforts and valuable comments and suggestions on our manuscript.
