HTML
--> --> -->2
1.1. Atmospheric predictability
The study of atmospheric predictability can be traced back to Lorenz (1963). Utilizing a three-variable ordinary differential equation, he found that the solutions are unstable and nonperiodic. After that, he studied the growth rate of the small initial errors and found that the error growth is strongly dependent on the background circulation patterns and varies from a few days to a few weeks (Lorenz, 1965). Later, he investigated the predictability of a flow containing different scales of motion by utilizing a two-dimensional barotropic vorticity equation and estimated that the atmospheric predictability was 16.8 days (Lorenz, 1969). His results also suggested that motions in small (large) scales have shorter (longer) saturation times.In addition to the simple atmospheric circulation model, Lorenz (1982) investigated predictability with the European Centre for Medium-Range Weather Forecasts (ECMWF) operational products from 1 December 1980 to 10 March 1981. He suggested that forecasts of instantaneous weather patterns nearly two weeks in advance appeared to be possible. Moreover, Simmons and Hollingsworth (2002) discussed the forecast skill of the ECMWF operational forecasts with its products from 1980 to 2001. Their results showed that forecasts still had the ability to be predicted in the three-week range, and these benefits mainly came from improvements in data assimilation, modeling and observing systems. With the reforecasts from July 2012 to July 2013, Buizza and Leutbecher (2015) found that the predictability of instantaneous grid points is approximately 17.0 days for the Northern Hemisphere and 21.5 days for the Southern Hemisphere. Furthermore, a considerably longer effective forecast time could be achieved with temporal and spatial filtering, which implies that the forecast time for different phenomena may differ.
The predictability sources for atmospheric motions come not only from the atmosphere itself, but also land, ocean and sea-ice conditions. For short-range forecasts, the atmospheric initial conditions and model parameterizations dominate the result. As the forecast lead time increases, external forcings such as land, ocean and sea ice have non-negligible impacts on the predictions (Liu et al., 2016). This is primarily related to the external thermodynamic processes and the external dynamic processes, which play secondary roles (Takaya et al., 2010; Ling et al., 2015). Thus, both the initial and boundary conditions are of importance for extended-range forecasts, particularly for high-impact weather events (Brunet et al., 2010).
In addition to the forecasting of general circulation patterns, forecasts of 2-m temperature are also important for midlatitude regions. Numerical results show that the 2-m temperature errors over the Northern Hemisphere start to saturate after two weeks during boreal winter. However, some forecast skill remains in weeks three and four after calibration (Guan et al., 2019). Moreover, Li et al. (2017) noted that numerical models can capture the features of cold surges, such as the frequency, intensity and location, with a lead time of about two weeks. Therefore, it is necessary to rethink the prediction limit of two weeks in numerical weather prediction.
2
1.2. Arctic midlatitude linkage
Due to rapid Arctic sea-ice loss and Arctic surface temperature warming, the linkage between the Arctic and the midlatitudes has received much attention in recent years (Budikova, 2009; Vihma, 2014; Gao et al., 2015). In conjunction with Arctic changes, Eurasia has experienced many extreme cold weather events over the past few decades, exhibiting extremely cold winters (Coumou and Rahmstorf, 2012; Cohen et al., 2014; Mori et al., 2014). The coincidence between Arctic changes and increased Eurasian extreme event occurrence has inspired many discussions on the possible linkage (Stroeve et al., 2012; Wang and Overland, 2009). It is probable that meridional temperature gradients have decreased due to Arctic warming, and have thereby weakened zonal winds. This change further leads to a wavier jet stream and slower-moving synoptic systems, which favors the occurrence of extreme events (Francis and Vavrus, 2012; Petoukhov et al., 2013; Screen and Simmonds, 2014).However, the linkage between the Arctic and midlatitudes is also modulated by the tropical oceans. Lee et al. (2011) noted that the Arctic surface air temperature is influenced by tropical convection, which further regulates midlatitude atmospheric circulations. Moreover, the Gulf Stream can affect ice in the Barents Sea, thus modulating the temperature in Eurasia (Sato et al., 2014). Matsumura and Kosaka (2019) showed that frequent Eurasian cold winters can be attributed not only to Arctic sea-ice loss, but also tropical Pacific cooling. Their results suggest that the Arctic and Eurasian climate anomalies are roughly in opposite phase at the surface during recent El Ni?o and La Ni?a-decay years.
Along with the retreat in the sea-ice extent, the sea-ice thickness (SIT) has also become thinner (Kwok and Rothrock, 2009). Both reconstructed observations (Lindsay and Schweiger, 2015) and reanalysis data (Zhang and Rothrock, 2003) have shown a great SIT reduction in the Arctic since 1979. There are much stronger upward heat fluxes and warmer temperatures with a thinner Arctic SIT, which further induce a significant negative sea level pressure in Eurasia and a negative North Atlantic Oscillation (NAO) response at 500 hPa (Rinke et al., 2006; Krinner et al., 2010; Sun et al., 2018). Further investigation revealed that warming from SIT loss is as large as one-third of the response from the sea-ice concentration (SIC) loss (Labe et al., 2018).
In addition to the linkage from the perspective of climatology, weather in the midlatitudes could be affected by the Arctic within two weeks. Relaxation experiments with the Integrated Forecasting System (IFS) from the ECMWF have been conducted to explore the influence of the Arctic on midlatitude weather prediction (Jung et al., 2014). They found that improved Arctic forecasts during wintertime have a positive influence on the accuracy of both medium- and extended-range predictions of the midlatitude geopotential height at 500 hPa in the Northern Hemisphere. This linkage between the Arctic and midlatitudes is also flow dependent, in which anomalous northerly winds lead to a stronger Arctic influence. The linkage in boreal winter is stronger than that in summer, which highlights the potential midlatitude forecast benefits from improved Arctic conditions in winter (Semmler et al., 2018). Specifically, the linkage between the Arctic and North Asia is strong during Scandinavian blocking episodes (Day et al., 2019). Moreover, the interannual variability of the Eurasian atmospheric circulation and temperature can be impacted by the Arctic troposphere via modifying large-scale atmospheric circulations, heat transport over the continent, and synoptic variations. Specifically, the Siberian high plays an important role in the linkage between the Arctic troposphere and variability in East Asia (Ye et al., 2018).
In addition to the role of the Arctic atmosphere, boundary conditions in the Arctic also play important roles in midlatitude atmospheric circulation evolution. Numerical results show that atmospheric circulation could respond to sea surface temperature and SIC variations within several days (Deser et al., 2007). Utilizing the IFS numerical model, Semmler et al. (2016) investigated the fast atmospheric response to sudden Arctic sea-ice thinning by introducing a 10-K sea-ice surface temperature warming. They found that the boundary layer turbulence is the most significant process that distributes anomalous vertical heat and that the quasi-equilibrium response is two months. Their work indicates that atmospheric circulation forecasts are affected by Arctic boundary conditions, especially for forecasts longer than 10 days.
2
1.3. Anomalous circulation patterns in the midlatitudes
Extreme weather events are usually associated with anomalous atmospheric circulation patterns such as blockings and the NAO. Due to the connection between the Arctic and midlatitudes, blocking can guide cold air from polar regions to the mid?low latitudes. For instance, the long persistent Ural blocking was the key process for severe snow and freezing rain in southern China during January 2008 (Tao and Wei, 2008; Zhou et al., 2009), and Asian blocking was an important factor for severe cold surges in eastern China during January 2016 (Cheung et al., 2016). In addition to blocking, the NAO can also trigger extreme cold events. For example, the extreme cold event in Europe during the winter of 2011/12, which was mainly caused by an atmospheric circulation transformation from positive NAO to eastern negative NAO (Luo et al., 2014), and the blizzard in the Middle East in December 2013, which was due to the atmospheric circulation associated with a positive NAO decay phase (Luo et al., 2015). Moreover, a blocking formation is usually associated with the positive NAO decay stage because energy disperses from the North Atlantic sectors to downstream areas (Yao and Luo, 2015). Numerical results indicate that the poor forecast skill of extreme events can be attributed to the difficulty in blocking and NAO event prediction (Lin and Wu, 2012).Previous studies have noted that the frequency of blocking in the midlatitudes is closely related to Arctic sea-ice loss (Liu et al., 2012; Barnes, 2013). However, blockings have different responses to the sea-ice anomalies in different regions. Specifically, sea-ice loss in the Barents and Kara seas can increase the frequency of Ural blocking events and their durations, thereby favoring cold surge occurrences in Eurasia (Luo et al., 2016; Yao et al., 2017).
The NAO has had a negative trend during past decades, which is probably caused by Arctic sea-ice loss (Wu et al., 2007; Overland et al., 2011; Cohen et al., 2014; Inoue et al., 2012). The increased baroclinicity induced by sea-ice loss and the interaction between the troposphere and stratosphere may be a possible mechanism (Jaiser et al., 2012, 2013). Moreover, the north center of the NAO exhibits clear shifts in response to different levels of sea-ice reduction, which shows that the NAO is sensitive to Arctic sea ice (Pedersen et al., 2016). The above results indicate that anomalous midlatitude atmospheric circulations, such as blocking and the NAO, which are modulated by Arctic sea ice, may be the linkage between Arctic changes and midlatitude responses.
Considering that the Arctic is a source of predictability for midlatitude weather forecasts and the tight linkage between the Arctic and midlatitudes, it is important to explore the Arctic influence on the predictability of Eurasian winter extreme weather events at weather time scales using case studies. This can help us understand the mechanism of extreme weather event formation and determine Arctic sensitive areas for Eurasian winter extreme weather event predictions. The determination of Arctic sensitive areas is helpful for capturing the Arctic signal of extreme weather events. On the other hand, it is also helpful to reduce the initial and boundary errors in extreme event forecasts to achieve improved forecast skill, not only for deterministic forecast skill improvement by reducing uncertainties in Arctic sensitive areas, but also for ensemble forecast skill improvement by providing better perturbed members.
2
2.1. Brief introduction to the CNOP approach
Generally, the equations governing atmospheric motions can be written aswhere U is the atmospheric state, F is the nonlinear operator and B is the boundary condition operator. x represents the location while t represents time.


Supposing there are some perturbations u0 in the initial condition and some perturbations g in the boundary condition. Then, the corresponding governing equations become
where u represents the difference from the reference state U caused by the perturbations in the initial and boundary conditions. The following optimization problem is used to assess the maximal influences of the initial and boundary perturbations, which can be written as
where J is the cost function defined by the considered problems. Usually, the perturbations are limited with certain constraints, i.e.,



Specifically, if only the initial perturbation is under discussion, the solution of Eq. (3) becomes



2
2.2. Applications of the CNOP approach in related investigations
The CNOP method has been applied in atmospheric and oceanic studies. Utilizing a quasi-geostrophic global spectral model with 21 truncations, the optimal precursors in the initial conditions are obtained with the CNOP method (Mu and Jiang, 2008). With this numerical model, Jiang et al. (2013) investigated the initial perturbations for triggering NAO onsets by the CNOP method. Dai et al. (2016) further discussed the relationship between the optimal precursors and the corresponding optimally growing initial errors obtained by the CNOP method. Their results indicated that random initial perturbations cannot develop and that only perturbations in specific patterns exhibit fast growth.In addition to initial perturbations, optimal boundary perturbations have been investigated in an ocean ecosystem model (Wang and Mu, 2015). The results revealed that nonlinear processes play important roles in the phytoplankton evolution caused by nutrient perturbations at the bottom boundary. These studies discussed the optimal initial and boundary perturbations respectively. However, for the optimal synergistic initial and boundary perturbations on weather and climate events, no investigations have been performed so far.
Moreover, the above investigations were conducted with relatively simple numerical models whose adjoint modules are accessible. Thus, the corresponding CNOP can be obtained easily. However, most complicated models in large dimensions have no accessible adjoint modules, so that CNOP computation could be a problem. Some intelligent algorithms, such as differential evolution (Storn and Price, 1997) and particle swarm optimization (Kennedy and Eberhart, 1995), should be utilized to solve the optimal problems.
2
3.1. Uncertainties in the Arctic SIC
Sea ice is the unique characteristic in the Arctic. However, the SIC is estimated from the passive microwave brightness temperature, and two widely used SIC products are derived from the NASA team (Cavalieri et al., 1984) and bootstrap (Comiso, 1986) algorithms, respectively. A previous study noted that the SICs derived from different algorithms have consistent variability in interannual time scales but yield different absolute SIC and sea-ice extent values (Kattsov et al., 2010). Specifically, Andersen et al. (2007) found that the NASA team algorithm underestimates ice cover by 4.4% in the central Arctic during winter, when passive microwave algorithms are considered the most reliable.However, SICs from bootstrap have high accuracy but they cannot be calculated in real time, and SICs from the NASA team algorithm are utilized in operational forecasts, although they have low accuracy. Figure 1 shows the monthly mean SIC in December 2018 derived from the National Snow and Ice Data Center (NSIDC). The monthly mean SICs derived from bootstrap and the NASA team algorithm are highly similar (Figs. 1a and b). However, the monthly mean SIC derived from the NASA team algorithm is underestimated in marginal seas, and these underestimations can be as large as 20% (Fig. 1c). As for daily SICs, the underestimations can be larger (Fig. 2). Therefore, an investigation of the influence of the SIC bias derived from different algorithms on weather forecasts and climate predictions is needed.
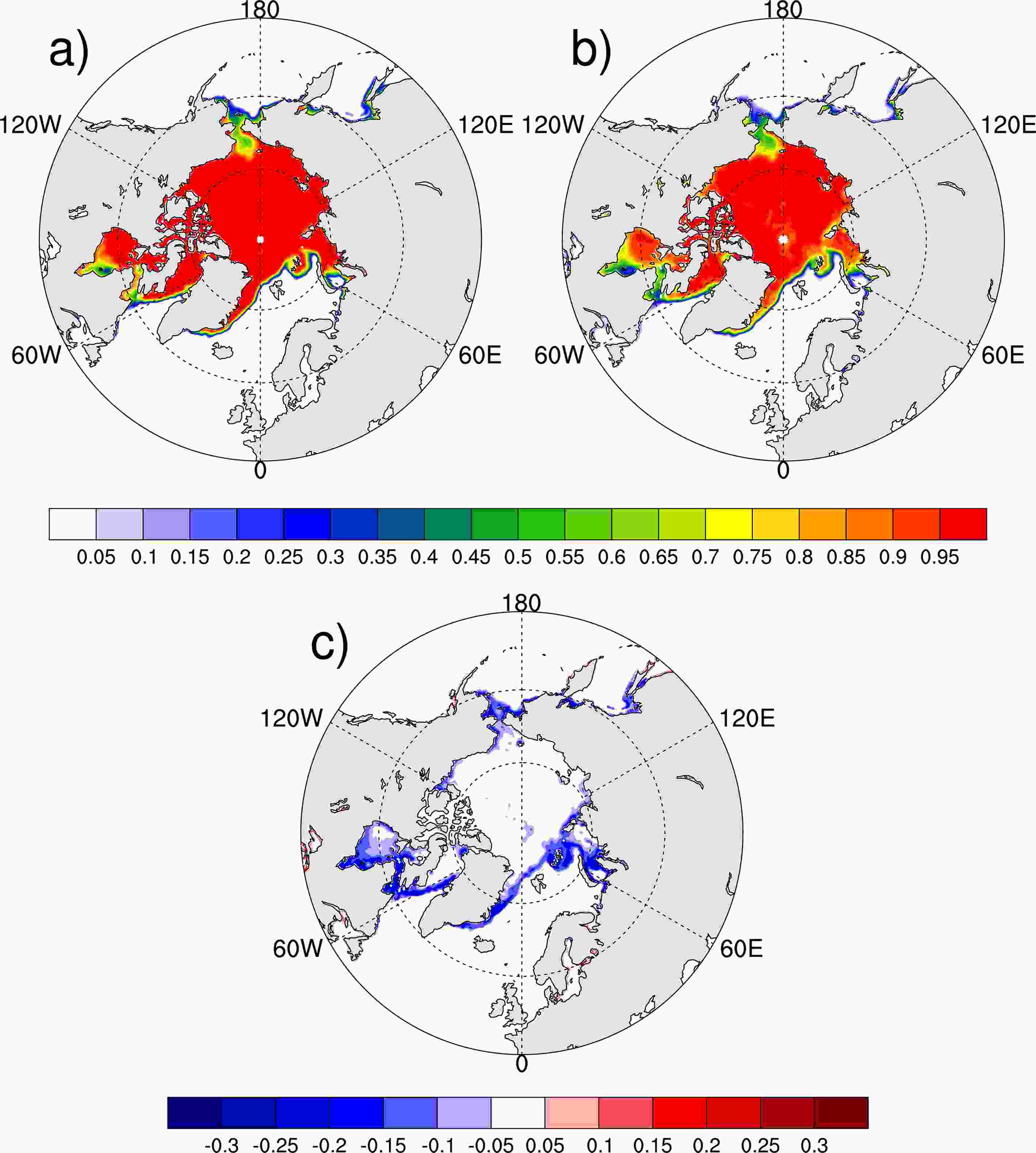 Figure1. Monthly mean SICs in December 2018 from the NSIDC (units: 1): (a) derived from the bootstrap algorithm (high accuracy but not in real time); (b) derived from the NASA team algorithm (low accuracy but in real time for operations); (c) difference between (a) and (b), i.e., (b) minus (a).
Figure1. Monthly mean SICs in December 2018 from the NSIDC (units: 1): (a) derived from the bootstrap algorithm (high accuracy but not in real time); (b) derived from the NASA team algorithm (low accuracy but in real time for operations); (c) difference between (a) and (b), i.e., (b) minus (a).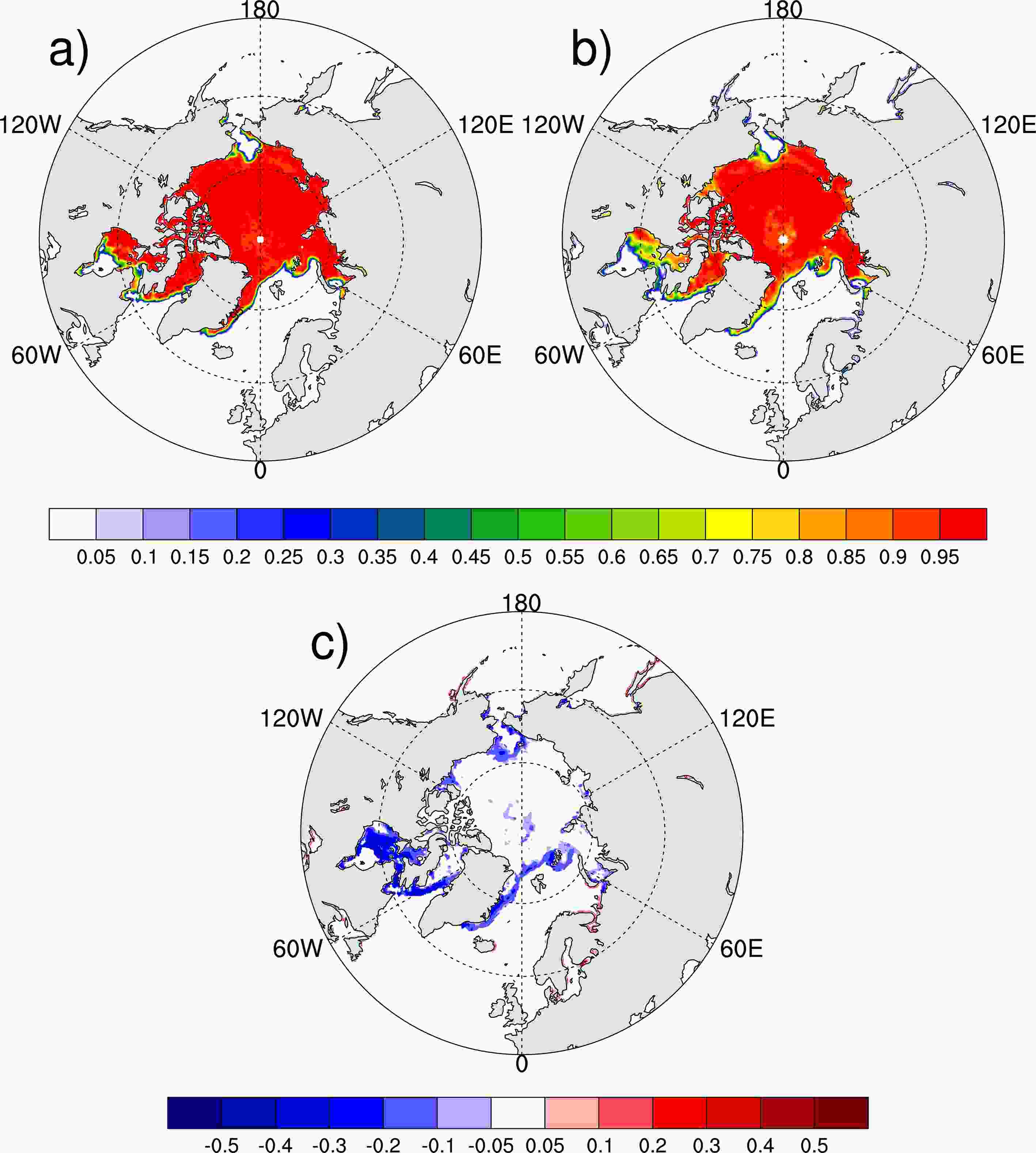 Figure2. As in Fig. 1, but for the SICs on 1 December 2018.
Figure2. As in Fig. 1, but for the SICs on 1 December 2018.2
3.2. Uncertainties in the Arctic SIT
In addition to the SIC, the SIT is another important characteristic of Arctic sea ice. There are fewer SIT data than SIC data due to the difficulties in SIT observations. However, the SIT is crucial for climate predictions because it affects the upward heat fluxes in the Arctic.SITs retrieved from the Soil Moisture and Ocean Salinity (SMOS) satellite are considered to have high quality for thin sea ice; however, they still have large uncertainties (Ricker et al., 2017). As noted by Kaleschke et al. (2012, 2015), the SMOS SITs retrieved from brightness temperatures are highly accurate over thin sea ice (< 1 m) but lose sensitivity over thick ice (> 1 m). Figure 3 shows the SITs and their corresponding uncertainties on 1 December 2018, which were retrieved from the SMOS satellite. As shown in Fig. 3, uncertainties in thin sea-ice regions can reach as large as the SITs there (dotted areas in Fig. 3b). Whether SIT uncertainties influence weather and climate predictions in the midlatitudes is unknown and should be further investigated.
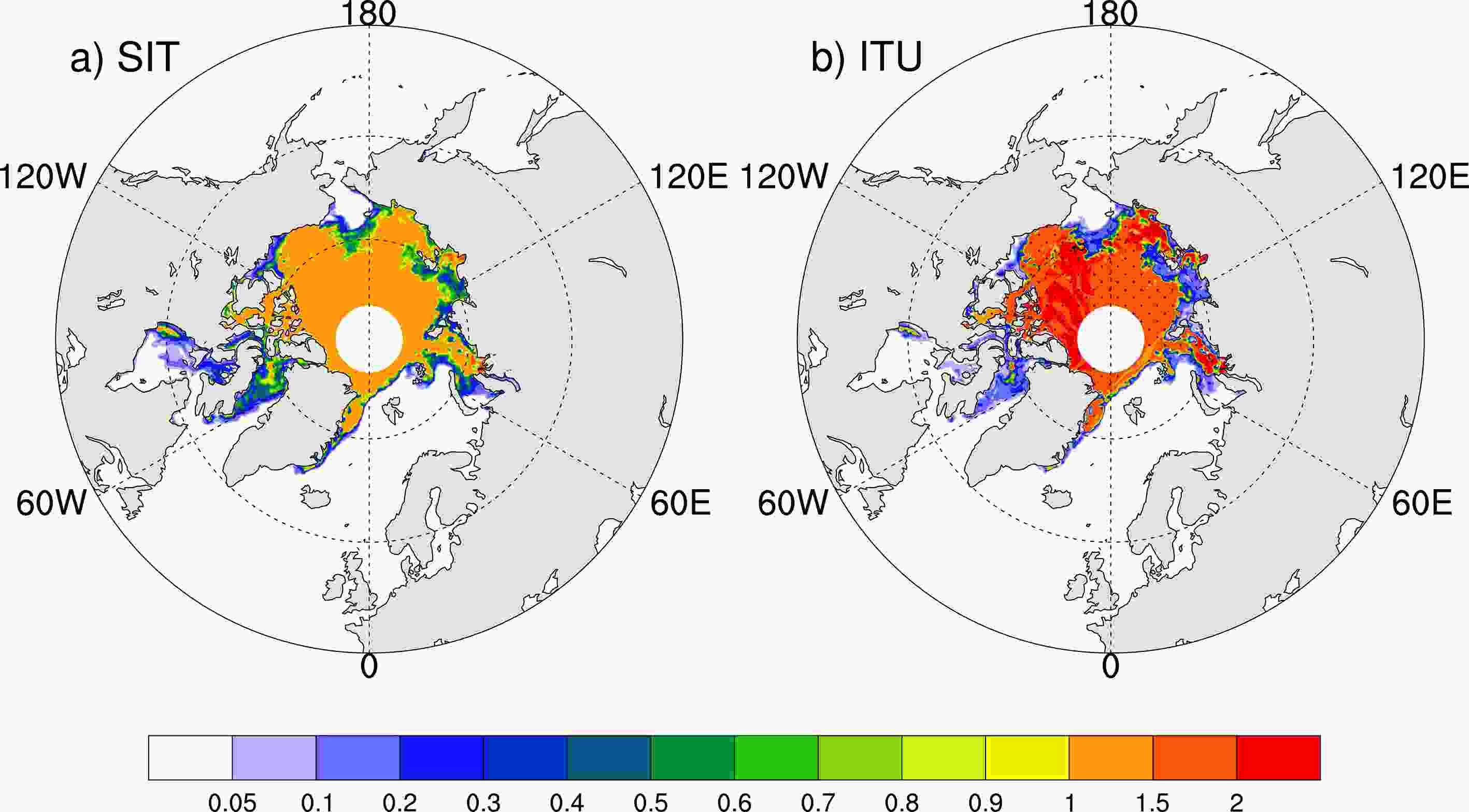 Figure3. (a) SITs on 1 December 2018 obtained from the SMOS satellite (units: m). (b) Corresponding SIT uncertainty (units: m), in which the dotted area indicates where the SIT uncertainty is larger than the SIT.
Figure3. (a) SITs on 1 December 2018 obtained from the SMOS satellite (units: m). (b) Corresponding SIT uncertainty (units: m), in which the dotted area indicates where the SIT uncertainty is larger than the SIT.2
3.3. Uncertainties in the Arctic atmosphere
Previous studies show that there are large uncertainties in Arctic atmospheric reanalysis data due to few observations in polar regions (Inoue et al., 2011; Screen and Simmonds, 2011; Jung et al., 2014). Figure 4 shows the monthly mean atmospheric ensemble spread in December 2018 from the fifth generation ECMWF reanalysis (ERA5) data, which can somewhat represent the uncertainties in atmospheric data (Hersbach et al., 2018). The ensemble spread in the Arctic is obviously larger than that in the midlatitudes for surface variables such as the mean sea level pressure and 2-m temperature (Figs. 4a and b). For the temperature and geopotential at 850 hPa, the spread in midlatitudes has large values, which suggests large uncertainties there (Figs. 4c and e). However, for the temperature and geopotential at 200 hPa, the uncertainties in the tropics are larger (Figs. 4d and f).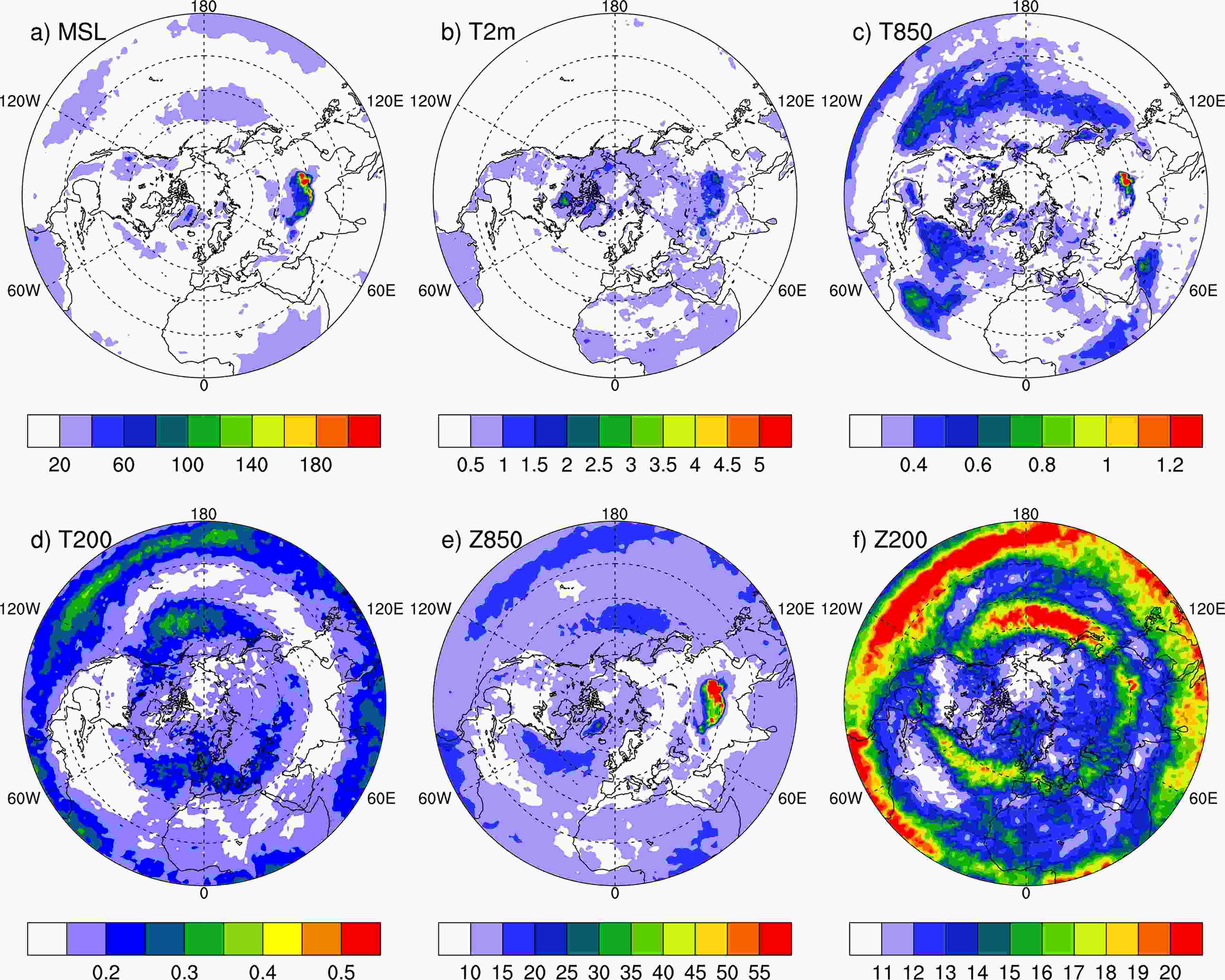 Figure4. Monthly mean atmospheric ensemble spread in December 2018 from ERA5: (a) mean sea level pressure (units: Pa); (b) 2-m temperature (units: °C); (c, d) temperature uncertainties at 850 hPa and 200 hPa, respectively (units: °C); (e, f) geopotential uncertainties at 850 hPa and 200 hPa, respectively (units: m2 s?2).
Figure4. Monthly mean atmospheric ensemble spread in December 2018 from ERA5: (a) mean sea level pressure (units: Pa); (b) 2-m temperature (units: °C); (c, d) temperature uncertainties at 850 hPa and 200 hPa, respectively (units: °C); (e, f) geopotential uncertainties at 850 hPa and 200 hPa, respectively (units: m2 s?2).Inoue et al. (2009) assimilated additional buoy data from the Arctic and found that the variability in the sea level pressure has been reduced significantly. The linkage between the Arctic and midlatitudes revealed by Jung et al. (2014) and Semmler et al. (2018) indicates that weather forecasts in the midlatitudes will be improved with more accurate Arctic initial conditions, especially for extreme weather events. Furthermore, Day et al. (2019) demonstrated by conducting observing system experiments that weather forecasts in North Asia can benefit from accurate Arctic initial conditions. Therefore, the influence of the initial uncertainty in the Arctic on midlatitude extreme weather events forecasts may be larger and should be further discussed.
2
4.1. Influence of Arctic atmospheric initial conditions on extreme weather events
Ensemble atmospheric forecasts with different initial datasets revealed that additional Arctic radiosonde observations are beneficial for persistent strong wind forecasts (Inoue et al., 2015). Furthermore, ensemble forecast experiments for the two winter storms over eastern Asia and North America in February 2015 show that errors and uncertainties in the upper troughs in the midlatitudes would be reduced by assimilating additional radiosonde observations from the Arctic, so that the forecast skills of these two storms are improved (Sato et al., 2017). Their results highlight the importance of Arctic initial conditions in Eurasian extreme event prediction. However, their work focused on a relatively short time period (i.e., 5.5 days) and the mid?high latitudes. For extreme events in mid?low latitudes with longer forecast time periods, whether their prediction could benefit from a better Arctic initial condition is unknown and should be investigated.2
4.2. Influence of Arctic SICs on extreme climate events
The linkage between Arctic SIC anomalies and Eurasian extreme events has recently been a point of discussion. Many investigations have focused on the statistical relationship between SIC anomalies and Eurasian extreme event frequency. Moreover, some investigations have been performed to reveal the role of Arctic sea-ice anomalies in Eurasian extreme events.There was a persistent cold event in Asia during late January to early February 2012. Wu et al. (2017) investigated the possible association between Arctic sea-ice loss and Arctic atmospheric circulations during the preceding summer. They noted that the sea level pressure in the Aleutian region played a critical role in this cold event by strengthening the Siberian high. Further numerical model simulation experiments illustrated that the combined impacts of both Arctic sea-ice anomalies and atmospheric initial conditions in the preceding summer favored the persistent cold winter weather.
Moreover, Xie et al. (2019) discussed the role of Arctic sea ice in the 2014/15 warm Eurasian winter. They found that the SIC has a large impact on winter temperature and pressure probability distribution functions by using two groups of large ensemble atmospheric model simulations under different SIC boundary conditions. Their results highlight the important role of the Barents SIC in favoring the occurrence of a warm winter in Eurasia.
However, there is something that we have to consider. These extreme events last only for several days. Therefore, background conditions, such as the SIC and sea surface temperature, can only increase the occurrence probability of extreme events. For individual extreme events, atmospheric circulation is the direct factor triggering their onsets.
Inspired by previous investigations, we believe that only Arctic perturbations in specific patterns have large impacts on extreme weather in the midlatitudes, while random perturbations have little impact on them. Therefore, the determination of the specific Arctic perturbation patterns can help us further understand the linkage between the Arctic and midlatitudes and the mechanism for Eurasian extreme event formation. However, the mechanism for extreme event formation may differ in different cases. Therefore, the role of the Arctic in these cases may differ as well. Thus, additional extreme cases should be investigated to reach common conclusions.
In addition, most studies have individually discussed the role of Arctic initial and boundary conditions. As different characteristics of the Arctic, we believe that the synergistic effect of Arctic initial and boundary perturbations could have a greater impact on weather in the midlatitudes. Therefore, we suggest that the Arctic synergistic effect should be used to describe the linkage between the Arctic and extreme weather events in the midlatitudes. These investigations can help improve the forecast skill of Eurasian extreme weather events, not only in deterministic forecasts by reducing uncertainties in Arctic sensitive areas, but also in ensemble forecasts by providing better perturbation members.
Acknowledgements. The authors are grateful to the anonymous reviewers and the Executive Editor-in-Chief for their insightful comments, which have helped improve the paper. This work was supported by the National Natural Science Foundation of China (Grant No. 41790475).
