0 引言
【研究意义】土壤重金属分布具有复杂的空间变异性和非平稳性,在对土壤重金属的调查中,通常利用合适的空间插值方法,对未知样点重金属含量值进行预测。研究土壤重金属与影响因子之间的相关性不仅可以为空间插值方法提供更加准确和可靠的辅助变量,从而提高调查成果质量,而且可以为土壤重金属的污染分析评价和防治提供解决思路。【前人研究进展】常用的土壤重金属空间插值方法主要包括克里格法和协同克里格法[1]。协同克里格法（Co-Kriging）可以视作普通克里格法的改进,通过用多个辅助变量对土壤重金属含量进行估值预测,较普通克里格法能有效提高预测精度[2]。以往研究影响因子和土壤重金属之间的相关关系多采用的是皮尔逊相关系数（pearson correlation coefficient,PCC）和主成分分析法（principal components analysis,PCA）,选择的影响因子多为连续数值型。例如章清等利用Pearson相关系数方法选择与土壤铜含量具有较高相关性的土壤因子（全钾、全铬、阳离子交换量、全铝、全氮（P<0.05））作为辅助变量,利用主成分分析（PCA）对辅助变量进行降维求总得分处理后与协同克里格插值相结合构建土壤铜含量空间模型（COKPCA）[3];郭龙等研究土壤pH、有机质、有效磷、速效钾、碱解氮与土壤属性指标变量之间的关系,选择与预测变量之间具有较高相关性的自变量作为辅助变量用以提高预测精度[4]。【本研究切入点】将影响因子作为辅助变量结合空间插值方法对土壤重金属进行空间预测是目前的研究热点。已有研究虽对土壤重金属的影响因子进行了分析,但主要围绕单个或少数几个连续数值型影响因子探讨,对于某些类别型影响因子尚缺乏综合全面的分析,同时也没有阐明各影响因子的相对重要程度和交互作用特征[5]。因此,对空间插值中辅助变量的选择研究仍有待完善。为了更加全面分析土壤重金属与影响因子相关性及其交互作用,为空间插值方法选择更佳的辅助变量,本研究利用地理探测器模型进行探测分析。该方法最大的优势在于没有过多的假设条件与约束,具有普适性,能有效地克服传统统计分析方法处理类别变量的局限性[6],并能快速、经济、有效、客观地探测出要素间的关系。如WANG等利用地理探测器研究中国和顺地区神经中枢缺陷疾病的致病因子[7];杨忍等利用地理探测器模型对中国村庄空间分布影响因子进行探测识别,同时解析乡村空间优化重组背景和模式[8];周磊等利用地理探测器模型研究京津冀PM2.5的污染风险因素[9]。【拟解决的关键问题】本研究利用地理探测器模型研究土壤重金属与影响因子之间及土壤重金属元素之间的相关性和交互作用,尝试解决以往研究方法在影响因子选择和处理上的选择度不高的问题,为土壤重金属空间预测模型中辅助变量的选择提供更加全面的分析和解释。1 材料与方法
1.1 研究区域概况
湘潭县位于湖南省中部偏东,湘江下游西岸,衡山北麓,长衡丘陵盆地北段,北纬27°20′—28°05′,东经112°25′—113°03′,属亚热带季风湿润气候,冬夏两季长,春秋两季短,雨水集中,光、温、水空间分布差异小,具有明显的大陆性气候特征。2013年湘潭县GDP增速为12.2%,第一、二、三产业的比重为分别为18.9%、52.1%、29%,以第二产业为主。研究区域选择湖南省湘潭县中部的5个乡镇,分别为杨嘉桥镇、河口镇、易俗河镇、梅林桥镇和谭家山镇,该区域内的农田灌溉水源主要来自湘江水及其支流水域,且人口密度大,路网密布,工业发达,历史上农田环境污染较重。1.2 数据来源
为获取有代表性的农田土壤样品,按照NY/T 395—2000《农田土壤环境质量监测技术规范》[10]的规定确定监测单元,采用简单随机的布点方法,以能代表监测区农田土壤环境质量为原则,同时考虑农田周围的河流、工厂和建设用地等情况,基本覆盖研究区内的主要农田。在作物生长期内采集0—20 cm耕层土壤,共789个采样样品。每个样品在采集过程中,都采用了GPS定位。土壤在室内风干,磨碎后过100目尼龙网筛,用来测定各重金属元素。土壤样品经HNO3-HCl-H2O2消解测定其Hg、As、Pb、Cd和Cr含量,采用原子吸收光谱仪分析消解液中重金属含量[11]。研究区内农田和采样数点的空间分布如图1所示。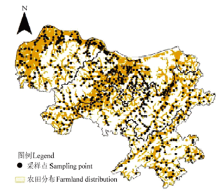
显示原图|下载原图ZIP|生成PPT图1研究区农田和土壤采样点空间分布图
-->Fig. 1Spatial distributions of farmland and soil sampling points in study area
-->
根据土壤中重金属的来源分析和土壤本身的特点,并考虑到易获取程度,本研究选择的影响因子为土壤pH、土壤类型、平均气温、平均相对湿度、高程数据和GDP。其中土壤pH、土壤类型为点数据,来源于2014年农业行业科研专项项目数据,与789个土壤采样点来源相同且以点为单位一一对应;平均气温、平均相对湿度、高程数据和GDP数据均来源于国家科技基础条件平台—国家地球系统科学数据共享平台（http://www.geodata.cn）。平均气温和平均相对湿度数据集利用NCEP/NCAR全球气候再分析资料中国区域气候要素数据及MODIS NDVI和DEM数据,将分辨率较低的NCEP/NCAR气候要素数据降尺度到1 km分辨率,提取2014年湘潭县1 km栅格逐年气候数据集;高程数据是将SRTM原始数据利用Matlab转换成ArcGIS能读取的GRID格式,对34个分区分块的数据进行拼接,提取出研究区域的1 km空间分辨率的高程数据;GDP数据是在综合分析了人类活动形成的土地利用格局与GDP的空间互动规律的基础上,建立分产业（一、二、三产业） GDP数量与土地利用类型的空间相关性模型。利用该模型对 GDP分县统计数据空间化,从而生成 1 km网格的 GDP空间分布数据。
1.3 地理探测器
地理探测器主要被用来分析土壤采样点中的5种重金属Pb、Cd、As、Cr和Hg与所选6种影响因子的相关性以及多种影响因子交互作用。主要是因为地理探测器q值具有明确的物理含义,没有线性假设,客观地探测出自变量解释了100×q%的因变量[12]。为了更加全面地分析土壤采样点中重金属与所选影响因子之间的相关关系,本研究应用地理探测器中的风险探测器、因子探测器、生态探测器和交互作用探测器[13]。风险探测器主要用于探测影响因子对土壤重金属是否具有风险性,用t统计量来检验：
$t_{\overline{y}_{h=1}-\overline{y}_{h=2}}=\frac{\overline{Y}_{h=1}-\overline{Y}_{h=2}}{[\frac{Var(\overline{Y}_{h=1})}{n_{h=1}}+\frac{Vae(\overline{Y}_{h=2})}{n_{h=2}}]^{1/2}}$（1）
式1中,$\overline{Y}_h$表示子区域h内的属性均值,此研究为某重金属元素含量;nh为子区域h内样本数量;Var表示方差。统计量t近似的服从Student's t分布,t值越大代表该影响因子对土壤重金属的空间分异性影响越大。零假设H0：$\overline{Y}_{h=1}-\overline{Y}_{h=2}$,如果在置信水平α下拒绝H0,则认为两个子区域间的属性均值存在着明显的差异。
因子探测器是探测某因子X多大程度上解释了属性Y的空间分异,用因子的解释力PD,H进行判断,PD,H的值域为[0,1],PD,H的值越大,表明目标属性Y的空间分异性越明显。PD,H计算公式为：
$SSW=\sum^{L}_{h=1} N_{h} \rho^{2}_{h}, SSW=N \rho^{2}$ （2）
$P_{D,H}=1-\frac{SSW}{SST}$ （3）
式2中,h=1,...,L为变量Y或因子X的分层,即分类或分区;Nh和N分别为层和全区的单元数;SSW和SST分别为层内方差之和和全区总方差。D为影响因子,H为目标土壤重金属含量的空间变化值,PD,H为D对H的解释力。
生态探测器用于比较影响因子X1和X2对目标属
性Y的空间分布的影响是否有显著的差异,以F统计量来衡量：
$F=\frac{N_{X1}(N_{x2-1})SSW_{X1}}{N_{X2}(N_{X1}-1)SSW_{X2}}$ （4）
$SSW_{X1}=\sum^{L1}_{h=1}N_{h} \rho^{2}_{h}, SSW_{X2}=\sum ^{L2}_{h=1}N_{h}\rho^{2}_{h}$ （5）
式4中,NX1及NX2分别表示两个因子X1和X2的样本量;SSWX1和 SSWX2分别表示由X1和X2形成的分层的层内方差之和;L1和 L2分别表示变量X1和X2分层数目。其中零假设H0：SSWX1=SSWX2。如果在α的显著性水平上拒绝H0,则表明两因子X1和X2对目标属性Y的空间分布的影响存在着显著的差异。
交互作用探测器是探测风险因子之间是否具有相互作用,判断公式如下：
协同：PD,H(D1∩D2)> PD,H(D1)或PD,H(D2)
双协同：PD,H(D1∩D2)> PD,H(D1)和PD,H(D2)
非线性协同：PD,H(D1∩D2)> PD,H(D1)+PD,H(D2)
拮抗：PD,H(D1∩D2)<PD,H(D1)+PD,H(D2)
单拮抗：PD,H(D1∩D2)<PD,H(D1)或PD,H(D2)
非线性拮抗：PD,H(D1∩D2)<PD,H(D1)和PD,H(D2)
相互独立：PD,H(D1∩D2)= PD,H(D1)+PD,H(D2)
由于进行风险分析时,对于面数据,自变量X即土壤重金属含量和因变量Y即影响因子的空间粒度是不同的,因此首先对面数据,例如平均气温、相对湿度、高程数据和GDP数据进行直接等分离散化,再将其与X分布叠加,然后利用ArcGIS软件提取每个离散点上的因变量与自变量值（Y,X）;对于点数据,包括土壤pH和土壤类型数据与土壤重金属采样点数据相对应,可以直接将这些点数据导入到地理探测器软件中进行计算。
地理探测器的具体实现采用GeoDetector软件（http://www.geodetector.org/）,该软件使用步骤包括数据采集与整理、读入样本（Y, X）数据、分析结果三部分。对于输入的面数据和点数据需要做匹配处理,连续型属性需要做离散化处理。软件运行结果主要包括 4个部分：比较不同影响因子对土壤采样点中的目标重金属含量的空间分异性影响是否显著;影响因子对土壤采样点中的目标重金属含量的空间分异性的解释力;不同的影响因子对目标重金属含量的空间分异性的影响是否具有显著差异;以及这些影响因子对目标重金属含量的空间分异性影响的交互作用。
2 结果
2.1 土壤重金属空间分布特征
根据2014年对湘潭县5个乡（镇）的土壤重金属789个采样点数据,利用ArcGIS软件对5种土壤重金属进行反距离插值处理,得到该区域5种土壤重金属的空间分布图（图2）。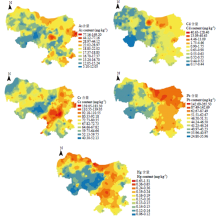
显示原图|下载原图ZIP|生成PPT图25 种土壤重金属空间分布图
-->Fig. 2Spatial distribution of five soils heavy metals
-->
如图2所示,研究区东部和北部土壤重金属As、Cd、Pb和Hg元素含量明显高于其他区域,呈现从西向东逐渐增加趋势。其中Hg含量较高的区域为湘江边上及东部工业发达区。土壤重金属元素Cr在南部区域的含量较高,且沿着国道有一定带状趋势。对Cr含量最高的区域进一步研究发现,此区域有国道与多条公路交错,交通发达,有丰富的矿石资源和多家化工企业,Cr的来源很有可能与此有关。土壤重金属可来源于土壤成土母质、污水灌溉、工业污染源排放、含重金属劣质化肥农药的使用和大气降尘等[14]。从土壤重金属元素与社会因子的直观相关性分析来看,研究区东部和北部是人口密集区,路网密布,工业发达,人类活动频繁,可能对农田土壤重金属的富集带来一定影响。
2.2 土壤重金属含量影响因子分析
2.2.1 风险探测 风险探测器揭示了各影响因子内部不同类别分区间的显著性差异。 本研究引入了多种较易获取的影响因子,包括土壤pH、土壤类型、平均气温、相对湿度、高程数据和GDP数据。各影响因子的空间分布如图3所示。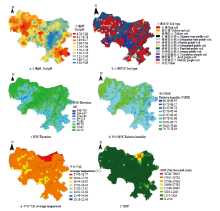
显示原图|下载原图ZIP|生成PPT图3影响因子空间分布图
-->Fig. 3Spatial distributions of influence factors
-->
在地理探测器计算中可以直接利用采样点中的土壤重金属数据,不需要再做离散化处理。对于影响因子中高程、平均气温等面数据,在提取影响因子在每个采样点上的数值的基础上,将每个采样点的5种土壤重金属Pb、Cd、As、Cr、和Hg分别作为目标属性Y1、Y2、Y3、Y4、Y5和Y6,6种影响因子分别作为自变量X1—X6,最后将每一条（Y,X）记录输入到GeoDetector中计算得到各因子的探测结果。探测结果表明,所有影响因子均存在差异性,说明所研究的影响因子对土壤重金属的空间分布具有风险性。
2.2.2 因子探测 利用因子探测器探测影响因子分别对5种土壤重金属元素的相对重要性,即各影响因子对每种重金属元素作为目标属性Y的解释力PD,H值（图4）。
结果表明,影响因子对5种土壤重金属的解释力PD,H既有一致性,又有差异性。GDP、平均温度和相对湿度对5种土壤重金属解释力较大（PD,H值均在0.5以上）。可能是由于GDP体现了工业发达程度,而工业排放是土壤重金属的重要来源。而平均温度和相对湿度可能从多个方面影响土壤重金属,例如通过影响成土母质的形成或土壤重金属的迁移和转化来间接影响土壤重金属的含量。土壤pH、土壤类型、高程对土壤重金属的解释力较小（PD,H值均在0.3以下）,其中土壤类型对于5种土壤重金属的解释力最低（PD,H值均在0.1以下）。高程对Cr的解释力明显大于其对Pb、Cd、Hg和As的解释力,可能是由于Pb、Cd、As和Hg主要来源于人为干扰输入,而Cr生成和迁移过程受地势影响较大。
显示原图|下载原图ZIP|生成PPT图4各影响因子对5种土壤重金属的解释力PD,H值
-->Fig. 4Effects of different factors on the explanatory power of five heavy metals in soils with PD,H value
-->
显示原图|下载原图ZIP|生成PPT图55种土壤重金属之间的解释力对比
-->Fig. 5Comparison of explanatory power between five heavy metals in soils
-->
本研究除了对影响因子进行因子探测,同时也对5种土壤重金属之间的解释力进行了探测,探测结果如图5所示。
图5结果表明,5种土壤重金属之间均有不同强弱的相关性。其中Cr对Cd的解释力最强,PD,H值达到0.95,然而Cd对Cr的解释力相对较小,PD,H值仅为0.24,表明Cr对Cd的影响要明显大于Cd对Cr的影响,可能是由于土壤中的Cr主要来源于岩石风化和工业废水,而Cd来源除了工业三废外,还有不合理的农药和化肥等的使用,相比Cr来源更加广泛。As对Cd的解释力最小,PD,H值仅为0.20,而Cd对As的解释力为0.43,表明As与Cd之间的相关性较弱。其他土壤重金属之间的相关性均较为显著。
2.2.3 生态探测 生态探测着重比较PD,H值的大小来探索一个影响因子对土壤重金属的影响是否比另一个影响因子大,即相对重要性是否显著,若显著,则记为Y,否则记为N。以Pb为例,生态探测结果如表1所示。
由表1可知,采用显著性水平为0.05的t检验。经检验,平均温度、相对湿度和GDP对Pb的影响与其他影响因子存在显著差异,而其他影响因子之间的解释力差异并不显著。
Table 1
表1
表1Pb生态探测结果
Table 1Pb ecological detection results
| 土壤pH Soil pH | 土壤类型 Soil type | 高程 Elevation | 平均温度 Average temperature | 相对湿度 Relative humidity | GDP | |
|---|---|---|---|---|---|---|
| 土壤pH Soil pH | ||||||
| 土壤类型Soil type | N | |||||
| 高程Elevation | N | N | ||||
| 平均温度Average temperature | Y | Y | Y | |||
| 相对湿度Relative humidity | Y | Y | Y | N | ||
| GDP | Y | Y | Y | N | N |
新窗口打开
2.2.4 交互探测 环境中土壤重金属的空间分布是由多种影响因子共同作用的结果。在实际环境中,也不可能存在单一因子或者单一性质的因素影响重金属的分布和变化。利用交互作用探测器探测影响因子对重金属元素空间分布变化的交互作用。对Pb元素而言,不同因子之间的交互作用强弱不同,有显著性差异（表2）。
Table 2
表2
表2不同影响因子对土壤重金属元素Pb影响的交互作用
Table 2Interaction of different influence factors on soil heavy metal element Pb
| 土壤pH Soil pH | 土壤类型 Soil type | 高程 Elevation | 平均温度 Average temperature | 相对湿度 Relative humidity | GDP | |
|---|---|---|---|---|---|---|
| 土壤pH Soil pH | 0.053 | |||||
| 土壤类型Soil type | 0.091 | 0.006 | ||||
| 高程Elevation | 0.518 | 0.165 | 0.077 | |||
| 平均温度Average temperature | 0.981 | 0.681 | 0.880 | 0.622 | ||
| 相对湿度Relative humidity | 0.981 | 0.681 | 0.880 | 0.622 | 0.622 | |
| GDP | 0.976 | 0.651 | 0.848 | 0.713 | 0.713 | 0.575 |
新窗口打开
对于目标土壤重金属各影响因子之间主要是双协同作用和非线性协同作用,不存在相互独立起作用的因子。平均气温、相对湿度和GDP对Pb均为双协同作用,其余影响因子对Pb均为非线性协同作用。GDP可以增强自然因子对土壤重金属空间分布变化的解释力,说明人类活动对土壤重金属的空间变化有一定影响。
本研究还对5种土壤重金属元素之间的交互作用进行了交互探测。交互探测结果表明,除了影响因子之间存在交互作用,5种土壤重金属元素之间同样存在一定交互作用。以Pb为目标属性,则其余4种土壤重金属之间的交互作用均为双协同作用,无非线性协同作用。以Cd为目标属性,则Pb∩Cr、As∩Cr、Cr∩Hg为双协同作用,其余为非线性协同作用;以As为目标属性,则除Cd∩Hg为非线性协同作用外,其余均为双线性协同作用;以Cr为目标属性,则其余4种土壤重金属之间的交互作用均为
非线性协同作用;以Hg为目标属性,则Cd∩As和As∩Cr为非线性协同作用,其余均为双协同作用。土壤重金属之间的交互作用从一定程度上可以反映土壤重金属的复合污染状况。土壤重金属的污染往往是多种重金属元素共同作用形成的。Pb和Cd之间为双线性协同作用,很有可能是Pb和Cd具有相同污染源,如污水灌溉等。通过重金属元素之间的交互作用,可以推测它们污染来源的关系,进一步确定污染源头。
2.2.5 地理探测器与Pearson相关系数对比分析
土壤重金属与影响因子之间的相关分析最常用的方法是Pearson相关系数。以重金属Pb为例,分别利用地理探测器和Pearson相关系数分析方法对Pb和6种影响因子进行相关性分析,结果如图6所示。
显示原图|下载原图ZIP|生成PPT图6地理探测器和Pearson分析Pb与影响因子相关性结果对比
-->Fig. 6Comparison of correlation between Pb and influence factors in geographical detectors and Pearson analysis
-->
从图6对比结果中发现,两种方法得到的结果有一定的相似性和差异性。相似性体现在两种方法均可以得到6种影响因子与Pb的相关性强弱的排序结果,差异性体现在两种方式获得的排序结果有差异。例如Pearson相关分析结果显示高程和土壤pH与Pb成负相关,而地理探测器相关分析结果并无负相关。这也说明了两种方法在相关分析方面的差异性。Pearson相关系数分析方法主要是衡量土壤重金属与影响因子之间的线性关系,同时可以根据相关系数的正负来判断影响因子与土壤重金属是属于正相关还是负相关。而地理探测器模型探测的是土壤重金属与影响因子之间的关联性,既包括线性关系,也包含非线性关系。如果Pearson相关系数不显著,表明土壤重金属与影响因子之间没有明显线性关系,但是不代表没有非线性关系。因此,从这个角度来看,地理探测器的相关分析结果可能更全面,更符合空间数据的特点。
3 讨论
3.1 土壤重金属空间特征与建模策略
土壤重金属空间数据探索性分析结果表明土壤重金属具有空间异质性,与诸多研究结果一致。产生空间分异性的原因是多样的,可能由于各层（类）的机理、因子或者主导因子不同导致不同的空间分异性。因此在数据分析开始时,应当首先进行空间异质性检验,确定是使用全局模型还是局域模型,是使用全局变量还是使用局域变量,是使用全局参数还是局域参数。用全局模型分析具有异质性的对象将掩盖对象的异质性,被混杂效应所干扰,甚至导致错误的结论[12],不同的对象性质对应不同的建模策略。经检验,本研究中的5种土壤重金属均有较强的空间异质性,符合地理探测器的适用条件。本研究通过对湘潭县域5种土壤重金属与6种影响因子分别进行风险探测、因子探测、生态探测和交互作用探测,得到与目标重金属有较强相关性的影响因子。在土壤重金属空间预测模型的建立中,既可以直接选择这部分影响因子作为辅助变量,也可以根据不同的对象性质和研究目的为土壤重金属空间预测模型选择不同的建模策略。选择多种影响因子作为辅助变量时,要考虑多个影响因子对土壤重金属的交互作用,使得选择的参数更加准确合理。3.2 多因子相关性分析问题
在多影响因子研究中,需要去除多个影响因子之间的冗余性和共线性。例如本研究中的平均气温、高程和相对湿度存在一定的共线性。在以往的研究中,为了有效的避免多重共线性问题,需要利用主成分分析方法对影响因子进行降维处理,而地理探测器在原理上解决了影响因子“多重共线”问题,而不局限于经典统计学预先指定的相乘或者单纯相加的模式,且具有更好的解释性。土壤重金属的空间分布是由多种影响因子共同作用的结果,不存在相互独立起作用的因子。对多个影响因子的选择上,根据影响因子的PD,H值大小选择合理数量的影响因子作为土壤重金属预测模型中的辅助变量。4 结论
4.1
风险探测器结果表明影响因子对土壤重金属存在风险性;因子探测器揭示了影响因子对5种土壤重金属的解释力PD,H的一致性和差异性。土壤重金属空间数据探索性分析结果表明,土壤重金属具有空间异质性。交互作用探测证明了土壤重金属的空间分布是由多种影响因子共同作用的结果,不同因子之间的交互作用强弱不同,有显著性差异。其中平均温度、GDP和相对湿度3种影响因子对5种土壤重金属的相关性较强。除了影响因子之间存在交互作用,5种土壤重金属元素之间同样存在双协同作用和非线性协同作用。土壤重金属之间的交互作用与土壤重金属的复合污染状况有一定联系。4.2 不同影响因子对于土壤重金属的影响程度不同。
在对土壤重金属与影响因子的相关性分析中,地理探测器有效地利用影响因子以及土壤重金属之间的交互作用,可以更加全面的分析和评估各影响因子对土壤重金属的影响,在研究空间数据的相关性和交互作用方面比经典的统计方法适用范围更广。The authors have declared that no competing interests exist.
