目前常用的变量选择方法有连续投影算法(Successive Projections Algorithm,SPA)[10]、无信息变量消除(Uninformative Variable Elimination,UVE)法[11-12]等。SPA是一种基于变量投影比较的特征波长选择方法。其通过比较某波长在其他波长上的投影,选择投影向量最大的波长作为待选波长,然后基于校正模型的均方根误差(Root Mean Square Error,RMSE)从待选波长集合中选择最终的特征波长。UVE在保留特征波长的同时消除无信息变量,是一种基于偏最小二乘(Partial Least Squares,PLS)模型回归系数的波长选择方法。该方法引入稳定性来评价模型中各变量的可靠性,从而确定最终选择的变量,在光谱变量的选择中得到了广泛的应用。这些方法的一个共同特点是,它们试图为给定的数据集选择一个固定的变量子集,而不考虑样本变化对变量选择的影响。
结合蒙特卡罗采样(Monte Carlo Sampling,MCS)技术建立变量选择方法可以有效地解决这一问题。例如,竞争自适应重采样(Competitive Adaptive Reweighted Sampling,CARS)[13]基于MCS和PLS回归系数选择特征变量。其首先通过MCS建立PLS模型,然后通过自适应加权采样保留模型中回归系数绝对值权重较大的波长作为新的子集,基于新的波长子集重新建立PLS模型,经过多次计算,选择交叉验证均方根误差(Root Mean Square Error of Cross Validation,RMSECV)最小的波长子集作为特征波长,降维性能较好。此外,其他变量选择方法包括蒙特卡罗无信息变量消除(Monte Carlo-Uninformative Variable Elimination,MC-UVE)[14]、模型种群分析(Model Population Analysis,MPA)[15]和变量互补网络(Variable Complementary Network,VCN)[16]等方法表明,结合MCS进行变量选择可以得到更好的预测结果。
本文搭建了葡萄籽总酚含量近红外高光谱预测系统,根据模型集群分析的思想,提出了将MCS和波长出现频次结合选择特征波长的方法,简称蒙特卡罗频率法(Monte Carlo Frequency,MCF)。该方法能够减少建模过程中的无信息变量及干扰变量,为开发葡萄籽总酚含量检测设备提供理论依据。
1 材料与方法 1.1 样本采集 试验样品来自陕西省杨凌盛唐酒庄,包括霞多丽、贵人香、8802、8803和雷司令5个白葡萄品种。采摘工作从葡萄转色期至成熟期进行,由于不同品种酿酒葡萄的成熟时间存在差异,采摘时间为2015年7月中旬至9月中旬。每个品种从转色期一周后开始,15天作为一个采摘周期,共采摘3次。每次采摘4组葡萄,每组20个葡萄(籽)作为一个样本。因此,每个品种包括12个样本,总计60个样本。将采摘的样本快速运送到实验室,手工将葡萄籽分离出来,拍摄其近红外高光谱图像,随后用蛋白质沉淀法[17]测量其总酚含量。
原始图像具有256个波长,去除两端包含噪音的波段,最终选择950~1 600 nm之间196个波长对应的光谱数据。为了去除高频随机噪声等干扰因素[18],采用S-G滤波[19]对数据进行预处理,预处理后的平均光谱如图 1所示。随机将样本按4:1的比例分为训练集和测试集,葡萄籽总酚含量分布如表 1所示。
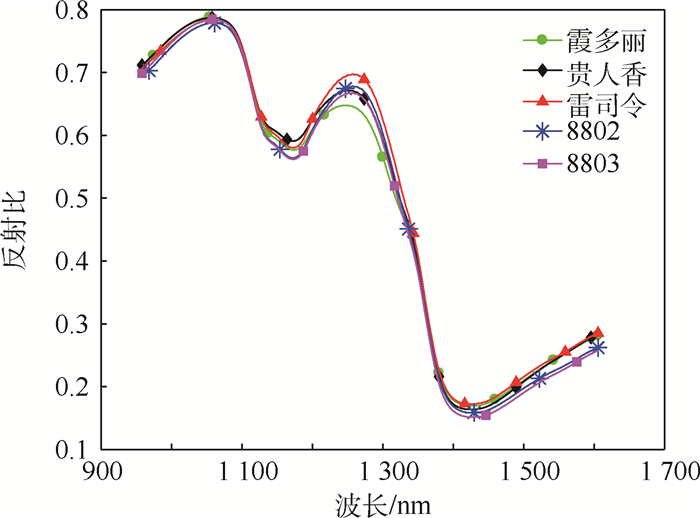 |
| 图 1 预处理后的5个品种葡萄籽平均光谱 Fig. 1 Average spectra of five types of pretreated grape seeds |
| 图选项 |
表 1 葡萄籽总酚含量分布统计 Table 1 Distribution statistics of total phenol content in grape seeds
| 参数 | 训练集 | 预测集 |
| 样本数 | 48 | 12 |
| 最小值/(g·L-1) | 1.720 8 | 2.192 7 |
| 最大值/(g·L-1) | 8.386 9 | 8.326 3 |
| 平均值/(g·L-1) | 4.531 9 | 4.972 3 |
| 标准偏差/(g·L-1) | 1.642 9 | 1.858 6 |
表选项
1.2 仪器设备 本文采用HyperSIS高光谱成像系统,包括IMSpector N17E型近红外成像光谱仪(Spectral Imaging Ltd.,Finland)、320像素×256像素的XEVA3616型面阵CCD相机(XenICs Ltd.,Belgium)、白光漫反射型卤钨白炽灯(4个)、高精度电动平移载物台和一台计算机。该系统的光谱分辨率为2.8 nm,采集的波长范围为900~1 700 nm,平台移动速度为20 mm/s,相机曝光时间为10 ms。本文方法均在MATLAB R2017a中实现。
1.3 预测模型 本文采用支持向量回归(Support Vector Regression,SVR)建立葡萄籽总酚的预测模型,用于比较MCF和其他常用变量选择方法的性能。SVR是一种适用于解决小样本、非线性及高维数据问题的方法[20-21]。SVR通过核函数,将低维空间向量映射到高维空间,在高维空间中构造线性决策函数来实现原空间中的非线性决策。考虑到高光谱数据和预测变量总酚含量之间映射关系的复杂性和非线性,利用SVR建模在一定程度上规避了过拟合风险。本文使用Libsvm[22]实现SVR方法。
1.4 评价指标 本文采用相关系数R2和RMSE作为回归模型的评价指标。R2越高,RMSE越低,表明模型的效果越好。R2和RMSE的计算公式分别为
 | (1) |
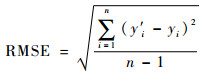 | (2) |
式中:y′i和yi分别为第i个样本的预测值和真实值;yi为样本的平均值;n为样本个数。
2 基于蒙特卡罗频率法选择波长变量 蒙特卡罗方法是一种基于随机数和概率统计来研究问题的技术。本文提出的MCF是一种基于MCS和波长出现频次的变量选择方法,该方法可以和多种回归方法结合,能够有效选择特征变量。
2.1 模型集群分析基本思想 模型集群分析[15]方法是首先通过MCS获取数据子集;然后针对每个子数据集,建立一个子模型;最后从样本空间、变量空间、参数空间或者模型空间中,对所有建立的集群子模型的参数进行统计分析,以获得有用信息。
2.2 基本原理 MCF选择特征波段主要采用MCS选择波长子集,然后利用波长子集建立大量回归子模型;选择RMSE较小的子模型,统计每个波长出现的频次;根据指数递减函数选择波长个数,选取频次最高的波长作为特征波长,具体步骤如下:
1) MCS选择波长子集。设样本的光谱矩阵X为n×q,表示矩阵由n个样本和q个波长组成;化学值Y由向量n×1表示。根据模型集群分析的建模思想,首先采用MCS对所有波长进行采样,每次随机选择p(p < q)个波长,可得到n×p的子光谱矩阵。将该过程重复N次(N>1 000),得到N个子数据集(Xsub, Y)i,i=1, 2, …,N。此过程不仅能得到N组不同变量的组合,还能确保每个变量具有相同的采样频率。
2) 将子数据集按4:1随机分为训练集和预测集,建立N个回归子模型。SVR是一种适用于解决小样本及高维数据问题的最常用的建模方法,因此本文采用SVR建立预测模型,然后计算N个子模型预测集的RMSE。
3) 计算波长出现的频率。将上述所有子模型按照预测RMSE从小到大进行排序,只保留预测结果较好的前K个子模型,计算这些模型中各个波段出现的频次f。一般波段出现频次越高,则认为该波段和化学值相关性越高,根据频次对波长进行重要性排序。f的计算公式为
 | (3) |
式中:i为波段序号;j表示保留的子模型;Fi表示波段i是否出现在模型j中,若出现则为1,否则为0;K为保留子模型的个数。
4) 根据指数递减函数选择波长个数。建立m个SVR回归模型,根据模型的预测RMSE选择最佳的特征波长个数。指数递减函数[13]定义为
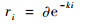 | (4) |
式中:ri为第i次选择的波长个数;?和k是由以下2个条件决定常数:
1) 在第一次运行中,所有q个波长都被用来建模。由于本文共采用了波段裁剪后的196个原始波长,因此r1=196。
2) 在第m(本文取m=40)次运行中,只保留2个波长,即r40=2。
在这2个条件下,?和k的计算公式分别为
 | (5) |
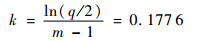 | (6) |
图 2所示为指数递减函数选择波长个数的过程。可以看出,波长个数呈递减趋势,并分为2个阶段,第1阶段波长数量下降较快,可快速去除出现频次少的波长;第2阶段波长数量下降缓慢,可有效保留出现频次较高的波段。
 |
| 图 2 MCF特征波长个数选择 Fig. 2 Selection of number of characteristic wavelengths by MCF |
| 图选项 |
3 结果与分析 3.1 不同波长选择方法的预测结果 为了验证提出方法的有效性,将MCF与SPA、CARS等2种方法分别结合SVR方法,预测葡萄籽中的总酚含量。
MCF通过MCS,每次从训练集中随机选择100个波段构建回归子模型。重复2 000次,并计算各子模型的RMSE。然后,对所有子模型进行排序,根据RMSE值由小到大,分别选择前10%、20%、30%、40%和50%的子模型,计算模型中每个波长出现的频率。根据式(4)的指数递减函数选择RMSE较小的波长数作为特征波长个数(见图 2),并找出出现频率最高的波长子集作为特征波长。实验表明,前30%的子模型预测性能最佳,因此,本文保留前30%子模型用于计算波长频率。各波段频次分布如图 3所示,最终MCF选择9个特征波长。
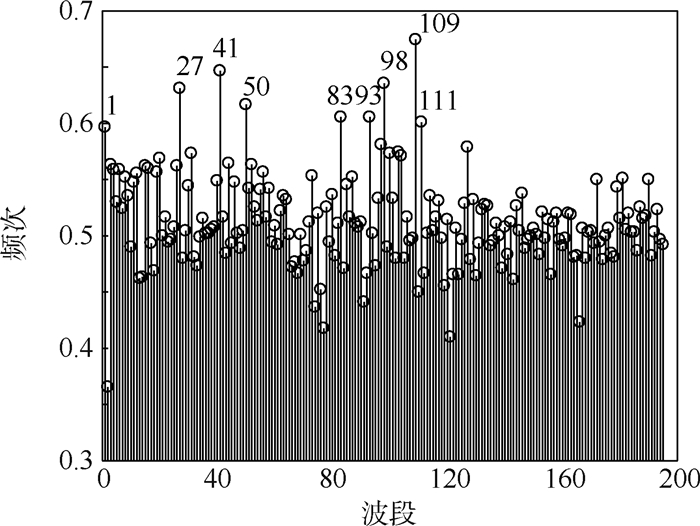 |
| 图 3 波段频次分布 Fig. 3 Frequency distribution of spectral bands |
| 图选项 |
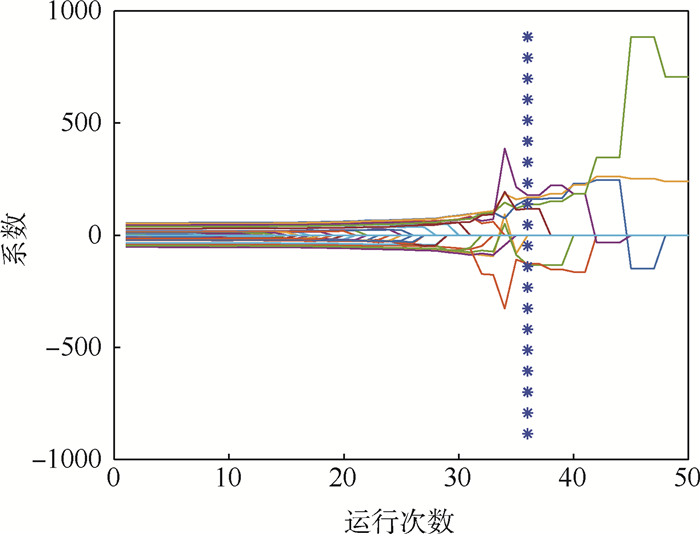 |
| 图 4 CARS方法波长的系数变化 Fig. 4 Coefficient variation of wavelength by CARS |
| 图选项 |
在SPA降维算法中,设置波长个数范围为2~49,根据训练集RMSE值确定最佳的光谱变量总数。当波长数量较少时,RMSE值较大,随着波长个数的增加,RMSE开始呈下降趋势,当选取18个波长时达到最小值。因此,SPA最终选择的波长个数为18。
图 4为采用CARS进行特征波长选择后,各波长的回归系数路径,设置采样次数为50次。每条线反映一个波长系数的变化。星号线处的临界点表示RMSECV的最优子集,星号之后由于有效波长的去除,RMSECV值开始增大。根据RMSECV值最小的原则,CARS共选择了7个特征波长。
图 5为3种方法选择的变量分布,直观地给出了方法所选变量的波长分布。可以看出,3种方法波长选择区间大致相同,主要集中在950~1 400 nm。由于高光谱图像光谱分辨率高,光谱曲线几乎连续分布,相邻波长之间数据相关性强,而MCF的特征波长分布较为均匀,说明该方法在去除冗余信息方面具有优势。此外,SPA选取18个特征波长,波长个数最多。CARS选择波长个数最少,其光谱包含的信息量少,因此可能导致模型效果不理想。可进一步根据回归模型的R2和RMSE比较3个方法的优劣。
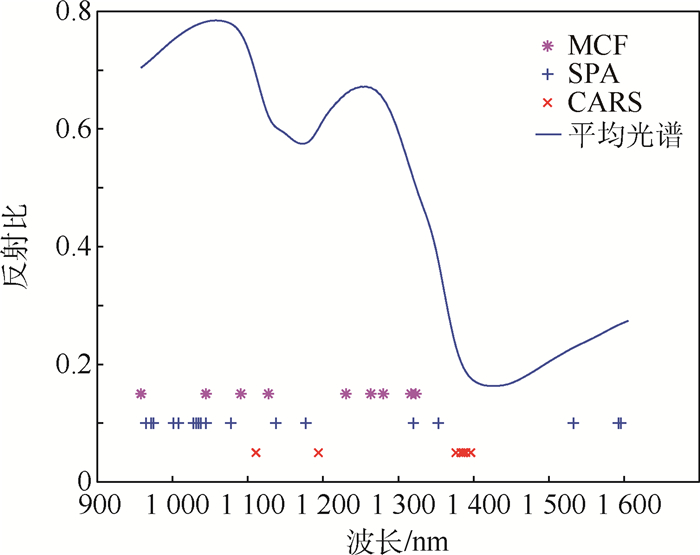 |
| 图 5 3种方法选择的变量分布 Fig. 5 Distribution of variables selected by three methods |
| 图选项 |
以总酚含量为因变量(Y),基于波长选择的光谱为自变量(矩阵X)构建SVR模型。采用高斯径向基函数(Radial Basis Function,RBF)作为SVR的核函数,通过网格寻优算法找到使分类模型最佳的惩罚函数c和核函数参数g,c和g寻优范围取[2-8,216]。通过训练集和预测集的R2和RMSE对模型性能进行评价。
不同降维方法对葡萄籽总酚含量预测结果如表 2所示。可以看出,全光谱模型的预测R2和RMSE分别约为0.90和0.42,表明总酚含量与高光谱数据高度相关。对比3种方法,MCF降维后模型具有最大的预测R2(0.91)和最小的RMSE(0.37),预测结果最好。该方法分别选择了958、1 044、1 091、1 127、1 230、1 264、1 280、1 317和1 323 nm处的特征波长。SPA选取波段个数最多,其模型结果略低于MCF,预测R2达到0.89。CARS选取波长个数最少,同时预测效果最差,预测相关系数均小于0.80。此外,MCF降维后的波长预测结果优于全波段,说明该波长选择方法可以提高模型的预测准确度。
表 2 不同降维方法的总酚预测结果比较 Table 2 Comparison of total phenol prediction results with different dimensionality reduction methods
| 方法 | 变量数 | (c,g) | 训练集 | 预测集 | |||
| R2 | RMSE | R2 | RMSE | ||||
| SVR | 196 | (256, 84.45) | 0.952 4 | 0.133 8 | 0.900 4 | 0.416 3 | |
| MCF-SVR | 9 | (362, 2 048) | 0.924 4 | 0.204 9 | 0.905 9 | 0.374 1 | |
| SPA-SVR | 18 | (2 896, 362) | 0.920 8 | 0.216 0 | 0.886 7 | 0.476 7 | |
| CARS-SVR | 7 | (256, 1 448) | 0.812 9 | 0.504 7 | 0.791 3 | 0.829 4 | |
表选项
3.2 MCF性能影响因素
3.2.1 采样次数 为了研究MCS次数对MCF性能的影响,将波长采样次数分别设置为1 000、2 000、3 000、4 000和5 000次,建立SVR子模型并统计各模型的预测RMSE值,箱型图如图 6所示。由图可得, 不同采样次数下N个模型的RMSE最大值、最小值和中值接近,RMSE分布无明显差别。结果表明,MCS次数对MCF的性能没有显著影响。因此,本文采用2 000次作为默认波长采样次数。
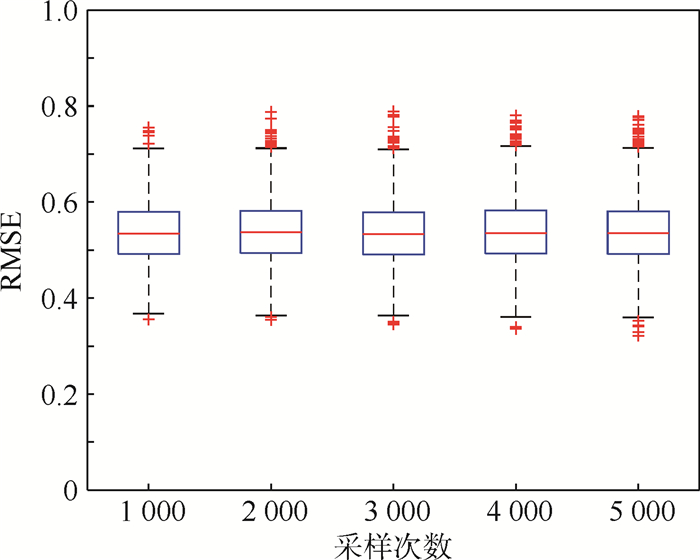 |
| 图 6 MCF不同采样次数的箱型图 Fig. 6 Box graph of MCF with different sampling times |
| 图选项 |
3.2.2 MCF结合不同回归方法 对MCF结合不同回归方法的性能进行比较。除SVR之外,还采用最小二乘回归(Partial Least Squares Regression,PLSR)法、RBF神经网络建立子模型选择特征波段。为了比较不同回归方法的波段选择效果,采用蒙特卡罗对波长采样2 000次,分别用SVR、PLSR和RBF这3种方法建立回归子模型,选择出现频次最高的前9个波长作为特征波长。用特征波长建立葡萄籽总酚的SVR预测模型,表 3为不同模型的预测结果。MCF结合3种回归方法进行波段选择,预测R2达到0.85~0.91,RMSE约为0.37~0.55。而其中采用SVR建立子模型进行波段选择时,预测效果最佳。
表 3 MCF结合不同回归方法的总酚预测结果比较 Table 3 Comparison of total phenol prediction results of MCF combined with different regression methods
| 回归方法 | (c, g) | 训练集 | 预测集 | |||
| R2 | RMSE | R2 | RMSE | |||
| SVR | (362, 2 048) | 0.924 4 | 0.204 9 | 0.905 9 | 0.374 1 | |
| PLSR | (20.55, 5 793) | 0.884 7 | 0.366 2 | 0.853 9 | 0.546 6 | |
| RBF | (862, 724) | 0.872 2 | 0.340 6 | 0.875 6 | 0.428 9 | |
表选项
4 结论 本文提出了一种基于MCS和波长出现频次结合的变量选择方法, 简称蒙特卡罗频率法(MCF)。
1) 针对葡萄籽总酚近红外高光谱,利用MCF进行特征波长选择,波长数目由196个减少到9个。
2) 采用SVR建立总酚的回归模型,预测R2和RMSE分别约为0.91和0.37。与其他变量选择方法相比,MCF在减少无信息变量和干扰变量的同时提高了模型的预测结果。
3) 讨论了MCS次数和不同回归方法对MCF性能的影响。结果表明,采样次数对MCF波长选择无显著影响,采用SVR建立子模型进行波段选择时,模型效果最佳。
因此,MCF可以作为一种有效的波长选择工具应用于高光谱数据分析,具有良好的预测性能。
致谢 感谢西北农林科技大学葡萄酒学院刘旭副教授及其团队在样本采集和葡萄籽总酚含量测量中的贡献。
参考文献
| [1] | 张保华, 李江波, 樊书祥, 等. 高光谱成像技术在果蔬品质与安全无损检测中的原理及应用[J]. 光谱学与光谱分析, 2014, 34(10): 2743-2751. ZHANG B H, LI J B, FAN S X, et al. Principle and application of high spectral imaging technology in nondestructive testing of fruit and vegetable quality and safety[J]. Spectroscopy and Spectral Analysis, 2014, 34(10): 2743-2751. DOI:10.3964/j.issn.1000-0593(2014)10-2743-09 (in Chinese) |
| [2] | CHEN S, ZHANG F, NING J, et al. Predicting the anthocyanin content of wine grapes by NIR hyperspectral imaging[J]. Food Chemistry, 2015, 172: 788-793. DOI:10.1016/j.foodchem.2014.09.119 |
| [3] | EIMASRY G, SU D W, ALLEN P, et al. Near-infrared hyperspectral imaging for predicting colour, pH and tenderness of fresh beef[J]. Journal of Food Engineering, 2012, 110(1): 127-140. DOI:10.1016/j.jfoodeng.2011.11.028 |
| [4] | LEO L, ROGER J M, HERRERO-LANGREO A, et al. Comparison of multispectral indexes extracted from hyperspectral images for the assessment of fruit ripening[J]. Journal of Food Engineering, 2011, 104(4): 612-620. DOI:10.1016/j.jfoodeng.2011.01.028 |
| [5] | GMES V M, FERNANDES A M, FAIA A, et al. Comparison of different approaches for the prediction of sugar content in new vintages of whole port wine grape berries using hyperspectral imaging[J]. Computers and Electronics in Agriculture, 2017, 140: 244-254. DOI:10.1016/j.compag.2017.06.009 |
| [6] | LI W, PRASAD S, FOWLER J E, et al. Locality-preserving dimensionality reduction and classification for hyperspectral image analysis[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(4): 1185-1198. |
| [7] | 宦克为, 刘小溪, 郑峰, 等. 基于蒙特卡罗特征投影法的小麦蛋白质近红外光谱测量变量选择[J]. 农业工程学报, 2013, 29(4): 266-271. HUAN K W, LIU X X, ZHENG F, et al. Selection of variables for wheat protein near infrared spectroscopy based on monte carlo characteristic projection[J]. Journal of Agricultural Engineering, 2013, 29(4): 266-271. (in Chinese) |
| [8] | 郝勇, 孙旭东, 潘圆媛, 等. 蒙特卡罗无信息变量消除方法用于近红外光谱预测果品硬度和表面色泽的研究[J]. 光谱学与光谱分析, 2011, 31(5): 1225-1229. HAO Y, SUN X D, PAN Y Y, et al. Monte-carlo method of elimination of uninformed variables was used to predict fruit hardness and surface color by near infrared spectroscopy[J]. Spectroscopy and Spectral Analysis, 2011, 31(5): 1225-1229. DOI:10.3964/j.issn.1000-0593(2011)05-1225-05 (in Chinese) |
| [9] | 顾章源, 刘翔, 苏枫, 等. 基于流形学习的多光谱优化波段选择算法研究[J]. 上海航天, 2017, 34(3): 40-46. GU Z Y, LIU X, SU F, et al. Research on multi-spectral optimal band selection algorithm based on manifold learning[J]. Aerospace Shanghai, 2017, 34(3): 40-46. (in Chinese) |
| [10] | ARAUJO M C U, SALDANHA T C B, GALVAO R K H, et al. The successive projections algorithm for variable selection in spectroscopic multicomponent analysis[J]. Chemometrics & Intelligent Laboratory Systems, 2001, 57(2): 65-73. |
| [11] | CENTNER V, MASSART D L, NOORD O E D, et al. Elimination of uninformative variables for multivariate calibration[J]. Analytical Chemistry, 1996, 68(21): 3851-3858. DOI:10.1021/ac960321m |
| [12] | MOROS J, KULIGOWSKI J, QINTAS G, et al. New cut-off criterion for uninformative variable elimination in multivariate calibration of near-infrared spectra for the determination of heroin in illicit street drugs[J]. Analytica Chimica Acta, 2008, 630(2): 150-160. DOI:10.1016/j.aca.2008.10.024 |
| [13] | LI H, LIANG Y, XU Q, et al. Key wavelengths screening using competitive adaptive reweighted sampling method for multivariate calibration[J]. Analytica Chimica Acta, 2009, 648(1): 77-84. DOI:10.1016/j.aca.2009.06.046 |
| [14] | CAI W, LI Y, SHAO X. A variable selection method based on uninformative variable elimination for multivariate calibration of near-infrared spectra[J]. Chemometrics & Intelligent Laboratory Systems, 2008, 90(2): 188-194. |
| [15] | LI H, LIANG Y, XU Q, et al. Model population analysis for variable selection[J]. Journal of Chemometrics, 2010, 24(7-8): 418-423. DOI:10.1002/cem.1300 |
| [16] | LI H, XU Q, ZHANG W, et al. Variable complementary network:A novel approach for identifying biomarkers and their mutual associations[J]. Metabolomics, 2012, 8(6): 1218-1226. DOI:10.1007/s11306-012-0410-z |
| [17] | HARBERTSON J F, PICCIOTTO E A, ACKERMANN K.Phenolic and anthocyanin assay for use with spectrophotometer[D].Davis, CA: University of California, 2005. |
| [18] | 褚小立, 袁洪福, 陆婉珍. 近红外分析中光谱预处理及波长选择方法进展与应用[J]. 化学进展, 2004, 16(4): 528-542. CHU X L, YUAN H F, LU W Z. Progress and application of spectral pretreatment and wavelength selection methods in nir analysis[J]. Progress in Chemistry, 2004, 16(4): 528-542. DOI:10.3321/j.issn:1005-281X.2004.04.008 (in Chinese) |
| [19] | GORRY P A. General least-squares smoothing and differentiation by the convolution (Savitzky-Golay) method[J]. Analytical Chemistry, 1990, 62(6): 570-573. |
| [20] | ZHANG C, GUO C, LIU F, et al. Hyperspectral imaging analysis for ripeness evaluation of strawberry with support vector machine[J]. Journal of Food Engineering, 2016, 179: 11-18. DOI:10.1016/j.jfoodeng.2016.01.002 |
| [21] | NI Z, XU L, XIAODUO J, et al. Determination of total iron-reactive phenolics, anthocyanins and tannins in wine grapes of skins and seeds based on near-infrared hyperspectral imaging[J]. Food Chemistry, 2017, 237: 811-817. DOI:10.1016/j.foodchem.2017.06.007 |
| [22] | CHANG C C, LIN C J. LIBSVM:A library for support vector machines[J]. ACM Transactions on Intelligent Systems and Technology, 2011, 2(3): 27. |
