在化工安全领域,爆炸碎片特性的研究主要利用Monte-Carlo方法仿真储罐爆炸碎片抛射轨迹[2]、构建爆炸碎片冲击失效模型[3]、预测沸腾液体膨胀蒸汽爆炸(BLEVE)事故中碎片的初始速度等[4]。在战斗部爆破领域,Gurney[5]以炸药质量和壳体质量的比值为基本参数提出了求解碎片飞散速度的Gurney公式,该公式应用最广泛;工程上,相关****基于炸药爆热提出了计算碎片速度的半经验公式[6],该公式对于单质炸药的计算精度较好,而混合炸药的计算误差较大;印立魁和蒋建伟[7]基于Gurney公式建立了多层球形战斗部爆炸破片初始速度的计算模型,给出了各层破片的平均初始速度。在航空航天领域,王卫杰等[8]针对液体火箭芯一级贮箱爆炸,推导了爆炸碎片初始速度(Fragment Initial Velocity, FIV)模型,模型中忽略了贮箱壳体的破坏能和传给空气介质的能量;美国国家航空航天局(NASA)基于图表法提出了求解柱形和球形高压容器爆炸碎片初始速度的方法[9],但该方法对容器内气体爆轰压强有一定的要求,适用范围受到限制。
本文基于能量守恒定律,考虑爆炸碎片动能、爆轰产物动能和内能、贮箱壳体的破坏能及其膨胀做功所消耗的能量,构建了贮箱爆炸FIV模型。基于量纲分析法,确定影响碎片初始速度的关键参量,利用AUTODYN软件中的光滑粒子流体动力学(Smooth Particle Hydrodynamics, SPH)算法进行数值仿真,分析贮箱壳体高径比、厚径比以及大气密度等对爆炸碎片初始速度的影响。
1 爆炸碎片初始速度模型 贮箱爆炸FIV模型基于以下假设:不考虑爆轰反应的过程,将化学反应区看作一个强间断面;将贮箱看作等壁厚的圆柱壳体,只考虑爆炸产物沿径向的飞散;推进剂全部参与爆轰反应,爆炸碎片初始速度的大小相同。
根据能量守恒定律,推进剂爆炸释放的总能量Et主要用于以下几部分:
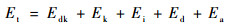 | (1) |
式中:Edk为贮箱爆炸碎片的动能;Ek为爆轰产物的动能;Ei为爆轰产物的内能;Ed为贮箱壳体的破坏能;Ea为贮箱壳体膨胀做功。
1) 推进剂爆炸释放的总能量
液体推进剂爆炸释放的总能量Et为
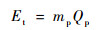 | (2) |
式中:mp为推进剂质量;Qp为推进剂爆热。
2) 爆炸碎片的动能
设爆炸一共产生的碎片数量为N,碎片初始速度为v0,由动能定律得
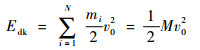 | (3) |
式中:mi为第i个碎片的质量;M为贮箱壳体的质量。
3) 爆轰产物的动能
若推进剂全部参与反应,根据质量守恒,爆轰产物的质量等于推进剂的质量,则爆轰产物动能Ek为
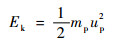 | (4) |
式中:up为爆轰产物的质点速度。
爆轰产物质点速度up与推进剂的爆速D之间的关系为[10]
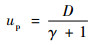 | (5) |
式中:γ为爆轰产物的多方指数,γ=3。
将式(5)代入式(4)得
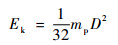 | (6) |
4) 爆轰产物的内能
单位质量爆轰产物的比内能ei、爆热Qp和爆速D之间的近似关系为[8]
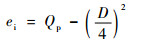 | (7) |
则爆轰产物的内能Ei为
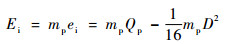 | (8) |
5) 贮箱壳体的破坏能
Hiroe[11]、胡永乐[12]、俞鑫炉[13]等分别研究了内部爆炸载荷作用下,不同金属材料(铝、钢、钛合金)圆柱壳体的动态变形和破坏模式。结果表明,在冲击波加载下,不同材料的圆柱壳体因径向膨胀发生动态塑性变形,产生剪切带,主要呈现出剪切型断裂特征。
若只考虑贮箱壳体在爆炸载荷作用下的剪切断裂,则贮箱壳体的破坏能Ed等于剪切变形能:
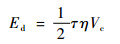 | (9) |
由剪切虎克定律得
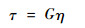 | (10) |
将式(10)代入式(9)得
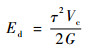 | (11) |
式中:τ为剪切应力;η为剪应变,无量纲;G为剪切弹性模量;Vc为贮箱壳体的体积。
6) 贮箱壳体膨胀做功
爆炸瞬间,在空气中形成的冲击波阵面压力pa为
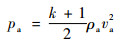 | (12) |
式中:k为空气的等熵绝热指数,对于强冲击波,k=1.2;ρa为未受冲击波扰动的空气密度;va为波阵面的空气质点速度。
空气冲击波的初始速度Da接近于推进剂的爆速D,而va与Da的关系式为
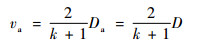 | (13) |
将式(13)代入(12)得
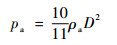 | (14) |
当地空气密度ρa随海平面高度y变化的一般表达式为
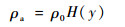 | (15) |
式中:ρ0为海平面的空气密度,ρ0=1.293 kg/m3; H(y)为空气密度修正系数[1]:
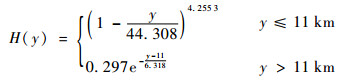 | (16) |
设爆轰瞬间作用于贮箱壳体上的空气冲击波阵面压力pa保持不变,则贮箱壳体等压膨胀时克服空气冲击波压力所做的功Ea,即
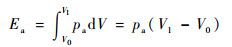 | (17) |
式中:V0为贮箱的初始体积;V1为贮箱完全膨胀后的体积。
根据剪切断裂判据[14],壳体完全膨胀后的半径rf和初始半径r0的关系式为
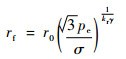 | (18) |
式中:pe为爆轰产物的压力;σ为贮箱材料的屈服应力;kr为修正系数,对于圆柱形壳体,kr=2,对于球形壳体,kr=3。
爆轰产物的压力pe与爆速D之间的关系为
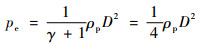 | (19) |
式中:ρp为推进剂的密度。
将式(14)、式(15)、式(18)和式(19)代入式(17)可得
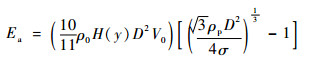 | (20) |
7) 爆炸碎片的初始速度
将式(2)、式(3)、式(6)、式(8)、式(11)和式(20)代入式(1),整理得爆炸碎片初始速度v0为
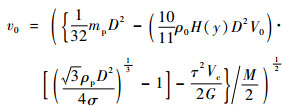 | (21) |
式(21)即为本文建立的贮箱爆炸FIV模型。
2 FIV模型验证 2.1 计算碎片初始速度的经验公式 1) Gurney公式
Gurney[5]针对不同形状的战斗部提出了预测爆炸碎片初始速度的经验公式,对于圆柱形壳体来说,有
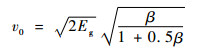 | (22) |
式中:
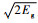
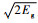
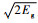
2) 工程半经验公式
工程上经常应用半经验公式计算碎片的初始速度为[6]
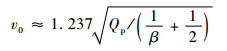 | (23) |
3) 王卫杰模型
王卫杰等[8]将火箭贮箱看作圆柱形壳体,推导了爆炸碎片初始速度的计算公式:
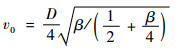 | (24) |
2.2 基于爆炸试验的模型验证 武汉理工大学孔祥韶等[15]开展了三硝基甲苯(TNT)炸药在Q235低碳钢圆柱壳体内的爆炸试验,壳体内径为110 mm,高度为160 mm,厚度为6 mm,装药量为1.9 kg。对于TNT炸药,ρp=1 630 kg/m3, D=6 900 m/s。
北京理工大学张奇等[16]开展了T-H-Al炸药在钢制圆柱壳体内的爆炸试验,壳体内填满炸药,壳体内径为120 mm,厚度为3.5 mm。对于T-H-Al炸药,ρp=1 752 kg/m3, D=7 054 m/s。
劳伦斯-利弗莫尔实验室开展了Comp B炸药在铜制圆柱壳体内的爆炸试验[17],壳体内填满炸药,壳体内径为25.4 mm,厚度为2.6 mm。对于Comp B炸药,ρp=1 720 kg/m3, D=7 980 m/s。
将文献[15-17]试验的相关参数分别代入FIV模型、Gurney公式、工程半经验公式、王卫杰模型开展计算,计算结果、试验结果及两者之间相对误差ε如表 1、表 2和表 3所示。
表 1 文献[15]爆炸试验数据及其理论计算结果 Table 1 Explosion test data in Ref.[15] and theoretical calculation results
| 理论模型 | v0/(m·s-1) | ε/% |
| FIV模型 | 1 356 | 12.3 |
| Gurney公式 | 1 486 | 23.1 |
| 工程半经验公式 | 1 621 | 34.3 |
| 王卫杰模型 | 1 469 | 21.7 |
| 注:文献[15]中v0=1 207 m/s。 | ||
表选项
表 2 文献[16]爆炸试验数据及其理论计算结果 Table 2 Explosion test data in Ref.[16] and theoretical calculation results
| 理论模型 | v0/(m·s-1) | ε/% |
| FIV模型 | 1 630 | 11.4 |
| Gurney公式 | 1 608 | 9.9 |
| 工程半经验公式 | 1 749 | 19.5 |
| 王卫杰模型 | 1 647 | 12.6 |
| 注:文献[16]中v0=1 463 m/s。 | ||
表选项
表 3 文献[17]爆炸试验数据及其理论计算结果 Table 3 Explosion test data in Ref.[17] and theoretical calculation results
| 理论模型 | v0/(m·s-1) | ε/% |
| FIV模型 | 1 461 | 14.1 |
| Gurney公式 | 1 482 | 15.8 |
| 工程半经验公式 | 1 616 | 26.3 |
| 王卫杰模型 | 1 490 | 16.4 |
| 注:文献[17]中v0=1 280 m/s。 | ||
表选项
由表 1、表 2和表 3可知,FIV模型计算的爆炸碎片初始速度与3组试验结果之间相对误差均小于15%,在误差允许范围内,与Gurney公式计算结果也吻合较好,验证了FIV模型的有效性。由于FIV模型考虑了贮箱的壳体变形和膨胀做功,因此计算结果比王卫杰模型更为准确。
3 爆炸碎片初始速度仿真分析 3.1 碎片初始速度影响参量的量纲分析 由FIV模型可知,影响爆炸碎片初始速度v0的参量包括:①推进剂方面:推进剂质量mp、爆速D;②贮箱壳体方面:壳体质量M、内径d、高度h、厚度b、屈服应力σ、剪切应力τ、剪切弹性模量G;③周围环境方面:空气密度ρa。
影响爆炸碎片初始速度的参量较多,若依次对其分析,工作量巨大,有必要利用量纲分析法确定其中的关键影响参量,开展针对性分析。
爆炸碎片初始速度v0可写成函数表达式:
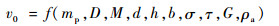 | (25) |
选取D、M和d为基本量,根据量纲分析π定理对式(25)进行无量纲化,得
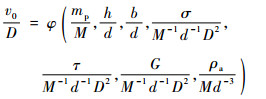 | (26) |
若壳体的材料特性不变,式(26)可以简化为
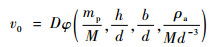 | (27) |
将液体推进剂质量mp换算为固体炸药质量me,式(27)可以写为
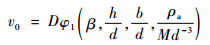 | (28) |
Gurney公式描述的是爆炸碎片初始速度v0与爆速D、炸药质量与壳体质量比值β的关系。但通过对FIV模型参量进行量纲分析可知,爆炸碎片初始速度v0还与贮箱壳体高径比h/d、厚径比b/d以及空气密度ρa等因素有关。
3.2 碎片初始速度影响因素的分析方法 卫星作为火箭的有效载荷,位于火箭上面级。卫星贮箱内携带易燃易爆的液体推进剂,在火箭发射过程中任何意外都有可能引发贮箱爆炸。探究卫星贮箱壳体的高径比h/d和厚径比b/d对爆炸碎片初始速度v0的影响,可以为贮箱结构设计提供参考;探究空气密度ρa对爆炸碎片初始速度v0的影响,有助于评估不同高度爆炸后碎片对周围设施设备和人员的危害。
若采用理论方法对爆炸碎片初始速度的影响因素开展分析,过程十分复杂;开展爆炸试验危险性较大;而数值仿真具有可重复性好、易操作、成本低等优点。基于传统网格法进行数值仿真,发生畸变的网格单元会被删除,而这些被删除的单元往往处于高应变率、大变形区域,导致无法准确统计爆炸碎片的平均速度。SPH算法是一种无网格法,避免了网格侵蚀的问题,因此,本文基于AUTODYN软件中的SPH算法研究贮箱壳体高径比h/d、厚径比b/d以及空气密度ρa对碎片初始速度v0的影响。
3.3 卫星贮箱爆炸仿真模型 液体推进剂爆炸要经历溅散、雾化、混合,以及高温蒸发形成可燃气体的过程,液相爆炸和气相爆炸同时进行,数值仿真难以复现其复杂的爆炸反应过程,且爆轰瞬间碎片初始速度的大小只与爆炸源能量有关,通常利用TNT炸药的爆炸过程来模拟液体推进剂的爆炸过程。根据能量相似原理将液体推进剂总量mp换算成TNT炸药质量mT,即
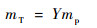 | (29) |
式中:Y为液体推进剂的TNT当量系数。
以装载液态肼的某卫星贮箱为研究对象,将贮箱看作等壁厚圆柱壳体,壳体内径为d=50 cm,高度为h=100 cm,厚度b=2 mm。贮箱满载状态下,液态肼质量mp=198.2 kg,TNT当量系数Y=0.93[18],则TNT炸药质量mT=184.3 kg,空气域为边长a=120 cm的立方体。TNT炸药采用JWL(Jones-Wilkins-Lee)状态方程;壳体材料钛合金采用Johnson-Cook本构模型和Stochastic破坏模型,最大失效应变取为0.23[19],其中A、B、C、n和m为本构模型参数,ρ为材料密度;空气域采用POLYNOMIAL多项式状态方程,通过改变空气密度来建立贮箱不同高度爆炸的模型。各材料参数见表 4。
表 4 TNT、钛和空气的材料参数 Table 4 Material parameters of TNT, titanium and air
| 材料 | ρ/(kg·m-3) | Qp/(kJ·kg-1) | D/(m·s-1) | A/MPa | B/MPa | C | n | m |
| TNT | 1 630 | 4 225 | 6 900 | |||||
| 钛 | 4 510 | 1 077 | 845 | 0.025 | 0.58 | 0.75 | ||
| 空气 | 1.293×10-4~2.8×10-4 |
表选项
根据模型的几何对称性,建立卫星贮箱的1/2模型,如图 1所示。贮箱壳体的SPH粒子大小为1 mm,炸药的SPH粒子大小为2 mm,空气的SPH粒子大小为4 mm,在炸药中心设置起爆点。TNT的爆炸反应大约在10-6 s数量级时间内完成,经多次仿真计算得到,在t=80 μs左右贮箱壳体完全破裂成碎片,因此将仿真计算时间设置为80 μs。
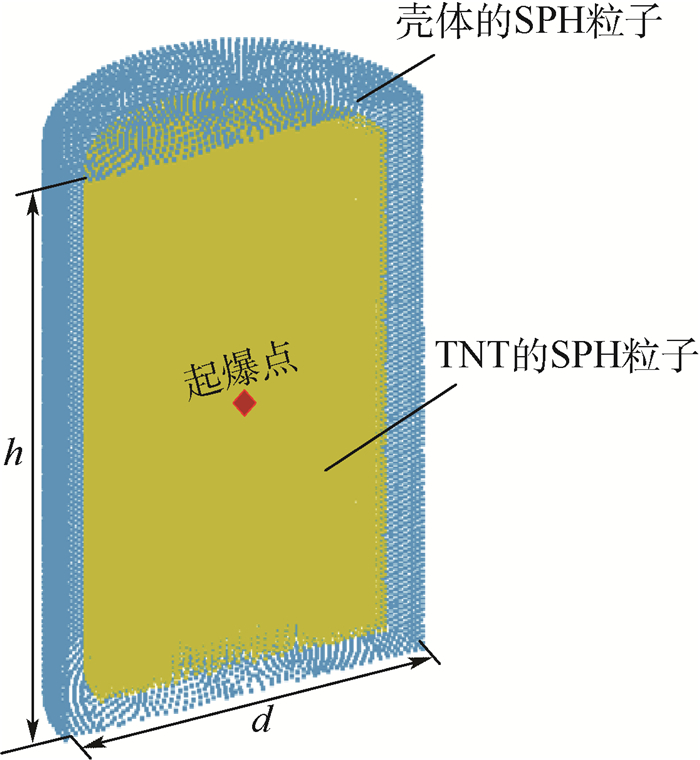 |
| 图 1 卫星贮箱的1/2仿真模型 Fig. 1 1/2 simulation model of satellite tank |
| 图选项 |
3.4 仿真结果与分析 为探究爆炸碎片初始速度与贮箱壳体高径比的关系,保持mT=184.3 kg、b=2 mm、ρa=1.293 kg/m3不变,考虑到工程实际,在0.41~5.83范围内改变壳体高径比h/d,进行10组数值仿真。数值计算完成后,通过AUTODYN软件后处理统计生成爆炸碎片的平均速度v0,将其看作爆炸碎片的初始速度,结果如表 5所示。表中,vG为利用Gurney公式计算的碎片初始速度,εG为Gurney公式与仿真结果之间的相对误差;vF为利用FIV模型计算的碎片初始速度; εF为FIV模型与仿真结果之间的相对误差。
表 5 不同高径比下碎片初始速度的仿真值与理论值 Table 5 Simulation and theoretical values of fragment initial velocity under different height-diameter ratios
| 序号 | d/cm | h/cm | h/d | v0/(m·s-1) | vG/(m·s-1) | εG /% | vF/(m·s-1) | εF /% |
| 1 | 35 | 204.1 | 5.83 | 2 804.5 | 3 138.2 | 11.9 | 2 674.7 | -4.63 |
| 2 | 40 | 156.2 | 3.91 | 2 817.6 | 3 174.9 | 12.7 | 2 754.8 | -2.23 |
| 3 | 45 | 123.5 | 2.74 | 2 831.4 | 3 203.6 | 13.1 | 2 882.3 | 1.80 |
| 4 | 50 | 100.0 | 2.00 | 2 848.5 | 3 227.6 | 13.3 | 2 951.8 | 3.63 |
| 5 | 55 | 82.6 | 1.50 | 2 867.3 | 3 247.6 | 13.3 | 3 036.2 | 5.89 |
| 6 | 60 | 69.4 | 1.16 | 2 898.4 | 3 264.3 | 12.6 | 3 134.9 | 8.16 |
| 7 | 65 | 59.2 | 0.91 | 2 925.0 | 3 278.7 | 12.1 | 3 179.1 | 8.69 |
| 8 | 70 | 51.0 | 0.73 | 2 943.9 | 3 291.4 | 11.8 | 3 249.6 | 10.4 |
| 9 | 75 | 44.4 | 0.59 | 2 955.6 | 3 302.3 | 11.7 | 3 286.6 | 11.2 |
| 10 | 80 | 39.1 | 0.49 | 2 962.2 | 3 311.7 | 11.8 | 3 296.5 | 11.3 |
| 11 | 85 | 34.6 | 0.41 | 2 966.8 | 3 320.4 | 11.9 | 3 301.4 | 11.3 |
表选项
表 5中仿真结果均比Gurney公式计算结果要小,原因是仿真中爆轰反应的总能量部分用于壳体变形和对外膨胀做功,爆炸碎片动能相应减少;仿真结果与FIV模型的计算结果更接近,出现误差的原因是仿真中材料参数设置和状态方程选取与FIV模型并不完全一致。仿真结果与理论计算值之间的相对误差均小于15%,在误差允许范围内,验证了仿真模型的有效性。绘制仿真得到的爆炸碎片初始速度v0随高径比h/d变化曲线,结果如图 2所示。
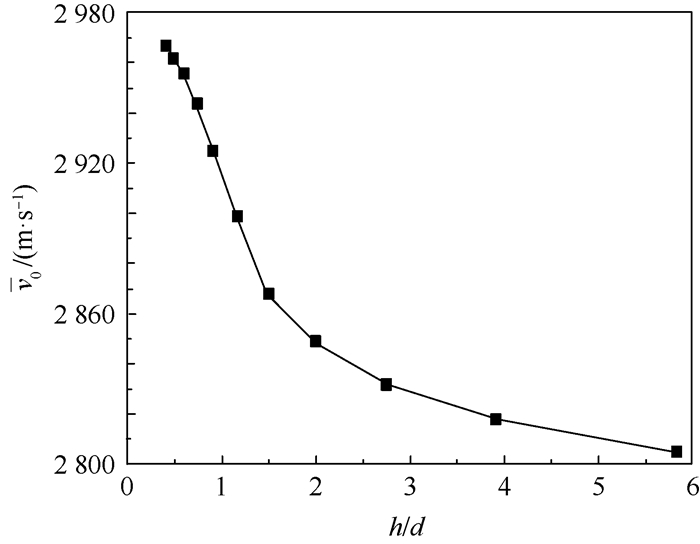 |
| 图 2 碎片初始速度随壳体高径比的变化曲线 Fig. 2 Curve of fragment initial velocity varying with height-diameter ratio of shell |
| 图选项 |
由图 2知,当h/d<1.50时,爆炸碎片初始速度随着高径比增大而急剧衰减,较小高径比的贮箱内,爆轰产物在轴向上分布较为集中,爆炸瞬间爆轰产物对壳体的冲击作用较大,更多的爆轰产物内能转化为爆炸碎片动能。当h/d>1.50时,初始速度的衰减幅度逐渐变缓。虽然贮箱高径比越大,发生意外爆炸后碎片初始速度越小,碎片对周围设施和人员的危害越小,但还要考虑卫星总体设计对贮箱尺寸的要求,合理选取高径比。
为探究爆炸碎片初始速度与贮箱壳体厚径比的关系,保持mT=184.3 kg、h=100 cm、ρa=1.293 kg/m3不变,考虑到工程实际,在0.001~0.01范围内改变壳体厚径比b/d进行数值仿真。图 3为爆炸碎片初始速度v0随壳体厚径比b/d的变化曲线。
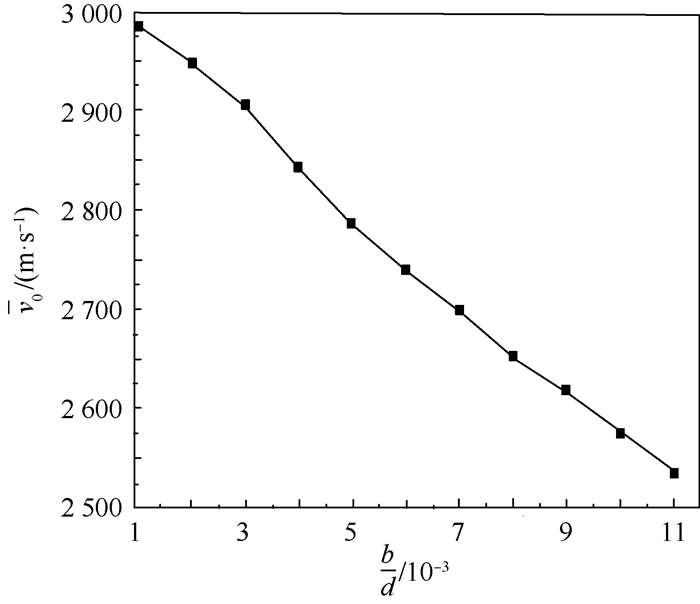 |
| 图 3 碎片初始速度随壳体厚径比的变化曲线 Fig. 3 Curve of fragment initial velocity varying with thickness-diameter ratio of shell |
| 图选项 |
由图 3知,随着壳体厚径比b/d的增加,爆炸碎片的初始速度近似呈线性减小趋势。在爆炸总能量一定的情况下,壳体厚径比b/d越大,用于壳体变形的能量越多,爆炸碎片的动能相应地减小,爆炸碎片初始速度减小。工程实际中需要结合贮箱对壳体质量和耐压性能的要求,合理选取壳体厚度。
空气密度随着海拔高度升高而减小,因此贮箱在不同高度爆炸时,壳体膨胀做功不同,爆炸碎片的初始速度也不同。为探究爆炸碎片初始速度v0与爆炸高度y、空气密度ρa的关系,保持贮箱壳体内径d=50 cm,高度h=100 cm,厚度b=2 mm不变,根据式(15)和式(16),在y=0~50 km范围内每间隔5 km改变爆炸高度,计算不同高度对应的空气密度ρa,对贮箱在不同密度的空气中爆炸进行数值仿真。图 4为空气密度ρa和爆炸碎片初始速度v0随高度y的变化曲线。
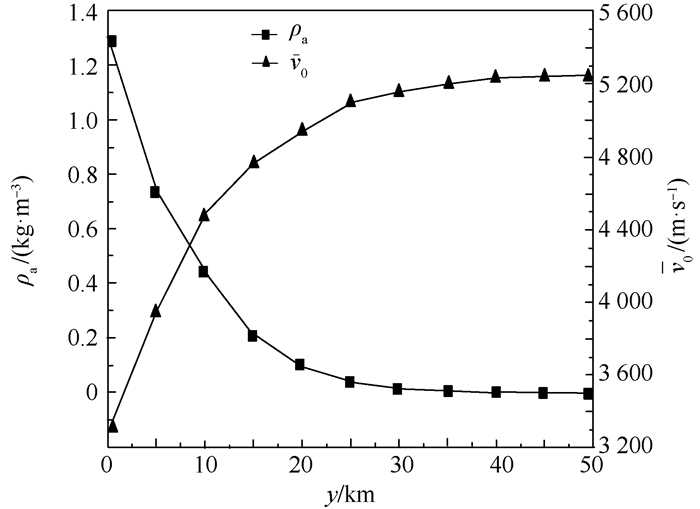 |
| 图 4 空气密度和碎片初始速度随高度的变化曲线 Fig. 4 Curves of air density and fragment initial velocity varying with height |
| 图选项 |
由图 4知,当y<20 km时,随着爆炸高度增加,空气密度大幅衰减,爆炸碎片初始速度迅速增长,这是由于在爆炸总能量一定的情况下,爆炸高度越高,空气密度越小,贮箱壳体向外膨胀克服空气冲击波压力做功越少,爆炸碎片的动能增加,碎片初始速度增大。当y>20 km时,碎片初始速度的增长趋于平缓。当y>40 km时,空气已经非常稀薄,可以忽略贮箱壳体的膨胀做功对爆炸碎片初始速度的影响。
4 结论 1) 基于能量守恒定律,构建了贮箱爆炸FIV模型;采用量纲分析法确定FIV模型中影响碎片初始速度的关键参量为壳体高径比h/d、厚径比b/d以及空气密度ρa。
2) 爆炸碎片的初始速度随着壳体高径比h/d增大而减小。当h/d<1.50时,初始速度迅速衰减,当h/d>1.50时,衰减幅度减小。工程实际中要结合卫星总体设计对贮箱尺寸的要求,合理选取高径比。
3) 爆炸碎片的初始速度随着壳体厚径比b/d增加近似呈线性减小趋势。工程实际中要结合卫星贮箱对壳体质量和耐压性能的要求,合理选取厚径比。
4) 随着爆炸高度y增加,空气密度ρa大幅衰减,爆炸碎片的初始速度增大;当y>20 km时,初始速度增长趋于稳定;当y>40 km时,可以忽略壳体膨胀做功对初始速度的影响。
参考文献
| [1] | 陈新华, 聂万胜. 液体推进剂爆炸危害性评估方法及应用[M]. 北京: 国防工业出版社, 2005: 226-233. CHEN X H, NIE W S. Evaluation method and application of liquid propellant explosion harmfulness[M]. Beijing: National Defense Industry Press, 2005: 226-233. (in Chinese) |
| [2] | 邢志祥, 蒋军成, 赵晓芳. 液化石油气储罐爆炸碎片抛射的蒙特卡罗分析[J]. 火灾科学, 2004, 13(1): 39-42. XING Z X, JIANG J C, ZHAO X F. Monte-Carlo analysis of the flight of missiles from LPG tank explosion[J]. Fire Safety Science, 2004, 13(1): 39-42. DOI:10.3969/j.issn.1004-5309.2004.01.006 (in Chinese) |
| [3] | 左哲. 基于蒙特卡罗法的储罐爆炸碎片冲击失效模型研究[J]. 中国安全科学学报, 2012, 22(3): 67-72. ZUO Z. Study on models of tank explosion fragments impact failure based on Monte Carlo method[J]. China Safety Science Journal, 2012, 22(3): 67-72. DOI:10.3969/j.issn.1003-3033.2012.03.011 (in Chinese) |
| [4] | 潘科, 许开立. 储罐爆炸事故中抛射碎片初始速度预测[J]. 东北大学学报(自然科学版), 2014, 35(7): 1047-1050. PAN K, XU K L. Prediction of the fragments initial velocity in tank explosions accident[J]. Journal of Northeastern University (Natural Science), 2014, 35(7): 1047-1050. DOI:10.3969/j.issn.1005-3026.2014.07.030 (in Chinese) |
| [5] | GURNEY R W.The initial velocities of fragments from bombs, shells and grenades: BRL report 405[R].Aberdeen: Ballistic Research Laboratory, 1943. |
| [6] | 张守中. 爆炸基本原理[M]. 北京: 国防工业出版社, 1988: 503-504. ZHANG S Z. Basic principles of explosion[M]. Beijing: National Defense Industry Press, 1988: 503-504. (in Chinese) |
| [7] | 印立魁, 蒋建伟. 多层球形预制破片战斗部破片初速场的计算模型[J]. 含能材料, 2014, 22(3): 300-305. YIN L K, JIANG J W. Calculation model of initial velocity field on multilayered spherical fragments warhead[J]. Chinese Journal of Energetic Materials, 2014, 22(3): 300-305. DOI:10.3969/j.issn.1006-9941.2014.03.006 (in Chinese) |
| [8] | 王卫杰, 沈怀荣, 李怡勇, 等. 液体火箭爆炸碎片模型研究[J]. 上海航天, 2013, 30(6): 35-38. WANG W J, SHEN H R, LI Y Y, et al. Study of liquid rocket explosion fragments model[J]. Aerospace Shanghai, 2013, 30(6): 35-58. DOI:10.3969/j.issn.1006-1630.2013.06.007 (in Chinese) |
| [9] | BAKER W E, KULESZ J J, RICHKER R E, et al.Workbook for predicting pressure wave and fragment effects of exploding propellant tanks and gas storage vessels: NASA-CR-34906[R].Washington, D.C.: NASA, 1977. |
| [10] | 恽寿榕, 赵衡阳. 爆炸力学[M]. 北京: 国防工业出版社, 2005: 18-20. YUN S R, ZHAO H Y. Explosion mechanics[M]. Beijing: National Defense Industry Press, 2005: 18-20. (in Chinese) |
| [11] | HIROE T, FUJIWARA K, HATA H, et al. Deformation and fragmentation behavior of exploded metal cylinders and the effects of wall materials, configuration, explosive energy and initiated locations[J]. International Journal of Impact Engineering, 2008, 35(12): 1578-1586. DOI:10.1016/j.ijimpeng.2008.07.002 |
| [12] | 胡永乐, 陈子辰, 王峰超, 等. 内部爆炸加载条件下圆柱钢壳的动态断裂[J]. 机械强度, 2010, 32(1): 99-104. HU Y L, CHEN Z C, WANG F C, et al. Dynamic fracture of cylindrical steel shell under inside-explosion loading[J]. Journal of Mechanical Strength, 2010, 32(1): 99-104. (in Chinese) |
| [13] | 俞鑫炉, 董新龙, 潘顺吉. 不同爆炸载荷下TA2钛合金圆管膨胀破坏过程[J]. 爆炸与冲击, 2018, 38(1): 148-154. YU X L, DONG X L, PAN S J. Fracture behaviors of explosively driven TA2 alloy cylinders under different loadings[J]. Explosion and Shock Waves, 2018, 38(1): 148-154. (in Chinese) |
| [14] | HOGGATT C, RECHT R. Fracture behavior of tubular bombs[J]. Journal of Applied Physics, 1968, 39(3): 1856. DOI:10.1063/1.1656442 |
| [15] | 孔祥韶, 吴卫国, 杜志鹏, 等. 圆柱形战斗部爆炸破片特性研究[J]. 工程力学, 2014, 31(1): 243-249. KONG X S, WU W G, DU Z P, et al. Research on fragments characteristic of cylindrical warhead[J]. Engineering Mechanics, 2014, 31(1): 243-249. (in Chinese) |
| [16] | ZHANG Q, MIAO C Q, LIN D C, et al. Relation of fragment with air shock wave intensity for explosion in a shell[J]. International Journal of Impact Engineering, 2003, 28: 1129-1141. DOI:10.1016/S0734-743X(03)00004-6 |
| [17] | KARPP R R, PREDEBON W W.Calculations of fragment velocities from naturally fragmenting munitions: ADB007377[R].Aberdeen: Ballistic Research Labooratory, 1979. |
| [18] | JULIEN H L, WOODS S S, RATHGEBER K, et al.Explosive events initiated by pyrovalves: AIAA-1999-2309[R].Reston: AIAA, 1999. |
| [19] | 刘旭阳.TC4钛合金动态本构关系研究[D].南京: 南京航空航天大学, 2010. LIU X Y.Dynamic constitutive relationship of TC4 titanium alloy[D].Nanjing: Nanjing University of Aeronautics and Astronautics, 2010(in Chinese). http://cdmd.cnki.com.cn/Article/CDMD-10287-1011252149.htm |
