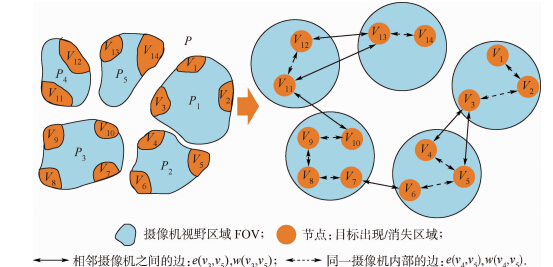
 |
| 图 1 摄像机网络与图模型建立示意图 Fig. 1 Example of camera network and its corresponding graph model |
| 图选项 |
2.1 基于网络拓扑的空间关联 空间关系定义了节点之间是否建立边,以及边的方向.图模型的建立过程中,如果两个节点之间在物理空间位置上一步可达,即不经过其他任何节点,则为它们之间建立一条边,边的方向定义为目标移动的方向.图 1中有5个摄像机,其视域(FOV)分别为P1~P5,vi∈V表示目标在FOV中的出现与消失区域,同一摄像机内部的目标运动轨迹用虚线箭头表示,不同摄像机之间的目标移动轨迹用实线箭头表示.这样的拓扑关系建立,能够满足跨摄像机下目标跟踪过程中的两个约束:约束1 如果跟踪目标在当前摄像机区域中的节点处能够监测到,则使用单摄像头跟踪算法对其进行持续跟踪,这时节点之间不需要进行目标关联计算,可将跟踪匹配时的不确定性降到最低.约束2 如果跟踪目标在某一节点处消失,则在图模型中使用广度优先策略(BFS,Breadth First Search)在其邻域(实线箭头)一步可达的节点处进行目标检测,对检测到的目标提取特征融合,再进行目标的匹配与关联.2.2 基于统计学习的时间关联 图模型中边的权重由目标在不同节点之间转移的概率决定,在实际应用系统中,采用统计学习方法为目标的运动建立时间约束,从而定义节点之间合理的权值w(vi,vj),vi,vj∈V.在实验过程中,首先对目标通过相邻vi和vj之间的时间进行统计,可以得到一组观测时间序列Tij=(t1,t2,…,tn),该观测序列的分布可以由高斯分布进行描述,也就是说节点vi和vj之间的边e(i,j)可以根据高斯分布N(e′ij,σ2ij)进行建模.通过训练数据,就可以由该分布的期望与方差来获得这条边的权重.实际情况下,想要获取一组观测序列的统计规律往往比较困难,这是由许多因素决定的:包括目标的运动规律、摄像机的地理位置、每天的监控环境变化等.本文中,利用事先获得的训练数据(如各个节点之间的通过时间),来近似地估计每条边的权重.在计算某一条边权时,对所有观测时间进行聚类并计算每个类内的方差.具体的操作过程中,σij是由当前边属于哪一个类而决定的.图 2是两个节点之间边权的直方图实例,从中可以看到,观测数据可以被划分为3个类别,每个类别中可以得到相应的方差值.本文使用的聚类方法为K-means,该算法可以自适应地决定聚类类别的数量.
 |
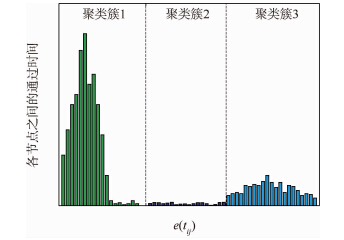| 图 2 通过训练数据学习而来的节点vi和vj之间边权统计直方图 Fig. 2 Histogram of edge weights between vi and vj learned during training phase |
| 图选项 |
文献[14]在求取图模型中最优边权时采用了一个期望权重相似度方程(EWS,Expected Weighted Similarity),本文受其启发,定义图模型的边权重为
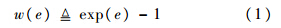
该权重方程能够为相应的边定义相似度最大的边权得分,如果p(e)～N(e′,σ),定义该边的能量为
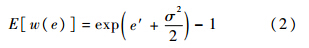
使用EWS方程定义的边权能量值既考虑了观测数据的均值也考虑了数据的方差.3 数据关联与相似性度量 3.1 特征提取与相似性度量 本节具体阐述了不同节点处观测到的目标相似性度量方法.Oin表示第i个节点处观测到的目标n.对于两个不同节点vi和vj处的两个目标关联性大小,本文使用下式进行度量：
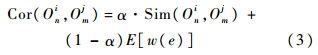
式中,Sim(Oin,Ojm)为目标表现特征项(AM),本文由两个目标区域的协方特征矩阵的相似性来度量,具体定义见下文.w(vi,vj)为目标时空关联项(GM,Graph Model),定义为两个节点之间的边权.对于算法中的参数,将设定一个最优化的经验范围,具体见本文实验部分.Tuzel等[15]在2006年将区域协方差描述子引入到目标特征匹配中去,这种基于图像二阶统计特性的协方差矩阵描述子(RC,Region Covariance)在目标检测与跟踪领域都得到了应用并且取得了良好的效果.为了提高跟踪的可靠性,本文使用RC来实现目标多特征的融合,对目标的外观表现模型进行表示.跟踪目标的每个像素点k生成一个d维的特征向量zk,该特征向量可以是像素的颜色、灰度、亮度、梯度等信息.本文中特征向量采用的是16位RGB颜色空间下均匀量化的直方图[16]与SURF特征[17].对于一个特定的大小为W×H的矩形区域R,使用{zk}k=1,2,…,s,s=W×H来表示R的d维的特征向量,并且使用以下的协方差矩阵来表示目标区域R:
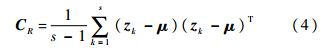
式中,
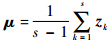,表示所有的点的均值化.式(4)中,正定的实对称矩阵CR由于在计算中本身就已经进行了去均值化,因此它对目标区域的亮度均值变化具有不变性.在目标识别的应用中,尺度不变性、旋转不变性和光照不变性具有非常重要的意义.在对运动目标进行提取与协方差矩阵表示之后,需要采用一定的相似性度量算法进行特征匹配,从而判定是否为同一目标.文献[18]给出了一种协方差矩阵之间的距离度量方法,对于两个协方差矩阵C1和C2,其相关性可表示为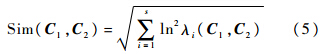
式中,{λi(C1,C2)}i=1,2,…,s是det(λC1－C2)=0中λ的解.
式中，正定的实对称阵
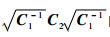的特征值是正实数,这样{λi(C1,C2)}i=1,2,…,s的计算即可以转化为对矩阵
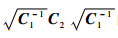的特征值的求解;E为单位矩阵.3.2 基于二部图匹配策略的目标关联 当目标在摄像机之间移动时,需要判断其最有可能出现的下一个节点,这是一个图像匹配的问题.传统的基于单幅图像匹配的重识别框架并不适用于跨摄像头跟踪任务,这是由于在某个摄像头下进行目标检测时有可能出现第一帧就检测错误的情况,而且由于监控环境的复杂性,跟踪目标经常会由于遮挡而出现跟踪框漂移的情况,为了避免上述两种情况可能导致的跟踪失败,本文采用了基于两个观测序列帧匹配的策略,这样可以降低匹配的错误率,修正误匹配.具体方法为:需要将目标消失节点vi处的观测序列Oi:{Oi1,Oi2,…,Oin}与目标可能出现的节点vj处的观测序列Oj:{Oj1,Oj2,…,Ojm}建立关联关系,具体如图 3所示.注意,依据之前建立的时空关联图模型,此处的vj应为vi一步可达的所有节点.为了求解一个最优的OiOj关联匹配,目标关联性问题可以转化为一个二部图匹配问题. |
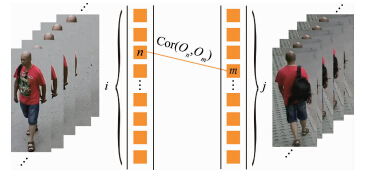| 图 3 视频帧序列的二部图匹配 Fig. 3 Bipartite frame sequence matching |
| 图选项 |
为了将问题形式化,本文定义两个矩阵:{Cor(Oin,Ojm)}N×M为得分矩阵,矩阵元素Cor(Oin,Ojm)表示节点vi中的检测目标Oin与节点vj中的检测目标Ojm相关联时产生的得分值,其中N=Oi,M=Oj.{X(Oin,Ojm)}N×M为0-1二值矩阵,如果目标Oin与目标Ojm相匹配,则X(Oin,Ojm)=1.特别地,这里需要定义一个约束:
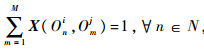,其作用是保证二值矩阵{X(Oin,Ojm)}N×M中每一行有且仅有一个1值,其余均为0值,即保证了Oi中所有观测对象在Oj中有且仅有唯一的对应.于是问题的目标方程即可表示为求解一个最大权重的完备匹配: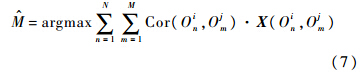
在解决二部图最大匹配问题的众多策略之中,匈牙利算法[19]是最为经典的算法之一,它可以在多项式时间内解决问题,该算法的复杂度为Ο(N3),其中N为观测帧序列Oi中的目标个数.本文使用匈牙利算法对式(7)进行求解,即可得到一个Oi到Oj的最大权完备匹配,并得到两个节点包含的观测序列的总体目标关联度M(vi,vj),这里需要设定一个阈值为0.5(见实验设计),当关联度大于该阈值时,认为是一个可信的匹配,否则认为该目标已经离开所有监控摄像机的可视范围.通过对节点vi所有一阶邻域的节点的关联度M进行排序,即可得到目标最有可能的出现节点vj:
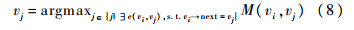
4 实 验4.1 实验设计 对多摄像机目标跟踪方法的研究一直都缺少相关的实验数据以及实验系统.本实验使用的数据来源于PKU-SVD-B数据集[20],本文建立如图 4所示的摄像机监控网络,用以模拟复杂监控网络中的若干单元,4个摄像机监控视域无重叠,采集视频在时间上保持同步,在每个摄像机独立监控的范围内首先需要对移动目标进行检测和分割[3],这里采用帧差法获取目标区域,然后采用TLD[6]算法在当前视域内进行跟踪.
 |
| 图 4 摄像机视域及网络拓扑 Fig. 4 Topology of camera views |
| 图选项 |
如图 4所示,所建立的图模型包含4个摄像机区域,9个节点,对于每个节点在时间轴上设置Fi(i=1,2,…,N)个观测帧序列,每个观测帧序列在时间轴上具有一定的范围(例如前后10帧).如果指定对象的运动轨迹依据图模型转移到该节点,则认为这条轨迹包含了对应的节点.对于某一个指定跟踪目标,在某个包含的节点范围内,当所有匹配帧和Ground Truth有超过50%的帧能够正确匹配上,则认为该跟踪对象在跨摄像头跟踪时得到了一个可信的匹配节点.对某一跟踪目标的评价指标为
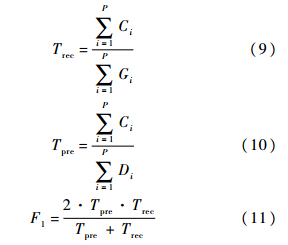
式中,Trec和Tpre分别表示召回率和准确率；P为总的节点个数；Gi(Gi
 |
| 图 5 5个目标跟踪实例 Fig. 5 Five examples of image of people in network |
| 图选项 |
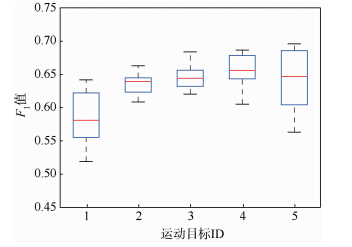
为了更好地评估算法性能，同时保证衡量标准的公正性,实验确保每种方法均使用相同的参数在全部5个跟踪实例上进行实验.对于式(3)中的参数α,根据Sim(·)项和E[w(e)]项的权重,首先,通过手工调整参数过程中确定的算法最佳性能的范围为0.05~0.15.然后,在对每个对象进行跟踪时,在经验范围内随机选择10组参数进行实验,图 6为每个跟踪实例的10组随机参数的结果得到的箱型图,即每个箱型柱由10组数据的分布得到.从中可以展示出每个实例的平均F1得分、上边缘值和下边缘值等,而且能更为细致地体现不同参数情况下算法性能的差异,大部分数据集中在平均值附近,说明在α的经验范围内算法性能比较稳定.
 |
| 图 6 在不同跟踪目标上的随机参数实验 Fig. 6 Experiment of random parameters in different tracking cases |
| 图选项 |
对比实验中,算法使用的最优参数为5组实例的平均F1得分最大情况下的参数.在表 1中列出了5组实例中目标最终轨迹的准确率、召回率和F1得分.本文结合目标表现模型与图模型时空关联的方法相比只使用表现模型的基线方法在跟踪的精度上能够得到提升(约10%的提升).传统的基于特征的识别方法没有加入时空关联约束,大部分目标由于在外观上难以分辨,会产生较多误匹配,因此准确率往往较低.表 1 目标跟踪精度及对比 Table 1 Tracking accuracy and comparison
| 目标ID | 方法对比 | 准确率 | 召回率 | F1值 |
| 1 | AM+GM | 0.5956 | 0.6006 | 0.5980 |
| AM | 0.4923 | 0.4950 | 0.4936 | |
| 2 | AM+GM | 0.6559 | 0.6264 | 0.6408 |
| AM | 0.5019 | 0.5996 | 0.5464 | |
| 3 | AM+GM | 0.6519 | 0.6592 | 0.6555 |
| AM | 0.5611 | 0.6040 | 0.5817 | |
| 4 | AM+GM | 0.6537 | 0.6590 | 0.6563 |
| AM | 0.5580 | 0.5976 | 0.5771 | |
| 5 | AM+GM | 0.6021 | 0.6878 | 0.6421 |
| AM | 0.5056 | 0.5590 | 0.5309 |
表选项
在目标识别、跟踪的应用中,好的算法应该对环境的变化有较强的鲁棒性.图 7中比较了只依赖AM跟踪与AM+GM方法在噪声与目标尺度变化方面的鲁棒性结果.使用高斯噪声对检测的帧序列进行模糊处理,可以清晰地发现随着噪声的逐渐增大,AM方法会逐渐失效,而加入了时空关联图模型辅助的方法则对噪声有一定的鲁棒性.与此同时,监控视频中的运动目标由于远离或者靠近摄像机,往往会产生较大幅度的尺度改变,实验表明,本文提出的方法对于跟踪目标的尺度大小也具有很好的鲁棒性.
 |
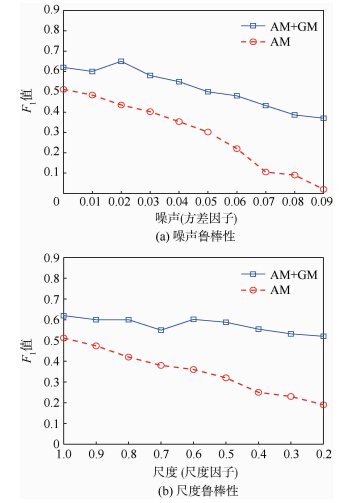| 图 7 跨摄像头跟踪时不同方法对噪声和尺度的鲁棒性 Fig. 7 Robustness of different approaches to noise and scale variances in object tracking |
| 图选项 |
5 结 论1) 本文提出了一种将特征融合与时空关联相结合来进行多摄像机监控环境下的目标跟踪方法.时空关联图模型能够为目标跟踪过程中的目标关联提供可靠的依据.2) 实验表明,本文的方法在实际应用中有着较好的适用性,相比于传统的基于特征模型跟踪的方法在跟踪精度方面有较大提高.3) 由于多摄像机网络的复杂性,目标移动过程中的时间延迟等因素,如何将算法进一步地扩大到更大范围的应用场景以及更多元的目标种类将是下一步的研究工作.
参考文献
| [1] | Wang X. Intelligent multi-camera video surveillance:a review[C]//Pattern Recognition Letters.Netherlands:Academic Press,Elsevier,2013,3(4):3-19. |
| Click to display the text | |
| [2] | Fu H,Ma H, Ming A.EGMM:an enhanced Gaussian mixture model for detecting moving objects with intermittent stops[C]//IEEE International Conference on Multimedia and Expo.Piscataway,NJ:IEEE,2011,7041(2):1-6. |
| Click to display the text | |
| [3] | Fu H,Ma H, Liu L.Robust human detection with low energy consumption in visual sensor network[C]//IEEE International Conference on Mobile Ad-hoc and Sensor Networks.Piscataway,NJ:IEEE,2011:91-97. |
| Click to display the text | |
| [4] | Zheng W S, Gong S,Xiang T.Reidentification by relative distance comparison[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2013,35(3):653-668. |
| Click to display the text | |
| [5] | Wu Y,Lim J, Yang M H.Online object tracking:a benchmark[C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE,2013,9(4):2411-2418. |
| Click to display the text | |
| [6] | Kalal Z, Mikolajczyk K,Matas J.Tracking-learning-detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2012,34(7):1409-1422. |
| Click to display the text | |
| [7] | Makris D,Ellis T, Black J.Bridging the gaps between cameras[C]//Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE,2004,2:II205-II210. |
| Click to display the text | |
| [8] | Stauffer C. Estimating tracking sources and sinks[C]//IEEE Conference on Computer Vision and Pattern Recognition Workshop.Piscataway,NJ:IEEE,2003:35. |
| Click to display the text | |
| [9] | Tieu K, Dalley G,Grimson W E L.Inference of non-overlapping camera network topology by measuring statistical dependence[C]//IEEE International Conference on Computer Vision.Piscataway ,NJ:IEEE,2005,2:1842-1849. |
| Click to display the text | |
| [10] | Loy C C, Xiang T,Gong S.Multi-camera activity correlation analysis [C]//IEEE Conference on Computer Vision and Pattern Recognition.Piscataway,NJ:IEEE,2009:1988-1995. |
| Click to display the text | |
| [11] | Wang X, Tieu K,Grimson W E L.Correspondence-free activity analysis and scene modeling in multiple camera views[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(1):56-71. |
| Click to display the text | |
| [12] | 刘少华,赖世铭, 张茂军.基于最小费用流模型的无重叠视域多摄像机目标关联算法[J].自动化学报,2010,36(10):1484-1489. Liu S H,Lai S M,Zhang M J.A min-cost flow based algorithm for objects association of multiple non-overlapping cameras[J].ACTA Automatica Sinica,2010,36(10):1484-1489(in Chinese). |
| Cited By in Cnki (3) | |
| [13] | 万九卿,刘青云. 基于高阶时空模型的视觉传感网络数据关联方法[J].自动化学报,2012,38(2):236-247. Wan J Q,Liu Q Y.Data association in visual sensor networks based on high-order spatio-temporal model[J].Acta Automatica Sinica,2012,38(2):236-247(in Chinese). |
| Cited By in Cnki (3) | |
| [14] | Song B, Roy-Chowdhury A K.Stochastic adaptive tracking in a camera network[C]//IEEE 11th International Conference on Computer Vision.Piscataway,NJ:IEEE,2007:1-8. |
| Click to display the text | |
| [15] | Tuzel O, Porikli F,Meer P.Region covariance:a fast descriptor for detection and classification[C]//European Conference on Computer Vision.Heidelberg:Springer,2006:589-600. |
| Click to display the text | |
| [16] | Gray D,Tao H. Viewpoint invariant pedestrian recognition with an ensemble of localized features[C]//European Conference on Computer Vision.Heidelberg:Springer,2008:262-275. |
| Click to display the text | |
| [17] | Bay H, Tuytelaars T,Van Gool L.Surf:speeded up robust features[C]//European Conference on Computer Vision.Heidelberg:Springer,2006:404-417. |
| Click to display the text | |
| [18] | Förstner W, Moonen B.A metric for covariance matrices[C]//Geodesy-the Challenge of the 3rd Millennium.Heidelberg:Springer,2003:299-309. |
| Click to display the text | |
| [19] | Kuhn H W. Variants of the Hungarian method for assignment problems[J].Naval Research Logistics Quarterly,1956,3(4):253-258. |
| Click to display the text | |
| [20] | Large-scale object tracking over a multiple-camera network[EB/OL] .The First IEEE International Conference on Multimedia Big Data.[2014-04-20].http://www.bigmm2015.org/Challenge.asp. |
| >Click to display the text |
