无自由参数型混合格式

删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

本站小编 Free考研考试/2021-12-25

气动声学以及电磁波传播的数值模拟在过去几十年里大量采用高阶数值格式.如今在湍流的大涡模拟以及直接数值模拟等数值模拟中,高阶数值格式也得到了广泛的应用.湍流问题中存在大范围的时间/空间尺度,低阶格式由于耗散过大,往往无法捕捉到流动中不稳定的、微小的尺度.高阶格式精度更高,有着很好的应用前景.然而,高阶格式在求解超音速可压缩流动问题时,仅有高精度还不能满足实际需求.为了准确地捕捉流动中的间断,还需要做到基本无数值振荡,并且具有较高的间断分辨率.总而言之,精度高、分辨率高、捕捉间断能力强、鲁棒性好的数值格式,是****们不断追求的目标^{[1, 2]}.有限差分格式可以分为显式格式和隐式格式.其中高阶的显式格式以ENO格式和WENO格式^{[3, 4]}为代表.这类格式能够实现高精度、高分辨率,并且具有良好的捕捉激波的能力.但是,在湍流的数值模拟中,ENO和WENO格式往往会表现出过大的耗散.WENO-Z^{[5, 6, 7]}格式通过对传统的WENO-JS格式中权重算子的改进,一定程度上减小了耗散,提高了分辨率.紧致格式是隐式格式.Lele^[8]最早系统地给出了具有类谱方法分辨率的非守恒型中心型紧致格式,能够在较小的模板上轻松地获得很高的精度.但是,由于这类紧致格式的耗散误差为零,最早只被应用于不可压缩流动问题的求解.Liu等^[9]对守恒型中心紧致格式进行了系统的介绍.尔后,****们通过各种手段将紧致格式推广到可压缩流动问题的模拟.其中,Adams等^[10]将ENO格式与紧致格式结合,以实现捕捉间断的能力.Pirozzoli^[11]依照同样的思路,将WENO格式与紧致格式结合起来.然而这些混合格式中,两种子格式间的相互切换显得有些“突然”,往往会在格式切换的附近造成数值振荡.为此,Ren等^[12]提出了新的权重计算方法,其中引入了自由参数r_c.国内****也提出了不同的引入自由参数的混合格式权重算法^{[13, 14]}.它们都表现出了优异的激波捕捉能力以及分辨率特性.但是,这类自由参数往往需要根据经验进行选取,需要进行大量的尝试,这就造成了使用上的不便.本文的目标就是要构造出一种无自由参数的权重算法^[15],在保持混合格式的高精度、高分辨率特性的同时,提高格式的易用性和鲁棒性. 1 混合格式的构造 1.1 控制方程考虑双曲型标量守恒律方程:

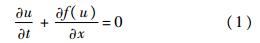
将计算区域等距离划分x_j=jΔx,j=0,1,…,N.守恒形式的半离散有限差分格式为

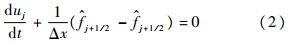
式中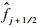为在半点j+1/2处的数值通量.本文称空间项的差分格式有k阶精度,是指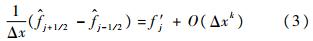

为了提高数值格式的鲁棒性,通常将数值通量分裂为正通量和负通量2个部分：

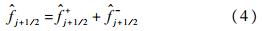
由于这2个部分的对称性,本文只讨论正通量的计算过程. 1.2 守恒型紧致格式本文构造了2种守恒型紧致格式^{[9, 11]}

这2种紧致格式的截断误差分别为

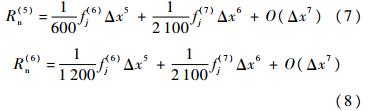
截断误差的第1和第2两项分别为格式中耗散误差以及色散误差的主项.不难看出,第2种紧致格式的耗散误差更小. 1.3 WENO-Z格式本文的混合格式采用WENO-Z格式^{[5, 6, 7]}.相比WENO-JS格式^[4],WENO-Z格式在极值点附近能够更好地保持高精度.为了论文的完整性,这里给出五阶WENO-Z的基本形式.

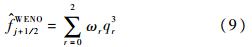
式中,q₃^r为候选模板的数值通量,详见文献^{[4, 5]};ω_r(r=0,1,2)是模板r的权重：

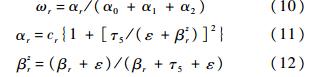
式中,c_r为理想权重;ε为一个极小数;β_r为候选模板的光滑因子：

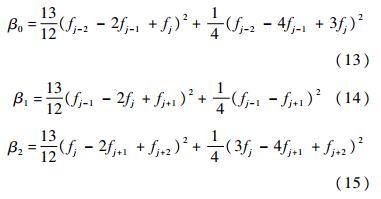
1.4 两种子格式的混合分别用c_j+1/2^compact,c_j+1/2^WENO表示紧致格式以及WENO格式的右端项,ξ,ψ,ζ表示紧致格式左端项的各项系数,令σ_j+1/2为紧致格式这一子格式的权重,那么混合格式的一般形式为

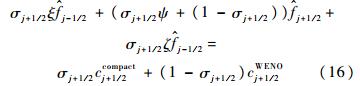
混合格式权重的理想状态是:在间断区域WENO-Z格式的权重为1,从而提高格式对间断的捕捉能力;在光滑区域紧致格式的权重为1,这样一来就能够保持混合格式在光滑区域的低耗散特性.本文将按照这一标准构造新的权重算子.混合格式的模板为[x_j－2,x_j－1,x_j,x_j+1,x_j+2],对光滑因子β₀,β₁,β₂进行Taylor展开分析：

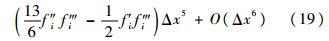
本文为混合格式中紧致格式的权重设计了新算子：

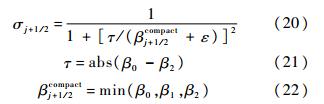
式中ε是一个极小的数,可以取计算机所能存储的最小浮点数,因此这并不能算作是自由参数.在光滑区域：

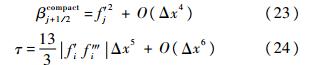
那么有

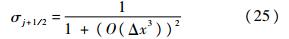
也就是说,在光滑区域,紧致格式的权重几乎就是1.当混合格式的总模板存在间断时,τ远大于β_j+1/2^compact,如此一来,紧致格式的权重就接近0.本文将这种新型算子称为Z型权重算子.Pirozzoli在文献^[11]中定义了一个简单的权重算子,这种算子造成了混合格式中两种子格式的切换过于突然,切换点会产生不容忽视的数值振荡乃至污染流场.为了克服上述问题Ren^[12]和武从海等^[14]提出了一个新的权重算子：

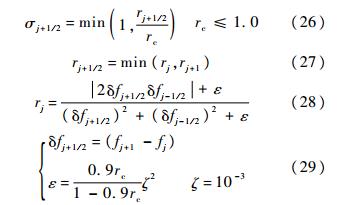
这种权重算子表现出了良好的分辨率以及对激波的精确捕捉能力.但是,该算子较为复杂,格式的表现很大程度上依赖算子中自由参数r_c的选取,r_c过小会造成计算无法进行.本文将这类算子称作R型算子.新权重算子Z避免了自由参数的引入以及逻辑判断的使用^[15].为了测试新算子的特性,主要将新算子的计算结果与R型算子的结果进行比较.本文用HCW-U表示式(5)型紧致格式与WENO-Z的混合格式,用HCW-UL表示式(6)型紧致格式与WENO-Z的混合格式.HCW-UL-Z型格式即为采用Z型权重的式(6)型迎风型低耗散紧致格式与WENO-Z格式的混合格式,文中提到的其他简称构成与此类似. 2 数值试验结果本文所涉及到的一、二维算例控制方程均为欧拉方程,时间离散采用三阶龙格库塔(RK)方法,这里不再赘述,详见文献^[4]. 2.1 激波管问题LAX问题是1D激波管问题的典型算例之一.在区间[-5.0,5.0]之内,以原点为分界点,左右两侧的气体初始状态不同.初始条件如下：

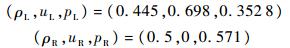
计算网格为200,计算终止时刻为t=1.3,CFL=0.3.本算例中R型权重算子取值为r_c=0.5.由图 1、图 2不难发现HCW-U以及HCW-UL采用Z型权重算子时,对激波以及接触间断的捕捉与采用R型权重时差不多.值得注意的是,这两种混合格式在采用R型权重算子时在膨胀波头造成的数值振荡都比采用Z型权重时严重,详见图 2中的局部放大图.

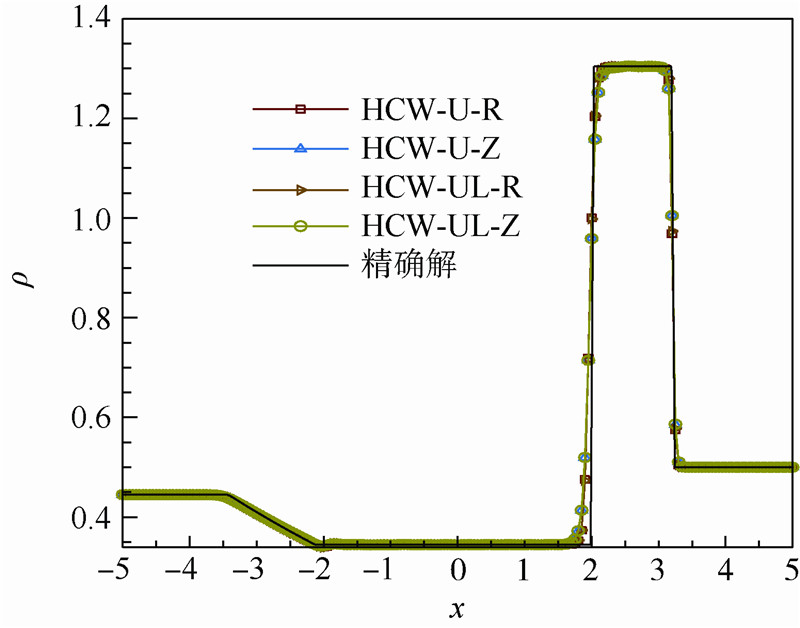图 1 HCW-U,HCW-UL,LAX问题,密度值Fig. 1 HCW-U,HCW-UL,LAX problem,density

图选项

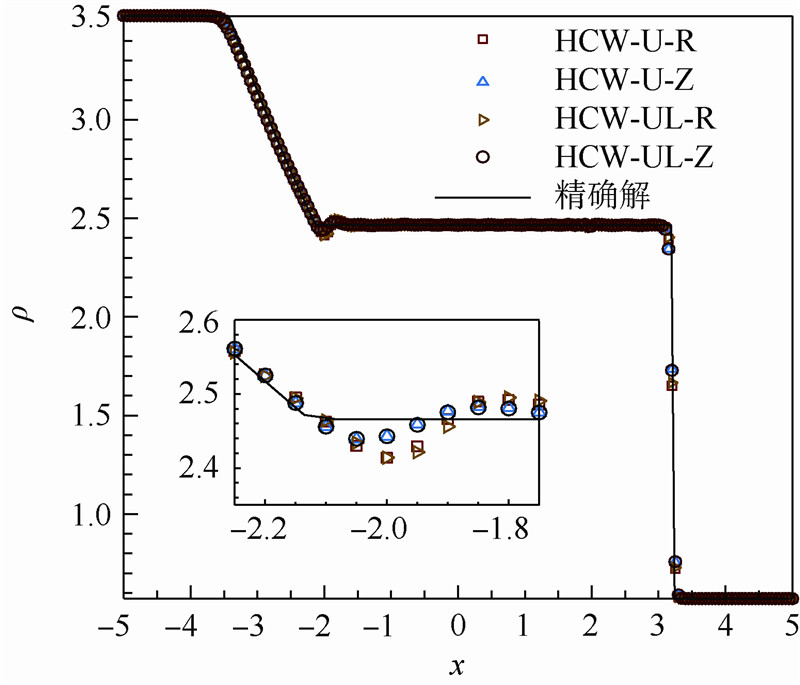图 2 HCW-U,HCW-UL,LAX问题,压强值Fig. 2 HCW-U,HCW-UL,LAX problem,pressure

图选项

2.2 激波与熵波的干涉本算例描述的是激波与熵波的干涉问题,其数值结果包含了间断以及不同尺度的波.该算例能够很好地测试数值格式对间断的捕捉能力以及分辨率特性.计算区域为^{[0, 10]},初始条件如下：

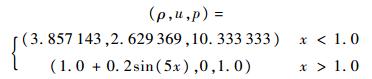
计算网格为301,计算终止时刻为t=1.8,CFL=0.1.混合格式采用R型权重时,r_c=0.5.该问题没有精确解,但是可以用五阶WENO格式在网格数为1601下的数值计算结果作为近似的精确解.为了便于观察,本文给出了密度在区间[5,7.4]内的数值结果,这一区间内密度的数值结果能够很好地说明格式的分辨率、耗散性质以及对间断的捕捉能力.从图 3、图 4可以清楚地看到,对于HCW-U以及HCW-UL格式,Z型权重与R型权重都表现出了对间断的良好捕捉能力以及对不同尺度波的分辨能力,混合格式相比于WENO-Z格式耗散大大降低,分辨率有了明显的提高.对比图 3、图 4,HCW-U以及HCW-UL计算效果并没有太显著的区别,尽管后者在理论上来说耗散比前者更小.

图 3 HCW-U,Osher-Shu问题,区间[5,7.4]密度值Fig. 3 HCW-U,Osher-Shu problem,density in[5,7.4]

图选项

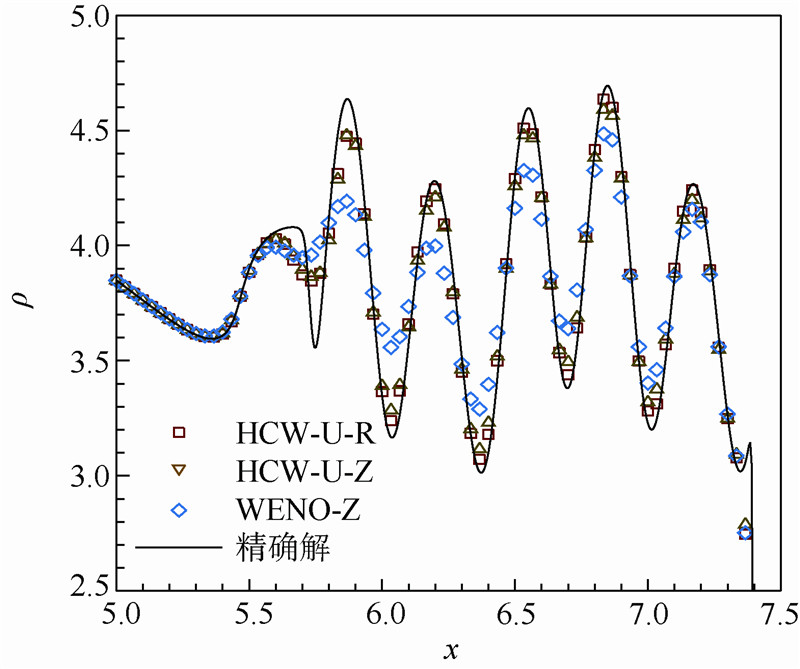图 4 HCW-UL,Osher-Shu问题,区间[5,7.4]密度值Fig. 4 HCW-UL,Osher-Shu problem,density in[5,7.4]

图选项

2.3 2D双马赫反射强激波的双马赫反射(DMR)问题是测试数值格式的分辨率以及对间断的捕捉特性的标准算例之一.该问题的计算区域为^{[0, 4]}×^{[0, 1]},初始条件为：马赫数为10、与x轴成60°斜激波在x=1/6处与底部边界相遇,激波上游(ρ,u,v,p)=(1.4,0,0,1),下游参数满足RH关系式.计算域的上边界条件是激波传播的精确解,左边界以及底部段为入流边界条件,右边界为出流边界条件,底部段为壁面边界.计算终止时间t=0.2,CFL=0.5.计算网格为 801×201.混合格式采用R型权重时,r_c=0.5.由于主要的流场信息都在^{[0, 3]}×^{[0, 1]}区间之内,本文仅仅给出了该区域内的密度云图,所有云图的等值线均为将区间2~22均分为50等份.对比图 5、图 6,可以清楚地看到，HCW-U-Z与HCW-U-R都很好地分辨出了滑移线的卷曲.HCW-UL-Z的计算结果由图 7给出,HCW-UL-R的计算结果略去.值得注意的是,采用R型权重计算时,如果r_c过小(以r_c=0.3为例),计算无法进行.Z型权重由于未引入自由参数,鲁棒性提高,在针对陌生问题进行数值求解时,则可以避免自由参数取得不当造成计算无法进行的问题,与此同时,保持了很好的分辨率特性.

图 5 HCW-U-R,DMR问题,密度云图,50条等值线Fig. 5 HCW-U-R,DMR problem,density contour,50 levels

图选项

图 6 HCW-U-Z,DMR问题,密度云图,50条等值线Fig. 6 HCW-U-Z,DMR problem,density contour,50 levels

图选项

图 7 HCW-UL-Z,DMR问题,密度云图,50条等值线Fig. 7 HCW-UL-Z,DMR problem,density contour,50 levels

图选项

3 结论1) 新权重算子(Z型)对间断的捕捉能力良好,同时相比R型权重能够抑制间断处数值振荡的传播.2) 相比于WENO-Z,采用Z型权重算子的混合格式HCW-Z耗散降低,分辨率提高.HCW-U与HCW-UL的数值结果并无明显区别.3) Z型权重算子的数值特性与R型权重算子(r_c=0.5)相比区别不明显,但是R型权重算子的计算效果依赖r_c的选取，使用受到局限.
参考文献

[1]	Wang Z J, Fidkowski K,Abgrall R,et al.High-order CFD methods:current status and perspective[J].Interntional Journal for Numerical Methods in Fluids,2012,72(8):811-845.
	Click to display the text
[2]	阎超,于剑, 徐晶磊,等.CFD模拟方法的发展成就与展望[J].力学进展,2011,41(5):562-589. Yan C,Yu J,Xu J L,et al.On the achievements and prospects for the methods of the computational fluid dynamics[J].Advances in Mechanics,2011,41(5):562-589(in Chinese).
	Cited By in Cnki (65)
[3]	Harten A,Osher S. Uniformaly high order accurate essentially nonoscillatory scheme,Ⅲ[J].Journal of Computational Physics,1987,71(2):231-303.
	Click to display the text
[4]	Shu C W, Osher S.Efficient implementation of essentially non-oscillatory shock-capturing schemes[J].Journal of Computational Physics,1988,77(2):439-471.
	Click to display the text
[5]	Borges R, Carmona M,Costa B,et al.An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics,2008,227(6):3191- 3211.
	Click to display the text
[6]	Henrick A K, Aslam T D,Powers J M.Mapped weighted essentially non-oscillatory schemes:achieving optimal order near critical points[J].Journal of Computational Physics,2005,207(2):542-567.
	Click to display the text
[7]	Castro M, Costa B,Don W S.High order weighted essentially non-oscillatory WENO-Z schemes for hyperbolic conservation laws[J].Journal of Computational Physics,2011,230(5):1766-1792
	Click to display the text
[8]	Lele S K. Compact finite difference schemes with spectral-like resolution[J].Journal of Computational Physics,1992,103(1):16-42.
	Click to display the text
[9]	Liu X L, Zhang S H, Zhang H X,et al.A new class of central compact schemes with spectral-like resolution Ⅰ :linear schemes[J].Journal of Computational Physics,248(1):235-256.

[10]	Adams N A, Shariff K.A high-resolution hybrid compact-ENO scheme for shock-turbulence interaction problems[J].Journal of Computational Physics,1996,127(1):27-51.
	Click to display the text
[11]	Pirozzoli S. Conservative hybrid compact-WENO schemes for shock-turbulence interaction[J].Journal of Computational Physics,2002,178(1):81-117.
	Click to display the text
[12]	Ren Y X, Liu M E,Zhang H X.A characteristic-wise hybrid compact-WENO scheme for solving hyperbolic conservation laws[J]. Journal of Computational Physics,2003,192(2):365-386.
	Click to display the text
[13]	Yu J, Yan C,Jiang Z H.A high resolution low dissipation hybrid scheme for compressible flows[J].Chinese Journal of Aeronautics,2011,24(4):417-424.
	Click to display the text
[14]	武从海,赵宁, 田琳琳.一种改进的紧致WENO混合格式[J].空气动力学报,2013,31(4):477-481. Wu C H,Zhao N,Tian L L.An improved hybrid cmpact-WENO scheme[J].Acta Aero Dynamica Sinica,2013,31(4):417-481(in Chinese).
	Cited By in Cnki
[15]	Shen Y Q, Zha G C.Generalized finite compact difference scheme for shock/complex flowfield interaction[J].Journal of Computational Physics,2011,230(12):4419-4436.
	Click to display the text