
 , 王浩乾, 程天庆, 洪楚航
, 王浩乾, 程天庆, 洪楚航 东北大学 医学与生物信息工程学院, 辽宁 沈阳 110169
收稿日期:2021-03-19
基金项目:国家自然科学基金资助项目(61801104,61902058);中央高校基本科研业务费专项资金资助项目(N2019002);东北大学第十五届(2021年)大学生创新训练计划项目(210249)。
作者简介:蒋芳芳(1983-),女,辽宁沈阳人,东北大学讲师.。
摘要:针对房颤事件中的节律异常特性, 提出应用相空间重构算法提取心冲击(ballistocardiogram, BCG)信号的二维节律特征, 并对重构过程中的最优嵌入维数和时间延迟参数进行了讨论.首先, 将心脏搏动视为非线性动力学系统, 应用相空间重构理论将一维时间序列映射到高维相空间中, 从而获取BCG信号中表征房颤过程节律异常的相空间轨迹特征.其次, 探讨了重构过程中适于房颤诊断的最优嵌入维数和时间延迟参数, 并结合卷积神经网络实现了对房颤的智能诊断.最终, 通过对59名受试者提取到的2 000组BCG数据进行十折交叉验证, 所提方法的分类准确率达到91.00%, 与基于经典时频特征的机器学习方法相比较, 有较为明显的提高, 从而验证了所提方法的优越性.
关键词:心冲击信号心电信号房颤检测相空间重构卷积神经网络
Atrial Fibrillation Detection Method Based on Phase Space Reconstruction Using Ballistocardiogram Signal
JIANG Fang-fang

 , WANG Hao-qian, CHENG Tian-qing, HONG Chu-hang
, WANG Hao-qian, CHENG Tian-qing, HONG Chu-hang School of Medicine & Biological Information Engineering, Northeastern University, Shenyang 110169, China
Corresponding author: JIANG Fang-fang, E-mail: jiangff@bmie.neu.edu.cn.
Abstract: Based on the arrhythmia characteristics of atrial fibrillation(AF), phase space reconstruction(PSR)is applied to extract the 2D rhythmic feature of the ballistocardiogram(BCG)signal. In the process of reconstruction, the optimal embedding dimensions and time delay parameters are discussed. Firstly, the heart beat is regarded as a non-linear dynamic system, and the 1D time series is mapped to the high-dimensional phase space, based on the phase space reconstruction theory, to obtain the 2D trajectory, which describes the abnormal rhythm of AF in BCG signal. Secondly, the optimal embedding dimension and time delay parameters of the reconstruction procedure for AF diagnosis are discussed, and the convolutional neural network(CNN) is applied to identify AF automatically. Finally, 2 000 BCG segments from 59 subjects are used to validate the classification performance. The accuracy reaches 91.00 % by means of the tenfold cross-validation. Compared to the machine learning method based on the classical time-frequency features, the accuracy is improved, which verifies the superiority of the proposed method.
Key words: ballistocardiogram(BCG) signalelectrocardiographic(ECG) signalatrial fibrillation(AF) detectionphase space reconstruction(PSR)convolutional neural network(CNN)
近年来心血管疾病的发病率逐年上升, 其高致残率和高死亡率严重危害人类健康[1].房颤作为一种常见的心律失常疾病, 其发病率也呈现逐年上升趋势, 且易导致心房血栓、缺血性脑卒中等恶性事件[2].由于房颤的发作具有时间不确定、临床表现不明显等特征, 故研究其日常实时、连续监测与诊断的方法尤为重要.
目前, 临床上多以心电图(electrocardiogram, ECG)作为房颤诊断的金标准.其主要表现为: 由心房活动异常引起的P波消失, 以及R-R间期紊乱等特征[3-5].由于ECG的检测过程需要在人体体表安装电极等装置, 且需要特定的检测设备及检测人员, 不但会对受试者的皮肤产生刺激, 其活动范围也会被约束, 不适于日常长期监测使用.因此, 面向家庭监测的非接触式房颤检测方法成为当今研究热点.
心冲击(ballistocardiogram, BCG)信号记录由心脏搏动与大动脉血液循环所导致的与心跳同步的身体振动, 是一种非接触式的心脏功能实时检测方法[6].目前, BCG在心率提取、心律变异等方面已取得较为显著的研究成果[7-8].关于房颤诊断的研究, 近几年也呈现上升趋势.Bruser等[9]提取了BCG信号的经典时频特征, 并应用机器学习算法开展了对房颤、窦性心律和体动的三分类研究.Yu等[10]通过小波变换提取BCG信号的时频特征, 应用机器学习分类器实现了房颤与非房颤的二分类诊断.Wen等[11]将BCG转换为能量信号, 并提取了新型的数据序列特征, 最终通过机器学习算法检测房颤.综上, 当前基于BCG信号的房颤诊断研究, 主要集中于应用机器学习分类器对信号的时频特征进行分类, 并取得了初步的成果, 能够证明应用BCG信号进行房颤检测的可行性.
但是, 基于时频特征的检测方法较为依赖于信号的波形变化, 而BCG信号受个体差异、不同检测装置、外界干扰等因素影响较大, 故难以保证房颤诊断精度的稳定性.因此, 本文提出应用相空间重构理论提取BCG信号的二维节律特征, 并结合卷积神经网络, 提高房颤诊断的自适应性与稳定性.通过对相空间重构过程中嵌入维数与时间延迟等参数的讨论, 探索面向房颤诊断的BCG信号新型特征提取方法, 为其在房颤等心血管疾病诊断中的实际应用提供一种可行的解决方案和崭新的研究方向.
1 实验数据本文采用基于聚偏氟乙烯(polyvinlidene fluoride, PVDF)压电薄膜传感器的卧姿BCG信号检测装置和CT-08S动态心电记录仪分别采集同步的BCG信号和ECG信号, 采样频率分别为125 Hz和200 Hz.其中, ECG信号作为房颤诊断的金标准, 主要起到为同步BCG信号设置标签的作用.共有59名受试者参与该实验, 男性34名, 女性25名, 年龄分布为27至93岁.记录时间均为8h(晚上12点至次日8点), 记录环境为医院病房卧姿采集方式.
为了解决不同采样率的问题, 本文对ECG信号进行降采样, 统一采样率为125 Hz.并根据房颤诊断的常用分帧方法, 设定分帧长度为24 s, 共计3 000采样点[12].将BCG数据分为房颤(AF)和非房颤(NAF)两类, 设定标签0为NAF, 1为AF.通过对原始信号进行筛选和预处理, 滤除波幅过大的体动及波幅过小的离床时段, 最终共获得2 000帧较为纯净的BCG数据, 其中AF与NAF各1 000帧.
2 方法2.1 方法描述本文所提方法流程如图 1所示.
图 1(Fig. 1)
 | 图 1 所提方法流程框图Fig.1 Flow chart of the proposed method |
主要工作包括: 选取合适的嵌入维数m和时间延迟τ进行相空间重构, 以保证所提二维节律特征对房颤的表征性能; 构建适于对二维节律特征进行分类的卷积神经网络模型.下面分别介绍这两部分的具体方法.
2.2 基于相空间重构的二维节律特征提取相空间重构是一种用于分析复杂系统的数学方法, 其将离散的一维时间序列x(t)转化为x(t)与x(t+τ), …, x[t+(m-1)τ]共同形成的m维空间, 其中τ为时间延迟, m为嵌入维数[13-15].通过高维映射实现对波形形态的实时量化, 在保证与原始序列相同的动态行为前提下, 挖掘时间序列中所隐含的动态信息, 从而弥补经典时频特征中有可能被丢失的潜在信息, 更适于处理较长的非平稳数据.因此, 考虑将一维BCG信号映射到高维的相空间中, 从而获取表征房颤节律异常的特征参数.
设单个时间序列x(t)=(x1, x2, …, xN), 其中N为x(t)中数据采样点数, 则延迟重构的状态向量为vi=(xi, xi+τ, xi+2τ, …, xi+(m-1)τ).基于时间序列x(t)的相空间重构表示为
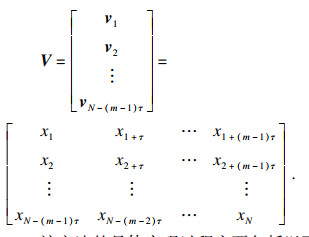 | (1) |
1) 确定延迟参数τ和嵌入维数m;
2) 通过延迟τ个采样点, 将BCG信号映射到m维相空间中, 获取其m维相空间轨迹;
3) 将m维相空间轨迹映射到二维平面上, 以提高其输入神经网络进行分类的效率.其中, 二维映射平面的选择要遵循高维信息最大化描述准则[13], 从而获取最优二维节律特征.
2.2.1 延时参数τ的确定延迟参数τ的选取, 直接影响重构相空间轨迹的表征性能.若τ选取过小, 则相空间轨迹会挤压于同一位置, 反之则会使各分量相互独立, 无法得到有效的特征[16].因此选取合适的τ值, 不仅能够有效反映心血管系统的特性, 而且能够提高后期房颤诊断的分类性能.目前, τ的选取方法主要包括: 自相关函数法(autocorrelation, AC)、互信息法(mutual information, MI)、嵌入窗法等[17-18].本文采用AC法和MI法两种方法, 对其所选τ值的分类性能进行比较, 以获取最优重构参数.
AC法所估算的τ值为自相关函数的过零点[19], 其计算公式为
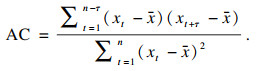 | (2) |
MI法所估算的τ值为互信息函数的局部最小值点[20], 其计算公式为
 | (3) |
AC法和MI法在估算τ值的过程中理论上仅需要提取首个过零点和局部最小值点.然而, 在实践中, 由于噪声和微小波动的存在, 真实的τ值之前可能会出现伪过零点或伪局部最小值点, 从而导致无法绘制出最优的相空间轨迹.因此, 本文选取了前三个过零点或局部最小值点τ1, τ2和τ3, 作为最优τ值的候选项, 而后通过实验确定最终的τ值.图 2为AC法前三个过零点处的τ1, τ2和τ3.图 3为MI法前三个局部最小值点处的τ1, τ2和τ3.
图 2(Fig. 2)
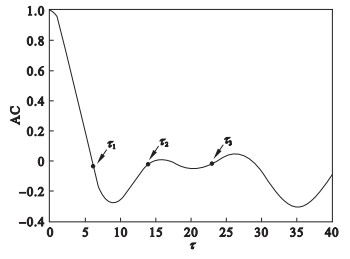 | 图 2 AC法估算τ值Fig.2 Estimate τ by AC method |
图 3(Fig. 3)
 | 图 3 MI法估算τ值Fig.3 Estimate τ by MI method |
2.2.2 嵌入维数m的确定嵌入维数m决定时间序列重构相空间的维度, 若m较小, 则吸引子无法完全展开, 反之则会使得计算量剧增, 误差变大[16].因此, 本文选择常用的虚假最近邻点法(false nearest neighbor, FNN)来选择最适合BCG信号重构的嵌入维数, 有效避免信息被隐藏的同时, 减小噪声的影响[21-23].该方法的原理为: 在足够大的维度d上相邻的两个点在维度d+1上并不相邻, 即虚假邻点.随着d的增大, 相空间重构轨迹会逐渐展开, 虚假邻近点也会逐步被消除, 从而得到能够还原动力学系统的相空间轨迹.当邻近点减少至可忽略, 则选取此时的d为嵌入维数m.该算法通过计算d与d+1维相空间之间欧氏距离的平方来确定邻近点数量, 其计算公式为
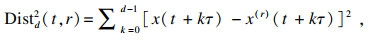 | (4) |
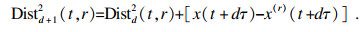 | (5) |
理论上, 若式(4)右侧第二项接近于零, 则选择此时的d作为相空间重构的最优嵌入维数.但由于虚假最近邻点接近零的过程耗时较长或无法完全实现, 因此实际情况下当虚假最近邻点小于某一阈值(1 % 或5 %),即选定d为合适的嵌入维数.将% FNN作为函数来表征d增加过程中虚假最近邻点的变化, 公式为
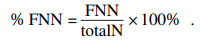 | (6) |
图 4为将BCG信号作为输入时所得FNN的变化情况.
图 4(Fig. 4)
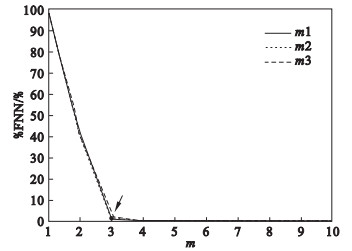 | 图 4 虚假最近邻点法估算m值Fig.4 Estimate m by false nearest neighbor method |
由图 4可见, 当m为3时% FNN值已小于5 %, 故本文选取3作为BCG信号相空间重构的最优嵌入维数.
2.3 基于卷积神经网络的房颤智能检测卷积神经网络(convolutional neural network, CNN)是一种包含卷积或相关计算且具有深度结构的前馈神经网络[24].由于卷积核参数的共享性和层间连接的稀疏性, 使得卷积神经网络能够以较少的计算量实现网格状的拓扑特性, 从而更适用于图像分析.
2.3.1 神经网络的输入由于信号的检测时间较长, 体动等因素的干扰致使信号出现基线漂移、不稳定等问题.本文沿(1, 1, 1)方向对相空间轨迹进行了坐标轴转换[25], 转换公式为
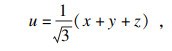 | (7) |
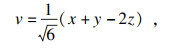 | (8) |
 | (9) |
2.3.2 神经网络结构本文基于相空间重构得到的二维节律特征, 设计了一个16层的卷积神经网络: 8层卷积层、4层池化层、1层flatten层、3层全连接层, 其框图如图 5所示.卷积层不仅可以对数据深入分析, 提取高维特征, 而且可以通过共享权值参数提高训练速度, 同时卷积之后的dropout操作提高了模型抗过拟合能力.池化层可以在保留特征的同时减少特征矩阵和网络参数, 也可以增加阻力避免过拟合.最后, Flatten层和全连接层对前向传播的特征进行处理, 并由softmax函数激活, 输出二分类结果.
图 5(Fig. 5)
 | 图 5 所设计的卷积神经网络结构Fig.5 Structure of the designed convolutional neural network |
3 实验与结果3.1 确定相空间重构参数3.1.1 时间延迟τ的选择为确定适于BCG信号房颤检测的时间延迟τ, 分别应用经典的AC法和MI法估算的AF与NAF数据的τ1, τ2和τ3值, 并绘制统计直方图如图 6、图 7所示.
图 6(Fig. 6)
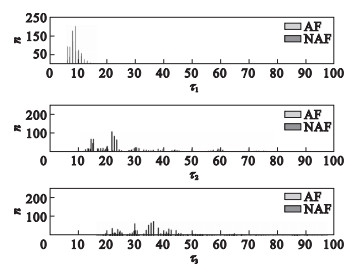 | 图 6 AC法估算τ值直方图Fig.6 Histogram of τ estimated by AC method |
图 7(Fig. 7)
 | 图 7 MI法估算τ值直方图Fig.7 Histogram of τ estimated by MI method |
由图 6与图 7可见, 通过AC法估算的τ值直方图分布较为杂乱, 无法显著区分AF与NAF.而MI法所估算的τ值直方图均趋于正态分布, 且对AF和NAF有一定的区分度.由此可见, MI法较AC法能避免噪声和其他微小波动对τ值计算的影响, 更适合于延迟参数的选择.此外, 通过比较图 7中τ1, τ2与τ3的直方图分布, 可见τ2和τ3较τ1可更明显地区分出AF和NAF, 而τ3相对于τ2具有更小的偏度, 这表明在大多数情况下τ3使得x(t)与x(t+1)有最小的依赖性.因此, 初步选定τ3为最佳延迟参数.
为定量验证以上结论, 分别应用两种方法估算了全部BCG分帧的τ值, 并绘制了τ1, τ2和τ3的分布箱线图, 如图 8、图 9所示.
图 8(Fig. 8)
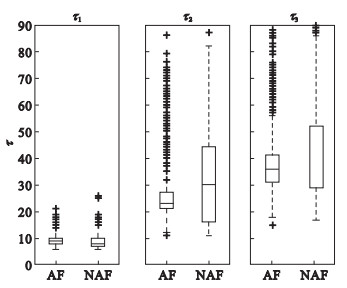 | 图 8 AC法估算τ值箱线图Fig.8 Boxplot of τ estimated by AC method |
图 9(Fig. 9)
 | 图 9 MI法估算τ值箱线图Fig.9 Boxplot of τ estimated by MI method |
通过比较可见, 在相同BCG数据下, MI法的异常值较少, 具有较好的鲁棒性, 箱体的上下线分布对于AF与NAF的区分度也最为明显, 与直方图分布显示结果一致.因此, 最终选定τ3为最佳延迟参数.
3.1.2 嵌入维数m的选择为定量验证2.2.2中初步选定的嵌入维数3, 本文应用FNN算法分别估算嵌入维数m1, m2和m3, 并绘制AF与NAF的分布箱线图, 如图 10所示.
图 10(Fig. 10)
 | 图 10 FNN估算m值箱线图Fig.10 Boxplot of m estimated by FNN |
由图 10可见, m1, m2与m3的平均值均介于2和3之间.同时, 根据相空间重构理论, 嵌入维数的选取应尽可能足够大, 以充分还原系统的动力学特性.因此, 最终选定m=3为最佳嵌入维数.
3.2 分类结果与性能比较3.2.1 二维节律特征获取应用m=3, τ=τ3绘制BCG信号的相空间轨迹, 并将其投影到与向量(1, 1, 1)正交的二维平面上.所获取的二维节律特征如图 11所示.
图 11(Fig. 11)
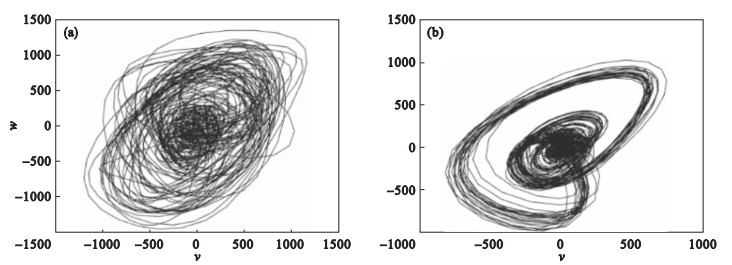 | 图 11 BCG信号的二维节律特征图Fig.11 2D rhythm feature of BCG signal (a)—τ3=7;(b)—τ3=5. |
由图 11可见, 通过选取适合的相空间重构参数, 所绘制的二维节律特征图可较为显著地区分出AF与NAF.
3.2.2 分类性能比较为验证所提方法的检测性能, 本文复现了文献[26]中的基于BCG信号的经典房颤诊断方法.通过提取BCG信号的17个经典时频特征(6个时域特征, 11个时频域特征), 作为机器学习分类器的输入, 以实现AF与NAF的区分.本文共比较了5个机器学习分类器, 分别为support vector machine(SVM), naive Bayesian(NB), bootstrap aggregated decision trees(BAT), random forests(RF)和decision tree(DT).
性能参数方面选取了准确率(Acc)、灵敏度(Sen)、精确度(Pre)、特异性(Spe)四个参数以评估所提方法的分类性能.其计算公式分别为
 | (10) |
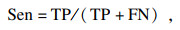 | (11) |
 | (12) |
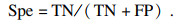 | (13) |
最终十折交叉验证所获得的混淆矩阵及对应的分类结果如表 1、表 2所示.
表 1(Table 1)
| 表 1 十折交叉验证混淆矩阵 Table 1 Confusion matrix of tenfold cross validation | ||||||||||||||||||||||||||||||||||||||||||||||||
表 2(Table 2)
| 表 2 分类性能对比 Table 2 Comparison of classification performance ?? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
通过对比可见:
1) 对于基于经典时频特征的机器学习分类方法, RF分类器的性能最佳, 这一结论与文献[26]的结论一致.但分类的绝对精度低于文献[26], 这主要由于本文所采用的实验数据量与受试者的人数均高于文献[26], 更接近日常筛查的数据环境, 而经典的时频特征对数据波形的差异性依赖较大, 从而导致分类精度的下滑.
2) 本文所提方法的分类性能总体优于基于经典时频特征的RF分类器.这主要由于本文所提取的二维节律特征, 较经典时频特征, 对房颤的异常节律信息有更显著的区分度.此外, 神经网络分类器较机器学习分类器具有更高的自适应性, 因此更适于多受试者的数据分类.由此验证了所提方法在日常房颤筛查中的优越性.
4 结论1) 通过讨论相空间重构过程中的时间延迟τ和嵌入维数m的最优解, 获取了BCG信号针对房颤诊断的最优重构参数.较经典时频特征, 提出了二维节律特征, 并在房颤检测方面取得了较为理想的表征效果, 为BCG信号相空间重构理论在心血管疾病诊断领域的应用提供了参考依据.
2) 针对重构轨迹的二维节律, 设计了自动诊断房颤的CNN分类器.并通过与经典机器学习分类器进行对比, 获得了更优的房颤分类性能.从而验证了端对端分类器的优越性, 为基于BCG信号的心血管疾病智能监测提供了新的研究思路.
参考文献
| [1] | 汤月霞, 颜晗. 风险评估指导心血管病预防研究进展[J]. 创伤与急危重病医学, 2020, 8(3): 214-216. (Tang Yue-xia, Yan Han. Risk sssessment guides advances in crdiovascular disease prevention research[J]. Trauma and Acute and Critical Care Medicine, 2020, 8(3): 214-216.) |
| [2] | 胡志成, 蒋超, 郑黎晖, 等. 2019年中国心房颤动医疗质量控制报告[J]. 中国循环杂志, 2020, 35(5): 427-437. (Hu Zhi-cheng, Jiang Chao, Zheng Li-hui, et al. 2019 China atrial fibrillation healthcare quality control report[J]. China Circulation Magazine, 2020, 35(5): 427-437. DOI:10.3969/j.issn.1000-3614.2020.05.003) |
| [3] | Ladavich S, Ghoraani B. Rate-independent detection of atrial fibrillation by statistical modeling of atrial activity[J]. Biomedical Signal Processing and Control, 2015, 18: 274-281. DOI:10.1016/j.bspc.2015.01.007 |
| [4] | Ledezma C A, Zhou X, Rodríguez B, et al. A modeling and machine learning approach to ECG feature engineering for the detection of ischemia using pseudo-ECG[J]. PLoS ONE, 2019, 14(8): e0220294. DOI:10.1371/journal.pone.0220294 |
| [5] | Daniel Z M, Christoph B, Patrick W, et al. Heartbeat cycle length detection by a ballistocardiographic sensor in atrial fibrillation and sinus rhythm[J]. Biomed Research International, 2015(19): 1-10. |
| [6] | Inan O T, Kovacs G T A, Giovangrandi L. Evaluating the lower-body electromyogram signal acquirm from the feet as a noise reference for standing ballistocardiogram measurements[J]. IEEE Transactions on Information Technology in Biommicine: A Publication of the IEEE Engineering in Mmicine and Biology Society, 2010, 14(5): 1188-1196. |
| [7] | CAO X R, Guo H, Tang J T. Heart rate extraction of ballistocardiogram based on Hilbert-Huang transformation[J]. Chinese Journal of Biomedical Engineering, 2019, 28(3): 118-124. |
| [8] | Liu W, Ren Y. A modified approach of peak extraction from BCG for heart rate estimation[J]. IOP Conference Series: Earth and Environmental Science, 2019, 252(4): 042086. DOI:10.1088/1755-1315/252/4/042086/pdf |
| [9] | Bruser C, Diesel J, Zink M D H, et al. Automatic detection of atrial fibrillation in cardiac vibration signals[J]. IEEE Journal of Biommical and Health Informatics, 2013, 17(1): 162-171. DOI:10.1109/TITB.2012.2225067 |
| [10] | Yu B, Zhang B Y, Xu L S, et al. Automatic detection of atrial fibrillation from ballistocardiogram(BCG)using wavelet features and machine learning[C]// Proceedings of 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society(EMBC). Berlin, 2019: 4322-4325. |
| [11] | Wen X, Huang Y Q, Wu X M, et al. A feasible feature extraction method for atrial fibrillation detection from BCG[J]. IEEE Journal of Biomedical and Health Informatics, 2020, 24(4): 1093-1103. DOI:10.1109/JBHI.2019.2927165 |
| [12] | 蒋芳芳, 徐敬傲, 李任, 等. 基于CNN的心冲击信号阵发性房颤自动检测方法[J]. 东北大学学报(自然科学版), 2019, 40(11): 1539-1543. (Jiang Fang-fang, Xu Jing-ao, Li Ren, et al. Automatic detection method of paroxysmal atrial fibrillation for ballistocardiagram based on CNN[J]. Journal of Northeastern University(Natural Science), 2019, 40(11): 1539-1543. DOI:10.12068/j.issn.1005-3026.2019.11.004) |
| [13] | Aston P J, Christie M I, Huang Y H, et al. Beyond HRV: attractor reconstruction using the entire cardiovascular waveform data for novel feature extraction[J]. Physiological Measurement, 2018, 39(2): 024001. DOI:10.1088/1361-6579/aaa93d |
| [14] | Peng F, Wen J, Zhang Y, et al. Monthly streamflow prediction based on random forest algorithm and phase space reconstruction theory[J]. Journal of Physics: Conference Series, 2020, 1637(1): 012091. DOI:10.1088/1742-6596/1637/1/012091/pdf |
| [15] | Zhang A, Xu Z. Chaotic time series prediction using phase space reconstruction based conceptor network[J]. Cognitive Neurodynamics, 2020, 14(6): 849-857. DOI:10.1007/s11571-020-09612-7 |
| [16] | 刘金海, 张化光, 冯健. 基于压力时间序列的输油管道在线泄漏故障诊断算法[J]. 东北大学学报(自然科学版), 2009, 30(3): 321-324. (Liu Jin-hai, Zhang Hua-guang, Feng Jian. On-line leak-detection method for pressure time series of oil pipeline[J]. Journal of Northeastern University(Natural Science), 2009, 30(3): 321-324.) |
| [17] | Huang S F, Horng C T, Chang C L, et al. Time delay autocorrelation analysis of EEG time series for the patients of early mild Alzheimer's disease[J]. Life Science Journal, 2017, 14(1): 78-81. |
| [18] | 李夕海, 刘代志, 张斌, 等. 基于重采样的混沌时间序列相空间重构研究[J]. 信号处理, 2006(2): 248-251. (Li Xi-hai, Liu Dai-zhi, Zhang Bin, et al. A resampling based phase space reconstruction for chaotic time series[J]. Journal of Signal Processing, 2006(2): 248-251. DOI:10.3969/j.issn.1003-0530.2006.02.026) |
| [19] | Michael T R, James J C, Carlo J D L, et al. Reconstruction expansion as a geometry-based framework for choosing proper delay times[J]. Physica D: Nonlinear Phenomena, 1994, 73(1/2): 82-98. |
| [20] | Lee J, Guo Y, Ravikumar V, et al. Towards the development of nonlinear approaches to discriminate AF from NSR using a single-lead ECG[J]. Entropy, 2020, 22(5): 531. DOI:10.3390/e22050531 |
| [21] | Kennel M B, Abarbanel H D I. False neighbors and false strands: a reliable minimum embedding dimension algorithm[J]. Physical Review E, 2002, 66(2): 026209. DOI:10.1103/PhysRevE.66.026209 |
| [22] | 刘树勇, 朱石坚, 俞翔. 确定相空间重构嵌入维数的研究[J]. 哈尔滨工程大学学报, 2008, 29(4): 374-381. (Liu Shu-yong, Zhu Shi-jian, Yu Xiang. Determinating the embedding dimension in phase space reconstruction[J]. Journal of Harbin Engineering University, 2008, 29(4): 374-381. DOI:10.3969/j.issn.1006-7043.2008.04.011) |
| [23] | Matilla-García M, Morales I, Rodríguez J M, et al. Selection of embedding dimension and delay time in phase space reconstruction via symbolic dynamics[J]. Entropy, 2021(2): 531. |
| [24] | Yadav S S, Jadhav S M. Deep convolutional neural network based medical image classification for disease diagnosis[J]. Journal of Big Data, 2019, 6(3): 1122-1131. DOI:10.1186/s40537-019-0276-2 |
| [25] | Jiang F F, Xu J A, Lu Z Y, et al. A transfer learning approach to detect paroxysmal atrial fibrillation automatically based on ballistocardiogram signal[J]. Journal of Medical Imaging and Health Informatics, 2019, 9(2): 1943-1949. |
| [26] | Cao L Y. Practical method for determining the minimum embedding dimension of a scalar time series[J]. Physica D: Nonlinear Phenomena, 1997, 110(1): 43-57. |
