, 宋帅1,2, 李昊1,2, 王英华1,2
, 宋帅1,2, 李昊1,2, 王英华1,2 1. 东北大学 机械工程与自动化学院, 辽宁 沈阳 110819;
2. 东北大学 航空动力装备振动及控制教育部重点实验室, 辽宁 沈阳 110819
收稿日期:2021-03-12
基金项目:辽宁省自然科学基金资助计划项目(2019-KF-04-03);国家自然科学基金资助项目(U1708255);中央高校基本科研业务费专项资金资助项目(N170308028)。
作者简介:钱文学(1975-),男,河北玉田人,东北大学副教授,博士。
摘要:为研究换刀机器人能沿特定路线平稳运动的问题, 对机器人模型进行运动学分析和轨迹规划.利用旋量理论推导出机器人的运动学模型, 结合蒙特卡洛法仿真得到了机器人末端工作空间的分布情况. 提出一种多节点多样条曲线运动的轨迹规划方法, 以关节位移、角速度和角加速度为评价指标, 分别采用3-3-3, 5-5-5和4-5-5样条曲线进行了轨迹规划.样机平台试验表明, 4-5-5混合多项式可以得到较平稳的加速度变化曲线, 有效解决了加速度发生阶跃和突变过大的现象.以上研究为机械臂复杂换刀路径的轨迹规划提供了基础.
关键词:换刀机器人运动学轨迹规划多节点混合样条曲线
Research on Tool-Changing Trajectory Planning of Tool-Changing Robots Based on Hybrid Spline Curves
QIAN Wen-xue1,2

 , SONG Shuai1,2, LI Hao1,2, WANG Ying-hua1,2
, SONG Shuai1,2, LI Hao1,2, WANG Ying-hua1,2 1. School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China;
2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems, Ministry of Education, Northeastern University, Shenyang 110819, China
Corresponding author: QIAN Wen-xue, E-mail: wxqian@mail.neu.edu.cn.
Abstract: In order to study the issue that the tool-changing robot can move smoothly along a specific route, kinematics analysis and trajectory planning of the robot model are carried out. The kinematics model of the robot is derived by using the screw theory combined with Monte Carlo simulation to obtain the distribution of the working space at the end of the robot. A trajectory planning method for multi-node and multiple-curve motion is proposed. The joint displacement, angular velocity and angular acceleration are used as the evaluation indicators, and 3-3-3, 5-5-5 and 4-5-5 spline curves are used to plan the trajectories respectively. The prototype platform test shows that the 4-5-5 mixed polynomial can obtain a relatively stable acceleration curve, which effectively solves the problem of excessive steps and sudden change in acceleration. The research provides a basis for the trajectory planning of complex tool-changing paths of manipulators.
Key words: tool-changing robotkinematicstrajectory planningmulti-nodehybrid spline curve
随着工业机器人的快速发展与广泛应用, 对其运行精度及可靠性的要求也越来越高.如何控制运行过程中的精度在最近机器人的发展史上一直是被重点研究的内容, 目前众多****针对相关研究已做了大量工作并取得了很多优秀成果[1].对于运行精度的研究, 轨迹规划是一个重要的研究内容和方向, 在轨迹规划过程中, 各关节的位移、速度和加速度是衡量运行精度的指标[2-3].
轨迹规划方法是利用多项式函数在初始位置和目标位置之间采用“内插”或“逼近”的方法来设定期望路径, 在笛卡尔空间中主要是针对机器人末端进行轨迹规划, 在关节空间进行轨迹规划是用各个关节角度随时间的函数来表示机器人的运动轨迹的变化[4-6].两种规划都需要保证轨迹是平滑连续的, 进而保证关节位移、角速度和角加速度是连续的, 使机器人整体运行平稳.
文献[7-8]利用3次样条函数在关节空间中对机器人进行了轨迹规划, 得到了各关节的运动学参数, 结果表明关节位移和速度满足连续要求, 但在开始和结束时的加速度值发生阶跃.文献[9-11]采用5次样条曲线的规划方法, 对机器人进行关节空间轨迹规划, 结果表明加速度是连续的, 但加加速度变化较大, 会使关节力变化较大.文献[12-14]采用高阶样条曲线方法获得了满足要求的运动学参数, 但采用高阶函数会增加计算机的运算量, 对实时控制关节运动是不利的.
因此, 本文针对换刀机器人特定工作路径, 结合多样条曲线函数插值方法, 以角位移、角速度和角加速度连续且无突变为目标进行规划.
1 基于旋量理论的工作空间分析机器人运动学主要研究机械臂的运动特性, 通过运动学方程研究机械臂的位置、速度、加速度及位置变量的所有高阶导数, 同时运动学分析也是研究机器人运动规划的理论基础.换刀机器人的整体结构如图 1所示, 其主要由基座、伸缩旋转结构、末端执行器及快换连接结构组成.
图 1(Fig. 1)
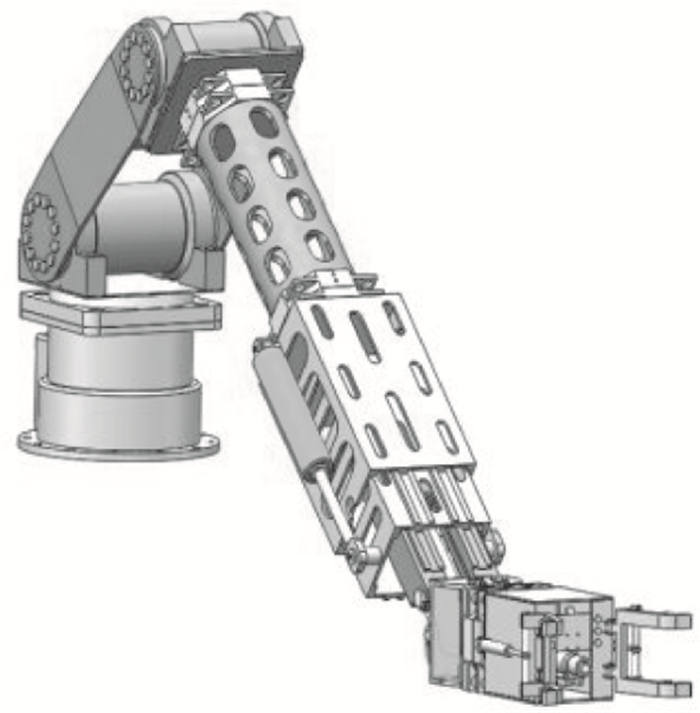 | 图 1 换刀机器人结构Fig.1 Tool-changing robot structure |
机器人的工作空间作为机器人工作能力的一个重要指标, 换刀机器人末端执行器的工作空间大小直接影响到末端能够到达位置范围的大小.本文利用旋量理论-蒙特卡洛方法, 通过随机抽样技术求解换刀机器人的工作空间.
刚体从一个坐标系到另一个坐标系的运动可由齐次变换矩阵G表示, G也被称为刚体的位姿矩阵.刚体的位姿矩阵G由刚体的位置矩阵P∈R3×1和姿态矩阵R∈SO(3)共同确定, 即
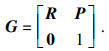 | (1) |
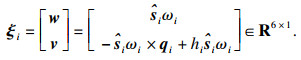 | (2) |
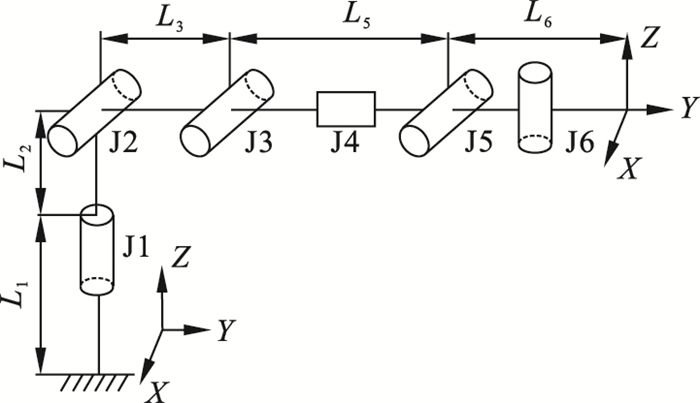 | 图 2 机器人简化结构及坐标系Fig.2 Simplified structure and coordinate system of the robot |
式中:
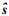
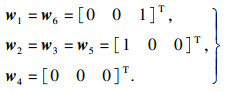 | (3) |
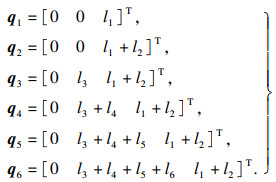 | (4) |
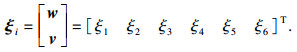 | (5) |
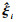
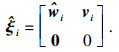 | (6) |
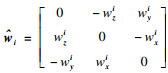
对于旋转关节, 运动旋量可以用矩阵指数积形式表达:
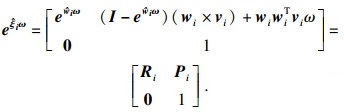 | (7) |
对于移动关节, 运动旋量的矩阵指数积形式为
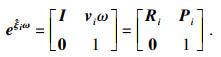 | (8) |
用Rodrigues公式将
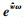
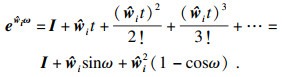 | (9) |
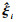
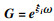
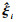
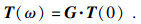 | (10) |
结合式(8)~式(10)可得换刀机器人基于旋量理论的运动学指数积公式[1]:
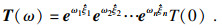 | (11) |
联立式(1)和式(11), 求得换刀机器人的末端位姿为
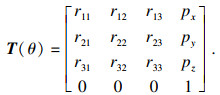 | (12) |
图 3(Fig. 3)
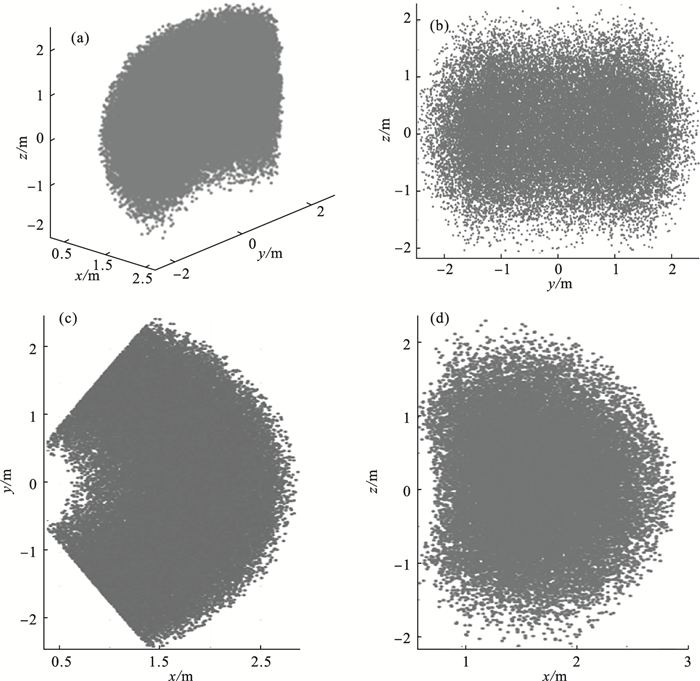 | 图 3 换刀机器人工作空间分布图及平面投影图Fig.3 Working space distribution diagram and plane projection diagram of the tool-changing robot (a)—工作空间三维图; (b)—yz平面图; (c)—xy平面图; (d)—xz平面图. |
由图 3可知, 在x轴方向最大工作半径为2.8 m, z轴方向半径为2 m, y轴方向最大工作半径为2.5 m, 分析结果表明, 设计的换刀机器人末端工作空间较大, 能满足换刀作业所需的空间要求.
2 轨迹规划针对换刀机器人在盾构机中进行换刀作业的工作特点, 对换刀机器人平移推动的工作路径进行轨迹规划, 在空间中的起始点和目标点的空间位姿如图 4所示(单位: m).
图 4(Fig. 4)
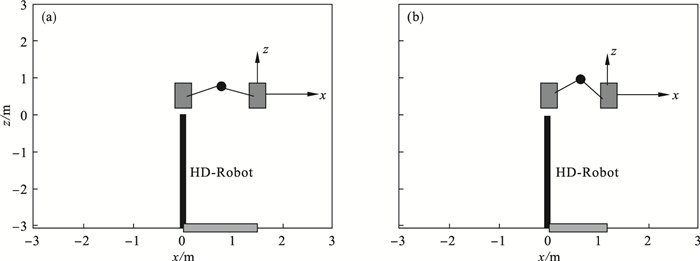 | 图 4 起始点和目标点的空间位姿Fig.4 Spatial pose of the starting point and the target point (a)—起始点; (b)—目标点. |
本文将起始点和目标点之间的轨迹通过关键点分成3段, 各关键点变量信息如表 1所示.分别采用3-3-3, 5-5-5和4-5-5混合多项式对换刀机器人进行关节轨迹规划.
表 1(Table 1)
| 表 1 各关键点处关节变量信息 Table 1 Joint variable information at each key point |
为了使计算过程简单, 对n段规划的轨迹中每一段所用的时间进行归一化处理:
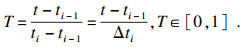 | (13) |
可得第i段轨迹的n次多项式方程:
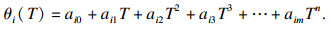 | (14) |
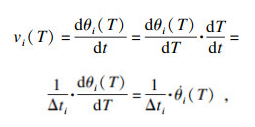 | (15) |
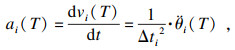 | (16) |
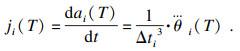 | (17) |
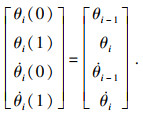 | (18) |
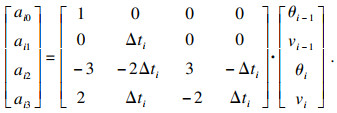 | (19) |
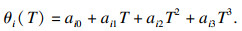 | (20) |
利用MATLAB, 将表 1中的值代入3-3-3多项式中进行仿真, 在关节空间中, 对换刀机器人进行轨迹规划, 其各关节的角位移、角速度和角加速度轨迹仿真图如图 5所示.
图 5(Fig. 5)
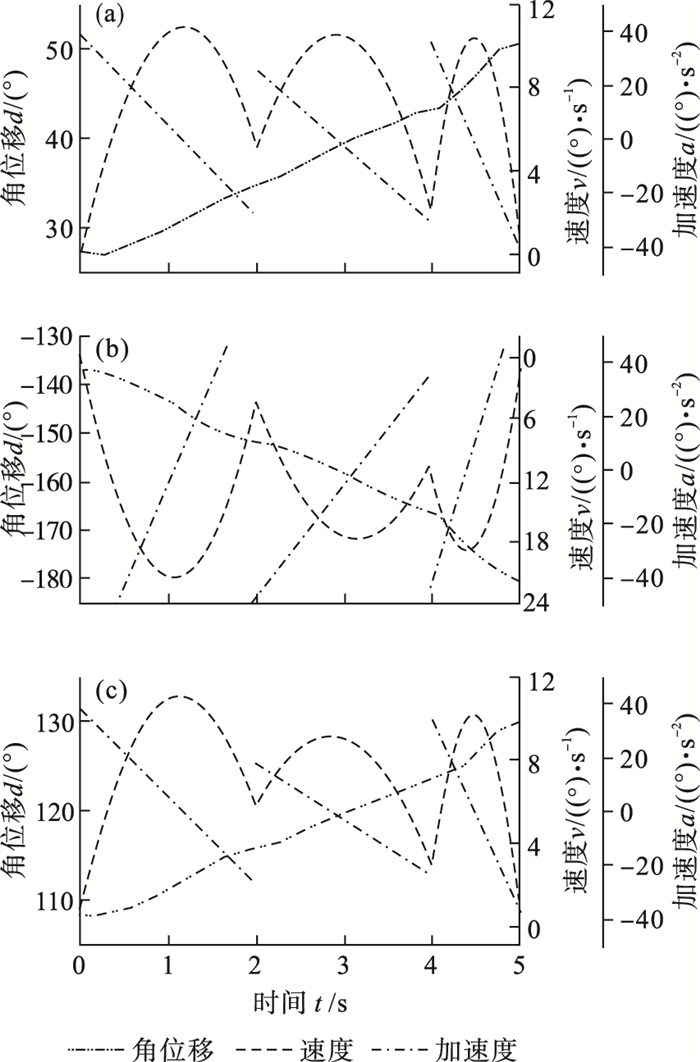 | 图 5 3-3-3多项式规划时旋转关节运动变量变化曲线Fig.5 Variation curves of rotation joint motion variables in 3-3-3 polynomial planning (a)—关节2; (b)—关节3; (c)—关节5. |
2.2 5-5-5混合多项式轨迹规划采用混合五次多项式时, 需要保证前一段轨迹结束的位置、速度、加速度及加加速度能够与后一段轨迹开始的位置、速度、加速度和加加速度连续, 故有以下约束关系:
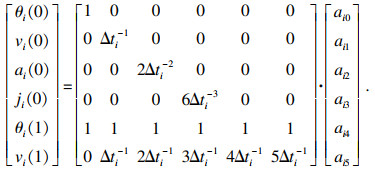 | (21) |
通过约束式(21), 可求得五次多项式的系数为
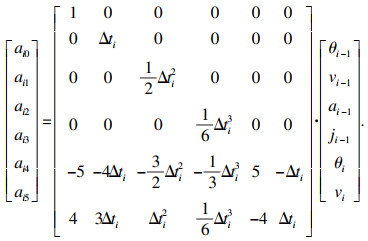 | (22) |
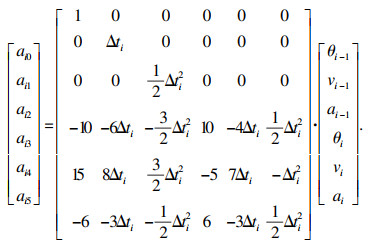 | (23) |
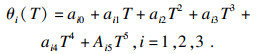 | (24) |
图 6(Fig. 6)
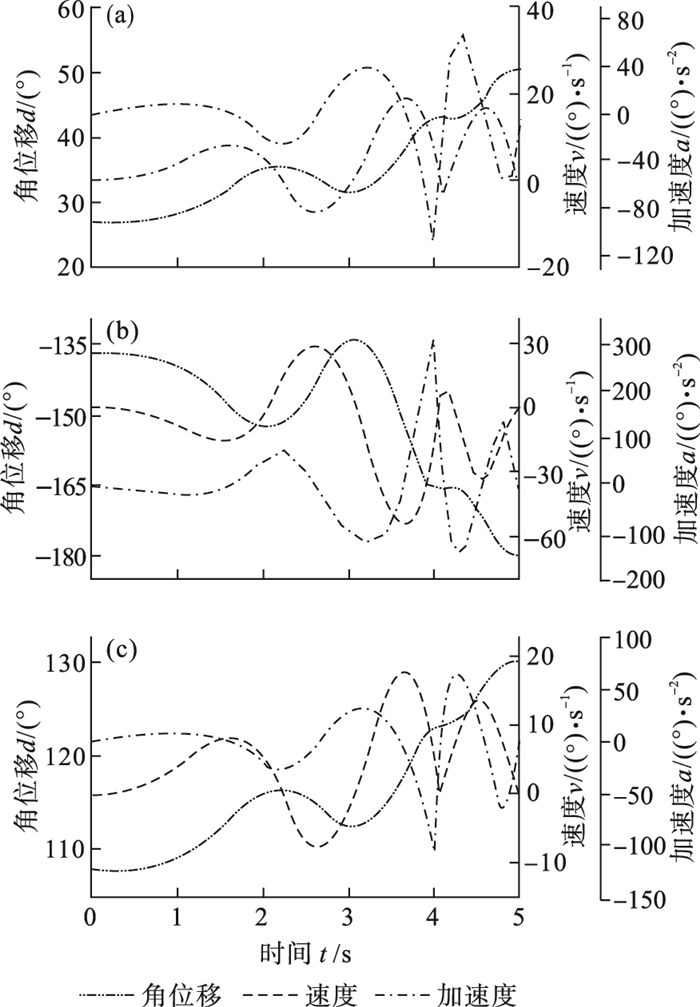 | 图 6 5-5-5多项式规划时旋转关节运动变量变化曲线Fig.6 Change curves of rotation joint motion variables in 5-5-5 polynomial planning (a)—关节2; (b)—关节3; (c)—关节5. |
2.3 4-5-5混合多项式轨迹规划本文引入四次多项式, 将三段轨迹规划为4-5-5模式, 其四次多项式有五个多项式系数, 需要五个约束方程, 即轨迹起始点的各关节位置、速度、加速度及目标点的关节位置和速度连续.约束方程为
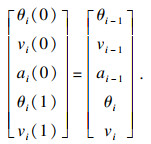 | (25) |
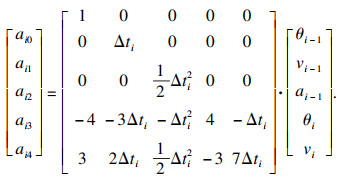 | (26) |
 | (27) |
图 7(Fig. 7)
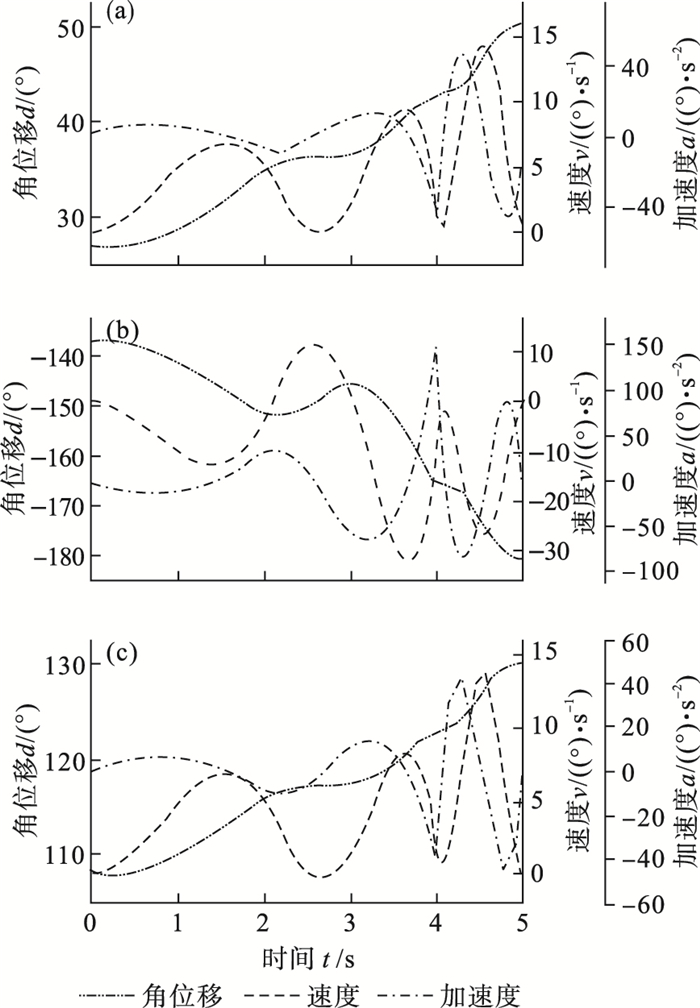 | 图 7 4-5-5多项式规划时旋转关节运动变量变化曲线Fig.7 Change curves of rotation joint motion variables in 4-5-5 polynomial planning (a)—关节2; (b)—关节3; (c)—关节5. |
由仿真结果可知, 采用4-5-5混合多项式进行轨迹规划可以保证速度和加速度的光滑连续, 且曲线峰值突变很小, 可以有效减少关节的冲击和震动.并且速度和加速度在起始点和目标点均能满足为零的要求.
2.4 换刀机器人末端运动学分析与试验对比换刀机器人系统如图 8所示, 为了验证换刀机器人的设计与分析的正确性, 将各关节运动变量输入到机器人关节控制器中, 进行运动试验, 通过试验测量和数值计算, 得到了机器人末端的空间位移曲线、速度曲线和加速度曲线.
图 8(Fig. 8)
 | 图 8 换刀机器人系统Fig.8 Tool-changing robot system |
通过以上算法分析, 确定了4-5-5混合多项式进行轨迹规划满足速度和加速的平稳连续的要求, 本节通过规划得到的各关节运动参数对末端轨迹、速度和加速度进行仿真, 从而建立末端运动学模型.通过式(12)可求得末端的运动轨迹, 如图 9所示.
图 9(Fig. 9)
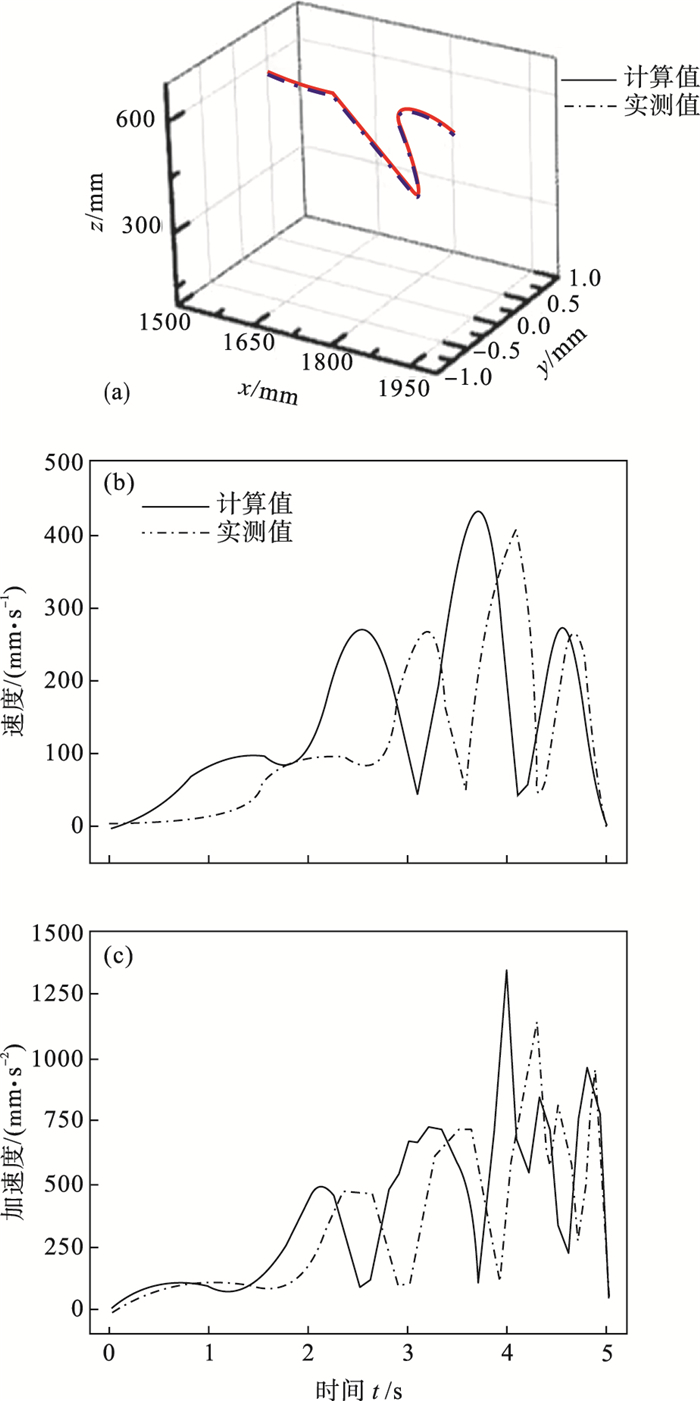 | 图 9 运动变量计算值与实测值对比曲线图Fig.9 Comparison curves between calculated and measured values of motion variables (a)—末端轨迹; (b)—末端速度; (c)—末端加速度. |
对式(10)两边求导, 可以得到末端标记点的速度
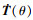
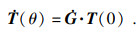 | (28) |
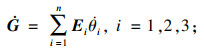 | (29) |
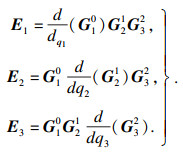 | (30) |
 | (31) |
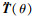
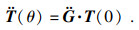 | (32) |
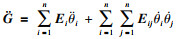
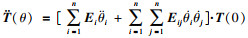
经整理可得
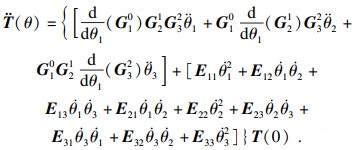 | (33) |
3 结论本文设计了一种模块化换刀机器人, 利用旋量理论-蒙特卡洛法对运动学进行了推导并对工作空间进行了仿真分析.以关节位移、角速度和角加速度为评价指标, 采用了3-3-3, 5-5-5和4-5-5多节点多样条曲线规划方案进行规划, 通过比较中间关键点处速度的连续性和整体过程中加速度的平稳性, 确定了4-5-5最优轨迹规划方案.与试验进行比较, 结果表明4-5-5多项式能有效解决三次多项式规划过程中加速度不连续和五次多项式引起加速度突变过大的现象.该方法具有普适性, 将采用多节点多样条曲线规划方法对机器人全局轨迹进行规划, 为机器人控制提供应用基础.
参考文献
| [1] | 邵君奕, 张传清, 陈雁, 等. 用于空间内曲面喷涂的冗余度机器人轨迹规划方法[J]. 清华大学学报(自然科学版), 2014, 54(6): 799-804. (Shao Jun-yi, Zhang Chuan-qing, Chen Yan, et al. Trajectory planning for redundant robots for internal surface spraying[J]. Journal of Tsinghua University(Science and Technology), 2014, 54(6): 799-804.) |
| [2] | Liu L, Chen C Y. Smooth trajectory planning for a parallel manipulator with joint friction and jerk constraints[J]. International Journal of Control, Automation and Systems, 2016, 8(14): 1022-1036. |
| [3] | Menasr R, Menasrij R. Smooth trajectory planning for robot using particle swarm optimization[C] //International Conference on Swarm Intelligence Based Optimization. Mulhouse: ICSIBO, 2014: 50-59. |
| [4] | Saravanan R, Ramabalan S, Balamurugan C, et al. Evolutionary trajectory planning for an industrial robot[J]. International Journal of Automation and Computing, 2010, 7(2): 190-198. DOI:10.1007/s11633-010-0190-8 |
| [5] | 房立金, 贺长林, 祝帅, 等. 串联多臂式巡检机器人控制策略及轨迹规划方法[J]. 东北大学学报(自然科学版), 2019, 40(5): 734-739. (Fang Li-jin, He Chang-lin, Zhu Shuai, et al. Control strategy and trajectory planning of serial multi-arm inspection robots[J]. Journal of Northeastern University(Natural Science), 2019, 40(5): 734-739.) |
| [6] | Chen G, Liu D, Wang Y F, et al. Path planning method with obstacle avoidance for manipulators in dynamic environment[J]. International Journal of Advanced Robotic Systems, 2018, 15(6): 1-18. |
| [7] | Abu-Dakka F J, Assad I F, Valero F, et al. Parallel populations genetic algorithm for the optimization of cubic pol ynomial joint trajectories for industrial robot[C]//International Conference on Intelligent Robotics and Applications. Aachen, 2011: 83-92. |
| [8] | 韩江, 谷涛涛, 夏链, 等. 基于混合插值的工业机器人关节轨迹规划算法[J]. 中国机械工程, 2018, 29(12): 1460-1466. (Han Jiang, Gu Tao-tao, Xia Lian, et al. Joint trajectory planning algorithm for industrial robots based on mixed interpolation[J]. China Mechanical Engineering, 2018, 29(12): 1460-1466. DOI:10.3969/j.issn.1004-132X.2018.12.012) |
| [9] | Krishnan J, Rajeev U P, Jayabalan J, et al. Optimal motion planning based on path length minimisation[J]. Robotics and Autonomous Systems, 2017, 94: 245-263. DOI:10.1016/j.robot.2017.04.014 |
| [10] | Sun Y, Wei X. Trajectory planning of palletizing robot based on quantic polynomial[J]. Packaging Engineering, 2017, 38(21): 159-163. |
| [11] | Wu J F, Wang H L, Zhang M H. On obstacle avoidance path planning in unknown 3D environments: a fluid-based framework[J]. ISA Transactions, 2020, 111: 249-264. |
| [12] | Liu H, Lai X, Wu W. Time-optimal and jerk-continuous trajectory planning for robot manipulators with kinematic constraints[J]. Robotics and Computer-Integrated Manufacturing, 2013, 29(2): 309-317. DOI:10.1016/j.rcim.2012.08.002 |
| [13] | 滕儒民, 李玉鑫, 王欣, 等. 基于凸优化的举高消防车时间最优轨迹规划[J]. 机械工程学报, 2019, 55(6): 138-144. (Teng Ru-min, Li Yu-xin, Wang Xin, et al. Time optimal trajectory planning of elevating fire truck based on convex optimization[J]. Journal of Mechanical Engineering, 2019, 55(6): 138-144.) |
| [14] | Zhang T, Zhang M, Zou Y. Time-optimal and smooth trajectory planning for robot manipulators[J]. International Journal of Control Automation and Systems, 2020, 19(3): 1-11. |