
 , 胡慧明, 张树磊
, 胡慧明, 张树磊 东北大学 信息科学与工程学院, 辽宁 沈阳 110819
收稿日期:2020-12-30
基金项目:国家自然科学基金资助项目(61873049);中央高校基本科研业务费专项资金资助项目(N180704013)。
作者简介:贾润达(1981-),男,辽宁沈阳人,东北大学副教授,博士生导师。
摘要:由于浓密脱水过程中浓密机的底流浓度难以在线检测, 本文提出了一种基于宽度学习的软测量建模方法, 用以解决底流浓度的在线检测问题.该方法精度高, 泛化能力强.首先,在浓密机内部安装压力传感器, 建立正常工况下的历史数据集; 然后, 利用宽度学习系统对软测量模型进行训练, 从而实现浓密机底流浓度的在线预测; 最后, 通过仿真实验验证了该方法的有效性.与传统的机器学习方法相比, 宽度学习方法具有更高的预测精度.
关键词:浓密机宽度学习底流浓度软测量深度学习
Soft Sensor of Underflow Concentration for Thickener Based on Broad Learning System
JIA Run-da

 , HU Hui-ming, ZHANG Shu-lei
, HU Hui-ming, ZHANG Shu-lei School of Information Science & Engineering, Northeastern University, Shenyang 110819, China
Corresponding author: JIA Run-da, E-mail: jiarunda@ise.neu.edu.cn.
Abstract: Since it is difficult to online measure the underflow concentration of the thickener in the thickening-dehydration process, a broad learning system(BLS) based soft sensor modeling method is proposed in this paper. The method has high precision and strong generalization capability. First, several pressure sensors are installed inside the thickener, and the historical dataset under normal operating conditions is established. Then, the soft sensor model is trained by employing the BLS method to online predict the underflow concentration of the thickener. Finally, the efficiency of the proposed method is verified by simulation experiments. Compared with other traditional machine learning methods, the BLS method has higher prediction accuracy.
Key words: thickenerbroad learning system (BLS)underflow concentrationsoft sensordeep learning
在湿法冶金过程中, 浓密机是进行固液分离、提高矿浆浓度的设备.近年来, 尽管浓密机的效率不断提升, 但浓密机的底流浓度仍然难以在线检测.底流浓度在线检测的难点在于: 检测方法主要采用射线浓度计, 维护困难且易造成环境污染; 沉降过程机理复杂; 浓密机内部运行状态不可见[1].因此, 由于无法在线检测底流浓度, 从而使浓密脱水过程的运行优化控制难以实现, 进而对下游工序的稳定生产造成影响.
传统的软测量是通过对设备机理的充分分析进行建模, 该方法依赖于研究人员对过程机理的理解, 但是, 运用机理建模难度高, 并且准确性难以保证.大数据时代到来, 以数据驱动的建模方法成为主流, 其中以机器学习为核心的数据建模方法有效解决了机理模型不清晰设备的软测量建模问题.
Nunez等[2]提出了一种基于神经网络模型的预测控制方案来控制浓密机的底流浓度, 该方法利用递归神经网络预测底流浓度, 采用粒子群优化(particle swarm optimization, PSO)算法对成本函数进行优化, 表明神经网络的现代体系结构可以用于过程控制, 本文进一步对该方法进行了补充, 将宽度学习网络应用于实际浓密脱水过程, 验证方法的可行性.Zhang等[3]提出了一种基于数据驱动的底流浓度软测量模型, 该模型采用数据协调方法来提高关键变量的预测可靠性, 提高模型精度, 并且数据协调方法可以减小其他变量导致的随机误差, 提高浓缩机的优化控制效果, 该方法是在理想情况下采用线性求解, 然而实际浓密脱水过程具有强非线性.Xiao等[4]通过分析浓密脱水过程特点, 建立混合模型, 利用基于整体分布优化算法的三层极值学习机模型对机理模型的预测误差进行补偿, 从而提高了底流浓度的预测精度.Yuan等[5]提出一种基于时差偏最小二乘法(time-difference partial least square, TD-PLS)的软测量方法,利用训练样本间的时间差值克服传感器表面结晶造成的数据漂移问题.Jia等[6]提出一种核偏鲁棒回归(kernel partial robust M-regression, KPRM)算法应用于底流浓度软测量建模过程, 该方法将原输入空间中的非线性结构转化为高维特征空间中的线性结构, 并通过选择合适的加权策略, 克服离群点对回归模型的影响.由于浓密脱水过程机理模型中包含较多的参数, 难以实际应用, 且实际生产数据中存在强噪声, 从而导致上述软测量模型难以实际应用, 同时泛化能力较差.
在宽度学习的研究中, Feng等[7]针对分类任务开发一种具有三重增量学习能力的广域网络梯度增强系统(broad network gradient boosting system,BNGBS), 采用贪婪算法进行求解.与传统的网络集成方法和多层网络相比, BNGBS利用级联的方式消除分类损失, 提高精度, 加快训练过程.此外, 利用三重增量学习方法, BNGBS无需从头进行训练, 即可实现快速的模型扩展.Chai等[8]提出一种由ObRF-BM(oblique random forests-batch multiclass)和ObRF-DIL(oblique random forests-dual-incremental learning)组成的新型ObRF(oblique random forests)学习系统.该方法对倾斜超平面进行解析计算, 免除了搜索最佳特征和分割阈值.此外, 将决策节点上的特征随机投影到高维空间, 增强集成模型的随机性, 提高了ObRF模型的性能.上述方法训练速度快、泛化能力强、误差小, 并且运用增量学习方法, 在添加新数据时, 不必重新训练模型, 但这些方法尚未在具有强噪声的实际工业过程中应用.
针对上述问题, 本文提出了一种基于宽度学习的浓密机底流浓度软测量方法, 其优点在于:
1) 利用传感器获得现场数据, 对数据进行分析, 根据变量关系, 利用ARX模型建立相应的底流浓度软测量模型;
2) 针对浓密脱水过程, 运用宽度学习方法对底流浓度和压力差等数据进行黑箱建模, 解决了机理模型在工业现场难以应用的难题;
3) 宽度学习相比于其他神经网络, 结构简单、训练速度快、更透明高效, 其数据拟合具有明显的优势, 将其应用在浓密脱水过程中, 取得了更好的效果.
本文提出的方法有效解决了底流浓度的在线检测问题, 为后续实现浓密机的优化控制奠定了基础.
1 浓密脱水过程简介在湿法冶金浓密脱水过程中, 浓密机和压滤机协同运作.浓密机是该过程的核心设备, 其原理是根据重力沉降作用来提高矿浆浓度, 有利于减少压滤时间, 降低生产成本; 压滤机则是进一步获得干矿粉的设备[9-10].某湿法冶金浓密脱水过程工艺流程如图 1所示.
图 1(Fig. 1)
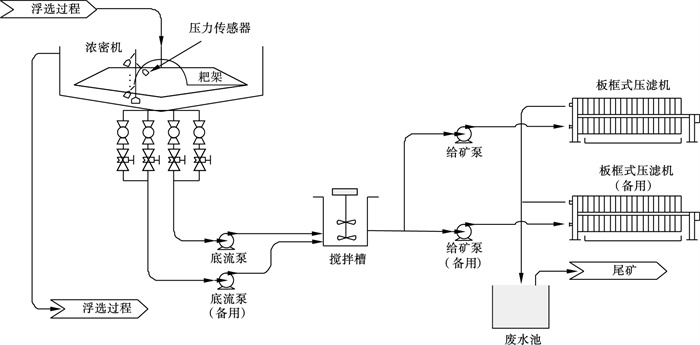 | 图 1 湿法冶金浓密脱水工艺流程图Fig.1 Flow chart of hydrometallurgy thickening-dehydration process |
由于压滤机是间歇工作, 在进行一次压滤后, 需要等待底流浓度达到期望值后才能进行下一次压滤, 因此, 定义每次压滤操作为一个批次, 在一个批次中, 矿浆首先通过渣浆泵输送到浓密机内进行沉降, 当浓密机的底流浓度达到期望值时开启底流泵, 将矿浆输出到搅拌槽内, 同时打开给矿泵压入压滤机进行压滤, 形成滤饼.当底流浓度低于某一设定值且一次压滤操作完成时, 关闭底流泵, 停止压滤操作.在此过程中, 底流浓度是关键变量, 并且难以获得, 因此需要对其建立软测量模型.如图 1所示, 可在浓密机内部靠近中心的位置安装多个压力传感器.将压力传感器安装在吊有重物的钢缆上, 将钢缆固定在浓密机耙架上防止在浓密机转动时压力传感器移动.一个批次内的底流浓度与压力关系如图 2所示, 在底流泵打开时内部压力下降, 相应的底流浓度下降; 底流泵关闭时, 内部压力上升, 底流浓度也上升.可以看出压力值与底流浓度呈正相关关系, 同时压力的测量值可以间接反映浓密机内部的浓度分布, 因此所获得的数据可以反映浓密机内部的运行状态.
图 2(Fig. 2)
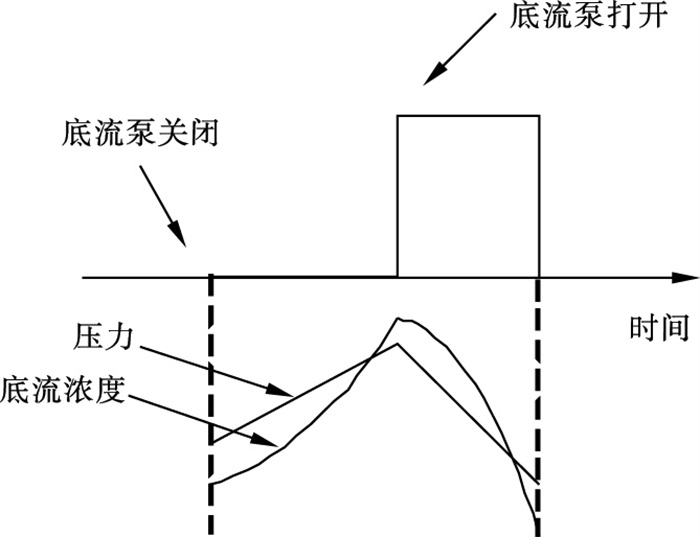 | 图 2 浓密脱水过程底流浓度随压力变化示意图Fig.2 Schematic diagram of underflow concentration varying with pressure in thickening-dehydration process |
2 基于宽度学习的底流浓度软测量2.1 宽度学习基本原理传统的神经网络训练时间长, 并且很容易陷入局部最优解, 因此研究人员开始研究简单的单层网络模型, 并提出宽度学习网络结构[11].宽度学习系统相较于其他神经网络的不同点在于, 输入权值矩阵通过稀疏自编码方式编码后, 在解码过程中选取最优权值, 而不是像其他神经网络随机更新权重[10].BLS训练的基本步骤如下:
步骤1 将输入样本进行线性变换, 将特征映射在特征平面上形成特征节点;
步骤2 在给定期望下, 运用稀疏自编码器优化特征节点的权重;
步骤3 利用激活函数将特征节点变为增强节点;
步骤4 将特征节点和增强节点连接作为输入信号, 输入到系统中, 经由连接矩阵线性输出;
步骤5 利用岭回归广义逆求解出连接矩阵.
宽度学习的结构图如图 3所示, 训练数据集为{X, Y} ∈ RN×(M+D).其中, M表示输入数据的维数, D表示输出数据的维数, N表示训练样本数, 每组映射包含特征节点ki个[11].映射特征函数可以表示为
图 3(Fig. 3)
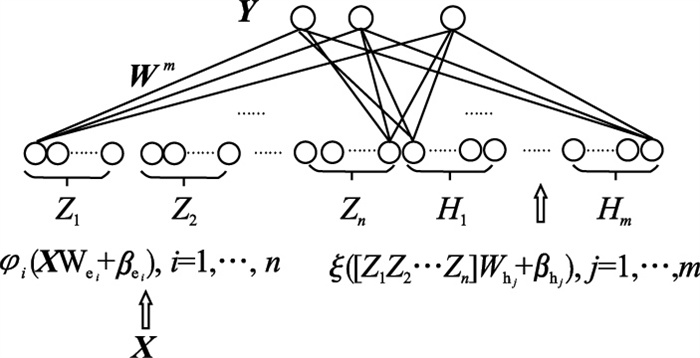 | 图 3 宽度学习结构图Fig.3 Structure diagram of broad learning system |
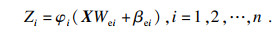 | (1) |
将所有特征节点Zi表示为Zn=[Z1, …, Zn], Zn作为增强节点的输入.因此M组增强节点的激活函数可表示为
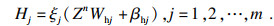 | (2) |
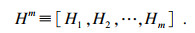 | (3) |
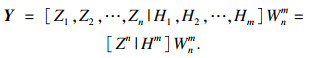 | (4) |
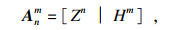 | (5) |
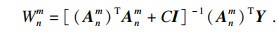 | (6) |
因为BLS是单层网络结构, 并且运用岭回归求解, 所以训练速度更快, 泛化能力更强[9].
2.2 稀疏自动编码器因为Wei, βei是随机初始化的输入权值和偏差,φ(·)是可自由选择的激活函数, 随机初始化虽然简便, 但是生成的随机特征常常具有不可预测性[14-15].为了克服这种随机性, BLS采用稀疏自编码思想来优化输入权值Wei.
提取训练数据中的稀疏特征, 用下面的公式来表示这个优化问题:
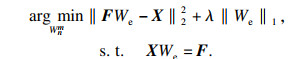 | (7) |
利用交替方向乘子法(alternating direction method of multipliers, ADMM)求解上述凸规划问题.可以将式(7)转化为一般问题:
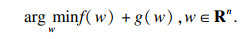 | (8) |
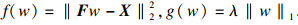
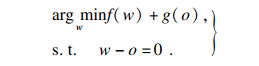 | (9) |
因此, 这个近似问题可以利用如下迭代步骤进行求解:
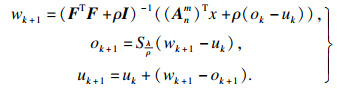 | (10) |
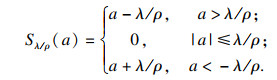 | (11) |
表 1(Table 1)
| 表 1 变量对应表 Table 1 Variable correspondence table |
图 4(Fig. 4)
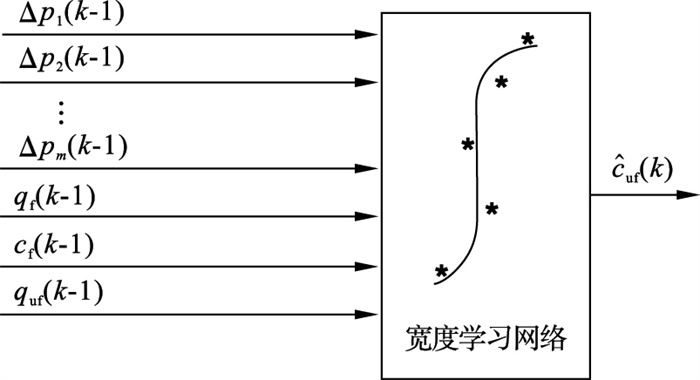 | 图 4 浓密机底流浓度软测量模型结构Fig.4 Soft sensor model structure of thickener underflow concentration |
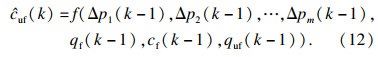 | (12) |
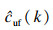
为了估计底流浓度
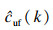
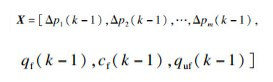 | (13) |
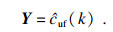 | (14) |
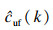
3 仿真实验3.1 数据生成研究团队通过浓密压滤过程机理模型和现场实际运行历史数据, 搭建了浓密脱水过程的仿真平台, 以模拟选矿厂的实际工艺层, 根据现场实际运行反馈, 该仿真平台可以稳定跟踪实际运行状态, 其预测误差满足工业实际运行需求, 因此可以模拟选矿厂实际浓密过程.本节将在“浓密脱水过程仿真平台”上验证所提方法的有效性.运用仿真平台模拟实际湿法冶金浓密过程, 利用实际工业过程数据对仿真平台中的机理模型进行辨识, 计算出浓密机内部的压力分布.利用一个班中前6个小时的数据进行测试, 加入1 % 的离群值, 5 % 的缺失值, 每隔27 s对数据进行采样, 共800个采样点, 组成训练集, 然后以相同方法生成另一个班的生产数据, 组成测试集进行测试.浓密脱水过程仿真平台的结构如图 5所示.通过浓密脱水过程仿真平台生成宽度学习训练数据集、测试数据集, 在仿真平台上进行实验,验证方法的可行性.
图 5(Fig. 5)
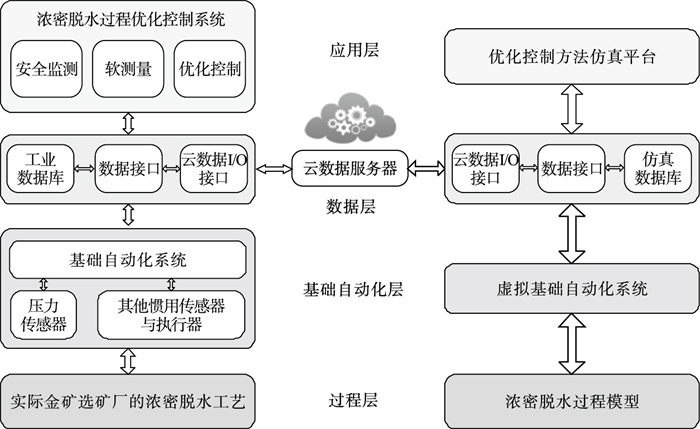 | 图 5 浓密脱水仿真平台Fig.5 Thickening-dehydration simulation platform |
3.2 数据预处理用浓密脱水仿真平台产生的数据对实际工厂数据进行模拟, 由于现场环境恶劣, 对压力传感器的测量值产生影响, 用于测量压力的传感器不可避免会出现数据丢失、记录错误等现象, 在对数据进行预处理后可以有效解决上述问题, 提高模型的准确性.
步骤1 归一化.实时采集到的数据, 数据量庞大, 大小相差很多, 并且压力传感器的测量值过小, 影响预测的准确率.利用归一化方法对数据进行预处理:
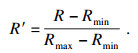 | (15) |
步骤2 缺失数据处理.本实验数据在浓密机正常工况下运行, 在传感器进行测量时, 计算传感器的数据缺失率约为5 %, 缺失率较小.
单个缺失数据可利用前后数据的平均值进行填补, 连续的缺失值采用K近邻补全算法[18].由于距离越近数据越相似, 当一组数据中缺失变量, 则利用其辅助变量与所有其他完整样本数据中辅助变量之间的欧氏距离, 找到它的k个最近邻样本, 缺失的变量用这k个最近邻样本的变量平均值来补充.常用欧氏距离表示:
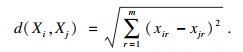 | (16) |
步骤3 离群值处理.利用全部数据建立预测模型, 对训练集数据进行预测, 计算出预测误差, 将预测误差大的数据点标记为离群点, 再利用预测值替代这些离群点, 重复上述步骤, 直到没有明显的离群点发现.
3.3 实验准备为了验证方法的有效性, 本文采用均方根误差(root mean square error, RMSE)和平均绝对误差(mean absolute error, MAE)对预测性能进行评价.利用Matlab 2018a实现BLS, 进行10次实验, 每次的实验RMSE均在0.006 2~0.008 6, 取均值0.007 3作为实验结果.为了评价BLS模型的有效性, 本文还采用了KPLS(kernel partial least squares, KPLS)和深度学习两种非线性回归方法对底流浓度进行了预测, KPLS采用高斯核将非线性数据投影到高维空间中, 在高维空间中构造线性PLS模型, 深度学习采用卷积神经网络, 第一、二隐层均为16节点.
BLS的参数有每个窗口的特征节点N1, 映射特征数N2, 增强节点数N3, 其中需要调整的为N2, N3.如图 6所示, 随着N2和N3的增加, 数据集的RMSE呈现先下降后上升的趋势, 过低的N2和N3会导致预测结果的RMSE较高, 过高的N2和N3会增加额外的计算量.经测试N2=18, N3=10 000时, 结果满足精度要求.
图 6(Fig. 6)
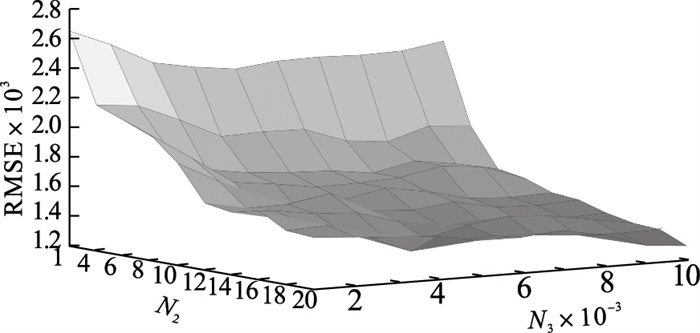 | 图 6 N2和N3对RMSE的影响Fig.6 Effect of N2 and N3 on RMSE |
3.4 结果分析实验结果如图 7~图 9所示, RMSE与MAE如表 2所示, 可得到如下结论.
图 7(Fig. 7)
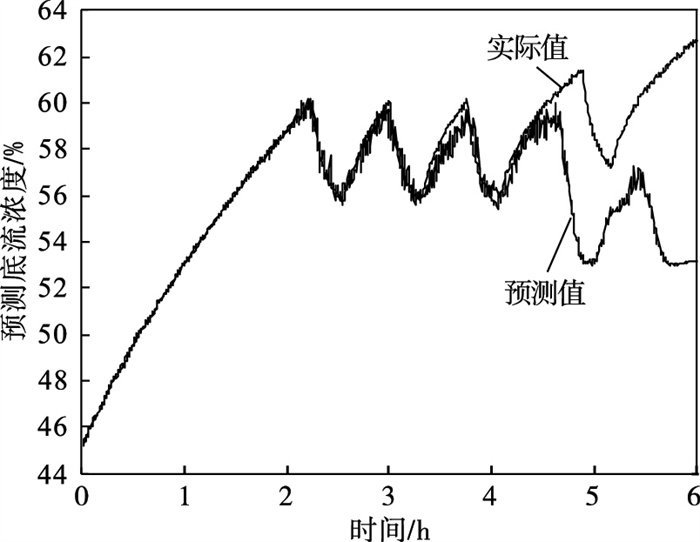 | 图 7 KPLS的预测效果Fig.7 Prediction effect of KPLS |
图 8(Fig. 8)
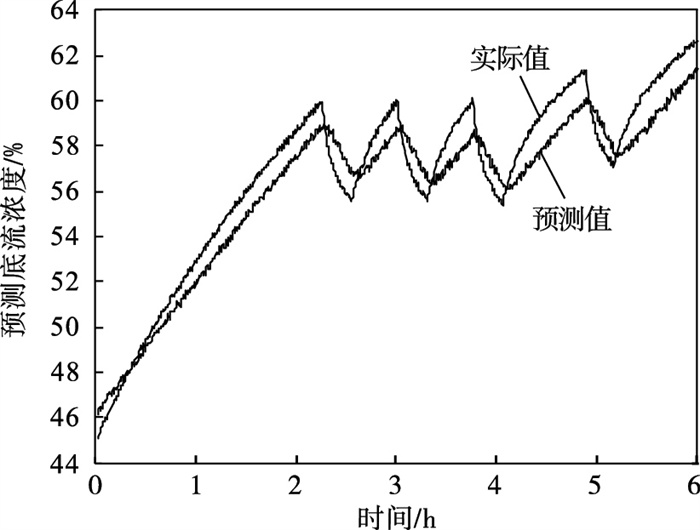 | 图 8 深度学习的预测效果Fig.8 Prediction effect of deep learning |
图 9(Fig. 9)
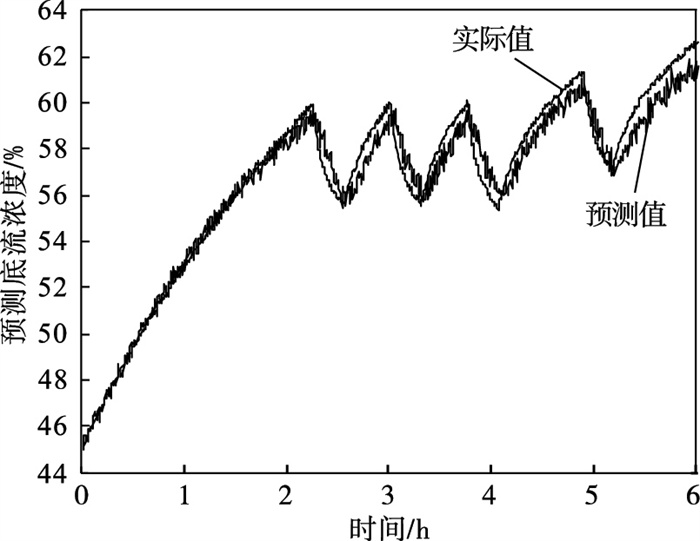 | 图 9 BLS的预测效果Fig.9 Prediction effect of BLS |
表 2(Table 2)
| 表 2 预测精度比较 Table 2 Prediction accuracy comparison |
1) 从预测精度来看, BLS获得的RMSE, MAE值明显小于KPLS和深度学习网络, BLS的预测性能更好, 泛化能力更强.
2) 从训练复杂度来看, BLS的复杂度明显小于深度学习网络.BLS所需要的训练的参数更少, 并且BLS不需要像深度学习网络一样进行反复迭代, 直接利用岭回归进行求解, 在数据量较大时, BLS求解速度明显更快.
3) 从泛化能力来看, 在4.5 h后, KPLS的预测性能明显下降, 深度学习网络的误差明显增大, 但BLS依然可以保持较好的效果, BLS网络在预测步数较远时仍然可以保持较好的效果.
4) 图 7~图 9进行对比, 可以看出相较于传统的KPLS方法和深度学习网络, BLS的拟合效果更好, 证明了宽度学习可以用于工业大数据的建模中, 并且效果更好.
4 结语本文针对湿法冶金浓密脱水过程底流浓度难以在线检测的问题, 提出一种基于BLS的底流浓度软测量方法.将这种方法应用于浓密机的底流浓度软测量, 得到了满意的预测效果.相比于KPLS方法和深度学习, 所提出的方法具有更高的预测精度和泛化能力.本文方法可为后续实现浓密机的优化控制奠定基础.
参考文献
| [1] | 范继涛, 朱勃霖. 矿产资源节约与综合利用先进技术推广的思考[J]. 中国矿业, 2013, 22(11): 23-26. (Fan Ji-tao, Zhu Bo-lin. Thinking for mineral resource saving and comprehensive utilization advanced technology popularization[J]. China Mining Industry, 2013, 22(11): 23-26. DOI:10.3969/j.issn.1004-4051.2013.11.006) |
| [2] | Nunez F, Langarica S, Diaz P, et al. Neural network-based model predictive control of a paste thickener over an industrial internet platform[J]. IEEE Transactions on Industrial Informatics, 2019, 16(4): 2859-2867. |
| [3] | Zhang H, Wang F, Zhang I, et al. Soft sensing model of underflow concentration for thickener process based on data reconciliation[C]//2020 Chinese Control and Decision Conference(CCDC). Hefei, 2020: 3337-3341. |
| [4] | Xiao D, Xie H, Jiang L, et al. Research on a method for predicting the underflow concentration of a thickener based on the hybrid model[J]. Engineering Applications of Computational Fluid Mechanics, 2020, 14(1): 13-26. DOI:10.1080/19942060.2019.1658228 |
| [5] | Yuan J, Wang S, Wang F, et al. A time-difference PLS based soft sensor method of underflow concentration for thickener in hydrometallurgy[C]//2017 29th Chinese Control and Decision Conference(CCDC). Chongqing, 2017: 248-253. |
| [6] | Jia R D, Mao Z Z, Chang Y Q, et al. Kernel partial robust M-regression as a flexible robust nonlinear modeling technique[J]. Chemometrics and Intelligent Laboratory Systems, 2010, 100(2): 91-98. DOI:10.1016/j.chemolab.2009.11.005 |
| [7] | Feng L, Zhao C, Chen C L P, et al. BNGBS: an efficient network boosting system with triple incremental learning capabilities for more nodes, samples, and classes[J]. Neurocomputing, 2020, 412: 486-501. DOI:10.1016/j.neucom.2020.06.100 |
| [8] | Chai Z, Zhao C. Multiclass oblique random forests with dual-incremental learning capacity[J]. IEEE Transactions on Neural Networks and Learning Systems,, 2020, 31(12): 5192-5203. DOI:10.1109/TNNLS.2020.2964737 |
| [9] | 桂卫华, 阳春华, 陈晓方, 等. 有色冶金过程建模与优化的若干问题及挑战[J]. 自动化学报, 2013, 39(3): 197-207. (Gui Wei-hua, Yang Chun-hua, Chen Xiao-fang, et al. Problems and challenges for modeling and optimizing nonferrous metallurgy processes[J]. Journal of Automatica Sinica, 2013, 39(3): 197-207.) |
| [10] | 马荣骏. 湿法冶金新发展[J]. 湿法冶金, 2007, 26(1): 1-12. (Ma Rong-jun. Novel development of hydrometallurgy[J]. Hydrometallurgy, 2007, 26(1): 1-12. DOI:10.3969/j.issn.1009-2617.2007.01.001) |
| [11] | Chen C L P, Liu Z. Broad learning system: an effective and efficient incremental learning system without the need for deep architecture[J]. IEEE Transactions on Neural Networks & Learning Systems, 2018, 29(1): 10-24. |
| [12] | Shuang F, Philip C C L. Fuzzy broad learning system: a novel neuro-fuzzy model for regression and classification[J]. IEEE Transactions on Cybernetics, 2018, 50(2): 414-424. |
| [13] | Chen C L P, Liu Z, Feng S. Universal approximation capability of broad learning system and its structural variations[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(4): 1191-1204. DOI:10.1109/TNNLS.2018.2866622 |
| [14] | Feng S, Ren W, Han M, et al. Robust manifold broad learning system for large-scale noisy chaotic time series prediction: a perturbation perspective[J]. Neural Networks, 2019, 117: 179-190. DOI:10.1016/j.neunet.2019.05.009 |
| [15] | Zhu L, Lian C, Zeng Z, et al. A broad learning system with ensemble and classification methods for multi-step-ahead wind speed prediction[J]. Cognitive Computation, 2020, 12(4): 654-666. |
| [16] | Senave M, Reynders G, Bacher P, et al. Towards the characterization of the heat loss coefficient via on-board monitoring: physical interpretation of ARX model coefficients[J]. Energy and Buildings, 2019, 195: 180-194. DOI:10.1016/j.enbuild.2019.05.001 |
| [17] | Baraldi P, Manginelli A A, Maieron M, et al. An ARX model-based approach to trial by trial identification of fMRI-BOLD responses[J]. Neuroimage, 2007, 37(1): 189-201. DOI:10.1016/j.neuroimage.2007.02.045 |
| [18] | Mcroberts R E, Tomppo E O, Finley A O, et al. Estimating areal means and variances of forest attributes using the k-nearest neighbors technique and satellite imagery[J]. Remote Sensing of Environment, 2015, 111(4): 466-480. |
