, 李伟鑫3 1. 东北大学秦皇岛分校 管理学院, 河北 秦皇岛 066004;
2. 河北省科普信息化工程技术研究中心, 河北 秦皇岛 066004;
3. 东北大学 信息科学与工程学院, 辽宁 沈阳 110819;
4. 燕山大学 经济管理学院，河北 秦皇岛 066004
收稿日期：2020-02-08
基金项目：国家自然科学基金资助项目(71401027); 国家重点研发计划项目(2020YFB1712802)；河北省自然科学基金资助项目(G2016501086)；河北省高等学校人文社会科学研究项目(SQ202002)。
作者简介：任嵘嵘(1975-)，女，河北秦皇岛人，东北大学副教授。
摘要：以往在研究第三方物流供应商的选择问题时, 通常假设第三方物流供应商(3PLS)对第四方物流集成商(4PLI)持风险中性态度, 而这与现实是不符的.为了使研究更加贴近实际, 考虑第三方物流供应商有风险态度的情况下, 第四方物流集成商通过多属性逆向拍卖方式对第三方物流供应商进行选择.通过案例设计和进行相关实验, 发现通过条件风险价值(conditional value at risk, CVaR)的风险度量方法对风险态度进行度量, 很好地将风险因素融合到了多属性逆向拍卖中, 打破了传统的第四方物流集成商选择时风险中性的假设, 并且将风险度量中常用的CVaR方法融合到了供应商选择中, 具有一定创新性.通过对不同风险厌恶程度以及风险中性的情况进行对比, 结果表明, 当3PLS为风险中性时对4PLI是最有利的, 当3PLS为风险厌恶时, 风险厌恶程度越小对4PLI越有利.
关键词：第四方物流集成商第三方物流供应商多属性逆向拍卖CVaR风险厌恶
Auction Mechanism Chosen by Third Party Logistics Suppliers Based on Risk Aversion
REN Rong-rong1,2, WANG Bo3, LU Fu-qiang4
, LI Wei-xin3 1. School of Management, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China;
2. Hebei Science Popularization Information Engineering Technology Research Center, Qinhuangdao 066004, China;
3. School of Information Science & Engineering, Northeastern University, Shenyang 110819, China;
4. School of Economics and Management, Yanshan University, Qinhuangdao 066004, China
Corresponding author: LU Fu-qiang, E-mail: fuqiang_lu@126.com.
Abstract: In the past, when researchers studied the selection of third-party logistics suppliers(3PLS), it was generally assumed that third-party logistics suppliers have a risk-neutral attitude towards fourth-party logistics integrators(4PLI), which is often inconsistent with reality. In order to make the research more realistic, considering that the third-party logistics providers have a risky attitude, the fourth-party logistics integrators select the third-party logistics suppliers through a multi-attribute reverse auction. Through case design and related experiments, it is found that the risk attitude is measured by the risk measurement method of conditional value at risk (CVaR), which integrates risk factors into the multi-attribute reverse auction, breaking the traditional assumption that the fourth-party logistics integrators assume risk neutrality when selecting them. Moreover, the commonly used CVaR method in risk measurement is integrated into supplier selection, which is innovative. Comparing different levels of risk aversion and risk neutrality, the result shows that 4PLI is the most beneficial when 3PLS is risk-neutral, and when 3PLS is under risk aversion, the lower the degree of risk aversion, the more beneficial it is for 4PLI.
Key words: fourth-party logistics integrator(4PLI)third-party logistics supplier(3PLS)multi-attribute reverse auctionCVaRrisk aversion
随着市场竞争的日益加剧和企业对物流服务的层次性和全面性要求的提高, 传统的第三方物流企业由于缺乏运作整个供应链的能力而逐渐不能满足企业的物流需求, 因而第四方物流作为供应链的集成商应运而生.第四方物流是由美国埃森哲公司提出的, 它是顺应全球物流外包要求具有提供"一站式"物流服务能力发展趋势的产物[1-2].随着物流市场需求的不断增长、基础设施和物流信息平台的不断完善, 第四方物流的发展十分迅速, 关于第四方物流研究也越来越多.在第四方物流运作中, 第三方物流供应商(3PLS)选择问题是研究热点之一[2].
拍卖是一种投标机制, 即根据一系列拍卖规则决定谁是赢家及赢家支付的价格[3].拍卖作为一种独特的价格生成机制、有效的资源配置方式以及重要的理论分析工具, 有着广泛的市场应用前景.近几十年, 逆向拍卖在买卖双方进行合作选择的过程中得到了迅速的发展和推广[4].早期的拍卖理论研究仅以价格来确定中标者[5], 主要讨论单一目标下最优机制的设计.之后, 许多****用实验证明如果采购方只看重价格, 最终获胜的往往是低价劣质的供应商[6], 多属性拍卖则可避免该类问题.多属性拍卖是拍卖人与投标人除了在价格之外还在其他属性上进行多重谈判的一种拍卖模式[7].Che最早提出了多属性拍卖模型, 但是Che的模型是建立在二维拍卖基础之上的, 即只包括价格和一个质量属性的模型[8].多属性拍卖一般应用在采购当中, 这时就成为多属性逆向拍卖, 比如在商品采购中不仅关心商品价格, 还要关注商品的质量、保修期、交货期和供应商信誉等.由于多属性逆向拍卖重视买卖双方的兴趣偏好差异, 极大地拓展了供应商的投标空间, 使供应商在投标时更能充分发挥和利用其自身的竞争优势, 在提供满足采购方需要的商品的同时, 保证自身一定的利润空间, 从而达到买卖双方"共赢"[9].陈德艳等[10]将买家风险态度引入到赢家选择模型, 并证明不同的风险态度会导致拍卖双方策略和拍卖结果的改变.以上文献都将多属性逆向拍卖引入物流运作中, 将风险因素考虑在内的研究较少, 且集中于买家风险态度的研究上[10-11], 忽视了在实际运作中每一个决策者都是有风险态度的, 并且风险态度极有可能对最终的结果产生影响.本文将条件风险价值(conditional value at risk, CVaR)[12]方法运用于多属性逆向拍卖机制的设计中, 以此来解决第四方物流运作中具有风险态度的第三方物流供应商选择问题.本文设计了完整的拍卖机制, 并通过对拍卖结果的分析得出3PLS的风险态度对拍卖结果的影响.
1 问题描述一个第四方物流集成商(4PLI)需要完成一项距离较远的运输任务, 在运输的过程中会经过不同的区域, 并且在每个区域都需要选择一个3PLS进行合作, 共同来完成该区域路径上的运输任务.因此, 该运输任务可分为多项子任务.在完成每一项子任务的过程中, 4PLI希望工期较短并且成本较低, 但两者往往不可兼顾.因此, 4PLI需要在综合考虑工期和成本两个因素的情况下, 选择合适的3PLS进行合作.而3PLS与4PLI进行合作时, 则希望工期越长越好, 且4PLI给出的报价越高越好.根据3PLS和4PLI的特点, 设计多属性逆向拍卖机制来解决4PLI对3PLS的选择问题.由于受到自然因素和社会因素(如天气、交通状况)的影响, 在运输的过程中第三方物流供应商可能会存在工期延误的风险, 于是, 3PLS在参与竞拍时需要考虑到这种延期风险.因此, 本文的研究重点在于4PLI具有风险厌恶态度对3PLS选择有何影响, 并对风险厌恶和风险中性情况下的拍卖结果进行了比较和分析.
基本假设为
1) 4PLI关于工期和成本的权重信息是公开的, 且在拍卖过程中是固定不变的;
2) 3PLS关于工期和成本的权重信息是私有的;
3) 3PLS的实际工期为竞价方案中的工期和影响工期随机因素的加和;
4) 在进行拍卖之前4PLI会对3PLS的基本资质进行筛选, 因此, 不会出现3PLS在第一轮就全部淘汰的情况.
2 拍卖框架设计2.1 拍卖流程设计一种多属性逆向拍卖的流程中, 由于在每一轮的拍卖中, 淘汰的供应商不只一个, 因此称为"多供应商淘汰拍卖".具体拍卖步骤如下:
步骤1??初始化信息.4PLI给出工期和成本的最小值, 每个3PLS给出一个工期和成本值, 然后进行协商, 确定该项任务工期和成本的最大值和最小值范围;
步骤2??4PLI公布第一轮拍卖保留值;
步骤3??3PLS根据4PLI公布的保留值计算其工期和成本以及CVaR值;
步骤4??3PLS判断CVaR值是否低于其保留值, 若CVaR值低于其保留值, 则将结果告知4PLI, 转步骤8, 否则转步骤5;
步骤5??4PLI判断3PLS的个数是否大于1, 若大于1, 则转步骤7, 否则转步骤6;
步骤6??4PLI判断3PLS的个数是否为0, 若为0, 则转步骤7, 否则转步骤9;
步骤7??4PLI按照其规则更新保留值, 4PLI的保留值更新规则: 当3PLS的个数大于1时, 更新后的保留值为上一轮的保留值加0.1;当3PLS的个数为0时, 取上一轮保留值与该轮保留值的中间值;
步骤8??退出拍卖;
步骤9??拍卖结束.
2.2 效用评价函数设计2.2.1 4PLI的效用评价函数对项目的工期和成本的效用评价函数进行归一化处理:
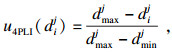 | (1) |
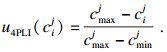 | (2) |
可以看出, 工期和成本越小, 其对应的效用值越大.
4PLI对3PLS的效用评价函数为
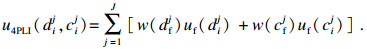 | (3) |
结合式(1)和式(2)可知, 式(3)中工期和成本越小, 最终的效用值就越大.
2.2.2 3PLS的效用评价函数对项目的工期和成本的效用评价函数进行归一化处理:
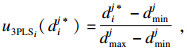 | (4) |
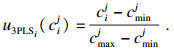 | (5) |
可以看出, 工期和成本越大, 其对应的效用值越大.
3PLS的效用评价函数为
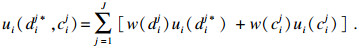 | (6) |
可以看出, 式(6)中工期和成本越大, 最终的效用值就会越大.
2.2.3 3PLS的CVaR模型1) CVaR模型概述.建立CVaR模型首先要定义风险价值VaR(value at risk).若3PLS的效用值为ui(dij, cij, ξ), 则VaR值表示为
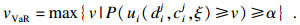 | (7) |
CVaR是在给定的条件和置信水平下, 效用低于某个给定VaR水平的平均值, CVaR值为
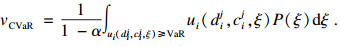 | (8) |
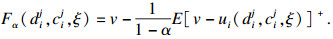 | (9) |
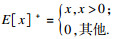
于是,
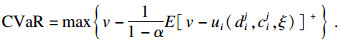 | (10) |
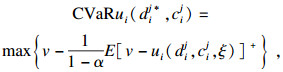 | (11) |
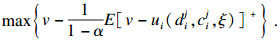 | (12) |
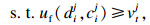 | (13) |
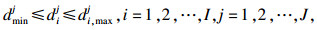 | (14) |
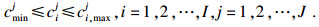 | (15) |
式(12)表示最大化3PLS的效用值；式(13)表示3PLS在拍卖中的效用值要满足4PLI的要求；式(14)表示3PLS的工期限制；式(15)表示3PLS的成本限制.
2.3 模型转换2.3.1 3PLS的CVaR模型的转换由于式(12)中含有随机变量, 不易直接求解, 需要对模型进行转化.蒙特卡洛方法[13]是求解随机优化问题的常用方法, 其基本思想是对随机变量进行随机模拟, 利用得到的随机样本将模型转化为确定性的优化问题, 然后对得到的确定性优化问题进行求解.
本文应用蒙特卡洛方法对CVaR模型中的随机变量进行处理.通过蒙特卡洛模拟得到随机变量ξ的独立分布的样本ξk, k=1, 2, 3, …, M, 其中M为样本容量.将样本代入模型, 式(12)~式(15)变为
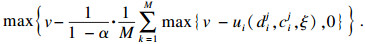 | (16) |
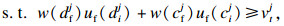 | (17) |
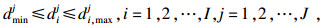 | (18) |
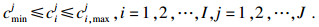 | (19) |
2.3.2 模型中v的表示
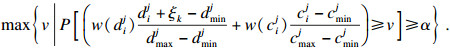 | (20) |
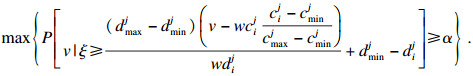 | (21) |
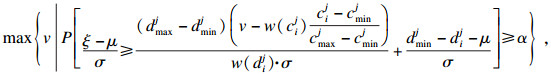 | (22) |
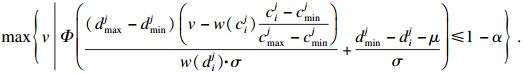 | (23) |
 |
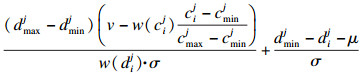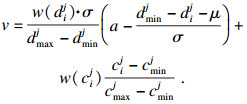 | (24) |
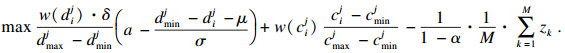 | (25) |
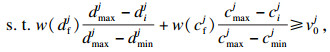 | (26) |
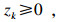 | (27) |
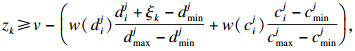 | (28) |
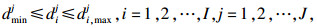 | (29) |
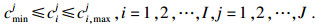 | (30) |
在进行拍卖之前, 双方首先要对该路段中成本和工期的最大值和最小值进行协商.在协商的过程中, 4PLI希望工期越短越好, 而成本越低越好, 因此4PLI给出工期和成本的最小值.而3PLS则希望4PLI完成的工期越长越好, 与4PLI成交的价格越高越好.
3.1 案例描述以区域A和区域B为例对本研究问题进行案例分析.在A到B之间, 有4个3PLS符合参与竞拍的条件.在竞拍前, 4PLI首先会公布相关的竞拍规则, 若3PLS能够接受, 则告知4PLI参加竞拍.4PLI在确定参加竞拍的3PLS的名单后, 4PLI会要求每一个3PLS提交自己所需的最大工期、成本以及权重等信息.4PLI也会给出相应的最低的工期、成本和权重信息.然后, 根据相关的拍卖规则进行3PLS的选择.本案例将从以下3个实验进行设计和分析：
实验Ⅰ??当各3PLS风险厌恶程度相同时, 拍卖过程的模拟；
实验Ⅱ??当各3PLS风险厌恶程度不同时, 拍卖过程的模拟；
实验Ⅲ??当3PLS分别为风险中性和风险厌恶时, 拍卖结果的比较.
3.2 初始信息1) 3PLS给出的工期、成本以及权重如表 1所示.
表 1(Table 1)
 表 1 3PLS的初始信息Table 1 Initial information of 3PLS
| 表 1 3PLS的初始信息 Table 1 Initial information of 3PLS |
2) 4PLI给出的工期和成本以及权重如表 2所示.
表 2(Table 2)
表 2 4PLI的初始信息Table 2 Initial information of 4PLI
| 表 2 4PLI的初始信息 Table 2 Initial information of 4PLI |
3) 经过协商后, 在区域A和区域B之间工期最大为420, 成本最大值为350.进行多轮拍卖时, 3PLS会有自己的保留值, 在此每个3PLS的保留值均为0.4.4PLI的初始保留值为0.3, 即v11=0.3, 上述4个3PLS全部符合标准.假设ξ服从正态分布, 即ξ~N(0, 100).并且样本容量取M=40.
3.3 实验分析实验Ⅰ??当各3PLS的风险厌恶程度相同时, 拍卖过程的模拟.
令3PLS的风险厌恶系数在区间[0.1, 0.9]变化时分别进行实验.
当3PLS的风险厌恶系数全部为0.1时, 具体拍卖如下：
步骤1??初始化信息, 相关的信息在3.2节中已经给出.
步骤2??4PLI公布第一轮的保留值.
步骤3??3PLS根据4PLI给出的保留值, 计算CVaR值.具体计算过程如下：
首先计算3PLS1的CVaR值, 由于3PLS1的风险厌恶系数为0.1, 通过查表得a=1.28, 代入式(24)中可以得到
 |
 |
 |
 |
 |
 |
 |
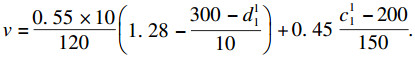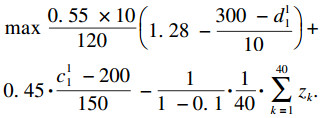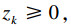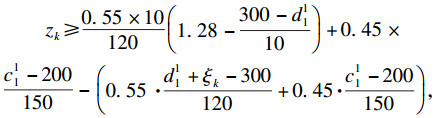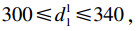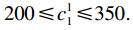由于其他3PLS的CVaR求解过程与3PLS1相同, 不再赘述.
通过计算可以得出3PLS在第一轮拍卖中的工期、成本以及CVaR值如表 3所示.
表 3(Table 3)
表 3 3PLS在第一轮拍卖中的信息Table 3 3PLS information in the first round of auction
| 表 3 3PLS在第一轮拍卖中的信息 Table 3 3PLS information in the first round of auction |
步骤4??通过计算结果可以看出, 第一轮拍卖结束后, 4个3PLS的CVaR值均高于自己的保留值, 所以均不退出拍卖.
步骤5??由于3PLS的个数大于1, 因此4PLI更新保留值进行下一轮拍卖.根据保留值的更新规则, 4PLI将保留值更新为0.4.重复上述步骤.由于计算过程相同，不再赘述.
由第一轮竞拍结果可知, 3PLS的个数仍然大于1, 4PLI将保留值更新为0.4进行第二轮拍卖.将保留值更新为0.4后, 通过计算得到3PLS在第二轮的拍卖信息如表 4所示.
表 4(Table 4)
表 4 3PLS在第二轮拍卖中的信息Table 4 3PLS information in the second round of auction
| 表 4 3PLS在第二轮拍卖中的信息 Table 4 3PLS information in the second round of auction |
通过表 4可以看出, 第二轮拍卖结束后, 所有3PLS对应的CVaR值均高于自己的保留值, 所以3PLS均不退出拍卖.根据保留值的更新规则, 4PLI将保留值更新为0.5, 进行下一轮拍卖.4PLI将保留值更新为0.5后, 通过计算可得第三轮拍卖中各个3PLS的相关信息如表 5所示.
表 5(Table 5)
表 5 3PLS在第三轮拍卖中的信息Table 5 3PLS information in the third round of auction
| 表 5 3PLS在第三轮拍卖中的信息 Table 5 3PLS information in the third round of auction |
通过表 5可以看出, 第三轮拍卖结束后, 3PLS均不退出拍卖.根据保留值的更新规则, 4PLI将保留值更新为0.6, 进行下一轮拍卖.保留值更新为0.6后, 通过计算可得各个3PLS的相关信息如表 6所示.
表 6(Table 6)
表 6 3PLS在第四轮拍卖中的信息Table 6 3PLS information in the fourth round of auction
| 表 6 3PLS在第四轮拍卖中的信息 Table 6 3PLS information in the fourth round of auction |
通过表 6可以看出, 第四轮拍卖结束后, 所有3PLS中的1, 3, 4退出拍卖.3PLS2最终获胜.每一轮拍卖中，各个3PLS对应的CVaR值如表 7所示.
表 7(Table 7)
表 7 3PLS在拍卖中的CVaR值Table 7 CVaR values of 3PLS in the auction
| 表 7 3PLS在拍卖中的CVaR值 Table 7 CVaR values of 3PLS in the auction |
由表 7可以看出, 当所有3PLS的风险厌恶系数为0.1时, 经过四轮拍卖, 3PLS2最终赢得拍卖, 且3PLS与4PLI最终成交的效用值为0.6, 而3PLS最终CVaR值为0.427.
3PLS风险厌恶系数从0.2变化至0.9的计算过程与上述步骤相同, 在此不再赘述.则3PLS风险厌恶程度相同, 风险厌恶系数从0.1变化至0.9时的拍卖结果如表 8所示(获胜者栏中的2表示第2个3PLS).
表 8(Table 8)
表 8 3PLS风险厌恶程度相同时的拍卖结果Table 8 3PLS auction results with the same risk aversion
| 表 8 3PLS风险厌恶程度相同时的拍卖结果 Table 8 3PLS auction results with the same risk aversion |
通过上述实验进行统计可得, 将3PLS的风险厌恶系数由0.1变化至0.9时, 最终的拍卖成交的效用值以及获胜者最终的CVaR变化情况如图 1所示.
由图 1可以看出, 3PLS的风险厌恶系数的不同, 会导致最终拍卖的成交的效用值不同以及最终3PLS的CVaR值的不同.随着3PLS的风险厌恶系数的增加, 拍卖最终成交单效用值逐渐降低, 所以3PLS对风险厌恶程度越大, 对4PLI越不利.同时通过图 1还可以看出, 两条曲线的拐点相同, 每当4PLI降低保留值, 3PLS的CVaR值会提高, 这是因为3PLS的风险厌恶较大时, 使得4PLI被迫增加拍卖轮次, 降低要求, 从而导致拍卖结果朝着有利于3PLS的风险发展.然而在拍卖轮次相同的情况下, 随着3PLS风险厌恶程度的增加, 其最终CVaR值是在波动中逐渐降低的.
图 1(Fig. 1)
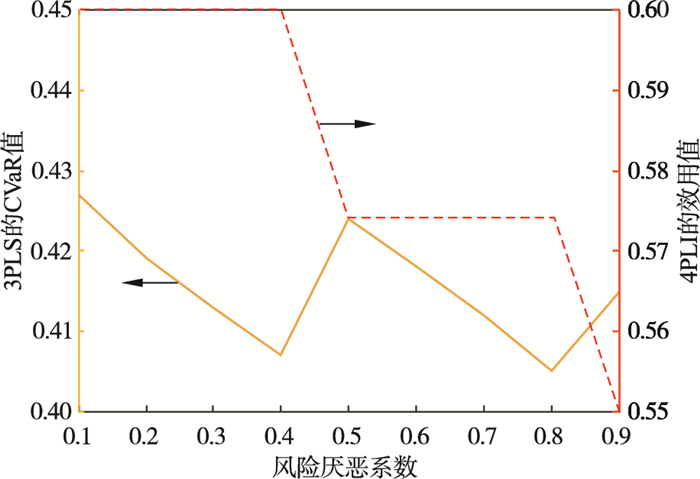 | 图 1 不同风险厌恶系数下获胜者CVaR值和成交的效用值Fig.1 CVaR value of winners and utility value of transactions under different risk aversion coefficients |
通过对不同风险厌恶程度下的拍卖结果分析可以看出, 所有3PLS的风险厌恶系数以相同的程度同时改变, 不会对最终拍卖的赢家产生影响.
实验Ⅱ??当各3PLS风险厌恶程度不同时, 拍卖过程模拟.
不同3PLS之间风险厌恶系数组合较多, 这里对4个较为典型的情况进行实验.
依次改变一个3PLS的风险厌恶系数, 令其为0.1, 其余三方的风险厌恶系数都为0.9.4个实验分别为
情况1??4个3PLS的风险厌恶系数分别为0.9, 0.9, 0.9, 0.1；
情况2??4个3PLS的风险厌恶系数分别为0.9, 0.9, 0.1, 0.9；
情况3??4个3PLS的风险厌恶系数分别为0.9, 0.1, 0.9, 0.9；
情况4??4个3PLS的风险厌恶系数分别为0.1, 0.9, 0.9, 0.9.
计算步骤与之前的求解步骤类似, 这里不再赘述.所得到的拍卖结果如表 9所示.
表 9(Table 9)
表 9 3PLS风险厌恶程度不同时的拍卖结果Table 9 3PLS auction results with different degrees of risk aversion
| 表 9 3PLS风险厌恶程度不同时的拍卖结果 Table 9 3PLS auction results with different degrees of risk aversion |
从上述实验结果可以看出, 当3PLS风险厌恶系数不相同时, 风险厌恶程度较低的3PLS更容易赢得拍卖.
实验Ⅲ??当3PLS分别为风险中性和风险厌恶时, 比较拍卖结果.
当α=0时, 以下模型描述了3PLS为风险中性的情况.
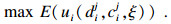 | (31) |
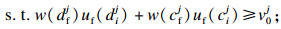 | (32) |
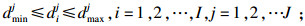 | (33) |
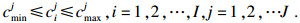 | (34) |
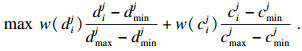 | (35) |
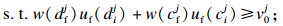 | (36) |
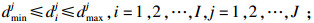 | (37) |
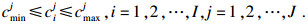 | (38) |
表 10(Table 10)
表 10 3PLS在拍卖中的CVaR值Table 10 3PLS CVaR values in the auction
| 表 10 3PLS在拍卖中的CVaR值 Table 10 3PLS CVaR values in the auction |
由表 10可以得出, 在风险中性情况下, 最终的获胜者仍然是3PLS2, 此时, 最终成交的效用值为0.625.
风险中性和风险厌恶情况下3PLS的CVaR值以及4PLI的效用值变化如图 2所示.
图 2(Fig. 2)
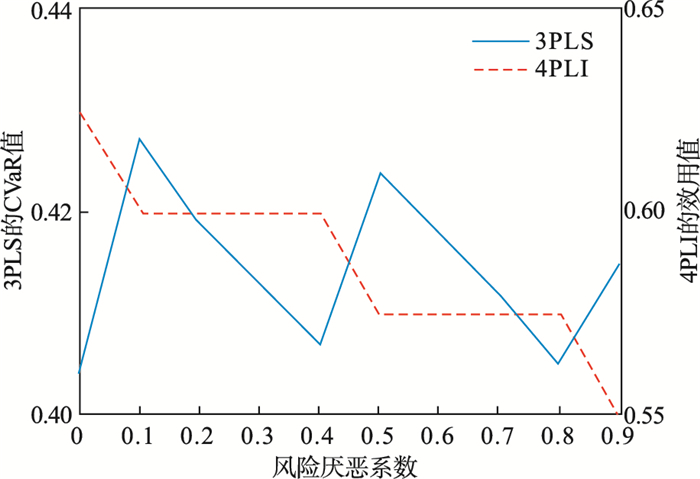 | 图 2 3PLS的CVaR值和4PLI的效用值变化Fig.2 Changes of CVaR value of 3PLS and utility value of 4PLI |
由图 2可以看出, 第三方物流供应商为风险中性时, 4PLI的效用值最高；随着3PLS风险厌恶程度的增加, 4PLI的效用呈现逐渐下降的趋势.
最终获胜者分别在不同风险厌恶程度和风险中性下CVaR值的变化如图 3所示.
图 3(Fig. 3)
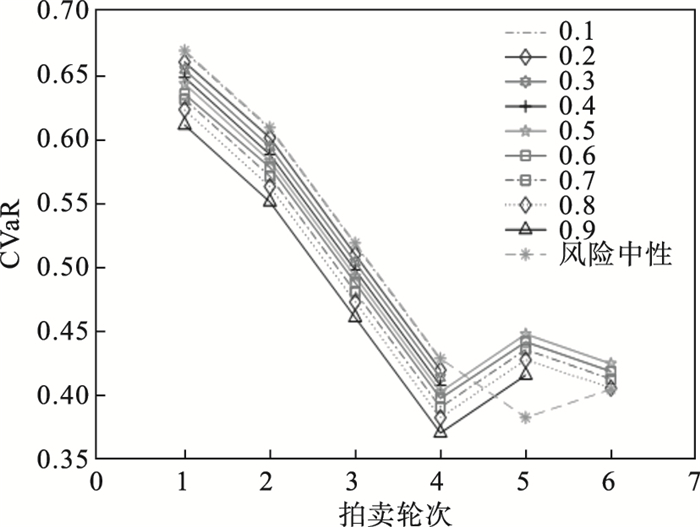 | 图 3 风险厌恶和风险中性下获胜者CVaR值的变化Fig.3 Changes in the CVaR value of winners under risk aversion and risk neutrality |
由图 3可知, 随着第三方物流供应风险厌恶程度的增大, 其CVaR值呈现逐渐降低的趋势.
综合以上3个实验的结果, 可以得出：
1) 从实验Ⅰ的结果可以看出, 当3PLS同时改变相同程度的风险厌恶程度时, 获胜者始终为3PLS2, 但是随着3PLS风险厌恶程度的增大, 3PLS与4PLI最终成交的效用值会变低, 即在这种多属性逆向拍卖机制下, 3PLS的风险厌恶程度越大, 对4PLI越不利.同时, 在不同的风险厌恶程度下, 最终的获胜者都为3PLS2, 说明在拍卖中, 第三物流供应商2比较占优势.将实验Ⅰ与实验Ⅱ的结果进行对比可以发现, 当3PLS风险厌恶程度较大时, 即使谁占有一定优势最终也不一定赢得拍卖.
2) 将实验Ⅱ以及对实验Ⅰ中同一3PLS不同风险厌恶下的拍卖最终给出的效用值进行对比可以看出, 3PLS风险厌恶程度越大, 其CVaR值越低, 即3PLS风险厌恶程度越大, 越难赢得拍卖.
3) 将实验Ⅰ和实验Ⅲ进行比较可以得出, 3PLS为风险中性时CVaR值较大, 因此在风险中性的情况下, 3PLS更容易赢得拍卖.同时通过3PLS和4PLI最终成交的效用值可以看出, 3PLS为风险中性时最终成交的效用值要大于3PLS为风险厌恶的情况.因此, 3PLS为风险中性对4PLI是最有利的, 且当3PLS为风险厌恶时, 风险厌恶程度越小对4PLI越有利.
4 结语本文设计了多属性逆向拍卖机制, 通过该机制对3PLS进行选择.针对3PLS对延期风险的厌恶, 通过CVaR方法对风险厌恶进行度量, 建立了相应的数学模型.通过案例设计和进行相关实验, 对不同风险厌恶程度以及风险中性的情况进行对比, 并分析不同风险厌恶程度和不同风险偏好下决策的行为以及风险偏好对决策结果的影响.发现3PLS为风险中性对4PLI是最有利的, 且当3PLS为风险厌恶时, 风险厌恶程度越小对4PLI越有利.本研究为行为特征下第四方物流运作中供应商的选择提供了一套可行方法.
参考文献
| [1] | 张宝来. 第三方物流发展与第四方物流研究[J]. 中国流通经济, 2012, 26(2): 44-48. (Zhang Bao-lai. The development of 3PL and the research on 4PL[J]. China Business and Market, 2012, 26(2): 44-48. DOI:10.3969/j.issn.1007-8266.2012.02.008) |
| [2] | Huang M, Tu J, Chao X L. Quality risk in logistics outsourcing: a fourth party logistics perspective[J]. European Journal of Operational Research, 2019, 276(3): 855-879. DOI:10.1016/j.ejor.2019.01.049 |
| [3] | 曾宪科, 冯玉强. 逆向多属性拍卖投标策略及收益性分析[J]. 管理科学学报, 2015, 18(9): 24-33. (Zeng Xian-ke, Feng Yu-qiang. Bidding strategies and revenue analysis for reverse multi-attribute auction[J]. Journal of Management Sciences in China, 2015, 18(9): 24-33. DOI:10.3969/j.issn.1007-9807.2015.09.003) |
| [4] | Qian X H, Fang S C, Huang M, et al. Bidding decisions with nonequilibrium strategic thinking in reverse auctions[J]. Group Decision and Negotiation, 2019, 28(4): 757-786. DOI:10.1007/s10726-019-09624-7 |
| [5] | Snir E M, Hitt L M. Costly bidding in online markets for IT services[J]. Management Science, 2003, 49(11): 1505-1520. |
| [6] | Farnia F, Frayret J M, LeBel L, et al. Multiple-round timber auction design and simulation[J]. International Journal of Production Economics, 2013, 146(1): 129-141. DOI:10.1016/j.ijpe.2013.06.012 |
| [7] | Rao C J, Xiao X P, Goh M, et al. Compound mechanism design of supplier selection based on multi-attribute auction and risk management of supply chain[J]. Computers & Industrial Engineering, 2017, 105: 63-75. |
| [8] | Che Y K. Design competition through multidimensional auctions[J]. RAND Journal of Economics, 1993, 24(4): 668-680. DOI:10.2307/2555752 |
| [9] | Baranwal G, Vidyarthi D P. A fair multi-attribute combinatorial double auction model for resource allocation in cloud computing[J]. The Journal of Systems and Software, 2015, 108: 60-76. DOI:10.1016/j.jss.2015.06.025 |
| [10] | 陈德艳, 汪定伟. 考虑风险态度的多属性逆向拍卖模型及机制设计[J]. 东北大学学报(自然科学版), 2019, 40(12): 1685-1689. (Chen De-yan, Wang Ding-wei. multi-attribute reverse auction model and mechanism design under the consideration of the risk attitude[J]. Journal of Northeastern University(Natural Science), 2019, 40(12): 1685-1689. DOI:10.12068/j.issn.1005-3026.2019.12.003) |
| [11] | Qian X H, Fang S C, Huang M, et al. Winner determination of loss-averse buyers with incomplete information in multi-attribute reverse auctions for clean energy device procurement[J]. Energy, 2019, 177: 276-292. DOI:10.1016/j.energy.2019.04.072 |
| [12] | Rockafelllar R T, Uryasev S. Optimization of contidional value at risk[J]. The Journal of Risk, 2000, 3(2): 21-41. |
| [13] | Chen J X, Liu Z Y, Zhu S L, et al. Design of limited-stop bus service with capacity constraint and stochastic travel time[J]. Transportation Research Part E, 2015, 83: 1-15. DOI:10.1016/j.tre.2015.08.007 |
| [14] | 樊梦, 王同科, 常慧宾. 非光滑函数的分数阶插值公式[J]. 计算数学, 2016, 38(2): 212-224. (Fan Meng, Wang Tong-ke, Chang Hui-bin. A fractional interpolation formula for non-smooth functions[J]. Mathematica Numerica Sinica, 2016, 38(2): 212-224.) |
