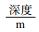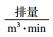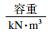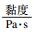, 宋沛, 陈玲霞, 胡凯
, 宋沛, 陈玲霞, 胡凯 郑州大学 水利科学与工程学院, 河南 郑州 450001
收稿日期:2020-06-18
基金项目:国家自然科学基金资助项目(41272339);河南省自然科学基金资助项目(182300410149)。
作者简介:王志荣(1963-),男,浙江嘉善人,郑州大学教授,博士生导师。
摘要:针对由水力裂缝触发的裂隙性储层涌水、突水等地质问题,首先根据弹性力学原理和断裂力学强度准则, 基于储层原生裂缝几何特性和压裂液渗流规律, 建立了垂直井工况下的起裂压力计算模型; 其次考虑煤储层的损伤本构关系, 将Dougill损伤因子与起裂压力公式相结合, 进一步建立了延伸压力的计算模型; 应用经典的PKN模型以及裂缝内净压力的非线性压降规律, 建立了改进的压裂缝扩展延伸模型.该模型揭示了裂缝性储层压裂长度L与压裂时间t之间的非线性关系, 显示出压裂缝的延伸距离随时间的增加而增长, 但前期增长较快, 后期基本趋于稳定.豫北焦作恩村区块三口试验井的计算结果, 与邻区位村区块微地震实测资料契合度较高, 从而验证了理论模型的正确性, 为现场压裂参数控制以及防治压裂缝突水提供了可靠的技术支撑.
关键词:垂直井断层突水起裂压力延伸压力压裂缝延伸模型
Fracture Extension Mechanism and Water Control Significance of Fractured Reservoir
WANG Zhi-rong

 , SONG Pei, CHEN Ling-xia, HU Kai
, SONG Pei, CHEN Ling-xia, HU Kai School of Hydraulic Science and Engineering, Zhengzhou University, Zhengzhou 450001, China
Corresponding author: WANG Zhi-rong, E-mail: wangzhirong513@sina.com.
Abstract: Aiming at geological problems such as water inrush in fractured reservoirs triggered by hydraulic fractures. Firstly, according to the principle of elastic mechanics and fracture mechanics strength criterion, based on the geometric characteristics of reservoir primary fracture and the seepage law of fracturing fluid, the calculation model of fracture initiation pressure under vertical well condition is established. Secondly, considering the damage constitutive relationship of coal reservoir, the Dougill damage factor is combined with the fracture initiation pressure formula to further establish the extension pressure calculation model. Using the classic PKN model and the nonlinear pressure drop law of the net pressure in the fracture, an improved fracture propagation model is established. The model reveals the non-linear relationship between fracture length L and fracturing time t in fractured reservoirs, showing that the extension distance of fractures increases with time, but it increases rapidly in the early stage and basically stabilizes in the later stage. The calculation results of three test wells in the Encun block of Jiaozuo in northern Henan Province are in good agreement with the microseismic data of the adjacent block, which verifies the correctness of the theoretical model and provides reliable technical support for on-site fracturing parameter control and prevention of fracture water inrush.
Key words: vertical wellfault inrushfractured pressureextension pressurefracture extension model
众所周知, 水力压裂是多场(应力场、渗流场、裂隙场)、多相(液体、气体、固体)相互耦合作用的复杂过程[1-3].近年来, 国内外许多****对压裂缝延伸扩展机理进行了大量探索与研究.韩金轩等[4]考虑裂缝动态渗透率和裂缝-孔隙型双重介质的综合影响, 建立了煤储层压裂液的滤失模型.张小东等[5-6]根据水力强化过程中裂缝扩展的分形特征, 基于分形理论提出了压裂过程中综合滤失系数的计算方法并建立了水力压裂缝扩展模型.李连崇等[7]对压裂缝延伸行为进行了数值模拟研究, 得出地应力、裂缝界面的强度和储层特性是影响裂缝延伸的主要因素.谭鹏等[8]基于压裂模拟实验, 研究了不同条件下水力裂缝非平面扩展规律的影响.张鹏海等[9]基于矩张量分析方法对压裂过程中裂缝延伸的时空过程及成缝机理进行了分析.贾奇锋等[10]对裂隙发育程度不同的煤体进行研究, 得出不同煤体结构煤水力压裂缝的延伸规律.然而华北型煤田水文地质条件较为独特, 下伏石炭、奥陶系岩溶含水层水头高且水量大, 太原组顶部L7+8灰岩距上覆主采二1煤层仅为20m左右.由于煤系地层裂隙发育且受多期断层切割, 形成了十分复杂的岩溶水水力网络联系[11], 造成地面井突水突气事故频发[12].所以迫切要求科学调配压裂时间, 达到控制压裂缝延伸及防治地下水害的目的[13-14].
迄今为止, 关于水力裂缝的延伸已进行了大量的研究, 但是, 关于裂隙性介质的研究进展, 水力压裂条件下储层的变形与破坏以及水力裂缝的延伸控制研究还较少.因此, 本文基于裂隙场与应力场时空耦合演化的新思路, 根据我国大水矿区低渗煤层的地质条件, 考虑原生裂缝特性和压裂液渗透特性, 建立垂直井起裂压力模型与延伸压力模型, 进而结合PKN模型探讨压裂缝时(t)空(L)之间的非线性耦合关系, 并应用焦作矿区试验井资料进行实例验证, 为指导我国复杂矿区的煤层气开发与实际施工提供理论依据.
1 工程背景我国华北型二叠纪煤系储层的地质条件极为复杂, 煤(岩)体原生裂隙与矿区断块构造极其发育, 主采二1煤层底板太原组、奥陶系岩溶水水头高且水量大.实践证明, 如不能精准控制起裂压力与压裂时间二者间的配置关系, 或将导致压裂缝盲目延伸至前方充水断层, 从而引发太原组或奥陶系岩溶水经断层向地面井大规模涌出, 造成矿区地下水污染与地面沉降, 甚至进一步诱发矿区地震等次生地质灾害.
2 垂直井压裂缝应力状态2.1 垂直井起裂压力模型2.1.1 射孔附加应力函数射孔集中力产生的附加应力是压裂缝起裂与扩展延伸的决定因素.通过井筒对井壁目标层施加泵压后, 一定范围内的储层便产生了由射孔集中力P带来的附加应力.设x为水平方向, 即射孔压裂方向; y为垂直方向.设水力压裂对于井筒具有对称性, 因而附加应力分量σx成为y轴的偶函数, 表达式为
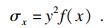 | (1) |
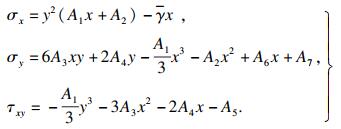 | (2) |
结合圣维南原理, 应力边界条件可表示为
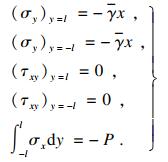 | (3) |
联立式(2)和式(3)即可得出附加应力各分量为
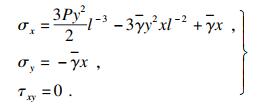 | (4) |
2.1.2 储层二次应力状态毋庸置疑, 地层初始应力也是起裂压力的重要影响因素.地层初始应力一般由两部分构成: 一部分是由地壳运动产生的构造应力, 构造应力差异巨大且难以测定; 另一部分是由地球引力产生的自重应力, 由上覆地层的密度决定.两种应力场在岩体中互相叠加, 形成了长期稳定的地层初始应力状态.为方便问题的讨论, 研究区储层初始应力[15]可表示为
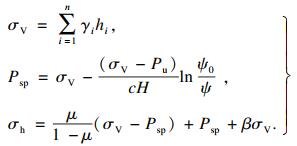 | (5) |
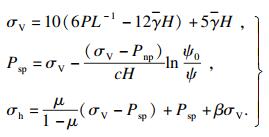 | (6) |
2.1.3 压裂层的破坏准则众所周知, 煤(岩)体内部一般赋存大量的有序原生裂缝, 压裂缝即在外部因素作用下最初由原生裂隙演化而成.根据断裂力学强度准则[16], 复合型裂纹的起裂判断条件, 可近似表达为
 | (7) |
2.1.4 起裂压力计算模型客观地说, 岩体内部发育的原生裂缝大都具有统计规律, 王志荣等[17]通过对豫北焦作矿区二1煤层的微观测试, 在定量分析原生裂缝的长度、宽度、密度等几何参数的基础上, 提出了裂缝特性指标T的新概念, 并判别为重要的压裂控制参数.考虑到压裂液在裂缝性储层运移过程中所产生的渗透力, 根据伯努利能量方程和差值法可得井筒附近径向和切向的渗透力为
 | (8) |
由水力学可知, 渗透力通常以体积力的形式施加于研究对象.引入体积力位置函数V, 根据弹性力学逆解法可得井筒周围应力分布为
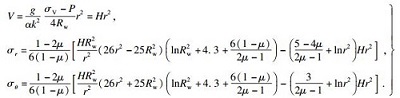 | (9) |
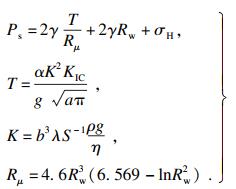 | (10) |
分析式(10)可知, 多场多相耦合作用下的起裂压力计算公式的影响因素主要有: 井壁应力场、压裂缝中的渗透场、原生裂缝场的几何特征(长度、宽度、密度)与裂缝粗糙度以及井孔工艺尺寸.全面考虑以上影响因素, 更能准确反映井壁储层的压裂行为, 使起裂压力的计算更加精确.
2.2 垂直井延伸压力模型延伸压力就是井壁储层在破裂后应力自然下降, 维持裂缝扩展延伸直至稳定的边界作用力.1976年Dougill将损伤力学引入岩体强度准则, 损伤本构研究成为当今岩土工程研究领域的热点之一[18].因此, 延伸压力的求解, 可以通过引入损伤变量D, 在起裂压力的基础上进行折减, 最终得出延伸压力的表达式.
2.2.1 损伤变量D的确定损伤变量D是描述岩石内部性质劣化, 表征其力学性能的重要参数.陈蕴生等[18]在研究非贯通裂隙性岩体的损伤本构关系时, 将裂隙的损伤归为两类, 分别为表征规则裂隙的奇异损伤与不规则裂隙的分布损伤, 其计算公式为
 | (11) |
表 1(Table 1)
| 表 1 损伤变量计算值 Table 1 Values of damage variable |
由于储层中奇异损伤与分布损伤二者几率大致相当, 符合概率统计规律, 故总损伤变量可视为奇异损伤变量与分布损伤变量的平均值:
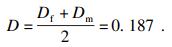 | (12) |
 | (13) |
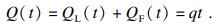 | (14) |
在压裂施工中, 压裂液充满压裂缝, 故压裂缝体积即为撑缝体积:
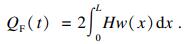 | (15) |
根据文献[19], 压裂缝内任一断面的缝宽与该处的净压力存在着函数关系, 结合压裂缝在延伸扩展过程中流体压降规律[20], 压裂缝宽度的计算公式为
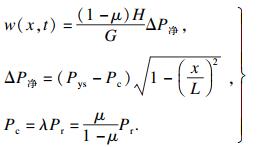 | (16) |
联立式(15)和式(16)即可得出压裂缝内的压裂液体积:
 | (17) |
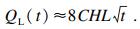 | (18) |
将式(17),式(18)代入式(14), 整理可得
 | (19) |
4 模型验证豫北焦作矿区是我国典型的大水矿区, 二叠系山西组二1煤层是矿区内主要可采煤层, 埋深一般位于155~800 m, 区内煤层厚度分布在4.32~7.10 m, 平均厚度为6.02 m.二1煤层多为块状煤, 但煤体结构复杂, 裂隙较发育, 坚固系数f 仅为0.2~0.5, 应属典型的碎裂-碎斑煤.据文献[20], 矿区煤体泊松比约为0.31, 弹性模量约为2.5 GPa, 储层压力约为4.14 MPa.
矿区水文地质条件极其复杂, 主采二1煤层下距太原组L7+8岩溶含水层仅仅10~25 m, 且石炭奥陶系各含水层水力联系较为密切.实际抽采中, 压裂缝时常延伸至前方断层含水层, 导致已施工的37口煤层气试验井, 2/3以上压裂后发生涌水突水事故.九里山井田JLS试-014与JLS试-016两口试验井, 其日平均产水量都在100 m3以上, 三个月试验期内的总涌水量都在1万m3以上.
4.1 储层的裂缝特性对豫北焦作恩村井田三口试验井实地采样, 按照国家标准(GB/T 18023—2000), (GB/T 8899—1998)以及煤炭行业标准(MT/T 968—2005)分别进行煤体裂隙的测试分析, 结果表明见表 2.
表 2(Table 2)
| 表 2 焦作矿区恩村区块储层工程地质参数一览表 Table 2 List of reservoir parameters of engineering geology of the Encun block in Jiaozuo district | ||||||||||||||||||||||||||||||||||||||
4.2 储层的施工参数恩村区块典型井施工参数如表 3所示, 现场压裂施工中采用活性水做压裂液、石英砂做支撑剂.根据宋佳等[21]关于压裂液滤失实验, 滤失系数C为8.3×10-3m/min0.5, 缝高H则取煤层的厚度.
表 3(Table 3)
| 表 3 焦作矿区恩村区块施工参数一览表 Table 3 List of construction parameters of the Encun block in Jiaozuo district | ||||||||||||||||||||||||||||||||||||||||||||||||
4.3 验证结果分析恩村井田煤储层裂缝宽度b在230~380 μm之间(表 2), 敏感度分析表明区内储层需要进行压裂改造.根据式(10)和表 3中的施工参数计算储层应力场相关参数, 其中主应力系数β=0.035[27], 将表 2,表 3中各计算参数和实测参数代入到式(13)中, 即可得三个试验井的延伸压力Pys值, 将该值与相关参数代入式(19)中, 得到压裂缝的一维时空演化规律(表 4与图 1).
表 4(Table 4)
| 表 4 裂缝延伸模型计算结果 Table 4 Results of fracture extension model | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
图 1(Fig. 1)
 | 图 1 压裂时间t与压裂半径L的关系Fig.1 Interaction between fracture time t and fracture radius L |
表 4中数据显示, 压裂缝随时间持续不断向前延伸, 压裂半径也随之不断增长.恩村井田EC试-007、EC试-008和EC试-011井压裂缝在延伸过程中均经历了加速延伸阶段与衰减增长阶段(图 1).加速延伸阶段压裂缝延伸速度较快, 但随着随着时间的持续, 在中后期压裂半径增长速度较为缓慢.分析可知, 随着压裂时间的增长, 压裂缝不断向前延伸并沟通大量原生裂缝, 压裂液滤失量逐渐增大, 导致延伸压力逐渐衰减, 压裂缝延伸速度也随之减缓.当延伸压力衰减至储层闭合压力时, 压裂缝延伸趋于停止.
GW试-002位于邻区位村井田中部, 主要产气二1煤层起裂压力为10.3 MPa.根据理论模型, 压裂时间从40 min增加到60 min时, 压裂半径计算值即从91.63 m增加到114.08 m, 将其与GW试-002现场微地震法实测值(82.4~109.5 m)进行对比, 发现二者较为吻合, 从而验证了理论模型对解决地下水害问题的有效性.
5 结论1) 裂隙性储层垂直井起裂压力计算模型显示, 储层的起裂压力不仅与外部地质条件有关(如储层的埋深、产状与地应力), 更取决于原生裂隙的几何特征(长度、宽度、密度).
2) 裂隙性储层压裂缝延伸模型阐明了地面井断层水防治的施工参数控制机理, 揭示了一定起裂压力条件下, 压裂半径L与压裂时间t之间的非线性关系, 即压裂缝的延伸距离随时间的增加而增长, 但前期增长较快, 后期减缓并最终趋于稳定.
3) 选择矿区内典型试验井对裂缝扩展模型进行实际验证.计算模型表明, 压裂时间维持在40~60 min时, 压裂半径为91.63~114.08 m, 上述理论值与焦作矿区GW试-002井的微地震实测值(82.4~109.5 m)较为吻合, 从而初步验证了压裂缝延伸模型的正确性.
参考文献
| [1] | 胡向志, 王志荣, 张振伦. 煤层气开发与"三软"矿区瓦斯抽采[M]. 郑州: 黄河水利出版社, 2011: 1-5. (Hu Xiang-zhi, Wang Zhi-rong, Zhang Zhen-lun. Development of CBM & gas drainage in "three soft" mining area[M]. Zhengzhou: The Yellow River Water Conservancy Press, 2011: 1-5.) |
| [2] | Adachi J, Siebrits E, Peirce A. Computer simulation of hydraulic fractures[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44: 739-757. DOI:10.1016/j.ijrmms.2006.11.006 |
| [3] | Wei Y, Economides M J. Transverse hydraulic fractures from a horizontal well[C]//SPE 94671 Presented at the 2005 SPE Annual Technical Conference and Exhibition. Dallas 2005. |
| [4] | 韩金轩, 杨兆中, 王会来, 等. 煤储层压裂液滤失计算模型[J]. 煤炭学报, 2014, 39. (Han Jin-xuan, Yang Zhao-zhong, Wang Hui-lai, et al. Leak-off model of fracturing fluid in coal seam[J]. Journal of China Coal Society, 2014, 39.) |
| [5] | 张小东, 张鹏, 刘浩, 等. 高煤级煤储层水力压裂裂缝扩展模型研究[J]. 中国矿业大学学报, 2013, 42(4): 573-579. (Zhang Xiao-dong, Zhang Peng, Liu Hao, et al. Fracture extended model under hydraulic fracturing engineering for high rank coal reservoirs[J]. Journal of China University of Mining & Technology, 2013, 42(4): 573-579.) |
| [6] | 张小东, 张硕, 杨艳磊, 等. 基于分形理论的煤储层水力压裂裂缝数值模拟[J]. 天然气地球科学, 2015, 26(10): 1992-1998. (Zhang Xiao-dong, Zhang Shuo, Yang Yan-lei, et al. Numerical simulation of fracture extending in coal seam under hydraulic fracturing engineering based on fractal theory[J]. Natural Gas Geoscience, 2015, 26(10): 1992-1998. DOI:10.11764/j.issn.1672-1926.2015.10.1992) |
| [7] | 李连崇, 张潦源, 黄波, 等. 薄互层储层水平井压裂裂缝延伸规律模拟分析[J]. 地下空间与工程学报, 2016, 12(6): 1577-1585. (Li Lian-chong, Zhang Liao-yuan, Huang Bo, et al. Numerical investigation on the propagation law of hydraulic fractures near horizontal wells in thin interbedded reservoir[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1577-1585.) |
| [8] | 谭鹏, 金衍, 侯冰, 等. 煤岩定向井水力裂缝起裂及非平面扩展实验[J]. 石油勘探与开发, 2017, 44(3): 439-445. (Tan Peng, Jin Yan, Hou Bing, et al. Experimental investigation on fracture initiation and non-planar propagation of hydraulic fractures in coal seams[J]. Petroleum Exploration and Development, 2017, 44(3): 439-445.) |
| [9] | 张鹏海, 张子麟, 李明, 等. 低渗储油层水力压裂裂缝延伸过程及成缝机理[J]. 东北大学学报(自然科学版), 2019, 40(5): 745-749. (Zhang Peng-hai, Zhang Zi-lin, Li Ming, et al. Extension process and fracture mechanism of hydraulic fractures in low permeability reservoir[J]. Journal of Northeastern University(Natural Science), 2019, 40(5): 745-749.) |
| [10] | 贾奇锋, 倪小明, 赵永超, 等. 不同煤体结构煤的水力压裂裂缝延伸规律[J]. 煤田地质与勘探, 2019, 47(2): 51-57. (Jia Qi-feng, Ni Xiao-ming, Zhao Yong-chao, et al. Fracture extension law of hydraulic fracture in coal with different structure[J]. Coal Geology & Exploration, 2019, 47(2): 51-57.) |
| [11] | 高柏, 王广才, 周来逊, 等. 华北型煤田岩溶水水文地球化学研究进展[J]. 水文地质工程地质, 2009, 36(3): 59-63. (Gao Bai, Wang Guang-cai, Zhou Lai-xun, et al. Advances in the study of hydrogeochemistry of karstic groundwater in coal mines in North China[J]. Hydrogeology & Engineering Geology, 2009, 36(3): 56-63.) |
| [12] | Wang Z R, Chen L X, Cheng C R, et al. Forecast of gas geological hazards for "three-soft" coal seams in gliding structural area[J]. Journal of China University of Mining and Technology, 2007, 17(4): 484-488. DOI:10.1016/S1006-1266(07)60130-8 |
| [13] | 王志荣, 韩中阳, 李树凯, 等. "三软"煤层注水压裂增透机理及瓦斯抽采施工参数确定[J]. 天然气地球科学, 2014, 25(5): 739-746. (Wang Zhi-rong, Han Zhong-yang, Li Shu-kai, et al. Mechanism of water-fracturing-induced permeability increment of "three soft" coal seam and construction parameters determination[J]. Natural Gas Geoscience, 2014, 25(5): 739-746.) |
| [14] | 王志荣, 贺平, 郭志伟, 等. 水力压裂条件下"三软"煤层压裂渗透模型及应用[J]. 天然气地球科学, 2017, 28(3): 349-355. (Wang Zhi-rong, He Ping, Guo Zhi-wei, et al. The research on permeable model of hydraulic fracture and its application in the "three soft" coal seam[J]. Natural Gas Geoscience, 2017, 28(3): 349-355.) |
| [15] | 张金才, 尹尚先. 页岩油气与煤层气开发的岩石力学与压裂关键技术[J]. 煤炭学报, 2014, 39(8): 1691-1699. (Zhang Jin-cai, Yin Shang-xian. Some technologies of rock mechanics applications and hydraulic fracturing in shale oil, shale gas and coalbed methane[J]. Journal of China Coal Society, 2014, 39(8): 1691-1699.) |
| [16] | 秦绪英, 陈有明, 陆黄生. 井中应力场的计算及其应用研究[J]. 石油物探, 2003(2): 271-275. (Qin Xu-ying, Chen You-ming, Lu Huang-sheng. Calculation of broehole stress with full-wave acoustic logging data and its application[J]. Geophysical Prospecting for Petroleum, 2003(2): 271-275.) |
| [17] | 王志荣, 贺平, 郭志伟, 等. 考虑裂缝特性指标的煤层气"垂直井"起裂压力计算方法[J]. 岩土力学, 2018, 39. (Wang Zhi-rong, He Ping, Guo Zhi-wei, et al. Calculation of initiation pressure of vertical well for coalbed methane considering crack characteristic index[J]. Rock and Soil Mechanics, 2018, 39.) |
| [18] | 陈蕴生, 韩信, 李宁, 等. 非贯通裂隙介质单轴受力条件下的损伤本构关系探讨[J]. 岩石力学与工程学报, 2005, 24. (Chen Yun-sheng, Han Xin, Li Ning, et al. Discussion on damage constitutive relation of non-interpenertrated crack media under uniaxial stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24.) |
| [19] | 王志荣, 郭志伟, 贺平, 等. 基于PKN分析的煤层气垂直井水力压裂时间计算模型[J]. 河南理工大学学报(自然科学版), 2018, 37(4): 24-30. (Wang Zhi-rong, Guo Zhi-wei, He Ping, et al. Calculation model on hydraulic fracturing time in gas vertical well based on PKN analysis[J]. Journal of Henan Polytechnic University(Natural Science), 2018, 37(4): 24-30.) |
| [20] | 刘浩. 高煤级煤储层水力压裂的裂缝预测模型及效果评价[D]. 焦作: 河南理工大学, 2010. (Liu Hao. The prediction model and evaluation for hydraulical fracture of high rank coal reservoirs [D]. Jiaozuo: Henan Polytechnic University, 2010. ) |
| [21] | 宋佳, 卢渊, 李永寿, 等. 煤岩压裂液动滤失实验研究[J]. 油气藏评价与开发, 2011, 1(1): 74-77. (Song Jia, Lu Yuan, Li Yong-shou, et al. Experiment research on fracture fluid dynamic filtration of coal rocks[J]. Reservoir Evaluation and Development, 2011, 1(1): 74-77.) |
| [22] | 蔡美峰, 何满潮, 刘东燕. 岩石力学与工程[M]. 北京: 科学出版社, 2013: 108-111. (Cai Mei-feng, He Man-chao, Liu Dong-yan. Rock mechanics and engineering[M]. Beijing: Science Press, 2013: 108-111.) |