
 , 于文鑫, 于长永
, 于文鑫, 于长永 东北大学秦皇岛分校 计算机技术学院, 河北 秦皇岛 066004
收稿日期:2020-01-08
基金项目:国家自然科学基金资助项目(61772124)。
作者简介:马海涛(1977-),男,黑龙江伊春人,东北大学讲师, 博士。
摘要:使用分段线性激活函数的神经网络(PLNN)在机器学习中得到广泛应用.本文给出了一种PLNN模型表达能力的度量值——线性区域数量, 并给出了线性区域的数学表示.分析了线性区域之间的关系并计算合并后的线性区域数量, 同时给出一种基于Z曲线的线性区域数量的计算方法.针对一个任务实例进行分析, 计算不同网络结构的线性区域数量及合并后的线性区域数量, 分析了线性区域数量与不同网络结构的准确性的关联.结果表明, 线性区域数量能够表现PLNN模型的表达能力, 对于选择网络超参数及解释模型边界具有研究意义.
关键词:机器学习分段线性神经网络表达能力线性区域
Relationship Between the Number of Linear Regions and Expressive Power of Piecewise Linear Neural Networks
MA Hai-tao, LU Jia-rui

 , YU Wen-xin, YU Chang-yong
, YU Wen-xin, YU Chang-yong School of Computer Technology, Northeastern University at Qinhuangdao, Qinhuangdao 066004, China
Corresponding author: LU Jia-rui, E-mail: 602037677@qq.com.
Abstract: The neural network with piecewise linear activation function(PLNN) is extensively applied in machine learning. This paper gives a measure of the expressive power of PLNN model, i.e., the number of linear regions, with the mathematical representation of linear regions presented. The relationship between linear regions is analyzed and the number of combined linear regions is calculated. A method for calculating the number of linear regions based on Z curve is developed. A case is given to calculate the number of linear regions of different network structures and the number of linear regions after merging, and the correlation between the number of linear regions and the accuracy of different network structures is analyzed. The results show that the number of linear regions can reflect the expressive power of PLNN model, which has great research significance for selecting network hyperparameters and explaining model boundaries.
Key words: machine learningpiecewise linear neural networkexpressive powerlinear region
神经网络, 特别是深度模型, 2006年以后在很多领域的应用中取得了十分好的效果, 是目前研究最深入、应用最广泛的学习模型, 其中分段线性神经网络(piecewise linear neural network, PLNN)是一类十分重要的网络模型.PLNN使用分段线性的激活函数, 其中较为典型的非饱和激活函数, 如relu家族中的PReLU, RReLU, Leaky ReLUs等, 在图像分类、动作识别、抵御对抗性攻击等[1-2]任务模型中取得很好的效果.由于对网络模型的解释研究滞后于网络模型取得的应用进展, 导致缺乏对模型行为的深入了解和解释, 使得当网络模型不能取得良好效果时, 无法对模型进行改进或优化.鉴于此, 一些致力于模型解释的工作已经展开.
最早在2014年Pascanu和Montúfa等[3-4]提出了PLNN的线性区域数概念, 并使用其数量的上界衡量网络的性能; 此后, 更多的****开始关注PLNN本身的基础性质.2016年, Eldan等[5]使用线性区域数比较了深、浅PLNN模型; Serra等[6]在2018年使用SAT概率推理方法近似了混合整数线性公式的解数量, 以此求解线性区域的概率下界.
受上述工作启发, Raghu等[7]使用轨迹长度作为PLNN表达能力的新度量值; Zhang等[8]首次建立了PLNN与热带几何之间的联系.
此外, 不少研究试图作出与模型无关的整体解释, 如文献[9]提出的LIME模型和文献[10]提出的Mask方法; 但其解释成果仍是局部的, 未能证明其可靠性.2018年Chu等[11]提出了OPENBOX方法, 将PLNN转换成一组数学上等价的线性分类器, 从而能够精确一致地解释一个整体的网络模型.
根据以上相关工作, 已有结论表明, PLNN神经网络等价于一组线性分类器.然而, PLNN神经网络的线性区域数量的计算方法、该数量与模型的表达能力, 以及模型的泛化准确定的关系仍不是十分明确, 有待进一步的验证和分析.本文针对上述问题进行了3方面的工作: ①给出计算PLNN激活模式的过程, 并说明线性区域数在数学上等于激活模式数量; ②提出线性区域可合并的概念, 使输出层标签相等的实例集合所对应的线性区域合并; ③对比了相同隐藏节点数、不同结构的线性区域数、合并区域数, 以及对应的精确度.
1 PLNN基础概念1.1 基本符号定义本文的研究对象为使用线性激活函数的神经网络.定义一个具有L层的网络模型Net, Net中网络层表示为li, i∈{1, …, L}.其中l1为网络的输入层, lL为网络的最终输出层.
Net模型中li层具有的节点个数为Ni, 隐藏层总节点个数为
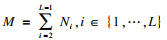
Net中自第2层开始的li层的偏置表示为Bi=[ b1i, …, bNii]T, i∈{2, …, L}, 网络总偏置矩阵表示为B=[B2, …, BL]T.
Net模型中前一层的神经元是通过全连接的形式与下一层相接, 因此用wjki表示li层中的第j个节点与li-1层中的第k个节点相连的边权, li-1层所有节点与li层第j个节点连接的权重矩阵表示为wji=[wj1i, …, wjNi-1i] T, 同时第li-1层所有节点与第li层所有节点的权重矩阵用Ni-1×Ni维的Wi表示, i∈{2, …, L}.
对于li层中的节点, i∈{2, …, L-1}, 每一个节点上的激活函数均使用ReLu函数, 即r(x)=max{0, x}.而输出层lL, 使用softmax函数作为激活函数.
1.2 PLNN定义根据以上基础符号, 定义Net网络的计算过程.当i=1时, 网络的输入表示为z1=x=[x1, …, xN1]T, x∈RN1是N1维的网络原始输入向量.
li层中的每个节点nji接收来自上一层节点的输入, 经过权重计算处理表示为yji, yji经过激活函数后的输出表示为zji, 即zji=r(yji).因此对于li层的加权和向量可以表示为yi=[y1i, …, yiNi]T, 而li层的输出向量也是li+1层的输入向量, 可以表示为zi=[z1i, …, ziNi] T.因此, 对于i∈{2, …, L-1}, li层的输出表示为
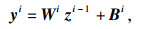 | (1) |
 | (2) |
由于Net模型中除输出层以外使用的激活函数都是线性激活函数ReLu, 因此整个网络可以视为一个等价的线性仿射函数f: RxN1→RNL.
2 线性区域计算方法2.1 线性区域的定义给定Net, 即给定权重与偏置矩阵.根据式(1)和式(2), 每当将一个实例x输入到Net计算后, Net中所有隐藏层节点都会根据ReLu函数判断一个不等式:
 | (3) |
因此, 给定网络模型Net所代表的线性映射函数f : X?RN1→Y?RNL, 用R?RN1表示Net的线性区域.当实例x输入到网络, 在隐藏层节点nji进行计算时, 根据式(3), 若yji大于0则输出yji的值, 即属于nji上的计算所代表的超平面的一侧线性区域Rj1i; 若yji小于0则输出0, 即属于超平面的另一侧的线性区域Rj0i.
而判断式(3)是否大于或等于0, 在数学层面上意味着可以将Net网络中的每个节点的输出视作两种状态: 0或1(原数据x).因此给定实例x, 节点nji的状态表示为sji=0/1, j∈{1, …, Ni}, 由以下公式定义:
 | (4) |
给定Net, 当Net的一个输入实例x的激活模式确定了, 同时也确定了此x所在的输入空间所属的线性区域, 即一种激活模式对应一个线性区域.多个实例x的激活模式若相同, 那么它们应同属一个线性区域; 因此可以计算输入集合X对应的激活模式种类数量, 用这个数值作为衡量网络表达能力的度量值.
当Net网络的隐藏层神经元总数为M时, 理论上此网络不同的激活模式的数量应为2M个.但由于网络模型的表达性能一般很难达到理论上的最高点, 其代表的函数计算复杂性一般也难以描述理论上所有的线性区域, 以及实际中预测的输入实例数据集之间总是存在关联, 因此通过计算输入实例集合所对应的不同激活模式数量总会远远小于2M个.
2.2 线性区域的计算给定网络模型Net, 给定具有P个实例的输入实例集合X, 通过不等式(3)可以确定地计算每一个输入实例xp∈X都对应着由M个不等式(3)组成的不等式组; 用Ep来表示这个不等式组, 同时用xp~Ep来表达对应关系, 其中p∈{1, …, P}, 同时Ep也确定了xp的激活模式Sp.
若有输入实例xp, xq∈X对应的Ep与Eq中的不等式完全相等, 则写作Ep=Eq(Sp=Sq), 这表示Ep与Eq代表了同一片线性区域R?RN1, 并且xp与xq也同属于这一片线性区域.
由以上定义可以总结为在这个线性子集区域R上的所有输入实例x, 都对应着由这一组不等式E所规定的分类规则, 最终整个网络模型Net所代表的线性函数f: X→Y可以由以下公式表达:
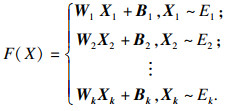 | (5) |
如上述内容所示, Wi与Bi是根据输入实例在网络中每一个隐藏层节点上的计算所决定的.假设Net网络模型固定, 实例x进入网络的l1层, 以全连接的形式输入到l2层, 根据式(1)和式(2)可得
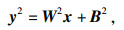 | (6) |
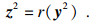 | (7) |
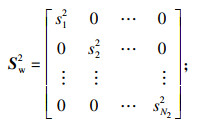 | (8) |
 | (9) |
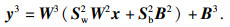 | (10) |
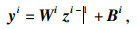 | (11) |
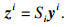 | (12) |
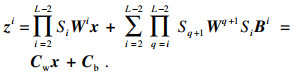 | (13) |
2.3 线性区域的合并本文提出了线性区域合并的概念, 即将输出层的分类标签加入划分线性区域的标准.例如本文实验是对数据集进行二分类, 分类标签分别是1类与0类.
给定网络模型Net, 共具有M个隐藏层节点.对于同属相同分类标签的两个激活模式集Si={s1i, …, sMi}, Sj={s1j, …, sMj}, 若它们M-1个同位置的状态码都相同, 并且仅有一个同位置的状态码相加为1, 即ski+skj=1, 则将第k位状态位合并为Qk.最终, Si与Sj合并为snewlv1={s1, …, Qk, …, sM}.
将仅合并过一个状态位的激活序列Slv1称为level.1的激活序列; 依此类推, 合并了两个状态位的激活序列Slv2称为level.2的激活序列.最终将原始激活模式集通过合并操作, 压缩为具有level激活序列的合并激活模式集.
下面给出实验数据示范合并过程: 图 1a为未经合并的4个原始激活序列, 经过第一轮合并操作后, 转变为2个各具有1位Q状态的level.1激活序列, 如图 1b所示; 再经过第二轮合并操作后, 转变为1个具有2位Q状态的level.2激活序列, 如图 1c所示.
图 1(Fig. 1)
 | 图 1 数据合并过程Fig.1 Data merging process (a)—原始激活序列;(b)—level.1激活序列;(c)—level.2激活序列. |
将原始线性区域数量通过合并操作压缩得更少, 可以在一定程度上使合并线性区域的决策边界更一般地表现出此决策的特征, 对于合并区域作用价值的研究将在未来展开.
3 实验3.1 实验准备本文的实验平台使用8 GB内存的i7处理器, 实验算法皆采用python语言编写.
为了取得能够尽可能遍历空间窗口的点集, 实验采用的数据集为Z-order空间填充曲线上的点, 如图 2所示.应用此点集作为网络模型Net的输入, 能够使不等式尽可能划分出更多的线性区域, 同时能在一定程度上得到此网络模型的最大表达能力及其能够达到的最高计算复杂性.
图 2(Fig. 2)
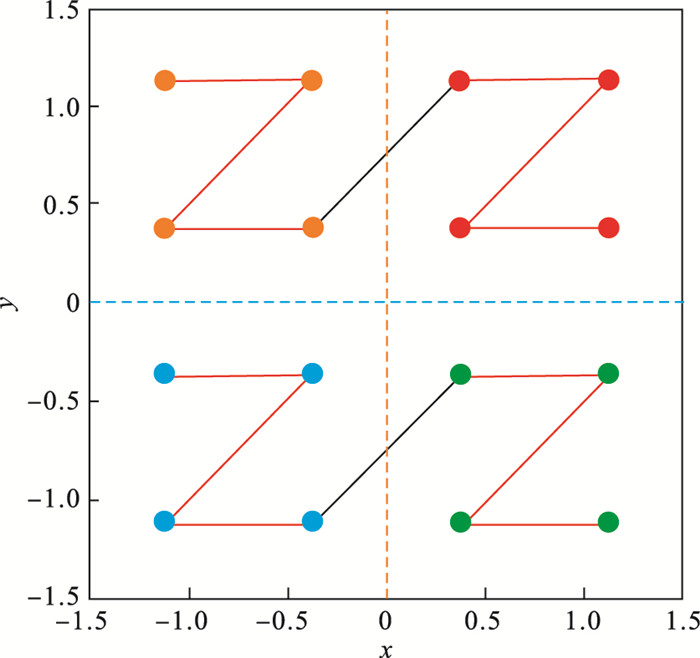 | 图 2 Z-order空间填充曲线Fig.2 Z-order space filling curve |
实验中采用的网络模型结构分为三种, 输入层l1与输出层lL保持不变, 分别都具有2个节点.中间层共22个节点, 构建了三种层分布: 具有2层中间层的网络模型A、具有3层中间层的网络模型B, 以及仅具有一层中间层的网络模型C.这三种网络模型中的隐藏层节点均采用ReLu函数作为激活函数, 输出层的激活函数则采用Softmax函数.
对三种网络模型A, B, C的中间层上分布的节点数量按一定规律进行调整.模型A根据层节点的分布又细分为9个模型, 同理模型B细分为27个模型; 而模型C因为仅有一层中间层, 22个隐藏层节点均在这一层中.
对A, B, C类共37个模型进行训练, 如图 3所示.用来训练的数据集是在一定空间内的一组二分类点集, 网络模型的功能即是对输入的数据点集进行二分类.最终所有37个模型的分类精度均达到97%以上.
图 3(Fig. 3)
 | 图 3 训练数据——二分类点集Fig.3 Training data —two classification point set |
开始实验时, 网络输入的数据集采用46个Z-order空间填充曲线, 点集中共有47=16 384个二维点.使用A, B, C类共37个模型对Z点集进行二分类, 同时计算这些模型得到的不同激活模型数量.
3.2 线性区域数量图 4所示为A类模型第1和第2隐藏层不同节点分布的子类模型所能够得到的线性区域数量, 即激活模式数量.
图 4(Fig. 4)
 | 图 4 A类模型的表达能力Fig.4 Expressive power of A-type model |
从图中可以看出, 隐藏层第1层的节点数量越少, 网络模型得到的线性区域数越少.当两个隐藏层之间的节点分布较为均匀, 如11∶11和13∶19, 网络的表达能力达到最大值; 而后随着第2层节点数量的减少, 网路模型能够划分的线性区域数又逐渐回落.这在一定程度上表示具有过少节点的中间层会降低网络的表达性能, 这种现象称为隐藏节点过少的局限性.
但对比具有同样过少节点的其他子模型, 如3∶19对比19∶3, 5∶17对比17∶5, 在这两组中, 后一种结构的子模型所划分的线性区域数均比前者多, 这一定程度上表示靠近网络输入层的隐藏层节点数量会限制后续网络的表达能力, 这个现象称为前期隐藏节点过少的制约性.
B类模型27个子模型的表达能力如图 5所示, B1, B2, B3系列模型均表现出了隐藏节点过少的局限性.中间层节点均匀分布的网络模型如8∶8∶6, 8∶6∶8, 6∶8∶ 8等子模型所划分的线性区域数更多一些, 并且对于三个不同系列, 均可见第1层隐藏层节点数过少的子模型表达能力不如第2层隐藏层节点数过少的子模型, 如2∶18∶2与2∶2∶18, 2∶10∶10与10∶2∶10等.保持第1层节点数量相等, 对比后两层节点数量翻转的模型, 如3∶16∶3与3∶3∶16, 9∶4∶9与9∶9∶4等, 都表现出前期隐藏节点过少的制约性.图中从6∶8∶8分布的子模型开始, 三个系列的模型有一个显著的反超趋势, 这正是因为第1层的节点数量制约了后续网络的表达性能.
图 5(Fig. 5)
 | 图 5 B类模型的表达能力Fig.5 Expressive power of B-type model |
选取B2系列与A类模型、C类模型一起作对比, 如图 6所示: 单隐藏层网络模型的表达能力远不及深层网络模型; 而三层的网络模型在节点分布较均匀时, 能够较多地超出二层模型所能划分的线性区域数, 仅有当层节点数量过少时才会制约三层网络模型的表达能力, 从而使得二层模型的表现更佳.
图 6(Fig. 6)
 | 图 6 三类模型的表达能力Fig.6 Expressive power of three types of models |
3.3 线性区域合并数量与精确度在合并线性区域的概念中, 由于引入了输出层分类标签的划分标准, 会存在激活序列相同但分类标签不同的情况, 这些激活序列会被重复计数, 因此原始线性区域数量会比3.2节中得到的区域数量更多, 需要对增多的原始线性区域进行合并操作.
选取A系列模型以及B1系列模型加入合并线性区域的操作, 并且计算了模型的精确度, 如图 7所示.由于合并操作不影响模型的分类计算, 因此合并前后模型的精确度是相同的.
图 7(Fig. 7)
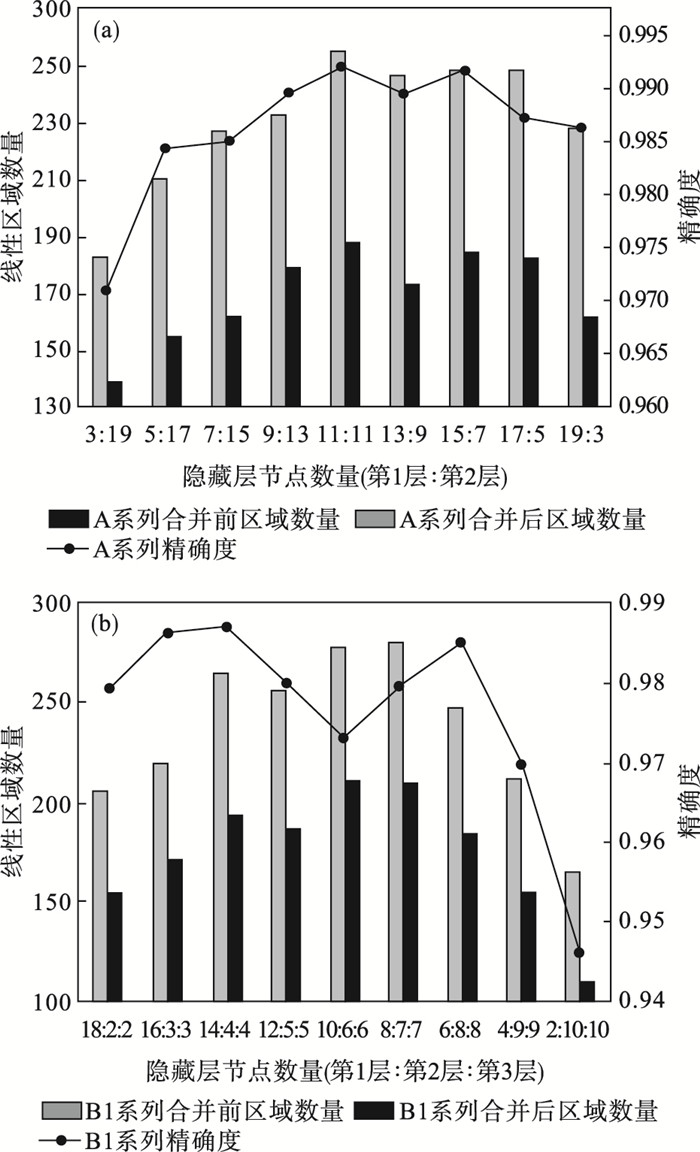 | 图 7 不同模型的合并区域数及精确度Fig.7 The number and accuracy of merging areas of different models (a)—A类模型;(b)—B1类模型. |
可以看到原始线性区域经过合并操作, 极大地压缩了原始区域数量, 这意味着计算出的同一标签下的线性区域, 其决策边界可能存在更加一般化的决策特征, 即合并后区域的决策特征.
从精确度的变化曲线可以看出, 精确度基本上是随线性区域数量的走势而变化的.这表明在一定程度上可以使用线性区域数量作为模型表达能力的度量单位.
最后选取A类模型中层节点分布为11∶11的子模型, 根据计算输入实例集合的激活模式, 将输入空间被划分后的线性区域可视化, 如图 8所示.从图中大致可以看出这些线性区域的边界可以构成一个半径为1的圆, 这正是网络模型对输入空间进行划分的结果.同时, 单独绘制了图 8中可合并的部分线性区域组, 如图 9所示.其中, 一些线性区域可以与其他不同的线性区域合并成不同的组合, 如图 9b和图 9c所示, 中间最大的线性区域与其他不同的3个线性区域构成了不同的合并组.
图 8(Fig. 8)
 | 图 8 线性区域的可视化Fig.8 Visualization of linear regions |
图 9(Fig. 9)
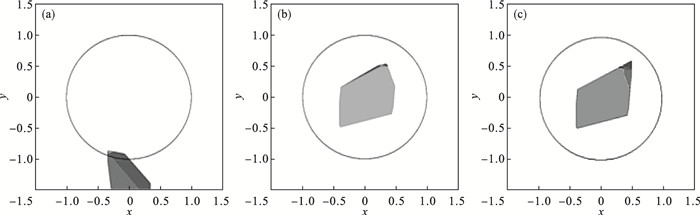 | 图 9 可合并的区域组Fig.9 Mergeable region groups (a)—图 8中区域Ⅰ;(b)—图 8中区域Ⅱ;(c)—图 8中区域Ⅲ. |
4 结语本文探究了分段线性神经网络的表达能力, 在原理上给出了线性区域的基础概念与相关的计算方式, 同时提出了合并线性区域的概念.在实验上通过三类模型所构建的线性区域, 一定程度上衡量了这些模型的表达能力.
通过本文的方法原理, 给出了一些如何使网络的表达能力较为优秀的途径.在未来的工作中, 将继续探索合并线性区域的决策特征是否能为模型带来更好的泛化能力等深入网络模型的原理及其作用.
参考文献
| [1] | Wang S H, Phillips P, Sui Y X, et al.Classification of Alzheimer's disease based on eight-layer convolutional neural network with leaky rectified linear unit and max pooling[J/OL].Journal of Medical Systems, 2018[2019-12-05].https://link.springer.com/article/10.1007/s10916-018-0932-7.DOI:10.1007/s10916-018-0932-7. |
| [2] | Croce F, Hein M.A randomized gradient-free attack on ReLU networks[C/OL] // Proceedings of 40th German Conference on Pattern Recognition.Stuttgart, 2018(2018-11-28)[2019-12-06].https://arxiv.org/pdf/1811.11493.pdf.DOI:10.1007/978-3-030-12939-2_16. |
| [3] | Pascanu R, Montúfar G, Bengio Y.On the number of response regions of deep feed forward networks with piece-wise linear activations[J/OL].(2014-02-14)[2020-01-04].https://arxiv.org/abs/1312.6098v4.DOI:10.1002/art.23474. |
| [4] | Montúfar G, Pascanu R, Cho K, et al.On the number of linear regions of deep neural networks[C] // Proceedings of the 27th International Conference on Neural Information Processing Systems.Cambridge, MA: MIT Press, 2014: 2924-2932. |
| [5] | Eldan R, Shamir O.The power of depth for feed forward neural networks[C/OL].(2015-12-12)[2019-12-05].https://arxiv.org/abs/1512.03965v1. |
| [6] | Serra T, Tjandraatmadja C, Ramalingam S.Bounding and counting linear regions of deep neural networks[C/OL].(2017-11-06)[2019-12-08].https://www.researchgate.net/publication/320920537_Bounding_and_Counting_Linear_Regions_of_Deep_Neural_Networks. |
| [7] | Raghu M, Poole B, Kleinberg J, et al.On the expressive power of deep neural networks[C] // Proceedings of the 34th International Conference on Machine Learning.Sydney, 2017: 2847-2854. |
| [8] | Zhang L W, Naitzat G, Lim L H.Tropical geometry of deep neural networks[C] // Proceedings of the 35th International Conference on Machine Learning.Stockholm, 2018: 5824-5832. |
| [9] | Ribeiro M T, Singh S, Guestrin C."Why should I trust you?": explaining the predictions of any classifier[C] // Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Demonstrations.San Diego, CA, 2016: 97-101. |
| [10] | Fong R, Vedaldi A.Interpretable explanations of black boxes by meaningful perturbation[C] // IEEE International Conference on Computer Vision.Venice, 2017: 3429-3437. |
| [11] | Chu L Y, Hu X, Hu J H, et al.Exact and consistent interpretation for piecewise linear neural networks: a closed form solution[C] // Processes of the 24th ACM SIGKDD International Reference on Knowledge Discovery & Data Mining.London, 2018: 1244-1253. |
