基于回归模型的Spark任务性能分析方法

阚忠良,李建中

(黑龙江大学 计算机科学技术学院, 哈尔滨 150080)



摘要:

为解决Spark任务运行过程中的性能评估与改进问题，本文提出一种基于启发式算法和支持向量机回归模型的Spark性能评价与分析方法.本文首先提出一种启发式性能评价算法，该方法采用Ganglia收集并处理Spark任务运行时的集群资源消耗数据，根据k-means算法划分任务类型，并根据任务类型确定启发式性能评价算法的评价指标和初始权重.然后，从Spark历史服务器中收集并处理任务运行效率数据，与集群资源消耗数据一并作为Spark任务运行时的状态数据.最后，根据状态数据迭代确定启发式性能评价算法的最终权重，以此建立Spark性能评价回归模型.本文随后提出一种基于支持向量机SVM回归算法(SVR)的Spark性能分析方法.该方法对Spark配置参数与整体性能建立回归模型，然后对该回归模型进行敏感度分析，找到能够影响Spark性能的重要参数.实验结果表明，启发式性能评价算法能够量化Spark任务资源消耗和运行效率等各方面性能，比较全面地评估任务的整体性能.基于SVR的性能分析方法能够比较有效地应用于Spark任务的实际分析中，形成初步的Spark任务性能调优建议.

关键词:  Spark  性能评价  回归模型  敏感度分析

DOI：10.11918/j.issn.0367-6234.201710009

分类号:TP311

文献标识码:A

基金项目:



Spark task performance analysis method based on regression model

KAN Zhongliang,LI Jianzhong

(School of Computer Science and Technology, Heilongjiang University, Harbin 150080, China)

Abstract:

To solve the problem of performance evaluation and improvement when the Spark tasks are performed, this paper proposes a Spark performance evaluation and an analysis method based on the heuristic algorithm and support vector machine regression model. A heuristic performance evaluation algorithm is proposed, which uses Ganglia to collect and process the consumption data of cluster resource when performing the Spark tasks. According to the k-means algorithm, the task type is determined and the evaluation index and the initial weight of the heuristic performance evaluation algorithm are determined according to the task type. The task efficiency data is collected and processed from the Spark history server, and it is regarded as the state data of the Spark run-time task along with the cluster resource consumption data. The final weight of the heuristic performance evaluation algorithm is determined according to the state data iteration process, and then the Spark Performance Evaluation Regression Model is established. A Spark performance analysis method based on support vector machine SVM regression algorithm (SVR) is proposed subsequently. This method establishes a regression model for the Spark configuration parameter and the overall performance, and then analyzes the sensitivity of the regression model to find important parameters that affect the performance of Spark. The experimental results show that the heuristic performance evaluation algorithm can quantify the performance of Spark task resource consumption and operation efficiency, and can comprehensively evaluate the overall performance of the task. The SVR-based performance analysis method can be applied to the actual analysis of Spark task effectively, which can form the initial tuning advice about the Spark mission performance.

Key words:  spark  performance evaluation  regression  sensitivity analysis


阚忠良, 李建中. 基于回归模型的Spark任务性能分析方法[J]. 哈尔滨工业大学学报, 2018, 50(3): 192-198. DOI: 10.11918/j.issn.0367-6234.201710009.
KAN Zhongliang, LI Jianzhong. Spark task performance analysis method based on regression model[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 192-198. DOI: 10.11918/j.issn.0367-6234.201710009.
作者简介 阚忠良(1969—)，男，博士，副教授;
李建中(1950—)，男，教授，博士生导师 通信作者 李建中，lijzh@hit.edu.cn 文章历史 收稿日期: 2017-10-09



Contents            -->Abstract            Full text            Figures/Tables            PDF


基于回归模型的Spark任务性能分析方法
阚忠良, 李建中    
黑龙江大学 计算机科学技术学院，哈尔滨 150080

收稿日期: 2017-10-09
作者简介: 阚忠良(1969—)，男，博士，副教授;
李建中(1950—)，男，教授，博士生导师
通信作者: 李建中，lijzh@hit.edu.cn


摘要: 为解决Spark任务运行过程中的性能评估与改进问题，本文提出一种基于启发式算法和支持向量机回归模型的Spark性能评价与分析方法.本文首先提出一种启发式性能评价算法，该方法采用Ganglia收集并处理Spark任务运行时的集群资源消耗数据，根据k-means算法划分任务类型，并根据任务类型确定启发式性能评价算法的评价指标和初始权重.然后，从Spark历史服务器中收集并处理任务运行效率数据，与集群资源消耗数据一并作为Spark任务运行时的状态数据.最后，根据状态数据迭代确定启发式性能评价算法的最终权重，以此建立Spark性能评价回归模型.本文随后提出一种基于支持向量机SVM回归算法(SVR)的Spark性能分析方法.该方法对Spark配置参数与整体性能建立回归模型，然后对该回归模型进行敏感度分析，找到能够影响Spark性能的重要参数.实验结果表明，启发式性能评价算法能够量化Spark任务资源消耗和运行效率等各方面性能，比较全面地评估任务的整体性能.基于SVR的性能分析方法能够比较有效地应用于Spark任务的实际分析中，形成初步的Spark任务性能调优建议.
关键词: Spark    性能评价    回归模型    敏感度分析    
Spark task performance analysis method based on regression model
KAN Zhongliang, LI Jianzhong    
School of Computer Science and Technology, Heilongjiang University, Harbin 150080, China


Abstract: To solve the problem of performance evaluation and improvement when the Spark tasks are performed, this paper proposes a Spark performance evaluation and an analysis method based on the heuristic algorithm and support vector machine regression model. A heuristic performance evaluation algorithm is proposed, which uses Ganglia to collect and process the consumption data of cluster resource when performing the Spark tasks. According to the k-means algorithm, the task type is determined and the evaluation index and the initial weight of the heuristic performance evaluation algorithm are determined according to the task type. The task efficiency data is collected and processed from the Spark history server, and it is regarded as the state data of the Spark run-time task along with the cluster resource consumption data. The final weight of the heuristic performance evaluation algorithm is determined according to the state data iteration process, and then the Spark Performance Evaluation Regression Model is established. A Spark performance analysis method based on support vector machine SVM regression algorithm (SVR) is proposed subsequently. This method establishes a regression model for the Spark configuration parameter and the overall performance, and then analyzes the sensitivity of the regression model to find important parameters that affect the performance of Spark. The experimental results show that the heuristic performance evaluation algorithm can quantify the performance of Spark task resource consumption and operation efficiency, and can comprehensively evaluate the overall performance of the task. The SVR-based performance analysis method can be applied to the actual analysis of Spark task effectively, which can form the initial tuning advice about the Spark mission performance.
Key words: spark    performance evaluation    regression    sensitivity analysis    
Apache Spark是基于内存的通用并行处理框架. 2012年加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)提出弹性分布式数据集(RDD)的概念. RDD是一种分布式内存抽象，它允许程序员以容错方式在大型集群上执行内存计算. Spark系统实现了RDD.实验显示，Spark比迭代应用的Hadoop快20倍，而且可以用5~7 s的延迟，交互式地扫描1TB数据集^[1].

由于Spark推出时间不长，用户对该平台运行任务的效率和性能不能很好地掌握，而且由于Spark基于内存实现的特性^[2]，导致Spark任务极容易造成内存溢出或资源浪费的问题.目前，针对Spark任务性能评价进行的工作较少，一般直接将任务运行时间作为Spark任务运行性能的评价指标[3-5]，没有考虑任务运行时的内存占用，shuffle效率等其他性能指标.在商业化软件中eBay^[6]，LinkedIn^[7]等公司推出一些第三方插件，如Apache Eagle，Dr. Elephant等，但是这些插件，一方面对Spark任务的性能监控和评价不够全面，另一方面，只是简单地展示目前的参数和任务运行时的状态数据，并没有很好地利用任务运行时的状态特征形成评价指标.因此在多数实际情况中，Spark任务评估仍然基本基于用户的经验.

在影响任务运行的性能的因素中，除了任务本身程序效率外，参数的配置也是极为重要的因素. Spark支持一系列工具，这导致Spark生态圈较为庞大，上层软件栈复杂多样，Spark可执行任务的种类也多种多样.不同的任务在相同的配置下会展现出截然不同的性能，因此需要根据任务的性能特征来具体分析Spark任务运行时的系统性能与配置参数之间的关系.

目前，针对Spark系统参数与性能关系建模进行的工作较少，比较具有代表性的是Spark官方网站的Tuning Spark文档以及Clouders上的有关博客，但也只是简单的参数设置建议，有关Spark参数评判和分析的研究大部分比较粗略，一般选取的参数很少，且只评价个别参数对某一性能指标的影响，或针对指定上层软件栈做参数的分析工作^[5].

1 性能监控Ganglia是一个可扩展的分布式监控系统，可用于集群或多个集群组成的Grid等高性能计算系统.它基于分层设计和多播的监听协议来监视集群内的状态，并使用树形结构连接并聚合节点之间的状态.它利用了XML，XDR，RRDtool等应用广泛的技术. Ganglia在每个节点的开销极低，并发性极强，因此被广泛使用^[8].

Ganglia可监控到的部分集群特征值如表 1所示.收集到的信息包括系统的平均负载，CPU使用情况，磁盘使用情况，内存使用情况，平均每秒进出包的数量，读写字节大小等.

表 1
表 1 部分Ganglia可监控参数及其说明 Table 1 Some parameters Ganglia monitored and the explanation 监控项 Load_one/个 Load_five/个 mem_total/KBs mem_free/KBs cpu_wio/%

说明 每分钟的系统平均负载 每5分钟的系统平均负载 物理内存总量 空闲内存大小 Cpu因io请求空闲时间百分比

监控值 load_one=0.0 load_five=0.0 mem_total=2 075 288.0 mem_cached=470 732.0 cpu_wio=0.2



监控项 disk_total/MBs disk_free/MBs pkts_in/个 pkts_out/个 cpu_idle/%

说明 磁盘总大小 剩余磁盘空间 每秒进来的包 每秒出去的包 Cpu非io请求空闲百分比

监控值 disk_total=133.9 disk_free=124.7 pkts_in=10.5 pkts_out=2.85 cpu_idle=99.6



表 1 部分Ganglia可监控参数及其说明 Table 1 Some parameters Ganglia monitored and the explanation


Spark官方系统提供了几种监控Spark运行程序的方法，包括web UI，Metrics以及第三方工具.如果Spark在YARN上运行，可以通过Spark history server(历史日志服务器)查看程序历史日志.

Spark历史日志文件默认格式为json类型，即用key-value键值对的格式存储各种信息.历史日志中保存程序运行时的详细信息，它以Spark任务的appid为索引，存储了任务运行时的状态信息，包括各个executor的运行信息，各阶段时间占总运行时间百分比，配置参数值等.

2 基于启发式算法的性能评价方法 2.1 系统性能向量建立定义集群资源消耗向量，α_i(α_cpu, α_io, α_network, α_disk, α_mem, α_load)用以量化集群资源的消耗大小.其中，α_cpu表示集群CPU使用百分比，α_io表示集群读写速度(bytes/s)；α_network表示集群网络丢包率；α_disk表示集群磁盘使用百分比；α_mem表示集群内存使用百分比；α_load表示集群负载.

定义任务运行效率向量，β_i(β_ComTime, β_{Shuffle Time}, β_{Shuffle Bytes}, β_GCTime, β_TotalTime, β_ResultsTime)用以衡量任务运行时的效率高低.其中，β_ComTime表示任务executor平均计算时间占总运行时间百分比；β_ShuffleTime表示任务Shuffle阶段平均时间占总时间百分比；β_ShuffleBytes表示任务Shuffle阶段平均读写大小(bytes)；β_GCTime表示任务GC阶段平均时间占总时间百分比；β_TotalTime表示任务总运行时间(ms)；β_ResultSTime表示任务结果序列化时间占总运行时间百分比.

定义系统性能向量γ_i(α_i, β_i)用以量化任务运行时系统的综合性能.其中，α_i表示集群资源使用向量；β_i表示任务运行效率向量.

2.2 基于k-means方法的任务类型划分k-均值聚类算法(k-means算法)作为数据挖掘中经典聚类算法之一，是一种被广泛使用的聚类算法.该算法是一种基于原型的聚类技术，算法使用质心定义原型，其中质心是一组点的均值^[9].

k-means聚类算法的基本原理是最小二乘法：将数据集的一个分区划分为k个集合，使分区的平方偏差之和最小^[10].具体来说，该算法将n个观测值分为k个集合，根据每个点与各集合中心的距离，将每个点都划分为离他最近的聚类，直到聚类收敛.

k-means算法将系统性能向量集合X，已知偏IO密集型任务系统性能向量集Y, 已知非IO密集型任务系统性能向量集Z和聚类簇数K作为输入. X，Y，Z中元素为历史任务的性能向量γ_i.

使用k-means的缺点之一是它需要最佳数量的簇(K)作为其输入.使用一个简单的启发式规则来确定K，因为原则上任何程序都可分为偏IO密集型和非IO密集型，所以选定K=2.尽管这种方法并不能保证找到最优解，但是此方法不要求手动解决问题以确定最佳聚类数.

k-means聚类结果显示，该方法趋向将性能特征相似的聚类，例如将α_cpu较高的任务聚成一簇.然而，k-means算法没有一个程式化的方法来确定哪一簇代表偏IO密集型，因此必须进一步处理.因此向系统提供多个有关任务的提示，首先利用一定的先验经验判断若干个任务(整体任务的子集)的类别，然后根据簇中已知类别的任务数目判断簇中任务的类型，选择多数任务所属的类别为该簇的类别.于是得到如下算法.

算法1?基于k-means的任务类型划分

输入：

系统性能向量集X，簇的数目K=2，阈值λ；

已知偏IO密集型任务系统性能向量集Y；

已知非IO密集型任务系统性能向量集Z.

误差平方和SSE_now←INF

随机选择K个中心点μ₁, μ₂…μ_k

do

??for x ∈ X:

?????i←argmin_j‖x-μ_j‖

?????x→C_i

??endfor

??for i∈[1, K]:

?????中心点${\mu _i} \leftarrow \frac{1}{{\left| {{C_i}} \right|}}\sum\limits_{x \in {C_i}} x $

??endfor

???SSE_old←SSE_now

???SSE_now←$\sum\limits_{i = 1}^K {\sum\limits_{x \in {C_i}} {} } $dist(μ_i, x)²

???ΔSSE ← SSE_old - SSE_now

until ΔSSE < λ

for i∈[1, K]:

????X1←C_i∩Y, X2←C_i∩Z

???if∣X1∣>∣X2∣

???????C_i为偏IO密集型任务集合

???else

???????C_i为非IO密集型任务集合

????endif

endfor

return各簇C_i类型和中心点μ_i.

算法结束.

在聚类之前必须保证性能向量的所有维度都是相同的数量级，否则结果将失去意义，因为数量级较大的维度将主导欧式距离的计算.通过对每个维度进行归一化处理，确保所有元数据都是相同的数量级.

实验中任务的集群资源消耗向量α_i各维度值为Ganglia收集的集群数据或集群数据的简单计算，任务的运行效率向量β_i各维度值可直接从Spark日志中获取.

2.3 启发式算法定义启发式算法(heuristic algorithm)是在搜索高维度解空间问题时，为了提高搜索效率而提出.启发式算法大多数具有随机行为，模仿生物或者物理过程(比如蚁群算法、模拟退火法等)，指导搜索算法的搜索方向，在可解空间中寻找到一个较好的解，但不保证找到全局最优解^[11].

启发式评价算法中涉及的定义和概念如下：目标任务性能向量γ_t：γ_t的每一维度γ_tj代表任务t在该维度的性能记录值.维度评价分数向量Score_t：对于γ_tj的每一维度j，评价分数值为Score_tj.权重向量w_t：对于不同的任务，在进行最后的综合分数评定时，不同的性能指标的重要性不同，所以定义权重向量w_t量化各个性能指标的重要性大小.对于Score_t的每一维度Score_tj，对应的权重值w_tj.最终评分FS_t= Score_t· w_t.

启发式评价算法过程如下：首先计算任务t的维度评价分数向量Score_t：Score_t的每一维度Score_tj，实际上是对γ_tj进行线性变换，将γ_tj映射到Score_t的每一维度Score_tj，计算公式如下：

${\rm{Scor}}{{\rm{e}}_{{t_j}}} = \frac{{60}}{{({M_j}-{B_j})}}*({M_j}-{\gamma _{{t_j}}})$

式中M_j为历史任务中j维度下最差性能记录值, B_j为历史任务中默认配置下任务的j维度性能记录值，γ_tj为目标任务t的j维度下性能记录值.注意，当γ_tj比M_j更差时，令M_j=γ_tj.

然后计算Score_t的权重向量w_t：w_t的初始值由任务t的类型确定. w_t的初始值，反映的是任务t所属类型下，大部分任务的性能瓶颈. w_t和Score_t的每个维度一一对应. Score_t的每一维度，是任务t在该维度上的得分值，反映了任务t在该维度上的性能优劣. w_t的每一维度，反映了Score_t对应维度的重要性大小. w_t计算过程如下：对于γ_t的每一维度γ_tj，若γ_tj=0，则：

${\mathit{\boldsymbol{w}}_{{t_{{\rm{TotalTime}}}}}} = {\mathit{\boldsymbol{w}}_{{t_{{\rm{TotalTime}}}}}} + {w_{{t_j}}}$

式中：w_tTotalTime代表Score_tTotalTime对应的权重向量.否则，根据γ_tj在γ_t所有维度中所占比重，小幅度调整w_tj的大小，并进行归一化处理.即根据任务t自身特性，调节任务t的权重向量.

最后计算任务t的最终评分：

${\rm{F}}{{\rm{S}}_{\rm{t}}} = \mathit{\boldsymbol{Scor}}{\mathit{\boldsymbol{e}}_t} \cdot {\mathit{\boldsymbol{w}}_t}.$

算法过程如下.

算法2?基于启发式的任务评价算法:

输入：待测任务t的系统性能向量γ_t，维度j的最差历史任务记录值M_j, 基准记录值B_j, 历史任务数据聚类后各簇C_i中心点μ_i和对应的权重向量初始值w_i，极小常量学习率ε.

μ_j=NearestNeighbor(γ_t, μ_i)

w_t←w_j

for Score_t每一维度Score_tj:

???if is Worse(γ_tj, M_j):

??????M_j=γ_tj

??????Score_tj=$\frac{{({M_j}-{\gamma _{{t_j}}})}}{{({M_j}-{B_j})}}*60$

endfor

for γ_t每一维度γ_tj:

???if γ_tj= 0:

??????w_tTotalTime←w_tTotalTime+w_tj

???else:

??????w_tj←w_tj+$\left( {{\gamma _{{t_j}}}/\sum\limits_{i = 0}^{11} {{\gamma _{{t_j}}} - {w_{{t_j}}}} } \right) \cdot \varepsilon $

endfor

w_t=normalization(w_t)

FS_t← Score_t* w_t

return FS_t

应用启发式算法对任务性能进行评价，可以使用户直观了解运行任务的性能优劣.当分数为60分左右时，表示当前设置的配置参数下任务的总体性能，与默认配置参数下相同类型任务的总体性能相似.分数越高，说明任务的总体性能越好，当分数高于100时，说明当前任务的性能优于历史数据中相同类型的其他任务.分数越低，意味着任务运行时表现的总体性能越差，例如，和历史任务中同类型的任务相比，该任务的运行时间可能比较长，或运行过程中资源消耗比较高等.用户可以通过自定义对性能评分的期望阈值，来选择对性能进行调优或停止调优.

2.4 启发式算法性能分析k-means聚类算法将问题归结为一个把数据空间划分为Voronoi cells的问题. k-means问题在计算上是困难的(NP-hard)；通常采用有效的启发式算法并快速收敛到局部最优^[12].这些算法类似于使用迭代方法处理高斯分布混合期望最大化算法.

k-means算法复杂度为O(NKq)，其中，N是样本数量，K是类别数，q是迭代次数.在本文实验中，K和q远小于N，因此算法复杂度近似可以看做是O(N)，在聚类算法中是相对高效的算法.

3 系统性能与配置参数的关系本文不旨在改变流应用(或查询)的结构，而是着重于寻找配置参数的调整与执行效率和资源消耗的关系，不试图构建系统的完整(封闭形式)数学模型，但将应用程序视为使用经验抽样优化的黑盒功能，与传统的基于成本的模型相反，采用在参数空间实验的方法，即构建由数据驱动的关系模型^[13].

为寻找影响系统性能的参数，本文试图构建参数向量X_i和系统性能向量γ_i之间的回归模型，并对该模型进行敏感性分析.

3.1 建立参数与系统性能的回归模型SVR算法的原理从设计最优准则线性分类器开始，旨在特征空间中找到最优超平面，最大化分类间隔.当特征空间线性不可分时，SVR使用核函数的方法，将低维特征空间投射到高维线性可分空间上，从而解决线性不可分问题.相较ANN等不保证求解全局最优解的方法，由于SVR的求解问题可表示成凸优化问题，所以SVR是求解全局最优的有效算法.除此之外，SVR算法使用核函数的方法表示内积，不需要实际求解样本在高维空间的特征值，避免了维度灾难；而且SVR优化的是基于结构化风险最小的准则函数，专注于少量的关键样本(支持向量)，泛化能力强.文中，相对于整个高维度参数空间，实验获取到的参数样本集属于小样本集合，为找到全局最优解，使用SVR算法，建立参数与性能之间的泛化模型^[14].

使用SVR算法建立回归模型，自变量为任务运行时的配置参数向量C，因变量为任务运行时的系统性能向量γ_i.根据Spark官方网站上的说明文档，从资源调配、内存调整、jvm垃圾回收三个方面选取7个Spark重要的配置参数构成配置参数向量C这7个参数均为数值型参数，实验中各参数的取值为最低值到实验条件允许的最大值中的随机值，否则，Spark将无法启动该任务.

利用SVR算法分类也有其缺点，SVR算法严重依赖核函数的选择和参数的设置，如何根据实际的数据模型选择合适的核函数从而构造SVR算法是个比较困难的问题，目前比较成熟的核函数及其参数的选择都是人为根据经验来选取的^[13].

SVR众多核函数中，应用最广泛的是径向基函数(RBF核函数). RBF核函数中最常用的是高斯核函数.高斯核函数类似高斯分布，理论上，高斯核函数可将低维空间映射到无穷维度空间，基于这个特性，高斯核函数可以应用于非线性分类中. linear线性核函数是RBF的一个特例，sigmoid在某些参数下和RBF的效果相似.高斯核函数的关键参数只有2个：惩罚系数和核参数，且取值范围在[0, 1]区间上.与高斯核函数相比，多项式polynomial核函数的取值范围在[0, +∞)区间上.因此，高斯核函数的复杂性较低，计算更为方便.此外，作为RBF核函数的特例，linear核函数的优点也是极为突出的：一是在数据线性可分时，linear的速度和效率都是非常可观的.二是linear核函数的参数相对RBF核函数来讲数量较少.因此，优先考虑RBF核函数拟合和linear核函数拟合.但是不能排除polynomial核函数在特定场合下对数据的拟合效果也很优秀，所以实验采用三种核函数进行对比.

3.2 对回归模型进行敏感度分析敏感性分析是研究数学模型或系统的输出中的不确定性来源的方法之一.为增加对回归模型中自变量和因变量之间关系的理解，识别对因变量影响较大的自变量，使用敏感性分析进一步对回归模型进行处理，寻求识别模型自变量和因变量之间的重要联系.

对于系统性能向量的每一维度，定义所有历史任务在该维度上的实际值构成一个向量y_fact，定义基于机器学习算法模型预测的系统性能向量y_pred，其与y_fact的欧氏距离作为模型预测误差度量，选择预测误差度最小的机器学习算法模型作为预测模型.

定义参数的敏感度为η，反映参数的变化量△X_i和预测值的变化量△y_pred之间的相关关系，具体计算公式如下

$\eta = \Delta \;y\_pred/\Delta {X_i}.$

式中：ΔX_i为参数i增加的微小变化量，具体为参数i可调整的最小单位; △y_pred为参数增加△X_i后y_pred的变化值.

对于性能向量得分最差的维度进行敏感度分析，敏感度值的大小反映参数对性能影响大小，敏感度值的符号反映参数对性能的影响方向，正号表明参数值增大可能会提升性能，负号表明参数值减小可能会提升性能.

4 应用实例与分析基于启发式算法的性能评价方法首先从Ganglia中提取集群资源消耗数据，建立集群资源消耗向量，然后对集群资源消耗向量进行k-means聚类，根据划分的类型确定启发式性能评价算法的初始权重，接下来从Spark history sever中抓取Spark运行日志，在日志中提取Spark任务运行效率数据，和集群资源消耗数据合并，作为系统性能向量，根据系统性能向量迭代计算最终的权重向量，以此建立Spark任务性能评估模型.

实验选取spark benchmark平台上2种类型的4个程序，包括wordcount(io密集型)，sort(计算密集型)，grep(计算密集型)，pagerank(计算密集型).在输入数据为10G的条件下，每个程序随机选取多种参数组合运行.聚类结果显示，不同类型的任务在运行时，集群资源消耗向量差异较大.集群资源消耗向量是基于Ganglia监控到的集群资源消耗值进行计算.以Ganglia监控到的cpu_idle和cpu_wio为例进行聚类结果说明. cpu_idle表示cpu空闲时间比，cpu_wio表示cpu因io操作导致的空闲时间比.聚类结果显示，偏io密集型的任务运行时，检测到的cpu_idle和cpu_wio值都较大.因为偏io密集型的任务运行时cpu空闲时间较多，且造成cpu空闲的主要原因是io操作.

本文基于动态变化的启发式参数评价算法，为904组实验程序进行评分.以app-1496760064578为例，由于该运行程序不存在shuffle阶段，因此权重向量weight由初始权重：

(0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1)变为(0.5, 0.1, 0, 0, 0.1, 0.1, 0, 0, 0.1, 0.1, 0.1, 0), 对应的非0性能指标为总运行时间，executor计算时间比，结果序列化时间比，GC时间比，内存使用比，丢包率和磁盘使用比7个.系统性能向量各维度值的比例几乎相近，因此最终的权重向量为(0.5, 0.1, 0, 0, 0.1, 0.1, 0, 0, 0.1, 0.1, 0.1, 0).系统性能总得分和各个维度的得分存储在MySQL中.实验数据表明该任务运行时GC时间比较大，可以调节能够影响GC时间的参数来提高任务运行效率，进而改善系统性能.

SVR模型参数及说明sklearn官方网站上用户文档有详细的说明.实验中选取3种常见的核函数，分别是rbf高斯核函数，linear线性核函数，poly二次多项式核函数.出于对模型精度考虑，选定目标函数的惩罚系数C为1e3，核函数系数为0.5.

使用904组对比实验建立回归模型，实验中采用平均相对误差(MRE)作为拟合程度的度量，即计算对应系统性能维度，实际值与SVR模型预测值的残差绝对值，与实际值的百分比.实验结果见表 2.实验数据表明，针对不同的系统性能维度，拟合程度最高的核函数不同.从整体上看，非线性SVR算法的精度与其他3种核函数下的SVR算法的精度相差不多，并没有明显提升.而线性核函数linear的SVR算法模型的速度和实际效果稍好一些.

表 2
表 2 各性能维度预测值与实际值的平均相对误差(MRE) Table 2 MRE of the predicted values of the performance dimensions SVR模型 总运行
时间/% Executor计算
时间比/% 结果序列化
时间比/% GC时间比/% 内存
使用比/% 丢包率/% 磁盘
使用比/%

SVR(rbf) 0.636 203 0.384 401 0.850 412 0.607 536 0.154 451 0.335 637 0.335 617

SVR(linear) 0.636 275 0.425 026 0.553 054 0.685 455 0.146 515 0.330 854 0.516 547

SVR(poly) 0.638 245 0.420 525 0.786 586 0.663 221 0.148 639 0.337 316 0.516 583

NuSVR() 0.851 822 0.407 567 1.061 122 0.621 806 0.127 876 0.205 162 0.113 426



表 2 各性能维度预测值与实际值的平均相对误差(MRE) Table 2 MRE of the predicted values of the performance dimensions


使用3种其他线性回归方法做相同实验，包括多项式回归函数，脊回归函数，线性逻辑回归函数，验证在该实验环境下，SVR模型的泛化能力比较强.实验中各性能维度下，平均相对误差结果显示见表 3.数据表明线性逻辑回归算法与SVR算法的精度总体上相差不多.而多项式回归函数和脊回归算法则存在严重过拟合问题.

表 3
表 3 各性能维度平均相对误差 Table 3 MRE of the predicted values of the performance dimensions 其他线性回归模型 总运行时间/% Executor计算时间比/% 结果序列化时间比/% GC时间比/% 内存使用比/% 丢包率/% 磁盘使用比/%

多项式线性回归 0.111 755 0.204 142 0.207 744 0.150 568 0.145 32 0.250 401 0.148 147

脊回归 0.211 749 0.204 142 0.207 565 0.150 565 0.145 305 0.250 338 0.148 027

线性逻辑回归 0.738 245 0.420 585 0.586 586 0.673 221 0.147 639 0.336 732 0.583 309



表 3 各性能维度平均相对误差 Table 3 MRE of the predicted values of the performance dimensions


为了对比SVR三种核函数的整体拟合效果，将得分为60分以上的任务作为性能优良类别，标记为类别0，将得分为60分以下的任务作为性能较差类别，标记为类别1，平均性能为类别总评.实验中使用交叉验证的方法，使用三种核函数建立的模型预估任务的类别.取准确度(precision), 召回率(recall)，和F1分数来评估模型的精确度.当test_size=0.5，即使用50%的数据进行模型训练，50%的数据用于模型测试时，实验数据如下图 1~3所示.

Figure 1
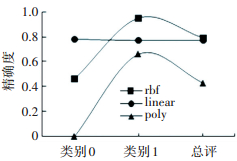图 1 精确度比较 Figure 1 Precision comparison


Figure 2
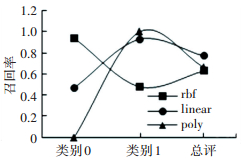图 2 召回率比较 Figure 2 Recall comparison


Figure 3
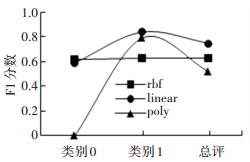图 3 F1分数比较 Figure 3 F1-score comparison


采用poly多项式核函数的模型综合拟合效果最差，rbf核函数和linear线性核函数的综合拟合效果较好. linear线性核函数是特殊的rbf核函数形式，比起rbf核函数，需要试验的参数更少，速度更快.多项式核函数需要调整的参数比rbf核函数更多，过拟合程度会更大.数据也显示，linear核函数模型对性能较差类别(类别1)的识别性能更好，准确率和召回率都远高于其他两种模型，而用户更关心性能瓶颈的存在及其原因，因此在本系统中，linear核函数的性能相对更好一些.

5 结论1) 量化了Spark任务性能的优劣程度，从任务自身运行效率和硬件资源消耗情况两方面入手分析spark任务运行时系统的综合性能.基于Ganglia收集的Spark任务运行时的集群资源消耗数据集，通过与Spark任务日志时间戳匹配，建立任务运行时的集群资源消耗向量，量化集群运行状态特征.本文在此基础上，根据k-means算法划分任务类型.聚类结果表明，所提取的特征对于所研究的两种任务类型具有比较好的可分性.

2) 定义了启发式性能评价方法，根据任务运行的具体状态特征，动态调整启发式性能评价模型.根据任务类型确定启发式算法的性能指标和初始权重，能够有效加速后续迭代过程，根据任务状态迭代计算最终权重，能够比较客观的反映任务运行效率和资源消耗等的各方面的性能，进而进行综合性能的合理评估.

3) 在对性能评估的基础上，尝试对性能与参数的关系进行回归分析.提出了对回归模型进行敏感度分析，通过对比敏感度大小发现影响性能的重要参数.采用SVR的4种核函数建立回归模型SVR，并且，通过与线性逻辑回归，多项式回归，脊回归算法模型的效果进行对比，证明SVR模型的泛化效果良好，过拟合现象并不严重.


参考文献
[1] ZAHARIA M, CHOWDHURY M, DAS T, et al. Resilient distributed datasets: a fault-tolerant abstraction for in-memory cluster computingC]//Gribble S, Katabi D. Proceedings of the 9th Usenix Conference on Networked Systems Design and Implementation. Berkeley, CA, USA: USENIX Association, 2012: 2-2.


[2] SHORO A G, SOOMRO T R. Big data analysis: apache spark perspective[J]. Global Journal of Computer Science and Technology, 2015, 15(1): 7-14. DOI:10.14445/22312803/IJCTT-V19P103


[3] FISCHER L, GAO S, BERNSTEIN A. Machines tuning machines: configuring distributed stream processors with bayesian optimization[C]//Raicu I. 2015 IEEE International Conference on Cluster Computing. Washington, DC, USA: IEEE Computer Society, 2015: 22-31. DOI: 10.1109/CLUSTER.2015.13.


[4] WANG K, KHAN M M H. Performance prediction for apache spark platform[C]//Zhu Yongxin, Ghazawi T E. 17th IEEEInternational Conference on High PERFORMANCE Computing and Communications. Washington, DC, USA: IEEE Computer Society, 2015: 166-173.


[5] 陈英芝. Spark shuffle的内存调度算法分析及优化[D]. 浙江: 浙江大学, 2016.
CHEN Yingzhi, Analysis and optimization of spark shuffle memory scheduling algorithm[D]. Zhejiang: Zhejiang University, 2016.


[6] GUPTA C, SINHA R, ZHANG Y. Eagle: User profile-based anomaly detection for securing hadoop clusters[C]// Cuzzocrea A, Hedges M. 2015 IEEE International Conference on Big Data. Washington, DC, USA: IEEE Computer Society, 2015: 1336-1343. DOI: 10.1109/BigData.2015.7363892.


[7] A Kshay Rai. LinkedIn开源Dr. Elephant. (2016. 4). http://www.infoq.com/cn/news/2016/04/Dr-Elephant-LinkedIn.


[8] MASSIE M L, CHUN B N, CULLER D E. The ganglia distributed monitoring system: design, implementation, and experience[J]. Parallel Computing, 2004, 30(7): 817-840. DOI:10.1016/j.parco.2004.04.001


[9] TAN Pangning, STEINBACH M, VIPIN. Introduction to data mining[M]. Posts & Telecom Press, USA: Pearson, 2010: 310-320.


[10] 郑兴鹏. K-Means聚集算法原理. (2017. 4). http://www.cnblogs.com/zhengxingpeng/p16670493.html.


[11] BEHESHTI Z, SHAMSUDDIN S M. A review of population-based meta-heuristic algorithm[J]. International Journal of Advances in Soft Computing & Its Applic, 2013, 5(1): 1-35.


[12] ZHU P, ZHU P, YANG X, et al. Optimized big data K-means clustering using map reduce[J]. Journal of Supercomputing, 2014, 70(3): 1249-1259. DOI:10.1007/s11227-014-1225-7


[13] FISCHER L, GAO S, BERNSTEIN A. Machines tuning machines: configuring distributed stream processors with bayesian optimization[C]//Antonino T. 2015 IEEE International Conference on CLUSTER Computing. Washington, DC, USA: IEEE Computer Society, 2015: 22-31. DOI: 10.1109/CLUSTER.2015.13.


[14] 刘泽燊, 潘志松. 基于Spark的并行SVM算法研究[J]. 计算机科学, 2016, 43(5): 238-242.
LIU Zeshen, PAN Zhisong. Research on parallel SVM algorithm based on spark[J]. Computer Science, 2016, 43(5): 238-242. DOI:10.11896/j.issn.1002-137X.2016.5.044