李建鹏1,张颖1,张瑞2,曹勇1
(1.哈尔滨工业大学 深圳研究生院, 广东 深圳 518055;2.深圳职业技术学院, 广东 深圳 518172)
摘要:
含有区间状态时滞的系统在实际中有重要的应用，如它可以方便地描述一类网络控制系统.本文对含有区间状态时滞的线性离散系统考虑了稳定性分析与状态反馈控制器设计问题.为研究该类系统的稳定性，通过引入二重求和和三重求和构造了新型的Lyapunov-Krasovskii泛函.在对所构造的泛函处理其差分的过程中，利用了基于Abel引理的有限和不等式技术以及时滞分割方法，进而提出了该类系统稳定的线性矩阵不等式充分性条件.相对于以往的Lyapunov泛函，本文所提出的Lyapunov-Krasovskii泛函包含更多的时滞信息，而且所采用的差分处理方法不涉及原系统的模型变化，因而所提出的渐近稳定充分条件具有较低保守性.另外，相对于以前存在的自由权矩阵方法，本文所提出的方法具有较少的可行性变量矩阵，因而能有效地降低计算量.基于所提出的稳定性条件，本文进一步提出了无记忆状态反馈镇定控制器的设计方法.所提出镇定控制器设计方法也通过线性矩阵不等式给出，具有很好的数值稳定性.最后，通过数值算例验证了所提方法的正确性和有效性.
关键词: 离散系统 区间时滞 稳定性 状态反馈
DOI：10.11918/j.issn.0367-6234.201701040
分类号:TU375.2
文献标识码:A
基金项目:国家自然科学基金重大项目(0,2);国家自然科学基金(61603111)
Stability analysis and controller design for discrete-time systems with interval time-varying delays
LI Jianpeng1,ZHANG Ying1,ZHANG Rui2,CAO Yong1
(1. Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China; 2. Shenzhen Polytechnic, Shenzhen 518172, China)
Abstract:
The systems with interval time-delay appearing in state variable have wide application, and can be used to describe a class of networked control systems. The stability analysis and the state feedback controller design are investigated for linear discrete-time systems with interval time delays. In order to investigate the stability, a new Lyapunov-Krasovskii functional is proposed by introducing the double summation and triple summation. In order to estimate the difference of the Lyapunov-Krasovskii functional, the Abel lemma based finite sum inequality technique and the time delay segmentation method are used as tools, and thus a sufficient condition is presented for the asymptotic stability of the considered systems in terms of linear matrix inequalities. Compared to the traditional Lyapunov functional, since the proposed Lyapunov-Krasovskii functional contains more information on delays, and the approach for estimating the difference does not involve model transformation, thus the presented sufficient condition for the asymptotic stability of the system is less conservative. In addition, compared with the previous free-weighting matrix method there exist less feasible matrix variables in the current method. Thus, the computational load can be effectively reduced. According to the derived stability criterion, a design approach for non-memory state feedback controllers is presented in terms of linear matrix inequalities, and thus has good numerical stability. Finally a numerical example is employed to illustrate the effectiveness of the methods proposed in this paper.
Key words: discrete-time system interval time delay stability state feedback
李建鹏, 张颖, 张瑞, 曹勇. 区间时变时滞离散系统的稳定性分析及控制器设计[J]. 哈尔滨工业大学学报, 2017, 49(11): 18-23. DOI: 10.11918/j.issn.0367-6234.201701040.
LI Jianpeng, ZHANG Ying, ZHANG Rui, CAO Yong. Stability analysis and controller design for discrete-time systems with interval time-varying delays[J]. Journal of Harbin Institute of Technology, 2017, 49(11): 18-23. DOI: 10.11918/j.issn.0367-6234.201701040.
基金项目 国家自然科学基金重大项目(61690210, 61690212);国家自然科学基金(61603111) 作者简介 李建鹏(1991—), 男, 硕士研究生 通信作者 张颖, zhangyinghit@126.com 文章历史 收稿日期: 2017-01-01
Contents -->Abstract Full text Figures/Tables PDF
区间时变时滞离散系统的稳定性分析及控制器设计
李建鹏1, 张颖1
, 张瑞2, 曹勇1 1. 哈尔滨工业大学 深圳研究生院, 广东 深圳 518055;
2. 深圳职业技术学院, 广东 深圳 518172
收稿日期: 2017-01-01
基金项目: 国家自然科学基金重大项目(61690210, 61690212);国家自然科学基金(61603111)
作者简介: 李建鹏(1991—), 男, 硕士研究生
通信作者: 张颖, zhangyinghit@126.com
摘要: 含有区间状态时滞的系统在实际中有重要的应用，如它可以方便地描述一类网络控制系统.本文对含有区间状态时滞的线性离散系统考虑了稳定性分析与状态反馈控制器设计问题.为研究该类系统的稳定性，通过引入二重求和和三重求和构造了新型的Lyapunov-Krasovskii泛函.在对所构造的泛函处理其差分的过程中，利用了基于Abel引理的有限和不等式技术以及时滞分割方法，进而提出了该类系统稳定的线性矩阵不等式充分性条件.相对于以往的Lyapunov泛函，本文所提出的Lyapunov-Krasovskii泛函包含更多的时滞信息，而且所采用的差分处理方法不涉及原系统的模型变化，因而所提出的渐近稳定充分条件具有较低保守性.另外，相对于以前存在的自由权矩阵方法，本文所提出的方法具有较少的可行性变量矩阵，因而能有效地降低计算量.基于所提出的稳定性条件，本文进一步提出了无记忆状态反馈镇定控制器的设计方法.所提出镇定控制器设计方法也通过线性矩阵不等式给出，具有很好的数值稳定性.最后，通过数值算例验证了所提方法的正确性和有效性.
关键词: 离散系统 区间时滞 稳定性 状态反馈
Stability analysis and controller design for discrete-time systems with interval time-varying delays
LI Jianpeng1, ZHANG Ying1
, ZHANG Rui2, CAO Yong1 1. Harbin Institute of Technology Shenzhen Graduate School, Shenzhen 518055, China;
2. Shenzhen Polytechnic, Shenzhen 518172, China
Abstract: The systems with interval time-delay appearing in state variable have wide application, and can be used to describe a class of networked control systems. The stability analysis and the state feedback controller design are investigated for linear discrete-time systems with interval time delays. In order to investigate the stability, a new Lyapunov-Krasovskii functional is proposed by introducing the double summation and triple summation. In order to estimate the difference of the Lyapunov-Krasovskii functional, the Abel lemma based finite sum inequality technique and the time delay segmentation method are used as tools, and thus a sufficient condition is presented for the asymptotic stability of the considered systems in terms of linear matrix inequalities. Compared to the traditional Lyapunov functional, since the proposed Lyapunov-Krasovskii functional contains more information on delays, and the approach for estimating the difference does not involve model transformation, thus the presented sufficient condition for the asymptotic stability of the system is less conservative. In addition, compared with the previous free-weighting matrix method there exist less feasible matrix variables in the current method. Thus, the computational load can be effectively reduced. According to the derived stability criterion, a design approach for non-memory state feedback controllers is presented in terms of linear matrix inequalities, and thus has good numerical stability. Finally a numerical example is employed to illustrate the effectiveness of the methods proposed in this paper.
Key words: discrete-time system interval time delay stability state feedback
实际系统测量元件或测量过程中总是不可避免地存在信号传递时间延迟，这种现象普遍存在，也深受学者的广泛关注和研究[1].区间时变时滞是学者们的研究热点[2-5]，而网络控制系统便是区间时变时滞动态系统的一个典型例子[6].利用频域法对时滞系统进行分析和设计，其求解并不容易，因而基于时域方法对时滞系统进行分析得到了广泛研究，特别是在系统存在不确定性时异常困难.时滞相关稳定性研究一般首先在时域空间内构造Lyapunov-Krasovskii泛函，通过模型变换以及交叉项界定技术或者自由权矩阵方法[7]得到系统稳定性的充分条件.其中自由权矩阵法直接对二次型积分项进行界定，避免了模型变换，获得了较小保守性的时滞相关稳定性条件[8].
具有区间时滞的离散系统的稳定性、镇定以及H∞控制问题同样也得到了广泛关注.文献[9]结合广义系统模型变换法和Moon不等式研究了离散系统的保代价控制问题.文献[10]研究了时变时滞离散系统输出反馈H∞控制问题.文献[11]应用自由权矩阵法求得时滞系统的稳定性判据.
本文结合增广型泛函[12]与时滞分割方法[13]构造新型的Lyapunov-Krasovskii泛函，在处理泛函过程中采用基于Abel引理的有限和不等式技术[14], 获得了保守性更小的稳定性分析结果.
1 问题描述考虑离散时滞系统
$\left\{ \begin{array}{l}\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + {\mathit{\boldsymbol{A}}_d}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right),\\\mathit{\boldsymbol{x}}\left( k \right) = \varphi \left( k \right),k = - {h_M}, - {h_M} + 1, \cdots ,0.\end{array} \right.$ (1)
式中:x(k)∈Rn为系统的状态向量，A, Ad∈Rn×n为恒定适维的系统矩阵，φ(k)为初始条件序列，时滞d(k)满足：
$0 \le {h_m} \le d\left( k \right) \le {h_M}.$ (2)
设计状态反馈控制律
$\mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{Kx}}\left( k \right).$ (3)
系统(1)在控制器(3)的作用下得到如下闭环系统:
$\left\{ \begin{array}{l}\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \mathit{\boldsymbol{Ax}}\left( k \right) + {\mathit{\boldsymbol{A}}_d}\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) + {\mathit{\boldsymbol{B}}_u}\mathit{\boldsymbol{u}}\left( k \right),\\\mathit{\boldsymbol{x}}\left( k \right) = \mathit{\boldsymbol{\varphi }}\left( k \right),k = - {h_M}, - {h_M} + 1, \cdots ,0.\end{array} \right.$ (4)
首先分析系统(1)的稳定性条件，然后设计状态反馈控制器(3)使系统(4)渐近稳定.
为便于表述，现将文中用到的引理归纳如下.
引理?1[15] (Schur补性质)????给定分块矩阵
$\mathit{\boldsymbol{S = }}\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{S}}_{11}}}&{{\mathit{\boldsymbol{S}}_{12}}}\\{\mathit{\boldsymbol{S}}_{12}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{22}}}\end{array}} \right].$
则下述条件是等价的：
1) S < 0；
2) S11 < 0，S22-S12TS11-1S12 < 0；
3) S22 < 0, S11-S12S22-1S12T < 0.
引理?2[14]????对于常数矩阵R，R=RT>0以及整数r2-r1>1有下述不等式成立：
$\sum\limits_{j = {r_1}}^{{r_2} - 1} {{\eta ^{\rm{T}}}\left( j \right)\mathit{\boldsymbol{R\eta }}\left( j \right)} \ge \frac{1}{{{\rho _1}}}\mathit{\boldsymbol{\nu }}_1^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\nu }}_1} + \frac{{3{\rho _2}}}{{{\rho _1}{\rho _3}}}\mathit{\boldsymbol{\nu }}_2^{\rm{T}}\mathit{\boldsymbol{R}}{\mathit{\boldsymbol{\nu }}_2}.$
其中
$\begin{array}{l}\mathit{\boldsymbol{\eta }}\left( j \right) = \mathit{\boldsymbol{x}}\left( {j + 1} \right) - x\left( j \right),{\rho _1} = {r_2} - {r_1},{\rho _2} = {r_2} - \\{r_1} - 1,{\rho _3} = {r_2} - {r_1} + 1,{\mathit{\boldsymbol{\nu }}_1} = \mathit{\boldsymbol{x}}\left( {{r_2}} \right) - \mathit{\boldsymbol{x}}\left( {{r_1}} \right),{\mathit{\boldsymbol{\nu }}_2} = \\\mathit{\boldsymbol{x}}\left( {{r_2}} \right) + \mathit{\boldsymbol{x}}\left( {{r_1}} \right) - \frac{2}{{{r_2} - {r_1} - 1}}\sum\limits_{j = {r_1} + 1}^{{r_2} - 1} {\mathit{\boldsymbol{x}}\left( j \right)} .\end{array}$
引理?3[16]????对于任意恒定适维矩阵Z>0及标量h2>h1>0，有下面不等式成立：
$\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( i \right)\mathit{\boldsymbol{Z\omega }}\left( i \right)} \ge \frac{1}{{{h_{12}}}}{\left( {\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {\mathit{\boldsymbol{\omega }}\left( i \right)} } \right)^{\rm{T}}}Z\left( {\sum\limits_{i = k - {h_2}}^{k - {h_1} - 1} {\mathit{\boldsymbol{\omega }}\left( i \right)} } \right).$
2 主要结果考虑系统(1)，设N为大于零的正整数，利用hi, i=1, 2, …, N+1, 对时滞区间进行如下分割：
${h_m} = {h_1} < {h_2} < , \cdots , < {h_N} < {h_{N + 1}} = {h_M},$
用δ表示子区间的长度：
$\delta = \left\{ \begin{array}{l}{h_{i + 1}} - {h_i} = \left\lfloor {\frac{{{h_M} - {h_m}}}{N}} \right\rfloor ,\;\;\;i = 1, \cdots ,N - 1;\\{h_M} - {h_i},\;\;\;\;\;i = N.\end{array} \right.$
其中
定理?1????对于给定的常数hm和hM，如果存在正定对称矩阵
$\mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\ * &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\ *&* &{{\mathit{\boldsymbol{P}}_{33}}}\end{array}} \right].$
Qi，Zi，Ri，i=2, 3, 以及适当维数的自由矩阵Y使得如下线性矩阵不等式成立：
${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_i} = \left[ {\begin{array}{*{20}{c}}{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{\theta }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}}\\ * &{ - {\mathit{\boldsymbol{P}}_{11}}}&0\\ *&* &{ - \mathit{\boldsymbol{U}}}\end{array}} \right] < {\bf{0}},i = 1,2, \cdots ,N.$ (5)
则系统(1)是渐近稳定的.在式(5)中，
${\mathit{\boldsymbol{Y}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}{\mathit{\boldsymbol{Y}}_1^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_2^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_3^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_4^{\rm{T}}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}{\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\boldsymbol{\theta }} = \left[ {\begin{array}{*{20}{c}}\mathit{\boldsymbol{A}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right];$
$\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{\varphi }}_{11}} = - {\mathit{\boldsymbol{P}}_{11}} + {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + \mathit{\boldsymbol{P}}_{12}^{\rm{T}}\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3} + }\\{\frac{{1 - 2{h_i}}}{3}{\mathit{\boldsymbol{Z}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2} - 2\frac{\delta }{{\delta + 1}}{\mathit{\boldsymbol{R}}_3};}\end{array}$
${\mathit{\boldsymbol{\varphi }}_{12}} = {\mathit{\boldsymbol{A}}^{\rm{T}}}\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right) - {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{P}}_{23}} - \frac{{{h_i} + 1}}{3}{\mathit{\boldsymbol{Z}}_2};$
${\mathit{\boldsymbol{\varphi }}_{13}} = \mathit{\boldsymbol{P}}_{12}^{\rm{T}}{\mathit{\boldsymbol{A}}_d} + {\mathit{\boldsymbol{Y}}_1},{\mathit{\boldsymbol{\varphi }}_{14}} = - {\mathit{\boldsymbol{A}}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{Y}}_1};$
${\mathit{\boldsymbol{\varphi }}_{15}} = {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2};$
${\mathit{\boldsymbol{\varphi }}_{16}} = {\left( {\mathit{\boldsymbol{A}} - \mathit{\boldsymbol{I}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} + {\mathit{\boldsymbol{P}}_{23}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{\delta + 1}}{\mathit{\boldsymbol{R}}_3};$
$\begin{array}{l}{\mathit{\boldsymbol{\varphi }}_{22}} = {\mathit{\boldsymbol{P}}_{22}} - {\mathit{\boldsymbol{P}}_{23}} - \mathit{\boldsymbol{P}}_{23}^{\rm{T}} + {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Q}}_2} - \frac{{2{h_i} + 5}}{3}{\mathit{\boldsymbol{Z}}_2} - \\\;\;\;\;\;\;\;\;\frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} + \frac{{1 - 2\delta }}{3}{\mathit{\boldsymbol{Z}}_3};\end{array}$
${\mathit{\boldsymbol{\varphi }}_{23}} = {\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right)^{\rm{T}}}{\mathit{\boldsymbol{A}}_d} + {\mathit{\boldsymbol{Y}}_2};$
${\mathit{\boldsymbol{\varphi }}_{24}} = {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{P}}_{33}} - \frac{{\delta + 1}}{3}{\mathit{\boldsymbol{Z}}_3} - {\mathit{\boldsymbol{Y}}_2};$
${\mathit{\boldsymbol{\varphi }}_{25}} = - {\mathit{\boldsymbol{P}}_{22}} + \mathit{\boldsymbol{P}}_{23}^{\rm{T}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2};$
${\mathit{\boldsymbol{\varphi }}_{26}} = - {\mathit{\boldsymbol{P}}_{23}} + \mathit{\boldsymbol{P}}_{33}^{\rm{T}} + {\mathit{\boldsymbol{Z}}_3};$
${\mathit{\boldsymbol{\varphi }}_{33}} = {\mathit{\boldsymbol{Y}}_3} + \mathit{\boldsymbol{Y}}_3^{\rm{T}};$
${\mathit{\boldsymbol{\varphi }}_{34}} = - \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{Y}}_3} + \mathit{\boldsymbol{Y}}_4^{\rm{T}};$
${\mathit{\boldsymbol{\varphi }}_{35}} = \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{12}},{\mathit{\boldsymbol{\varphi }}_{36}} = \mathit{\boldsymbol{A}}_d^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}};$
${\mathit{\boldsymbol{\varphi }}_{44}} = {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Q}}_3} - \frac{{2\delta + 5}}{3}{\mathit{\boldsymbol{Z}}_3} - \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3} - {\mathit{\boldsymbol{Y}}_4} - \mathit{\boldsymbol{Y}}_4^{\rm{T}};$
${\mathit{\boldsymbol{\varphi }}_{45}} = - \mathit{\boldsymbol{P}}_{23}^{\rm{T}},{\mathit{\boldsymbol{\varphi }}_{46}} = - {\mathit{\boldsymbol{P}}_{33}} + {\mathit{\boldsymbol{Z}}_3} + \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3};$
${\mathit{\boldsymbol{\varphi }}_{55}} = - \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} - \frac{1}{{{h_s}}}{\mathit{\boldsymbol{R}}_2},{\mathit{\boldsymbol{\varphi }}_{56}} = 0;$
${\mathit{\boldsymbol{\varphi }}_{66}} = - \frac{2}{{\delta - 1}}{\mathit{\boldsymbol{Z}}_3} - \frac{1}{{{h_d}}}{\mathit{\boldsymbol{R}}_3};$
$\begin{array}{l}\mathit{\boldsymbol{U = }}\frac{{{h_i} + 1}}{6}h_i^2{\mathit{\boldsymbol{Z}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3} + \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2}{\mathit{\boldsymbol{R}}_2} + \\\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{2}{\mathit{\boldsymbol{R}}_3};\end{array}$
${h_s} = \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2},{h_d} = \frac{{\delta \left( {\delta + 1} \right)}}{2}.$
证明????首先证明定理1在d(k)∈[h2, h3]子区间段时成立，进而将结论推广到一般的时滞区间中，即d(k)=[hi, hi+1](i=1, 2, …, N)时，定理1成立.
构造如下L-K泛函：
${\mathit{\boldsymbol{V}}_2}\left( k \right) = {\mathit{\boldsymbol{V}}_{21}}\left( k \right) + {\mathit{\boldsymbol{V}}_{22}}\left( k \right) + {\mathit{\boldsymbol{V}}_{23}}\left( k \right),$
${\mathit{\boldsymbol{V}}_{21}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\ * &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\ *&* &{{\mathit{\boldsymbol{P}}_{33}}}\end{array}} \right]{\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right),$
${\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = {\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)}&{\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} }&{\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} }\end{array}} \right]^{\rm{T}}},$
$\begin{array}{l}{\mathit{\boldsymbol{V}}_{22}}\left( k \right) = \sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){Q_2}\mathit{\boldsymbol{x}}\left( i \right)} + \sum\limits_{i = k - {h_3}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( i \right)} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_2}\left( {{h_2} + 1} \right)}}{6}\sum\limits_{\theta = - {h_2}}^{ - 1} {\sum\limits_{i = k + \theta }^{k + 1} {\mathit{\Delta } {x^{\rm{T}}}\left( i \right){Z_2}\mathit{\Delta } x\left( i \right)} } + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{\theta = - {h_3}}^{ - {h_2} - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {x^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } ,\end{array}$
$\begin{array}{l}{\mathit{\boldsymbol{V}}_{23}}\left( k \right) = \sum\limits_{m = - {h_2}}^{ - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{m = - {h_3}}^{ - {h_2} - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } .\end{array}$
对V2(k)做前向差分，则有：
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{V}}_{21}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( {k + 1} \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\varepsilon }}_2}\left( {k + 1} \right) - \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;2\mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) + \mathit{\Delta } \mathit{\boldsymbol{\varepsilon }}_2^{\rm{T}}\left( k \right)\mathit{\boldsymbol{P}}\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right),\end{array}$
其中:
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{\varepsilon }}_2}\left( k \right) = \\{\left[ {\begin{array}{*{20}{c}}{\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)}&{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right)}&{{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right)}\end{array}} \right]^{\rm{T}}},\end{array}$
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) = {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left( {{\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3}} \right)\mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left[ {\frac{{{h_2} + 1}}{6}h_2^2{\mathit{\boldsymbol{Z}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3}} \right]\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_2}\left( {{h_2} + 1} \right)}}{6}\sum\limits_{i = k - h_2}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) - } \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} .\end{array}$
应用引理2，得到
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) \le {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left( {{\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3}} \right)\mathit{\boldsymbol{x}}\left( k \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - } \right.\\\;\;\;\left. {{h_2}} \right){\mathit{\boldsymbol{Q}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Q}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right)\left[ \begin{array}{l}\frac{{{h_2} + 1}}{6}h_2^2{\mathit{\boldsymbol{Z}}_2} + \\\;\;\;\;\;\;\frac{{\delta + 1}}{6}{\delta ^2}{\mathit{\boldsymbol{Z}}_3}\end{array} \right]\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) + \\\;\;\;\frac{{1 - 2{h_2}}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( k \right) - \\\;\;\;\frac{{2\left( {{h_2} + 1} \right)}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){Z_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) + 2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){Z_2}\sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\\;\;\;\frac{{2{h_2} + 5}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - \\\;\;\;\frac{2}{{{h_2} - 1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) + \\\;\;\;\left( {2 + \frac{4}{{{h_2} - 1}}} \right){\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_2}\sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\\;\;\;\frac{2}{{{h_2} - 1}}\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}} \sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} + \\\;\;\;\frac{{1 - 2\delta }}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_2}} \right) - \\\;\;\;\frac{{2\left( {\delta + 1} \right)}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\\;\;\;2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_2}} \right){\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\\;\;\;\frac{{2\delta + 5}}{3}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right) + \\\;\;\;\left( {2 + \frac{4}{{\delta - 1}}} \right){\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\\;\;\;\frac{2}{{\delta - 1}}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right)} {\mathit{\boldsymbol{Z}}_3}\sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} - \\\;\;\;\frac{2}{{\delta - 1}}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( {k - {h_3}} \right){\mathit{\boldsymbol{Z}}_3}\mathit{\boldsymbol{x}}\left( {k - {h_3}} \right),\\\;\;\;\mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) = {h_s}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\\;\;\;\sum\limits_{j = - {h_2}}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } + \\\;\;\;{h_d}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \sum\limits_{j = - {h_3}i}^{ - {h_2} - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } .\end{array}$
应用引理3，可得到：
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) \le {h_s}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) + {h_d}\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( k \right) - \\\;\;\;\;\;\;\;\;\;\frac{1}{{{h_s}}}\left[ {h_2^2{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{x}}\left( k \right) - 2{h_2}\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\boldsymbol{x}}\left( k \right)} + } \right.\\\;\;\;\;\;\;\;\;\;\left. {\sum\limits_{i = k - {h_2}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}} \sum\limits_{i = k - {h_2}}^{k - 1} {\mathit{\boldsymbol{x}}\left( i \right)} } \right] - \frac{1}{{{h_d}}}\left[ {{\delta ^2}{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( k \right){\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{x}}\left( k \right) - } \right.\\\;\;\;\;\;\;\;\;\;\left. {2\delta \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\boldsymbol{x}}\left( k \right)} + \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}} \sum\limits_{i = k - {h_3}}^{k - {h_2} - 1} {\mathit{\boldsymbol{x}}\left( i \right)} } \right],\end{array}$
$\begin{array}{l}\mathit{\Delta } {\mathit{\boldsymbol{V}}_2}\left( k \right) = \mathit{\Delta } {\mathit{\boldsymbol{V}}_{21}}\left( k \right) + \mathit{\Delta } {\mathit{\boldsymbol{V}}_{22}}\left( k \right) + \mathit{\Delta } {\mathit{\boldsymbol{V}}_{23}}\left( k \right) + \\\;\;\;2{\eta ^{\rm{T}}}\left( k \right)\mathit{\boldsymbol{Y}}\left[ {\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right) - \left( {k - {h_3}} \right) - } \right.\\\;\;\;\left. {\sum\limits_{i = k - {h_3}}^{k - d\left( k \right) - 1} {\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } \right] \le {\eta ^{\rm{T}}}\left( k \right)\left( {\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + {\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}\mathit{\pmb{\Upsilon}} + } \right.\\\;\;\;\left. {{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}} \right)\eta \left( k \right).\end{array}$
基于Schur补引理，即可证得当i=2时定理1成立.
不失一般性，当d(k)∈[hi, hi+1], i=1, 2, …, N时，构造如下的L-K泛函：
$\mathit{\Delta } {\mathit{\boldsymbol{V}}_i}\left( k \right) = {\mathit{\boldsymbol{V}}_{i1}}\left( k \right) + {\mathit{\boldsymbol{V}}_{i2}}\left( k \right) + {\mathit{\boldsymbol{V}}_{i3}}\left( k \right),$
${\mathit{\boldsymbol{V}}_{i1}}\left( k \right) = \mathit{\boldsymbol{\varepsilon }}_i^{\rm{T}}\left( k \right)\left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\boldsymbol{P}}_{12}}}&{{\mathit{\boldsymbol{P}}_{13}}}\\ * &{{\mathit{\boldsymbol{P}}_{22}}}&{{\mathit{\boldsymbol{P}}_{23}}}\\ *&* &{{\mathit{\boldsymbol{P}}_{33}}}\end{array}} \right]{\mathit{\boldsymbol{\varepsilon }}_i}\left( k \right),$
$\begin{array}{l}{\mathit{\boldsymbol{V}}_{i2}}\left( k \right) = \sum\limits_{i = k - {h_i}}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_2}x\left( i \right)} + \sum\limits_{i = k - {h_i} + 1}^{k - 1} {{\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Q}}_3}x\left( i \right)} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{h_i}\left( {{h_i} + 1} \right)}}{6}\sum\limits_{\theta = - {h_i}}^{ - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) + } } \\\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{6}\sum\limits_{\theta = - {h_i} + 1}^{ - {h_i} - 1} {\sum\limits_{i = k + \theta }^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{Z}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } ,\end{array}$
$\begin{array}{l}{\mathit{\boldsymbol{V}}_{i3}}\left( k \right) = \sum\limits_{m = - {h_i}}^{ - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_2}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right) + } } } \\\;\;\;\;\;\;\;\;\;\;\;\;\;\sum\limits_{m = - {h_{i + 1}}}^{ - {h_i} - 1} {\sum\limits_{j = m}^{ - 1} {\sum\limits_{i = k + j}^{k - 1} {\mathit{\Delta } {\mathit{\boldsymbol{x}}^{\rm{T}}}\left( i \right){\mathit{\boldsymbol{R}}_3}\mathit{\Delta } \mathit{\boldsymbol{x}}\left( i \right)} } } .\end{array}$
采用同样的方法可证明d(k)∈[hi, hi+1], i=1, 2, …，N时，系统(1)渐近稳定.
说明?1????定理1针对每一段时滞分割区间设计了新的L-K泛函，其中增广项Vi1(k), i=1, 2, …, N和三重求和项Vi3(k), i=1, 2, …, N, 充分利用了系统的时滞信息，为降低结论的保守性起到积极作用.在泛函差分处理过程中不涉及模型变换，而是利用文献[14]所提出的基于Abel引理的有限和不等式，直接给出Lyapunov泛函差分更紧的上界，因此可减少结论的保守性和计算的复杂性.
根据定理1可以进一步推导出使离散时滞系统(4)保持渐近稳定的镇定器设计方法.
定理?2????考虑离散时滞系统(4)，给定时滞上下界hm、hM，如果存在正定对称矩阵
$\mathit{\boldsymbol{\bar P}} = \left[ {\begin{array}{*{20}{c}}\mathit{\boldsymbol{X}}&{{{\mathit{\boldsymbol{\bar P}}}_{12}}}&{{{\mathit{\boldsymbol{\bar P}}}_{13}}}\\ * &{{{\mathit{\boldsymbol{\bar P}}}_{22}}}&{{{\mathit{\boldsymbol{\bar P}}}_{23}}}\\ *&* &{{{\mathit{\boldsymbol{\bar P}}}_{33}}}\end{array}} \right].$
Qi，Zi，Ri，i=2, 3，X，J以及
$\begin{array}{l}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varXi} }}}_i} = \left[ {\begin{array}{*{20}{c}}{{{\left[ {{{\mathit{\boldsymbol{\bar \varphi }}}_{ij}}} \right]}_{6 \times 6}}}&{\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}}&{\mathit{\boldsymbol{X}}{\mathit{\pmb{\Upsilon}}^{\rm{T}}}}&\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}&\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}\\ * &{ - \mathit{\boldsymbol{X}}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\\ *&* &{\mathit{\boldsymbol{\bar U}} - 2\mathit{\boldsymbol{X}}}&{\bf{0}}&{\bf{0}}\\ *&*&* &{ - \mathit{\boldsymbol{J}}}&{\bf{0}}\\ *&*&*&* &{\mathit{\boldsymbol{J}} - 2\mathit{\boldsymbol{X}}}\end{array}} \right] < 0,\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 1,2, \cdots ,N.\end{array}$ (6)
则在如下状态反馈控制器的作用下系统(4)渐近稳定:
$\mathit{\boldsymbol{u}}\left( k \right) = \mathit{\boldsymbol{Kx}}\left( k \right) = \mathit{\boldsymbol{\hat K}}{\mathit{\boldsymbol{X}}^{ - 1}}\mathit{\boldsymbol{x}}\left( k \right),$
其中:
${\mathit{\boldsymbol{Y}}^{\rm{T}}} = \left[ {\begin{array}{*{20}{c}}{\mathit{\boldsymbol{Y}}_1^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_2^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_3^{\rm{T}}}&{\mathit{\boldsymbol{Y}}_4^{\rm{T}}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \left[ {\begin{array}{*{20}{c}}{\mathit{\boldsymbol{A}} + {\mathit{\boldsymbol{B}}_u}\mathit{\boldsymbol{K}}}&{\bf{0}}&{{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}{A + {B_u}K}&0&{{A_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\bar \Gamma } = {\left[ {\begin{array}{*{20}{c}}{{{\bar P}_{12}}}&{{{\bar P}_{13}} -{{\bar P}_{12}}}&0&{ -{{\bar P}_{13}}}&{{{\bar P}_{12}}}&{{{\bar P}_{13}}}&{\bf{0}}&{\bf{0}}\end{array}} \right]^{\rm{T}}},$
$\mathit{\Lambda = }{\left[ {\begin{array}{*{20}{c}}{{{\left( {AX + {B_u}\hat K} \right)}^{\rm{T}}}}&{\bf{0}}&{\mathit{\boldsymbol{X}}{\mathit{\boldsymbol{A}}_d}}&{\bf{0}}&{\bf{0}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right]^{\rm{T}}},$
$\begin{array}{l}{{\mathit{\boldsymbol{\bar \varphi }}}_{11}} = - \mathit{\boldsymbol{X}} + {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar Q}}}_2} + {{\mathit{\boldsymbol{\bar Q}}}_3} + \frac{{1 - 2{h_i}}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{{\mathit{\boldsymbol{\bar R}}}_2} - \\\;\;\;\;\;\;\;\;2\frac{\delta }{{\delta + 1}}{{\mathit{\boldsymbol{\bar R}}}_3},\end{array}$
${{\mathit{\boldsymbol{\bar \varphi }}}_{12}} = - {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar P}}}_{23}} - \frac{{{h_i} + 1}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{13}} = {{\mathit{\boldsymbol{\bar Y}}}_1},$
${{\mathit{\boldsymbol{\bar \varphi }}}_{14}} = - {{\mathit{\boldsymbol{\bar P}}}_{23}} - {{\mathit{\boldsymbol{\bar Y}}}_1},{{\mathit{\boldsymbol{\bar \varphi }}}_{15}} = - {{\mathit{\boldsymbol{\bar P}}}_{12}} + {{\mathit{\boldsymbol{\bar P}}}_{22}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{{h_i} + 1}}{{\mathit{\boldsymbol{\bar R}}}_2},$
${{\mathit{\boldsymbol{\bar \varphi }}}_{16}} = - {{\mathit{\boldsymbol{\bar P}}}_{13}} + {{\mathit{\boldsymbol{\bar P}}}_{23}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{\delta + 1}}{{\mathit{\boldsymbol{\bar R}}}_3},$
$\begin{array}{l}{{\mathit{\boldsymbol{\bar \varphi }}}_{22}} = {{\mathit{\boldsymbol{\bar P}}}_{22}} - {{\mathit{\boldsymbol{\bar P}}}_{23}} - \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}} + {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Q}}}_2} - \frac{{2{h_i} + 5}}{3}{{\mathit{\boldsymbol{\bar Z}}}_2} - \\\;\;\;\;\;\;\;\;\;\frac{2}{{{h_i} - 1}}{{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{{1 - 2\delta }}{3}{{\mathit{\boldsymbol{\bar Z}}}_3},\end{array}$
${{\mathit{\boldsymbol{\bar \varphi }}}_{23}} = {{\mathit{\boldsymbol{\bar Y}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{24}} = {{\mathit{\boldsymbol{\bar P}}}_{23}} - {{\mathit{\boldsymbol{\bar P}}}_{33}} + \frac{{\delta + 1}}{3}{{\mathit{\boldsymbol{\bar Z}}}_3} - {{\mathit{\boldsymbol{\bar Y}}}_2},$
$\begin{array}{l}{{\mathit{\boldsymbol{\bar \varphi }}}_{25}} = - {{\mathit{\boldsymbol{\bar P}}}_{22}} + \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}} + {{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{2}{{{h_i} - 1}}{{\mathit{\boldsymbol{\bar Z}}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{26}} = - {{\mathit{\boldsymbol{\bar \varphi }}}_{23}} + \\\;\;\;\;\;\;\;\;\mathit{\boldsymbol{\bar P}}_{33}^{\rm{T}} + {{\mathit{\boldsymbol{\bar Z}}}_3},\end{array}$
${{\mathit{\boldsymbol{\bar \varphi }}}_{33}} = {{\mathit{\boldsymbol{\bar Y}}}_3} + \mathit{\boldsymbol{\bar Y}}_3^{\rm{T}},{{\mathit{\boldsymbol{\bar \varphi }}}_{34}} = - {{\mathit{\boldsymbol{\bar Y}}}_3} + {{\mathit{\boldsymbol{\bar Y}}}_4},{{\mathit{\boldsymbol{\bar \varphi }}}_{35}} = {{\mathit{\boldsymbol{\bar \varphi }}}_{36}} = 0,$
${{\mathit{\boldsymbol{\bar \varphi }}}_{44}} = {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Q}}}_3} - \frac{{2\delta + 5}}{3}{{\mathit{\boldsymbol{\bar Z}}}_3} - \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3} - {{\mathit{\boldsymbol{\bar Y}}}_4} - \mathit{\boldsymbol{\bar Y}}_4^{\rm{T}},$
${{\mathit{\boldsymbol{\bar \varphi }}}_{45}} = - \mathit{\boldsymbol{\bar P}}_{23}^{\rm{T}},{{\mathit{\boldsymbol{\bar \varphi }}}_{46}} = - {{\mathit{\boldsymbol{\bar P}}}_{33}} + {{\mathit{\boldsymbol{\bar Z}}}_3} + \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3},$
${{\mathit{\boldsymbol{\bar \varphi }}}_{55}} = - \frac{2}{{{h_i} - 1}}{\mathit{\boldsymbol{Z}}_2} - \frac{1}{{{h_s}}}{\mathit{\boldsymbol{R}}_2},{{\mathit{\boldsymbol{\bar \varphi }}}_{56}} = 0,$
${{\mathit{\boldsymbol{\bar \varphi }}}_{66}} = - \frac{2}{{\delta - 1}}{{\mathit{\boldsymbol{\bar Z}}}_3} - \frac{1}{{{h_d}}}{{\mathit{\boldsymbol{\bar R}}}_3},$
$\begin{array}{l}\mathit{\boldsymbol{\bar U = }}\frac{{{h_i} + 1}}{6}h_i^2{{\mathit{\boldsymbol{\bar Z}}}_2} + \frac{{\delta + 1}}{6}{\delta ^2}{{\mathit{\boldsymbol{\bar Z}}}_3} + \frac{{{h_i}\left( {{h_i} + 1} \right)}}{2}{{\mathit{\boldsymbol{\bar R}}}_2} + \\\;\;\;\;\;\;\;\frac{{\delta \left( {\delta + 1} \right)}}{2}{{\mathit{\boldsymbol{\bar R}}}_3}.\end{array}$
证明????用Ak=A+BuK替换定理1条件中的A，可得
${\mathit{\boldsymbol{ \boldsymbol{\varXi} }}_i} = \left[ {\begin{array}{*{20}{c}}{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}\mathit{\boldsymbol{U}}}\\ * &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\ *&* &{ - \mathit{\boldsymbol{U}}}\end{array}} \right] < {\bf{0}}\;\;i = 1,2, \cdots ,N.$ (7)
其中
$\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{\varphi }}_{11}} = - {\mathit{\boldsymbol{P}}_{11}} + \mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_{12}} + \mathit{\boldsymbol{P}}_{12}^{\rm{T}}{\mathit{\boldsymbol{A}}_k} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Q}}_2} + {\mathit{\boldsymbol{Q}}_3} + }\\{\frac{{1 - 2{h_i}}}{3}{\mathit{\boldsymbol{Z}}_2} - \frac{{2{h_i}}}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2} - 2\frac{\delta }{{\delta + 1}}{\mathit{\boldsymbol{R}}_3},}\end{array}$
${\mathit{\boldsymbol{\varphi }}_{12}} = \mathit{\boldsymbol{A}}_k^{\rm{T}}\left( {{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{12}}} \right) - {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{P}}_{23}} - \frac{{{h_i} + 1}}{3}{\mathit{\boldsymbol{Z}}_2},$
${\mathit{\boldsymbol{\varphi }}_{14}} = - \mathit{\boldsymbol{A}}_k^{\rm{T}}{\mathit{\boldsymbol{P}}_{13}} - {\mathit{\boldsymbol{P}}_{23}} - {\mathit{\boldsymbol{Y}}_1},$
${\mathit{\boldsymbol{\varphi }}_{16}} = {\left( {{\mathit{\boldsymbol{A}}_k} - I} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{13}} + {\mathit{\boldsymbol{P}}_{23}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{\delta + 1}}{\mathit{\boldsymbol{R}}_3},$
${\mathit{\boldsymbol{\varphi }}_{15}} = {\left( {{\mathit{\boldsymbol{A}}_k} - I} \right)^{\rm{T}}}{\mathit{\boldsymbol{P}}_{12}} + {\mathit{\boldsymbol{P}}_{22}} + {\mathit{\boldsymbol{Z}}_2} + \frac{2}{{{h_i} + 1}}{\mathit{\boldsymbol{R}}_2},$
$\mathit{\pmb{\Upsilon}} = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{A}}_k} - \mathit{\boldsymbol{I}}}&{\bf{0}}&\mathit{\boldsymbol{B}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right],$
$\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} = \left[ {\begin{array}{*{20}{c}}{{\mathit{\boldsymbol{A}}_k}}&{\bf{0}}&\mathit{\boldsymbol{B}}&{\bf{0}}&{\bf{0}}&{\bf{0}}\end{array}} \right].$
$\left[ {\begin{array}{*{20}{c}}{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}\\ * &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\ *&* &{ - {\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{U}}^{ - 1}}{\mathit{\boldsymbol{P}}_{11}}}\end{array}} \right] < {\bf{0}};\;\;i = 1,2, \cdots ,N.$
由于
$ - {\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{U}}^{ - 1}}{\mathit{\boldsymbol{P}}_{11}} \le \mathit{\boldsymbol{U}} - 2{\mathit{\boldsymbol{P}}_{11}}.$
则有下面不等式成立：
$\left[ {\begin{array}{*{20}{c}}{{{\left[ {{\mathit{\boldsymbol{\varphi }}_{ij}}} \right]}_{6 \times 6}}}&{{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}&{{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}{\mathit{\boldsymbol{P}}_{11}}}\\ * &{ - {\mathit{\boldsymbol{P}}_{11}}}&{\bf{0}}\\ *&* &{\mathit{\boldsymbol{U}} - 2{\mathit{\boldsymbol{P}}_{11}}}\end{array}} \right] < {\bf{0}};\;\;i = 1,2, \cdots ,N.$ (8)
将式(8)左右同乘
${\rm{diag}}\left\{ {\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1},\mathit{\boldsymbol{P}}_{11}^{ - 1}} \right\},$
并令X=P11-1，
$\left[ {\begin{array}{*{20}{c}}{{{\left[ {{{\mathit{\boldsymbol{\bar \varphi }}}_{ij}}} \right]}_{6 \times 6}}}&{\mathit{\boldsymbol{P}}_{11}^{ - 1}{\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}^{\rm{T}}}}&{\mathit{\boldsymbol{P}}_{11}^{ - 1}{\mathit{\pmb{\Upsilon}} ^{\rm{T}}}}\\ * &{ - \mathit{\boldsymbol{P}}_{11}^{ - 1}}&{\bf{0}}\\ *&* &{\mathit{\boldsymbol{\bar U}} - 2\mathit{\boldsymbol{P}}_{11}^{ - 1}}\end{array}} \right] + \mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} < 0.$ (9)
其中i=1, 2, …, N，因为
$\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} \le \mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}{\mathit{\boldsymbol{J}}^{ - 1}}{{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}} + \mathit{\boldsymbol{ \boldsymbol{\varLambda} }}{\mathit{\boldsymbol{P}}_{11}}\mathit{\boldsymbol{J}}{\mathit{\boldsymbol{P}}_{11}}{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{T}}}.$
应用矩阵的Schur补性质可知式(9)等价于式(6)，因此定理2得证.
3 仿真算例例?1????考虑时变时滞离散系统：
$\begin{array}{l}\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}}{0.8}&0\\{0.05}&{0.9}\end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\begin{array}{*{20}{c}}{ - 0.1}&0\\{ - 0.2}&{ - 0.1}\end{array}} \right]\mathit{\boldsymbol{x}}\left( {k - d\left( k \right)} \right).\end{array}$
给定时滞下限hm，利用定理1得到的时滞上限hM列于表 1中.
表 1
表 1 给定hm使系统稳定的hM Table 1 hM guaranteeing the stability of the system for given hm 方法 hm 6 10 15 20 25 文献[17] hM 14 15 18 22 26
文献[18] hM 14 17 20 24 29
定理1(N=2) hM 16 19 23 26 31
定理1(N=3) hM 19 22 24 27 32
表 1 给定hm使系统稳定的hM Table 1 hM guaranteeing the stability of the system for given hm
例?2????考虑如下时滞系统
$\begin{array}{*{20}{c}}{\mathit{\boldsymbol{x}}\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}}{0.5}&{0.3}\\{0.2}&1\end{array}} \right]\mathit{\boldsymbol{x}}\left( k \right) + \left[ {\begin{array}{*{20}{c}}{0.1}&{0.4}\\{0.2}&{0.1}\end{array}} \right]\mathit{\boldsymbol{x}}\left( {k - } \right.}\\{\left. {d\left( k \right)} \right) + \left[ {\begin{array}{*{20}{c}}1\\1\end{array}} \right]\mathit{\boldsymbol{u}}\left( k \right).}\end{array}$
当初始值为x(0)=[-2??2]T，
Figure 1
图 1 开环响应曲线 Figure 1 Response of the open-loop systems 对于给定的时滞下界hm，运用定理2，选取N=2可得到保证系统渐近稳定的时滞上界hM以及控制器K，分别列于表 2中.
表 2
表 2 给定时滞下限时滞上界及控制器增益 Table 2 Delay upper bound and controller gain for given delay lower bound hm hM 控制器增益K 2 12 [-0.331 3??-0.722 0]
5 13 [-0.345 6??-0.744 2]
8 15 [-0.381 1??-0.769 3]
11 18 [-0.420 8??-0.819 7]
表 2 给定时滞下限时滞上界及控制器增益 Table 2 Delay upper bound and controller gain for given delay lower bound
假设系统初始值为x(0)=[-2??2]T，状态时滞为
Figure 2
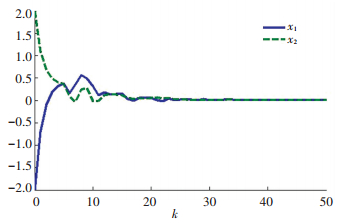图 2 闭环响应曲线 Figure 2 Response of the closed-loop systems 4 结论基于一种新的时滞分割方法，研究了一类区间时变时滞离散系统的稳定性分析和状态反馈控制器设计问题，得到新的低保守性结果.具体而言，在构造L-K泛函时，使用了增广型泛函和时滞分割相结合的方法，在泛函的差分处理过程中借助于基于Abel引理的有限和不等式技术保证了结论具有较小的保守性.在数值仿真算例中，通过与以往结果进行比较，验证了所得的结果正确和有效.
参考文献
[1]张冬梅, 俞立. 线性时滞系统稳定性分析综述[J].控制与决策, 2008(8): 841-849.
ZHANG Dongmei, YU Li. Survey on the stability analysis of linear time-delay systems[J].Control and Decision, 2008(8): 841-849.
[2] LEE S Y, LEE W I, PARK P G. New stability criteria for linear systems with interval time-varying delays via an extended state vector[C]. // Proceedings of the 10th Asia Control Conference. Beijing: IEEE, 2015: 1-6.
[3]JIANG X, HAN Q L. New stability criteria for linear systems with interval time-varying delay[J].Automatica, 2008, 44(10): 2680-2685.DOI: 10.1016/j.automatica.2008.02.020
[4]HE Y, WANG Q G, LIN C, et al. Delay-range-dependent stability for systems with time-varying delay[J].Automatica, 2007, 43(2): 371-376.DOI: 10.1016/j.automatica.2006.08.015
[5]PENG C, TIAN Y C. Delay-dependent robust stability criteria for uncertain systems with interval time-varying delay[J].Journal of Computational & Applied Mathematics, 2008, 214(2): 480-494.
[6]QIU Xiang, TENG You. Network-based guaranteed cost control of discrete time-delay systems[J].Journal of Zhejiang University of Technology, 2014, 42(4): 400-404.
[7]HE Y, WU M, SHE J H, et al. Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays[J].Systems & Control Letters, 2004, 51(1): 57-65.
[8]吴敏, 何勇. 时滞系统鲁棒控制--自由权矩阵方法[M]. 北京: 科学出版社, 2008.
WU Min, HE Yong. Robust control for time delay systems-Free-weighting matrix method[M]. Beijing: Science Press, 2008.
[9]FRIDMAN E, SHAKED U. Stability and guaranteed cost control of uncertain discrete delay Systems[J].International Journal of Control, 2005, 78(4): 235-246.DOI: 10.1080/00207170500041472
[10]XU S, CHEN T. Robust H∞ control for uncertain discrete-time systems with time-varying delays via exponential output feedback Controllers[J].Systems & Control Letters, 2004, 51(3-4): 171-183.
[11]HE Y, WU M, LIU G P, et al. Output feedback stabilization for a discrete-time system with a time-varying delay[J].IEEE Transactions on Automatic Control, 2008, 53(10): 2372-2377.DOI: 10.1109/TAC.2008.2007522
[12]HE Y, WANG Q G, LIN C, et al. Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems[J].International Journal of Robust & Nonlinear Control, 2005, 15(18): 923-933.
[13]WANG C, SHEN Y. Delay partitioning approach to robust stability analysis for uncertain stochastic systems with interval time-varying delay[J].IET Control Theory & Applications, 2012, 6(7): 875-883.
[14]ZHANG X M, HAN Q L. Abel lemma-based finite-sum inequality and its application to stability analysis for linear discrete time-delay systems[J].Automatica, 2015, 57: 199-202.DOI: 10.1016/j.automatica.2015.04.019
[15]GHAOUI L El, FERON E, BALAKRISHNAN V. Linear matrix inequalities in system and control theory[M]. Philadelphia: Society for Industrial and Applied mathematics, 1994: 2473-2474.
[16] GU K. An integral inequality in the stability problem of time-delay systems[C]//Proceedings of IEEE Conference on Decision & Control. Sydney, NSW: Institute of Electrical and Electronics Engineers Inc., 2000: 2805-2810.
[17]GAO H, CHEN T. New results on stability of discrete-time systems with time-varying state delay[J].IEEE Transactions on Automatic Control, 2007, 52(2): 328-334.DOI: 10.1109/TAC.2006.890320
[18]ZHANG B, XU S, ZOU Y. Improved stability criterion and its application in delayed controller design for discrete-time systems[J].Automatica, 2008, 44(11): 2963-2967.DOI: 10.1016/j.automatica.2008.04.017
