Le Wang,Muchun Yu
(China Academy of Launch Vehicle Technology, Beijing 100076, China)
Abstract:
A three-dimensional state space method has been developed for the calculation of dynamic response of plates with two free edges and two simply supported edges. A complex damping model was introduced, then the exact solutions which satisfy all the governing equations and boundary conditions were obtained. In order to overcome the difficulty of satisfying all the stress conditions at free edges, the displacement functions of free edges were assumed. The boundary conditions were strictly satisfied when the convergence rate was good. The computing time was evidently less than that of finite element method. The comparison of the solution with those of finite element method show that there is an excellent agreement for displacements. When the imaginary parts of normal stress deviated, the finite element results showed existence of shear stresses at top and bottom surfaces, and the boundary conditions of FEM model were not strictly satisfied.
Key words: three-dimensional exact solution state space method free edge response
DOI:10.11916/j.issn.1005-9113.18044
Clc Number:O326
Fund:
Le Wang, Muchun Yu. Three-Dimensional Exact Solution for Dynamic Damped Response of Plates with Two Free Edges[J]. Journal of Harbin Institute of Technology (New Series), 2019, 26(3): 79-90. DOI: 10.11916/j.issn.1005-9113.18044.

Corresponding author Le Wang, E-mail: aabeau@163.com Article history Received: 2018-04-22
Contents Abstract Full text Figures/Tables PDF
Three-Dimensional Exact Solution for Dynamic Damped Response of Plates with Two Free Edges
Le Wang

 , Muchun Yu
, Muchun Yu China Academy of Launch Vehicle Technology, Beijing 100076, China
Received: 2018-04-22
Corresponding author: Le Wang, E-mail: aabeau@163.com
Abstract: A three-dimensional state space method has been developed for the calculation of dynamic response of plates with two free edges and two simply supported edges. A complex damping model was introduced, then the exact solutions which satisfy all the governing equations and boundary conditions were obtained. In order to overcome the difficulty of satisfying all the stress conditions at free edges, the displacement functions of free edges were assumed. The boundary conditions were strictly satisfied when the convergence rate was good. The computing time was evidently less than that of finite element method. The comparison of the solution with those of finite element method show that there is an excellent agreement for displacements. When the imaginary parts of normal stress deviated, the finite element results showed existence of shear stresses at top and bottom surfaces, and the boundary conditions of FEM model were not strictly satisfied.
Keywords: three-dimensional exact solution state space method free edge response
1 Introduction Plates and shell panels are widely used in modern industry especially in aerospace engineering. In practice, it is very important to exactly calculate the response of plates when they are subjected to dynamic excitations.
The exact solutions are of particular interest[1-2], and three-dimensional analyses of laminated plates are regarded as benchmarks for two-dimensional or finite element methods. Giving up any initial assumptions of stress or displacement models, all the fundamental equations can be strictly satisfied, and the exact solutions can be obtained.
Owing to the complexity of the problem, lots of three-dimensional exact solutions are for plates with simply supported edges[3-12]. The boundary conditions of the fully simply supported edges can be easily satisfied by assuming the solution in the form of Fourier series at once. For a plate with infinite width, the cylindrical bending problem arises. This problem with the boundary conditions of two edges simply supported has been extensively investigated[6, 13-17]. Sheng et al.[18]presented an exact solution for thick laminated piezoelectric plates with two edges clamped and two edges simply supported by assuming appropriate boundary functions. By using the state space method, Zhang et al.[19] investigated the interlaminar stresses and displacements near the free edges and ply cracks. For plates with free edges, the difficulty of strictly satisfying the stress boundary conditions at a free edge is to make a normal stress and two shear stresses to be zero simultaneously.
All these works deal with the problem of static or free vibration of plates, but ignore the effects of damping. Kapuria and Achary[20] and Kapuria and Nair[21] presented exact three-dimensional solution for dynamics of simply supported rectangular cross-ply hybrid plates with damping. Loredo[22] studied the exact solution for damped harmonic response of simply supported general laminates. In his work, laminates made of different materials were studied. The results agreed perfectly with those of three-dimensional FEM analysis. It was found that the particular boundary conditions used in the 3D FEM model were suitable to the study, while the results were not so good when other set of boundary conditions were used.
In this paper, a three-dimensional state space method has been developed for the calculation of dynamic response of plates with two free edges and two simply supported edges. A complex damping model was introduced, then the exact solutions which satisfy all the governing equations and boundary conditions were obtained. The comparison of the solution with those of finite element method shows that there is an excellent agreement for displacements. When the imaginary parts of normal stress deviated, the finite element results showed existence of shear stresses τyz and τzx at top and bottom surfaces. The present theory offers better solution than the finite element analysis.
2 Basic Equations and Solutions 2.1 The Problem and Basic Equations We consider a plate with length a, width b and total thickness h, as shown in Fig. 1. The z direction is determined by the right-handed coordinate system. The two edges at x=0, a is simply supported and the two edges at y=0, b are free. The uniformly distributed dynamical pressure qeiωt is applied to the top surface of the plate.
Fig.1
 Fig.1 Coordinate system and edges of a plate
Fig.1 Coordinate system and edges of a plate The displacements along x, y, and z directions are written as U, V, W, the normal stresses σx, σy, σz, the shear stresses τyx, τyz, τzx, and the lateral boundary conditions are
$\left\{ \begin{array}{l}W = V = {\sigma _x} = 0\;{\rm{at}}\;x = 0,a\\{\sigma _y} = {\tau _{yz}} = {\tau _{yx}} = 0\;{\rm{at}}\;y = 0,b\end{array} \right.$ (1)
The constitutive equations are
$\left\{ \begin{array}{l}{\sigma _x}\\{\sigma _y}\\{\sigma _z}\\{\tau _{yz}}\\{\tau _{xz}}\\{\tau _{xy}}\end{array} \right\} = \left[ {\begin{array}{*{20}{c}}{{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0&0\\{{C_{12}}}&{{C_{22}}}&{{C_{23}}}&0&0&0\\{{C_{13}}}&{{C_{23}}}&{{C_{33}}}&0&0&0\\0&0&0&{{C_{44}}}&0&0\\0&0&0&0&{{C_{55}}}&0\\0&0&0&0&0&{{C_{66}}}\end{array}} \right]\left\{ \begin{array}{l}{\xi _x}\\{\xi _y}\\{\xi _z}\\{\gamma _{yz}}\\{\gamma _{xz}}\\{\gamma _{xy}}\end{array} \right\}$ (2)
where Cij(i, j=1, 2, …6) are elastic constants for the plate. The following equations can be obtained by eliminating stress σx, σy and τxy from equilibrium, geometric and constitutive equations:
$\frac{\partial }{{\partial Z}}\left\{ \begin{array}{l}U\\V\\Z\\X\\Y\\W\end{array} \right\} = \mathit{\boldsymbol{D}}\left\{ \begin{array}{l}U\\V\\Z\\X\\Y\\W\end{array} \right\}$ (3)
$\mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}}0&0&0&{{C_8}}&0&{ - \alpha }\\0&0&0&0&{{C_9}}&{ - \beta }\\0&0&0&{ - \alpha }&{ - \beta }&{{\xi ^2}}\\{{\xi ^2} - {C_2}{\alpha ^2} - {C_6}{\beta ^2}}&{ - \left( {{C_3} + {C_6}} \right)\alpha \beta }&{{C_1}\alpha }&0&0&0\\{ - \left( {{C_3} + {C_6}} \right)\alpha \beta }&{{\xi ^2} - {C_6}{\alpha ^2} - {C_4}{\beta ^2}}&{{C_5}\beta }&0&0&0\\{{C_1}\alpha }&{{C_5}\beta }&{{C_7}}&0&0&0\end{array}} \right]$ (4)
where
$X = {\tau _{zx}},Y = {\tau _{zy}},Z = {\sigma _z}$
$\alpha = \partial /\partial x,\beta = \partial /\partial y,{\xi ^2} = \rho {\partial ^2}/\partial {t^2}$
${C_1} = - {C_{13}}/{C_{33}},{C_2} = {C_{11}} - C_{13}^2/{C_{33}}$
${C_3} = {C_{12}} - {C_{13}}{C_{23}}/{C_{33}},{C_4} = {C_{22}} - C_{23}^2/{C_{33}}$
${C_5} = - {C_{23}}/{C_{33}},{C_6} = {C_{66}},{C_7} = 1/{C_{33}}$
${C_8} = 1/{C_{55}},{C_9} = 1/{C_{44}}$
ρ is the density of the material.
The stresses σx, σy and τxy can be expressed as
$\left\{ \begin{array}{l}{\sigma _x}\\{\sigma _y}\\{\tau _{xy}}\end{array} \right\} = \left[ {\begin{array}{*{20}{c}}{{C_2}\alpha }&{{C_3}\beta }&{ - {C_1}}\\{{C_3}\alpha }&{{C_4}\beta }&{ - {C_5}}\\{{C_6}\beta }&{{C_6}\alpha }&0\end{array}} \right]\left\{ {\begin{array}{*{20}{c}}U\\V\\Z\end{array}} \right\}$ (5)
2.2 Solutions to the Problem Internal friction is the main damping for a continuous plate, so with the complex damping model being adopted, the constitutive equation of uniaxial stressed sate is
$\sigma = \left( {1 + {\rm{i}}\gamma } \right)E\xi $ (6)
where γ is the material damping coefficient.
The displacement functions of free edges at y=0, b are separately written as V(0)(x, z, t) and V(b)(x, z, t). We assume
$\left\{ \begin{array}{l}U = \bar U + \frac{b}{2}{\left( {1 - \frac{y}{b}} \right)^2}\alpha {V^{\left( 0 \right)}}\left( {x,z,t} \right) - \\\;\;\;\;\;\;\frac{b}{2}{\left( {\frac{y}{b}} \right)^2}\alpha {V^{\left( b \right)}}\left( {x,z,t} \right)\\V = \bar V + \left( {1 - \frac{y}{b}} \right){V^{\left( 0 \right)}}\left( {x,z,t} \right) + \left( {\frac{y}{b}} \right){V^{\left( b \right)}}\left( {x,z,t} \right)\end{array} \right.$ (7)
Eq.(3) can be written into state-space form.
$\frac{\partial }{{\partial z}}{\left[ {\bar U\;\bar V\;Z\;X\;Y\;W} \right]^{\rm{T}}} = \mathit{\boldsymbol{D}}{\left[ {\bar U\;\bar V\;Z\;X\;Y\;W} \right]^{\rm{T}}} + \mathit{\boldsymbol{B}}$ (8)
where
$\mathit{\boldsymbol{B}} = {\left[ {{B_1}\;{B_2}\;{B_3}\;{B_4}\;{B_5}\;{B_6}} \right]^{\rm{T}}}$ (9)
$\left\{ \begin{array}{l}{B_1} = - \frac{b}{2}{\left( {1 - \frac{y}{b}} \right)^2}\frac{\partial }{{\partial z}}\alpha {V^{(0)}}(x,z,t) + \\\;\;\;\;\;\;\;\frac{b}{2}{\left( {\frac{y}{b}} \right)^2}\frac{\partial }{{\partial z}}\alpha {V^{(b)}}(x,z,t)\\{B_2} = - \left( {1 - \frac{y}{b}} \right)\frac{\partial }{{\partial z}}{V^{(0)}}(x,z,t) - \\\;\;\;\;\;\;\;\left( {\frac{y}{b}} \right)\frac{\partial }{{\partial z}}{V^{(b)}}(x,z,t)\\{B_3} = 0\\{B_4} = \frac{b}{2}{\left( {1 - \frac{y}{b}} \right)^2}\left( {{\xi ^2}\alpha {V^{\left( 0 \right)}}(x,z,t) - } \right.\\\;\;\;\;\;\;\left. {{C_2}{\alpha ^3}{V^{\left( 0 \right)}}(x,z,t)} \right) - \frac{b}{2}{\left( {\frac{y}{b}} \right)^2}\left( {{\xi ^2}\alpha {V^{\left( b \right)}}(x,z,t) - } \right.\\\;\;\;\;\;\;\left. {{C_2}{\alpha ^3}{V^{\left( b \right)}}(x,z,t)} \right) + \frac{{{C_3}}}{b}\left[ {\alpha {V^{\left( 0 \right)}}(x,z,t) - } \right.\\\;\;\;\;\;\;\;\left. {\alpha {V^{\left( b \right)}}(x,z,t)} \right]\\{B_5} = \left( {1 - \frac{y}{b}} \right)\left( {{C_3}{\alpha ^2}{V^{\left( 0 \right)}}(x,z,t) + {\xi ^2}{V^{\left( 0 \right)}}(x,z,t)} \right) + \\\;\;\;\;\;\;\;\left( {\frac{y}{b}} \right)\left( {{C_3}{\alpha ^2}{V^{\left( b \right)}}(x,z,t) + {\xi ^2}{V^{\left( b \right)}}(x,z,t)} \right)\\{B_6} = {C_1}\left[ {\frac{b}{2}{{\left( {1 - \frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( 0 \right)}}(x,z,t) - } \right.\\\;\;\;\;\;\;\;\left. {\frac{b}{2}{{\left( {\frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( b \right)}}(x,z,t)} \right] + \\\;\;\;\;\;\;\;\frac{{{C_5}}}{b}\left( { - {V^{\left( 0 \right)}}(x,z,t) + {V^{\left( b \right)}}(x,z,t)} \right)\end{array} \right.$ (10)
Stresses σx, σy and τxy can be written as
$\left\{ \begin{array}{l}{\sigma _x} = {C_2}\alpha \bar U + {C_3}\beta \bar V - {C_1}Z + \\\;\;\;\;\;\;{C_2}\left[ {\frac{b}{2}{{\left( {1 - \frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( 0 \right)}}\left( {x,z,t} \right) - } \right.\\\;\;\;\;\;\;\left. {\frac{b}{2}{{\left( {\frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( b \right)}}\left( {x,z,t} \right)} \right] + \\\;\;\;\;\;\;\frac{{{C_3}}}{b}\left[ { - {V^{\left( 0 \right)}}\left( {x,z,t} \right) + {V^{\left( b \right)}}\left( {x,z,t} \right)} \right]\\{\sigma _y} = {C_3}\alpha \bar U + {C_4}\beta \bar V - {C_5}Z + \\\;\;\;\;\;\;{C_3}\left[ {\frac{b}{2}{{\left( {1 - \frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( 0 \right)}}\left( {x,z,t} \right) - } \right.\\\;\;\;\;\;\;\left. {\frac{b}{2}{{\left( {\frac{y}{b}} \right)}^2}{\alpha ^2}{V^{\left( b \right)}}\left( {x,z,t} \right)} \right] + \\\;\;\;\;\;\;\frac{{{C_4}}}{b}\left[ { - {V^{\left( 0 \right)}}\left( {x,z,t} \right) + {V^{\left( b \right)}}\left( {x,z,t} \right)} \right]\\\tau_{x y}=C_{6} \beta \overline{U}+C_{6} \alpha \overline{V}\end{array} \right.$ (11)
To solve Eq.(8), we write the solution of the state space equation as a form of double-trigonometric function, assuming
$\left\{ \begin{array}{l}\bar U = \sum\limits_m {\sum\limits_n {{{\bar U}_{mn}}\left( z \right)\cos \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \\\bar V = \sum\limits_m {\sum\limits_n {{{\bar V}_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\sin \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \\Z = \sum\limits_m {\sum\limits_n {{Z_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \\X = \sum\limits_m {\sum\limits_n {{X_{mn}}\left( z \right)\cos \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \\Y = \sum\limits_m {\sum\limits_n {{Y_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\sin \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \\W = \sum\limits_m {\sum\limits_n {{W_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } \end{array} \right.$ (12)
$\left\{ \begin{array}{l}{V^{\left( 0 \right)}} = \sum\limits_m {V_m^{\left( 0 \right)}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}{e^{{\rm{i}}\omega t}}} \\{V^{\left( b \right)}} = \sum\limits_m {V_m^{\left( b \right)}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}{e^{{\rm{i}}\omega t}}} \end{array} \right.$ (13)
For each combination of m and n, letting ζ=mπ/a, η=nπ/b, then
$\frac{{\rm{d}}}{{{\rm{d}}z}}{\mathit{\boldsymbol{R}}_{mn}} = {\mathit{\boldsymbol{D}}_{mn}}{\mathit{\boldsymbol{R}}_{mn}} + {\mathit{\boldsymbol{B}}_{mn}}$ (14)
where
${\mathit{\boldsymbol{R}}_{mn}} = {\left[ {{{\bar U}_{mn}}\left( z \right)\;{{\bar V}_{mn}}\left( z \right)\;{Z_{mn}}\left( z \right)\;{X_{mn}}\left( z \right)\;{Y_{mn}}\left( z \right)\;{W_{mn}}\left( z \right)} \right]^{\rm{T}}}$ (15)
${\mathit{\boldsymbol{B}}_{mn}} = {\left[ {{B_{mn,1}}\;{B_{mn,2}}\;{B_{mn,3}}\;{B_{mn,4}}\;{B_{mn,5}}\;{B_{mn,6}}} \right]^{\rm{T}}}$ (16)
${\mathit{\boldsymbol{D}}_{mn}} = \left[ {\begin{array}{*{20}{c}}0&0&0&{{C_8}}&0&{ - \zeta }\\0&0&0&0&{{C_9}}&\eta \\0&0&0&\zeta &{ - \eta }&{ - \rho {\omega ^2}}\\{ - \rho {\omega ^2} + {C_2}{\zeta ^2} + {C_6}{\eta ^2}}&{ - \left( {{C_3} + {C_6}} \right)\zeta \eta }&{{C_1}\zeta }&0&0&0\\{ - \left( {{C_3} + {C_6}} \right)\zeta \eta }&{ - \rho {\omega ^2} + {C_6}{\zeta ^2} + {C_4}{\eta ^2}}&{ - {C_5}\eta }&0&0&0\\{ - {C_1}\zeta }&{{C_5}\eta }&{{C_7}}&0&0&0\end{array}} \right]$ (17)
when n≠0:
$\left\{ \begin{array}{l}{B_{mn,1}} = - \frac{2}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\frac{\partial }{{\partial z}}V_m^{\left( 0 \right)}\left( z \right)\zeta + \frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\frac{\partial }{{\partial z}}V_m^{\left( b \right)}\left( z \right)\zeta \\{B_{mn,2}} = - \frac{2}{{n{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial z}}V_m^{\left( 0 \right)}\left( z \right) + \frac{2}{{n{\rm{ \mathsf{ π} }}}}\cos n{\rm{ \mathsf{ π} }}\frac{\partial }{{\partial z}}V_m^{\left( b \right)}\left( z \right)\\{B_{mn,3}} = 0\\{B_{mn,4}} = \left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\left[ {V_m^{\left( 0 \right)}\left( z \right) - \cos n{\rm{ \mathsf{ π} }}V_m^{\left( b \right)}\left( z \right)} \right]\\{B_{mn,5}} = \left( { - \rho {\omega ^2} - {C_3}{\zeta ^2}} \right)\frac{2}{{n{\rm{ \mathsf{ π} }}}}\left[ {V_m^{\left( 0 \right)}\left( z \right) - \cos n{\rm{ \mathsf{ π} }}V_m^{\left( b \right)}\left( z \right)} \right]\\{B_{mn,6}} = - {C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\left[ {V_m^{\left( 0 \right)}\left( z \right) - \cos n{\rm{ \mathsf{ π} }}V_m^{\left( b \right)}\left( z \right)} \right]\end{array} \right.$ (18)
when n=0:
$\left\{ \begin{array}{l}{B_{mn,1}} = - \frac{b}{6}\frac{\partial }{{\partial z}}V_m^{\left( 0 \right)}\left( z \right)\zeta + \frac{b}{6}\frac{\partial }{{\partial z}}V_m^{\left( 6 \right)}\left( z \right)\zeta \\{B_{mn,2}} = 0\\{B_{mn,3}} = 0\\{B_{mn,4}} = \left[ {\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{b}{6} + \frac{{{C_3}}}{6}\zeta } \right]\left[ {V_m^{\left( 0 \right)}\left( z \right) - } \right.\\\;\;\;\;\;\;\;\;\;\;\left. {V_m^{\left( b \right)}\left( z \right)} \right]\\{B_{mn,5}} = 0\\{B_{mn,6}} = \left( { - {C_1}{\zeta ^2}\frac{b}{6} - \frac{{{C_5}}}{b}} \right)\left[ {V_m^{\left( 0 \right)}\left( z \right) - V_m^{\left( b \right)}\left( z \right)} \right]\end{array} \right.$ (19)
From Eqs.(7), (12) and (13), it can be seen that the lateral boundary conditions are satisfied except for σy=0 at y=0, b. The rest of the problem is to obtain Vm(0)(z) and Vm(b)(z) by utilizing the remaining lateral boundary conditions. For this reason, the plate is split into sufficient layers to ensure both Vm(0)(z) and Vm(b)(z) are linear within every layer, as shown in Fig. 2. Assume the number of layers is p, so the number of layer edges along the thickness direction is p+1.
Fig.2
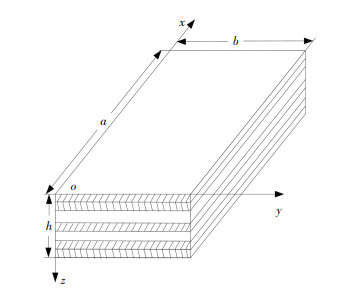 Fig.2 Laminated thick plate
Fig.2 Laminated thick plate Inside the jth layer, suppose the values of Vm.j(0)(z) at the jth and the (j+1)th layer edge are Am, j and Am, j+1, and the values of Vm.j(b)(z) at the jth and the (j+1)th layer edge are Bm, j and Bm, j+1, then
$\left\{ \begin{array}{l}V_{m,j}^{\left( 0 \right)}\left( z \right) = \frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - z}}{A_{m,j}} + \frac{{z - {z_j}}}{{{z_{j + 1}} - z}}{A_{m,j + 1}}\\V_{m,j}^{\left( b \right)}\left( z \right) = \frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - z}}{B_{m,j}} + \frac{{z - {z_j}}}{{{z_{j + 1}} - z}}{B_{m,j + 1}}\end{array} \right.$ (20)
Letting
${\mathit{\boldsymbol{L}}_{m,j}} = {\left[ {{A_{m,j}}{B_{m,j}}} \right]^{\rm{T}}},{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{m,j}}\left( z \right) = {\left[ {V_{m,j}^{\left( 0 \right)}\left( z \right)V_{m,j}^{\left( b \right)}\left( z \right)} \right]^{\rm{T}}}$
Eq.(20) can be written as
${\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{m,j}}\left( z \right) = \frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - z}}{\mathit{\boldsymbol{L}}_{m,j}} + \frac{{z - {z_j}}}{{{z_{j + 1}} - z}}{\mathit{\boldsymbol{L}}_{m,j + 1}}$ (21)
For each combination of m and n, the solution of Eq.(14) is
$\begin{array}{l}{\mathit{\boldsymbol{R}}_{mn}}\left( {{z_{j + 1}}} \right) = {e^{{\mathit{\boldsymbol{D}}_{mn,j}}\left( {{z_{j + 1}} - {z_j}} \right)}}{\mathit{\boldsymbol{R}}_{mn}}\left( {{z_j}} \right) + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\int_{{z_j}}^{{z_{j + 1}}} {{e^{{\mathit{\boldsymbol{D}}_{mn,j}}\left( {{z_{j + 1}} - \tau } \right)}}{\mathit{\boldsymbol{B}}_{mn}}\left( \tau \right){\rm{d}}\tau } \end{array}$ (22)
Letting
${\mathit{\boldsymbol{B}}_{mn,j}}\left( \tau \right) = {\mathit{\boldsymbol{C}}_{mn,j}}\left( \tau \right){\mathit{\boldsymbol{L}}_{m,j}} + {\mathit{\boldsymbol{\bar C}}_{mn,j}}\left( \tau \right){\mathit{\boldsymbol{L}}_{m,j + 1}}$ (23)
${\mathit{\boldsymbol{B}}_{mn,j}}\left( z \right) = {\mathit{\boldsymbol{N}}_{mn,j}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{m,j}}\left( z \right)$ (24)
where
${\mathit{\boldsymbol{N}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{ - \frac{2}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\frac{\partial }{{\partial z}}\zeta }&{\frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\frac{\partial }{{\partial z}}\zeta }\\{ - \frac{2}{{n{\rm{ \mathsf{ π} }}}}\frac{\partial }{{\partial z}}}&{\frac{2}{{n{\rm{ \mathsf{ π} }}}}\cos n{\rm{ \mathsf{ π} }}\frac{\partial }{{\partial z}}}\\0&0\\{\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}}&{\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\left( { - \cos n{\rm{ \mathsf{ π} }}} \right)}\\{\left( { - \rho {\omega ^2} - {C_3}{\zeta ^2}} \right)\frac{2}{{n{\rm{ \mathsf{ π} }}}}}&{\left( {\rho {\omega ^2} + {C_3}{\zeta ^2}} \right)\frac{2}{{n{\rm{ \mathsf{ π} }}}}\cos n{\rm{ \mathsf{ π} }}}\\{ - {C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}}&{{C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\cos n{\rm{ \mathsf{ π} }}}\end{array}} \right],n \ne 0$ (25)
${\mathit{\boldsymbol{N}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{ - \frac{b}{6}\frac{\partial }{{\partial z}}\zeta }&{\frac{b}{6}\frac{\partial }{{\partial z}}\zeta }\\0&0\\0&0\\{\left[ {\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{b}{6} + \frac{{{C_3}}}{b}\zeta } \right]}&{\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{b}{6} - \frac{{{C_3}}}{b}\zeta }\\0&0\\{ - {C_1}{\zeta ^2}\frac{b}{6} - \frac{{{C_5}}}{b}}&{{C_1}{\zeta ^2}\frac{b}{6} + \frac{{{C_5}}}{b}}\end{array}} \right],n = 0$ (26)
then
$\left\{ \begin{array}{l}{\mathit{\boldsymbol{C}}_{mn,j}}\left( z \right) = {\mathit{\boldsymbol{N}}_{mn,j}}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}\\{{\mathit{\boldsymbol{\bar C}}}_{mn,j}}\left( z \right) = {\mathit{\boldsymbol{N}}_{mn,j}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}\end{array} \right.$ (27)
${\mathit{\boldsymbol{C}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{\frac{2}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\zeta \frac{{ - 1}}{{{z_{j + 1}} - {z_j}}}}\\{\frac{2}{{n{\rm{ \mathsf{ π} }}}}\frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{2}{{n{\rm{ \mathsf{ π} }}}}\cos n{\rm{ \mathsf{ π} }}\frac{{ - 1}}{{{z_{j + 1}} - {z_j}}}}\\0&0\\{\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}&{\left( {\rho {\omega ^2} - {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\cos n{\rm{ \mathsf{ π} }}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}\\{\left( { - \rho {\omega ^2} - {C_3}{\zeta ^2}} \right)\frac{{2b}}{{n{\rm{ \mathsf{ π} }}}}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}&{\left( {\rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{2}{{n{\rm{ \mathsf{ π} }}}}\cos n{\rm{ \mathsf{ π} }}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}\\{ - {C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}&{{C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\cos n{\rm{ \mathsf{ π} }}\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}\end{array}} \right],n \ne 0$ (28)
${\mathit{\boldsymbol{C}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{\frac{b}{6}\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{b}{6}\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}\\0&0\\0&0\\{\left[ {\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{b}{6} + \frac{{{C_3}}}{b}\zeta } \right]\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}&{\left[ {\left( {\rho {\omega ^2}\zeta - {C_2}{\zeta ^3}} \right)\frac{b}{6} - \frac{{{C_3}}}{b}\zeta } \right]\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}\\0&0\\{\left( { - {C_1}{\zeta ^2}\frac{b}{6} - \frac{{{C_5}}}{b}} \right)\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}&{\left( {{C_1}{\zeta ^2}\frac{b}{6} + \frac{{{C_5}}}{b}} \right)\frac{{{z_{j + 1}} - z}}{{{z_{j + 1}} - {z_j}}}}\end{array}} \right],n = 0$ (29)
${\mathit{\boldsymbol{\bar C}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{ - \frac{2}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}b\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}\\{ - \frac{2}{{n{\rm{ \mathsf{ π} }}}}\frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{n{\rm{ \mathsf{ π} }}}}\frac{1}{{{z_{j + 1}} - {z_j}}}}\\0&0\\{\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}&{\left( {\rho {\omega ^2}\zeta - {C_2}{\zeta ^3}} \right)\frac{{2b\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}\\{\left( { - \rho {\omega ^2} - {C_3}{\zeta ^2}} \right)\frac{2}{{n{\rm{ \mathsf{ π} }}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}&{\left( {\rho {\omega ^2} + {C_3}{\zeta ^2}} \right)\frac{{2\cos n{\rm{ \mathsf{ π} }}}}{{n{\rm{ \mathsf{ π} }}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}\\{ - {C_1}{\zeta ^2}\frac{{2b}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}&{{C_1}{\zeta ^2}\frac{{2b\cos n{\rm{ \mathsf{ π} }}}}{{{n^2}{{\rm{ \mathsf{ π} }}^2}}}\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}\end{array}} \right],n \ne 0$ (30)
${\mathit{\boldsymbol{\bar C}}_{mn,j}} = \left[ {\begin{array}{*{20}{c}}{ - \frac{b}{6}\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}&{\frac{b}{6}\zeta \frac{1}{{{z_{j + 1}} - {z_j}}}}\\0&0\\0&0\\{\left[ {\left( { - \rho {\omega ^2}\zeta + {C_2}{\zeta ^3}} \right)\frac{b}{6} + \frac{{{C_3}}}{b}\zeta } \right]\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}&{\left[ {\left( {\rho {\omega ^2}\zeta - {C_2}{\zeta ^3}} \right)\frac{b}{6} - \frac{{{C_3}}}{b}\zeta } \right]\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}\\0&0\\{\left( { - {C_1}{\zeta ^2}\frac{b}{6} - \frac{{{C_5}}}{b}} \right)\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}&{\left( {{C_1}{\zeta ^2}\frac{b}{6} + \frac{{{C_5}}}{b}} \right)\frac{{z - {z_j}}}{{{z_{j + 1}} - {z_j}}}}\end{array}} \right],n = 0$ (31)
The dynamical load qeiωt can be written as
$q{e^{{\rm{i}}\omega t}} = \sum\limits_m {\sum\limits_n {{q_{mn}}\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } $ (32)
where
${q_{mn}} = \left\{ {\begin{array}{*{20}{c}}\begin{array}{l}4q/m{\rm{ \mathsf{ π} }},\\0,\\0,\end{array}&\begin{array}{l}n = 0,m = 1,3,5, \cdots \cdots \\n = 0,m = 2,4,6, \cdots \cdots \\n \ne 0\end{array}\end{array}} \right.$ (33)
Substituting Eq.(23) for Eq.(22), the following equation is obtained:
${\mathit{\boldsymbol{R}}_{mn,j + 1}} = {e^{{\mathit{\boldsymbol{D}}_{mn,j}}\left( {{z_{j + 1}} - {z_j}} \right)}}{\mathit{\boldsymbol{R}}_{mn,j}} + {\mathit{\boldsymbol{M}}_{mn,j}}{\mathit{\boldsymbol{L}}_{m,j}} + {\mathit{\boldsymbol{\bar M}}_{mn,j}}{\mathit{\boldsymbol{L}}_{m,j + 1}}$ (34)
where j > 0, and
$\left\{ \begin{array}{l}{\mathit{\boldsymbol{M}}_{mn,j}} = \int_{{z_j}}^{{z_{j + 1}}} {{e^{{\mathit{\boldsymbol{D}}_{mn,j}}\left( {{z_{j + 1}} - \tau } \right)}}{\mathit{\boldsymbol{C}}_{mn,j}}\left( \tau \right){\rm{d}}\tau } \\{{\mathit{\boldsymbol{\bar M}}}_{mn,j}} = \int_{{z_j}}^{{z_{j + 1}}} {{e^{{\mathit{\boldsymbol{D}}_{mn,j}}\left( {{z_{j + 1}} - \tau } \right)}}{{\mathit{\boldsymbol{\bar C}}}_{mn,j}}\left( \tau \right){\rm{d}}\tau } \end{array} \right.$ (35)
Letting
${\mathit{\boldsymbol{R}}_{mn,j}} = {\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{mn,j}}{\mathit{\boldsymbol{R}}_{mn,1}} + {\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{mn,j}}$ (36)
${\mathit{\boldsymbol{J}}_{mn,j,i}} = \left\{ \begin{array}{l}{e^{{\mathit{\boldsymbol{D}}_{mn,j - i}}\left( {{z_{j - i + 1}} - {z_j}} \right)}},1 \le i \le j - 1\\\mathit{\boldsymbol{I}},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;i = 0\end{array} \right.$ (37)
${\mathit{\boldsymbol{F}}_{mn,j,i}} = \left\{ \begin{array}{l}\prod\limits_{k = 1}^i {{\mathit{\boldsymbol{J}}_{mn,j,k}}} ,1 \le i \le j - 1\\\mathit{\boldsymbol{I}},\;\;\;\;\;\;\;\;\;\;\;\;i = 0\end{array} \right.$ (38)
then
${\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_{mn,j}} = {\mathit{\boldsymbol{F}}_{mn,j,j - 1}}$ (39)
Πmn, j is expressed as follows, which can be proved with mathematical induction.
${\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{mn,j}} = \left\{ \begin{array}{l}\sum\limits_{i = 0}^{j - 2} {\left( {{\mathit{\boldsymbol{F}}_{mn,j,i}}{M_{mn,j - i - 1}}{L_{m,j - i - 1}} + } \right.} \\\;\;\;\;\left. {{F_{mn,j,i}}{{\bar M}_{mn,j - i - 1}}{L_{m,j - i}}} \right),2 \le j \le p + 1\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1\end{array} \right.$ (40)
Letting
${\mathit{\boldsymbol{G}}_{mn,j,i}} = {\mathit{\boldsymbol{F}}_{mn,j,i}}{\mathit{\boldsymbol{M}}_{mn,j - i - 1}},{\mathit{\boldsymbol{\bar G}}_{mn,j,i}} = {\mathit{\boldsymbol{F}}_{mn,j,i}}{\mathit{\boldsymbol{\bar M}}_{mn,j - i}}$ (41)
then
${\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{mn,j}} = \left\{ \begin{array}{l}\sum\limits_{i = 0}^{j - 2} {\left( {{G_{mn,j,i}}{L_{m,j - i - 1}} + } \right.} \\\;\;\;\;\;\;\;\left. {{{\bar G}_{mn,j,i}}{L_{m,j - i}}} \right),\;\;\;\;\;\;\;\;\;2 \le j \le p + 1\\0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 1\end{array} \right.$ (42)
With Eqs.(11), (12) and (13), σy can be rewritten as follows:
$\begin{array}{l}{\sigma _y} = {C_3}\sum\limits_m {\sum\limits_n {{{\bar U}_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}\left( { - \frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right){e^{{\rm{i}}\omega t}}} } + \\\;\;\;\;\;\;\;\;{C_4}\sum\limits_m {\sum\limits_n {{{\bar V}_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}\left( {\frac{{n{\rm{ \mathsf{ π} }}}}{b}} \right){e^{{\rm{i}}\omega t}}} } - \\\;\;\;\;\;\;\;\;{C_5}\sum\limits_m {\sum\limits_n {{Z_{mn}}\left( z \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}{e^{{\rm{i}}\omega t}}} } + \\\;\;\;\;\;\;\;\;{C_3}\frac{b}{2}{\left( {1 - \frac{y}{b}} \right)^2}\sum\limits_m {V_m^{\left( 0 \right)}\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}\left( { - 1} \right){{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2}{e^{{\rm{i}}\omega t}}} + \\\;\;\;\;\;\;\;\;{C_3}\frac{{{y^2}}}{{2b}}\sum\limits_m {V_m^{\left( 0 \right)}\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}{{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2}{e^{{\rm{i}}\omega t}}} + \\\;\;\;\;\;\;\;\;\frac{{{C_4}}}{b}\sum\limits_m {\left( { - V_m^{\left( 0 \right)} + V_m^{\left( b \right)}} \right)\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}{e^{{\rm{i}}\omega t}}} \end{array}$ (43)
Letting
$\left\{ \begin{array}{l}{\sigma _y} = \sum\limits_m {{f_m}\sin \frac{{m{\rm{ \mathsf{ π} }}x}}{a}{e^{{\rm{i}}\omega t}}} \\{f_m} = {C_3}\sum\limits_n {{{\bar U}_{mn}}\left( z \right)\cos \frac{{m{\rm{ \mathsf{ π} }}y}}{b}\left( { - \frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)} + \\\;\;\;\;\;\;\;{C_4}\sum\limits_n {{{\bar V}_{mn}}\left( z \right)\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}\left( {\frac{{n{\rm{ \mathsf{ π} }}}}{b}} \right)} - \\\;\;\;\;\;\;\;{C_5}\sum\limits_n {{Z_{mn}}\left( z \right)\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}} + \\\;\;\;\;\;\;\;{C_3}\left[ { - \frac{b}{2}{{\left( {1 - \frac{y}{b}} \right)}^2}V_m^{\left( 0 \right)}{{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2} + } \right.\\\;\;\;\;\;\;\;\left. {\frac{{{y^2}}}{{2b}}V_m^{\left( b \right)}{{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2}} \right] + \frac{{{C_4}}}{b}\left( { - V_m^{\left( 0 \right)} + V_m^{\left( b \right)}} \right)\end{array} \right.$ (44)
$\left\{ \begin{array}{l}{\mathit{\boldsymbol{k}}_{1,mn}} = \left[ {\begin{array}{*{20}{c}}{{C_3}\left( { - \frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}}&{{C_4}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}\left( {\frac{{n{\rm{ \mathsf{ π} }}}}{b}} \right)}&{ - {C_5}\cos \frac{{n{\rm{ \mathsf{ π} }}y}}{b}}\end{array}} \right]\\{\mathit{\boldsymbol{k}}_{2,m}} = \left[ {\begin{array}{*{20}{c}}{ - \frac{b}{2}{{\left( {1 - \frac{y}{b}} \right)}^2}{C_3}{{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2} - \frac{{{C_4}}}{b}}&{{C_3}\frac{{{y^2}}}{{2b}}{{\left( {\frac{{m{\rm{ \mathsf{ π} }}}}{a}} \right)}^2} + \frac{{{C_4}}}{b}}\end{array}} \right]\end{array} \right.$ (45)
then
$\begin{array}{l}{f_m} = \sum\limits_n {{\mathit{\boldsymbol{k}}_{1,mn}}{{\left[ {\begin{array}{*{20}{c}}{{{\bar U}_{mn}}\left( z \right)}&{{{\bar V}_{mn}}\left( z \right)}&{{Z_{mn}}}\end{array}} \right]}^{\rm{T}}}} + \\\;\;\;\;\;\;\;{\mathit{\boldsymbol{k}}_{2,m}}{\left[ {\begin{array}{*{20}{c}}{V_m^{\left( 0 \right)}}&{V_m^{\left( b \right)}}\end{array}} \right]^{\rm{T}}}\end{array}$ (46)
According to Eq.(36), we get
$\begin{array}{l}{\left\{ {\begin{array}{*{20}{c}}{\bar U}\\{\bar V}\\Z\end{array}} \right\}_{mn,j}} = {\left[ {\begin{array}{*{20}{c}}{{\pi _{11}}}&{{\pi _{12}}}&{{\pi _{16}}}\\{{\pi _{21}}}&{{\pi _{22}}}&{{\pi _{26}}}\\{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\end{array}} \right]_{mn,j}}{\left\{ {\begin{array}{*{20}{c}}{\bar U}\\{\bar V}\\W\end{array}} \right\}_{mn,1}} + \\\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}}{{\pi _{13}}}&{{\pi _{14}}}&{{\pi _{15}}}\\{{\pi _{23}}}&{{\pi _{24}}}&{{\pi _{25}}}\\{{\pi _{33}}}&{{\pi _{34}}}&{{\pi _{35}}}\end{array}} \right]_{mn,j}}{\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}_{mn,1}} + {\left\{ {\begin{array}{*{20}{c}}{{{\bar \pi }_1}}\\{{{\bar \pi }_2}}\\{{{\bar \pi }_3}}\end{array}} \right\}_{mn,j}}\end{array}$ (47)
Since the stresses on the bottom surface are zero, then
$\begin{array}{l}0 = {\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}_{mn,p + 1}} = \left[ {\begin{array}{*{20}{c}}{{\pi _{31}}\;{\pi _{32}}\;{\pi _{33}}\;{\pi _{34}}\;{\pi _{35}}\;{\pi _{36}}}\\{{\pi _{41}}\;{\pi _{42}}\;{\pi _{43}}\;{\pi _{44}}\;{\pi _{45}}\;{\pi _{46}}}\\{{\pi _{51}}\;{\pi _{52}}\;{\pi _{53}}\;{\pi _{54}}\;{\pi _{55}}\;{\pi _{56}}}\end{array}} \right] \cdot \\\;\;\;\;\;\;\;{\left\{ {\begin{array}{*{20}{c}}{\bar U}\\{\bar V}\\Z\\X\\Y\\W\end{array}} \right\}_{mn,1}} + {\left\{ {\begin{array}{*{20}{c}}{{{\bar \pi }_3}}\\{{{\bar \pi }_4}}\\{{{\bar \pi }_5}}\end{array}} \right\}_{mn,j}}\end{array}$ (48)
$\begin{array}{l}{\left\{ \begin{array}{l}{\bar U}\\{\bar V}\\W\end{array} \right\}_{mn,1}} = \left[ {\begin{array}{*{20}{c}}{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\\{{\pi _{41}}}&{{\pi _{42}}}&{{\pi _{46}}}\\{{\pi _{51}}}&{{\pi _{52}}}&{{\pi _{56}}}\end{array}} \right]_{mn,p + 1}^{ - 1} \cdot \\\;\;\;\;\;\left( { - {{\left[ {\begin{array}{*{20}{c}}{{\pi _{33}}}&{{\pi _{34}}}&{{\pi _{35}}}\\{{\pi _{43}}}&{{\pi _{44}}}&{{\pi _{45}}}\\{{\pi _{53}}}&{{\pi _{54}}}&{{\pi _{55}}}\end{array}} \right]}_{mn,p + 1}}{{\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}}_{mn,1}} - {{\left\{ {\begin{array}{*{20}{c}}{{{\bar \pi }_3}}\\{{{\bar \pi }_4}}\\{{{\bar \pi }_5}}\end{array}} \right\}}_{mn,p + 1}}} \right)\end{array}$ (49)
Substituting Eq.(49) for Eq.(47), we have
$\begin{array}{l}{\left\{ \begin{array}{l}{\bar U}\\{\bar V}\\Z\end{array} \right\}_{mn,j}} = {\mathit{\boldsymbol{H}}_{mn,j}}{\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}_{mn,1}} + {\mathit{\boldsymbol{S}}_{mn,j}}{\left\{ {\begin{array}{*{20}{c}}{{{\bar \pi }_3}}\\{{{\bar \pi }_4}}\\{{{\bar \pi }_5}}\end{array}} \right\}_{mn,p + 1}} + \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left\{ {\begin{array}{*{20}{c}}{{{\bar \pi }_1}}\\{{{\bar \pi }_2}}\\{{{\bar \pi }_3}}\end{array}} \right\}_{mn,j}}\end{array}$ (50)
where
$\left\{ \begin{array}{l}{H_{mn,j}} = - {\left[ {\begin{array}{*{20}{c}}{{\pi _{11}}}&{{\pi _{12}}}&{{\pi _{16}}}\\{{\pi _{21}}}&{{\pi _{22}}}&{{\pi _{26}}}\\{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\end{array}} \right]_{mn,j}}\left[ {\begin{array}{*{20}{c}}{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\\{{\pi _{41}}}&{{\pi _{42}}}&{{\pi _{46}}}\\{{\pi _{51}}}&{{\pi _{52}}}&{{\pi _{56}}}\end{array}} \right]_{mn,p + 1}^{ - 1} \cdot \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\left[ {\begin{array}{*{20}{c}}{{\pi _{33}}}&{{\pi _{34}}}&{{\pi _{35}}}\\{{\pi _{43}}}&{{\pi _{44}}}&{{\pi _{45}}}\\{{\pi _{53}}}&{{\pi _{54}}}&{{\pi _{55}}}\end{array}} \right]_{mn,p + 1}} + {\left[ {\begin{array}{*{20}{c}}{{\pi _{13}}}&{{\pi _{14}}}&{{\pi _{15}}}\\{{\pi _{23}}}&{{\pi _{24}}}&{{\pi _{25}}}\\{{\pi _{33}}}&{{\pi _{34}}}&{{\pi _{35}}}\end{array}} \right]_{mn,j}}\\{S_{mn,j}} = - {\left[ {\begin{array}{*{20}{c}}{{\pi _{11}}}&{{\pi _{12}}}&{{\pi _{16}}}\\{{\pi _{21}}}&{{\pi _{22}}}&{{\pi _{26}}}\\{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\end{array}} \right]_{mn,j}}\left[ {\begin{array}{*{20}{c}}{{\pi _{31}}}&{{\pi _{32}}}&{{\pi _{36}}}\\{{\pi _{41}}}&{{\pi _{42}}}&{{\pi _{46}}}\\{{\pi _{51}}}&{{\pi _{52}}}&{{\pi _{56}}}\end{array}} \right]_{mn,p + 1}^{ - 1}\end{array} \right.$ (51)
We can define
$\left\{ \begin{array}{l}\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{mn,j}^{\left( {3,4,5} \right)} = \left[ {{{\bar \pi }_3}{{\bar \pi }_4}{{\bar \pi }_5}} \right]_{mn,j}^{\rm{T}}\\\mathit{\boldsymbol{ \boldsymbol{\bar \varPi} }}_{mn,j}^{\left( {1,2,3} \right)} = \left[ {{{\bar \pi }_1}{{\bar \pi }_2}{{\bar \pi }_3}} \right]_{mn,j}^{\rm{T}}\end{array} \right.$ (52)
$\left\{ \begin{array}{l}\mathit{\boldsymbol{G}}_{mn,j,i}^{\left( {3,4,5} \right)} = {\left[ {\begin{array}{*{20}{c}}{{g_{31}}\;{g_{32}}}\\{{g_{41}}\;{g_{42}}}\end{array}} \right]_{mn,j,i}}\\\mathit{\boldsymbol{\bar G}}_{mn,j,i}^{\left( {3,4,5} \right)} = {\left[ {\begin{array}{*{20}{c}}{{{\bar g}_{31}}\;{{\bar g}_{32}}}\\{{{\bar g}_{41}}\;{{\bar g}_{42}}}\\{{{\bar g}_{51}}\;{{\bar g}_{52}}}\end{array}} \right]_{mn,j,i}}\\\mathit{\boldsymbol{G}}_{mn,j,i}^{\left( {1,2,3} \right)} = {\left[ {\begin{array}{*{20}{c}}{{g_{11}}\;{g_{12}}}\\{{g_{21}}\;{g_{22}}}\\{{g_{31}}\;{g_{32}}}\end{array}} \right]_{mn,j,i}}\\\mathit{\boldsymbol{\bar G}}_{mn,j,i}^{\left( {1,2,3} \right)} = {\left[ {\begin{array}{*{20}{c}}{{{\bar g}_{11}}\;{{\bar g}_{12}}}\\{{{\bar g}_{21}}\;{{\bar g}_{22}}}\\{{{\bar g}_{31}}\;{{\bar g}_{32}}}\end{array}} \right]_{mn,j,i}}\end{array} \right.$ (53)
Then, according to Eqs.(42), (52), and (53), Eq.(50) is expressed as follows:
$\begin{array}{l}{\left\{ {\begin{array}{*{20}{c}}{\bar U}\\{\bar V}\\Z\end{array}} \right\}_{mn,j}} = {\mathit{\boldsymbol{H}}_{mn,j}}{\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}_{mn,1}} + {\mathit{\boldsymbol{S}}_{mn,j}}\sum\limits_{i = 0}^{p + 1 - 2} {\left( {\mathit{\boldsymbol{G}}_{mn,p + 1,i}^{\left( {3,4,5} \right)}{\mathit{\boldsymbol{L}}_{m,p + 1 - i - 1}} + } \right.} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{\bar G}}_{mn,p + 1,i}^{\left( {3,4,5} \right)}{\mathit{\boldsymbol{L}}_{m,p + 1 - i}}} \right) + \sum\limits_{i = 0}^{j - 2} {\left( {\mathit{\boldsymbol{G}}_{mn,j,i}^{\left( {1,2,3} \right)}{\mathit{\boldsymbol{L}}_{m,j - i - 1}} + } \right.} \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. {\mathit{\boldsymbol{\bar G}}_{mn,j,i}^{\left( {1,2,3} \right)}{\mathit{\boldsymbol{L}}_{m,j - i}}} \right)\end{array}$ (54)
The boundary conditions of σy=0 at y=0, b must be satisfied at every layer edge for random x, so
$\begin{array}{l}0 = {f_{m,j}} = \sum\limits_n {{k_{1,mn}}{\mathit{\boldsymbol{H}}_{mn,j}}{{\left\{ {\begin{array}{*{20}{c}}Z\\X\\Y\end{array}} \right\}}_{mn,1}}} + \sum\limits_n {\left[ {{k_{1,mn}}{S_{mn,j}}} \right. \cdot } \\\;\;\;\;\;\;\left. {\sum\limits_{i = 0}^{p + 1 - 2} {\left( {\mathit{\boldsymbol{G}}_{mn,p + 1,i}^{\left( {3,4,5} \right)}{\mathit{\boldsymbol{L}}_{m,p + 1 - i - 1}} + \mathit{\boldsymbol{\bar G}}_{mn,p + 1,i}^{\left( {3,4,5} \right)}{\mathit{\boldsymbol{L}}_{m,p + 1 - i}}} \right)} } \right] + \\\;\;\;\;\;\;\sum\limits_n {\left[ {{k_{1,mn}}\sum\limits_{i = 0}^{j - 2} {\left( {\mathit{\boldsymbol{G}}_{mn,j,i}^{\left( {1,2,3} \right)}{\mathit{\boldsymbol{L}}_{m,j - i - 1}} + \mathit{\boldsymbol{\bar G}}_{mn,j,i}^{\left( {1,2,3} \right)}{\mathit{\boldsymbol{L}}_{m,j - i}}} \right)} } \right]} + \\\;\;\;\;\;\;{k_{2,m}}{\mathit{\boldsymbol{L}}_{m,j}}\end{array}$ (55)
This is an equation of Lm, j. For every m, the number of unknowns and equations are both 2(1+p), so Lm, j can be solved, and all the stresses and displacements are calculated, then the complete solution can be determined.
3 Numerical Examples and Discussion As an example, let us consider a plate with length a=1 m and width b=1 m. The thickness-length ratio h/a is taken as 0.1. The material of the plate is aluminum which is isotropic. Young's modulus for the plate is 70 GPa, Poisson's ratio is 0.33, and the material damping coefficient is 0.01, q=1 Pa, f=500 Hz, p=20. The solution has converged with few series. In this example, m=1, 3, …, 15, n=0, 2, ..., 14. In this paper, the three-dimensional elastic solution of dynamic response of a plate with two free edges is given for the first time. Comparison is made between the current three-dimensional solution including real and imaginary parts and that of finite element results at x=a/4, y=b/4, as shown in Figs. 3-11. The finite element results are obtained from a three-dimensional MSC.Nastran model in direct frequency response analysis. It should be mentioned that the solution of displacements by finite element method is primitive. Since the solution of stresses is derivative, this will result in the discontinuity of stresses of a single node within adjacent elements. So in this paper, the average value is taken as the stress component of a node.
Fig.3
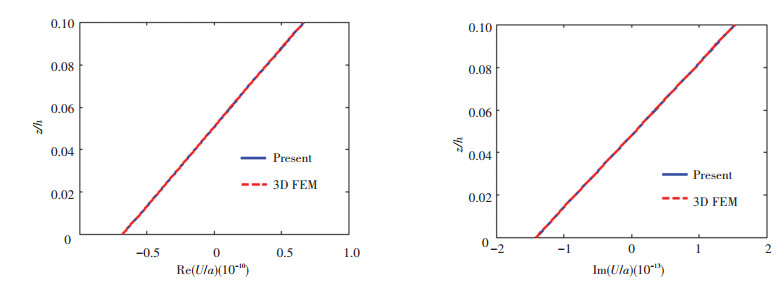 Fig.3 Through-thickness variation of U
Fig.3 Through-thickness variation of U Fig.4
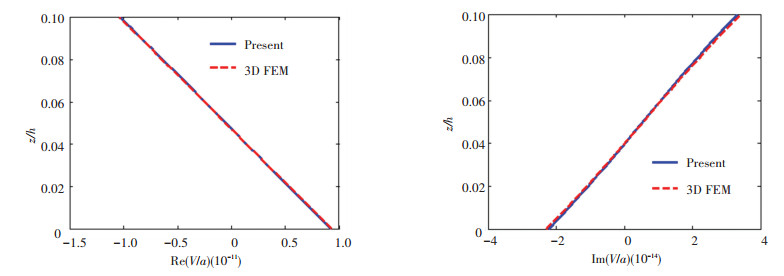 Fig.4 Through-thickness variation of V
Fig.4 Through-thickness variation of V Fig.5
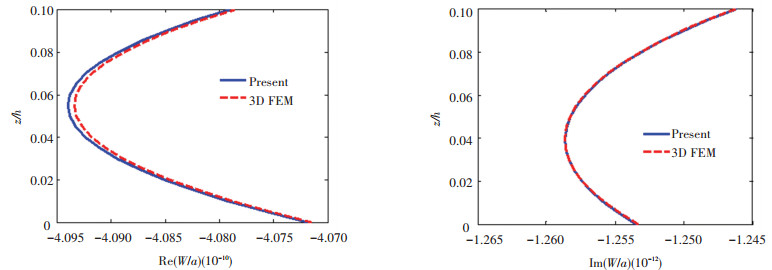 Fig.5 Through-thickness variation of W
Fig.5 Through-thickness variation of W Fig.6
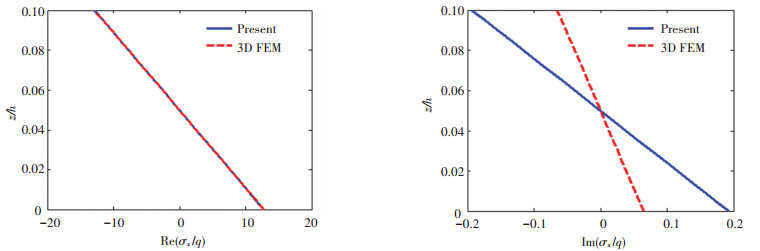 Fig.6 Through-thickness variation of σx
Fig.6 Through-thickness variation of σx Fig.7
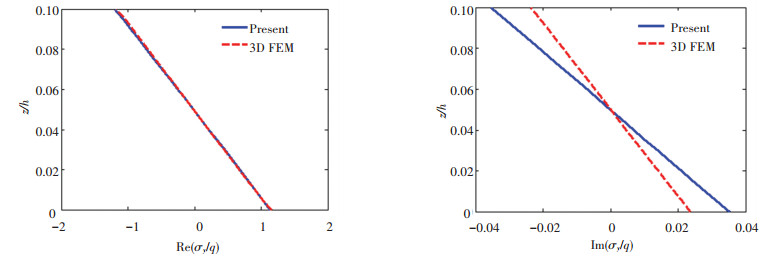 Fig.7 Through-thickness variation of σy
Fig.7 Through-thickness variation of σy Fig.8
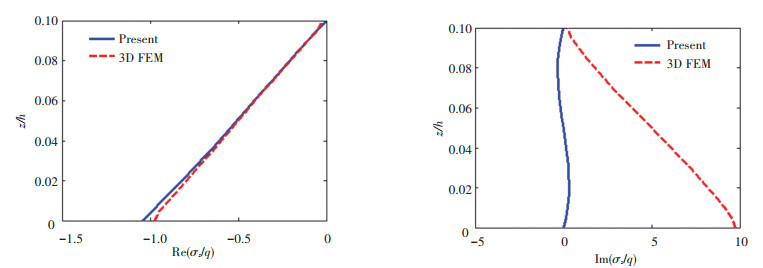 Fig.8 Through-thickness variation of σz
Fig.8 Through-thickness variation of σz Fig.9
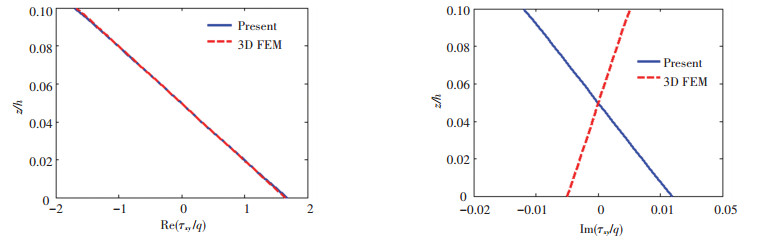 Fig.9 Through-thickness variation of τxy
Fig.9 Through-thickness variation of τxy Fig.10
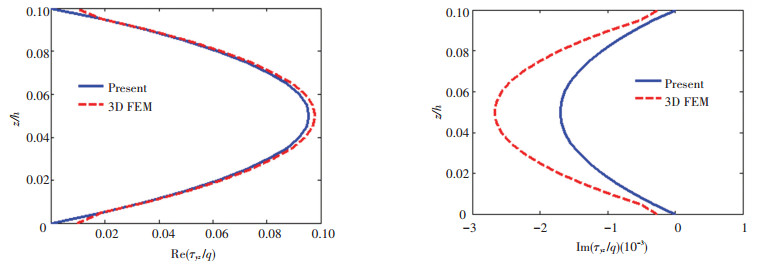 Fig.10 Through-thickness variation of τyz
Fig.10 Through-thickness variation of τyz Fig.11
 Fig.11 Through-thickness variation of τzx
Fig.11 Through-thickness variation of τzx By comparing the present solution with the finite element results, it is evident that there is an excellent agreement for displacements, as the results of displacements by finite element method are primitive. With dynamical pressure applied to the top surface, the real and imaginary parts of U and V are approximately linear along the thickness direction, while the results of W is nonlinear along the thickness direction.
The comparison of normal stresses has shown that the real parts are very close. While the imaginary parts deviate, the imaginary part of σz in finite element model at the top surface is not zero. In contrast, the imaginary part of q is zero. It is clear that the present solution of shear stresses can satisfy the free conditions at the top and bottom surfaces of the plate, while the finite element results show existence of τyz and τzx at both surfaces, thus the boundary conditions are not strictly satisfied.
The numbers of unknowns for every m is 42 as the plate is split into 20 layers in the example. However, the finite element model in MSC.Nastran is built of 60×60×20 six-sided solid elements with a total of 78141 nodes, then the computing time of this paper is evidently less than that of finite element method.
4 Concluding Remarks A three-dimensional state space method has been developed for the calculation of dynamic response of a plate with two free edges and two simply supported edges. Based on equilibrium, geometric and constitutive equations, the complex damping model was introduced, then the exact solutions which satisfy all the governing equations and boundary conditions were obtained.
In order to overcome the difficulty of satisfying all the stress conditions at free edges, the displacement functions of free edges were assumed. The boundary conditions were strictly satisfied while the convergence rate was good. The computing time was evidently less than that of finite element method.
The comparison of the solutions with those of finite element method show that there is an excellent agreement for displacements. While the imaginary parts of normal stress deviated, the finite element results showed existence of shear stresses τyz and τzx at both surfaces, so the boundary conditions were not strictly satisfied. It is apparent that the present theory offers better solution than the finite element analysis.
It should be pointed out that although the dynamical pressure is assumed to be uniform, according to the derivation process, the method proposed in this paper is suitable for random distributed loads and laminated composite structures.
References
[1] Zhang H, Jiang J Q, Zhang Z C. Three-dimensional elasticity solutions for bending of generally supported thick functionally graded plates. Applied Mathematics and Mechanics (English Edition), 2014, 35(11): 1467-1478. DOI:10.1007/s10483-014-1871-7 (
 0)
0)[2] Yuan J H, Chen W Q. Exact solutions for axisymmetric flexural free vibrations of inhomogeneous circular Mindlin plates with variable thickness. Applied Mathematics and Mechanics (English Edition), 2017, 38(4): 505-526. DOI:10.1007/s10483-017-2187-6 (
 0)
0)[3] Alibeigloo A. Three-demensional thermoelasticity solution of functionally graded carbon nanotube reinforced composite plate embedded in piezoelectric sensor and actuator layers. Compos. Struct., 2014, 118(1): 482-495. DOI:10.1016/j.compstruct.2014.08.004 (
 0)
0)[4] Chen W Q, Ding H J. On free vibration of a functionally graded piezoelectric rectangular plate. Act. Mech., 2002, 153(3-4): 207-216. DOI:10.1007/BF01177452 (
 0)
0)[5] Chen W Q, Cai J B, Ye G R, et al. Exact three-dimensional solutions of laminated orthotropic piezoelectric rectangular plates featuring interlaminar bonding imperfections modeled by a general spring layer. International Journal of Solids and Structures, 2004, 41(18-19): 5247-5263. DOI:10.1016/j.ijsolstr.2004.03.010 (
 0)
0)[6] Chen W Q, Lee K Y. Three-dimensional exact analysis of angle-ply laminates in cylindrical bending with interfacial damage via state-space method. Compos. Struct, 2004, 64(3-4): 275-283. DOI:10.1016/j.compstruct.2003.08.010 (
 0)
0)[7] Chen W Q, Zhou Y Y, Lü C F, et al. Bending of multiferroic laminated rectangular plates with imperfect interlaminar bonding. Europ. J. Mech. A/Solids., 2009, 28(4): 720-727. DOI:10.1016/j.euromechsol.2009.02.008 (
 0)
0)[8] Kashtalyan M, Menshykova M. Three- dimensional elastic deformation of a functionally graded coating/substrate system. Int. J. Solids Struct., 2007, 44(16): 5272-5288. DOI:10.1016/j.ijsolstr.2006.12.035 (
 0)
0)[9] Lee J S, Jiang L Z. Exact electroelastic analysis of piezoelectric laminae via state space approach. Int. J. Solids Struct., 1996, 33(7): 977-990. DOI:10.1016/0020-7683(95)00083-6 (
 0)
0)[10] Moslemi A, Neya B N, Amiri J V. 3-D elasticity buckling solution for simply supported thick rectangular plates using displacement potential functions. Appl. Math. Modelling, 2016, 40(11-12): 5717-5730. DOI:10.1016/j.apm.2015.12.034 (
 0)
0)[11] Pan E, Heyliger P R. Free vibrations of simply supported and multilayered magneto-electro- elastic plates. J. Sound Vib., 2002, 252(3): 429-442. DOI:10.1006/jsvi.2001.3693 (
 0)
0)[12] Vel S, Batra R C. Exact solution for rectangular sandwich plates with embedded piezoelectric shear actuators. AIAA Journal, 2001, 39(7): 1363-1373. DOI:10.2514/2.1455 (
 0)
0)[13] Chen W Q, Cai J B, Ye G R. Exact solutions of cross-ply laminates with bonding imperfections. AIAA J., 2003, 41(11): 2244-2250. DOI:10.2514/2.6817 (
 0)
0)[14] He W M, Qiao H, Chen W Q. Analytical solutions of heterogeneous rectangular plates with transverse small periodicity. Composites Part B: Engineering, 2012, 43(3): 1056-1062. DOI:10.1016/j.compositesb.2011.09.010 (
 0)
0)[15] He W M, Chen W Q, Qiao H. In-plane vibration of rectangular plates with periodic inhomogeneity: Natural frequencies and their adjustment. Compos. Struct., 2013, 105: 134-140. DOI:10.1016/j.compstruct.2013.05.013 (
 0)
0)[16] He W M, Chen W Q, Hua Q. Two-scale analytical solutions of multilayered composite rectangular plates with in-plane small periodic structure. Europ. J. Mech. A/Solids., 2013, 40: 123-130. DOI:10.1016/j.euromechsol.2013.01.005 (
 0)
0)[17] Pan E, Heyliger P R. Exact solutions for magneto-electro-elastic laminates in cylindrical bending. Int. J. Solids Struct., 2003, 40(24): 6859-6876. DOI:10.1016/j.ijsolstr.2003.08.003 (
 0)
0)[18] Sheng H Y, Wang H, Ye J Q. State space solution for thick laminated piezoelectric plates with clamped and electric open-circuited boundary conditions. Int. J. Mech. Sci., 2007, 49(7): 806-818. DOI:10.1016/j.ijmecsci.2006.11.012 (
 0)
0)[19] Zhang D X, Ye J Q, Sheng H Y. Free-edge and ply cracking effect in cross-ply laminated composites under uniform extension and thermal loading. Compos. Struct., 2006, 76(4): 314-325. DOI:10.1016/j.compstruct.2005.04.021 (
 0)
0)[20] Kapuria S, Achary G G S. Exact 3D piezoelasticity solution of hybrid cross-ply plates with damping under harmonic electro- mechanical loads. J. Sound Vib., 2005, 282(3-5): 617-634. DOI:10.1016/j.jsv.2004.03.030 (
 0)
0)[21] Kapuria S, Nair P G. Exact three-dimensional piezothermoelasticity solution for dynamics of rectangular cross-ply hybrid plates featuring interlaminar bonding imperfections. Comp. Sci Techn., 2010, 70(5): 752-762. DOI:10.1016/j.compscitech.2010.01.006 (
 0)
0)[22] Loredo A. Exact 3D solution for static and damped harmonic response of simply supported general laminates. Compos. Struct., 2013, 108(1): 625-634. DOI:10.1016/j.compstruct.2013.09.059 (
 0)
0)