
 , 陆芊芊1,2, 陈学舜1, 王自发1,3,4
, 陆芊芊1,2, 陈学舜1, 王自发1,3,41. 中国科学院大气物理研究所, 大气边界层物理和大气化学国家重点实验室, 北京 100029;
2. 广西壮族自治区气候中心, 南宁 530022;
3. 中国科学院区域大气环境研究卓越创新中心, 厦门 361021;
4. 中国科学院大学, 北京 100049
收稿日期: 2020-06-22; 修回日期: 2020-07-28; 录用日期: 2020-07-28
基金项目: 中科院重点部署项目(No.ZDRW-CN-2018-1-03);国家重点研发计划项目(No.2018YFC0830802);国家重大科技基础设施项目"地球系统数值模拟装置"
作者简介: 葛宝珠(1984-), 男, 副研究员, E-mail: gebz@mail.iap.ac.cn
通讯作者(责任作者): 葛宝珠
摘要:放射性核素大气扩散模式可以模拟放射性核素在不同尺度下的大气输送与扩散,为核电站选址、核事故应急提供科学依据.本文总结了目前广泛用于模拟核素扩散的多种模式,详细比较了各模式对放射性核素的衰变、输送和扩散、干/湿沉降和重力沉降以及辐射剂量等处理方法,总结归纳各个模式模拟的差异性.最后,对放射性核素大气扩散模式发展前景做了展望.对有针对性地提高模式模拟能力以及明确模式的发展方向具有重要的意义.
关键词:放射性核素放射性衰变输送和扩散沉降辐射剂量
A review of the numerical simulations of the atmospheric dispersion of radionuclides
GE Baozhu1,3

 , LU Qianqian1,2, CHEN Xueshun1, WANG Zifa1,3,4
, LU Qianqian1,2, CHEN Xueshun1, WANG Zifa1,3,41. State Key Laboratory of Atmospheric Boundary Layer Physics and Atmospheric Chemistry, Institute of Atmospheric Physics, Chinese Academy of Sciences, Beijing 100029;
2. Guangxi Climate Center, Nanning 530022;
3. CAS Center for Excellence in Regional Atmospheric Environment, Xiamen 361021;
4. University of Chinese Academy of Sciences, Beijing 100049
Received 22 June 2020; received in revised from 28 July 2020; accepted 28 July 2020
Abstract: The radionuclide numerical models are applied to predict the advection and diffusion of radionuclides in the atmosphere at different scales, based on which decisions are made on site selection for nuclear power plants as well as emergency response to a nuclear accident. This paper summarizes the various numerical models used to predict and simulate the atmospheric dispersion of radionuclides with a thorough comparison of decay processes, the advection and diffusion, dry/wet deposition process and the radiation exposure in different models. Three different types of the radionuclide numerical models are studied, e.g., Gaussian, Lagrangian and Eulerian, and their limitations and advantages are categorized. Finally, prospect for future development of the models is concluded. This review is informative in improving the numerical models for various applications.
Keywords: radionuclidesdecaytransport and dispersiondepositionradiation dose
1 引言(Introduction)核能是当今乃至未来重要的能源, 它蕴含巨大能量的同时也存在巨大的风险(陈达等, 2012).原子弹的爆炸、核事故中核反应堆的泄露, 甚至是正常工作的核设施, 都会释放放射性核素(姬文超, 2008).放射性核素在大气中主要经过输运、扩散、迁移和转化4个过程(刘爱华, 2012), 在短时间内产生大范围的影响, 对自然环境、人类身体健康和公共安全造成极大的破坏(潘自强, 2000; 黄越承, 2006).数值模式是研究放射性核素迁移扩散的一种有效手段, 应用数值模式模拟能快速有效地评估放射性物质泄漏的污染范围和区域.我国有众多用于国防、科研以及能源发电的核设施, 模拟放射性核素的扩散, 一方面能够提前假设事故情景, 模拟放射性核素的扩散路径和范围, 对保护人民和国家财产安全免受或少受放射性辐射危害具有非常重要的意义.另一方面, 可以为核电站选址提供科学依据, 尽可能地将核设施放置于对人民和国家损害最小的地方.
20世纪80年代切尔诺贝利事故之后, 核扩散模式研究兴起(崔慧玲, 2012), 核事故应急软件的开发也得到了快速发展(杨晔, 2015).近年来, 越来越多的模式应用于放射性核素迁移扩散, 刘爱华等(2011)根据模式描述方法的不同将放射性核素扩散模式分为高斯烟羽模型、拉格朗日模型以及欧拉模型, 以此为基点开展综述研究, 在介绍各类模式的原理及优缺点的同时展示了近20年模式的发展.崔慧玲等(2012)总结了近20年核扩散模式的进展, 并对目前放射性核素长距离迁移模式的应用及今后的发展方向进行了综述.Leel?ssy等(2018)对模拟放射性核素扩散的模式从物理机制、数值方法到应用做了一个综述, 认为虽然扩散模式发展迅速, 但是模型精度仍存在严重的瓶颈, 误差的主要来源是时间演化的不确定性.
一个完整的放射性核素扩散模式, 包括放射性核素的衰变模块、放射性核素的输送和扩散模块、放射性核素的干、湿沉降模块和重力沉降模块以及辐射剂量的诊断等.已有的综述研究已经将核扩散模式的原理以及各类模式的优缺点, 都进行了系统的总结(刘爱华等, 2011; 崔慧玲等, 2012; Leel?ssy et al., 2018).然而, 这些研究, 在模式的主要模块、模块的影响因素以及该模块在各模式中模拟能力的差异性等方面的讨论仍比较欠缺.因此, 本文在之前综述研究的基础上, 对模式主流的4个模块:放射性核素的衰变、输送和扩散、大气沉降以及辐射剂量诊断的物理机制和各个模式对这些模块的模拟能力进行系统性的收集、归纳和总结.文章首先对目前核扩散模式的发展做一个系统性的总结, 形成放射性核素扩散模式选择的参考列表, 然后重点对模式组成的4个模块的物理机制、模式应用的差异进行归纳总结, 为有针对性地提高模式模拟能力以及明确模式的发展方向提供科学依据.
2 模式模拟原理(Principle of model simulation)放射性核素释放之后在大气中主要经过输运、扩散、迁移和转化4个过程, 这些过程由大气传输方程描述:
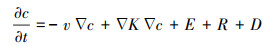 | (1) |
将数值天气预报模式(NWP)和大气扩散模式集于一体, 利用NWP模式模拟气象场由此驱动大气扩散模式, 数值模式通过求解大气传输方程, 输出放射性核素的浓度、沉积量及辐射剂量等结果.
2.1 放射性核素迁移扩散气象预报模式放射性核素的大气运输过程受天气控制, 因此扩散模式需要气象场的驱动.对于简单的局地尺度模拟, 可使用固定监测点的气象观测数据.然而, 单个度量的空间代表性是非常有限的, 三维空间的结构气象参数只能用数值天气预报(NWP)模式来描述.因此模式模拟时将大气扩散模型与NWP模式耦合, 利用NWP模式模拟出大气扩散模式的气象驱动场.扩散模拟的精度很大程度上取决于耦合的NWP模型的精度, 例如进行轨迹计算时, 任何风场数据的不准确, 都是轨迹模式误差的最大来源(Brandt et al., 1998).常见的一些NWP模式有(Pielke, 1984; Pielke et al., 1992; Pielke et al., 1998; Stohl et al., 2002):ALADIN、COAMPS、ECMWF、ETA、GFS、MASS、MM5/WRF和RAMS等.
2.2 放射性核素迁移扩散模式近年来放射性核素迁移扩散模式的基本理论发展得较为成熟, 虽然没有取得突破性的进展, 但是各种模式的应用发展却十分活跃.表 1在Leel?ssy等(2018)的基础上, 补充总结了近年来应用于放射性核素扩散模拟的大气扩散模式, 将各个模式分成高斯模式、拉格朗日模式、欧拉模式、CFD模式以及拉格朗日-欧拉嵌套模式5类, 从模式名称、模式类型、研发机构、模式关注点以及适用范围5个方面, 直观展现近年来相关研究****在核扩散模拟领域的成果.
表 1(Table 1)
| 表 1 一组非详尽的应用于放射性核素扩散模拟的大气扩散模式 Table 1 A non-exhaustive collection of atmospheric dispersion models for dispersion of radionuclides | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 一组非详尽的应用于放射性核素扩散模拟的大气扩散模式 Table 1 A non-exhaustive collection of atmospheric dispersion models for dispersion of radionuclides
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
高斯模型(Mikkelsen et al., 1998; 姚仁太等, 2003; Leel?ssy et al., 2011; Connan et al., 2013; Korsakissok et al., 2013; Jeong et al., 2014)以K理论为基础, 基于稳定状态下, 羽流在x方向上随风速呈非随机变化, 在y方向和垂直z方向呈高斯分布.高斯模型概念清晰, 有较多的假定条件故而模型简单, 运算快速, 在核应急情况下, 能迅速给出模拟结果, 但是模型是基于理想情况简化而来的, 因此与其他模型相比计算结果精度不高(Connan et al., 2013), 该类模型一般适用于核事故早期较短时间且近距离范围内的模拟, 能够迅速地确定放射性核素扩散的大致方向, 采取应急措施.
拉格朗日模型是一组描述许多粒子运动的一阶随机模态, 它是目前放射性核素扩散模拟应用最多且较为成熟的模式, 尤其是在日本福岛核事故中, 应用十分广泛(Chino et al., 2011; Katata et al., 2012a; 2012b; Mcginnity et al., 2012; Stohl et al., 2012; Terada et al., 2012; 李航等, 2013; 梁志超等, 2013; Povinec et al., 2013; 王鹏飞等, 2013; Draxler et al., 2015; Leadbetter et al., 2015; Saito et al., 2015; Mészáros et al., 2016), 该模型侧重于放射性核素扩散轨迹的模拟.对于RAPTAD、LODI和STADIUM模式(Wu et al., 2006; Becker et al., 2007; Bradley, 2007)笔者主要介绍模式的原理.GEARN、FLEXPART、HYSPLIT和NAME等模式用于模拟福岛核事故的放射性核素浓度、干湿沉积量以及剂量率的水平空间分布(Chino et al., 2011; Stohl et al., 2012; Katata et al., 2012a; 2012b; Mcginnity et al., 2012; 李航等, 2013; 梁志超等, 2013; 王鹏飞等, 2013; Leadbetter et al., 2015; Saito et al., 2015; Draxler et al., 2015).核事故往往影响范围很大, 其半衰期通常为几天至几十年, 甚至百年以上, 因此有必要针对其全球扩散影响进行评估.Povinec等(2013)和Mészáros等(2016)分别应用IMS模式和RAPTOR模式, 对福岛事故的全球扩散进行模拟, 结果表明日本福岛事故可在10 d至一个月内显著影响欧洲、北美、亚洲等地区放射性核物质的大气浓度.其它拉格朗日类型的模式包括RIMPUFF、ParModel、MLDP0、SNAP和RePLaT等(余琦, 2000;Saltbones et al., 2000;姚仁太等, 2005;Nelson et al., 2006;Barescut et al., 2012;Rolph et al., 2014;Haszpra, 2016;Leel?ssy et al., 2017;Liu et al., 2017), 这些模式均被应用于相应的事故模拟中, 验证了该类模式在放射性核素长距离扩散模拟中的能力.
欧拉模式基于大气传输方程的数学解, 可以很好地模拟放射性核素的大尺度长距离迁移扩散, 还可以模拟其在垂直方向上的空间分布, 不足之处在于近源模拟和原始方程的闭合问题上存在困难.CMAQ模式(Morino et al., 2011; 聂新旺等, 2012; Morino et al., 2013; 费建芳等, 2014)、WRF-Chem模式(Huh et al., 2013; Hu et al., 2014)用于模拟福岛核事故中放射性核素的浓度以及干湿沉积量的水平空间分布, 另外, 聂新旺等(2014)和费建芳等(2012)还发现, 放射性核素的浓度随高度向东倾斜, 而这一结果是拉格朗日模型无法得到的.此外, 包括法国的ldX模式(Saunier et al., 2013)、日本的SPRINTARS模式(Takemura et al., 2011)、德国的EMAC模式(Christoudias et al., 2013)和EURAD模式(Lujaniene et al., 2013)、美国的GATOR-GCMOM模式(Ten Hoeve et al., 2012)以及芬兰的SILAM模式(Langner et al., 1998)对福岛核事故中放射性核素的全球扩散模拟, 得到的扩散影响范围, 及浓度和沉积的水平空间分布与观测值都较吻合.而在放射性物质的沉降模拟方面, Syrakov等(2009)、张彦等(2008)、Langner等(1998)分别利用欧洲的EMAP模式、日本的CFORS Ⅱ模式以及的瑞典的MATCH模式在放射性核素的衰变及沉积量模拟中的可行性.
CFD是计算流体力学模型(Vach et al., 2011; Vervecken et al., 2015), 通过求解Navier-Stokes方程, 得到复杂的微尺度风场和湍流场.其适用于核电站2 km范围以内, 它可以模拟主流模式的模拟盲区, 对小尺度的扩散模拟有较好的效果.
各种类型的模式都存在本身的固有缺陷, 即使进行了修正优化, 其模拟效果和应用范围仍然受限, 若将两种以上模式嵌套使用, 模式之间取长补短, 会产生较好的效果.Brandt等(2000)将拉格朗日模型与欧拉模型耦合起来, 利用拉格朗日模型计算近源区的初始输运和扩散, 欧拉模型计算远距离的输运和扩散, 得到了很好的模拟效果.
表 1中, 可以用来进行全球尺度模拟的模式有:ParModel(姚仁太等, 2005)、LODI(Bradley, 2007)、MLDP0(Stocki et al., 2012)、IMS(Povinec et al., 2013)、RAPTOR(Mészáros et al., 2016)、STADIUM(Becker et al., 2007)、ldX(Saunier et al., 2013)、SPRINTARS(Takemura et al., 2011)、EMAC(Christoudias et al., 2013)、EURAD(Lujaniene et al., 2013)、GATOR-GCMOM(Ten Hoeve et al., 2012)和SILAM(Paatero et al., 2012)模式, 这些模式都属于拉格朗日粒子模型和欧拉模型, 说明这两种类型的模式在长距离输送和扩散方面较为擅长.
2.3 模式性能评估以2011年3月日本福岛核事故为例, 本研究对比分析了各模式在此次事故中的模拟性能.高斯模式类型中以Px模式为例(Korsakissok et al., 2013), 在事故点周边20 km范围内, Px模式表现较好, 模拟结果中52%的辐射计量率在观测值的2倍之内(FAC2), 而85%的数据在观测值的5倍之内(FAC5).但是在离事故点较远的站点(Iwaki)仅有约9%的数据在FAC2中和16%的数据在FAC5中.同时模拟和观测的分数偏差为0.44, 这表示高估趋势, 相关系数为0.72, 时间价值因数(FMT)为0.43.模拟的峰值到达时间比观测晚6~18 h.相比于高斯模式, 拉格朗日模式模拟的范围更大, 如世界气象组织(WMO)开展的“大气传输-扩散-沉降模式比较”(ATDM)中, 详细比较包括MLDP0、HYSPLIT、NAME、RATM以及FLEXPART在内的18个不同拉格朗日模式和不同参数化方案的模拟结果, 选用的观测数据选择距离事故点110 km的Tokai-mura站点.从对比结果上看, 对137Cs浓度模拟的相关系数为0.1~0.45, 平均百分比偏差FB为-128%~12%, 与《环境空气质量模型遴选工作指南》(下称《指南》)中-67%~67%的要求相比偏差较大, 但多模式集合平均结果为满足《指南》中的要求, 为-50%.137Cs沉降的结果较好, 相关系数在0.7以上, 集合平均FB为-4%.欧拉模式以ldX模式(Saunier et al., 2013)和在环境大气中更为流行的CMAQ模式为例(Morino et al., 2011), ldX模式模拟的3月15—16日期间日本全境内136Cs的活性浓度稍微高估了2~3倍, 137Cs的模拟结果与测量结果较为一致.而131I浓度被高估, 但仍在观测值的2倍之内.从辐射剂量率看, 约80%的模拟结果处在FAC2以内.CMAQ模式结果则表明, 沉降模拟高估约20%的131I和80%137Cs.尽管不同模式模拟结果和观测数据之间存在一些差异, 这很可能是由于排放、运输处理的不确定性以及模型中的沉积过程造成的.当可以获得更准确的排放数据时, 模拟的准确性将会提高.
3 放射性核素扩散迁移模式主要模块(The modules of the radionuclide dispersion models)3.1 放射性衰变绝大多数的核素是不稳定的, 它们会自发的锐变, 变成另一种核素, 同时放出各种射线, 这就叫做放射性衰变.核事故中放射性核素扩散的同时会伴随核素衰变现象, 因此在模拟扩散时需要考虑因核素衰变造成的核素浓度值的降低, 如果模式忽略放射性核素的衰变, 可能会导致模式输出的放射性核素浓度偏高.几乎所有的模式都会考虑核素的放射性衰变, 计算核衰变带来的核素浓度降低, 需要考虑放射性核素本身的性质, 如半衰期等.放射性核素种类众多, 目前大部分模式在应用的时候关注最多的放射性核素是131I和137Cs.在核素的衰变过程中, 关键参量是衰变系数, 与半衰期有关.如果考虑到扩散迁移等过程, 除了衰变系数以外, 直接的浓度也是关键的影响因子, 这就与大气扩散过程直接相关.因此放射性核素在大气中的衰变过程不仅需要考虑不同物质的衰变系数, 同时也需要考虑因大气扩散、沉降等因素引起的浓度变化, 是一个复杂的物理过程.
不同的模式对于放射性衰变会有不同的处理, 这里对几种常用的处理方法进行介绍:①直接独立地计算出因核素衰变造成的核素变化.Nelson等(2006)在文章中给出了NAME模式(拉格朗日粒子)的放射性衰变质量控制方程:
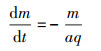 | (2) |
② 将放射性衰变引起的浓度减少作为大气传输方程中的一项.Girard等(2014)在Polair3D模型中的平流扩散方程表示为:
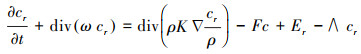 | (3) |
Ten Hoeve等(2012)在GATOR-GCMOM模式中将131I的地表浓度表示为:
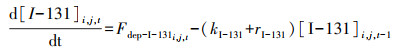 | (4) |
该种方法在各个模式中应用较广, 且多为欧拉模式, 譬如WRF-Chem模式(Hu et al., 2014).
③ 将放射性衰变表示成衰变修正因子考虑到源强的损耗里, 与由干湿沉积引起的损耗一起, 修正源强.CALFUFF模式用的就是这种方法(崔慧玲, 2012), 另外, 高斯烟羽模式(姬文超, 2008; 刘爱华, 2012)也常这样处理核素的放射性衰变:
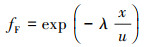 | (5) |
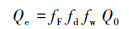 | (6) |
从模式分类上来说, 欧拉模式的放射性衰变多采用第二种方法, 高斯模式和拉格朗日模式多采用第一、三种方法, 但并不绝对.欧拉模式是基于大气传输方程的数学解, 第二种方法将放射性衰变作为大气传输方程的其中一项更贴合欧拉模式的原理, 各个模块相互影响使数值解更精确;第三种方法考虑放射性衰变对源强的损耗, 对源强进行修正, 使输入的源项信息更符合真实情况, 进而提高模式输出的准确性.第二种方法将放射性衰变考虑在模式的物理化学过程, 第三种方法则着眼于模式输入, 二者从不同的角度实现模式模拟结果的优化.从操作难度上看, 第三种方法较简单, 它与放射性核素在大气中的平流输送与扩散是分开的, 因此在放射性核素迁移扩散研究的初期, ****多采用该种方法.模式计算放射性衰变损耗的方法是多样的, 即使各类模式使用的方法都有偏向, 但是选择是自由的, 也可以根据模式的需求进行设计.
3.2 放射性核素的输送与扩散进入大气中的放射性核素, 受大气水平运动、湍流扩散运动, 以及各种不同尺度的扰动运动而被输送、混合和稀释, 称为核素的扩散, 大气的水平运动对核素具有输送作用.由于影响扩散过程的气象条件、地形、下垫面状况及核素本身的复杂性, 放射性核素在大气中的输送与扩散的过程十分复杂.放射性核素的扩散模拟基于大气传输方程(式(1)), 而模式中的大气传输方程多表示为浓度的表达式, 核素的输送与扩散在模式中主要由大气传输方程的平流扩散项和湍流扩散项表征.与放射性衰变一样, 不同的模式, 放射性核素浓度的表达式不同, 笔者以高斯、拉格朗日和欧拉3种不同模式, 对比放射性核素迁移扩散方法.
高斯模式的浓度表达式是在大气传输方程的基础上, 经过各种假设条件, 简化大气传输方程并求解方程的解析式得到的.高斯模式通常假设核素在风场方向的平流输送项远大于湍流扩散项, 湍流扩散项对整个污染物的扩散可忽略(杨晔, 2015).Leel?ssy等(2011)在ALOHA模式中, 将浓度分布表达为:
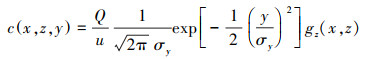 | (7) |
拉格朗日粒子模型主要基于Weil模型, 用大量标记粒子的释放来表征污染物的连续排放, 使它们在流场的平均风中输送, 同时又用一系列的随机位移来模拟湍流扩散, 并跟踪它们的运动轨迹, 最后统计粒子在时间和空间上的总体分布, 从而得出放射性核素的扩散规律(池兵等, 2006).拉格朗日模式采用的坐标随气流一起移动, 因此其输送-扩散方程中不再出现平流项:
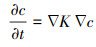 | (8) |
欧拉模式对大气传输方程保留得最为完整, 把实际大气中平流扩散、湍流扩散、放射性衰变、大气沉降及源等因素都考虑到了.Hu等(2014)给出了WRF-Chem模式中欧拉平流-扩散-反应方程:
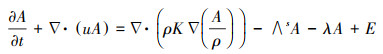 | (9) |
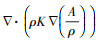
3.3 干、湿沉降和重力沉降在放射性核素的输送和扩散过程中, 沉降是主要机制之一, 沉降的作用是使放射性核素在空气中的浓度降低.在没有降水的条件下, 核素通过碰撞、静电作用、化学反应或气体通过与表面成分或潮湿的溶质发生化学反应而沉积到地面、牧草、作物的叶面上或表面上, 从而使烟羽中的核素浓度降低, 这种效应即为干沉降.依靠地球引力场的作用, 利用核素颗粒与流体的密度差异, 使之发生相对运动而沉降, 即重力沉降, 只有颗粒较大, 气速较小时, 重力沉降的作用才较明显.有降水的条件下, 会造成烟羽中放射性核素的湿沉降, 导致大气中的放射性核素向地面沉积.在放射性核素的全球扩散模拟中, 干沉降作用比湿沉降的影响更为重要, 与局地范围的模拟结果相比, 全球范围的沉降模拟结果与真实情况更接近(Christoudias et al., 2013).对于局地尺度的扩散模拟, 沉降量占放射性核素收支的40%左右(Morino et al., 2011), 对于不同种类的放射性核素干、湿沉降的比例也有所不同.因此, 大气沉降在放射性核素扩散模式中具有重要的作用, 并且不同的模拟尺度对模式沉降模块的要求也不同.
核事故释放的气载放射性核素通常都是较小的粒子(如半径小于μm)或气体, 对于小粒子核素, 随着粒径变小, 重力沉降的作用逐渐可以忽略, 目前的模式大多只考虑干、湿沉降.与放射性衰变类似, 模式对大气沉降过程的处理有两种主流方法:①将其作为模式物理化学过程的重要一项, 与其他项共同作用影响放射性核素浓度, 采用这种方法的多为欧拉模式(Ten Hoeve et al., 2012; Girard et al., 2014; Hu et al., 2014).②将其造成的损耗作为修正因子对源强进行修正, 采用这种方法的多为高斯模式和拉格朗日模式(姬文超, 2008; 崔慧玲, 2012).模式的差异不仅体现在处理方法上, 还体现在不同沉降方案的选择上.
RATM模式(Saito et al., 2015)对于放射性气溶胶粒子, 湿沉降只考虑云下清除过程, 云下湿清除率:
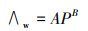 | (10) |
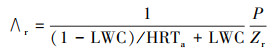 | (11) |
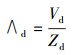 | (12) |
3.4 辐射剂量诊断辐射剂量可以表征放射性核素通过照射对人体产生的危害大小, 是衡量核事故对环境和人体健康的危害性的一个重要指标, 放射性核素主要通过以下几种方式对人体造成辐射损伤, ①烟羽直接造成空气浸没外照射和皮肤外照射;②因干、湿沉积累积在土壤表面对人体造成的地面沉积外照射;③吸入烟羽中的放射性核素对人体产生的吸入内照射;④食入受照植物、动物产品或饮水对人体产生的食入内照射.辐射剂量诊断根据扩散模型输出的各个途径的浓度值, 经过辐射剂量诊断模块估算出相应的辐射剂量对核事故影响进行评估.剂量的估算需要考虑事故的不同阶段, 在事故早期辐射剂量主要由空气浸没外照射、地面沉积外照射和吸入内照射引起的, 事故中后期则主要关注地面沉积外照射、吸入内照射和食入内照射.
根据国际原子能机构(IAEA) (IAEA, 2001)的报告, 各个途径的年有效剂量可通过以下公式计算:
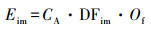 | (13) |
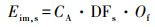 | (14) |
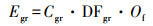 | (15) |
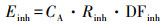 | (16) |
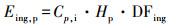 | (17) |
总有效剂量为所有核素的所有照射途径的有效剂量之和, 即
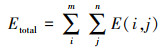 | (18) |
表 2(Table 2)
| 表 2 131I和137Cs有效剂量转换因子 Table 2 The effective dose coefficient of 131I and 137Cs | |||||||||||||||||||||||||||||||||||||
表 2 131I和137Cs有效剂量转换因子 Table 2 The effective dose coefficient of 131I and 137Cs
| |||||||||||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 剂量降低因子Of和呼吸率Rinh Table 3 The fraction of the year for which the hypothetical critical group member is exposed to this particular pathway Of and the inhalation rate Rinh | ||||||||||||
表 3 剂量降低因子Of和呼吸率Rinh Table 3 The fraction of the year for which the hypothetical critical group member is exposed to this particular pathway Of and the inhalation rate Rinh
| ||||||||||||
造成辐射损伤的途径多种多样, 上文也只是列举出最主要的几种方式, 辐射剂量的计算具有一定的复杂性, 很多模式在模拟时没有加入辐射剂量的计算模块.目前考虑了辐射剂量计算的模式主要有:pX模式(Korsakissok et al., 2013)、PRWDA21模式、GEARN模式(Katata et al., 2012)、HYSPLIT模式(Rolph et al., 2014)、ldX模式(Saunier et al., 2013)、Polair3D模式(Girard et al., 2014)、RIMPUFF模式(余琦等, 2000)、CALLPUFF模式(崔慧玲, 2012)、EMAC模式(Christoudias et al., 2013)、WRF-chem模式(胡啸峰等, 2016)、EMAP模式(Syrakov et al., 2009).其中, 前5种模式在目前的研究中只计算了空气浸没外照射的剂量.EMAC模式(Christoudias et al., 2013)可以计算吸入内照射剂量和沉积外照射剂量.WRF-Chem模式(胡啸峰等, 2016)可以估算核电站周边131I和137Cs的空气浸没外照射年有效剂量、地表沉积外照射年有效剂量、吸入内照射年有效剂量和总有效剂量, EMAP模式(Syrakov et al., 2009)能在核事故应用模拟中计算37种不同放射性核素在核事故早期的有效剂量、空气淹没和地面照射的有效剂量、吸入的有效剂量和甲状腺的吸收剂量.由于计算的复杂性和数据的缺乏, 目前这些模式都是针对核事故早期进行辐射剂量评价, 缺少食入内照射有效剂量的估算.
4 问题与展望(Question and prospects)数值模式是模拟放射性核素扩散迁移的有效工具, 越来越多的数值天气预报模式和大气扩散模式被尝试用于放射性核素的扩散模拟, 虽然实现了方法多样化, 但是模式精度的瓶颈依旧无法突破(Leel?ssy et al., 2018).从模拟准确度较差的高斯模式发展到精度更高的拉格朗日模型和欧拉模型, 在模式应用上取得了较大的进步.然而, 放射性核素的扩散模拟不仅与扩散模式有关, 输入源强的准确度、与大气扩散模式耦合的NWP模式的预报效果等, 都与放射性核素扩散模拟精度密切相关.提高模式的模拟结果, 不仅要从扩散模式着手, 还要注重源项的反演以提高输入源强的准确性.目前, 应用于放射性核素扩散模拟的模式众多, 仍有研究者陆续引进新的模式, 若在不断尝试新的大气扩散模式的同时, 兼以考虑源项的反演以及提高气象场精度, 对放射性核素模拟的发展更有价值和意义.另一方面, 提升NWP模式的预报准确性和模式精度, 多次尝试选择最佳的NWP模式与大气扩散模式的耦合方案.将提高模式精度作为另一个目标, 将几百米级别高精度的微尺度扩散模式和中小尺度大气扩散模式耦合, 形成兼顾核应急评估和区域及全球预测为一体的核事故评估系统.同时自适应网格数值模式的发展在核事故的模拟方面也可以起到十分重要的作用.
在模式应用方面, 考虑辐射剂量诊断的模式较少且已有的考虑辐射剂量诊断的模式对辐射剂量的考虑不够全面, 影响辐射剂量的途径是复杂而多样的, 考虑得越全面对辐射剂量的估算更准确, 更能说明核事故或放射性核素释放对人产生的影响情况.若能深入研究辐射剂量诊断的模块, 形成一套对人体健康影响的模型系统, 将非常具有实用性.
5 结论(Conclusions)大气扩散模式被广泛地应用于放射性核素的扩散模拟中, 放射性核素经历放射性衰变、输送和扩散、干湿沉降和重力沉降过程由本地释放到全球.大多数模式都具有区域模拟能力, ParMode、LOD、MLDP0、IMS、RAPTOR、STADIUM、ldX、SPRINTARS、EMAC、EURAD、GATOR-GCMOM和SILAM模式具有模拟全球尺度放射性核素扩散的能力.对于放射性衰变和大气沉降过程, 欧拉模式多将其作为模式物理化学过程的重要一项, 与源项、平流项、湍流项共同作用影响放射性核素浓度;高斯模式和拉格朗日模式通常将其造成的损耗作为修正因子对源强进行修正.辐射剂量是衡量核事故对环境和人体健康的危害性的一个重要指标, 目前pX、PRWDA21、GEARN、HYSPLIT、ldX、Polair3D、RIMPUFF、CALLPUFF、EMAC、WRF-chem、EMAP模式均可应用辐射剂量的估算.
参考文献
| Becker A, Wotawa G, Geer L E D, et al. 2007. Global backtracking of anthropogenic radionuclides by means of a receptor oriented ensemble dispersion modelling system in support of Nuclear-Test-Ban Treaty verification[J]. Atmospheric Environment, 41(21): 4520-4534. DOI:10.1016/j.atmosenv.2006.12.048 |
| Bradley, Michael M. 2007. NARAC: an emergency response resource for predicting the atmospheric dispersion and assessing the consequences of airborne radionuclides[J]. Journal Environmental Radioact, 96(1): 116-121. |
| Brandt J R, Christensen J H, Frohn L M, et al. 2000. Numerical modelling of transport, dispersion, and deposition-validation against ETEX-1, ETEX-2 and Chernobyl[J]. Environmental Modelling & Software, 15(6): 521-531. |
| Brandt J, Bastrup-Birk A, Christensen J H, et al. 1998. Testing the importance of accurate meteorological input fields and parameterizations in atmospheric transport modelling using dream-validation against ETEX-1[J]. Atmospheric Environment, 32(24): 4167-4186. DOI:10.1016/S1352-2310(98)00170-8 |
| 陈达. 2012. 核能与核安全: 日本福岛核事故分析与思考[J]. 南京航空航天大学学报, 44(5): 597-602. DOI:10.3969/j.issn.1005-2615.2012.05.001 |
| 池兵, 方栋, 李红. 2006. 随机游走大气扩散模型在核事故应急中的开发和应用[J]. 核科学与工程, 26(1): 39-45. DOI:10.3321/j.issn:0258-0918.2006.01.007 |
| 崔慧玲. 2012. CALPUFF模式用于放射性核素不同尺度的迁移扩散研究[D]. 太原: 太原理工大学 |
| 崔慧玲, 姚仁太, 徐向军. 2012. 放射性核素长距离迁移模拟研究进展[J]. 辐射防护, 32(4): 240-247. |
| Chino M, Nakayama H, Nagai H, et al. 2011. Preliminary estimation of release amounts of 131I and 137Cs accidentally discharged from the fukushima daiichi nuclear power plant into the atmosphere[J]. Journal of Nuclear Science and Technology, 48(7): 1129-1134. DOI:10.1080/18811248.2011.9711799 |
| Christoudias T, Lelieveld J. 2013. Modelling the global atmospheric transport and deposition of radionuclides from the Fukushima Dai-ichi nuclear accident[J]. Atmospheric Chemistry Physics, 13(3): 1425-1438. DOI:10.5194/acp-13-1425-2013 |
| Connan O, Smith K, Organo C, et al. 2013. Comparison of RIMPUFF, HYSPLIT, ADMS atmospheric dispersion model outputs, using emergency response procedures, with 85Kr measurements made in the vicinity of nuclear reprocessing plant[J]. Journal of Environmental Radioactivity, Journal of Geophysical Research, 117: C11014. DOI:10.1029/2012JC007933 |
| Draxler R, Arnold D, Chino M, et al. 2015. World Meteorological Organization's model simulations of the radionuclide dispersion and deposition from the Fukushima Daiichi nuclear power plant accident[J]. Journal of Environmental Radioactivity, 139: 172-184. DOI:10.1016/j.jenvrad.2013.09.014 |
| Estournel C, Bosc E, Bocquet M, et al. 2012. Assessment of the amount of cesium-137 released into the Pacific Ocean after the Fukushima accident and analysis of its dispersion in Japanese coastal waters[J]. Journal of Geophysical Research, 117(11). |
| 费建芳, 王鹏飞, 程小平. 2014. 日本大地震福岛核污染物扩散传输区域模拟研究[J]. 中国科学: 地球科学, (2): 271-282. |
| Girard S, Korsakissok I, Mallet V. 2014. Screening sensitivity analysis of a radionuclides atmospheric dispersion model applied to the Fukushima disaster[J]. Atmospheric Environment, 95(95): 490-500. |
| Girard S, Mallet V, Korsakissok I, et al. 2016. Emulation and Sobol' sensitivity analysis of an atmospheric dispersion model applied to the Fukushima nuclear accident[J]. Journal of Geophysical Research: Atmospheres, 121(7): 3484-3496. DOI:10.1002/2015JD023993 |
| 郝燕波, 余琦, 曲静原. 2002. 大气扩散模型ATSTEP在核应急决策支持系统中的应用研究[J]. 核动力工程, 23(4): 102-107. DOI:10.3969/j.issn.0258-0926.2002.04.026 |
| 胡啸峰, 陈鹏, 曾昭龙. 2016. 基于WRF的放射性物质大气扩散模拟的环境辐射剂量估算方法[J]. 安全与环境工程, 23(2): 135-142. |
| 黄越承. 2006. 切尔诺贝利事故对健康、环境和社会经济的影响[J]. 中华放射医学与防护杂志, 26(3): 309-312. DOI:10.3760/cma.j.issn.0254-5098.2006.03.045 |
| Haszpra T. 2016. Time-reversibility in atmospheric dispersion[J]. Atmosphere, 7(1). DOI:10.3390/atmos7010011 |
| Hu X, Li D, Huang H, et al. 2014. Modeling and sensitivity analysis of transport and deposition of radionuclides from the Fukushima Daiichi accident[J]. Atmospheric Chemistry and Physics, 14(2): 11065-11092. |
| Huh C A, Lin C Y, Hsu S C. 2013. Regional dispersal of fukushima-derived fission nuclides by East Asia Monsoon[J]. Aerosol & Air Quality Research, 13(2): 8. |
| IAEA, 2001. Generic models for use in assessing the impact of discharges of radioactive substances to the environment[M]. Safety Report Series No. 19, International Atomic Energy Agency, Vienna |
| 姬文超. 2008. 核电站气载放射性核素浓度和辐射剂量计算[D]. 广州: 暨南大学 |
| Jeong H, Park M, Jeong H, et al. 2014. Terrain and building effects on the transport of radioactive material at a nuclear site[J]. Annals of Nuclear Energy, 68(3): 157-162. |
| Katata G, Ota M, Terada H, et al. 2012a. Atmospheric discharge and dispersion of radionuclides during the Fukushima Dai-ichi Nuclear Power Plant accident. Part Ⅰ: Source term estimation and local-scale atmospheric dispersion in early phase of the accident[J]. Journal of Environmental Radioactivity, 109: 103-113. DOI:10.1016/j.jenvrad.2012.02.006 |
| Katata G, Terada H, Nagai H, et al. 2012b. Numerical reconstruction of high dose rate zones due to the Fukushima Dai-ichi Nuclear Power Plant accident[J]. Journal of Environmental Radioactivity, 111(5): 2-12. |
| Korsakissok I, Mathieu A, Didier D. 2013. Atmospheric dispersion and ground deposition induced by the Fukushima Nuclear Power Plant accident: A local-scale simulation and sensitivity study[J]. Atmospheric Environment, 70(4): 267-279. |
| 李航, 张宏升, 蔡旭晖, 等. 2013. 日本福岛核电站泄漏事故污染物扩散的数值模拟与事故释放源项评估[J]. 安全与环境学报, 13(5): 265-270. |
| 梁志超, 费建芳, 程小平. 2013. 地形对日本福岛核事故放射性粒子扩散影响的敏感性研究[J]. 环境科学研究, 26(12): 1259-1267. |
| 刘爱华. 2012. 核设施气载核素浓度及辐射剂量计算研究[D]. 上海: 上海交通大学 |
| 刘爱华, 蒯琳萍. 2011. 放射性核素大气弥散模式研究综述[J]. 气象与环境学报, 27(4): 59-65. |
| Langner J, Robertson L, Persson C, et al. 1998. Validation of the operational emergency response model at the Swedish Meteorological and Hydrological Institute using data from etex and the chernobyl accident[J]. Atmospheric Environment, 32(24): 4325-4333. DOI:10.1016/S1352-2310(98)00175-7 |
| Leadbetter S J, Hort M C, Jones A R, et al. 2015. Sensitivity of the modelled deposition of Caesium-137 from the Fukushima Dai-ichi nuclear power plant to the wet deposition parameterisation in NAME[J]. Journal of Environmental Radioactivity, 139(Sp. Iss. SI): 200-211. |
| Leel?ssy á, Mészáros R, Lagzi I. 2011. Short and long term dispersion patterns of radionuclides in the atmosphere around the Fukushima Nuclear Power Plant[J]. Journal of Environmental Radioactivity, 102(12): 1117-1121. DOI:10.1016/j.jenvrad.2011.07.010 |
| Leel?ssy á, Mészáros R, Kovács A, et al. 2017. Numerical simulations of atmospheric dispersion of iodine-131 by different models[J]. PLOS ONE, 12(2): e0172312. DOI:10.1371/journal.pone.0172312 |
| Leel?ssy á, Lagzi I, Kovács A, et al. 2018. A review of numerical models to predict the atmospheric dispersion of radionuclides[J]. Journal of Environmental Radioactivity, 182: 20-33. DOI:10.1016/j.jenvrad.2017.11.009 |
| Liu Y, Li H, Sun S, et al. 2017. Enhanced air dispersion modelling at a typical Chinese nuclear power plant site: Coupling RIMPUFF with two advanced diagnostic wind models[J]. Journal of Environmental Radioactivity, 175-176: 94-104. DOI:10.1016/j.jenvrad.2017.04.016 |
| Lujaniene G, By?enkien S, Povinec P. 2013. Fukushima radionuclides in Vilnius/Lithuania aerosols: Modelling of aerosol transport[J]. Applied Radiation and Isotopes, 81: 330-334. DOI:10.1016/j.apradiso.2013.03.072 |
| Mcginnity P, Currivan L, Duffy J, et al. 2012. Assessment of the impact on ireland of the 2011 Fukushima Nuclear Accident[R]. Ireland |
| Mészáros R, Vincze C, Lagzi I. 2010. Simulation of accidental release using a coupled transport (TREX) and numerical weather prediction (ALADIN) model[J]. Id?járás, 114(3): 101-120. |
| Mészáros R, Leel?ssy á, Kovács T, et al. 2016. Predictability of the dispersion of Fukushima-derived radionuclides and their homogenization in the atmosphere[J]. Scientific Reports, 6: 19915. DOI:10.1038/srep19915 |
| Mikkelsen T, Thykiernielsen S, Astrup P, et al. 1998. MET-RODOS: A comprehensive atmospheric dispersion module[J]. Radiation Protection Dosimetry, 73(73): 45-56. |
| Morino Y, Ohara T, Watanabe M, et al. 2011. Atmospheric behavior, deposition, and budget of radioactive materials from the Fukushima Daiichi nuclear power plant in March 2011[J]. Geophysical Research Letters, 38(7). DOI:10.1029/2011GL048689 |
| Morino Y, Ohara T, Watanabe M, et al. 2013. Episode analysis of deposition of radiocesium from the Fukushima Daiichi Nuclear Power Plant Accident[J]. Environmental Science & Technology, 47(5): 2314-2322. |
| 聂新旺, 王益柏, 孙守勋, 等. 2012. 应用Models-3/CMAQ对2011年3月日本福岛核泄漏的数值研究[J]. 气象, 38(10): 1182-1188. DOI:10.7519/j.issn.1000-0526.2012.10.003 |
| Nelson N, Kitchen K P, Maryon R H. 2006. A study of the movement of radioactive material discharged during the windscale fire in October 1957[J]. Atmospheric Environment, 40(1): 58-75. DOI:10.1016/j.atmosenv.2005.08.013 |
| 潘自强. 2000. 核事故对健康与环境的影响[J]. 核科学与工程, 20(3): 205-210. DOI:10.3321/j.issn:0258-0918.2000.03.003 |
| Paatero J, Vira J, Siitari-Kauppi M, et al. 2012. Airborne fission products in the high Arctic after the Fukushima nuclear accident[J]. Journal of Environmental Radioactivity, 114: 41-47. DOI:10.1016/j.jenvrad.2011.12.027 |
| Pielke R A. 1984. Mesoscal meteorological modeling[M]. San Diego: Academic Press, 1-2. |
| Pielke R A, Cotton W R, Walko R L, et al. 1992. A comprehensive meteorological modeling system-RAMS[J]. Meteorology and Atmospheric Physics, 49(1): 69-91. |
| Pielke R A, Uliasz M. 1998. Use of meteorological models as input to regional and mesoscale air quality models-limitations and strengths[J]. Atmospheric Environment, 32(8): 1455-1466. DOI:10.1016/S1352-2310(97)00140-4 |
| Povinec P P, Gera M, Holy' K, et al. 2013. Dispersion of Fukushima radionuclides in the global atmosphere and the ocean[J]. Appl Radiat Isot, 81(2): 383-392. |
| Rolph G D, Ngan F, Draxler R R. 2014. Modeling the fallout from stabilized nuclear clouds using the HYSPLIT atmospheric dispersion model[J]. J Environ Radioact, 136: 41-55. DOI:10.1016/j.jenvrad.2014.05.006 |
| Saito K, Shimbori T, Draxler R. 2015. JMA's regional atmospheric transport model calculations for the WMO technical task team on meteorological analyses for Fukushima Daiichi Nuclear Power Plant accident[J]. Journal of Environmental Radioactivity, 139: 185-199. DOI:10.1016/j.jenvrad.2014.02.007 |
| Saltbones J R, Foss A, Bartnicki J. 2000. Threat to Norway from potential accidents at the Kola nuclear power plant. Climatological trajectory analysis and episode studies[J]. Atmospheric Environment, 34(3): 407-418. DOI:10.1016/S1352-2310(99)00246-0 |
| Saunier O, Mathieu A, Didier D, et al. 2013. An inverse modeling method to assess the source term of the Fukushima Nuclear Power Plant accident using gamma dose rate observations[J]. Atmospheric Chemistry and Physics, 13(22): 11403-11421. DOI:10.5194/acp-13-11403-2013 |
| Stocki T J, Ungar R K, D'amours R, et al. 2012. North Korean nuclear test of October 9th, 2006:The utilization of health Canada's radionuclide monitoring network and environment Canada's atmospheric transport and dispersion modelling[J]. Radioprotection, 46(6): S529-S534. |
| Stohl A, Eckhardt S, Forster C, et al. 2002. A replacement for simple back trajectory calculations in the interpretation of atmospheric trace substance measurements[J]. Atmospheric Environment, 36(29): 4635-4648. DOI:10.1016/S1352-2310(02)00416-8 |
| Stohl A, Seibert P, Wotawa G, et al. 2012. Xenon-133 and caesium-137 releases into the atmosphere from the Fukushima Dai-ichi nuclear power plant: determination of the source term, atmospheric dispersion, and deposition[J]. Atmospheric ChemIstry and Physics, 12(5): 2313-2343. |
| Syrakov D, Veleva B, Prodanova M, et al. 2009. The Bulgarian Emergency Response System for dose assessment in the early stage of accidental releases to the atmosphere[J]. Journal of Environmental Radioactivity, 100(2): 151-156. |
| Takemura T, Nakamura H, Takigawa M, et al. 2011. A numerical simulation of global transport of atmospheric particles emitted from the Fukushima Daiichi Nuclear Power Plant[J]. SOLA, 7: 101-104. |
| Ten Hoeve J E, Jacobson M Z. 2012. Worldwide health effects of the Fukushima Daiichi nuclear accident[J]. Energy & Environmental Science, 5(9): 8743-8757. |
| Terada H, Katata G, Chino M, et al. 2012. Atmospheric discharge and dispersion of radionuclides during the Fukushima Dai-ichi Nuclear Power Plant accident. Part Ⅱ: verification of the source term and analysis of regional-scale atmospheric dispersion[J]. Journal of Environmental Radioactivity, 112(5): 141-154. |
| Vach M, Duong V M. 2011. Numerical modeling of flow fields and dispersion of passive pollutants in the vicinity of the Temelín Nuclear Power Plant[J]. Environmental Modeling & Assessment, 16(2): 135-143. DOI:10.1007/s10666-010-9239-x |
| Vervecken L, Camps J, Meyers J. 2015. Dynamic dose assessment by Large Eddy Simulation of the near-range atmospheric dispersion[J]. Journal of Radiological Protection, 35(1): 165-178. |
| 王鹏飞, 费建芳, 程小平, 等. 2013. 气旋活动对福岛核污染物扩散影响的模拟研究[J]. 环境科学研究, 26(1): 50-56. |
| Wu J, Lu C H, Chang S J, et al. 2006. Three-dimensional dose evaluation system using real-time wind field information for nuclear accidents in Taiwan[J]. Nuclear Inst & Methods in Physics Research A, 565(2): 812-820. |
| 杨晔. 2015. 基于拉格朗日粒子模型的放射性核素迁移模拟研究[D]. 北京: 华北电力大学 |
| 姚仁太, 郝宏伟, 胡二邦, 等. 2003. RODOS系统中两种大气弥散模型链的比较[J]. 辐射防护, 23(3): 146-155. |
| 姚仁太, 徐向军, 郝宏伟, 等. 2005. 远东地区核风险厂址释放的气载放射性污染物长距离迁移的模拟[J]. 辐射防护, 25(4): 193-205. |
| 余琦, 刘原中. 2000. 拉格朗日烟团模型在核事故早期应急决策中的应用[J]. 清华大学学报(自然科学版), 40(12): 6-9. |
| 余琦, 刘原中. 2001. 分段烟羽模型和烟团模型在核事故应急中的应用比较[J]. 核科学与工程, 21(3): 288-292. |
| 张彦. 2008. 高空核试验放射性烟云扩散的数值模拟研究[J]. 安全与环境学报, 8(3): 115-121. |
| 张彦, 郑毅, 王自发. 2008. 基于RAMS/CFORS Ⅱ模式一次低空核试验放射性烟云扩散的数值模拟[J]. 气候与环境研究, 13(6): 717-726. |
