 , 赵胜豪2, 廖朋辉2, 钱瑜1,3
, 赵胜豪2, 廖朋辉2, 钱瑜1,3

1. 南京大学污染控制与资源化研究国家重点实验室, 南京 210023;
2. 南京国环科技股份有限公司, 南京 210042;
3. 南京大学环境学院, 南京 210023
收稿日期: 2020-04-27; 修回日期: 2020-06-12; 录用日期: 2020-06-12
基金项目: 国家重点研发计划项目(No.2016YFC0207603)
作者简介: 刘泽宇(1996-), 男, E-mail:zyliu0830@foxmail.com
通讯作者(责任作者): 钱瑜, E-mail:yqian@nju.edu.cn
摘要:场地污染调查是开展场地风险评估和修复的基础,随着我国颁布建设用地土壤风险管控标准等文件,提出风险筛选值和管制值的分级管控体系,我国土壤污染调查工作对于精确掌握污染物浓度梯度及空间分布有了更高的要求,因而如何构建高效采样布点方法变得尤为重要.本研究以南京市某砷工业污染场地为例,开展了优化布点方法与调查精度的研究.首先,在初查数据的基础上,运用指示克里格的方法预测土壤污染概率,参考城市土壤背景值开展阈值设定,提取加密布点区域,之后结合场地历史生产资料与自然信息布设加密点位,最终将插值预测污染结果与非加密、均匀加密、真实情况结果进行对比,验证方法精度.结果表明:本方法符合国际中基于设计抽样以达到场地调查简单、经济、客观的理念,适用于数据存在明显空间相关性的场地;该方法获得的污染区域面积占比为8.32%,与8.57%的现实情况较为接近,但普通法得到的污染面积比相对未加密情况不升反降,可能的原因是在非污染区域增设点位会造成阈值边缘区域在模拟时往清洁区域偏移,污染区域被误判为清洁,反而造成结果偏差;在目前我国环境管理对超阈范围重点关注的背景下,该方法既能够节约布点成本,又精确化预测场地污染超标范围,为后续的场地修复和治理工作提供帮助.
关键词:土壤污染调查优化布点指示克里格精度对比
Optimization and accuracy comparative analysis of sampling methods in an Arsenic pollution site survey
LIU Zeyu1,3
 , ZHAO Shenghao2, LIAO Penghui2, QIAN Yu1,3
, ZHAO Shenghao2, LIAO Penghui2, QIAN Yu1,3

1. State Key Laboratory of Pollution Control and Resource Reuse, Nanjing 210023;
2. Nanjing Guohuan Science and Technology Co, Nanjing 210042;
3. School of the Environment, Nanjing University, Nanjing 210023
Received 27 April 2020; received in revised from 12 June 2020; accepted 12 June 2020
Abstract: Contaminated site survey, as the basis of risk assessment and remediation, should be accurate in describing pollutant concentration and spatial distribution because of the stringent Soil Environmental Quality Risk Control Standard in China, which stipulated a multilevel risk control system. Therefore, it's important to study on sampling methods with both high efficiency and high accuracy. In the case of an Arsenic polluted industrial site in Nanjing, indicator kriging method was used to predict pollution probability of the whole site according to the first-round regular investigation with 82 sampling points. Then high pollution area was identified and 20 more sampling points were located in these area. Finally, Arsenic distribution was simulated in four situations including regular sampling, high pollution probability sampling (20 more calculated points), common increased sampling (20 more random points), and fully increased sampling (100 more points), and the investigation accuracy was evaluated. The results show that sampling based on contamination probability forecast is in accordance with the principal of simple, economical and objective, and is an optimized method for sites with large spatial difference of pollution. The proportion of Polluted areas calculated by this method is 8.32%, close to 8.57% obtained from the fully increased sampling, which could be considered as the real situation. While the proportion of common increased sampling is even lower than the regular situation with only first-round sampling, indicating that more sampling points in unpolluted area could make miscarriage and deviation. In conclusion, the sampling method based on kriging interpolation can guarantee the survey accuracy in limited cost, and provide support for contaminated site remediation scientifically.
Keywords: contaminated site surveysampling optimizationindicator kriging methodaccuracy comparison
1 引言(Introdution)土壤场地调查作为获得污染空间分布信息与环境状况的重要手段, 其调查结果的精度将对场地后续的污染风险评价与决策管理的合理性产生直接的影响(谢云峰等, 2016).在场地调查全过程中, 点位布设、样品采集、运输、含量分析等不同的环节皆会给调查结果带来误差, 但由于土壤污染流动性差, 场地常伴随明显的污染空间异质性和不连续性(李锋等, 2019), 因此在土壤调查过程中对点位位置进行优化相较于提高样品检验精度或采样精度更能影响结果(Crumbling et al., 2001; Theocharopoulos et al., 2001), 尤其是在工业场地中.Jenkins等对土壤中三硝基甲苯的污染研究表明, 至少95%的变异度是由于调查点位布设所带来的, 而含量分析对于变异度的影响比例不超过5%(Jenkins et al., 1997).Gustavsson等发现在土壤污染调查研究中, 抽样误差是分析误差的20倍以上(Bj?rn et al., 2006).因此, 科学合理地选择采样布点方法, 将会是获得场地精准调查结果的重要保障.
目前, 实际工作与科研中运用较多的土壤调查布点方法主要包括判断性布点和非判断性布点两类(姜成晟等, 2009).我国的《场地环境监测技术导则》(HJ25.2-2014)也对不同的点位布设方法进行了阐述.判断性布点是在掌握了背景信息的基础上, 于潜在污染嫌疑较大的区域进行增设点位, 即加密布点;而非判断性布点则是在缺乏场地相关信息时, 只能选择采取的加密方法, 如网格布点法、系统随机布点法等.但因为目前在我国土壤污染防治过程中, 尤为关注污染超标区域的位置、范围、污染程度, 如2018年颁布的《建设用地土壤污染风险管控标准》(GB36600-2018)与《农用地土壤污染风险管控标准》(GB15618-2018)中对土壤各类污染物划定了筛选值与管制值, 对于超过不同限值的情况后续需采取不同应对措施.因此, 如何在节约成本的基础上, 优化布设点位, 精准获取污染超标区域实际情况, 将对于后续的土壤污染防治工作带来巨大帮助.
近年来, 运用地统计学方法进行土壤污染调查与加密布点的研究成为了热点之一(Kai-Wei et al., 2005; 谢云峰等, 2016; Fernando et al., 2017; Hashemi et al., 2017; Ersoy et al., 2018; 郝易成等, 2019; Eljebri et al., 2019; 林莎等, 2020).该方法是基于土壤污染的空间自相关, 运用空间插值或条件模拟方法, 预测污染分布、优化布点方案、提高模拟精度(Barth et al., 1984).也有研究对不同加密位置和数量的预测结果进行对比, 发现加密点数量并非越多越能提高估计精度(郝易成等, 2019).总体来说, 国际中已有不少相关研究, 但我国结合本土实际情况所提出的土壤加密布点方法研究还相对较少, 且从污染超标区域的角度分析的研究也欠缺.因此本研究以南京市某工业场地中污染空间异质性较大的重金属砷(As)为研究对象, 从分析污染超标区域的角度, 对比未加密布点、普通均匀加密法(简称普通法)与污染概率加密法(简称概率加密法)的各类预测结果, 分析差异与原因, 希望能为后续工业场地污染调查与修复工作提供参考与帮助.
2 材料与方法(Materials and methods)2.1 研究场地概况研究区位于江苏省南京市雨花台区, 规划用地面积101572 km2(约152.4亩), 具体位置为龙翔路以南、经九路以东、机场二通道以西、纬四路以北.该区域自20世纪70年代陆续建设8家单位, 主要为化工企业和研究所, 部分企业曾生产农药如喹诺酮, 而砷作为许多农药的原料之一也被大量使用.该场地全部单位于2015年前后完成搬迁及拆除, 并改变为居住用地, 规划建设单身公寓.根据国家和地方相关法律法规要求, 为保障地块再开发利用的环境安全, 须对该地块开展污染调查.
2.2 数据采集结合场地原工厂分布情况与实际地理状况, 参考20 m×20 m网格, 生产区布点间距控制为40 m左右, 非生产区布点间距适当稀疏, 本案例初查点位为82个(图 1), 后续再次布点100个, 共182个样点, 每个样点均采用五点法采样, 采样深度为20 cm.为防止采样机械对于样品的污染, 运用采样机器提取的土壤需要用木铲进行剔除筛选后采样.
图 1(Fig. 1)
 |
| 图 1 场地土壤初查点位布设图 Fig. 1Locations of initial sampling sites |
2.3 样品测定土壤样品中的砷测定按照《土壤质量总汞、总砷、总铅的测定》(GB-T 22105.2—2008)的要求, 经加热消解后, 按序加入硫脲与硼氢化钾, 由氩气导入石英原子化器进行原子态转化, 后采用荧光光度计进行检测, 根据荧光光度进行砷浓度定量.
2.4 研究方法2.4.1 土壤污染调查加密布点方法本研究为解决区域土壤局部污染超标明显的问题, 提出基于污染概率的土壤调查加密布点方法.首先通过土壤污染初步调查布点的情况判定是否存在明显局部超标区域, 若存在, 则采用概率制图方法求取场地污染超标概率, 通过划定阈值提取符合区域作为后续加密布点的区域.
概率制图方法包括有地统计条件模拟法、指示克里格法等, 因本研究数据为非正态有偏数据, 因而采用指示克里格法.指示克里格法是一种常用的地质统计学方法, 属于非线性克里格方法的范畴, 它表示某点超过预先设定的一个阈值概率, 其能在不必去除重要而实际存在的特异质条件下保证模拟的有效性, 适用于非正态数据.该方法也在大量土壤研究中普遍使用(赵玉杰等, 2009; 杨奇勇等, 2011; 吕建树等, 2012; 刘玉娟等, 2014).通过指示克里格求取的污染概率取值范围为0~1, 值越高则代表污染超标的可能性越大, 即越可能为污染土壤, 反之则越可能为清洁土壤(Xie et al., 2011; 刘庚等, 2013).
在获得污染概率范围后, 根据相应方法设定阈值, 划分清洁与污染土壤.因城市土壤背景值常在指示克里格法中被用作阈值(刘玉娟等, 2014), 本研究以此为基础进行适度变换, 以南京市土壤砷背景值为界, 假设超过背景值则为受到污染, 在总体布点插值结果上划定污染区域作为对照组, 然后划分不同概率阈值, 如0.2、0.3等, 分析不同情况下所得污染区域与对照组的契合性, 通过面积契合性对比与误差分析, 阈值为0.2情况下结果最佳, 因此设定0.2为本研究最终阈值.确定阈值后将所划污染区域作为后续加密区域.
获得加密区域后, 结合场地历史生产资料与自然信息等选择适宜位置进行加密.如原本为工厂生产区、原料或废物储藏区等污染嫌疑较大, 且恰好处于加密范围内的区域, 则需要重点多布设点位.
同时为进行对比, 在场地均匀布设同等数量的加密点位, 作为普通加密布点方案;并在两类加密点位与初查点位的基础之上, 继续均匀布设至182个点位, 统称总体点位.理论上布设点数量越多, 插值结果越接近于真实情况, 因此假设以总体点位的预测结果近似代表案例区土壤真实情况.
2.4.2 加密精度分析方法因重点关注污染区域, 所以能否精确表示污染区域范围便作为反应方法精度的指标.本研究参照《土壤环境质量建设用地土壤风险管控标准(试行)》(GB36600—2018), 通过数据正态转换和半变异函数拟合后, 运用普通克里格分别对总体点位、初查点位、普通加密点位、污染概率加密点位进行污染区域预测, 通过将预测区域栅格化, 通过计算各单元格的预测平均浓度, 划分是否属于污染超标区域, 从而统计污染区域面积及其占比.
以总体点位预测的污染范围与面积为参照, 分别对未加密点位、普通法、概率加密法的预测结果进行污染区域面积定量对比与污染范围定性对比, 并求取不同加密方法的效率.式(1)为精度计算方法, 式(2)为布点效率计算方法.
 | (1) |
 | (2) |
2.5 数据处理工具土壤点位砷浓度数据的正态转化与描述性统计运用SPSS完成, 空间结构分析和半变异拟合采用GS+7.0软件.污染概率求取、空间插值、污染制图与空间统计运用GIS 10.5软件.
3 结果与讨论(Results and discussion)3.1 加密布点结果对82个初查点位进行描述性统计分析, 原始数据不符合正态分布, 最大值为87.90 mg·kg-1, 最小值为1.33 mg·kg-1, 均值为13.61 mg·kg-1.
基于初查点位数据, 以砷的筛选值20.00 mg·kg-1作为阈值, 运用指示克里格法插值获得的污染概率分布图(图 2a), 污染概率范围为0~0.8, 高值区域主要集中在场地西北角, 其他位置存在轻度起伏, 但整体污染概率偏低, 可能的原因为区域污染含量偏低或样本量少(谢云峰等, 2016).结合南京市土壤背景值, 通过对比不同阈值下的污染区域重叠性及误差分析, 设定拟合效果最好的0.2为最终阈值, 提取出概率0.2~0.8的污染区域(2b).
图 2(Fig. 2)
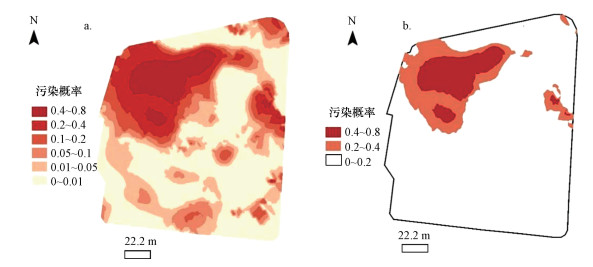 |
| 图 2 污染概率分布图 (a.运用指示克里格预测的污染概率分布图;b.提取的加密区域) Fig. 2Map of contamination probability |
以提取出的污染区域作为概率加密区域, 结合场地原始生产资料与自然信息, 并考虑数据的有限性, 于区域内布设20个加密点位, 作为概率加密方案(图 3a); 同时于全场地内均匀布设等量点位作为普通加密方案(图 3b).
图 3(Fig. 3)
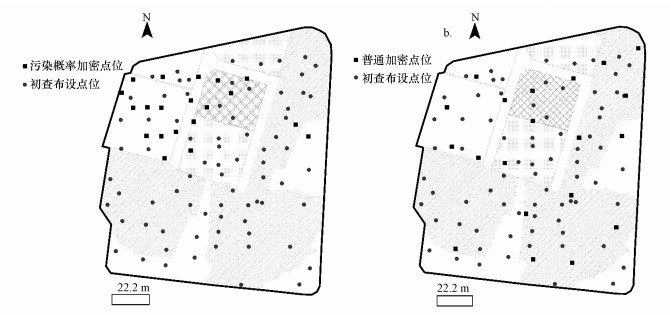 |
| 图 3 加密布点图 (a.基于污染概率加密布点图;b.普通加密布点图) Fig. 3Map of sampling design optimization |
3.2 精度分析结果及讨论分别针对初查点位、普通加密点位、概率加密点位、总体点位的污染数据进行描述性统计, 并通过正态转换、半方差函数拟合, 运用普通克里格模拟各方案下的污染分布情况, 通过GIS将结果栅格转换、划分区域网格后统计独立网格平均污染浓度超标个数, 最终计算污染面积并开展污染范围制图, 结果见图 4与表 1.
图 4(Fig. 4)
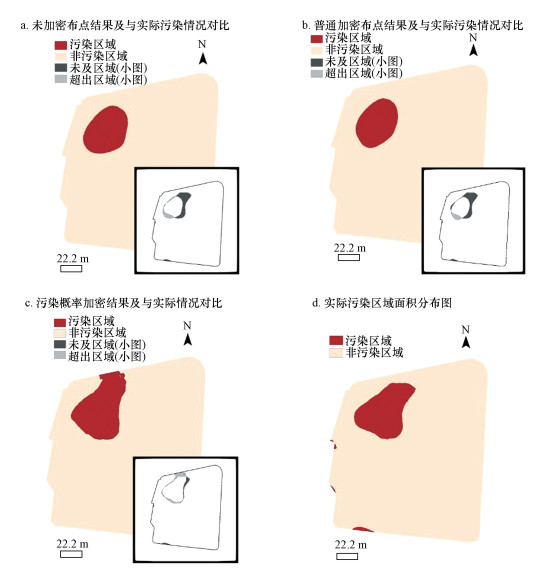 |
| 图 4 污染区域分布及对比图 (a.未加密布点污染区域图;b.普通加密布点污染区域图;c.污染概率加密污染区域图;d.实际污染区域图) Fig. 4Map of pollution area and comparison |
表 1(Table 1)
| 表 1 各布点情况统计分析结果 Table 1 Statistical analysis results of each sampling situation | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 1 各布点情况统计分析结果 Table 1 Statistical analysis results of each sampling situation
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
由表 2可得, 几种布点情况下半变异函数的R2分别为0.71、0.79、0.83, 表明数据经过变换后拟合的半变异函数都能取得稳健的效果, 能够满足克里格插值的要求.普通与概率加密法块金值(C0)与基台值(C0+C)的比值分别为8.13%和0.2%, 表明两种加密方法的数据都具有较强的空间相关性, 后者的空间相关性尤为明显.变程两者分别为53.90和52.60, 表明两者空间相关性作用范围相差不大.
在面积精度对比上, 总体布点获得的污染面积占区域整体面积8.57%, 前文中假设了以总体布点结果代表真实情况, 即场地实际污染面积占比为8.57%.而未进行加密布点的初查布点求取占比为5.37%, 与实际情况存在较大偏差;普通法污染面积占比仅5.12%, 相比未加密情况面积预测效果反而下降, 可能的原因是基于克里格法的原理, 于非污染区域增多布设点位比例(由均值从13.61下降为13.32可得)反而会使部分阈值边缘区域在模拟时往清洁区域偏移, 造成原本为污染区域误判为清洁区域;污染概率加密布点的占比为8.32%, 明显接近于真实情况, 表明运用该方法能有效提高污染面积预测精度.通过计算, 在本案例内普通法和概率加密法布设每个加密点位的精度效率为-0.15%与1.72%.
根据图 4也可对结果开展定性判断, 概率加密法求取的污染面积图对比阴影更少, 更接近于实际污染状况, 而未加密布点污染面积图、普通法污染面积图与实际情况相差较大, 尤其是变化边界处, 存在明显差异.
3.3 不足与局限本研究亦存在不足与局限, 具体如下:①若以平方根误差(RMSE)的角度来评判, 该方法效果相较于普通加密布点并不能带来明显提高.即该方法适用于高效确定污染超标区域, 但若想获得场地较精确的污染全面空间分布特征, 此方法并不适用.②本研究通过假设总体布点模拟结果为真实情况, 本身即会带来一定的误差.而污染概率加密法中于加密区域进行点位位置选择是基于场地历史生产分布情况、自然信息等进行人为的选择, 并不一定是最佳布设点位, 因而对于预测结果精度会带来影响.若后续继续开展深入研究, 则需要针对点位的合理选择继续优化.③因加密方法仅布设20个点位, 于场地边界处并未加设点位, 并未有效模拟出场地边界处的污染情况.因而才会出现总体布点污染超标范围图中西与西南方向边界处有狭小污染超标区域但加密方法的图中没有.这也是此加密方法的局限, 若加密点位皆布设在场地内部而非边界, 则对于边界污染状况预测精度较低.
4 结论(Conclusions)本研究提出的加密方法核心原理为通过确定污染嫌疑较大的区域, 根据污染物的空间分布规律加设点位从而提高污染超标面积预测精度, 符合国际中提出的基于设计的抽样以达到场地调查简单、经济、客观的目的(Patrick et al., 2020).与目前基于模拟退火算法的各类加密方法相似, 皆为基于初步结果进行再次参数化计算, 以达到优化点位区域的效果(Gábor et al., 2019; 李佳燕, 2019).且该方法适用于数据存在明显空间相关性的场地, 如工业场地中多环芳烃、重金属等存在较强空间相关性的情况下(Wang et al., 2013; 钟山等, 2014).
以往的研究经验表示, 在区域内布设点位越多, 调查的结果应越接近于真实情况.但计算结果反映普通法得到的污染面积比相对未加密情况不升反降, 反而偏离真实情况.造成的主要原因可能为在非污染区域增多点位反而会使部分阈值边缘区域在模拟时往清洁区域偏移, 使得污染区域被误判为清洁区域, 造成结果偏差.郝易成等也在研究中提到, 若在不合适的区域加密布点反而会降低效率(郝易成等, 2019).该结果可能是由于局部案例的特殊性造成, 但具有一定借鉴意义.
概率加密法的预测结果为8.32%, 相较于普通法的5.12%明显接近于真实情况, 该结果也与谢云峰等人的研究结果相似, 在其研究中提出的加密方法将污染区面积的估计误差降低至4.10%(谢云峰等, 2016).综上, 说明针对局部区域污染浓度明显偏高的场地, 运用科学方法在污染嫌疑大的区域内加设点位能在优化点数的基础上大大提高污染超标范围的预测精度.因而鉴于目前我国突然管理中对于超阈范围的重点关注, 污染概率加密法能在实际工作中既节约布点成本, 又较精确预测获得场地污染超标范围, 提高调查效率, 有助于后续的场地修复和治理.
综上, 本研究结合国内外加密布点经验, 结合我国城市土壤背景值与工业场地特征, 提出一套基于污染概率的加密布点方法.能够在目前我国环境管理中对于超阈范围重点关注的背景之下, 既节约布点成本, 又较精确地预测场地污染超标范围, 使得调查效率提高, 为后续的场地修复和治理工作提供帮助.
参考文献
| Barth D S, Mason B J. 1984. Soil sampling quality assurance user's guide[J]. N.V. EPA, 600/4-84-043. |
| BJ?RN G, Karin L, Andres L. 2006. Comparison of analytical error and sampling error for contaminated soil[J]. Journal of Hazardous Materials, 138(2): 252-260. DOI:10.1016/j.jhazmat.2006.01.082 |
| Crumbling D M, Lynch K, Howe R, et al. 2001. Peer Reviewed:Managing uncertainty in environmental decisions[J]. American Chemical Society, 19: 404A-409A. |
| Eljebri S, Mounir M, Faroukh A T, et al. 2019. Application of geostatistical methods for the spatial distribution of soils in the irrigated plain of Doukkala, Morocco[J]. Springer International Publishing, 5(2): 669-687. |
| Ersoy A, Yünsel T Y. 2018. The assessment of soil contamination by heavy metals using geostatistical sequential Gaussian simulation method[J]. Taylor & Francis, 24(8): 2142-2161. |
| Fernado S F, Antonio M G, ávila Z C, et al. 2017. Spatial distribution of heavy metals and the environmental quality of soil in the northern plateau of Spain by geostatistical methods[J]. Pubmed, 14(6): 568. |
| Gábor S, Péter L, Katalin T, et al. 2019. Optimization of second-phase sampling for multivariate soil mapping purposes:Case study from a wine region, Hungary[J]. Geoderma, 352: 373-384. DOI:10.1016/j.geoderma.2018.02.030 |
| 郝易成, 师华定, 白中科, 等. 2019. 土壤污染调查加密布点区域优化及效率研究[J]. 农业环境科学学报, 38(5): 1036-1042. |
| Hashemi M, Ahanger A G, Bameri A, et al. 2017. Survey and zoning of soil physical and chemical properties using geostatistical methods in GIS (Case study:Miankangi region in Sistan)[J]. Directory of Open Access Journals, 30(2): 443-458. |
| 姜成晟, 王劲峰, 曹志冬. 2009. 地理空间抽样理论研究综述[J]. 地理学报, 64: 368-380. |
| Jenkins T F, Grant C L, Brar G S, et al. 1997. Sampling error associated with collection and analysis of soil samples at TNT-contaminated sites[J]. Field Analytical Chemistry & Technology, 1(3): 151-163. |
| Kai W J, Dar Y L, Yun L T. 2005. Adaptive sampling based on the cumulative distribution function of order statistics to delineate heavy-metal contaminated soils using kriging[J]. Pubmed, 138(2): 268-277. |
| 李锋, 刘思源, 李艳, 等. 2019. 工业发达城市土壤重金属时空变异与源解析[J]. 环境科学, 40: 934-944. |
| 李佳燕. 2019.基于模拟退火算法的矿区复垦土壤监测样点布设研究[D].北京: 中国地质大学(北京) |
| 林莎, 贺康宁, 王莉, 等. 2020. 基于地统计学的黄土高寒区典型林地土壤水分盈亏状况研究[J]. 生态学报, 40: 728-737. |
| 刘庚, 毕如田, 张朝, 等. 2013. 某焦化场地苯并(a)芘污染空间分布范围预测的不确定性分析[J]. 环境科学学报, 33: 587-593. |
| 刘玉娟, 喻根, 郭旻欣. 2014. 淮南土壤Pb含量的指示克里格估值研究[J]. 安徽农业科学, 42: 2870-2871+2889. |
| 吕建树, 张祖陆, 刘洋, 等. 2012. 日照市土壤重金属来源解析及环境风险评价[J]. 地理学报, 67: 971-984. |
| Patrick G, Wayne Roper L, Thomas F, et al. 2020. Guiding soil sampling strategies using classical and spatial statistics:A review[J]. Agronomy Journal, 112(1): 493-510. DOI:10.1002/agj2.20048 |
| Theocharopoulos S P, Wagner G, Sprengart J, et al. 2001. European soil sampling guidelines for soil pollution studies[J]. Science of the Total Environment, 264(1/2): 51-62. |
| Wang X T, Miao Y, Zhang Y, et al. 2013. Polycyclic aromatic hydrocarbons (PAHs) in urban soils of the megacity Shanghai:Occurrence, source apportionment and potential human health risk[J]. Science of the Total Environment, 447: 80-89. DOI:10.1016/j.scitotenv.2012.12.086 |
| 谢云峰, 曹云者, 杜晓明, 等. 2016. 土壤污染调查加密布点优化方法构建及验证[J]. 环境科学学报, 36: 981-989. |
| Xie Y F, Chen T B, Li M, et al. 2011. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods:accuracy and uncertainty analysis[J]. Chemosphere, 82(3): 468-476. DOI:10.1016/j.chemosphere.2010.09.053 |
| 杨奇勇, 杨劲松, 余世鹏. 2011. 禹城市耕地土壤盐分与有机质的指示克里格分析[J]. 生态学报, 31: 2196-2202. |
| 钟山, 高慧, 张漓衫, 等. 2014. 平原典型垃圾焚烧厂周边土壤重金属分布特征及污染评价[J]. 生态环境学报, 23(1): 164-169. |
| 赵玉杰, 唐世荣, 李野, 等. 2009. 普通及指示克里格法在水稻禁产区筛选中的应用[J]. 环境科学学报, 29: 1780-178. |
