 , 胡东滨1,2
, 胡东滨1,2
 , 李权3
, 李权31. 中南大学 商学院, 长沙 410083;
2. 湖南省两型社会与生态文明协同创新中心, 长沙 410083;
3. 中国地质大学(武汉) 环境学院, 武汉 430074
收稿日期: 2020-02-14; 修回日期: 2020-04-09; 录用日期: 2020-04-09
基金项目: 新时代矿产资源开发与生态保护协调发展的理论与实证研究(No.71991483);中国工程院咨询研究项目(No.2019-XY-037);中南大学中央高校基本科研业务费专项资金资助项目(No.1053320184048)
作者简介: 郑霞(1993-), 女, E-mail:610975507@qq.com
通讯作者(责任作者): 胡东滨, E-mail:hdbin@163.com
摘要:针对大气污染物浓度的精准预测问题,运用小波分解将污染物浓度一维序列分解为高维信息,结合气象及污染物浓度数据,构建了基于小波分解的支持向量机预测模型.最后将模型应用于长沙市2018年PM2.5和O3-8 h的浓度预测.结果表明:①在其他参数不变的条件下,该模型在平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)、一致性水平(IA)和相关系数(R)指标上均优于未经小波分解的预测模型;②在考虑其他污染物对PM2.5浓度的影响后,预测模型评价指标MAE、MAPE和RMSE分别减少了5.57%、9.91%和3.44%,有着更小的误差;③在考虑气象因素对O3-8 h浓度的影响后,预测模型评价指标MAE、MAPE和RMSE分别减少了1.59%、3.54%和0.82%,同样也有更小的误差.由此可以看出,本文所提模型能够有效预测大气污染物浓度,为相关研究提供了方法参考.
关键词:污染物小波分解支持向量机灰色关联分析长沙
Study on prediction model of atmospheric pollutant concentration based on wavelet decomposition and SVM
ZHENG Xia1
 , HU Dongbin1,2
, HU Dongbin1,2
 , LI Quan3
, LI Quan31. Business School, Central South University, Changsha 410083;
2. Resource-conserving & Environment-friendly Society and Ecological Civilization 2011 Collaborative Innovation Center of Hunan Province, Changsha 410083;
3. School of Environmental Studies, China University of Geosciences, Wuhan 430074
Received 14 February 2020; received in revised from 9 April 2020; accepted 9 April 2020
Abstract: Responding to the problem of accurate prediction of air pollutant concentrations, this paper decomposes the one-dimensional sequence of pollutant concentrations into high-dimensional information based on wavelet decomposition and creates a support vector machine (SVM) prediction model on the basis of meteorological and pollutant concentrations data. The model is applied to predict the PM2.5 and O3-8 h concentration in Changsha in 2018. It is concluded that: ① With the presupposition that other parameters are fixed, indicators including mean absolute error (MAE), mean absolute percentage error (MAPE), root mean square error (RMSE), consistency level (IA), and correlation coefficient (R) in this predication model all perform better than that in predication model without wavelet decomposition.② When the impact of other pollutants on PM2.5 concentration is taken into account, the indicators of MAE, MAPE and RMSE are cut by 5.57%, 9.91% and 3.44% respectively, i.e. with much smaller errors.③ After considering the impact of meteorological factors on O3-8 h concentration, indicators of MAE, MAPE, and RMSE are reduced by 1.59%, 3.54%, and 0.82% respectively, also with smaller errors. It can be seen that the prediction model proposed in this paper could effectively predict the air pollutants concentration. As a result, it provides important reference for future related researches.
Keywords: interaction of pollutantswavelet decompositionsupport vector machinegrey correlation analysisChangsha
1 引言(Introduction)近年来, 工业和技术的发展让以煤炭为主的能源消耗不断增加, 大气污染问题变得日益严重, 给人体健康带来极大危害的同时也制约着经济的发展.因此, 为促进生态文明建设, 推动人与自然和谐发展, 建立准确、有效的大气污染物浓度预测模型是十分有必要的.
大气污染物浓度预测研究开始于20世纪60年代, 主要针对污染物预测进行定性研究.到80年代后, 随着大气污染自动监测系统和监测站网的日趋完善, 大气污染物研究逐渐转向了定量预测.目前, 国内外大多****主要运用模式法和统计法对大气污染物浓度进行预测.模式法较复杂, 不易获取精确的污染源信息及气象时空分布资料, 且预测结果易受污染物排放量和选定变量的影响, 预测精度较低(Zhang et al., 2012);统计法建模过程简单、易操作, 推广性强, 且对基础数据要求较低, 更适合实时发布空气质量预报.常用的统计方法有:多元线性回归(Goyal et al., 2006; 胡玉筱等, 2015)、自回归移动平均(Kumar et al., 2010; Zafra et al., 2017)、神经网络(Zhang et al., 2013; 王国胜等, 2015; Perez et al., 2016)、支持向量机(Moazami et al., 2016; 王黎明等, 2017)等.多元线性回归和自回归移动平均方法很好地预测非线性变化序列;神经网络方法存在过拟合和局部最优问题(杨晓帆等, 1994);支持向量机作为高维非线性模型, 以结构风险化为目标, 有效克服了以上方法的不足(常涛, 2006), 因此被广泛应用于污染物浓度预测.随着研究的进一步深入, 将多种方法组合预测的方式逐渐盛行, 并取得了较好的拟合效果(Jiang et al., 2017;Wang et al., 2017; Liu et al., 2019).此外, 小波分解对非平稳信号具有较好的处理能力, 能有效地从信号中提取有用信息, 因而成为大气污染分析的新兴方法, 如顾昊元等(2015)利用小波基函数, 建立了小波神经网络预测模型, 并将该模型对松江区PM2.5浓度进行短期预测, 结果表明该模型有着更高的预测精度.
虽然越来越多的方法应用于大气污染物浓度预测, 但在SVM模型输入因子方面大多为污染物浓度一维序列和气象参数, 而大气污染物来源复杂(自然环境、人类活动、汽车尾气排放等), 其浓度变化是一个非线性非平稳的动态过程, 一维序列数据不能很好地表达污染物浓度潜在信息, 且不同污染物之间也存在一定的关联性.为了弥补以上缺陷, 本文根据小波分解原理, 将大气污染物浓度一维序列转换为高维信息, 同时考虑气象条件及污染物浓度相互关联程度, 构建基于小波分解和支持向量机的大气污染物浓度预测模型, 并用粒子群算法对模型参数进行优化, 最后将优化后的模型应用于长沙市PM2.5和O3-8 h浓度预测.
2 数据与方法(Data and methods)2.1 研究数据本文所用数据为长沙市2015—2018年空气质量数据和气象历史逐日数据.其中, 2015年1月1日—2017年12月31日的730组数据作为训练集, 2018年1月1日—2018年12月31日的365组数据作为测试集.空气质量数据来源于长沙市环境监测中心(http://106.37.208.233:20035), 主要为PM2.5、PM10、NO2、SO2、CO和O3-8 h浓度(除CO浓度单位为mg·m-3外, 其他均为μg·m-3), 并用10个监测站点的日均浓度作为本文研究数据;气象数据来自中国气象数据网(https://data.cma.cn/), 主要包括温度(℃)、湿度(1%)、降水量(mm)、气压(hPa)、风速(m·s-1)、风向和日照(h).
2.2 支持向量机原理支持向量机(Support Vector Machine, SVM)是一种基于统计学VC维理论和结构风险最小化理论的模式识别方法(汪海燕等, 2014).通过选择不同核函数进行非线性分类, 能够很好地处理小样本、非线性和高维模式识别等复杂问题(Saunders et al., 2002), 因此被广泛应用于大气污染物浓度预测(蔡旺华, 2018; 李建新等, 2019).其基本原理是将训练样本向量映射到一个高维空间中, 通过选取该方法中的核函数, 找到一个可以将训练样本划分为两类数据的最优超平面, 从而区别不同类别的数据样本(陈晋音等, 2018).当样本数据不可分时, 在特征空间中, 最优超平面所对应的模型可表示为:
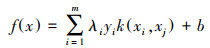 | (1) |
2.3 小波分解与重构原理小波分解与重构是小波变换的核心, 其根据图像特点, 通过改变伸缩因子a和平移因子v, 将不同频率的信号图像分解为高频信息和低频信息(Kushwaha et al., 2019).图 1为三层小波分解原理.其中, Y(t)为原始数据信息, D1、D2和D3分别表示每层高频数据部分, 对应原始数据细节;A1、A2和A3分别表示每层低频数据部分, 对应原始数据大体轮廓.
图 1(Fig. 1)
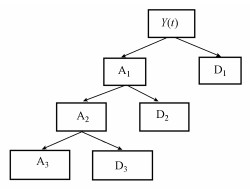 |
| 图 1 三层小波分解示意图 Fig. 1The diagram of three-layer wavelet decomposition |
由图 1可见, 小波分解只对数据低频部分进行处理, 把每层低频信号再次分解成一个低频的粗略逼近部分和一个高频的细节部分, 然后通过重构的方式将原始信号不同时频的信息构成新的序列组.相比一维原始序列, 新的序列组能更有效、准确地表达数据潜在信息, 从而使SVM模型预测精度更好.小波分解公式如下, 其逆变换就为重构公式.
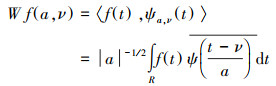 | (2) |
3 模型构建与性能评价指标(Model construction and performance evaluation indicators)3.1 模型构建步骤图 2给出了预测模型构建的流程, 根据流程模型构建具体步骤为:
图 2(Fig. 2)
 |
| 图 2 基于小波分解和SVM的模型流程示意图 Fig. 2The process diagram based on wavelet decomposition and SVM model |
① 污染物浓度历史一维数据的小波分解与重构.结合小波分解原理, 利用MATLAB软件编程, 将污染物浓度历史一维数据集{Y1, Y2, Y3, …Yt}经过m层分解后得到高维数据信息{Y′1, Y′2, Y′3, …Y′t}.其中Y′t=(Ami-1, D1i-1, …Dmi-1), i=1, 2, …t.
② 构建污染物浓度最优影响因子集.本文综合考虑气象因素和其他污染物对预测污染物浓度的影响, 运用灰色关联分析构建污染物浓度最优影响因子集, 结合步骤①一起作为SVM模型输入向量.
③ 训练SVM预测模型.根据输入向量构造训练样本集训练SVM, 结合训练样本数据特点, 选择相应的参数, 并用粒子群算法(particle swarm optimization, PSO)优化参数, 得到最终的预测模型f(X′i).
④ 大气污染物浓度预测与模型性能分析.运用预测模型f(X′i)对污染物t+1时期的浓度进行预测, 并与实际真实值作比较分析模型性能.
⑤ 不同模型对比分析.在控制其他参数不变的情况下, 将本文所提模型与其他模型进行对比, 进一步说明本文模型的可行性和合理性.
3.2 模型性能评价指标为验证预测模型的有效性, 选取平均绝对误差(MAE)、平均绝对百分比误差(MAPE)、均方根误差(RMSE)、一致指标(IA)和相关系数(R)作为衡量模型性能的指标.通常, MAE、MAPE和RMSE值越小, IA和R值越大, 说明模型预测结果越准确.
4 结果与分析(Result and analysis)4.1 污染物浓度变化特征图 3为长沙市2015—2018年PM2.5和O3-8 h浓度逐日变化特征.通过分析每年具体数据, 发现PM2.5在4年里日均浓度分别为12~220、12~212、3~284和8~270 μg·m-3, 最高值分别高达国家24 h平均二级标准限值(75 μg·m-3)的2.93、2.83、3.79和3.60倍, 超标率分别高达25.75%、20.49%、20.27%和13.42%;O3-8 h在4年里日均浓度为11~202、7~221、8~230和8~229 μg·m-3, 其最高值分别是国家日最大8 h平均二级标准限值(160 μg·m-3)的1.26、1.38、1.44和1.43倍, 超过二级标准的天数分别为37、23、28和32 d, 有恶化的趋势.此外, PM2.5和O3-8 h浓度有明显的季节差异.图 3中, PM2.5每年浓度变化均呈“U”型分布, 最高点均出现在1—2月份, 最低点均出现在6—7月份, 而O3-8 h则刚好相反.
图 3(Fig. 3)
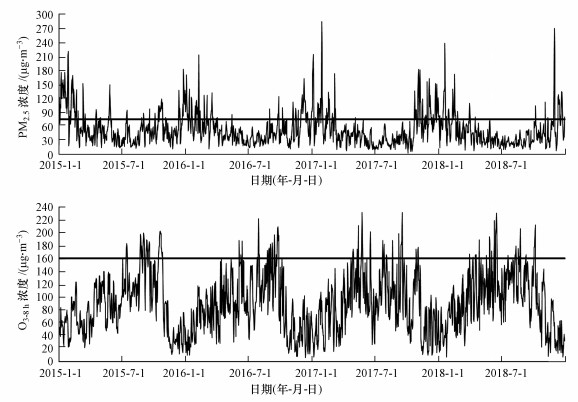 |
| 图 3 长沙市2015—2018年PM2.5和O3-8 h日均浓度变化(直线为二级标准) Fig. 3Daily average concentration of major pollutants in Changsha from 2015 to 2018 (Straight line is the second-level standard) |
基于长沙市PM2.5和O3-8 h浓度变化特点, 分析其差异特征主要受长沙市地形气候特征、其他污染物和能源结构等因素影响.从地形气候特征上看, 长沙市东北、西北两端山地环绕, 南部丘岗起伏, 北部平坦开阔, 地势由南向北倾斜, 呈开口朝北的马蹄形结构, 加上常年主导西北风, 秋冬季节城市风速偏小, 大气低层有明显的逆温现象, 不利于大气污染物扩散, 增加了大气污染累计效应;夏季降水较多, 雨水的冲刷作用降低了PM2.5的浓度, 但高温和日照时长的增加, 更易于发生光化学反应, 增加了大气中O3-8 h浓度;秋冬季是长沙少雨季, 盛行西北风, 易携带京津冀地区大量污染物, 使PM2.5浓度升高.从其他污染物上看, CO、NO2、PM10及SO2浓度对长沙市PM2.5浓度的增加有较长时间的影响(邓洋, 2017), 同时, 工业生产燃煤排放的SO2、氮氧化合物(NOx)和挥发性有机物(VOCS)在高温下二次转化也增加了O3和PM2.5浓度(严茹莎等, 2016; 曹军骥, 2016).从能源结构上看, 长沙市能源结构主要由煤、燃料油、电力和天然气构成, 随着长沙市经济不断发展, 产业结构由“二一三”转变为“二三一”, 工业生产和服务业燃煤量不断增加, 排放大量粉尘和NOx, 一定程度上增加了大气环境中PM2.5和O3浓度.此外, 随着社会的发展, 长沙市车辆保有量逐渐增加, 汽车尾气的排放在一定程度上加大了PM2.5污染(陈晓红等, 2015; 杨平安等, 2016).
表 1(Table 1)
| 表 1 长沙市2016—2018年夏季温度及日照值 Table 1 Summer temperature and sunshine value in Changsha city from 2016 to 2018 | ||||||||||||||||
表 1 长沙市2016—2018年夏季温度及日照值 Table 1 Summer temperature and sunshine value in Changsha city from 2016 to 2018
| ||||||||||||||||
4.2 基于灰色关联分析的影响因子选择从4.1节中对长沙市污染物浓度变化特征原因分析可以看出, 温度、降水、风速等气象条件都会引起PM2.5和O3浓度变化, 相关研究也进一步证实了这些观点(堵晖, 1992; Hafner et al., 2005).此外, 4.1节相关文献分析中也表明大气污染物的相互作用在一定程度上也会影响PM2.5和O3浓度(严茹莎等, 2016; 曹军骥, 2016), 同时, 颗粒物也可以通过对光化学辐射吸收或散射作用改变光解速率, 改变大气中自由基浓度, 进而影响O3浓度(杨开放等, 2019).
基于以上分析, 本文综合考虑气象因素和其他污染物对预测污染物浓度的影响, 收集了长沙市2015年1月1日—2018年12月31日4年内20个特征的相关数据, 具体包括6种大气污染物浓度(SO2、NO2、CO、O3-8 h、PM2.5和PM10)和14种气象因子(平均气温、日最高气温、日最低气温、平均气压、日最高气压、日最低气压、平均相对湿度、平均风速、最大风速、最大风速的风向、极大风速、极大风速的风向、20—20时累计降水量和日照时数).运用灰色关联分析计算PM2.5和O3-8 h与每个影响因子之间的关联度.具体步骤为:
① 数据归一化:本文采用均值法对原始数据进行归一化处理;
② 根据
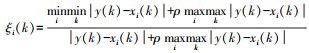
③ 根据公式
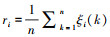
表 2(Table 2)
| 表 2 2015—2018年长沙市预测污染物与影响因子关联度 Table 2 Correlation degree of predicted pollutants and effect factors in Changsha from 2015 to 2018 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 2 2015—2018年长沙市预测污染物与影响因子关联度 Table 2 Correlation degree of predicted pollutants and effect factors in Changsha from 2015 to 2018
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 3(Table 3)
| 表 3 预测污染物最优影响因子集 Table 3 The optimal effect factor subset of predicted pollutants | ||||||
表 3 预测污染物最优影响因子集 Table 3 The optimal effect factor subset of predicted pollutants
| ||||||
4.3 污染物浓度数据小波分解与重构在小波分解过程中, 由于Daubechies小波基函数适宜特征提取, 因此被广泛应用并表现出良好的性能(Da Silva et al., 2019).本文选用db1函数, 根据小波分解相关理论, 运用MATLAB进行相关算法编程, 分别对PM2.5和O3-8 h浓度数据进行8层分解与重构, 得到训练数据集{Y′1, Y′2, Y′3, …Y′t}.Y′t由低频信息和高频信息重构组成, 低频信息是剔除高频信息后的序列, 体现污染物浓度大体变化趋势, 与气象因素和前一日污染物浓度密切相关;高频信息体现污染物浓度局部细节, 影响因素主要是异常突发性因素, 如风速或风向的局部变化、汽车尾气的随机排放等.图 4为PM2.5和O3-8 h浓度小波分解重构结果, 从上往下分别是原始数据信息、低频近似信息和第1~8层高频信息.
图 4(Fig. 4)
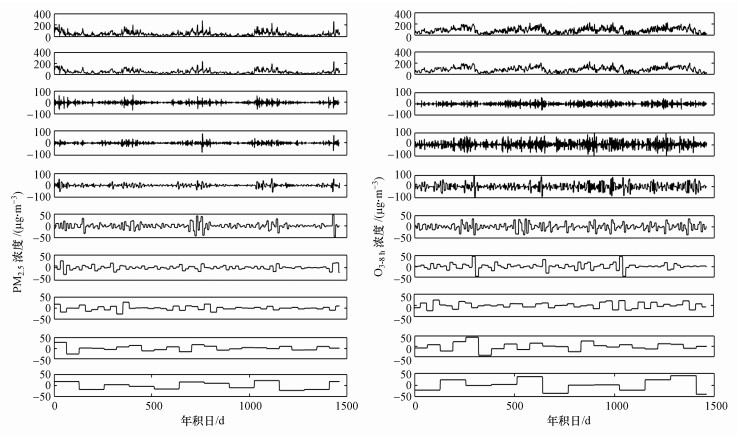 |
| 图 4 PM2.5和O3-8 h浓度小波分解与重构 Fig. 4Wavelet decomposition and reconstruction of PM2.5 and O3-8 h concentration |
4.4 基于小波分解和SVM的大气污染物浓度预测将污染物最优影响因子集和小波分解重构数据共同作为SVM的输入向量, 对长沙市2018年PM2.5和O3-8 h浓度进行预测, 结果如图 5所示.其中蓝线代表预测值, 红线代表实际值.可以看出, 本文所提模型(模型2)的大多预测值都能够很好地拟合其真实值, 只有个别极值与真实值相差较大.模型对PM2.5浓度和O3-8 h浓度预测的性能指标MAE分别为12.4291 μg·m-3和16.3718 μg·m-3, MAPE分别为33.37%和23.46%, IA分别为0.8721和0.9313(表 4).与其他模型相比, 本文模型误差小, 预测精度较高.
图 5(Fig. 5)
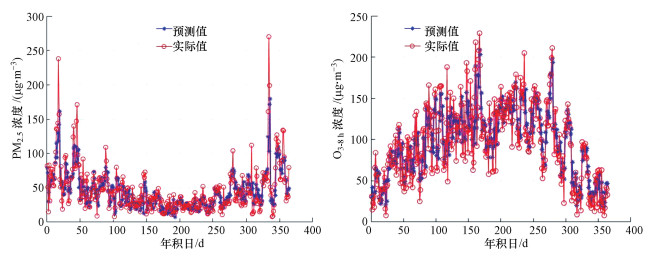 |
| 图 5 PM2.5和O3-8 h预测结果 Fig. 5The prediction results of PM2.5 and O3-8 h concentration |
表 4(Table 4)
| 表 4 不同模型性能比较 Table 4 Performance comparison of different models | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
表 4 不同模型性能比较 Table 4 Performance comparison of different models
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4.5 不同模型预测结果比较为进一步说明模型2的可行性, 在控制其他参数不变的条件下, 本文将模型2分别与模型1(不考虑污染物浓度小波分解重构数据)、模型3(不考虑污染物间的相互关联程度)和模型4(不考虑气象因素对预测污染物浓度的影响)进行了对比, 不同模型的性能评价指标值如表 4所示.可以看出, 不论是PM2.5还是O3-8 h, 模型1在MAE、MAPE、RMSE、IA和R指标上的性能均低于模型2、模型3和模型4.其中, MAE指标差异最明显:模型1对PM2.5浓度预测的MAE为14.1534 μg·m-3, 分别在模型2、模型3和模型4基础上增加了12.19%、7%和12.78%;对O3-8 h浓度预测的MAE为27.6760 μg·m-3, 分别在模型2、模型3和模型4基础上增加了40.84%、40.55%和39.89%.此外, 在模型输入因子方面, 相比于只考虑气象因素(模型3), 模型2对PM2.5浓度预测的MAE、MAPE、和RMSE分别从13.1621 μg·m-3、37.04%和20.9220 μg·m-3降低为12.4291 μg·m-3、33.37%和20.2013 μg·m-3;相比于只考虑污染物间相互关联程度(模型4), 模型2对O3-8 h浓度预测的MAE、MAPE和RMSE分别从16.6361 μg·m-3、24.32%和22.4188 μg·m-3降低为16.3718 μg·m-3、23.46%和22.2341 μg·m-3.以上可以看出, 本文模型对污染物浓度预测有着更小的误差.
在其他类似研究中, Lu等(2005)建立了考虑气象因素(温度、湿度、风速、风向和日照)的SVM预测模型, 并将模型应用于香港市区PM2.5浓度预测, 其MAE值为17.657 μg·m-3.宋国军等(2018)构建了基于回归树气象分类的ARIMA-SVM模型, 并对沈阳市不同监测站点的PM2.5浓度进行预测, 模型性能评价指标MAPE均值为41.2%.张建磊等(2007)利用O3历史浓度一维数据, 运用最小二乘支持向量机模型对其浓度进行预测, 最后模型预测精度只有71.75%.与以上模型性能评价指标相比, 本文模型对PM2.5和O3-8 h浓度预测的误差更小, 预测精度更高.分析原因可能为:本文考虑了其他大气污染物对PM2.5和O3-8 h浓度的影响, 且将PM2.5和O3-8 h浓度的高维分解重构数据作为SVM模型的输入向量, 更加体现了SVM模型高维非线性特点, 一定程度上提高了模型预测精度.总的来说, 本文提出的预测模型能够有效预测污染物浓度.
5 结论(Conclusions)1) 作为高维非线性学习算法, SVM用于大气污染物浓度预测取得了较好的效果.但由于大气污染物浓度一维历史数据维度较低, 不能完整地表达出原始数据特点, 在一定程度上制约了SVM预测模型的泛化能力.
2) 运用小波分解将大气污染物浓度一维历史数据转换为高维数据, 新的高维特征向量更好地表达了大气污染物浓度时序数据在不同频率下的相关信息.相比大气污染物浓度一维历史数据, 将不同时频下的高维数据作为SVM模型输入向量, 更好体现了SVM模型高维非线性的特点, 减少了模型预测误差, 提高了模型预测精度.
3) 对于突发大气污染事件或极端天气造成的大气污染物浓度随机极值点, 本文提出的预测模型无法进行准确预测.可能原因为这些突发性污染事件比较随机, 而SVM学习算法未能很好地挖掘该类信息.因此, 在以后的研究中需要对本文模型进行进一步改进.
4) 由不同模型性能评价结果可以看出, 气象因素和其他大气污染物对预测模型精度都有一定影响.其中, 气象因素对O3-8 h浓度预测影响较大, 其他大气污染物对PM10浓度预测影响较大.因此, 本文将气象因素和其他大气污染物浓度共同作为SVM模型的输入变量, 更加科学合理, 在一定程度上能够提高预测精度, 为政府和相关部门进行大气污染防治提供方法参考.
参考文献
| 蔡旺华. 2018. 运用及其学习方法预测空气中臭氧浓度[J]. 中国环境管理, 10(2): 78-84. |
| 曹军骥. 2016. 中国大气PM2.5污染的主要成因与控制对策[J]. 科技导报, 34(20): 74-80. |
| 常涛. 2006. 支持向量机在大气污染预报中的应用研究[J]. 气象, 32(12): 61-65. |
| 陈晋音, 熊晖, 郑海斌. 2018. 基于粒子群算法的支持向量机的参数优化[J]. 计算机科学, 45(6): 203-209. |
| 陈晓红, 唐湘博, 田耘, 等. 2015. 基于PCA-MLR模型的城市区域PM2.5污染来源解析实证研究-以长株潭城市群为例[J]. 中国软科学, (1): 139-149. DOI:10.3969/j.issn.1002-9753.2015.01.015 |
| Da Silva P C L, Da Silva J P, Garcia A R G. 2019. Daubechies wavelets as basis functions for the vectoril beam propagation method[J]. Journal of Electromagnetic Waves and Application, 33(8): 1027-1041. DOI:10.1080/09205071.2019.1587319 |
| 邓洋. 2017. 长沙市PM2.5与空气污染物之间的动态关系[J]. 工程技术研究, 1(1): 1-2+8. DOI:10.3969/j.issn.1671-3818.2017.01.001 |
| 堵晖. 1992. 逆温层状态下的大气扩散模式[J]. 中国环境监测, 8(2): 28-29. |
| Goyal P, Chan A T, Jaiswal N. 2006. Statistical models for the prediction of respirable suspended particulate matter in urban cities[J]. Atmospheric Environment, 40(11): 2068-2077. DOI:10.1016/j.atmosenv.2005.11.041 |
| 顾昊元, 肖翔, 袁陈晨, 等. 2015. 基于小波神经网络的松江区PM2.5浓度预测[J]. 上海工程技术大学学报, 29(2): 83-86. |
| Hafner W D, Hites R A. 2005. Effects of wind and air trajectory directions on atmospheric concentrations of persistent organic pollutants near the great lakes[J]. Environmental Science & Technology, 39(20): 7817-7825. |
| 胡玉筱, 段显明. 2015. 基于高斯烟羽的多元线性回归模型的PM2.5扩散和预测研究[J]. 干旱区资源与环境, 29(6): 86-92. |
| Jiang P, Dong Q L, Li P Z. 2017. A novel hybrid strategy for PM2.5 concentration analysis and prediction[J]. Journal of Environmental Management, 196: 443-457. DOI:10.1016/j.jenvman.2017.03.046 |
| Kumar U, Jain V K. 2010. ARIMA forecasting of ambient air pollutants(O3, NO, NO2, and CO)[J]. Stochastic Environmental Research & Risk Assessment, 24(5): 751-760. |
| Kushwaha V, Pindoriya N M. 2019. A SARIMA-RVFL hybrid model assisted by wavelet decomposition for very short-term solar PV power generation forecast[J]. Renewable Energy, 140: 124-139. DOI:10.1016/j.renene.2019.03.020 |
| 李建新, 刘小生, 刘静, 等. 2019. 基于MRMR-HK-SVM模型的PM2.5浓度预测[J]. 中国环境科学, 39(6): 2304-2310. DOI:10.3969/j.issn.1000-6923.2019.06.009 |
| Liu H, Jin K R, Duan Z. 2019. Air PM2.5 concentration multi-step forecasting using a new hybrid modeling method:Comparing cases for four cities in China[J]. Atmospheric Pollution Research, 10(5): 1588-1600. DOI:10.1016/j.apr.2019.05.007 |
| Lu W Z, Wang W J. 2005. Potential assessment of the "support vector machine" method in forecasting ambient air pollutant trends[J]. Chemosphere, 59(5): 693-701. DOI:10.1016/j.chemosphere.2004.10.032 |
| Moazami S, Noori R, Amiri B J, et al. 2016. Reliable prediction of carbon monoxide using developed support vector machine[J]. Atmospheric Pollution Research, 7(3): 412-418. DOI:10.1016/j.apr.2015.10.022 |
| 南国卫, 孙虎. 2017. 基于灰色关联模型对陕西省O3浓度影响因素分析[J]. 环境科学学报, 37(12): 4519-4527. |
| Perez P, Gramsch E. 2016. Forecasting hourly PM2.5 in Santiago de Chile with emphasis on night episodes[J]. Atmospheric Environment, 124: 22-27. DOI:10.1016/j.atmosenv.2015.11.016 |
| Saunders C, Stitson M O, Weston J, et al. 2002. Support vector machine[J]. Computer Science, 1(4): 1-28. DOI:10.1007/978-3-642-27733-7_299-3 |
| 宋国君, 国潇丹, 杨啸, 等. 2018. 沈阳市PM2.5浓度ARIMA-SVM组合预测研究[J]. 中国环境科学, 38(11): 4031-4039. DOI:10.3969/j.issn.1000-6923.2018.11.005 |
| 王国胜, 郭联金, 董晓清, 等. 2015. 深圳市区空气污染的人工神经网络预测[J]. 环境工程学报, 9(7): 3393-3399. |
| 汪海燕, 黎建辉, 杨风雷. 2014. 支持向量机理论及算法研究综述[J]. 计算机应用研究, 31(5): 1281-1286. DOI:10.3969/j.issn.1001-3695.2014.05.001 |
| 王黎明, 吴香华, 赵天良, 等. 2017. 基于距离相关系数和支持向量机回归的PM2.5浓度滚动统计预报方案[J]. 环境科学学报, 37(4): 1268-1276. |
| Wang P, Zhang H, Qin Z D, et al. 2017. A novel hybrid-Garch model based on ARIMA and SVM for PM2.5 concentrations forecasting[J]. Atmospheric Pollution Research, 8(5): 850-860. DOI:10.1016/j.apr.2017.01.003 |
| 严茹莎, 李莉, 安静宇, 等. 2016. 上海市夏季臭氧生成与其前体物控制模拟研究[J]. 环境污染与防治, 38(1): 30-35, 40-40. |
| 杨开放, 魏游. 2019. 臭氧污染形成机制及影响因素的研究进展[J]. 环境研究与监制, 32(4): 1-4. |
| 杨平安, 刘琼, 李军成. 2016. 长沙市区PM2.5浓度的主要因素分析及预测[J]. 环境研究与监制, 29(1): 11-16. |
| 杨晓帆, 陈延槐. 1994. 人工神经网络固有的优点和缺点[J]. 计算机科学, 21(2): 23-26. |
| Zafra C, Angel Y, Torres E. 2017. ARIMA analysis of the effect of land surface coverage on PM10 concentrations in a high-altitude megacity[J]. Atmospheric Pollution Research, 8: 660-668. DOI:10.1016/j.apr.2017.01.002 |
| Zhang H, Liu Y, Shi R, et al. 2013. Evaluation of PM10 forecasting based on the artificial neural network model and intake fraction in an urban area:a case study in Taiyuan City, China[J]. Journal of the Air & Waste Management Association, 63(7): 755-763. |
| Zhang H, Zhang W, Palazoglu A, et al. 2012. Prediction of ozone levels using a hidden markov model(HMM) with gamma distribution[J]. Atmospheric Environment, 62: 64-73. DOI:10.1016/j.atmosenv.2012.08.008 |
| 张建磊, 乐群, 束炯. 2007. 最小二乘支持向量机在臭氧浓度时间序列预测中的试应用[J]. 江苏环境科技, 20(3): 43-45. DOI:10.3969/j.issn.1674-4829.2007.03.015 |
